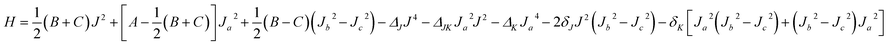DOI:
10.1039/C9RA03782A
(Paper)
RSC Adv., 2019,
9, 20925-20930
Theoretical calculation of a full-dimensional ab initio potential energy surface and prediction of infrared spectra for Xe–CS2
Received
20th May 2019
, Accepted 17th June 2019
First published on 4th July 2019
Abstract
An effective four-dimensional (4D) ab initio potential energy surface (PES) for Xe–CS2 which explicitly involves the intramolecular Q1 symmetric stretching and Q3 antisymmetric stretching vibrational coordinates of CS2 is constructed. The computations are carried out employing single- and double-excitation coupled-cluster theory with a non-iterative perturbation treatment of triple excitations [CCSD(T)] method with a large basis set. Two vibrationally averaged potentials at the ground and ν1 + ν3 (ν1 = 1, ν3 = 1) excited states are obtained by integrating the 4D potentials over the Q1 and Q3 coordinates. The potentials have a T-shaped global minimum and two equivalent linear local minima. The radial discrete variable representation/angular finite basis representation and the Lanczos algorithm are employed to calculate the rovibrational energy levels for Xe–CS2. The infrared band origin shift associated with the fundamental band of CS2 is predicted, which is red-shifted by −1.996 cm−1 in the ν1 + ν3 region. In addition, we further predict the spectroscopic parameters for the ground and the ν1 + ν3 excited states of Xe–CS2. Compared with the previous Rg–CS2 (Rg = He, Ne, Ar, Kr) complexes, we found that the complexes of the rare gas atoms with CS2 display obvious regularities.
I. Introduction
The linear CX2 (X = O, S) molecules play an important role in the investigation of atmosphere. While complexes consisting of small linear molecules (CO2, OCS, CS2) bound to a rare gas (Rg) have had a remarkable growth in interest in spectroscopic studies. Such studies are aimed at advancing our understanding of the weak intermolecular forces and dynamics of these bound molecules. As we know, CO2 exists extensively in nature and absorbs infrared radiation in the ground. Accordingly, complexes containing CO2 have been widely investigate both experimentally1–7 and theoretically.8–25 As an analog of CO2, CS2 is one of the sulfur compounds in the Earth’s atmosphere and has also been widely studied because sulfur is a key element in the spectroscopy of giant planets. In addition, some interesting differences were explored for Rg–CS2 compared to Rg–CO2.
Experimentally, the first infrared spectra for the Rg–CS2 complexes26 with Rg = He, Ne, Ar were studied in the CS2 ν3 region. Meanwhile, Mivehvar et al. also reported the high resolution spectra of the He–CS2 complex in the ν1 + ν3 region (2185 cm−1). In their work, the structures were T-shaped and the spectroscopic parameters were presented. Theoretically, a number of ab initio potential energy surfaces (PESs) for Rg–CS2 were constructed at different levels of theory. For instance, Farrokhpour and co-workers27 first determined the PESs for the Rg–CS2 complexes using CCSD(T) theory with the aug-cc-pVDZ basis set. Soon after, Zang et al.28 reported the two-dimensional PES for the Rg–CS2 (Rg = He, Ne, Ar) complexes by using the aug-cc-pVTZ basis set at the CCSD(T) level. However, these theoretical studies have obtained the PESs that encompass only two intermolecular vibration coordinates and a fixed CS2 geometry. The results showed that the spectral pattern in the infrared region cannot be properly identified. Thus, construction of the PESs that involve the intramolecular vibration modes of CS2 is needed. Recently, we calculated a 3D PES of the Rg–CS2 complex29,30 including the antisymmetric stretching Q3 coordinate of the CS2 monomer, and showed a good agreement with the experimental infrared data. In order to explore more detailed spectral information for Rg–CS2, we further carried out the calculation of a four-dimensional PES of the Rg–CS2 (ref. 31–33) complexes, which incorporates the Q1 symmetric and Q3 anti-symmetric stretching coordinates of CS2. We have successfully reported the 4D PESs for the complexes of the lighter rare gas atoms with CS2 by this method. To our knowledge, the experimental and theoretical information in the ν1 + ν3 region are absent for Xe–CS2.
In order to discover the trends and diversities among the Rg–CS2 complexes, we present a reliable 4D PES for Xe–CS2 with CS2 in the ν1 + ν3 region by applying the CCSD(T) method with the aug-cc-pVQZ basis set. This paper is arranged as follows: in Section II, we show the computational details that include ab initio and rovibrational energy levels. The discussion of the PES, the calculated rovibrational bound states, and the predicted infrared spectra are presented in Sections III–IV. Finally, a brief conclusion is given in Section V.
II. Computational details
A. Ab initio calculations
For the Xe–CS2 dimer, the Jacobi coordinates (R, θ, Q1, Q3) are employed to describe the geometry. In the geometric variables, R denotes the intermolecular distance between the center of mass of CS2 to the Xe atom, the angle of the vector R with respect to the CS2 molecule is defined as θ. Q1 and Q3 are the normal mode coordinates, which describe the ν1 symmetric stretching vibration and ν3 antisymmetric stretching vibration of CS2, respectively. Here, the intramolecular vibrational coordinates (Q1, Q3) can be simply defined as| |
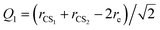 | (1) |
| |
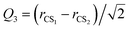 | (2) |
where rCS1 and rCS2 mean the two C–S bond lengths of CS2, re is the average bond length derived from experimental spectra data.34 The two-dimensional Q1 and Q3 potential curves were computed at the CCSD(T) level to determine the energy levels and wave functions for the Q1 and Q3 modes. The coordinate scaling method35 was employed to adjust the two-dimensional potential in order to reproduce the experimental frequencies for the fundamental band.34 We generated 25 potential optimized discrete variable representation (PODVR)36,37 grid points corresponding to Q1 = −0.122411, −0.044046, −0.027968, −0.101203, −183772a0, Q3 = −0.245743, −0.116813, 0.0, 0.116813, 0.245743a0 for the ground state, and Q1 = −0.139155, −0.060791, 0.011220, 0.084454, 0.167022a0, Q3 = −0.247934, −0.117859, 0.0, 0.117859, 0.247934a0 for the ν1 + ν3 (ν1 = 1, ν3 = 1) excited state.
The ab initio potential energies were computed for a total of about 9000 discrete points. A relatively dense grid was calculated with 27 values of R ranging from 5.50a0 to 24.00a0 and 13 points of θ from 0° to 180° at intervals of 15°. The four dimensional PES for Xe–CS2 was performed using the CCSD(T)38 method. The aug-cc-pVQZ basis set of Woon and Dunning39 was used for carbon and sulfur atoms, and the quasirelativistic pseudopotential aug-cc-pVQZ-PP40 basis set was used for the Xe atom, supplemented with an additional set of bond functions (3s3p2d1f1g).41 The full counterpoise procedure (FCP)42 was selected to correct the basis set superposition error (BSSE). The vibrationally averaged 2D potentials Vν1+ν3(R,θ) were obtained by averaging the 4D potential over the Q1 and Q3 vibrational coordinates, which can be written as
| |
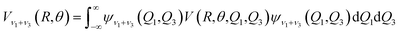 | (3) |
The cubic spline interpolation was employed to generate the averaged PESs for
R and
θ coordinates. The root-mean-square (rms) deviation is about 0.08 cm
−1 in the final fit. All calculations were carried out using the MOLPRO package.
43
B. Calculations of rovibrational energy levels
With the Born–Oppenheimer approximation, the vibrational averaged 2D intermolecular Hamiltonian of the Xe–CS2 complex can be written as44,45| |
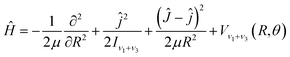 | (4) |
where μ is the reduced mass of the Xe–CS2 complex, Ĵ and ĵ are the angular momentum operators for the total and monomer rotations. Iν1+ν3 represents the vibrationally averaged rotational moment of the inertia of CS2, which can be defined by the following equation,| |
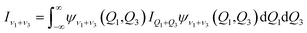 | (5) |
Based on the PES, the rovibrational Hamiltonian and wave functions were calculated with the radial DVR/angular FBR method.46,47 In our work, 120 sine-DVR48 grid points were used for the radial coordinate R. For the angular coordinate, we selected 90 DVR grids and 89 basis functions of associated Legendre polynomials. The Lanczos algorithm method49,50 was used to diagonalize the Hamiltonian matrix, and we selected 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Lanczos iterations to obtain the eigenvalues and eigenvectors. For the angular part, the parity-adapted rotational basis for the three Euler angles (α,β,γ) can be written as
000 Lanczos iterations to obtain the eigenvalues and eigenvectors. For the angular part, the parity-adapted rotational basis for the three Euler angles (α,β,γ) can be written as
| |
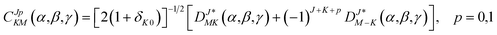 | (6) |
where
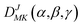
were the normalized rotational functions for Xe–CS
2, the space-inversion parity
p = 0 or 1 illustrates that the basis is even or odd under inversion. The total parity was given by (−1)
J+P.
III. Potential energy surface
The contour plot of the vibrationally averaged 2D ν1 + ν3 excited state PES is showed in Fig. 1, which clearly displays that the global minimum is a T-shaped configuration at R = 3.97 Å and θ = 90.0° with a well depth of 413.875 cm−1. In addition, there are two equivalent linear local minima at R = 5.56 Å and θ = 0° or 180° with a depth of 248.045 cm−1. In our PES, between the two minima, there are two saddle points with an energy barrier of 187.997 cm−1 relative to the global minimum, located at R = 5.08 Å and θ = 45° or 135°. In order to compare the Xe–CS2 complex with the other Rg–CS2 complexes, the differences in the geometries and well depths between the Rg–CS2 complexes31–33,51,52 are listed in Table 1. One can see that the Rg–CS2 complexes have similar shapes, such as the T-shaped global minimum, two linear local minima, and two saddle points. However, there are some deviations among the Rg–CS2 complexes. For example, the depth of the global and local minima become deeper from He–CS2 to Xe–CS2, which indicates the intermolecular interactions become stronger with the increasing mass of the rare gas atom. For another, the well depth of Xe–CS2 is much larger than the other Rg–CS2 complexes, which means the Xe atom is strongly hindered from free motion around the CS2 molecule. In addition, the minimum energy distance gradually become larger from He–CS2 to Xe–CS2. Compared with the previous theoretical study of the potential,51 the contour plots look almost the same as those for our work, and the positions and energies of the stationary points are shifted only slightly.
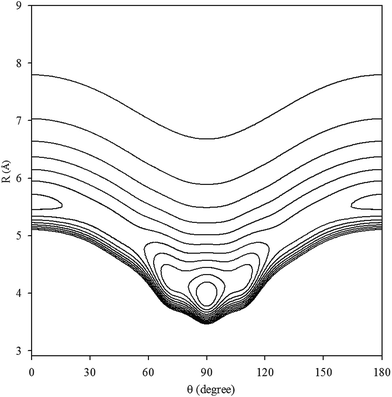 |
| | Fig. 1 Contour plot (in cm−1) of the averaged intermolecular potential energy surface for Xe–CS2 with CS2 at the ν1 + ν3 excited state. | |
Table 1 The stationary geometries (Å and deg) and well depths (cm−1) of Rg–CS2 (Rg = He, Ne, Ar, Kr, Xe)
| Rg–CS2 |
Global minimum |
Local minimum |
Saddle point |
| He–CS2 (ref. 31) |
(3.36, 90, −52.68) |
(5.00, 0/180, −32.11) |
(4.56, 59/121, −21.39) |
| Ne–CS2 (ref. 33) |
(3.44, 90, −104.35) |
(5.03, 0/180, −67.15) |
(4.56, 44/136, −51.12) |
| Ar–CS2 (ref. 32) |
(3.68, 90, −279.77) |
(5.26, 0/180, −173.47) |
(4.92, 39/141, −146.75) |
| Kr–CS2 (ref. 52) |
(3.76, 90, −367.06) |
(5.39, 0/180, −226.16) |
(4.92, 45/135, −203.49) |
| Xe–CS2 (ref. 51) |
(3.97, 90, −414.77) |
(5.56, 0/180, −243.66) |
(5.08, 46/134, −224.37) |
| Xe–CS2 |
(3.97, 90, −413.88) |
(5.56, 0/180, −248.04) |
(5.08, 45/135, −225.88) |
IV. Bound states of rovibrational energy levels and infrared spectra
Based on the potential, the energy levels of the bound states were calculated. In order to simplify our writing, we label the ν1 + ν3 of CS2 as the ν5 vibrational state for Xe–CS2. In Table 2, we display the first twenty pure vibrational bound states of the Xe–CS2 complex for the ground and ν5 states of CS2. As seen in Table 2, the first bound state for the ν5 state is −374.239 cm−1, which reveals the zero-point energy is 39.636 cm−1 relative to global minimum, only about one-tenth of the global well depths. Due to the deep well and high barrier for Xe–CS2, the bound states are much deeper than the other Rg–CS2 complexes.31–33,52 The ν1 + ν3 band origin shift is determined by Δv = E05 − E00,53 where E0v are the ground state energies of Xe–CS2 with the CS2 monomer in the corresponding ν vibrational state. Meanwhile, we further predicted the infrared band origin shift of Xe–CS2, which is −1.996 cm−1 indicating that is negative (red-shift) in sign and large in magnitude. In addition, the band origin shifts of the other Rg–CS2 complexes26,29–33,51,52 are listed in Table 3, together with the Rg–CO2 complexes.2,6 One can see that the tendency of the CS2 shifts are similar to CO2. Besides, the results indicate the lighter complexes (He, Ne) tend to positive (blue shifts), while the larger complexes (Ar, Kr, Xe) tend to negative (red-shifts). The predicted ν1 + ν3 band shift for Xe–CS2 (−1.996 cm−1) is larger than that for Xe–CO2 (−1.447 cm−1), revealing that Xe–CS2 has a larger weakening of the vdW bond upon vibrational excitation in the ν1 + ν3 region.
Table 2 The calculated energy levels (in cm−1) for the first twenty vibrational bound states of Xe–CS2 with CS2 at the ground and the ν1 + ν3 excited states
| Ground state |
ν5 state |
| N |
|
N |
|
N |
|
N |
|
| 0 |
−372.243 |
10 |
−276.947 |
0 |
−374.239 |
10 |
−278.046 |
| 1 |
−340.903 |
11 |
−275.624 |
1 |
−342.887 |
11 |
−276.971 |
| 2 |
−330.927 |
12 |
−273.955 |
2 |
−335.591 |
12 |
−275.602 |
| 3 |
−312.666 |
13 |
−266.022 |
3 |
−314.627 |
13 |
−266.029 |
| 4 |
−308.886 |
14 |
−258.545 |
4 |
−310.894 |
14 |
−259.381 |
| 5 |
−308.813 |
15 |
−257.516 |
5 |
−310.755 |
15 |
−259.247 |
| 6 |
−298.008 |
16 |
−256.517 |
6 |
−299.059 |
16 |
−256.907 |
| 7 |
−295.275 |
17 |
−252.014 |
7 |
−296.373 |
17 |
−253.608 |
| 8 |
−284.470 |
18 |
−251.523 |
8 |
−285.564 |
18 |
−253.276 |
| 9 |
−283.164 |
19 |
−245.973 |
9 |
−284.769 |
19 |
−246.196 |
Table 3 The vibrational shifts of band origin for Rg–CS2, compared with Rg–CO2 (in cm−1)
In Fig. 2, we present the contour plots of the wave functions of Xe–CS2 with CS2 at the ground state. It is clear from Fig. 2 that the vibrational ground state is localized around the T-shaped global minimum. The first two vibrational excited states are characterized predominantly by bending and stretching vibrations, respectively, while the corresponding wave functions are distributed and exhibit a strong mixing between the bending and stretching vibration modes for the higher vibrational excited states. The calculated average distance 〈R〉 and the average angle 〈θ〉 for the ground state are 3.99 Å and 87.85°, respectively, which is very close to the global minimum (R = 3.97 Å and θ = 90°). The radial dispersion 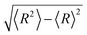 and angular dispersion
and angular dispersion 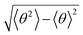 are 0.14 Å and 2.15°, respectively. Therefore, the ground state is rigid.
are 0.14 Å and 2.15°, respectively. Therefore, the ground state is rigid.
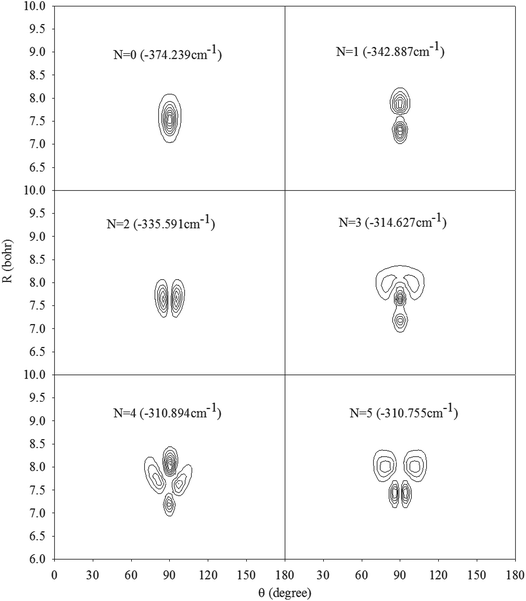 |
| | Fig. 2 Contour plots of the wave functions for the lowest six vibrational states of Xe–CS2 with CS2 at the ν1 + ν3 excited state. | |
The rovibrational energies of Xe–CS2 are labeled by the asymmetric rotor quantum numbers JKaKc, where J denotes the total angular momentum, Ka and Kc represent the projections of J onto the a and c principal axes of inertia. The rovibrational energy levels consist of four blocks, (even/even), (even/odd), (odd/even), and (odd/odd) for different combination parity of (j/p). The rovibrational energies of Xe–CS2 for the vibrational ground and ν1 + ν3 excited states are shown in Table 4, and the total angular momentum J ranges from 0 to 5.
Table 4 The rovibrational energy levels (in cm−1) of Xe–CS2 with CS2 at the ground and ν1 + ν3 excited states
| Level |
J |
E (JKaKc) |
| Even/Even |
Even/Odd |
Odd/Even |
Odd/Odd |
| Ground state |
0 |
−372.243 (000) |
|
|
|
| 1 |
|
−372.203 (101) |
−372.113 (110) |
−372.116 (111) |
| 2 |
−372.122 (202) |
−371.770 (221) |
−372.040 (212) |
−372.028 (211) |
| −371.769 (220) |
| 3 |
−371.649 (322) |
−372.002 (303) |
−371.902 (312) |
−371.925 (313) |
| −371.648 (321) |
−371.207 (330) |
−371.208 (331) |
| 4 |
−371.843 (404) |
−371.488 (423) |
−371.772 (414) |
−371.734 (413) |
| −371.487 (422) |
−370.430 (441) |
−371.047 (432) |
−371.046 (431) |
| −370.430 (440) |
| 5 |
−371.288 (524) |
−371.644 (505) |
−371.525 (514) |
−371.580 (515) |
| −370.229 (542) |
−371.284 (523) |
−370.846 (532) |
−370.846 (533) |
| −370.229 (541) |
−369.436 (550) |
−369.436 (551) |
| ν5 state |
0 |
−374.239 (000) |
|
|
|
| 1 |
|
−374.199 (101) |
−374.110 (110) |
−374.114 (111) |
| 2 |
−374.119 (202) |
−373.770 (221) |
−374.037 (212) |
−374.026 (211) |
| −373.770 (220) |
| 3 |
−373.650 (322) |
−373.999 (303) |
−373.900 (312) |
−373.923 (313) |
| −373.649 (321) |
−373.213 (330) |
−373.214 (331) |
| 4 |
−373.839 (404) |
−373.489 (423) |
−373.770 (414) |
−373.732 (413) |
| −373.487 (422) |
−372.442 (441) |
−373.053 (432) |
−373.052 (431) |
| −372.442 (440) |
| 5 |
−373.288 (524) |
−373.641 (505) |
−373.522 (514) |
−373.579 (515) |
| −372.241 (542) |
−373.284 (523) |
−372.851 (532) |
−372.852 (533) |
| −372.241 (541) |
−371.456 (550) |
−371.456 (551) |
The rovibrational energy levels within J ≤ 3 are used to fit to a Watson asymmetric top Hamiltonian54 employing the a-type reduction in the Ir representation,
| |
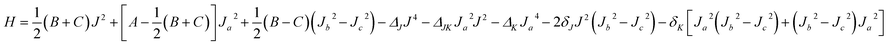 | (7) |
The fitted molecular spectroscopic constants for the Xe–CS2 complex are given in Table 5. Because the energy levels for Xe–CS2 at the ground state are almost equal to the ν1 + ν3 excited state, the molecular parameters of the two states are very similar. The calculated inertial defects Δ0 of this complex with CS2 at the ground state and the ν1 + ν3 excited state are around 1.07 amu Å2 and 1.13 amu Å2, respectively. For Rg–CS2 (Rg = He,31 Ne,33 Ar,32 Kr52), the inertial defects Δ0 in the ground state were found to be 6.14, 3.09, 2.93, 2.32 amu Å2, respectively. The decrease in the inertial defects reveals that the vdW complexes are more rigid with the increase in the mass of the rare gas atom. The asymmetry parameter κ, κ = (2B − A − C)/(A − C) (equal to −1 for the symmetric prolate top) is −0.917 and −0.916 for this complex with CS2 at the ground and the ν1 + ν3 excited states, respectively.
Table 5 The calculated spectroscopic constants (in cm−1) and the inertial defects Δ0 (in amu Å2) for the Xe–CS2 complex with CS2 at the ground and the ν1 + ν3 excited states
| |
Ground state |
ν5 state |
| A |
0.108321 |
0.107674 |
| B |
0.022038 |
0.022023 |
| C |
0.018291 |
0.018261 |
| ΔK |
−2.443 × 10−7 |
−3.110 × 10−7 |
| ΔJK |
3.748 × 10−7 |
3.258 × 10−7 |
| ΔJ |
4.563 × 10−6 |
8.778 × 10−6 |
| δK |
2.050 × 10−6 |
2.225 × 10−6 |
| δJ |
9.176 × 10−9 |
2.993 × 10−9 |
| Δ0 |
1.07 |
1.13 |
V. Conclusions
In this paper, a new four-dimensional potential energy surface for the Xe–CS2 complex including the Q1 and Q3 normal modes was constructed. We calculated the intermolecular potential with five PODVR grid points for the Q1 and Q3 normal modes, respectively, using the CCSD(T) method with the aug-cc-pVQZ basis set plus bond functions. Based on the ab initio potential points, two vibrationally averaged PESs of the Xe–CS2 complex were generated. We found that each potential energy surface has a T-shaped global minimum and two equivalent local linear minima. The bound rovibrational energy levels of Xe–CS2 were obtained by employing the radial DVR/angular FBR method and the Lanczos algorithm. The predicted band origin shift is −1.996 cm−1. Meanwhile, we found that the Rg–CS2 complexes have very similar features. For example, each PES is characterized by a T-shaped global minimum. For another, the regularities were represented among the complexes from He–CS2 to Xe–CS2. It is expected that the work on the Rg–CS2 complexes in the ν1 + ν3 region of CS2 should be useful for further theoretical and experimental studies.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21705011).
References
- G. T. Fraser, A. S. Pine and R. D. Suenram, J. Chem. Phys., 1988, 88, 6157 CrossRef CAS.
- R. W. Randall, M. A. Walsh and B. J. Howard, Faraday Discuss. Chem. Soc., 1988, 85, 13 RSC.
- M. Iida, Y. Ohsbima and Y. Endo, J. Phys. Chem., 1993, 97, 357 CrossRef CAS.
- A. S. Pine and G. T. Fraser, J. Chem. Phys., 1988, 89, 100 CrossRef CAS.
- T. Konno, S. Fukuda and Y. Ozaki, Chem. Phys. Lett., 2006, 421, 421 CrossRef CAS.
- M. J. Weida, J. M. Sperhac and D. J. Nesbitt, J. Chem. Phys., 1994, 101, 8351 CrossRef CAS.
- Y. J. Xu and W. Jäger, J. Mol. Spectrosc., 1998, 192, 435 CrossRef CAS PubMed.
- G. A. Parker, M. Keil and A. Kuppermann, J. Chem. Phys., 1983, 78, 1145 CrossRef CAS.
- M. Keil and G. A. Parker, J. Chem. Phys., 1985, 82, 1947 CrossRef CAS.
- L. Beneventi, P. Casavecchia, F. Vecchiocattivi, G. G. Volpi, U. Buck, C. Lauenstein and R. Schinke, J. Chem. Phys., 1988, 89, 4671 CrossRef CAS.
- C. F. Roche, A. Ernesti, J. M. Huston and A. S. Dickinson, J. Chem. Phys., 1996, 104, 2156 CrossRef CAS.
- P. J. Marshall, M. M. Szczesniak, J. Sadlej, G. Chalasinski, M. A. ter Horst and C. J. Jameson, J. Chem. Phys., 1996, 104, 6569 CrossRef CAS.
- J. M. Hutson, A. Ernesti, M. M. Law, C. F. Roche and R. J. Wheatley, J. Chem. Phys., 1996, 105, 9130 CrossRef CAS.
- G. S. Yan, M. H. Yang and D. Q. Xie, J. Chem. Phys., 1998, 109, 10284 CrossRef CAS.
- F. Negri, F. Ancliotto, G. Mistura and F. Toigo, J. Chem. Phys., 1999, 111, 6439 CrossRef CAS.
- H. Ran and D. Q. Xie, J. Chem. Phys., 2008, 128, 124323 CrossRef PubMed.
- Y. L. Cui, H. Ran and D. Q. Xie, J. Chem. Phys., 2009, 130, 224311 CrossRef PubMed.
- R. Chen, E. Q. Jiao, H. Zhu and D. Q. Xie, J. Chem. Phys., 2010, 133, 104302 CrossRef PubMed.
- R. Chen and H. Zhu, J. Theor. Comput. Chem., 2012, 11, 1175 CrossRef CAS.
- R. Chen, H. Zhu and D. Q. Xie, Chem. Phys. Lett., 2011, 511, 229 CrossRef CAS.
- M. Chen and H. Zhu, J. Theor. Comput. Chem., 2012, 11, 537 CrossRef CAS.
- H. Li and R. J. Le Roy, Phys. Chem. Chem. Phys., 2008, 10, 4128 RSC.
- H. Li, N. Blinov, P.-N. Roy and R. J. Le Roy, J. Chem. Phys., 2009, 130, 144305 CrossRef PubMed.
- Y. L. Cui, H. Ran and D. Q. Xie, J. Theor. Comput. Chem., 2008, 7, 707 CrossRef CAS.
- C. J. Xie, R. Chen, H. Zhu and D. Q. Xie, Chem. Res. Chin. Univ., 2009, 9, 1851 Search PubMed.
- F. Mivehvar, C. Lauzin, A. R. W. McKellar and N. Moazzen-Ahmadi, J. Mol. Spectrosc., 2012, 281, 24 CrossRef CAS.
- H. Farrokhpour and M. Tozihi, Mol. Phys., 2013, 111, 779 CrossRef CAS.
- L. M. Zang, W. Dai, L. M. Zheng, C. X. Duan, Y. P. Lu and M. H. Yang, J. Chem. Phys., 2014, 140, 114310 CrossRef PubMed.
- T. Yuan and H. Zhu, Theor. Chem. Acc., 2014, 133, 1537 Search PubMed.
- T. Yuan, X. L. Sun, Y. Hu and H. Zhu, J. Chem. Phys., 2014, 141, 104306 CrossRef PubMed.
- J. Shang, T. Yuan and H. Zhu, Theor. Chem. Acc., 2016, 135, 1 Search PubMed.
- J. Shang, T. Yuan and H. Zhu, Chem. Phys. Lett., 2016, 648, 147 CrossRef CAS.
- M. Qin, J. Shang, Q. Hong and H. Zhu, Mol. Phys., 2017, 115, 379 CrossRef CAS.
- J. S. Wells, M. Schneider and A. G. Maki, J. Mol. Spectrosc., 1988, 132, 422 CrossRef CAS.
- J. M. Bowman and B. Gazdy, J. Chem. Phys., 1991, 94, 816 CrossRef CAS.
- H. Wei and T. Carrington, J. Chem. Phys., 1992, 97, 3029 CrossRef CAS.
- J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225 CrossRef CAS.
- M. Meuwly and J. M. Hutson, J. Chem. Phys., 2003, 119, 8873 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- T. B. Pedersen, B. Fernandez, H. Koch and J. Makarewicz, J. Chem. Phys., 2001, 115, 8431 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- H. J. Werner, P. J. Knowles, R. D. Amos, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, S. T. Elbert, C. Hampel, R. Lindh, A. W. Lloyd, W. Meyer, A. Nicklass, K. Peterson, R. Pitzer, A. J. Stone, P. R. Taylor, M. E. Mura, P. Pulay, M. Schutz, H. Stoll and T. Thoorstcinsso, Molpro, version 2000.1, a package of ab initio programs, 2000, see http://www.molpro.net Search PubMed.
- J. Tennyson and B. T. Sutcliffe, Mol. Phys., 1984, 51, 887 CrossRef CAS.
- S. Miller and J. Tennyson, J. Mol. Spectrosc., 1988, 128, 530 CrossRef CAS.
- S. Y. Lin and H. Guo, J. Chem. Phys., 2002, 117, 5183 CrossRef CAS.
- R. Q. Chen, G. B. Ma and H. Guo, Chem. Phys. Lett., 2000, 320, 567 CrossRef CAS.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982 CrossRef CAS.
- C. J. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255 CrossRef.
- H. G. Yu, J. Chem. Phys., 2002, 117, 8190 CrossRef.
- T. Yuan, M. L. Yang and H. Zhu, Comput. Theor. Chem., 2015, 88, 1070 Search PubMed.
- Q. Hong, M. Qin and H. Zhu, Acta Chim. Sin., 2018, 76, 138 CrossRef.
- F. Paesani and K. B. Whaley, J. Chem. Phys., 2004, 121, 4180 CrossRef CAS PubMed.
- J. K. G. Watson, J. Chem. Phys., 1967, 46, 1935 CrossRef CAS.
Footnote |
| † Miao Qin and Xiuchan Xiao contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab and
Hua Zhuc
*ab and
Hua Zhuc
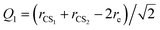
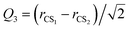
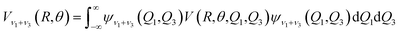
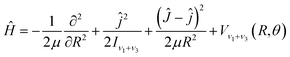
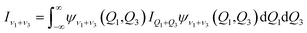
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Lanczos iterations to obtain the eigenvalues and eigenvectors. For the angular part, the parity-adapted rotational basis for the three Euler angles (α,β,γ) can be written as
000 Lanczos iterations to obtain the eigenvalues and eigenvectors. For the angular part, the parity-adapted rotational basis for the three Euler angles (α,β,γ) can be written as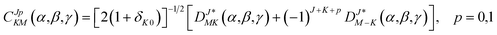
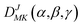 were the normalized rotational functions for Xe–CS2, the space-inversion parity p = 0 or 1 illustrates that the basis is even or odd under inversion. The total parity was given by (−1)J+P.
were the normalized rotational functions for Xe–CS2, the space-inversion parity p = 0 or 1 illustrates that the basis is even or odd under inversion. The total parity was given by (−1)J+P.

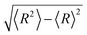 and angular dispersion
and angular dispersion 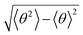 are 0.14 Å and 2.15°, respectively. Therefore, the ground state is rigid.
are 0.14 Å and 2.15°, respectively. Therefore, the ground state is rigid.