Open Access Article
Open Access ArticleSize engineering optoelectronic features of C, Si and CSi hybrid diamond-shaped quantum dots
H. Ouarrada,
F.-Z. Ramadan a and
L. B. Drissi*abc
a and
L. B. Drissi*abc
aLPHE, Modeling & Simulations, Faculty of Science, Mohammed V University, Rabat, Morocco. E-mail: ldrissi@fsr.ac.ma
bCPM, Centre of Physics and Mathematics, Faculty of Science, Mohammed V University, Rabat, Morocco
cHassan II Academy of Science and Technology, Rabat, Morocco
First published on 11th September 2019
Abstract
Based on the density functional theory and many-body ab initio calculations, we investigate the optoelectronic properties of diamond-shaped quantum dots based graphene, silicene and graphene–silicene hybrid. The HOMO–LUMO (H–L) energy gap, the exciton binding energy, the singlet–triplet energy splitting and the electron–hole overlap are all determined and discussed. Smaller nanostructures show high chemical stability and strong quantum confinement resulting in a significant increase in H–L gap and exciton binding energy. On the other hand, the larger configurations are reactive which implies characteristics favorable to possible electronic transport and conductivity. In addition, the typically strong splitting between singlet and triplet excitonic states and the big electron–hole overlap make these QDs emergent systems for nanomedicine applications.
I. Introduction
Nanomaterials, especially semiconductor quantum dots (QDs), are of immense interest for bioimaging and clinical diagnosis.1–3 Owing to the strong quantum confinement, these small particles possess several unique properties such as, size, wavelength-dependent luminescence, and low photo-bleaching, which make them the perfect candidates for in vitro and in vivo bioimaging probes.4,5To fabricate graphene quantum dots, there are two main ways, namely the top-down and bottom-up approaches. The top-down method consists in breaking carbonaceous materials such as graphene sheets, graphene oxide or graphite to GQDs/GOQDs, through chemical oxidation and exfoliation,6 hydrothermal synthesis,7 electrochemical synthesis,8 UV-assisted synthesis9 and microwaves.10 Top-down methods can not control the shape and the size of quantum dots. However, the “bottom-up” technique can produce GQDS from small organic molecules such as polycyclic aromatic hydrocarbon molecules using stepwise chemical synthesis, pyrolysis or carbonization techniques.11–13 The same synthesis process can be used to fabricate SiQDs by using fine powders of CaSi2 as raw materials, and PtO2 powders.14
In nanochemistry and nanobiophotonics, graphene quantum dots (CQDs) play an important role thanks to their physicochemistry, their biocompatibility, their strong tunable photoluminescence and their low toxicity.15,16 Moreover, the presence of localized states at the zigzag edges makes these hexagonal nanostructures more affected than the armchair ones. Recent advances in synthetic approaches like top-down and bottom-up methods have made possible the production of QDs with a variety of shapes and sizes.17,18 Polystyrene-nanosphere lithography as well as swift heavy ion beam methods have been carried out to fabricate well-aligned graphene quantum dots.19,20 The synthesized CQDs inherit the superior thermal and mechanical properties of their parent graphene sheet.21
Referring to recent experimental studies, the reduction of the QD's diameter intensifies the presence of quantum confinement, which mainly affects the behavior of CQDs visible photoluminescence and their peak red absorption and its intensity.22 Additionally, tuning CQD's photoluminescence using solvothermal synthesis revealed an evident redshift when varying their size and the amount of oxidation surface.23 Consequently, the control of the preparation conditions as well as the choice of the manufacturing process opens the gap and tunes the optical properties of these nanostructures.24,25
In parallel, the theoretical calculations have proven that many factors, namely; the size, the shape such as triangular and hexagonal, the edge configuration (zigzag/armchair),26,27 the atom type,28 the application of the electric field, the chemical modification29,30 which includes adsorption, substitution31 as well as functionalization,32,33 have a great impact on the optoelectronic properties and chemical reactivity of QDs. Indeed, they tailor the highest occupied-lowest unoccupied molecular orbital (HOMO)–(LUMO) energy gap.34–36 They also induce a significant modification in optical absorption leading to remarkable enhancements in the overlap between electron and hole wave functions and tunable singlet–triplet energy splitting.28,37 Photoluminescence is also highly sensitive to size variation, which allows the production of a large class of multicolored fluorescent QDs.38 Moreover, the increase in quantum confinement strongly affects the chemical stability and the different global reactivity parameters of nanostructures, in particular the hardness, the softness, the electrophilicity index and the electronegativity.39,40
Time-dependent DFT studies on electronic excitations in CQDs, especially optically dark ones, reveal their crucial role in fabricating optical devices.41 Employing other methods such as the tight-binding model, many-body perturbation theory and large-scale electron-correlated calculations, the energy gap dependence on different shapes and edges as well as its control by an applied external field have been reported.42–44 Moreover, an interplay between size and covalent edge functionalization has been studied in the framework of Hartree–Fock based semiempirical methods for the highly distorted graphene nanoflakes.45 All the resulted features make CQDs suitable for many applications in optoelectronic, bioimaging, photothermal and photodynamics therapy, biosensing, nanofluidics and organic photovoltaic devices.46–48
Obviously, many parameters influence the luminescent behavior of QD's. This study aims to modulate and adapt the QDs characteristics to nanomedical use, through size control and base-material variation. To do so, we investigate three different diamond-shaped QDs, namely graphene CQDs, silicene SiQDs and graphene–silicene hybrid C-SiQDs. The effect of size on the chemical and optoelectronic properties of nanostructures has been emphasized using the first principles density functional theory calculations. Quasiparticle (QP) corrections as well as charge carrier interactions are included by employing the GW (Green function G and screened Coulomb interaction W) approximation and the BSE (Bethe–Salpeter equation), given their very important role in improving the accuracy of calculated physical properties of nanomaterials. It is shown that the variation in QD's size controls the HOMO–LUMO gap and the exciton binding energy, leading to an adjustment of their luminescent property. Additionally, the chemical stability and reactivity are also evaluated through determining the global hardness, the chemical potential and the electrophilicity index. The luminescent behavior as well as the nature of the excitons in the studied QDs are explored by calculating the singlet–triplet energy splitting and the electron–hole overlap. It is found that a significant overlap and exchange splitting of excitons, results in a high fluorescence quantum yield in all QDs compared to typical yields observed in semiconductor nanostructures. Finally, the high sensitivity of the optoelectronic properties to size variations and base-material makes these QDs suitable for biomedical and luminescent devices for detection and treatment.
The paper is structured as follows: Section 2 describes the computational method used. In Section 3, we report and discuss in detail the results obtained. Finally, the last section presents a summary and conclusion of the work.
II. Computational details
First-principles simulations are performed using the density-functional theory (DFT) as implemented in the Quantum Espresso (QE) simulation package.49 Numerical calculations are provided within the framework of generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE)50 for the exchange–correlation functional. Norm-conserving pseudopotentials51 and plane-wave basis set with a kinetic energy cutoff of 60 Ry are used. Since quantum dots are zero dimensional and the systems are non-periodic, only the Γ-point of the Brillouin zone is considered for structural, electronic and optical properties. Geometric optimization is performed under force and under stress on the atoms, until all forces and energy are less than 10−3 eV Å−1 and 10−4 eV Å−1 respectively.To perform quasi-particle (QP) calculations within the many-body perturbation theory, the exchange–correlation potential Vxc used in the DFT is replaced by a nonlocal self-energy operator 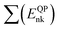 defined as:52
defined as:52
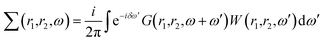 | (1) |
These non-self consistent GW calculations are performed using the YAMBO program suite.53 The Coulomb potential has been truncated at the edges of QDs in both the GW and BSE calculations where only Γ-point has been used. Excitonic properties were calculated by solving Bethe–Salpeter equations (BSE).52 To build the electron–hole interaction kernel, 600 bands were used.
To predict the chemical stability and to interpret the reactivity of the considered QDs, we compute the global hardness (η) and the chemical potential (μ). These crucial parameters are given in terms of the total energy (E) of an N-electron system and its external potential ν(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) as follows:54,55
) as follows:54,55
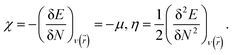 | (2) |
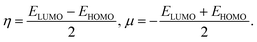 | (3) |
The electrophilicity index ω, that gives the electrophilicity power of a molecule and measures the chemical stability of the system, takes the following form,54,55
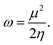 | (4) |
III. Results and discussion
The present study considers three types of diamond-shaped quantum dots, namely graphene (C), silicene (Si) and silicene–graphene hybrid (SiC) quantum dots (QDs), with a varying number of carbon and silicon atoms. Diamond shaped quantum dots present an excellent nanomaterial for examining the effect of size and edges on optoelectronic properties. This particularity is owing to their specific shape that gather the two edge configurations, namely zigzag edges and armchair corners, in addition to the strong zigzag edges dependence on size variation. Furthermore, certain counterparts of this class of QDs, notably, the pyrene C16H10 and dibenzo[bc,kl]coronene C30H14 molecules were successfully fabricated.56,57 This fact makes it easier to compare some of our findings with the experimental results.In the studied configurations displayed in Fig. 1, the zigzag edges and armchair corners are hydrogen passivated, since it has been proved that the graphene nanoribbons with passivated edges are more stable than the unpassivated ones.58,59 The configurations are divided into three categories. Each category consists of three different sizes, namely QD16H10, QD30H14 and QD48H18, where 16, 30 and 48 refer to the number of C and/or Si atoms, while 10, 14 and 18 represent the number of hydrogen atoms that passivate the border. More precisely, 9 configurations are considered: (i) CQDs that have point group symmetry D2h: this first category comprises the following structures C16H10, C30H14 and C48H18. (ii) SiCQDs with C2v symmetry: this second class of hybrid QDs is represented by Si8C8H10, Si15C15H14 and Si24C24H18. (iii) Finally, the SiQDs whose point group is C2h: the components of this third family are labelled as Si16H10, Si30H14 and Si48H18.
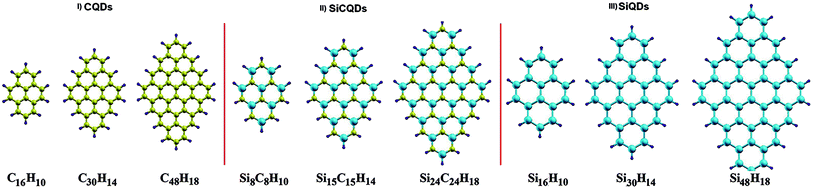 | ||
| Fig. 1 Quantum dots structures. Carbon (C), silicon (Si) and hydrogen (H) atoms are colored in yellow, cyan and purple. | ||
Unlike graphene quantum dots and SiC hybrid quantum dots which are planar structures, silicene quantum dots are buckled structures like their counterpart silicene sheet.60 Both CQDs and SiCQDs are sp2 atoms hybridized, while hybridization is between sp3 and sp2 in SiQDs. As shown in Table 1, the vertical and horizontal sizes are modified according to the type and number of atoms.
| C16H10 | C30H14 | C48H18 | Si8C8H10 | Si15C15H14 | Si24C24H18 | Si16H10 | Si30H14 | Si48H18 | |
|---|---|---|---|---|---|---|---|---|---|
| Horizontal size | 6.83 | 8.56 | 10.21 | 9.32 | 11.76 | 14.11 | 11.81 | 14.85 | 17.99 |
| Vertical size | 9.26 | 11.48 | 13.98 | 13.52 | 16.87 | 20.71 | 17.78 | 22.26 | 27.415 |
| EGGAg | 2.61 | 1.32 | 0.65 | 1.93 | 0.72 | 0.18 | 1.05 | 0.51 | 0.24 |
| EGWg | 6.63 | 4.28 | 3.09 | 5.11 | 3.10 | 1.896 | 3.55 | 2.38 | 1.80 |
| μ | 3.58 | 3.4754 | 3.3406 | 3.49 | 3.24435 | 2.8538 | 3.91 | 3.522085 | 3.3787 |
| η | 1.30 | 0.6585 | 0.3234 | 0.96 | 0.35925 | 0.09 | 0.52 | 0.26 | 0.12 |
| ω | 4.91 | 9.171 | 17.2536 | 6.31 | 20.242 | 45.2454 | 14.60 | 23.854 | 47.5651 |
| EXb | 3.21 | 1.81 | 1.61 | 2.51 | 1.16 | 1.08 | 1.99 | 1.154 | 1.09 |
| MXe–h | 0.253 | 0.203 | 0.326 | 0.192 | 0.155 | 0.496 | 0.209 | 0.216 | 0.671 |
| RX | 2.169 | 3.218 | 2.700 | 2.818 | 4.60 | 2.671 | 3.026 | 3.881 | 2.341 |
| ΔXS–T | 1.27 | 1.62 | 1.37 | 0.67 | 0.23 | 0.37 | 0.66 | 0.63 | 0.26 |
| IH/L | 0.90 | 0.908 | 0.933 | 0.567 | 0.406 | 0.658 | 0.871 | 0.887 | 0.918 |
| Transitions | H−1 → L+1 | H−2 → L+2 | H−1 → L+1 | H → L | H → L | H−1 → L+1 | H−1 → L+1 | H−2 → L+2 | H−1 → L+1 |
| H → L | H−1 → L+1 | H → L | H → L | H → L | H−1 → L+1 | H → L | |||
| H → L | H → L | ||||||||
| ε0 | 1.0676 | 1.2377 | 1.661 | 1.01 | 1.350 | 2.509 | 1.253 | 1.610 | 2.826 |
Before focussing on the optical and electronic properties of QDs, it is necessary to study the chemical stability of these systems.
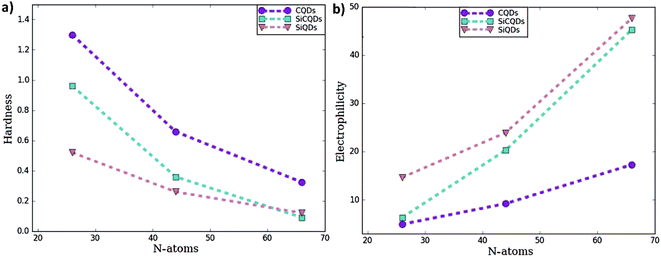
To predict the chemical behavior of the compounds, it is crucial to analyze the results reporting the hardness. Notice that harder molecules have a larger HOMO–LUMO gap (as shown in eqn (3)), which means higher chemical stability and larger excitation energy. Consequently, their electron density is more resistive to change than in a soft molecule.
In our case, CQDs are the most stable structures having the lowest global reactivity, followed by SiCQDs configurations. Indeed, the highest chemical hardness corresponds to the CQDs, as summarized in Table 1 and displayed in Fig. 2. It ranges between 1.30 eV for the smallest size and 0.32 eV for the biggest one. However, silicene QDs show the lowest chemical hardness, which means they are the most reactive configurations. In each QDs class, the greatest hardness coincides with the smallest size which is the most stable structure while the largest of QDs has a highest electrophilicity. The result is in good agreement with,61,62 which show that the increment of atoms amount in graphene-doped nanostructures increases their hardness and reduce their electrophilicity values. Therefore, these QDs exhibit the favorable character of the high electrophilicity required for possible electronic transport and conductivity.
To address the electronic properties, both the GGA-DFT and GW approximations are used. Since quantum confinement in QDs is stronger, GGA-DFT calculations are not the practical method to calculate the energy gap. Nevertheless, it is employed in the geometry optimization and also to determine the ground-state Kohn–Sham wave functions because this approximation represents the first step of the many-body ab initio computations such as the GW approximation, which includes many body effects. Consequently, GW provides a significant correction to the GGA-DFT gap energy.63
Fig. 3 and Table 1 lists the HOMO–LUMO gap. It is clear that the QDs gaps are strongly influenced by two main factors: (1) the type of atoms constituting the QD's and (2) the QDs size since when it increases, the gap energy decreases due to the quantum confinement effect. More precisely, it is found that the HOMO–LUMO energies are inversely proportional to the size of the three classes. This characteristic behavior of quantum dots allows to tune their properties by controlling their size in concordance with the works ref. 43 and 44 reporting the effect of size on the graphene QDs using different approaches. At this stage, one could highlight that the GW-corrections enlarge the gap energy in QDs relative to their 2D counterparts.64–67
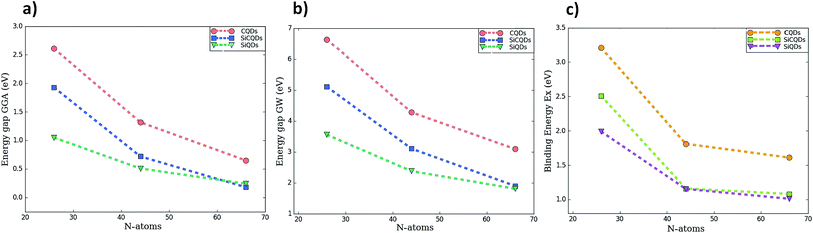 | ||
| Fig. 3 The variation of HOMO–LUMO gap calculated by two methods (a) GGA (b) GW correction, and (c) exciton binding energy as function of the number of atoms composing the QDs. | ||
To shed more light on the impact of the atoms type present in the structures on the gap energy, we compare the results of CQDs, SiQDs and SiCQDs with an equal and fixed atoms number, namely 16, 30 and 48. The data in Table 1 show that the gap decreases starting from graphene passing through SiC to the silicene structure. This can be attributed to the horizontal and vertical increment of the Si atom concentration, which aggrandizes the total size. Note also that silicon has a more metallic behavior than carbon which is more electronegative. As a result carbon loses its electrons less readily than silicon. This strongly affects the electronic and optical properties, as investigated in ref. 28 and 30 where it was pointed out that the HOMO–LUMO gaps are tuned by doping CQD's with Si atoms and by the position and the concentration of BN substituent respectively.
To achieve deeper insight into the variation of the H–L gaps, Fig. 4 illustrates the charge distribution of Frontier molecular orbitals for all structures. In all the smallest nanostructures, the spatial distribution of the HOMO and LUMO is located entirely on the zigzag edges as well as in the armchair corners. More precisely, the contribution to the HOMO originates the most from atoms in armchair corners. However, the contribution to the LUMO comes from atoms in zigzag edges. This is clear for the smallest hybrid Si8C8H10 QDs where LUMO is mainly issued from silicon atoms, while carbon atoms contribute the most to the HOMO. Furthermore, the increment of the QD's size results in not only an increased amount of atoms in the entire structure, but also more prominent zigzag edges. It follows that besides the more pronounced contribution of the atoms located at the zigzag edges, additional contributions of the atoms located in the whole structure, excluding the backbone atoms, are added as shown in Fig. 4. This explains the significant evolution of the H–L energy gap in large structures with respect to smaller configurations. Similar findings on the gap depending on size variation were also discussed in earlier works.28,44
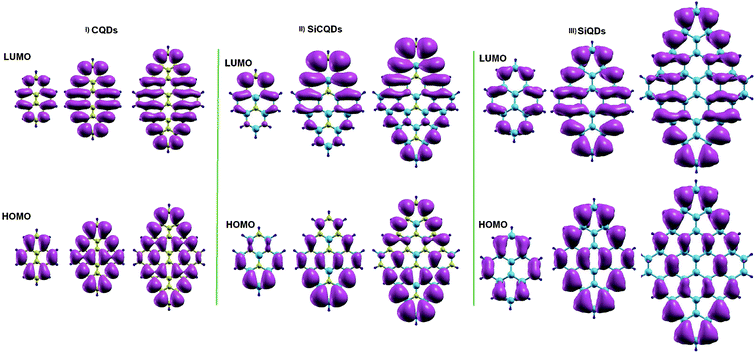 | ||
| Fig. 4 Isosurface charge densities for the lowest unoccupied (LUMO) and the highest occupied molecular orbital (HOMO). | ||
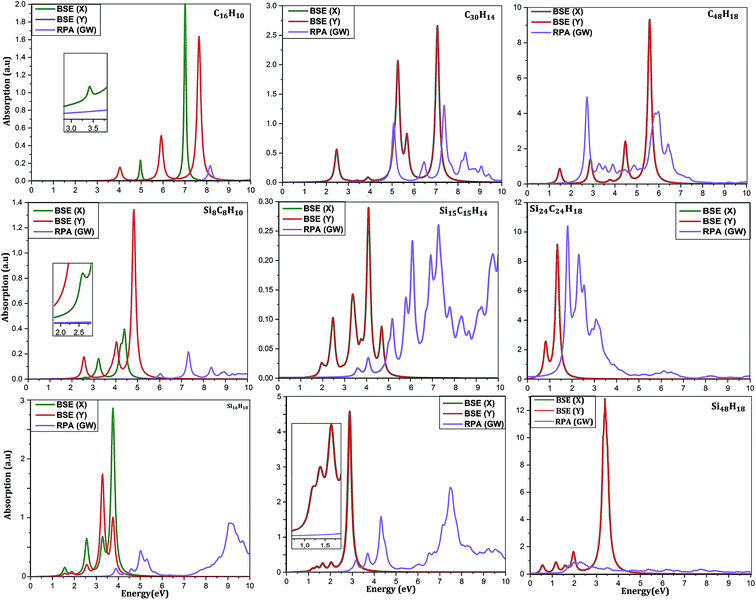
To reveal other potential applications of CQDs, SiCQDs, and SiQDs, it is necessary to study their optical properties. Fig. 5 displays the optical absorption spectra determined within the framework of the GW approximation employing two different methods: (1) Random Phase Approximation (RPA) that ignores the electron–hole interaction and (2) Bethe–Salpeter Equation (BSE) that includes correlation effects.
An accurate analysis of the spectra represented in Fig. 5 and the values reported in Table 1 show similar behavior for each category of QDs. A red-shift of the first peak is observed due to the increasing size of the QD's. As a result, the exciton binding energy increases with the strong electron–hole interaction induced by the weak screening and the reduced dimensionality. Note also that the absorption spectra describing the three smallest configurations, namely C16H10, Si8C8H10 and Si16H10, is remarkably modified as the direction of the light polarized changes. This result indicates the optically anisotropic nature of these compounds, which concurs well with our previous work.28 For larger sized configurations, the BSE absorption curves as well as the exciton binding energy values Eb become equivalent regardless of the light polarization direction. Consequently, one deduce that large structures are quite symmetrical than smaller ones. Due to this isotropy, the rest of the discussion only reports the effect of the X-light polarization as the results will be the same for the Y-one.
For CQDs, it turns out that in pyrene (C16H10) and dibenzo[bc,kl]coronene (C30H14),the first exciton is located at 3.42 eV and 2.47 eV which is in excellent agreement with 3.34 eV and 2.54 eV respectively obtained in experiments.44,68 For C48H18 quantum dot, that we are not yet aware of its synthesis, the optical gap of 1.41 eV is consistent with 1.48 eV reported in ref. 44. In the silicene–graphene hybrids (SiCQDs), the exciton binding energy is 2.51 eV, 1.16 eV, and 1.08 eV for Si8C8H10, Si15C15H14 and Si24C24H18 respectively, which is lower than CQDs but greater than 1.99, 1.15 and 1.09 eV observed for Si16H10, Si30H14 and Si48H18 respectively. Compared with their 1D and 2D analogues, the present QDs display higher binding energies attributed to the quantum confinement effect that originates from a more important electron–hole overlap.64–70
A more intuitive picture of the effects of size variation on the optical excitations of the studied QDs is illustrated in Fig. 6, which displays the spatial distributions of the exciton. It is clear that for the smaller structures of CQD and SiQD, the electron spreads all along the zigzag edges. The increase in size leads to an additional contribution of electrons located in the center of the corresponding systems. In the case of SiCQDs, the exciton is mainly placed in the LUMO region as deduced from Fig. 4. Additionally, the CQDs exhibit the smallest exciton radius with respect to the other categories, which confirms the strong excitonic effect in these structures. Further insight on the optical features is derived from the analysis of the optical transitions corresponding to the lowest dark and highest bright excited states listed in Table 1. Notably, for graphene and silicene structures, dominated transitions are H → L and H+1 → L−1 together. Whereas for SiCQDs, the contribution originates principally from H → L transitions. It is therefore remarkable that transitions in CQDs and SiQDs involve more Frontier orbitals. As a result, more transitions contribute to the bright states leading to the activation of additional orbitals and the enhancement of the excitonic features, especially the Bohr radius. In contrast, SiCQDs exhibit a minor contribution of transitions which explain the difference in their optical behavior.
 | ||
| Fig. 6 Electron distribution of the exciton along X-direction. The hole is represented by the black dot. | ||
The singlet–triplet splitting energy 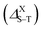 values strongly depend on the size variation and the base-material, as it is depicted in Table 1. Obviously, the largest splitting values were obtained for CQDs that exhibit a very pronounced e–h overlap (90–93%). Closer splitting values are found in SiCQDs and SiQDs, leading to an equivalent luminescent yield for both materials, regardless of their separate overlap amounts. Therefore, the control and adaptation of the singlet–triplet splitting, through various factors, represent a useful mean to tailor excitons for diverse applications in photonics, optoelectronics and nanomedicine. On the other hand,
values strongly depend on the size variation and the base-material, as it is depicted in Table 1. Obviously, the largest splitting values were obtained for CQDs that exhibit a very pronounced e–h overlap (90–93%). Closer splitting values are found in SiCQDs and SiQDs, leading to an equivalent luminescent yield for both materials, regardless of their separate overlap amounts. Therefore, the control and adaptation of the singlet–triplet splitting, through various factors, represent a useful mean to tailor excitons for diverse applications in photonics, optoelectronics and nanomedicine. On the other hand, 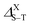 provides informations on the excitons migration, their population on excited states as well as the photoluminescence behavior in nanostructures. According to ref. 71, our structures can be classified into 4 categories depending on the photoluminescence process.
provides informations on the excitons migration, their population on excited states as well as the photoluminescence behavior in nanostructures. According to ref. 71, our structures can be classified into 4 categories depending on the photoluminescence process.
More precisely, normal fluorescence occurs in structures with splitting values range between 0.5 and 1 eV, namely the smallest silicene–graphene hybrid Si8C8H10 as well as the two Si16H10 and Si30H14 configurations. Meanwhile, when 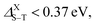 thermally activated delayed fluorescence (TADF) takes place, which is the case for the two larger SiCQDs and the largest Si48H18QDs. Finally, for graphene nanostructures, which exhibit the highest splitting values ranging between 1.27 and 1.67 eV, two processes can happen. Indeed, depending on the ratio ET1/ES1 (where ET1 and ES1 are the energies of triplet and singlet first excited states respectively), we can have the triplet–triplet annihilation (TTA) category if ET1/ES1 ≥ 0.5 eV or the singlet fission (SF) in the case ET1/ES1 < 0.5 eV. It follows that the pyrene C16H10 exhibits a TTA luminescence referred to as pyrene-type luminescence in the literature,72 while the SF behavior is manifest in the two largest configurations C30H14 and C48H18. Compared to typical carbon-based materials such as graphene73 and carbon nanotubes,74 current QDs show greater singlet–triplet splitting, which means stronger fluorescence and different photoluminescence quantum yields that render them promising for various applications. For further details, it is known that the TTA and TADF structures have great potential for organic light-emitting diodes (OLEDs) while SF systems are highly emphasized for solar cells.
thermally activated delayed fluorescence (TADF) takes place, which is the case for the two larger SiCQDs and the largest Si48H18QDs. Finally, for graphene nanostructures, which exhibit the highest splitting values ranging between 1.27 and 1.67 eV, two processes can happen. Indeed, depending on the ratio ET1/ES1 (where ET1 and ES1 are the energies of triplet and singlet first excited states respectively), we can have the triplet–triplet annihilation (TTA) category if ET1/ES1 ≥ 0.5 eV or the singlet fission (SF) in the case ET1/ES1 < 0.5 eV. It follows that the pyrene C16H10 exhibits a TTA luminescence referred to as pyrene-type luminescence in the literature,72 while the SF behavior is manifest in the two largest configurations C30H14 and C48H18. Compared to typical carbon-based materials such as graphene73 and carbon nanotubes,74 current QDs show greater singlet–triplet splitting, which means stronger fluorescence and different photoluminescence quantum yields that render them promising for various applications. For further details, it is known that the TTA and TADF structures have great potential for organic light-emitting diodes (OLEDs) while SF systems are highly emphasized for solar cells.
IV. Conclusion
In conclusion, the first principles calculations based on density functional and many-body perturbation theories were carried out to reveal the importance of the size variation in manipulating the stability as well as the optoelectronic behavior of the diamond-shaped quantum dots. It was reported that the strong quantum confinement present in the smallest nanostructures results in a pronounced increase in H–L gap and noticeable global reactivity. This result provides an index of the utility of these QDs in fabricating potential electronic transport and conductivity for electronic devices. In addition, the optical profile of the systems has been shown to be size-dependent owing to the crucial modification of the exciton binding energy and the Bohr radius, also due to the suppression of the optical anisotropy and the red-shift of absorption peaks with increasing size. The radiative transitions from the singlet to triplet first excited states seem highly predictable due to the large exchange splitting, attributed to the strong electron–hole overlap. All the findings of this work have shown that quantum confinement effects and the base-material tailor and control the optoelectronic properties of QDs, thus offering a promising diversity of characteristics required for a wide range of emerging nanomedical and optoelectronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge “Académie Hassan II des Sciences et Techniques-Morocco” for financial support.References
- W. H. Zhang, X. X. Hu and X. B. Zhang, Dye-doped fluorescent silica nanoparticles for live cell and in vivo bioimaging, Nanomaterials, 2016, 6, 81 CrossRef.
- J. Lin, Y. Huang, and P. Huang, Graphene-Based Nanomaterials in Bioimaging, in Biomedical Applications of Functionalized Nanomaterials, 2018, pp. 247–287 Search PubMed.
- L. S. Li and X. Yan, Colloidal graphene quantum dots, J. Phys. Chem. Lett., 2010, 17, 2572–2576 CrossRef.
- J. Yao, M. Yang and Y. Duan, Chemistry, biology, and medicine of fluorescent nanomaterials and related systems: new insights into biosensing, bioimaging, genomics, diagnostics, and therapy, Chem. Rev., 2014, 114, 6130–6178 CrossRef CAS.
- S. Zhu, Y. Song, X. Zhao, J. Shao, J. Zhang and B. Yang, The photoluminescence mechanism in carbon dots (graphene quantum dots, carbon nanodots, and polymer dots): current state and future perspective, Nano Res., 2015, 8, 355–381 CrossRef CAS.
- M. Xie, Y. Su, X. Lu, Y. Zhang, Z. Yang and Y. Zhang, Blue and green photoluminescence graphene quantum dots synthesized from carbon fibers, Mater. Lett., 2013, 93, 161–164 CrossRef CAS.
- D. Pan, J. Zhang, Z. Li and M. Wu, Hydrothermal route for cutting graphene sheets into blue-luminescent graphene quantum dots, Adv. Mater., 2010, 22, 734–738 CrossRef CAS.
- Y. Li, Y. Hu, Y. Zhao, G. Shi, L. Deng, Y. Hou and L. Qu, An electrochemical avenue to green-luminescent graphene quantum dots as potential electron-acceptors for photovoltaics, Adv. Mater., 2011, 23, 776–780 CrossRef CAS.
- A. K. Swain, D. Li and D. Bahadur, UV-assisted production of ferromagnetic graphitic quantum dots from graphite, Carbon, 2013, 57, 346–356 CrossRef CAS.
- M. K. Kumawat, M. Thakur, R. B. Gurung and R. Srivastava, Graphene Quantum Dots from Mangifera indica: Application in Near-Infrared Bioimaging and Intracellular Nanothermometry, ACS Sustainable Chem. Eng., 2017, 5, 1382–1391 CrossRef CAS.
- R. Liu, D. Wu, X. Feng and K. Müllen, Bottom-up fabrication of photoluminescent graphene quantum dots with uniform morphology, J. Am. Chem. Soc., 2011, 133, 15221–15223 CrossRef CAS.
- Y. Dong, J. Shao, C. Chen, H. Li, R. Wang, Y. Chi, X. Lin and G. Chen, Blue luminescent graphene quantum dots and graphene oxide prepared by tuning the carbonization degree of citric acid, Carbon, 2012, 50, 4738–4743 CrossRef CAS.
- G. Chen, Z. Zhuo, K. Ni, N. Y. Kim, Y. Zhao, Z. Chen, B. Xiang, L. Yang, Q. Zhang, Z. Lee, X. Wu, R. S. Ruoff and Y. Zhu, Rupturing C60 molecules into graphene-oxide-like quantum dots: structure, photoluminescence, and catalytic application, Small, 2015, 11, 5296–5304 CrossRef CAS PubMed.
- P. Hu, L. Chen, J. E. Lu, H. W. Lee and S. Chen, Silicene Quantum Dots: Synthesis, Spectroscopy, and Electrochemical Studies, Langmuir, 2018, 34, 2834–2840 CrossRef CAS.
- M. Bacon, S. J. Bradley and T. Nann, Graphene quantum dots, Part. Part. Syst. Charact., 2014, 31, 415–428 CrossRef CAS.
- X. T. Zheng, A. Ananthanarayanan, K. Q. Luo and P. Chen, Glowing graphene quantum dots and carbon dots: properties, syntheses, and biological applications, Small, 2015, 11, 1620–1636 CrossRef CAS.
- X. Li, S. P. Lau, L. Tang, R. Ji and P. Yang, Multicolour light emission from chlorine-doped graphene quantum dots, J. Mater. Chem. C, 2013, 1, 7308–7313 RSC.
- F. Chen, W. Gao, X. Qiu, H. Zhang, L. Liu, P. Liao, W. Fu and Y. Luo, Graphene quantum dots in biomedical applications: Recent advances and future challenges, Frontiers in Laboratory Medicine, 2017, 1, 192–199 CrossRef.
- S. D. Oh, J. Kim, D. H. Lee, J. H. Kim, C. W. Jang, S. Kim and S. H. Choi, Structural and optical characteristics of graphene quantum dots size-controlled and well-aligned on a large scale by polystyrene-nanosphere lithography, J. Phys. D: Appl. Phys., 2015, 49, 025308 CrossRef.
- P. Mishra and B. R. Bhat, Synthesis and characterization of graphene quantum dots and their size reduction using swift heavy ion beam, Radiat. Eff. Defects Solids, 2018, 1–7 Search PubMed.
- Y. Liu and P. Wu, Graphene Quantum Dot Hybrids as Efficient Metal-Free Electrocatalyst for the Oxygen Reduction Reaction, ACS Appl. Mater. Interfaces, 2013, 5, 3362–3369 CrossRef CAS.
- S. Kim, S. W. Hwang, M. K. Kim, D. Y. Shin, D. H. Shin, C. O. Kim, S. B. Yang, J. H. Park, E. Hwang, S. H. Choi and G. Ko, Anomalous behaviors of visible luminescence from graphene quantum dots: interplay between size and shape, ACS Nano, 2012, 6, 8203–8208 CrossRef CAS.
- B. P. Qi, X. Zhang, B. B. Shang, D. Xiang and S. Zhang, Solvothermal tuning of photoluminescent graphene quantum dots: from preparation to photoluminescence mechanism, J. Nanopart. Res., 2018, 20, 20 CrossRef.
- P. Tian, L. Tang, K. S. Teng and S. P. Lau, Graphene quantum dots from chemistry to applications, Mater. Today Chem., 2018, 10, 221–258 CrossRef CAS.
- J. Lu, P. S. E. Yeo, C. K. Gan, P. Wu and K. P. Loh, Transforming C 60 molecules into graphene quantum dots, Nat. Nanotechnol., 2011, 6, 247 CrossRef CAS.
- A. D. Güçlü, P. Potasz and P. Hawrylak, Excitonic absorption in gate-controlled graphene quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155445 CrossRef.
- C. Mansilla Wettstein, F. P. Bonafé, M. B. Oviedo and C. G. Sànchez, Optical properties of graphene nanoflakes: shape matters, J. Chem. Phys., 2016, 144, 224305 CrossRef.
- F.-Z. Ramadan, H. Ouarrad and L. B. Drissi, Tuning Optoelectronic Properties of the Graphene-Based Quantum Dots C16−xSixH10 Family, J. Phys. Chem. A, 2018, 122, 5016–5025 CrossRef CAS.
- G. S. Kumar, R. Roy, D. Sen, U. K. Ghorai, R. Thapa, N. Mazumder, S. Saha and K. K. Chattopadhyay, Amino-functionalized graphene quantum dots: origin of tunable heterogeneous photoluminescence, Nanoscale, 2014, 6, 3384–3391 RSC.
- S. Sanyal, A. K. Manna and S. K. Pati, BN-decorated graphene nanoflakes with tunable opto-electronic and charge transport properties, J. Mater. Chem. C, 2014, 2, 2918–2928 RSC.
- S. S. Yamijala, A. Bandyopadhyay and S. K. Pati, Electronic properties of zigzag, armchair and their hybrid quantum dots of graphene and boron-nitride with and without substitution: a DFT study, Chem. Phys. Lett., 2014, 603, 28–32 CrossRef CAS.
- K. R. Geethalakshmi, T. Y. Ng and R. Crespo-Otero, Tunable optical properties of OH-functionalised graphene quantum dots, J. Mater. Chem. C, 2016, 4, 8429–8438 RSC.
- J. Feng, H. Dong, L. Yu and L. Dong, The optical and electronic properties of graphene quantum dots with oxygen-containing groups: a density functional theory study, J. Mater. Chem. C, 2017, 5, 5984–5993 RSC.
- F. Zhang, F. Liu, C. Wang, X. Xin, J. Liu, S. Guo and J. Zhang, Effect of lateral size of graphene quantum dots on their properties and application, ACS Appl. Mater. Interfaces, 2016, 8, 2104–2110 CrossRef CAS.
- R. Das, N. Dhar, A. Bandyopadhyay and D. Jana, Size dependent magnetic and optical properties in diamond shaped graphene quantum dots: a DFT study, J. Phys. Chem. Solids, 2016, 99, 34–42 CrossRef CAS.
- P. Zhang, Q. Hu, X. Yang, X. Hou, J. Mi, L. Liu and M. Dong, Size effect of oxygen reduction reaction on nitrogen-doped graphene quantum dots, RSC Adv., 2018, 8, 531–536 RSC.
- R. Zhang, S. Qi, J. Jia, B. Torre, H. Zeng, H. Wu and X. Xu, Size and refinement edge-shape effects of graphene quantum dots on UV-visible absorption, J. Alloys Compd., 2015, 623, 186–191 CrossRef CAS.
- M. A. Sk, A. Ananthanarayanan, L. Huang, K. H. Lim and P. Chen, Revealing the tunable photoluminescence properties of graphene quantum dots, J. Mater. Chem. C, 2014, 2, 6954–6960 RSC.
- H. Chermette, Chemical reactivity indexes in density functional theory, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. K. Chattaraj and U. Sarkar, Effect of Spherical Confinement on Chemical Reactivity, J. Phys. Chem. A, 2003, 107, 4877–4882 CrossRef CAS.
- S. Schumacher, Photophysics of graphene quantum dots: insights from electronic structure calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081417 CrossRef.
- M. Zarenia, A. Chaves, G. A. Farias and F. M. Peeters, Energy levels of triangular and hexagonal graphene quantum dots: a comparative study between the tight-binding and Dirac equation approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245403 CrossRef.
- Y. Li, H. Shu, S. Wang and J. Wang, Electronic and optical properties of graphene quantum dots: the role of many-body effects, J. Phys. Chem. A, 2015, 119, 4983–4989 CrossRef CAS.
- T. Basak, H. Chakraborty and A. Shukla, Theory of linear optical absorption in diamond-shaped graphene quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205404 CrossRef.
- C. Cocchi, D. Prezzi, A. Ruini, M. J. Caldas and E. Molinari, Electronics and Optics of Graphene Nanoflakes: Edge Functionalization and Structural Distortions, J. Phys. Chem. A, 2012, 116, 17328–17335 CAS.
- Y. Liu, X. Dong and P. Chen, Biological and chemical sensors based on graphene materials, Chem. Soc. Rev., 2012, 41, 2283–2307 RSC.
- B. Tian, C. Wang, S. Zhang, L. Feng and Z. Liu, Photothermally enhanced photodynamic therapy delivered by nano-graphene oxide, ACS Nano, 2011, 5, 7000–7009 CrossRef CAS.
- M. Miansari, J. R. Friend, P. Banerjee, M. Majumder and L. Y. Yeo, Graphene-based planar nanofluidic rectifiers, J. Phys. Chem. A, 2014, 118, 21856–21865 CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo and A. Dal Corso, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Electron-hole excitations and optical spectra from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927 CrossRef CAS.
- A. Marini, C. Hogan, M. Grüning and D. Varsano, Yambo: an ab initio tool for excited state calculations, Comput. Phys. Commun., 2009, 180, 1392–1403 CrossRef CAS.
- P. K. Chattaraj and S. Giri, Stability, Reactivity, and Aromaticity of Compounds of a Multivalent Super Atom, J. Phys. Chem. A, 2007, 111, 11116–11121 CrossRef CAS.
- J. Padmanabhan, R. Parthasarathi, V. Subramanian and P. K. Chattaraj, Electrophilicity-Based Charge Transfer Descriptor, J. Phys. Chem. A, 2007, 111, 1358–1361 CrossRef CAS.
- H. S. Jang, Y. Wang, Y. Lei and M. P. Nieh, Controllable formation of pyrene (C16H10) excimers in polystyrene/tetrabutylammonium hexafluorophosphate films through solvent vapor and temperature annealing, J. Phys. Chem. A, 2013, 117, 1428–1435 CrossRef CAS.
- W. J. Simonsick and R. A. Hites, Characterization of high molecular weight polycyclic aromatic hydrocarbons by charge exchange chemical ionization mass spectrometry, Anal. Chem., 1986, 58, 2114–2121 CrossRef CAS.
- P. Koskinen, S. Malola and H. Häkkinen, Self-passivating edge reconstructions of graphene, Phys. Rev. Lett., 2008, 101, 115502 CrossRef.
- Ç. Ö. Girit, J. C. Meyer, R. Erni, M. D. Rossell, C. Kisielowski, L. Yang, C. H. Park, M. F. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Graphene at the edge: stability and dynamics, Science, 2009, 323, 1705–1708 CrossRef.
- P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Silicene: compelling experimental evidence for graphene like two-dimensional silicon, Phys. Rev. Lett., 2012, 108, 155501 CrossRef.
- A. S. Rad, First principles study of Al-doped graphene as nanostructure adsorbent for NO2 and N2O: DFT calculations, Appl. Surf. Sci., 2015, 357, 1217–1224 CrossRef CAS.
- V. Sharma, S. Narayan, S. D. Dabhi, S. Shinde and P. K. Jha, Sensing behavior of a graphene quantum dot phenalenyl towards toxic gases, AIP Conf. Proc., 2018, 050047 CrossRef.
- G. Onida, L. Reining and A. Rubio, Electronic excitations: density functional versus many-body Green-function approaches, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- L. B. Drissi and F. Z. Ramadan, Many Body Effects Study of Electronic and Optical Properties of Silicene-Graphene Hybrid, Phys. E, 2015, 68, 38–41 CrossRef CAS.
- L. B. Drissi, F. Z. Ramadan and K. Junior, Optoelectronic Properties in 2D GeC and SiC Hybrids: DFT and Many Body Effect Calculations, Mater. Res. Express, 2018, 5, 015061 CrossRef.
- M. S. Hybertsen and S. G. Louie, Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390 CrossRef CAS.
- T. Y. Lü, X. X. Liao, H. Q. Wang and J. C. Zheng, Tuning the indirect-direct band gap transition of SiC, GeC and SnC monolayer in a graphene-like honeycomb structure by strain engineering: a quasiparticle GW study, J. Mater. Chem., 2012, 22, 10062–10068 RSC.
- E. Clar and W. Schmidt, Correlations between photoelectron and ultraviolet absorption spectra of polycyclic hydrocarbons: the terrylene and peropyrene series, Tetrahedron, 1978, 34, 3219–3224 CrossRef CAS.
- D. Prezzi, D. Varsano, A. Ruini, A. Marini and E. Molinari, Optical properties of graphene nanoribbons: the role of many-body effects, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041404 CrossRef.
- C. D. Spataru, S. Ismail-Beigi, L. X. Benedict and S. G. Louie, Excitonic effects and optical spectra of single-walled carbon nanotubes, Phys. Rev. Lett., 2004, 92, 077402 CrossRef.
- T. Chen, L. Zheng, J. Yuan, Z. An, R. Chen, Y. Tao, H. Li, X. Xie and W. Huang, Understanding the control of singlet-triplet splitting for organic exciton manipulating: a combined theoretical and experimental approach, Sci. Rep., 2015, 5, 10923 CrossRef.
- C. Bohne, E. B. Abuin and J. C. Scaiano, Characterization of the triplet-triplet annihilation process of pyrene and several derivatives under laser excitation, J. Am. Chem. Soc., 1990, 112, 4226–4231 CrossRef CAS.
- S. Huang, Y. Liang and L. Yang, Exciton spectra in two dimensional graphene derivatives, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075441 CrossRef.
- V. Perebeinos, J. Tersoff and P. Avouris, Radiative Lifetime of Excitons in Carbon Nanotubes, Nano Lett., 2005, 5, 2495–2499 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |