Open Access Article
Open Access ArticleAn evaluation on the extraction capability of anion exchange membranes for high-precision sulfur isotope measurement by multiple-collector inductively coupled plasma mass spectrometry
Liu Willow
Yang
a,
Chenhui
Liu
 *ab and
Tao
Yang
*a
*ab and
Tao
Yang
*a
aState Key Laboratory for Mineral Deposits Research, School of Earth Sciences and Engineering, Nanjing University, Nanjing 210093, P. R. China. E-mail: cliu@nju.edu.cn; yangtao@nju.edu.cn
bKey Laboratory of Marine Mineral Resources, Ministry of Land and Resources, Guangzhou 510075, P. R. China
First published on 2nd October 2019
Abstract
Anion exchange membranes (AEMs) are adept at extracting sulfate for sulfur isotope analyses by multiple-collector inductively coupled plasma mass spectrometry (MC-ICP-MS) from natural samples typically with low sulfate concentrations. But up to now, their capability for sulfate extraction is still lacking adequate research. In this study, a series of detailed tests on AEMs for sulfate extraction were developed, which included the tolerance of pH, the effect of competitive anions, and the lowest concentration limit of sulfate uploading. The optimal scope of pH for sulfate exchange is from 3 to 11. Approximately over 90% of sulfate recoveries and reliable sulfur isotope analyses can be achieved when the concentrations of nitrate, chloride, phosphate, carbonate, and bicarbonate are limited in 0.5 mmol per L per cm2 of a piece of AEM. In practice, we suggest that the applicable concentrations are able to increase to 10 times, except for phosphate. The lowest uploading concentration of sulfate that can be adsorbed by the AEM without sulfur isotope fractionation is further detected as 0.5 μmol L−1 though the recovery of sulfate decreases when its concentration is lower than 0.01 mmol L−1. This research offers insight into realizing accurate and precise sulfur isotope analyses for natural freshwater and marine pore water by MC-ICP-MS.
1. Introduction
In recent years, multiple-collector inductively coupled plasma mass spectrometry (MC-ICP-MS) has become increasingly popular in rapid and precise measurements of sulfur isotopic compositions in various sulfur-bearing materials, such as sulfate and sulfide minerals,1–3 seawater and marine pore water sulfate,4–7 and rainwater and soil solution,8 even including medical serum and plasma.9 Comparing with the traditional technique of gas-source isotope ratio mass spectrometry (GS-IRMS),10–16 MC-ICP-MS requires a lower quantity sulfur injection (5–40 nmol sulfur4) and is free from oxygen isotope correction for the produced sulfur dioxide gas (up to 1–3‰ shift in δ34S values17). However, MC-ICP-MS has three potential shortages, i.e. instrument mass bias, spectral interferences, and non-spectral interferences (also referred to as matrix effects). The former two can be overcome effectively by the method of standard-sample bracketing (SSB) and media-to-high mass resolution (m/Δm > 2700) detection, while the matrix effects can only be solved by chemical purification or matrix-matched treatment before isotope measurements.2,3,5–8 Considering that the natural sample is a complex mixture, it appears difficult and cumbersome to prepare a full-matched standard for every sample that contains various matrix elements. Therefore, pre-purification may be an efficient and reasonable approach to obtain accurate and precise sulfur isotope ratios in natural samples.An ion exchange membrane is a polymer or copolymer modified by ionic groups, which can be used for collecting and condensing the ion of interest from sample solutions.18 Comparing with the ion exchange resin traditionally used for chemical purification,2,4,19–24 the ion exchange membrane performs better at low concentration but high sample volume.8,25 Anion exchange membranes (AEMs) were widely applied in field and laboratory sample treatments, and particularly in extracting phosphorus compounds (organic and condensed inorganic phosphorus) from soil-water, rainwater, river, and sediments.26–30 Kwon et al.25 firstly used AEM for soil sulfate collection and found that the existence of competitive anions (e.g., nitrate and chloride) only lowered the sulfate absorption on the resin membranes but almost did not produce sulfur isotope fractionation (< 1‰). Afterward, Hanousek et al.8 developed a more detailed test on matrix separation of AEM and chose MC-ICP-MS for direct analyses of sulfur isotopes in rainwater and soil solutions, which were often low in sulfate concentrations (down to 0.04 mmol L−1) but ample for sample amount. They indicated that some common cations including calcium, potassium, sodium, and lithium could be quantitatively removed during the sulfate exchange, but nitrate and chloride ions would compete with sulfate and decrease its recovery. However, these studies have placed more weight on highlighting the necessity of matrix separation for reliable sulfur isotope analyses rather than evaluating the extent to which change in concentrations of competitive ions could impact on sulfate extraction. Meanwhile, the lowest uploading concentration of sulfate that can be adsorbed by AEM without sulfur isotope fractionation is still not determined.
To solve these two questions, we performed a detailed investigation to evaluate the sulfate extraction capability of AEM in this study. First, the pH tolerance of AEM was determined to provide an optimal pH scope for the subsequent tests. As the common anions accompanied with sulfate in nature, nitrate, chloride, phosphate, carbonate, and bicarbonate were chosen to determine the influence of their competitiveness on sulfate absorption. Afterward, the pure sulfate solution was diluted to detect the lowest concentration limit of sulfate uploading. During these tests, the changes in sulfur isotopic compositions before and after the sulfate extraction were measured by MC-ICP-MS. Finally, two geological applications about sulfur isotope analyses of natural freshwater and marine pore water by MC-ICP-MS were further provided.
2. Materials and methods
2.1 Preparation of sample solutions
All sample solutions were prepared in an ultra-clean lab. All vials and bottles were cleaned for more than 24 h in 10% w/w nitric acid (HNO3) and rinsed with deionized water (prepared by a Milli-Q system at 18.2 MΩ cm) over three times. To investigate the effect of sulfur isotope fractionation during the ion exchange, we chose ammonium sulfate ((NH4)2SO4) powder (99.0% w/w purity; CAS no.7783-20-2; Nanjing Chemical Reagent Co., Ltd., China) with known sulfur isotopic composition (see below) to prepare sample solutions. Detailed preparation procedures were listed as follows:(a) A series of 0.3 mmol L−1 sulfate solutions were prepared for pH controlling tests with different pH values ranging from ca. 1.2 to 12.5. High-purity nitric acid and ammonium hydroxide (NH3·H2O) were added to adjust pH values. The pH values were verified by a pH meter (Sartorius PB-10, Germany) after being corrected using a series of standard solutions (pH = 4.00, 7.00, and 10.01).
(b) Six groups of samples were prepared by adding competitive ions, nitrate (NO3−), chloride (Cl−) (Chinese national standard solutions GSB 04-1772-2004 and GSB 04-1770-2004, respectively; 1000 μg mL−1), phosphate (PO43−), carbonate (CO32−), and bicarbonate (HCO3−) (dissolved from analytical reagent solid powders with CAS no. 25447-33-0, 506-87-6, and 1066-33-7, respectively) into 0.3 mmol L−1 sulfate solutions. These anions were added separately in the first five groups at the concentrations of 0.15, 0.3, 1.5, 3, 15, 30, 150, and 300 mmol L−1. In the last group, each solution contained both nitrate and chloride but halved in their concentrations. Afterward, the concentration of sulfate was changed with the sequential addition of nitrate as the competitive ion. These solutions contained 0.03, 0.06, 0.15, 0.3, 0.6, and 1.5 mmol L−1 of sulfate, respectively. For each concentration of sulfate, nitrate was introduced to obtain a constant array of atomic ratio (including 0.4, 1, 2, 4, and 10) of nitrate/sulfate. All prepared solutions were adjusted to neutral by adding ammonium hydroxide, which corresponded to the optimal pH range concluded from the controlling tests (see Section 3.1 below).
(c) Six pure sulfate solutions with decreasing sulfate concentrations (including 0.3, 0.05, 0.01, 0.005, 0.001, and 0.0005 mmol L−1) were made to detect the lowest concentration of sulfate uploading.
Several natural freshwater and seawater samples were also applied to validate the sulfate extraction effects. The natural freshwater samples with low levels of sulfate (roughly below 2 mmol L−1) were collected from the Lake Taihu, China and the surface runoff of Aksu region, Xinjiang, China, respectively (see Table 6 below). These samples were further diluted to sulfate concentration of ca. 0.3 mmol L−1 before AEM treatments. In addition, to simulate the marine pore water with different concentrations of sulfate and chloride, the Atlantic Seawater (OSIL, salinity = 35.0 ± 0.2%) was diluted 100, 200, 500, and 1000 times, respectively.
2.2 Extraction using anion exchange on membranes
The AEM in use (551642S, BDH-ROLABO, VWR International, EC) is the polystyrene-divinylbenzene copolymer base adulterated with quaternary-ammonium as ionic groups18 and is provided in 12.5 × 12.5 cm sheet with ferric chloride (FeCl3) preloaded. It was cut into 1 × 3 cm pieces (6 cm2 for both sides) and pretreated according to the procedures described by Hanousek et al.8 Each piece of AEM was placed into 0.5 mol L−1 nitric acid for 1 hour cleaning and then regenerated within 0.5 mol L−1 sodium bicarbonate (NaHCO3) for 4 h. After the pretreatment, the AEM pieces were uploaded with sample solutions and shaken for 16 h. The sulfate absorbed in the membranes were subsequently eluted with 2% w/w nitric acid for 1 hour desorption. Lastly, the used AEM pieces were cleaned by 0.5 mol L−1 nitric acid.2.3 Concentration and isotope analyses
All measurements were performed at State Key Laboratory for Mineral Deposits Research, School of Earth Sciences and Engineering, Nanjing University, Nanjing, China.Sulfate sulfur concentrations before and after extraction procedures were determined using an Element XR single-collector inductively coupled plasma mass spectrometer (Thermo Scientific, Bremen, Germany) with the configuration and operating parameters listed in Table 1. A sequence of standard solutions with sulfate sulfur concentrations of 1, 10, 20, 50, and 100 μg kg−1 (GSB 04-1773-2004(b); 1000 μg mL−1) were diluted to construct the standard curve in linear calibration, which had a correlation coefficient greater than 0.9999 and the relative standard deviation lower than 5%. All measured solutions contained 10 μg kg−1 Rh as the internal normalization reference. The recovery of sulfate was calculated by dividing the concentrations of sulfate before and after extraction procedures.
| Mass spectrometer setup | ||
| ICP-MS | Thermo Scientific Element XR | Thermo Scientific Neptune Plus |
| Cooling gas flow rate | ca. 15 L min−1, argon | ca. 15 L min−1, argon |
| Auxiliary gas flow rate | ca. 1.25 L min−1, argon | ca. 1.1 L min−1, argon |
| Sample gas flow rate | ca. 1.05 L min−1, argon | ca. 0.95 L min−1, argon |
| Extraction lens | ca. −2000 V | ca. −2000 V |
| Interface cones | Ni cones | Ni cones |
| Analyzer pressure | ca. 10−9 torr | ca. 10−9 torr |
| RF forward power | ca. 1175 W | ca. 1200 W |
| RF reflect power | ca. 5 W | ca. 2 W |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Data acquisition parameters | ||
| Mass resolution mode | Medium resolution (m/Δm > 2500) | Medium resolution (m/Δm ≈ 3500) |
| Acquisition mode | Static | Static |
| Detection system | Analog | Faraday cups |
| Cup configuration | 32S | 32S (C), 33S (H2), 34S (H3) |
| Signal analysis protocol | 3 runs and 4 passes | 4.194 s integration per cycle, 40 cycles per block, 1 block |
| Wash-out time | ca. 200 s | ca. 200 s |
A Neptune Plus multiple-collector inductively coupled plasma mass spectrometer (Thermo Scientific, Bremen, Germany) was used for sulfur isotope ratio measurement. The signals of sulfur isotopes were acquired on the interference-free plateau in medium-to-high mass resolution mode to eliminate the isobaric interferences from oxygen species (e.g., 16O2+). Standard-sample bracketing (SSB) method was applied to determine the sulfur isotopic composition of the recovered solution after extraction procedures. More detailed parameters of apparatus and operation were illustrated in Table 1. The ammonium sulfate (ibid) at the same sulfur concentration was chosen as the working standard and the sulfur isotope deviation of the recovered solution relative to the standard was defined as:
| Δ34S (‰) = (Rsam/Rstd − 1) × 1000 | (1) |
| δ34S (‰ VCDT) = Δ34S + δ34Sstd | (2) |
3. Results and discussion
3.1 pH controlling tests
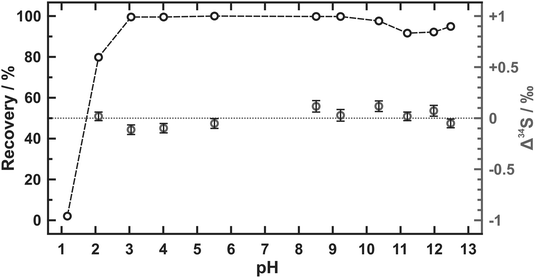
The results of pH tolerance tests are listed in Table 2 and plotted in Fig. 1. Over 90% of sulfate is recovered from the samples in a pH range from 3.1 to 12.5 but the percentage value of the sulfate recovery declines sharply as the pH value lowers than 3. Similar recoveries (tested pH values including 1.1, 1.4, 2.0, 11.4, 11.9, and 12.6) were also accomplished by Hanousek et al.8 though there existed a little difference (93% of sulfate recovered) in the case that pH value was equal to 2. The sulfur isotope changes after the sulfate recovery (Δ34S) are further determined in our study. Only quite small values of Δ34S are yielded at pH values between 2.1 and 12.5 (avg. 0.01 ± 0.16‰ (2SD)) even though sulfate is not totally recovered when pH value equals 2.1. Yet the piece of AEM appears inactive after being soaked in strong alkaline conditions (pH ≥ 12), which becomes dark brown and cannot refresh after the regeneration. Therefore, the pH range from 3 to 11 is recommended for the sulfate extraction using AEM where almost no sulfur isotope fractionation is observed.| pH | Recoverya/% | Δ 34Sb/‰ |
|---|---|---|
| a All uploading sample solutions have 0.3 mmol L−1 of sulfate. The volumes of uploading and eluting solutions are both 10 mL. b The calculated internal uncertainties are given as 2SE. n.d. = not detected. | ||
| 1.17 | 2.0 | n.d. |
| 2.09 | 79.8 | +0.02 ± 0.04 |
| 3.05 | 99.5 | −0.11 ± 0.05 |
| 4.01 | 99.5 | −0.10 ± 0.05 |
| 5.51 | 100.0 | −0.05 ± 0.05 |
| 8.51 | 99.8 | +0.12 ± 0.06 |
| 9.23 | 99.8 | +0.03 ± 0.06 |
| 10.36 | 97.6 | +0.12 ± 0.05 |
| 11.20 | 91.6 | +0.02 ± 0.04 |
| 11.98 | 92.2 | +0.07 ± 0.05 |
| 12.48 | 94.9 | −0.05 ± 0.04 |
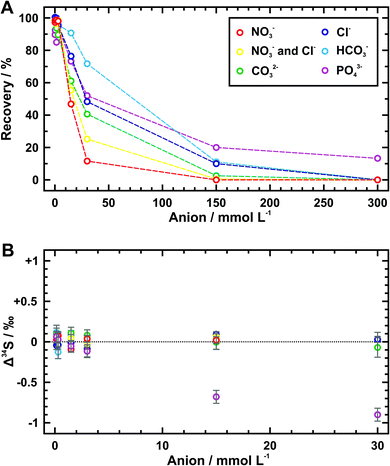
3.2 Anion competition tests and exchange capacity evaluation
As shown in Table 3 and Fig. 2A, the amount of exchanged sulfate decreases with increasing concentration of every competitive anion tested here, but their gradients are obviously different. Specifically, the sulfate recoveries are increasingly affected by an order of phosphate, bicarbonate, chloride, carbonate, and nitrate when they are at the same concentration. This may result from different adsorption abilities of these anions towards the quaternary-ammonium resinous exchanger, because it accords with the order of preferred affinity towards uptake (SO42− > NO3− > Cl− > HCO3−).32 So that it is not difficult to explain why the recovery data of samples with half concentration of nitrate and chloride fall in between those containing them separately. In fact, most of the phosphate ion (PO43−) would be hydrolyzed to the hydrogen phosphate ion (HPO42−) at pH values between 7 and 10 (i.e., the pH range of phosphate-bearing samples tested here). For samples of phosphate concentration lower than 30 mmol L−1, the hydrolysis of phosphate under almost neutral conditions (pH ≈ 7) can also yield some dihydrogen phosphate ion (H2PO4−), which may have a higher affinity for the membrane exchange sites compared with the bicarbonate ion. This could be the reason why the recoveries below 30 mmol L−1 of phosphate are generally close to those of chloride at the same concentrations (Fig. 2A).| Competitive anion/mmol L−1 | Recoverya/% | Δ 34Sb/‰ | ||||
|---|---|---|---|---|---|---|
| NO3− | Cl− | PO42− | CO32− | HCO3− | ||
| a All uploading sample solutions have 0.3 mmol L−1 of sulfate. The volumes of uploading and eluting solutions are both 10 mL. b The calculated internal uncertainties are given as 2SE. n.d. = not detected. | ||||||
| 0.15 | 97.3 | +0.03 ± 0.04 | ||||
| 0.3 | 98.5 | +0.08 ± 0.05 | ||||
| 1.5 | 98.8 | −0.09 ± 0.04 | ||||
| 3 | 98.0 | +0.04 ± 0.04 | ||||
| 15 | 46.9 | +0.02 ± 0.04 | ||||
| 30 | 11.6 | n.d. | ||||
| 150 | 0.0 | n.d. | ||||
| 300 | 0.0 | n.d. | ||||
| 0.15 | 100.4 | −0.04 ± 0.05 | ||||
| 0.3 | 99.1 | −0.04 ± 0.05 | ||||
| 1.5 | 99.9 | −0.01 ± 0.05 | ||||
| 3 | 95.5 | −0.09 ± 0.04 | ||||
| 15 | 76.4 | +0.09 ± 0.03 | ||||
| 30 | 48.3 | +0.03 ± 0.04 | ||||
| 150 | 10 | n.d. | ||||
| 300 | 0.0 | n.d. | ||||
| 0.15 | 89.6 | +0.06 ± 0.07 | ||||
| 0.3 | 92.4 | +0.03 ± 0.09 | ||||
| 1.5 | 85.0 | −0.05 ± 0.07 | ||||
| 3 | 94.6 | −0.12 ± 0.08 | ||||
| 15 | 73.3 | −0.68 ± 0.08 | ||||
| 30 | 52.0 | −0.90 ± 0.08 | ||||
| 150 | 20.0 | n.d. | ||||
| 300 | 13.3 | n.d. | ||||
| 0.15 | 98.6 | +0.10 ± 0.07 | ||||
| 0.3 | 98.0 | +0.02 ± 0.09 | ||||
| 1.5 | 93.7 | +0.11 ± 0.07 | ||||
| 3 | 89.6 | +0.08 ± 0.07 | ||||
| 15 | 61.1 | −0.01 ± 0.09 | ||||
| 30 | 40.6 | −0.07 ± 0.12 | ||||
| 150 | 2.6 | n.d. | ||||
| 300 | 0.0 | n.d. | ||||
| 0.15 | 100.4 | +0.12 ± 0.09 | ||||
| 0.3 | 98.6 | −0.13 ± 0.08 | ||||
| 1.5 | 96.8 | +0.08 ± 0.06 | ||||
| 3 | 95.9 | −0.10 ± 0.08 | ||||
| 15 | 90.7 | +0.00 ± 0.09 | ||||
| 30 | 71.7 | +0.03 ± 0.09 | ||||
| 150 | 11.1 | n.d. | ||||
| 300 | 0.0 | n.d. | ||||
| 0.075 | 0.075 | 97.7 | +0.06 ± 0.04 | |||
| 0.15 | 0.15 | 97.9 | +0.06 ± 0.04 | |||
| 0.75 | 0.75 | 96.4 | +0.05 ± 0.04 | |||
| 1.5 | 1.5 | 98.6 | −0.02 ± 0.05 | |||
| 7.5 | 7.5 | 55.3 | +0.06 ± 0.04 | |||
| 15 | 15 | 25.2 | n.d. | |||
| 75 | 75 | 0.5 | n.d. | |||
| 150 | 150 | 0.0 | n.d. | |||
Maximum sulfate recoveries (approximately > 90%) are achieved within the concentration threshold of 3 mmol L−1 for every competitive anion (i.e., 0.5 mmol per L per cm2 of AEM piece), except that the threshold of bicarbonate can extend to 15 mmol L−1. When the anion concentration exceeds this threshold, despite only partial sulfate is exchanged by AEM, there exists negligible Δ34S values (avg. 0.02 ± 0.10‰ (2SD)) as indistinguishable as those of high sulfate recoveries (avg. 0.01 ± 0.15‰ (2SD)) (Table 3 and Fig. 2B). The only exceptions are phosphate-bearing samples. Over 0.6‰ of Δ34S values are observed at the phosphate concentration higher than 15 mmol L−1. Low recoveries of sulfate denote that some phosphate ion can simultaneously be absorbed in the membranes and then be eluted together with sulfate. As a result, such obvious sulfur isotope fractionation could be associated with matrix effects from phosphorus. Thus, for the sulfate sample with nitrate, chloride, carbonate, or bicarbonate, the reliable sulfur isotopic composition can be acquired as long as a sufficient amount of sulfate for measurement (5 μg g−1 of sulfur at least) is recovered. But for the phosphate-bearing sample, equally convincing sulfur isotope measurement is only obtained as its concentration stays within 3 mmol L−1. In practice, the applicable concentrations of these competitive anions can extend to 5 mmol per L per cm2 of AEM piece except for phosphate which should be limited to 0.5 mmol per L per cm2 of AEM piece.
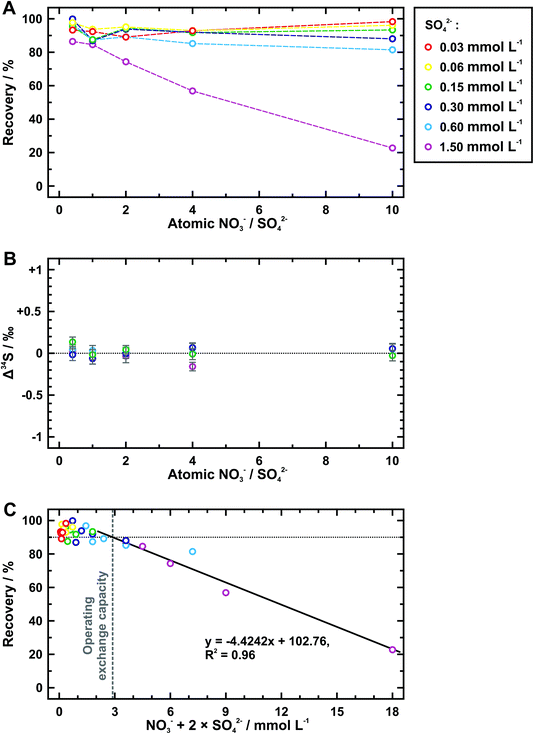
Nitrate is further taken as the competitive ion to evaluate the exchange capacity of AEM. Table 4 shows the recovery and isotopic results tested from six groups of sample solutions, which have different sulfate concentrations but a constant array of the atomic ratio between nitrate and sulfate. When the concentration of sulfate is no more than 0.6 mmol L−1, most data points of the sulfate recovery gather around 90% and the difference among them cannot be clearly identified except for those at the nitrate/sulfate ratio of 10 (Fig. 3A). A distinct decrease in the sulfate recovery with the ratio of nitrate to sulfate is observed at 1.5 mmol L−1 of sulfate. In addition, samples with a sufficient amount of sulfate available for Δ34S analyses (avg. 0.01 ± 0.13‰ (2SD)) verify no detectable sulfur isotope fractionation during extraction procedures (Fig. 3B). When replacing the nitrate/sulfate ratio with the anion equivalent concentration (i.e., the sum of nitrate concentration and two times of sulfate concentration) and still retaining the sulfate recovery as the Y-axis, we find that the data points show a decreasing trend following the same linear function (Fig. 3C). The operating exchange capacity can be defined as the maximum moles of exchanged anions per unit area of AEM piece at the maximum sulfate recovery,33 which is calculated from the anion equivalent concentration (=2.88 mmol L−1) at which the fitting line extends upward to 90% of sulfate recovery. According to this, the operating exchange capacity of the AEM used here is of 4.8 μmol cm−2 (=2.88 mmol L−1 × 10 mL/6 cm2). Conversely, the anion equivalent concentration at the lower intercept of the fitting line at the zero recovery of sulfate represents the total exchange capacity,34 whose value is 38.7 μmol cm−2 (= 23.23 mmol L−1 × 10 mL/6 cm2).
| Atomic NO3−/SO42− | NO3−/mmol L−1 | Recoverya/% | Δ 34Sb/‰ |
|---|---|---|---|
| a The volumes of uploading and eluting solutions are both 10 mL. b The calculated internal uncertainties are given as 2SE. n.d. = not detected. | |||
| 0.03 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.012 | 93.3 | n.d. |
| 1 | 0.03 | 92.4 | n.d. |
| 2 | 0.06 | 89.1 | n.d. |
| 4 | 0.12 | 92.8 | n.d. |
| 10 | 0.3 | 98.3 | n.d. |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 0.06 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.024 | 97.7 | n.d. |
| 1 | 0.06 | 93.7 | n.d. |
| 2 | 0.12 | 95.1 | n.d. |
| 4 | 0.24 | 93.0 | n.d. |
| 10 | 0.6 | 96.1 | n.d. |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 0.15 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.06 | 95.3 | +0.14 ± 0.06 |
| 1 | 0.15 | 87.5 | −0.02 ± 0.06 |
| 2 | 0.3 | 94.4 | +0.04 ± 0.05 |
| 4 | 0.6 | 91.8 | −0.01 ± 0.07 |
| 10 | 1.5 | 93.3 | −0.03 ± 0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 0.3 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.12 | 99.8 | −0.02 ± 0.07 |
| 1 | 0.3 | 86.9 | −0.06 ± 0.07 |
| 2 | 0.6 | 93.8 | +0.00 ± 0.06 |
| 4 | 1.2 | 91.9 | +0.07 ± 0.05 |
| 10 | 3 | 88.0 | +0.06 ± 0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 0.6 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.24 | 96.8 | +0.05 ± 0.05 |
| 1 | 0.6 | 87.4 | +0.03 ± 0.06 |
| 2 | 1.2 | 89.2 | +0.02 ± 0.06 |
| 4 | 2.4 | 85.2 | +0.06 ± 0.07 |
| 10 | 6 | 81.4 | +0.05 ± 0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 1.5 mmol L−1 of SO 4 2− | |||
| 0.4 | 0.6 | 86.4 | +0.03 ± 0.06 |
| 1 | 1.5 | 84.6 | −0.06 ± 0.07 |
| 2 | 3 | 74.3 | −0.03 ± 0.08 |
| 4 | 6 | 56.8 | −0.16 ± 0.05 |
| 10 | 15 | 22.7 | n.d. |
3.3 Lowest concentration tests of sulfate uploading
For different uploading concentrations of sulfate, the volumes of uploading and eluting solutions are changed to condense and recover the sufficient amount of sulfate for isotope analyses. Table 5 shows that almost all (> 97%) of the sulfate in uploading solutions can be extracted by AEM if its concentration is higher than 0.01 mmol L−1. Below this concentration threshold, the recoveries of sulfate decrease obviously (< 70%), which may result from deficient contact between the surface of the AEM piece and scarce sulfate ions in a large volume of diluted solution. However, considering the observed Δ34S values no higher than 0.15‰, a credible sulfur isotopic composition for trace sulfate samples (even down to 0.5 μmol L−1 of SO42−) can still be attained after condensing and extracting by AEM.4. Implications for geological applications
4.1 Sulfur isotope analyses of sulfate in natural freshwater
Sulfate in natural freshwater samples from river, lake, glacier, rainwater, groundwater, and soil-water typically keeps at low concentration levels though they often vary by large orders of magnitude from 10−1 to 105 μmol L−1.8,35–43 These freshwater reservoirs may play an important part in environmental sulfur cycles on account of their large volumes. So, it is quite essential for obtaining the accurate and precise sulfur isotopic composition of these freshwater sulfate.Conventionally, collecting and condensing sulfate is performed by column chromatography.2,4,19,24,44 However, for the samples in large volume with low sulfate concentration, this method becomes helpless and powerless.8,25 From our AEM tests above (see Section 3.3), the uploading concentration of sulfate can lower down to 0.5 μmol L−1 and there is negligible sulfur isotope fractionation during extraction procedures. Such concentration value is of the same magnitude as the minimum concentration of the freshwater sulfate. Meanwhile, the amount of competitive anions in natural freshwater samples (e.g., the concentrations of nitrate and chloride normally range from 0.03 to 6300 and 0.13 to 3500 μmol L−1, respectively37–43) would not have a greater impact on the sulfate recovery (see Section 3.2). Therefore, the AEM can provide an effective tool to extract sulfate from natural freshwater for accurate and precise δ34S analysis by MC-ICP-MS.
Three water samples from lake and surface runoff were taken as real applications here. These samples contain only trace amounts of sulfate (≤ 2 mmol L−1). As the major competitive anions, the concentrations of chloride and nitrate are lower than 2.5 mmol L−1 and 0.2 mmol L−1, respectively. In this case, the influence of their competitiveness on sulfate absorption can be ruled out. As shown in Table 6, over 95% of sulfate is extracted after AEM treatment and thus the reliable and accurate δ34S values can be obtained.
| Sample IDa | SO42−/mmol L−1 | Cl−/mmol L−1 | NO3−/mmol L−1 | Recovery/% | δ 34Sb/‰ VCDT |
|---|---|---|---|---|---|
| a Samples S1 and S2 are from the Lake Taihu, China. Sample S3 is from the surface runoff of Aksu region, Xinjiang, China. b The calculated internal uncertainties are given as 2SE. | |||||
| S1 | 1.92 | 2.23 | 0.01 | 100.0 | +1.75 ± 0.07 |
| S2 | 2.02 | 2.08 | 0.06 | 101.7 | +1.57 ± 0.07 |
| S3 | 1.05 | 1.24 | 0.19 | 96.5 | +9.06 ± 0.09 |
4.2 Sulfur isotope analyses of sulfate in marine pore water
The anoxic marine sediments are the largest reservoirs of methane at the global scale and the release of methane would have a dramatic impact on global climate changes, carbon cycles, and the partial pressure of methane in the atmosphere.45–47 However, about 90% of the produced methane has no chance to emit into seawater or air due to the consumption via aerobic oxidation of methane (AOM) before reaching the seafloor.48,49 This process often occurs at the base of the sulfate reduction zone where the concentration of sulfate left in pore water is typically less than 5 mmol L−1.50–52 Besides, the δ34S values of the remaining sulfate tend to the maximum since the pore water sulfate becomes more enriched in 34S as its concentration decreases with depth.53,54Considering that pore water samples have almost the same matrix ions (principally sodium) as seawater while the sulfate concentrations vary with depth, Bian et al.6 proposed a convenient method to determine δ34S values of sulfate in pore water by combining matrix-matching with concentration-matching by MC-ICP-MS. This method requires a 100-times dilution of pore water samples beforehand. In this case, the pore water sample initially containing 5 mmol L−1 of sulfate will be diluted to 0.05 mmol L−1. However, replicate δ34S analyses of 0.05 mmol L−1 of sulfate by MC-ICP-MS may generate a considerable uncertainty.7 This denotes that Bian et al.'s method falls ill with very low sulfate concentrations (< 5 mmol L−1) which may be relative to the process of AOM.
The diluted Atlantic seawater was applied to simulate the samples of marine pore water. For all samples diluted from 100 to 1000 times, the recoveries of sulfate maintain a high level of over 94% and those sulfur isotopic compositions show no difference from the mean δ34S value of seawater (ca. +21.0‰ VCDT55) (Table 7). Within this range of dilution factors, the concentration of sulfate is as low as 0.03 mmol L−1 and the concentration of competitive chloride is generally not higher than 6 mmol L−1 (i.e., 1 mmol per L per cm2 of AEM piece). Based on our AEM tests about the effect of anion competition (see Section 3.2), it will not bring a considerable influence on sulfate recovery. Thus, for the AOM-related pore water samples, the prior extraction of sulfate using AEM is highly recommended for accurate and precise δ34S analysis by MC-ICP-MS.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We appreciate the valuable suggestions from anonymous reviewers for their precious comments and suggestions, which significantly improved the manuscript. Thanks for Qiong Guo from School of the Environment, Nanjing University, who provided the natural freshwater samples from Lake Taihu. This study was supported by the Opening Foundation of the Key Laboratory of Marine Mineral Resources, Ministry of Land and Resources, China (Grant No. KLMMR-2017-B-04), the National Science and Technology Major Project of China (Grant No. 2016ZX05004-004), the National Natural Science Foundation of China (Grant No. 41806059), and the Fundamental Research Funds for the Central Universities (Grant No. 0206-14380044).References
- P. R. D. Mason, J. Košler, J. C. M. de Hoog, P. J. Sylvester and S. Meffan-Main, J. Anal. At. Spectrom., 2006, 21, 177–186 RSC.
- P. R. Craddock, O. J. Rouxel, L. A. Ball and W. Bach, Chem. Geol., 2008, 253, 102–113 CrossRef CAS.
- Z.-Y. Zhu, S.-Y. Jiang, C. L. Ciobanu, T. Yang and N. J. Cook, Chem. Geol., 2017, 450, 223–234 CrossRef CAS.
- G. Paris, A. L. Sessions, A. V. Subhas and J. F. Adkins, Chem. Geol., 2013, 345, 50–61 CrossRef CAS.
- A.-J. Lin, T. Yang and S.-Y. Jiang, Rapid Commun. Mass Spectrom., 2014, 28, 750–756 CrossRef CAS.
- X.-P. Bian, T. Yang, A.-J. Lin and S.-Y. Jiang, Talanta, 2015, 132, 8–14 CrossRef CAS.
- C. Liu, X.-P. Bian, T. Yang, A.-J. Lin and S.-Y. Jiang, Talanta, 2016, 151, 132–140 CrossRef CAS.
- O. Hanousek, T. W. Berger and T. Prohaska, Anal. Bioanal. Chem., 2016, 408, 399–407 CrossRef CAS.
- E. Albalat, P. Telouk, V. Balter, T. Fujii, V. P. Bondanese, M.-L. Plissonnier, V. Vlaeminck-Guillem, J. Baccheta, N. Thiam, P. Miossec, F. Zoulim, A. Puisieux and F. Albarède, J. Anal. At. Spectrom., 2016, 31, 1002–1011 RSC.
- P. Fritz, R. Drimmie and V. Nowicki, Anal. Chem., 1974, 46, 164–166 CrossRef CAS.
- B. W. Robinson and M. Kusakabe, Anal. Chem., 1975, 47, 1179–1181 CrossRef CAS.
- C. E. Rees, Geochim. Cosmochim. Acta, 1978, 42, 383–389 CrossRef CAS.
- A. Giesemann, H.-J. Jäger, A. Norman, H. Krouse and W. Brand, Anal. Chem., 1994, 66, 2816–2819 CrossRef CAS.
- N. V. Grassineau, D. P. Mattey and D. Lowry, Anal. Chem., 2001, 73, 220–225 CrossRef CAS.
- S. A. Studley, E. M. Ripley, E. R. Elswick, M. J. Dorais, J. Fong, D. Finkelstein and L. M. Pratt, Chem. Geol., 2002, 192, 141–148 CrossRef CAS.
- D. Xia, H. Ye, Y. Xie, C. Yang, M. Chen, Z. Dang, X. Yi and G. Lu, RSC Adv., 2017, 7, 43310–43318 RSC.
- B. Fry, S. R. Silva, C. Kendall and R. K. Anderson, Rapid Commun. Mass Spectrom., 2002, 16, 854–858 CrossRef CAS PubMed.
- A. W. Cheesman, B. L. Turner and K. R. Reddy, Soil Sci. Soc. Am. J., 2010, 74, 1607–1612 CrossRef CAS.
- I. Akira, Bull. Chem. Soc. Jpn., 1958, 31, 600–605 CrossRef.
- L. E. Smythe and R. N. Whittem, Analyst, 1961, 86, 83–94 RSC.
- R. Self, Biomed. Mass Spectrom., 1979, 6, 361–373 CrossRef CAS.
- A. Götz and K. G. Heumann, Int. J. Mass Spectrom. Ion Processes, 1988, 83, 319–330 CrossRef.
- J. B. Finley, J. I. Drever and J. T. Turk, Water, Air, Soil Pollut., 1995, 79, 227–241 CrossRef CAS.
- A. Das, C.-H. Chung, C.-F. You and M.-L. Shen, J. Anal. At. Spectrom., 2012, 27, 2088–2093 RSC.
- J.-S. Kwon, B. Mayer, S.-T. Yun and M. Nightingale, J. Environ. Qual., 2008, 37, 501–508 CrossRef CAS.
- W. M. H. Saunders, N. Z. J. Agric. Res., 1964, 7, 427–431 CrossRef CAS.
- P. Qian, J. J. Schoenau and W. Z. Huang, Commun. Soil Sci. Plant Anal., 1992, 23, 1791–1804 CrossRef CAS.
- M. J. McLaughlin, P. A. Lancaster, P. W. G. Sale, N. C. Uren and K. I. Peverill, Plant Soil, 1993, 155, 223–226 CrossRef.
- L. R. Cooperband and T. J. Logan, Soil Sci. Soc. Am. J., 1994, 58, 105–114 CrossRef CAS.
- R. G. Myers, S. J. Thien and G. M. Pierzynski, Soil Sci. Soc. Am. J., 1999, 63, 1229–1237 CrossRef CAS.
- C. Paton, J. Hellstrom, B. Paul, J. Woodhead and J. Hergt, J. Anal. At. Spectrom., 2011, 26, 2508–2518 RSC.
- C. E. Harland, Ion Exchange: Theory and Practice, Royal Society of Chemistry, 2007 Search PubMed.
- S. Li, Y. Qiu and X. Guo, J. Appl. Polym. Sci., 2009, 114, 2307–2314 CrossRef CAS.
- V. J. Inglezakis and H. P. Grigoropoulou, Microporous Mesoporous Mater., 2003, 61, 273–282 CrossRef CAS.
- D. R. Lovley and M. J. Klug, Appl. Environ. Microbiol., 1983, 45, 187–192 CAS.
- A. Döscher, H. W. Gäggeler, U. Schotterer and M. Schwikowski, Water, Air, Soil Pollut., 1995, 85, 603–609 CrossRef.
- A. Abdelouas, W. Lutze, W. Gong, E. H. Nuttall, B. A. Strietelmeier and B. J. Travis, Sci. Total Environ., 2000, 250, 21–35 CrossRef CAS.
- A. I. López-Archilla, I. Marin and R. Amils, Microb. Ecol., 2001, 41, 20–35 Search PubMed.
- J. Chen, F. Wang, X. Xia and L. Zhang, Chem. Geol., 2002, 187, 231–255 CrossRef CAS.
- G. P. Hu, R. Balasubramanian and C. D. Wu, Chemosphere, 2003, 51, 747–755 CrossRef CAS.
- M. Zunckel, C. Saizar and J. Zarauz, Atmos. Environ., 2003, 37, 1601–1611 CrossRef CAS.
- N. Neubert, A. R. Heri, A. R. Voegelin, T. F. Nägler, F. Schlunegger and I. M. Villa, Earth Planet. Sci. Lett., 2011, 304, 180–190 CrossRef CAS.
- U. Özkan and F. Gökbulak, Catena, 2017, 149, 158–166 CrossRef.
- E. Le Gendre, E. Martin, B. Villemant, P. Cartigny and N. Assayag, Rapid Commun. Mass Spectrom., 2017, 31, 137–144 CrossRef CAS.
- J. P. Kennett, Methane Hydrates in Quaternary Climate Change: The Clathrate Gun Hypothesis, American Geophysical Union, 2003 Search PubMed.
- A. V. Milkov, Earth-Sci. Rev., 2004, 66, 183–197 CrossRef CAS.
- V. Krey, J. G. Canadell, N. Nakicenovic, Y. Abe, H. Andruleit, D. Archer, A. Grubler, N. T. M. Hamilton, A. Johnson, V. Kostov, J.-F. Lamarque, N. Langhorne, E. G. Nisbet, B. O'Neill, K. Riahi, M. Riedel, W. Wang and V. Yakushev, Environ. Res. Lett., 2009, 4, 034007 CrossRef.
- K. Knittel and A. Boetius, Annu. Rev. Microbiol., 2009, 63, 311–334 CrossRef CAS.
- P. Regnier, A. W. Dale, S. Arndt, D. E. LaRowe, J. Mogollón and P. Van Cappellen, Earth-Sci. Rev., 2011, 106, 105–130 CrossRef CAS.
- B. B. Jørgensen, A. Weber and J. Zopfi, Deep Sea Res., Part I, 2001, 48, 2097–2120 CrossRef.
- W. S. Borowski, in Proc. ODP, Sci. Results, ed. A. M. Tréhu, G. Bohrmann, M. E. Torres and F. S. Colwell, Ocean Drilling Program, College Station, TX, 2006, vol. 204, ch. 19, pp. 1–13 Search PubMed.
- P. Meister, B. Liu, T. G. Ferdelman, B. B. Jørgensen and A. Khalili, Geochim. Cosmochim. Acta, 2013, 104, 183–193 CrossRef CAS.
- B. B. Jørgensen, M. E. Böttcher, H. Lüschen, L. N. Neretin and I. I. Volkov, Geochim. Cosmochim. Acta, 2004, 68, 2095–2118 CrossRef.
- W. S. Borowski, N. M. Rodriguez, C. K. Paull and W. Ussler III, Mar. Pet. Geol., 2013, 43, 381–395 CrossRef CAS.
- C. E. Rees, W. J. Jenkins and J. Monster, Geochim. Cosmochim. Acta, 1978, 42, 377–381 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |