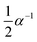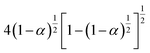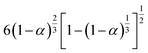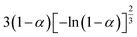Open Access Article
Open Access ArticleMultistage kinetic analysis of DMAA/MBAM polymer removal from gelcast ceramic parts using a multi-stage parallel reaction model and model-free method
Jing Li ab,
Jindi Huang
ab,
Jindi Huang *a and
Ruiming Yinc
*a and
Ruiming Yinc
aSchool of Energy and Mechanical Engineering, Jiangxi University of Science and Technology, Nanchang, 330013, P. R. China. E-mail: hjd041@163.com
bSchool of Metallurgy and Environment, Central South University, Changsha, 410083, P. R. China
cCollege of Metallurgical Engineering, Hunan University of Technology, Zhuzhou, 412008, P. R. China
First published on 30th August 2019
Abstract
This work aims to develop an effective method for investigating the multistage debinding kinetics and reaction mechanisms of removing N,N-dimethylacrylamide/N,N′-methylenebisacrylamide (DMAA/MBAM) polymer from gelcast ceramic parts. Thermogravimetry (TG) and pyrolysis-gas chromatography/mass spectrometry (Py-GC/MS) experiments were performed to investigate the thermal degradation characteristics and the main compounds produced during the pyrolysis of DMAA/MBAM polymer within green components. A multi-stage parallel reaction model (M-PRM) was proposed to separate the overlapping peaks in the dα/dT curves. The kinetic parameters (activation energy E and pre-exponential factor k0) of each substage were calculated using model-free methods (Flynn–Wall–Ozawa, Starink, Friedman and Kissinger–Akahira–Sunose) and an activation energy variable model. In addition, the most appropriate kinetic mechanism function f(α) of each substage was analyzed and discussed via Málek's procedure and the Šesták–Berggren (SB) model. The results showed that the DMAA/MBAM polymer burnout in green components can be divided into three substages through a three-stage parallel reaction model (3-PRM). The values of E (Friedman method) for substages 1 to 3 were E(α) = 139.862 − 110.481α + 156.161α2 − 88.714α3 kJ mol−1, E(α) = 160.791 + 152.496α − 236.906α2 + 163.724α3 kJ mol−1 and E(α) = 72.132 + 452.830α − 669.039α2 + 507.015α3 kJ mol−1, respectively. The average values of E showed an increasing tendency from substages 1 to 3, and a kinetic compensation effect was also observed between the E and k0 in each substage. The kinetic mechanism analysis revealed that the reaction mechanisms for substages 1 to 3 were f(α) = (1 − α)0.668α3.049(−ln(1 − α))−3.874, f(α) = (1 − α)0.700α3.177(−ln(1 − α))−3.962 and f(α) = (1 − α)1.049α−0.161(−ln(1 − α))0.518, respectively. It is expected that the research results can be extended to investigate the multiplex debinding of binders or polymers for various colloidal molding techniques.
1 Introduction
Gelcasting is an emerging colloidal molding technology for near-net shaping of ceramic parts.1–3 This technique ingeniously utilizes the in situ polymerization of the gel system to form a three-dimensional network to enwrap and immobilize ceramic particles, allowing them to keep the desired shape of green bodies.4 The gelcasting processing mainly consists of four steps: preparation of ceramic slurries with low viscosity and high solids content, injection of slurries into the mold, demolding and drying, and debinding and sintering. The development of a reasonable debinding process, which is a critical step in the gelcasting process, is essential for obtaining compact and defect-free sintered bodies.5,6 At present, the main methods for removing polymer or binder are classified into four categories: catalytic debinding,7 solvent debinding,8,9 thermal debinding10,11 and wicking debinding.12 For gelcasting, the organic polymer formed by the polymerization of the monomer is insoluble in the solvent and does not melt; thus, it cannot be removed by processes such as wicking debinding and solvent debinding. The related reports mainly use the thermal debinding technique.13–15Removing gel from gelcast green components is a complex process involving various physical and chemical reactions, such as the diffusion of residual moisture, the degradation reaction of the polymer, mass transfer and heat transfer in porous media and evolution of stress and strain,16,17 as shown in Fig. 1. If the gel is not completely removed, then the polymeric residues will be passed to the next process, influencing the final properties of the sintered bodies. If the gel is removed too quickly, defects such as voids and cracks may form, and these defects will also be passed to the next process, further affecting the microstructure of the ceramic parts during sintering. These effects are signs that the key to thermal debinding is successfully controlling the degradation of the polymer while ensuring complete removal without introducing defects in the green parts. Accordingly, systematic research on debinding kinetics is necessary. At present, single-step reaction models such as the Kissinger,18 Ozawa,18 Coats–Redfern integration14 and model-free19 methods have been used to estimate thermal debinding kinetic parameters such as activation energy and pre-exponential factor. However, the rate control mechanism of the binder or polymer pyrolysis during thermal debinding has not been reported. Shi et al.17 assumed that the burnout of the polymeric binder is controlled by diffusion reactions and proposed a diffusion-controlled model for predicting the debinding kinetics of binder within powder compacts. It is known that different polymers have different thermal stabilities and may be controlled by multiple reaction mechanisms. Usually, it is difficult to accurately describe kinetic behavior with complex variations in apparent activation energy caused by changes in the reaction mechanism via a single-step reaction model.20 Therefore, understanding the reaction mechanism and determining the limiting step of the thermal debinding process can provide a fundamental theoretical basis for obtaining more accurate kinetic parameters.
Currently, as a low-toxicity monomer, DMAA has attracted great interest for gelcasting various ceramic materials with low gel concentrations (e.g., porous Si3N4 ceramics,2 ZTA composites,21 ZrO2,22 SiO2,23 Al2O3,1,24 AlN25); however, very limited research on its debinding behavior and reaction mechanisms has been conducted. In contrast, many investigations have concentrated on the thermal stability of DMAA/MBAM polymer through experimental thermogravimetric (TG) analysis.21,26 In an earlier work, we developed a three-parallel-distributed activation energy model to predict debinding behavior and estimate kinetic parameters.27 The reported theoretical predictions of pyrolysis kinetics of DMAA/MBAM polymer agree well with experimental findings. However, explicit debinding mechanisms, which are extremely important for determining the controlling mechanisms of mass transport in the green components during the overall debinding process, have not been revealed.
The present study is intended to seek an effective method of investigating the multistage debinding kinetics and reaction mechanisms of DMAA/MBAM polymer pyrolysis in gelcast ceramic parts. The main purpose is to obtain insight into the multiple debinding mechanisms to provide useful and reliable theoretical support for the design and optimization of multistep thermal debinding technology. The thermal degradation characteristics of DMAA/MBAM polymer within green parts were investigated by thermogravimetry experiments, and the main compounds in the fast pyrolysis of DMAA/MBAM polymer were identified by pyrolysis-gas chromatography/mass spectrometry (Py-GC/MS). A multi-stage parallel reaction model (M-PRM) was proposed to analyze and separate the overlapping peaks in dα/dT curves. The kinetic parameters of each substage were calculated using model-free methods. In addition, the most appropriate kinetic mechanism function of each substage was analyzed and discussed via Málek's procedure and the Šesták–Berggren (SB) model.
2 Experimental methods
2.1 Raw materials
For gelcasting, a low toxicity aqueous gel system using DMAA (Kowa Co., Ltd., Japan) and MBAM (Aladdin Industrial Co., Ltd., China) as the monomer and crosslinker, respectively, was used for polymerization. Ammonium polyacrylate (NH4PAA, Shenzhen Highrun Chemical Industry Co. Ltd., China), (NH4)2S2O8 (APS) and N,N,N′,N′-tetramethylethylene-diamine (TEMED, Aladdin Industrial Co., Ltd., China) were used as dispersant, initiator and catalyst, respectively, according to the approach reported in our previous work.27,28Y-α-SiAlON, with a composition of Y0.5Si9.75Al2.25O0.75N15.25 (m = 1.5, n = 0.75), was selected for investigation. Additional amounts of 3 wt% Y2O3 and 6 wt% Ce2O3 were used to promote sintering densification. The raw materials were α-Si3N4 (SN-E10, UBE Industries, Ube, Japan), AlN (d = 2.0 μm, purity of 99.9%, Aladdin Industrial Co., Ltd., China), Al2O3 (d = 0.5 μm, purity of 99.9%, AKP-50, Sumitomo Chemical, Japan), Y2O3 (grade fine, purity of 99.9%, H.C. Stark, Germany) and Ce2O3 (d = 5 μm, purity of 99.9%, Aladdin Industrial Co., Ltd., China). To avoid the flocculation of the suspension caused by the hydrolysis reaction of AlN powder in aqueous solution, thermal oxidation treatment was used to obtain AlN with a modified surface (called M-AlN) to obtain hydrolytic resistance, following the approach reported by Li et al.29
2.2 Green body preparation
The gelcasting process of a green body includes the following steps. (1) The premixed solution is prepared by dissolving DMAA, MBAM (DMAA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MBAM = 16
MBAM = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, DMAA + MBAM = 12.4 wt%) and NH4PAA (1.0 wt%) in deionized water. The pH value of the premixed solution was adjusted to approximately 11 by NH3·H2O. (2) The suspensions are prepared by adding mixture powders into the premixed solution. The solid loading of the suspensions was 40 vol%. To increase the dispersion uniformity of the slurry, the Si3N4, Al2O3, Y2O3 and Ce2O3 were first added to the slurry under constant stirring and ball milled for 3 h in a planetary mill using ZrO2 balls. The rotating rate was 255 rpm, and the weight ratio of ball-to-powder-to water was 1.9
1, DMAA + MBAM = 12.4 wt%) and NH4PAA (1.0 wt%) in deionized water. The pH value of the premixed solution was adjusted to approximately 11 by NH3·H2O. (2) The suspensions are prepared by adding mixture powders into the premixed solution. The solid loading of the suspensions was 40 vol%. To increase the dispersion uniformity of the slurry, the Si3N4, Al2O3, Y2O3 and Ce2O3 were first added to the slurry under constant stirring and ball milled for 3 h in a planetary mill using ZrO2 balls. The rotating rate was 255 rpm, and the weight ratio of ball-to-powder-to water was 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4. Then, M-AlN was added, and the planetary mill was run without ZrO2 balls for 30 min to prevent the wear of the dense alumina film of M-AlN flowed by degassing for 30 min. (3) The gelation process of the slurry proceeded by adding 1.0 wt% initiator and catalyst. The suspensions were cast into a cylindrical mold (∅ 35 mm × 25 mm) and then cured at room temperature until the DMAA and MBAM were fully polymerized. Then, they were demolded in a drying oven at 60 °C for 24 h. (4) The drying process is performed. The demolded wet ceramic parts were moved to a temperature and humidity test chamber and dried under controlled temperature and humidity conditions to avoid cracking and uneven shrinkage of the body due to the rapid evaporation of water. Then, the green bodies were obtained for subsequent thermal analysis.
0.4. Then, M-AlN was added, and the planetary mill was run without ZrO2 balls for 30 min to prevent the wear of the dense alumina film of M-AlN flowed by degassing for 30 min. (3) The gelation process of the slurry proceeded by adding 1.0 wt% initiator and catalyst. The suspensions were cast into a cylindrical mold (∅ 35 mm × 25 mm) and then cured at room temperature until the DMAA and MBAM were fully polymerized. Then, they were demolded in a drying oven at 60 °C for 24 h. (4) The drying process is performed. The demolded wet ceramic parts were moved to a temperature and humidity test chamber and dried under controlled temperature and humidity conditions to avoid cracking and uneven shrinkage of the body due to the rapid evaporation of water. Then, the green bodies were obtained for subsequent thermal analysis.
2.3 TG analysis
The green body sample was grinded to pass through a 100-mesh sieve for the nonisothermal TG experiment. The TG analysis of the green body was performed using a thermo gravimetric analyzer (STA-449 F3 Jupiter, NETZSCH, Germany) at heating rates of 2.5, 5, 10, 15, and 20 °C min−1. In the experiment, approximately 14 ± 0.5 mg of sample was placed on the crucible of the thermal analyzer. The temperature range was 35–900 °C. Pure Argon (>99.999%), and a flowrate of 40 ml min−1 was applied for all experiments.2.4 Py-GC/MS analysis
The pyrolysis mechanism of the DMAA/MBAM polymer was investigated by analytical Py-GC/MS (Shimadzu QP2010 GCMS-EGA FRONTERE3030D PY). The pyrolysis temperatures were set to 240, 385 and 450 °C for 90 s; then, the pyrolysis gases were introduced into the GC/MS via a transfer line for on-line analysis. The temperature program for GC is as follows: the oven was heated from 200 °C (isothermal for 3 min) to 240 °C (isotherm for 15 min) at a heating rate of 5 °C min−1; pure Ar (99.999%) was used as the carrier gas at a flow rate of 1.0 ml min−1; and the split ratio was 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The MS conditions were as follows: the ion source was EI mode (70 eV) with a temperature of 200 °C, and the mass was scanned from m/z 2 to 600 amu. The chromatographic peaks were identified based on the NIST mass spectra library.
1. The MS conditions were as follows: the ion source was EI mode (70 eV) with a temperature of 200 °C, and the mass was scanned from m/z 2 to 600 amu. The chromatographic peaks were identified based on the NIST mass spectra library.
3 Kinetic modeling
The primary purpose for investigating the pyrolysis kinetics is to obtain the multiplex debinding mechanisms of the DMAA/MBAM polymer and further to predict the entire pyrolysis process. In this study, the kinetic parameters (activation energy E and pre-exponential factor k0) and reaction mechanisms are estimated by following various kinetic models. The flow diagram of the DMAA/MBAM polymer pyrolysis kinetic analysis is shown in Fig. 2.3.1 Theory of kinetic triplets
The decomposition rate (dα/dt) of the DMAA/MBAM polymer for nonisothermal reactions is expressed by the following equation:
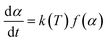 | (1) |
| α = (m0 − mt)/(m0 − m∞) | (2) |
k(T) = k0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/RT) exp(−E/RT)
| (3) |
The nonisothermal kinetic equation can be expressed as follows:
 | (4) |
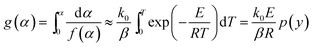 | (5) |
 | (6) |
3.2 Theory of model-free methods
In thermal degradation kinetic analysis, model-free methods can be used to obtain the activation energy for any reaction progress without considering reaction mechanism.19,30 In this study, four commonly used model-free methods, namely, the Flynn–Wall–Ozawa (FWO), Starink, Friedman and Kissinger–Akahira–Sunose (KAS) methods, are used to study the pyrolysis process of the DMAA/MBAM polymer during debinding.The FWO method is established based on Doyle's approximation.31 After rearranging and taking the common logarithm, Doyle's approximation equation, that is, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(y) = −5.331 − 1.052y, is substituted into eqn (5), and the following linear relationship is obtained:
p(y) = −5.331 − 1.052y, is substituted into eqn (5), and the following linear relationship is obtained:
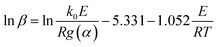 | (7) |
 .
.
The Starink method32,33 is considered to have the highest accuracy, and its equation is expressed as:
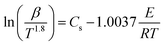 | (8) |
For the same value of α of the DMAA/MBAM polymer at different heating rates, ln(β) is plotted vs. 1/T for the FWO method, and ln(β/T1.8) is plotted vs. 1/T for the Starink method. The values of E are estimated from the slope of the regression lines.
The KAS method uses the Coats–Redfern approximation, which is p(y) = exp(−y)/y2, therefore, eqn (5) is rearranged as 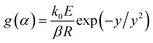 . Then, the logarithm of both sides of the rearranged equation is taken; thus, the mathematical expression is proposed as:34
. Then, the logarithm of both sides of the rearranged equation is taken; thus, the mathematical expression is proposed as:34
 | (9) |
Under isoconversional conditions, ln(β/T2) is plotted vs. 1/T, and the apparent activation energy E can be determined according to the slopes of the regression lines of −E/R at different heating rates.
The differential Friedman approach has recently been considered the most accurate method, and is established without approximation algorithms.19 The equation is expressed as:
 | (10) |
If the regression lines of  vs. 1/T for the Friedman method are plotted, then the apparent activation energy E can be determined according to the slopes of the regression lines at different heating rates.
vs. 1/T for the Friedman method are plotted, then the apparent activation energy E can be determined according to the slopes of the regression lines at different heating rates.
3.3 Model-fitting method
dαi/dT = k0,i/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ei/RT)fi(αi) exp(−Ei/RT)fi(αi)
| (11) |
The weighted factor of parallel reaction stage i is calculated by eqn (12):
 | (12) |
Then, α and E for the overall pyrolysis reaction process can be written as:
 | (13) |
 | (14) |
M-PRM uses a multipeak fitting method to separate the overlapping peaks in the reaction rate (dα/dT) or differential thermogravimetric (DTG) curve. In this study, the Gaussian distribution function eqn (15) is used to fit the dα/dT curve. The Levenberg–Marquardt algorithm is used for curve fitting.
 | (15) |
 | (16) |
After taking the common logarithm, the eqn (16) can be written as:
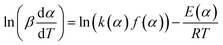 | (17) |
 vs. 1/T can be plotted at the same fractional extent of conversion α from a series of non-isothermal thermogravimetric experiments at different heating rates. The activation energy E(α) can be estimated from the slope of the regression lines of
vs. 1/T can be plotted at the same fractional extent of conversion α from a series of non-isothermal thermogravimetric experiments at different heating rates. The activation energy E(α) can be estimated from the slope of the regression lines of 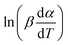 vs. 1/T. On this basis, the model parameters (p5, p6, p7 and p8) can be obtained by polynomial regression fitting.
vs. 1/T. On this basis, the model parameters (p5, p6, p7 and p8) can be obtained by polynomial regression fitting.
Based on the data of f(α), E(α), dα/dt, T and α, the unknown model parameters (p1, p2, p3 and p4) can be obtained by minimizing the objective function (OF) using the generalized reduced gradient (GRG) method in Microsoft Excel Solver.36
 | (18) |
3.4 Determination of the mechanism function
 | (19) |
The most appropriate kinetic mechanism function f(α) is deduced from the theoretical curve of y(α).
Arbitrarily, αi, y(αi) (i = 1, 2, …, j) and α = 0.5, y(0.5) are substituted into the following equation, and the theoretical master plot f(α)G(α)/f(0.5)G(0.5) vs. α can be obtained.
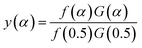 | (20) |
Substituting, αi, Ti, (dα/dt)i (i = 1, 2, …, j) and α = 0.5, T0.5, (dα/dt)0.5 into eqn (19) provides the experimental master plot of (T/T0.5)2(dα/dt)/(dα/dt)0.5 vs. α.
 | (21) |
If the experimental plot overlaps with the theoretical plot or if the experimental data points all fall on a certain theoretical plot, then the chosen f(α) can be considered to be the most likely kinetic mechanism function. The common functions of the kinetic mechanism for f(α) and G(α) are summarized in Table 1.20,33
| f(α) = (1 − α)nαm[−ln(1 − α)]p | (22) |
Based on the data of dα/dt, T and α, the unknown model parameters (m, n and p) can be obtained by minimizing the objective function (OF) using the generalized reduced gradient (GRG) method in Microsoft Excel Solver.36
| OF = ∑[y(α)exp − y(α)pred]2 | (23) |
4 Results and discussion
4.1 TG and Py-GC/MS analysis
Fig. 3 shows the TG and DTG curves of the DMAA/MBAM polymer in the gelcast green bodies obtained at 2.5, 5, 15 and 20 °C min−1. As illustrated in Fig. 3, it can be seen that both TG and DTG curves show similar trends for all heating rates. From the TG curves in Fig. 3, a small mass loss is found at a temperature below 200 °C, which should correspond to the removal of residual moisture (free/bound water) absorption in the polymer. The large mass loss in the temperature range of 200–900 °C correspond to the main pyrolysis stage of the DMAA/MBAM polymer, where large amounts of light gases were given off. Additionally, the thermal degradation of the DMAA/MBAM copolymer mainly occurs in two temperature ranges: 200–300 °C and 300–600 °C. As shown in the DTG curves in Fig. 3, two strong peaks were observed and the peak maximum temperatures for DMAA/MBAM polymer degradation at heating rates of 2.5, 5, 15 and 20 °C min−1 are presented in Table 2. From Table 2, the maximum loss rate (temperature of peak 2) for DMAA/MBAM polymer pyrolysis occurred at 399 °C, 401 °C, 405 °C and 411 °C at the heating rates of 2.5, 5, 15 and 20 °C min−1, respectively.| Heating rate (°C min−1) | 2.5 | 5 | 15 | 20 |
|---|---|---|---|---|
| Peak 1 (°C) | 210 | 212 | 220 | 268 |
| Peak 2 (°C) | 399 | 401 | 405 | 411 |
| Height (peak 1) (%/°C) | 0.05 | 0.07 | 0.15 | 0.73 |
| Height (peak 2) (%/°C) | 0.08 | 0.28 | 1.23 | 1.66 |
| Maximum mass loss (%) | 9.79 | 9.32 | 8.42 | 9.21 |
However, both TG and DTG curves presented some differences with an increase in the heating rates. As shown in TG curves, the mass loss of the sample decreased slightly with an increase in the heating rate at a temperature below 420 °C. Here, taking 2.5 °C min−1 as an example, approximately 76.5 wt% polymer in the sample was burnt out, and the mass loss of is approximately 7.5%. But there is no obvious trend of the ultimate maximum mass loss with an increase the heating rate in the temperature range of 420–900 °C. As shown in Table 2, the ultimate mass loss observed at 900 °C for heating rate of 2.5, 5, 15 and 20 °C min−1 are 9.79%, 9.32%, 8.42% and 9.21%, respectively. The reasons for this phenomenon might be attributed to the following two points: (1) the sample is more susceptible to cracking at high heating rates, leading to the pyrolysis gas of the polymer to be released more quickly, which may not occur at a lower heating rate. (2) When the heating rates are increased, the partial polymer cannot adequately rapidly pyrolyze and release their volatiles, thereby resulting in hysteresis. Moreover, as seen from Fig. 3, the DTG curves are offset to a high temperature area with an increase in the heating rate, and the degradation temperature was delayed as the heating rate increased. This phenomenon should be due to the fact that more thermal energy was provided for the pyrolysis at the higher heating rate.
The types of gas products and their proportions (in terms of the percentage peak area) during the thermal degradation process of DMAA/MBAM copolymer are identified by Py-GC/MS at different temperatures (240, 385 and 450 °C). The total ion count (TIC) of the main compounds resulting from polymer degradation are presented in Fig. 4 and Table 3. As shown in Fig. 4 and Table 3, the main chemical compositions of the products of gel pyrolysis are the amides and ammonia species with carbon numbers ranging from C3–C12. Moreover, cyclohexane and cyclohexylamine species, which were the main ring compounds, were mainly detected at 380 °C and 450 °C, whereas ring compounds were scarce at the final pyrolysis temperature of 240 °C. The high temperature leads to a remarkable increase in the characteristic compounds (N,N-dimethyl-2-propenamide and trimethylamine, etc.) and cyclic compounds (cyclohexane-1,4-cis-dicarboxamide and N-methyl-n-propyl-cyclohexanamine, etc.). When the pyrolysis temperature increases from 240 °C to 450 °C, the relative content of N,N-dimethyl-2-propenamide (DMAA monomer) increases from 19.9% to 26.30%, and the relative content of cyclohexane-1,4-cis-dicarboxamide can reach 16.98%. This finding is because more energy is provided to the pyrolysis reaction at a higher temperature, which promotes the breakage of carbon chains in the long chain and the ring opening in the side chain. Therefore, the thermal degradation mechanism of the DMAA/MBAM polymer is mainly divided into two types: depolymerization reactions and random cleavage reactions. The former starts from the chain terminal or weak bonds in the molecule. Once free radical molecules are formed, the C–H and C–O bonds on the adjacent carbon atom are liable to cleavage, thereby causing a chain reaction of monomer loss; the latter is mainly the breakage of the main chain, side groups and end groups occurring inter- or intramolecularly.
 | ||
| Fig. 4 Details of GC-MS chromatograms with the main identified compounds in the fast pyrolysis of DMAA/MBAM polymer at different final pyrolysis temperatures. (a) 240 °C, (b) 385 °C and (c) 450 °C. | ||
| No. | Compound | Formula | Molar mass | CAS no. | Relative content/area% |
|---|---|---|---|---|---|
| 1 | Trimethylamine | C3H9N | 59 | 75-50-3 | 17.46 |
| 2 | 2,4-Pentanedia-mine, 2-methyl- | C6H16N2 | 116 | 21586-21-0 | 7.48 |
| 3 | 2-Propanone, 1-(dimethylamino)- | C5H11NO | 101 | 15364-56-4 | 0.47 |
| 4 | Formamide, N,N-dimethyl- | C3H7NO | 73 | 68-12-2 | 1.06 |
| 5 | Acetamide, N,N-dimethyl- | C4H9NO | 87 | 127-19-5 | 1.86 |
| 6 | 2-Propenamide, N,N-dimethyl- | C5H9NO | 99 | 2680-03-7 | 26.3 |
| 7 | 2,3-Dimethyl-4-hydroxy-2-butenoic lactone | C6H8O2 | 112 | 1575-46-8 | 0.48 |
| 8 | 5-Amino-1,3-dimethylpyra-zole | C5H9N3 | 111 | 3524-32-1 | 0.69 |
| 9 | 2H-Azepin-2-one, 1,5,6,7-tetrahydro | C6H9NO | 111 | 2228-79-7 | 1.20 |
| 10 | N,N-Dimethyl cyanoacetamide | C5H8N2O | 112 | 7391-40-4 | 0.41 |
| 11 | Cyclopentane-cis-1,3-dicarboxamide | C7H12N2O2 | 156 | 0-00-0 | 0.31 |
| 13 | Octanamide, N,N-dimethyl- | C10H21NO | 171 | 1118-92-9 | 1.51 |
| 14 | Octahydro-2H-pyrido(1,2-a)pyrimidin | C8H14N2O | 154 | 24025-00-1 | 6.8 |
| 17 | 4-Cyclopentene-1,3-dione, 4-propyl | C8H10O2 | 138 | 58940-74-2 | 0.33 |
| 18 | Cyclohexanecarboxa-mide, N,N-dimethyl-2-oxo- | C9H15NO2 | 169 | 52631-32-0 | 0.68 |
| 21 | 7-Octynamide, N,N-dimethyl- | C10H17NO | 167 | 35066-53-6 | 0.29 |
| 12, 24 | Cyclopentane-trans-1,3-dicarboxamide | C11H20N2O2 | 212 | 59219-51-1 | 4.16 |
| 15, 19, 20 | N,N-Dimethylheptanamide | C9H19NO | 157 | 1115-96-4 | 11.05 |
| 16, 22, 23, 26, 27, 28 | Cyclohexane-1,4-cis-dicarboxamide | C12H22N2O2 | 226 | 35541-94-7 | 16.98 |
4.2 Traditional overall thermal debinding kinetics analysis
The model-free method, also known as the isoconversion method, was used to estimate the thermal debinding kinetics of the DMAA/MBAM polymer for gelcast ceramic parts at heating rates of 2.5, 5, 15 and 20 °C min−1. Fig. 5 illustrates the relationship between E and α (range from 0.025 to 0.975) during the overall debinding process obtained from the FWO, KAS, Friedman and Starink methods. As shown in Fig. 5, the correlation coefficients (R2) of the linear fits for the four methods are all greater than 0.91 in the conversion range from 0.05–0.7, but the R2 values are very low in the conversion range below 0.05 and above 0.7. Therefore, the estimated E values at these conversion ranges were inaccurate. This situation may be caused the high heterogeneous characters, which are the comprehensive effects of the secondary or autocatalytic reactions, diffusion, etc. Moreover, the changing trend in activation energies obtained by different methods is consistent, but there are obvious fluctuations in values. As the pyrolysis continued, the apparent activation energy in each stage increases at first, then decreases and subsequently increases in the conversion range from 0.05–0.7. The apparent activation energy ranges for the FWO, KAS, Friedman and Starink methods are 221.49–327.56, 222.22–333.27, 121.75–490.08 and 222.47–333.17 kJ mol−1, respectively. The large variation in E indicates that the thermal degradation of DMAA/MBAM copolymer has multiple complex reaction mechanisms during debinding. | ||
| Fig. 5 E and R2 of the pyrolysis of DMAA/MBAM polymer obtained by the FWO, KAS, Friedman and Starink methods. | ||
It has been shown that the activation energies calculated by the FWO, Starink, Friedman and KAS methods usually differ from each other due to their intrinsic nature.19,39 The FWO, KAS and Starink methods are based on different approximation algorithms of the temperature integral, which are obtained under the assumption that the activation energy is independent of conversion under isoconversional conditions. Hence, the errors associated with kinetic measurements from the three methods should be dependent on the magnitude of the variation of the activation energy with respect to conversion.19 Obviously, this situation is not applicable to multistep processes in this study, and a systematic error may be introduced, particularly for the FWO integral method,40 which is consistent with the solution results in this work. For the Friedman method, it is established without approximation algorithms, but tends to be more sensitive to experimental noise.41
4.3 Multipeak fitting result analysis
M-PRM is used to separate the overlapping peaks in dα/dT curves. Fig. 6 gives the fitting results of the subpeaks corresponding to the substages of the debinding process. As shown in Fig. 6a–d, the total thermal debinding process is a weighted composition of the pyrolysis reactions of three pseudocomponents. The three subpeaks exhibit consistent distribution characteristics at different heating rates. Among the three subpeaks, peak 3 has the widest distribution, while peaks 1 and 2 present narrow distributions, indicating that the pyrolysis of pseudo component 3 is the strongest pyrolysis stage. In substage 1, weak bonds (such as C–O, C–N) in the polymer side chains break to form characteristic compounds such as ammonia and amines, as shown in Fig. 4. As the temperature increases, cyclization conditions are generated intramolecularly. In addition to the abovementioned characteristic compounds, cyclic compounds such as cyclohexane and cyclohexylamine are cleaved from the macromolecular chain, and the process includes substage 2. Substage 3 runs through the entire pyrolysis temperature range and possibly includes monomer depolymerization and the carbonization or coking reaction of the molecular chain at the later stage. However, there are some differences in the weighted factors of each subpeak at different heating rates, as tabulated in Table 4. In addition, as the heating rate increases, the temperature range of each subpeak shifts to high-temperature areas, which is related to the delay of pyrolysis of each pseudo component due to inadequate reaction time and heat hysteresis at high heating rates. | ||
| Fig. 6 Gaussian distribution multipeak fitting for the dα/dT curves at different heating rates. (a) 2.5 °C min−1, (b) 5 °C min−1, (c) 15 °C min−1 and (d) 20 °C min−1. | ||
| Subpeaks | Weighted factor (wi) | |||
|---|---|---|---|---|
| 2.5 °C min−1 | 5 °C min−1 | 15 °C min−1 | 20 °C min−1 | |
| Peak 1 | 0.122 | 0.116 | 0.154 | 0.170 |
| Peak 2 | 0.404 | 0.378 | 0.438 | 0.430 |
| Peak 3 | 0.379 | 0.423 | 0.409 | 0.409 |
To further improve the accuracy of E and k0, the FWO, KAS, Friedman and Starink methods are applied to estimate the kinetic parameters of each substage analyzed above. Due to space limitations, only the Arrhenius plot of ln(dα/dt) vs. 1/T obtained using Friedman method is illustrated in Fig. 7. Table 5 summarizes the fitting equations and the correlation coefficients (R2) calculated by the FWO, KAS, Friedman and Starink methods within the conversion range from 0.1–0.9. As shown in Table 5, the R2 values of almost all the plots are larger than 0.99, reflecting that all four methods can appropriately describe the pyrolysis stage of each subpeak. Compared to the traditional global thermal debinding kinetics analysis, the reliability of the kinetic equations of each subpeak is significantly increased after multipeak fitting.
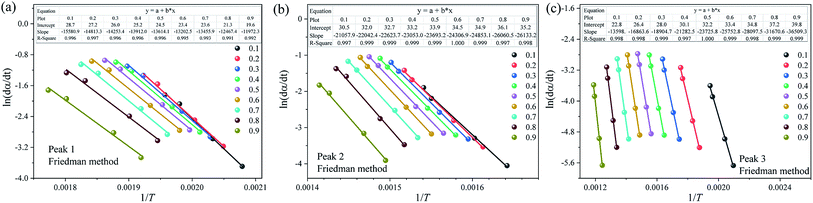 | ||
| Fig. 7 Arrhenius plot of ln(dα/dt) vs. 1/T of each pyrolysis stage at different conversion rates using the Friedman method. (a) Peak 1, (b) peak 2 and (c) peak 3. | ||
| Sub-peaks | α | KAS method | FWO method | Starink method | Friedman method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitting equation | R2 | Fitting equation | R2 | Fitting equation | R2 | Fitting equation | R2 | ||||||
| Slope | Intercept | Slope | Intercept | Slope | Intercept | Slope | Intercept | ||||||
| Peak 1 | 0.1 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657.40 657.40 |
23.16 | 0.993 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648.70 648.70 |
37.57 | 0.994 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756.53 756.53 |
24.60 | 0.993 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580.92 580.92 |
28.71 | 0.996 |
| 0.2 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901.33 901.33 |
21.10 | 0.997 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908.74 908.74 |
35.54 | 0.997 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002.08 002.08 |
22.54 | 0.997 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813.31 813.31 |
27.19 | 0.997 | |
| 0.3 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291.93 291.93 |
19.53 | 0.996 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311.24 311.24 |
34.00 | 0.997 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393.86 393.86 |
20.98 | 0.996 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253.36 253.36 |
26.01 | 0.996 | |
| 0.4 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014.45 014.45 |
18.71 | 0.997 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042.78 042.78 |
33.20 | 0.998 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117.28 117.28 |
20.16 | 0.997 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912.01 912.01 |
25.21 | 0.996 | |
| 0.5 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752.28 752.28 |
17.94 | 0.998 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 789.63 789.63 |
32.45 | 0.998 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856.02 856.02 |
19.39 | 0.998 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614.14 614.14 |
24.46 | 0.996 | |
| 0.6 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345.37 345.37 |
16.88 | 0.996 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392.51 392.51 |
31.40 | 0.996 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450.08 450.08 |
18.33 | 0.996 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202.48 202.48 |
23.41 | 0.995 | |
| 0.7 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486.00 486.00 |
16.88 | 0.996 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543.23 543.23 |
31.42 | 0.996 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 591.73 591.73 |
18.33 | 0.996 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455.88 455.88 |
23.57 | 0.993 | |
| 0.8 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703.20 703.20 |
15.12 | 0.995 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771.23 771.23 |
29.68 | 0.996 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810.00 810.00 |
16.57 | 0.995 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467.41 467.41 |
21.27 | 0.991 | |
| 0.9 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 294.38 294.38 |
13.96 | 0.996 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378.41 378.41 |
28.55 | 0.996 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402.78 402.78 |
15.42 | 0.996 | −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.30 972.30 |
19.57 | 0.992 | |
| Peak 2 | 0.1 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158.87 158.87 |
19.51 | 0.996 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416.92 416.92 |
34.40 | 0.996 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284.67 284.67 |
21.00 | 0.996 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 057.91 057.91 |
30.49 | 0.997 |
| 0.2 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 308.29 308.29 |
20.78 | 0.997 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587.44 587.44 |
35.70 | 0.998 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436.21 436.21 |
22.27 | 0.997 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042.44 042.44 |
32.00 | 0.999 | |
| 0.3 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769.69 769.69 |
21.13 | 0.997 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062.84 062.84 |
36.07 | 0.998 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899.00 899.00 |
22.62 | 0.997 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623.69 623.69 |
32.74 | 0.999 | |
| 0.4 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169.29 169.29 |
21.43 | 0.997 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474.45 474.45 |
36.39 | 0.998 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299.80 299.80 |
22.92 | 0.997 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053.01 053.01 |
33.20 | 0.999 | |
| 0.5 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863.64 863.64 |
22.18 | 0.998 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.47 180.47 |
37.16 | 0.998 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995.32 995.32 |
23.68 | 0.998 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 693.16 693.16 |
33.90 | 0.999 | |
| 0.6 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475.86 475.86 |
22.81 | 0.998 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804.10 804.10 |
37.81 | 0.999 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608.69 608.69 |
24.31 | 0.998 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.88 306.88 |
34.51 | 1.000 | |
| 0.7 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074.89 074.89 |
23.35 | 1.000 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416.91 416.91 |
38.37 | 1.000 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209.09 209.09 |
24.85 | 1.000 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853.11 853.11 |
34.87 | 0.999 | |
| 0.8 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092.11 092.11 |
24.47 | 0.999 | −25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447.76 447.76 |
39.51 | 0.999 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227.67 227.67 |
25.98 | 0.999 | −26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060.51 060.51 |
36.06 | 0.997 | |
| 0.9 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610.47 610.47 |
24.70 | 1.000 | −25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986.23 986.23 |
39.76 | 1.000 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748.04 748.04 |
26.20 | 1.000 | −26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133.22 133.22 |
35.18 | 0.998 | |
| Peak 3 | 0.1 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675.85 675.85 |
15.13 | 0.998 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 666.77 666.77 |
29.54 | 0.998 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774.94 774.94 |
16.57 | 0.998 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598.24 598.24 |
22.81 | 0.998 |
| 0.2 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830.03 830.03 |
18.03 | 0.998 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933.06 933.06 |
32.66 | 0.998 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940.34 940.34 |
19.50 | 0.998 | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863.61 863.61 |
26.41 | 0.998 | |
| 0.3 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736.18 736.18 |
19.15 | 0.998 | −18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920.33 920.33 |
33.92 | 0.998 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 854.60 854.60 |
20.63 | 0.998 | −18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904.71 904.71 |
27.98 | 0.999 | |
| 0.4 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058.95 058.95 |
21.11 | 0.997 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311.00 311.00 |
35.99 | 0.997 | −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184.16 184.16 |
22.59 | 0.997 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282.46 282.46 |
30.14 | 0.997 | |
| 0.5 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 435.54 435.54 |
23.03 | 0.999 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753.44 753.44 |
38.01 | 0.999 | −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567.33 567.33 |
24.53 | 0.999 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725.80 725.80 |
32.20 | 1.000 | |
| 0.6 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397.50 397.50 |
24.19 | 0.998 | −25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779.77 779.77 |
39.26 | 0.999 | −24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535.73 535.73 |
25.69 | 0.998 | −25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752.78 752.78 |
33.43 | 0.999 | |
| 0.7 | −26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689.84 689.84 |
25.57 | 0.998 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140.74 140.74 |
40.74 | 0.999 | −26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 834.93 834.93 |
27.09 | 0.998 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097.48 097.48 |
34.78 | 0.998 | |
| 0.8 | −30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.25 148.25 |
28.03 | 0.999 | −31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680.58 680.58 |
43.31 | 0.999 | −30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301.48 301.48 |
29.56 | 0.999 | −31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670.58 670.58 |
37.18 | 0.999 | |
| 0.9 | −34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838.05 838.05 |
30.91 | 0.999 | −36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482.43 482.43 |
46.33 | 0.999 | −35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002.49 002.49 |
32.45 | 0.999 | −36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509.31 509.31 |
39.79 | 0.999 | |
Fig. 8 shows the E vs. α curves of the three substages estimated via the FWO, KAS, Friedman and Starink methods. As shown in Fig. 8, the variation in the activation energy along with conversion show similar tends for all the four methods. The activation energy values of substages 2 and 3 basically show an increasing trend, while the activation energy values of substage 1 basically shows a decreasing trend, which agrees with the dominant reactants corresponding to the pseudo-components of each substage analyzed above. Moreover, the average values of E showed an increasing tendency from substages 1 to 3. However, there are some difference in the values of activation energy estimated by the four methods. For the FWO, KAS and Starink methods, the apparent activation energy curves of each subpeak substantially overlap for the three methods, and the difference in the values of E is very small. The values of activation energy calculated by the Friedman method exhibit some differences with other three methods, but the deviations are within acceptable 6% in terms of the average activation energy for each substage. These differences may be attributed to experimental errors and mathematical approximations in the different methods.
 | ||
| Fig. 8 The dependence of E on the degree of α for subpeaks in the entire debinding process using the FWO, KAS, Friedman and Starink methods. (a) Peak 1, (b) peak 2 and (c) peak 3. | ||
Then, the activation energy variable model is used to determine the dependency between the activation energies and conversion for three different subpeaks. Take the differential (Friedman) and the integral (FWO) as examples, for the differential (Friedman) method, the activation energies of substages 1 to 3 are E(α) = 139.862 − 110.481α + 156.161α2 − 88.714α3 kJ mol−1, E(α) = 160.791 + 152.496α − 236.906α2 + 163.724α3 kJ mol−1 and E(α) = 72.132 + 452.830α − 669.039α2 + 507.015α3 kJ mol−1, respectively. For the integral (FWO) method, the activation energies of substages 1 to 3 are E(α) = 152.665 − 123.087α + 182.724α2 − 103.190α3 kJ mol−1, E(α) = 150.604 + 132.938α − 200.494α2 + 139.979α3 kJ mol−1 and E(α) = 69.668 + 426.576α − 631.607α2 + 480.782α3 kJ mol−1, respectively. Compared with substages 1 and 2, the fluctuation range of the apparent activation energy of substage 3 is larger (113–303 kJ mol−1). This phenomenon indicates that substage 3 may follow a different kinetics mechanism.
Fig. 9 shows the kinetic compensation effect between the apparent activation energy E and the pre-exponential factor k0 (obtained by the Friedman method) of each substage separated by an M-PRM. It can be seen from Fig. 9 that the R2 of plots of E and ln(k0) for each subpeak are relatively high, indicating that the E and k0 of each substage exhibit a kinetic compensation effect.
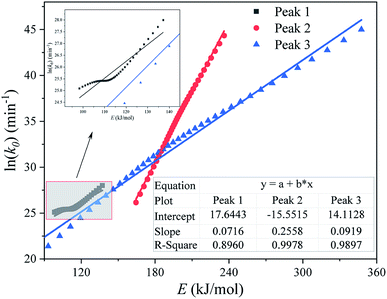 | ||
| Fig. 9 Plot of ln(k0) vs. E (calculated by the Friedman method) for each substage of the pyrolysis process of the DMAA/MBAM polymer during the debinding process. | ||
4.4 Determination of the most appropriate mechanism function f(α)
To further determine the kinetic mechanism of the removal of DMAA/MBAM polymer from gelcast ceramic parts, the mechanism function of the thermal debinding stages is determined by Málek's procedure.32 The results of the experimental and theoretical master plots depicted in Fig. 10 demonstrate the most appropriate mechanism function for each substage at different heating rates. It can be seen from Fig. 10 that the substages corresponding to the pyrolysis process of the pseudocomponents do not follow a single-process reaction mechanism. At different heating rates, each substage can be divided into two zones with α = 0.5 in the experimental plots as the boundary. The first and second substages follow the same kinetics mechanism, and the most appropriate mechanism function for the pyrolysis processes of pseudo components 1 and 2 are the reaction-order model (F2) in the conversion range of 0 < α < 0.5; however, the most appropriate mechanism function changes to the 3D Zhuravlev–Lesokhin–Tempelman mechanism model (D-ZLT3) in the conversion range of 0.5 < α < 1. For the third substage, the kinetic mechanism of the pyrolysis process of pseudo component 3 is well fit by a 3D Diffusion-Jander model (D-J3) (0 < α < 0.5) and an Avrami–Erofeev model (A4) (0.5 < α < 1) mechanism model. | ||
| Fig. 10 Standard y(α) and experimentally derived master plots against different α values at different heating rates. (a) 2.5 °C min−1, (b) 5 °C min−1, (c) 15 °C min−1 and (d) 20 °C min−1. | ||
Furthermore, the SB model is applied to determine the mechanism function of the complex debinding processes for the three substages at different heating rates.32,37 Using the E(α) and k0 obtained from the differential Friedman and integral (FWO) methods, the optimized parameters (n, m, p) for SB model are summarized in Table 6, and the fitting results of the SB model are depicted in Fig. 11. It can be seen from Fig. 11, the R2 values of the nonlinear regression fitting equation for each subpeak are all greater 0.99, indicating that the SB model can interpret the thermal degradation mechanism of DMAA/MBAM polymer. The reaction mechanism of the DMAA/MBAM pyrolysis is complex, which is the combined effects of the reaction order, power law, and diffusion mechanisms. The reaction mechanisms for substages 1 to 3 are f(α) = (1 − α)0.668α3.049(−ln(1 − α))−3.874, f(α) = (1 − α)0.700α3.177(−ln(1 − α))−3.962 and f(α) = (1 − α)1.049α−0.161(−ln(1 − α))0.518, respectively.
| Parameter | Peak 1 | Peak 2 | Peak 3 | |
|---|---|---|---|---|
| Weighted factor | wi | 0.149 | 0.439 | 0.412 |
| SB | n | 0.668 | 0.700 | 1.049 |
| m | 3.049 | 3.177 | −0.161 | |
| p | −3.874 | −3.962 | 0.518 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Differential (Friedman) | ||||
| ln(k(α)) | p1 | 28.309 | 25.174 | 18.920 |
| p2 | −13.087 | 40.646 | 53.097 | |
| p3 | 19.766 | −60.199 | −76.419 | |
| p4 | −9.978 | 39.651 | 50.662 | |
| E(α) | p5 | 139.862 | 160.791 | 72.132 |
| p6 | −110.481 | 152.496 | 452.830 | |
| p7 | 156.161 | −236.906 | −669.039 | |
| p8 | −88.714 | 163.724 | 507.015 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Integral (FWO) | ||||
| ln(k(α)) | p1 | 31.389 | 23.217 | 18.124 |
| p2 | −16.678 | 37.640 | 49.514 | |
| p3 | 26.793 | −54.330 | −71.448 | |
| p4 | −13.923 | 35.869 | 47.801 | |
| E(α) | p5 | 152.665 | 150.604 | 69.668 |
| p6 | −123.087 | 132.938 | 426.576 | |
| p7 | 182.724 | −200.494 | −631.607 | |
| p8 | −103.190 | 139.979 | 480.782 | |
 | ||
| Fig. 11 SB model y(α) and experimentally derived master plots against different α values at different heating rates. (a) 2.5 °C min−1, (b) 5 °C min−1, (c) 15 °C min−1 and (d) 20 °C min−1. | ||
Therefore, the kinetic mechanism does not change at different heating rates. A high heating rate may complicate the pyrolysis reaction process (shown in Fig. 4), but has almost no effect on the reaction mechanism. This effect is because the pyrolysis reaction of each substage is controlled by the dominant reactants, that is, the three pseudo-components, when the pyrolysis is stable, which also reveals the thermal stability and inherent reactivity of the DMAA/MBAM polymer.
4.5 Model prediction
The comparison between the experimental and SB model predicted α and dα/dT curves of the pyrolysis process of the DMAA/MBAM polymer over the whole degradation run at a heating rate of 10 °C min−1 is shown in Fig. 12. It can be seen from Fig. 12 that the α and dα/dT curves predicted by integral (FWO) and differential (Friedman) model-fit basically overlap, which indicates that the two methods have similar accuracy with respect to the SB model. It is also found that the SB model predicted values are very close to the experimental α and dα/dT values, except at lower (<0.05) and higher (>0.95) conversions. This deviation may be due to the complex multiple reactions that occur throughout the active pyrolysis process. The predicted values are in good agreement with the experimental values and the maximum error is less than 9%, which indicates that the SB model can be used for the prediction of the thermal degradation course over the whole degradation run. | ||
| Fig. 12 Experimental and SB model predicted α and dα/dT curves of the pyrolysis process of the DMAA/MBAM polymer at a heating rate of 10 °C min−1. | ||
5 Conclusions
This work investigated the thermal degradation characteristics of DMAA/MBAM copolymer through TG and Py-GC/MS experiments. M-PRM was proposed to separate the overlapping peaks in the dα/dT curves. The kinetic parameters (E, k0) of each substage were calculated using the FWO, KAS, Friedman and Starink methods. In addition, the reaction mechanism of each substage was analyzed and discussed by Málek's procedure and the SB model. The main conclusions are as follows:(1) TG analysis showed that the dehydration stage occurs at temperatures below 200 °C, and the thermal degradation of the DMAA/MBAM copolymer mainly occurs in two temperature ranges: 200–300 °C and 300–600 °C. Py-GC/MS analysis showed that the relevant monomers of copolymerization and the characteristic compounds generated from gel pyrolysis are primarily amides and ammonia species. Moreover, cyclohexane and cyclohexylamine species, which were the main ring compounds, were mainly detected at 385 °C and 450 °C, whereas ring compounds were scarce at the final pyrolysis temperature of 240 °C.
(2) A three-stage parallel reaction model was able to accurately describe the thermal debinding behavior and multiplex reaction mechanisms of removing DMAA/MBAM polymer from gelcast ceramic parts. The activation energies of substages 1 to 3 calculated by the Friedman method and activation energy variable model are E(α) = 139.862 − 110.481α + 156.161α2 − 88.714α3 kJ mol−1, E(α) = 160.791 + 152.496α − 236.906α2 + 163.724α3 kJ mol−1 and E(α) = 72.132 + 452.830α − 669.039α2 + 507.015α3 kJ mol−1, respectively. The average values of E showed an increasing trend from substages 1 to 3, and a kinetic compensation effect was also found between the E and k0 of each substage.
(3) The kinetic mechanism determined by SB model revealed that the reaction mechanism for substages 1 to 3 are f(α) = (1 − α)0.668α3.049(−ln(1 − α))−3.874, f(α) = (1 − α)0.700α3.177(−ln(1 − α))−3.962 and f(α) = (1 − α)1.049α−0.161(−ln(1 − α))0.518, respectively. The α and dα/dT curves predicted by SB model were in good agreement with the experimental values, indicating that the SB model was an effective tool for the prediction of the thermal degradation course of DMAA/MBAM copolymer during the whole debinding process.
Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This work was funded by the Science and Technology Program of Education Department of Jiangxi Province in China (GJJ170527). We are grateful for the technical assistance and the use of facilities at the Shanghai Yuyi Analytical & Testing Center, China and the Shanghai Buke Analytical & Testing Center, China.Notes and references
- T. Deng, Y. Wang, A. Dufresne and N. Lin, Carbohydr. Polym., 2018, 181, 111–118 CrossRef CAS PubMed.
- S. Yin, L. Pan, L. Guo, Y. Liu, Y. Feng, T. Qiu and J. Yang, Ceram. Int., 2018, 44, 7569–7579 CrossRef CAS.
- L. Montanaro, B. Coppola, P. Palmero and J.-M. Tulliani, Ceram. Int., 2019, 45, 9653–9673 CrossRef CAS.
- P. Jamshidi, N. Lu, G. Liu, E. Herny and M. M. Attallah, Ceram. Int., 2018, 44, 3440–3447 CrossRef CAS.
- B. Paulina and S. Mikolaj, J. Therm. Anal. Calorim., 2012, 109, 773–782 CrossRef.
- G. Chen, P. Cao, G. Wen and N. Edmonds, Mater. Chem. Phys., 2013, 139, 557–565 CrossRef CAS.
- G. Fu, N. Loh, S. Tor, B. Tay, Y. Murakoshi and R. Maeda, Appl. Phys. A: Mater. Sci. Process., 2005, 81, 495–500 CrossRef CAS.
- W.-W. Yang, K.-Y. Yang, M.-C. Wang and M.-H. Hon, Ceram. Int., 2003, 29, 745–756 CrossRef CAS.
- R. K. Enneti, T. S. Shivashankar, S.-J. Park, R. M. German and S. V. Atre, Powder Technol., 2012, 228, 14–17 CrossRef CAS.
- L. Liu, N. Loh, B. Tay, S. Tor, Y. Murakoshi and R. Maeda, Mater. Lett., 2007, 61, 809–812 CrossRef CAS.
- S. M. Ani, A. Muchtar, N. Muhamad and J. A. Ghani, Ceram. Int., 2014, 40, 2819–2824 CrossRef.
- L. Gorjan, A. Dakskobler and T. Kosmač, J. Am. Ceram. Soc., 2012, 95, 188–193 CrossRef CAS.
- J. Xue, M. Dong, J. Li, G. Zhou and S. Wang, J. Am. Ceram. Soc., 2010, 93, 928–930 CrossRef CAS.
- H. Yuan, C. Jia, X. Zhang, K. Bekouche and Z. Wang, Chinese Journal of Engineering, 2016, 38, 102–107 Search PubMed.
- L. Zhang, L. Zhang, L. Wang, H. Zhou, P. Liu, Z. Li and Y. Huang, Rare Met. Mater. Eng., 2008, 37, 697–701 Search PubMed.
- S. J. Lombardo, J. Am. Ceram. Soc., 2015, 98, 57–65 CrossRef CAS.
- Z. Shi, Z. Guo and J. Song, Acta Mater., 2002, 50, 1937–1950 CrossRef CAS.
- M. Belgacem, B. Thierry and G. Jean-Claude, Powder Technol., 2013, 235, 192–202 CrossRef CAS.
- M. Salehi, F. Clemens, T. Graule and B. Grobéty, Appl. Energy, 2012, 95, 147–155 CrossRef CAS.
- M. Hu, Z. Chen, S. Wang, D. Guo, C. Ma, Y. Zhou, J. Chen, M. Laghari, S. Fazal, B. Xiao, B. Zhang and S. Ma, Energy Convers. Manage., 2016, 118, 1–11 CrossRef CAS.
- C. Zhang, T. Qiu, J. Yang and J. Guo, Mater. Sci. Eng., A, 2012, 539, 243–249 CrossRef CAS.
- H.-X. Xu, T. Qiu, J. Yang and J. Guo, J. Inorg. Mater., 2011, 26, 1105–1110 CrossRef CAS.
- W. Wan, C. e Huang, J. Yang, J. Zeng and T. Qiu, J. Electron. Mater., 2014, 43, 2566–2572 CrossRef CAS.
- J. Tong and D. Chen, Ceram. Int., 2004, 30, 2061–2066 CrossRef CAS.
- L. Shen, X. Xu, W. Lu and B. Shi, Ceram. Int., 2016, 42, 5569–5574 CrossRef CAS.
- J. Guo, T. Qiu, J. Yang, Y. Feng, C. Zhang, W. Zhang and T. Guo, Ceram. Int., 2012, 38, 2905–2911 CrossRef CAS.
- J. Li, C. Zhang, R. Yin and W. Zhang, Ceram. Int., 2019, 45, 8166–8174 CrossRef CAS.
- J. Li, C. Zhang, R. Yin and W. Zhang, RSC Adv., 2019, 9, 8415–8425 RSC.
- Y. Q. Li, T. Qiu and J. Xu, Mater. Res. Bull., 1997, 32, 1173–1179 CrossRef CAS.
- A. S. Khan, Z. Man, M. A. Bustam, C. F. Kait, Z. Ullah, A. Nasrullah, M. I. Khan, G. Gonfa, P. Ahmad and N. Muhammad, J. Mol. Liq., 2016, 223, 754–762 CrossRef CAS.
- J. H. Flynn, Thermochim. Acta, 1997, 300, 83–92 CrossRef CAS.
- Y. Sun, F. Bai, X. Lü, C. Jia, Q. Wang, M. Guo, Q. Li and W. Guo, Energy, 2015, 82, 705–713 CrossRef CAS.
- M. Starink, Thermochim. Acta, 1996, 288, 97–104 CrossRef CAS.
- C. Xie, J. Liu, X. Zhang, W. Xie, J. Sun, K. Chang, J. Kuo, W. Xie, C. Liu, S. Sun, M. Buyukada and F. Evrendilek, Appl. Energy, 2018, 212, 786–795 CrossRef CAS.
- G. Sun, H. Sun, Y. Liu, B. Zhao, N. Zhu and K. Hu, Polymer, 2007, 48, 330–337 CrossRef CAS.
- I. Ali, H. Bahaitham and R. Naebulharam, Bioresour. Technol., 2017, 235, 1–11 CrossRef CAS.
- P. Šimon, Thermochim. Acta, 2011, 520, 156–157 CrossRef.
- J. Šesták and G. Berggren, Thermochim. Acta, 1971, 3, 1–12 CrossRef.
- S. Vyazovkin and C. A. Wight, Thermochim. Acta, 1999, 340–341, 53–68 CrossRef CAS.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- P. Budrugeac, Polym. Degrad. Stab., 2001, 74, 125–132 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |