Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Percolation analysis of the electrical conductive network in a polymer nanocomposite by nanorod functionalization†
Ruibin Maab,
Guangyao Muab,
Huan Zhangc,
Jun Liu ab,
Yangyang Gao
ab,
Yangyang Gao *ab,
Xiuying Zhao*ab and
Liqun Zhang
*ab,
Xiuying Zhao*ab and
Liqun Zhang *ab
*ab
aKey Laboratory of Beijing City on Preparation and Processing of Novel Polymer Materials, Beijing University of Chemical Technology, 10029, China. E-mail: gaoyy@mail.buct.edu.cn; zhaoxy@mail.buct.edu.cn; zhanglq@mail.buct.edu.cn
bState Key Laboratory of Organic-Inorganic Composites, Beijing University of Chemical Technology, 100029, China
cAerospace Research Institute of Materials and Processing Technology, Beijing, 100076, China
First published on 7th November 2019
Abstract
Chemical functionalization of nanofillers is an effective strategy to benefit the formation of the conductive network in the matrix which can enhance the electrical conductivity of polymer nanocomposites (PNCs). In this work, we adopted a coarse-grained molecular dynamics simulation to investigate the effect of the nanorod (NR) functionalization on the conductive probability of PNCs under the quiescent state or under a shear field. It is found that the direct aggregation structure of NRs is gradually broken down with increasing the NR functionalization degree λA, which improves their dispersion state. Moreover, a local bridging structure of NRs sandwiched via one polymer layer is formed at high λA. Corresponding to it, the percolation threshold of PNCs first quickly decreases, then increases and last slightly decreases again with the increase of λA, which exhibits an anti N-type under the quiescent state. Meanwhile, it shows a non-monotonic dependence on the interaction between polymer and the functionalized beads which reaches the lowest value at the moderate interaction. However, the percolation threshold is nearly independent of λA under the shear field. Compared with in the quiescent state, the decrease or the increase of the percolation threshold can be tuned by λA under the shear field. The significant change in the percolation threshold is attributed to the orientation and the dispersion state of NRs under the shear field, which affects the conductive network. Especially, we found that the dispersion state of NRs is different for different λA under the shear field. However, the percolation threshold is similar which indicates that the dispersion state of NRs is not completely correlated to the conductive network. In summary, this work presents some further understanding of how the NR functionalization affects the electrical conductivity of PNCs.
1. Introduction
Addition of small amounts of conductive nanofillers (such as carbon nanotubes (CNTs), graphene, carbon black (CB)) into a polymer matrix can increase the electrical conductivity of polymer nanocomposites (PNCs) by orders of magnitude.1–3 If the filler concentration is above the percolation threshold, the conductive network will be formed in the matrix which can be understood by percolation theory.4 Generally, the formation of the conductive network depends on both the properties of the polymer matrix and the filler and the processing conditions (such as tensile field and shear field).5–7 It is important to reduce the percolation threshold of PNCs which can improve the electrical conductivity and reduce cost in industrial applications.In experiments, a lot of effect is devoted to understand the relationship between the experimental parameters and the electrical conductivity, which aims to enhance electrical property of PNCs.8,9 For example, the dependence of the percolation threshold on the aspect ratio of CNTs can be described by a mode which could optimize the CNTs processing conditions.10 In addition, the surface functionalization of CNTs is used to form the conductive PNCs with a low percolation threshold.11,12 Moreover, the percolation threshold can be further reduced by controlling the CB in one phase of the composite blend.13 The tensile and shear fields are necessary during the processing of PNCs which exerts a great influence on the conductive network. Compared with under the quiescent state, the decrease or the increase of the electrical conductivity under the shear field is determined by the initial dispersion state of filler.14–16 To better understand how the shear field affects the electrical conductivity, it is necessary to characterize the conductive network.17,18 However, experimental techniques are unable to intuitively analyze the variation of the conductive network and electrical properties. Computer simulations have an obvious advantage in analyzing the electrical conductive behavior of PNCs. Currently, by employing a three-dimensional Monte Carlo model, the dependence of the fiber aspect ratio on the percolation threshold is investigated which exhibits an exponential relationship.19,20 With the same model, it is found that the aspect ratio of CNTs determines the percolation threshold rather than the tunneling barrier height.21 In addition, the size polydisperse will improve the percolation threshold which is approximately inversely upon the weight-averaged aspect ratio.22 For comparable sizes of fillers, nanorods can form a percolating network at lower concentration than nanoplates and nanospheres.23 Furthermore, it is reported that the average conductive pathway density of CNTs dominates the anisotropy of the electrical property which depends heavily on CNT alignment structure.24 By considering the CNT structural distortion in the developed percolation network model, the effect of the temperature on the electrical conductivity is clarified.25 The conductive stability of PNCs firstly declines and then rises with the filler concentration at a constant strain, and the minimum corresponds to the percolation threshold.26 The shear field will induce the alignment of CNTs parallel to the shear direction which affects the electrical conductivity of PNCs.27 Interestingly, as the shear rate is above a critical value, CNTs form the direct contact aggregation which reduces the electrical conductivity.28 Especially, the partial alignment of CNTs can result in maximum electrical conductivity of PNCs rather than complete alignment.29,30
In fact, because of the self-attraction of CNTs, CNTs show an aggregation structure which is the main cause for the low electrical conductivity of PNCs. Among the various methods,31–35 the chemical functionalization of CNTs seems much more effective than others to achieve the uniform dispersion of CNTs in the matrix. However, the effect of the nanorod (NR) functionalization on the conductive behavior of PNCs has not been investigated to our knowledge, especially under the shear field. In this work, by adopting a coarse-grain model, first the microstructure of the NR aggregation is analyzed for different NR functionalization degree. Then, the conductive probabilities of PNCs are calculated under the quiescent state and under the shear field. By calculating the main cluster size and the number of clusters in the conductive network, the relationship between the conductive probability and the NR functionalization degree is well clarified.
2. Model and simulation methods
In this work, we adopted a coarse-grained model of the NRs filled PNCs. The classic bead-spring model is adopted to simulate polymer chains which consist of thirty beads.36 The total number of polymer beads is fixed to be 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for each system. Each NR contains ten beads, which consists of the strong (A) and weak (B) beads, the only difference being the interaction energy with polymers. The NR functionalization degree is defined as λA = NA/(NA + NB) which varies from 0.0, 0.1, 0.2, 0.4, 0.6, 0.8 to 1.0 in this work. Here, NA and NB are the number of A and B beads in one NR, respectively. σ and m are used to stand for the diameter and mass of each bead respectively. When mapping the coarse-grained model to a real polymer, each bond in this model corresponds to three to six covalent bonds along the backbone of a real chemical chain.36
000 for each system. Each NR contains ten beads, which consists of the strong (A) and weak (B) beads, the only difference being the interaction energy with polymers. The NR functionalization degree is defined as λA = NA/(NA + NB) which varies from 0.0, 0.1, 0.2, 0.4, 0.6, 0.8 to 1.0 in this work. Here, NA and NB are the number of A and B beads in one NR, respectively. σ and m are used to stand for the diameter and mass of each bead respectively. When mapping the coarse-grained model to a real polymer, each bond in this model corresponds to three to six covalent bonds along the backbone of a real chemical chain.36
The truncated and shifted Lenard–Jones (TSLJ) potential is adopted to describe the non-bonded interactions between all beads:
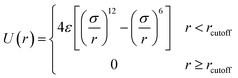 | (1) |
The bonded interaction between the adjacent beads including both polymer chains and NRs is represented by a stiff finite extensible nonlinear elastic (FENE) potential:
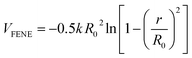 | (2) |
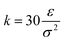 and R0 = 1.5σ, guaranteeing a certain stiffness of the bonds while avoiding high-frequency modes and chain crossing.
and R0 = 1.5σ, guaranteeing a certain stiffness of the bonds while avoiding high-frequency modes and chain crossing.
The rod-like character of the NR is enforced by a bending potential, given by
| Uangle = K(θ − θ0)2 | (3) |
It is noted that it is not our aim to study a specific polymer. Thus, the reduced LJ units σ and ε are set to be unity, which means that all calculated quantities are dimensionless. Following our previous works,37–39 first all the polymer chains and NRs are put into a large box. Then, the NPT ensemble is used to compress the system for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ where τ is the reduce time unit. Temperature and pressure are set to be T* = 1.0 and P* = 0.0 respectively by using the Nose–Hoover temperature thermostat and pressure barostat. It is noted that the glass transition temperature of polymer chains is
000τ where τ is the reduce time unit. Temperature and pressure are set to be T* = 1.0 and P* = 0.0 respectively by using the Nose–Hoover temperature thermostat and pressure barostat. It is noted that the glass transition temperature of polymer chains is 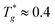 which is lower than our simulation temperature (T* = 1.0). Periodic boundary conditions are employed in all three directions. The velocity-Verlet algorithm is applied to integrate the equations of motion with a timestep of δt = 0.001. Next, a further equilibration is performed for 50000τ under NVT ensemble with T* = 1.0. We have checked that polymer chains and NRs have experienced fully relaxed, reaching their equilibrated states for all systems. The equilibrium number density of polymer beads reaches nearly 0.85 which is corresponding to the density of polymer melts. Such equilibrated structures are then used as starting structures for production runs of the structural and dynamical analysis. All simulation runs are carried out by using the large scale atomic/molecular massively parallel simulator (LAMMPS).40
which is lower than our simulation temperature (T* = 1.0). Periodic boundary conditions are employed in all three directions. The velocity-Verlet algorithm is applied to integrate the equations of motion with a timestep of δt = 0.001. Next, a further equilibration is performed for 50000τ under NVT ensemble with T* = 1.0. We have checked that polymer chains and NRs have experienced fully relaxed, reaching their equilibrated states for all systems. The equilibrium number density of polymer beads reaches nearly 0.85 which is corresponding to the density of polymer melts. Such equilibrated structures are then used as starting structures for production runs of the structural and dynamical analysis. All simulation runs are carried out by using the large scale atomic/molecular massively parallel simulator (LAMMPS).40
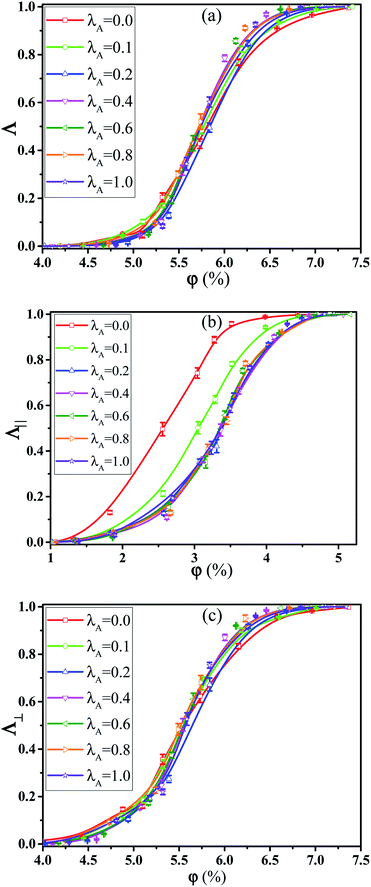
It is noted that the electrical properties of the PNCs are correlated to the conductive network. To determine whether the conductive network is formed, a criterion is used to check whether any two NRs are connected. Any two NRs are considered to be connected once their gap is less than the tunneling distance (TD) which can reflect the contact conductance between NRs.41 High TD indicates the high contact conductance. Here, the tunneling distance is chosen to be 1.0σ from the two aspects (one is the sandwiched polymer chain,42 another is that the ratio of CNT diameter to the maximum TD is nearly 1.0 in experiment43). It is noted that TD will impact upon the percolation threshold. However, it does not influence the trend of the results. At the beginning of the computational implementation, each NR is assigned a site number and a cluster number. The site number is equal to the cluster number, ranging from 1 to N where N is the total number of NRs. Then, each NR is checked for connection with others. If two NRs are connected, they will be assigned a common cluster number. Finally, all the NRs with the same cluster number are in the same cluster while NRs with different cluster numbers are not connected. Once the NR network spans one direction continuously from one side to another, the system is conductive in this direction. If the NR network spans the three-dimensional directions continuously, it is homogeneously conductive in three directions. Finally, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibrated configurations are dumped which are divided into ten independent blocks. Then we calculated the quantities separately in each block, determine average and standard deviation of the average, and use standard deviation as error bar. The time interval between two continuous frames is 10τ. Then, the number of the configurations is counted which is conductive in the three-dimensional directions or in one direction. Here, the conductive probability Λ, the directional conductive probability Λ‖ parallel to the shear field direction, and the directional conductive probability Λ⊥ perpendicular to the shear direction are used to represent the probability of forming the filler network, which spans the systems in the three-dimensional directions, parallel to the shear direction, and perpendicular to the shear direction respectively. It is noted that the size effect of the simulation box is considered where the conclusions are not changed. Meanwhile, the directional conductive probabilities along the different directions are similar under the quiescent state which indicates that the chosen size is reasonable.
000 equilibrated configurations are dumped which are divided into ten independent blocks. Then we calculated the quantities separately in each block, determine average and standard deviation of the average, and use standard deviation as error bar. The time interval between two continuous frames is 10τ. Then, the number of the configurations is counted which is conductive in the three-dimensional directions or in one direction. Here, the conductive probability Λ, the directional conductive probability Λ‖ parallel to the shear field direction, and the directional conductive probability Λ⊥ perpendicular to the shear direction are used to represent the probability of forming the filler network, which spans the systems in the three-dimensional directions, parallel to the shear direction, and perpendicular to the shear direction respectively. It is noted that the size effect of the simulation box is considered where the conclusions are not changed. Meanwhile, the directional conductive probabilities along the different directions are similar under the quiescent state which indicates that the chosen size is reasonable.
3. Results and discussion
3.1 Conductive property of PNCs
〈P2(r)〉 = (3〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 − 1)/2 θ〉 − 1)/2
| (4) |
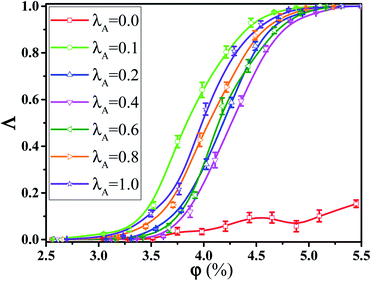 | ||
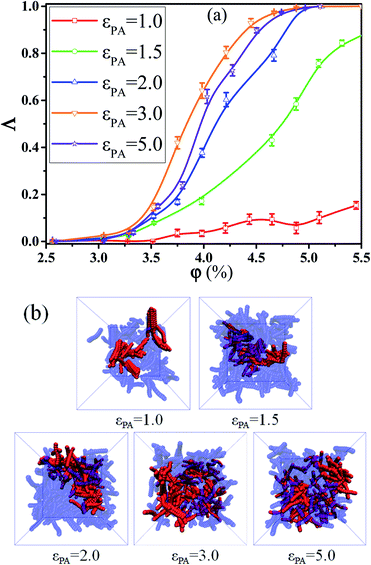
Fig. 1 Conductive probability Λ as a function of the nanorod (NR) volume fraction φ for different NR functionalization degree λA. (T* = 1.0, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0). = 0.0). | ||
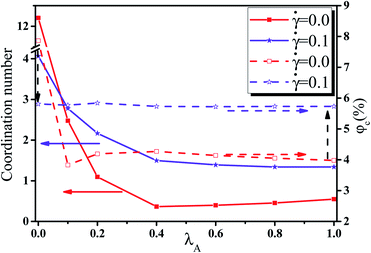
First, we investigated the effect of the NR functionalization degree λA on the conductive probability of PNCs by fixing the shear rate = 0.1. Fig. 7 presented the dependence of Λ, Λ‖, and Λ⊥ on λAfor different φ in a steady shear flow. To clearly present it, the percolation threshold φc of PNCs at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1 is obtained in Fig. 7(a) and shown in Fig. 2 for different λA. It is interesting to find that the φc is nearly independent of the λA at
= 0.1 is obtained in Fig. 7(a) and shown in Fig. 2 for different λA. It is interesting to find that the φc is nearly independent of the λA at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1 (namely the similar Λ), which is different with φc at
= 0.1 (namely the similar Λ), which is different with φc at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0 in Fig. 2. This is actually consistent with the experimental result.50 To better understand it, the φc at
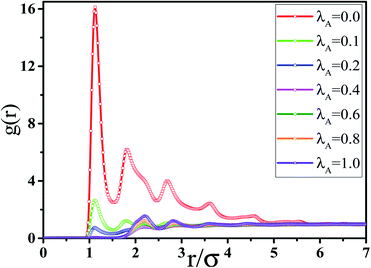
= 0.0 in Fig. 2. This is actually consistent with the experimental result.50 To better understand it, the φc at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0 and 0.1 are presented together in Fig. 2. Then, we characterized how the shear field changes the conductive network. First, the inter-NR RDF under the shear field is calculated for different λA in Fig. S7.† Compared with those at
= 0.0 and 0.1 are presented together in Fig. 2. Then, we characterized how the shear field changes the conductive network. First, the inter-NR RDF under the shear field is calculated for different λA in Fig. S7.† Compared with those at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0 in Fig. 3, the peaks at r = 1σ and 2σ are found to gradually decrease for λA = 0.0 at
= 0.0 in Fig. 3, the peaks at r = 1σ and 2σ are found to gradually decrease for λA = 0.0 at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1, which indicates the breakage of the direct contact aggregation of NRs. Thus, the shear field induces the decrease in φc for λA = 0.0. However, they show an increase for λA ≥ 0.1 which reflects the breakage of the original conductive network. As a result, this leads to the increase in φc for λA ≥ 0.1 under the shear field. Next, the local order of the NR aggregation 〈P2(r)〉is presented in Fig. S8(a).† Similarly, compared with those at
= 0.1, which indicates the breakage of the direct contact aggregation of NRs. Thus, the shear field induces the decrease in φc for λA = 0.0. However, they show an increase for λA ≥ 0.1 which reflects the breakage of the original conductive network. As a result, this leads to the increase in φc for λA ≥ 0.1 under the shear field. Next, the local order of the NR aggregation 〈P2(r)〉is presented in Fig. S8(a).† Similarly, compared with those at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0 in Fig. S3(a),† the fluctuation of 〈P2(r)〉 is very small at r < 3σ at
= 0.0 in Fig. S3(a),† the fluctuation of 〈P2(r)〉 is very small at r < 3σ at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1, especially for λA = 0.0. This also indicates that the shear field induces the breakage of the direct contact aggregation of NRs. Meanwhile, the orientation of NRs along the shear direction is responsible for the non-zero value of 〈P2(r)〉 at long distance r. In addition, the number of the nearest neighbor NRs surrounding one NR (Nnum) is calculated. From Fig. S8(b),† compared with that at
= 0.1, especially for λA = 0.0. This also indicates that the shear field induces the breakage of the direct contact aggregation of NRs. Meanwhile, the orientation of NRs along the shear direction is responsible for the non-zero value of 〈P2(r)〉 at long distance r. In addition, the number of the nearest neighbor NRs surrounding one NR (Nnum) is calculated. From Fig. S8(b),† compared with that at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.0 in Fig. S3(b),† the Nnum at the maximum probability distribution PN decreases for λA = 0.0 at
= 0.0 in Fig. S3(b),† the Nnum at the maximum probability distribution PN decreases for λA = 0.0 at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1. However, the PN decreases at Nnum = 0 while it increases at Nnum = 1. These results indicate that the shear field exerts a significant effect on the conductive network. To better explain it, we turned to Λ‖ and Λ⊥, which determine the Λ. It is noted that two directional conductive probabilities along the gradient direction and the vorticity direction are averaged as the directional conductive probability perpendicular to the shear direction Λ⊥ because they are very similar. As shown in Fig. 7(b), Λ‖ first shows a decrease with λA from 0.0 to 0.1 and then keeps unchanged with λA, which is generally related to both the dispersion state and the orientation of NRs. Thus, we characterized the orientation degree of NRs for different λA, which is described by the second-order Legendre polynomials 〈P2〉. It is given by 〈P2〉 = (3 〈cos2
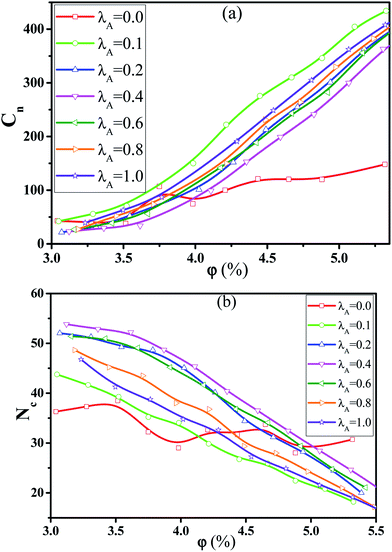
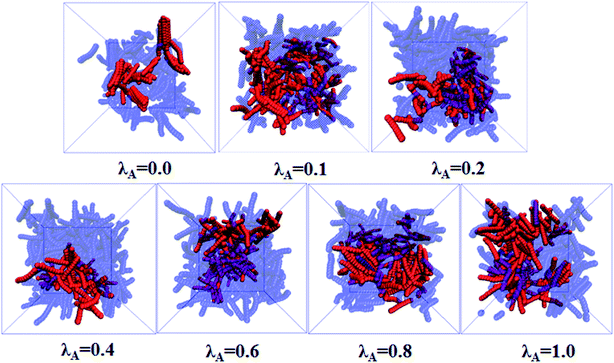
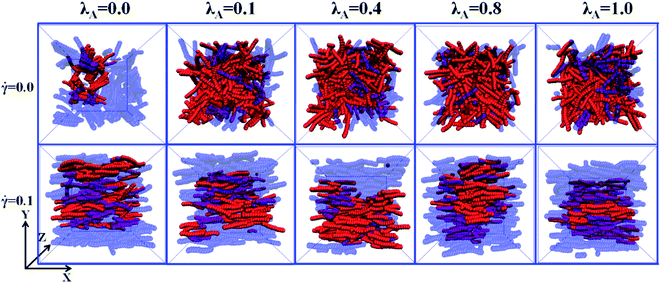
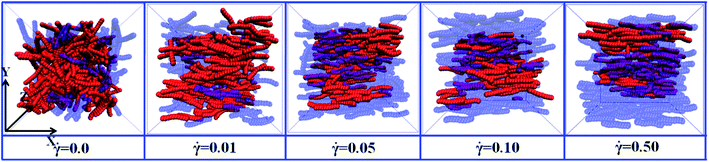
= 0.1. However, the PN decreases at Nnum = 0 while it increases at Nnum = 1. These results indicate that the shear field exerts a significant effect on the conductive network. To better explain it, we turned to Λ‖ and Λ⊥, which determine the Λ. It is noted that two directional conductive probabilities along the gradient direction and the vorticity direction are averaged as the directional conductive probability perpendicular to the shear direction Λ⊥ because they are very similar. As shown in Fig. 7(b), Λ‖ first shows a decrease with λA from 0.0 to 0.1 and then keeps unchanged with λA, which is generally related to both the dispersion state and the orientation of NRs. Thus, we characterized the orientation degree of NRs for different λA, which is described by the second-order Legendre polynomials 〈P2〉. It is given by 〈P2〉 = (3 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 − 1)/2, where θ denotes the angle between the end-to-end vector of NRs and the shear direction. As shown in Fig. S9,† it is found that the 〈P2〉 first increases and then keeps nearly unchanged with the increase of λA, which is consistent with Λ‖. In addition, it is noted that the PN at Nnum = 3 or 4 for λA = 0.0 and 0.1 is larger than that for λA ≥ 0.2 in Fig. S8(b).† This indicates that more NRs connect 3 to 4 other NRs for λA = 0.0 and 0.1, which can help to form the conductive network along the shear direction. It is noted than Λ‖ is larger than Λ⊥. Thus, Λ strongly depends on Λ⊥, rather than Λ‖. From Fig. 7(c), Λ⊥ exhibits a similar trend with Λ. Similarly, we calculated the main cluster size Cn to analyze the conductive network in Fig. S10.† The results indicate that Cn is nearly similar for different λA which is consistent with Λ. To intuitively observe the NR conductive network, Fig. 8 presents the snapshots of some typical systems (φ = 5.75%) with different λA. It clearly shows that NRs gradually align along the shear direction. Meanwhile, Cn (the number of red beads) is similar for different λA. In summary, the original conductive network is broken down and a new one forms under the shear field. Compared with under the quiescent state, the breakage of the direct contact aggregation structure of NRs enhances Λ and reduces φc for λA = 0.0 under the shear field; However, φc increases for λA ≥ 0.1. Thus, compared with under the quiescent state, the decrease or the increase of the conductive probability depends on the initial dispersion state of NRs under the shear field, which can be tuned by λA.
θ〉 − 1)/2, where θ denotes the angle between the end-to-end vector of NRs and the shear direction. As shown in Fig. S9,† it is found that the 〈P2〉 first increases and then keeps nearly unchanged with the increase of λA, which is consistent with Λ‖. In addition, it is noted that the PN at Nnum = 3 or 4 for λA = 0.0 and 0.1 is larger than that for λA ≥ 0.2 in Fig. S8(b).† This indicates that more NRs connect 3 to 4 other NRs for λA = 0.0 and 0.1, which can help to form the conductive network along the shear direction. It is noted than Λ‖ is larger than Λ⊥. Thus, Λ strongly depends on Λ⊥, rather than Λ‖. From Fig. 7(c), Λ⊥ exhibits a similar trend with Λ. Similarly, we calculated the main cluster size Cn to analyze the conductive network in Fig. S10.† The results indicate that Cn is nearly similar for different λA which is consistent with Λ. To intuitively observe the NR conductive network, Fig. 8 presents the snapshots of some typical systems (φ = 5.75%) with different λA. It clearly shows that NRs gradually align along the shear direction. Meanwhile, Cn (the number of red beads) is similar for different λA. In summary, the original conductive network is broken down and a new one forms under the shear field. Compared with under the quiescent state, the breakage of the direct contact aggregation structure of NRs enhances Λ and reduces φc for λA = 0.0 under the shear field; However, φc increases for λA ≥ 0.1. Thus, compared with under the quiescent state, the decrease or the increase of the conductive probability depends on the initial dispersion state of NRs under the shear field, which can be tuned by λA.
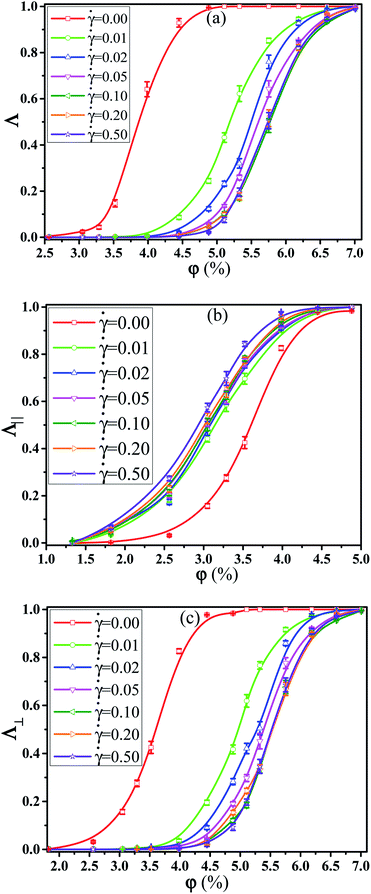
At last, the effect of the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) on the conductive probability of PNCs is investigated at λA = 0.1 where the system shows the highest conductive probability under the quiescent state. Fig. 9 presents the change of Λ, Λ‖, and Λ⊥ with
on the conductive probability of PNCs is investigated at λA = 0.1 where the system shows the highest conductive probability under the quiescent state. Fig. 9 presents the change of Λ, Λ‖, and Λ⊥ with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . From Fig. 9(a), it is found that the Λ first decreases and then keeps unchanged with the increase of
. From Fig. 9(a), it is found that the Λ first decreases and then keeps unchanged with the increase of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , which indicates the breakage of the conductive network under the shear field. As shown in Fig. S11,† φc increases slowly from 3.85% to 5.75% when
, which indicates the breakage of the conductive network under the shear field. As shown in Fig. S11,† φc increases slowly from 3.85% to 5.75% when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) varies from 0.0 to 0.1. Then, it keeps nearly unchanged with further increasing
varies from 0.0 to 0.1. Then, it keeps nearly unchanged with further increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to 0.5. This is because the shear field destroys the conductive network which is reflected by the decrease of Cn in Fig S12.† From Fig. 9(b), Λ‖ exhibits a continuous increase with
to 0.5. This is because the shear field destroys the conductive network which is reflected by the decrease of Cn in Fig S12.† From Fig. 9(b), Λ‖ exhibits a continuous increase with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) from 0.0 to 0.5, which is attributed to the high orientation degree of NRs in Fig. S13† and the relatively dispersion structure of NRs in Fig. S14.† Λ⊥ shows a similar trend with Λ as the increase of
from 0.0 to 0.5, which is attributed to the high orientation degree of NRs in Fig. S13† and the relatively dispersion structure of NRs in Fig. S14.† Λ⊥ shows a similar trend with Λ as the increase of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The significant decrease of the λ⊥ is attributed to the breakage of the inter-NR connection perpendicular to the shear direction. At last, we presented the snapshots of the conductive network for different
. The significant decrease of the λ⊥ is attributed to the breakage of the inter-NR connection perpendicular to the shear direction. At last, we presented the snapshots of the conductive network for different ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (φ = 5.50%) in Fig. 10. It is found that the Cn gradually decreases when
(φ = 5.50%) in Fig. 10. It is found that the Cn gradually decreases when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) increases from 0.0 to 0.1. Then, it nearly keeps unchanged with further increasing
increases from 0.0 to 0.1. Then, it nearly keeps unchanged with further increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) which is consistent with the Λ. In total, the orientation and the dispersion state of NRs along the shear direction changes with
which is consistent with the Λ. In total, the orientation and the dispersion state of NRs along the shear direction changes with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) which synergistically affects the conductive network and conductive probability.
which synergistically affects the conductive network and conductive probability.
4. Discussion
When mapping the coarse-grained model to real polymers, the interaction parameter ε is about 2.5–4.0 kJ mol−1 for the common polymers,36 indicating that εpA = 5.0 (in units of ε) is about 12.5–20.0 kJ mol−1. It has been reported that the interaction strengths of the natural rubber with adsorption sites on carbon black vary from 13 to 35 kJ mol−1,51 and they are mainly attributed to van der Waals forces. In addition, for the adopted coarse-grained model, the persistence length is about 0.676σ. For real polymers, the persistence length varies from 0.35 nm to 0.76 nm,52 which indicates that σ is roughly about 1 nm. Meanwhile, we have calculated the rotational diffusion coefficient (Dr) of nanorod, which is about 1.42 × 10−4τ−1.53 The shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is between 0.01τ−1 and 0.5τ−1 in our simulation, which is higher than that in the real physical experiments. As a result, the Peclet number
is between 0.01τ−1 and 0.5τ−1 in our simulation, which is higher than that in the real physical experiments. As a result, the Peclet number 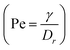 roughly varies from 70 to 3500, which is comparable with the experimental Peclet numbers.54 Thus, our simulation results can reflect the real experiments.
roughly varies from 70 to 3500, which is comparable with the experimental Peclet numbers.54 Thus, our simulation results can reflect the real experiments.
According to the previous works, the electrical conductivity is strongly dependent on the conductive network, which is affected by the polymer–filler interactions,12 the aspect ratio,55 shape,56 flexibility,23 and alignment24 of filler, etc. In this work, we mainly focused on the effect of the NR functionalization on the conductive behavior of PNCs under the quiescent state and under the shear field. In experiments,57 the percolation threshold varies from 0.01 vol% to 4.75 vol% in different CNT filled PNCs, which is smaller than our results (from 3.83% to 7.86%). To explain this difference, firstly both the aspect ratio of CNTs and the chain length in experiments are much greater than those in this work because of the limitation of computational power. Secondly, in the simulation, the conductive probability is adopted to qualitatively reflect the electrical conductivity, but not quantitatively. Meanwhile, the conductive probability just changes from 0.0 to 1.0 (one order of magnitude) in the simulation which also depends on the tunneling distance. However, the electrical conductivity can change over more than 10 orders of magnitude near the percolation threshold in experiments.57 Therefore, quantitative comparison between the experiments and our simulation is difficult. In addition, some experimental works58,59 reported that the chemical functionalization of CNTs increases the compatibility between polymer matrix and CNTs, which, in turn, causes a significant increase in the electrical conductivity. However, it is difficult to decide the optimal functionalization degree of CNT where the PNCs exhibits the maximum electrical conductivity. Meanwhile, the other work60 indicated the decrease of the electrical conductivity. In general, the functionalization of CNT breaks the conjugate planar structure which reduces the inherent conductivity of the CNT. However, it is not considered in the current model. Furthermore, the electrical conductivity of PNCs can be obtained by the electrical network model via the filler network24,61,62 which can be used to further optimize our model in the further. In total, our simulation can roughly reflect the above experimental systems. The main new phenomena revealed here are summarized below: (1) the percolation threshold of PNCs first decreases, then increases and last slightly decreases again with the increase of λA, which exhibits an anti N-type under the quiescent state. However, the percolation threshold is nearly independent of the λA under the shear field. (2) Compared with in the quiescent state, the decrease or the increase of the conductive probability under the shear field depends on the λA. (3) Even though the dispersion state of NRs is different, the percolation threshold is similar for different λA under the shear field, which indicates that the dispersion state of NRs is not completely correlated to the conductive network.
5. Conclusions
In this work, by adopting a coarse-grained molecular dynamics simulation, we investigated the effect of nanorod (NR) functionalization on the conductive probability of PNCs under the quiescent state or under the shear field. The self-attractive NRs form a direct contact aggregation structure with the local order in the matrix. Then, the NR functionalization induces the breakage of the aggregation structure of NRs, which improves their dispersion state. Last a local bridging structure of NRs sandwiched via one polymer layer is formed at high functionalization degree λA. As a result, the percolation threshold of PNCs first quickly decreases, then increases and last slightly decreases again with increasing λA, which exhibits an anti N-type under the quiescent state. Meanwhile, the percolation threshold first decreases and the increase with the increase of the interaction between polymer and the functionalized beads which reaches the lowest value at the moderate interaction. However, it is nearly independent of the λA under the shear field. Compared with in the quiescent state, the shear induces the breakage of the NR aggregation for λA = 0.0 which enhances the conductive probability. However, the conductive network is broken down under the shear field for λA > 0.0 which reduces the conductive probability. Thus, compared with in the quiescent state, the decrease or the increase of the conductive probability under the shear field depends on the λA. Interestingly, the dispersion state of NRs is different for different λA under the shear field. However, the conductive probability is similar. This reflects that the dispersion state of NRs is not completely correlated to the conductive network. In summary, this work presents that the NR functionalization is an effective method to tune and control the conductive network, which can help fabricate PNCs with high electrical conductivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported from the National Natural Science Foundation of China (21704003, 51973012), National 973 Basic Research Program of China 2015CB654700 (2015CB654704), the Foundation for Innovative Research Groups of the NSF of China (51221002 and 51521062) and the start-up funding of Beijing University of Chemical Technology for excellent introduced talents (buctrc201710). The authors acknowledge the National Supercomputer Center in Lvliang and Guangzhou.References
- A. Mora, F. Han and G. Lubineau, Results Phys., 2018, 10, 81–90 CrossRef.
- G. Sui, W. Yu, Q. Zhang, F. Chen and Q. Fu, Polymer, 2017, 123, 65–72 CrossRef CAS.
- B. Guo, Z. Tang and L. Zhang, Prog. Polym. Sci., 2016, 61, 29–66 CrossRef CAS.
- I. Balberg, Philos. Mag. B, 1987, 56, 991–1003 CAS.
- H. Deng, L. Lin, M. Ji, S. Zhang, M. Yang and Q. Fu, Prog. Polym. Sci., 2014, 39, 627–655 CrossRef CAS.
- K. Hilarius, D. Lellinger, I. Alig, T. Villmow, S. Pegel and P. Pötschke, Polymer, 2013, 54, 5865–5874 CrossRef CAS.
- F. Grillard, C. Jaillet, C. Zakri, P. Miaudet, A. Derré, A. Korzhenko, P. Gaillard and P. Poulin, Polymer, 2012, 53, 183–187 CrossRef CAS.
- R. M. Mutiso and K. I. Winey, Prog. Polym. Sci., 2015, 40, 63–84 CrossRef CAS.
- I. Alig, P. Pötschke, D. Lellinger, T. Skipa, S. Pegel, G. R. Kasaliwal and T. Villmow, Polymer, 2012, 53, 4–28 CrossRef CAS.
- J. Li, P. C. Ma, W. S. Chow, C. K. To, B. Z. Tang and J. K. Kim, Adv. Funct. Mater., 2007, 17, 3207–3215 CrossRef CAS.
- Y. Zeng, P. Liu, J. Du, L. Zhao, P. M. Ajayan and H.-M. Cheng, Carbon, 2010, 48, 3551–3558 CrossRef CAS.
- Y. Bréchet, J. Y. Cavaillé, E. Chabert, L. Chazeau, R. Dendievel, L. Flandin and C. Gauthier, Adv. Eng. Mater., 2001, 3, 571–577 CrossRef.
- Y. Pan, X. Liu, X. Hao and D. W. Schubert, Phys. Chem. Chem. Phys., 2016, 18, 32125–32131 RSC.
- T. Skipa, D. Lellinger, W. Böhm, M. Saphiannikova and I. Alig, Polymer, 2010, 51, 201–210 CrossRef CAS.
- T. Skipa, D. Lellinger, M. Saphiannikova and I. Alig, Phys. Status Solidi B, 2009, 246, 2453–2456 CrossRef CAS.
- I. Alig, D. Lellinger, M. Engel, T. Skipa and P. Pötschke, Polymer, 2008, 49, 1902–1909 CrossRef CAS.
- J. Xu, W. Florkowski, R. Gerhardt, K.-s. Moon and C.-P. Wong, J. Phys. Chem. B, 2006, 110, 12289–12292 CrossRef CAS.
- R. H. Schmidt, I. A. Kinloch, A. N. Burgess and A. H. Windle, Langmuir, 2007, 23, 5707–5712 CrossRef CAS.
- H. M. Ma and X. L. Gao, Polymer, 2008, 49, 4230–4238 CrossRef CAS.
- G. Wang, C. Wang, F. Zhang and X. Yu, Comput. Mater. Sci., 2018, 150, 102–106 CrossRef CAS.
- W. S. Bao, S. A. Meguid, Z. H. Zhu, Y. Pan and G. J. Weng, J. Appl. Phys., 2013, 113, 234313 CrossRef.
- R. M. Mutiso, M. C. Sherrott, J. Li and K. I. Winey, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 86, 278–281 Search PubMed.
- S. Kwon, H. W. Cho, G. Gwon, H. Kim and B. J. Sung, Phys. Rev. E, 2016, 93, 032501 CrossRef.
- S. Gong, Z. H. Zhu and S. A. Meguid, Polymer, 2015, 56, 498–506 CrossRef CAS.
- S. Gong, Y. Wang, Z. Xiao, Z. Li, Z. X. Wang, R. S. Lei and Z. H. Zhu, Compos. Sci. Technol., 2017, 149, 48–54 CrossRef CAS.
- Y. Feng, N. Ning, L. Zhang, M. Tian, H. Zou and J. Mi, J. Chem. Phys., 2013, 139, 024903 CrossRef.
- A. E. Eken, E. J. Tozzi, D. J. Klingenberg and W. Bauhofer, J. Appl. Phys., 2011, 109, 084342 CrossRef.
- G. Kwon, Y. Heo, K. Shin and B. J. Sung, Phys. Rev. E, 2012, 85, 011143 CrossRef PubMed.
- C. Jizhe and N. Mohammad, Modell. Simul. Mater. Sci. Eng., 2016, 24, 065004 CrossRef.
- F. Du, J. E. Fischer and K. I. Winey, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 121404 CrossRef.
- R. Socher, B. Krause, M. T. Müller, R. Boldt and P. Pötschke, Polymer, 2012, 53, 495–504 CrossRef CAS.
- F. Qin and C. Brosseau, J. Appl. Phys., 2012, 111, 061301 CrossRef.
- M. T. Müller, B. Krause, B. Kretzschmar and P. Pötschke, Compos. Sci. Technol., 2011, 71, 1535–1542 CrossRef.
- K. Menzer, B. Krause, R. Boldt, B. Kretzschmar, R. Weidisch and P. Pötschke, Compos. Sci. Technol., 2011, 71, 1936–1943 CrossRef CAS.
- B. J.-P. Adohi, A. Mdarhri, C. Prunier, B. Haidar and C. Brosseau, J. Appl. Phys., 2010, 108, 074108 CrossRef.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- X. Duan, H. Zhang, J. Liu, Y. Gao, X. Zhao and L. Zhang, Polymer, 2019, 168, 138–145 CrossRef CAS.
- Y. Gao, R. Ma, H. Zhang, J. Liu, X. Zhao and L. Zhang, RSC Adv., 2018, 8, 30248–30256 RSC.
- F. Li, X. Duan, H. Zhang, B. Li, J. Liu, Y. Gao and L. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 21822–21831 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Y. Wang, G. J. Weng, S. A. Meguid and A. M. Hamouda, J. Appl. Phys., 2014, 115, 193706 CrossRef.
- Y. Gao, J. Liu, J. Shen, L. Zhang and D. Cao, Polymer, 2014, 55, 1273–1281 CrossRef CAS.
- C. Li, E. T. Thostenson and T.-W. Chou, Appl. Phys. Lett., 2007, 91, 223114 CrossRef.
- S. Nam, H. W. Cho, S. Lim, D. Kim, H. Kim and B. J. Sung, ACS Nano, 2013, 7, 851–856 CrossRef CAS.
- S. Khani, S. Jamali, A. Boromand, M. J. A. Hore and J. Maia, Soft Matter, 2015, 11, 6881–6892 RSC.
- Y. Gao, D. Cao, J. Liu, J. Shen, Y. Wu and L. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 22959–22968 RSC.
- L. Su, P. Wang, Z. Xu, M. Peng and D. Chen, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 369–373 CrossRef CAS.
- M. E. Tuckerman, C. J. Mundy, S. Balasubramanian and M. L. Klein, J. Chem. Phys., 1997, 106, 5615–5621 CrossRef CAS.
- A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef.
- W. Bauhofer, S. C. Schulz, A. E. Eken, T. Skipa, D. Lellinger, I. Alig, E. J. Tozzi and D. J. Klingenberg, Polymer, 2010, 51, 5024–5027 CrossRef CAS.
- J. Léopoldès, C. Barrès, J. L. Leblanc and P. Georget, J. Appl. Polym. Sci., 2004, 91, 577–588 CrossRef.
- P. C. Hiemenz and T. P. Lodge, in Polymer Chemistry, CRC Press, London, New York, 2007, p. 587 Search PubMed.
- T. Zhao and X. Wang, Polymer, 2013, 54, 5241–5249 CrossRef CAS.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999, p. 663 Search PubMed.
- S. I. White, R. M. Mutiso, P. M. Vora, D. Jahnke, S. Hsu, J. M. Kikkawa, J. Li, J. E. Fischer and K. I. Winey, Adv. Funct. Mater., 2010, 20, 2709–2716 CrossRef CAS.
- X.-Y. Qi, D. Yan, Z. Jiang, Y.-K. Cao, Z.-Z. Yu, F. Yavari and N. Koratkar, ACS Appl. Mater. Interfaces, 2011, 3, 3130–3133 CrossRef CAS PubMed.
- W. Bauhofer and J. Z. Kovacs, Compos. Sci. Technol., 2009, 69, 1486–1498 CrossRef CAS.
- R. Ramasubramaniam, J. Chen and H. Liu, Appl. Phys. Lett., 2003, 83, 2928–2930 CrossRef CAS.
- N. G. Sahoo, S. Rana, J. W. Cho, L. Li and S. H. Chan, Prog. Polym. Sci., 2010, 35, 837–867 CrossRef CAS.
- A. Sulong, N. Muhamad, J. Sahari, R. Ramli, B. Deros and J. Park, Eur. J. Sci. Res., 2009, 29, 13–21 Search PubMed.
- S. Gong, Z. H. Zhu, J. Li and S. A. Meguid, J. Appl. Phys., 2014, 116, 194306 CrossRef.
- F. Nilsson, J. Krückel, D. W. Schubert, F. Chen, M. Unge, U. W. Gedde and M. S. Hedenqvist, Compos. Sci. Technol., 2016, 132, 16–23 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra04680a |
| This journal is © The Royal Society of Chemistry 2019 |