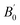Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic, optical and thermoelectric properties of Fe2ZrP compound determined via first-principles calculations
Esmaeil Pakizeh *a,
Jaafar Jalilianb and
Mahnaz Mohammadi
*a,
Jaafar Jalilianb and
Mahnaz Mohammadi c
c
aFaculty of Petroleum and Gas, Yasouj University, Gachsaran, 75813-56001, Iran. E-mail: e.pakizeh@yu.ac.ir; esmaeil_pakizeh@yahoo.com
bDepartment of Physics, Faculty of Science, Yasouj University, Yasouj, Iran
cDepartment of Physics, Faculty of Science, Qom University of Technology, Qom, Iran
First published on 19th August 2019
Abstract
In this study, based on the density functional theory and semi-classical Boltzmann transport theory, we investigated the structural, thermoelectric, optical and phononic properties of the Fe2ZrP compound. The results of the electronic band structure analysis indicate that Fe2ZrP is an indirect band gap semiconductor in the spin-down state with the band gap of 0.48 eV. Thermoelectric properties in the temperature range of 300–800 K were calculated. Fe2ZrP exhibits the high Seebeck coefficient of 512 μV K−1 at room temperature along with the huge power factor of 19.21 × 1011 W m−1 K−2 s−1 at 800 K, suggesting Fe2ZrP as a potential thermoelectric material. The Seebeck coefficient decreased with an increase in temperature, and the highest value was obtained for p-type doped Fe2ZrP when the optimum carrier concentration was 0.22 × 1023 cm−3; the n-type doped Fe2ZrP had high electrical conductivity than the p-type doped Fe2ZrP. Thermal conductivity increased with an increase in chemical potential. Optical calculations illustrated that there was a threshold in the imaginary dielectric function for the spin-down channel. Spin-dependent optical calculations showed that the intraband contributions affected only the spin-up optical spectra due to the free-electron effects. Generally, the results confirmed that the intraband contribution had the main role in the optical spectra in the low energy infra-red and visible ranges of light. We also presented the phononic properties and found that these materials were dynamically stable.
1. Introduction
Thermoelectric (TE) effect involves direct energy conversion by electrons in materials and is thus considered an alternative and “green” energy source. The TE effect has various advantages in industrial applications.1–3 The Peltier and Seebeck effects are the main TE effects. Using the Peltier effect, the TE device can cool materials. On the other hand, via the Seebeck effect, thermal energy can be transformed into electric energy, and this phenomenon is called TE power generation.4 The performance of a thermoelectric material is described by the figure of merit ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature. Thus, to realize efficient energy conversion, a favorable thermoelectric material should possess high ZT, which indicates that a high Seebeck coefficient, high electrical conductivity, and low thermal conductivity are required for achieving efficient energy conversion.5–8In recent years, Heusler compounds have been theoretically investigated, and their TE properties have attracted significant attention from researchers.9–17 Generally, Heusler compounds have the stoichiometric composition XYZ or X2YZ and crystallize in the L21 structure, where X and Y are transition or rare-earth metals and Z is the main group element.18 These materials are half-metallic, where one spin channel shows metallicity, whereas the other spin channels are completely semiconducting. Because of this feature, half-metallic Heusler alloys can be considered as the most important class of spintronic materials.19–23 Half-metallic material alloys have been found in some kinds of materials such as full16,24–29 and half Heusler alloys,15,30,31 binary compounds32–34 and 2D materials.35–37
Recently, in a theoretical study, the effect of Ge substitution on the thermoelectric properties of the Heusler-type alloy Fe2MnSixGe1−x has been investigated by Reshak.13 It has been reported that the Seebeck coefficient (S) for Fe2MnGe exhibits an n-type behavior over the entire concentration range. In contrast, Fe2MnSi has a positive S of up to 250 μV K−1. Comtesse et al.14 have reported the spin polarization TE properties of Co-based half-metallic Heusler compounds using the fully relativistic screened Korringa–Kohn–Rostoker theory. The transport coefficients of Co-based half-metallic Heusler materials are strongly influenced in spin polarization cases. The thermoelectric properties of the CrVNbZn Heusler compound have been investigated by Kara et al. based on the Boltzmann transport theory.9 It has been reported that a unique sharp electronic band, with highest contribution from valence electronic states, increases the TE figure of merit. Bhat et al. have focused on the TE performance of the ferromagnetic CoFeCrAs Heusler alloy. This material presents high S and huge power factor at room temperature.11 The thermoelectric behaviors of Ru2VZ (Z = Si, Ge and Sn) half-metallic full-Heusler compounds have been investigated by Yalcin.12 The TE parameters, such as Pauli magnetic susceptibility, electrical conductivity, S, thermal conductivity and power factor, were obtained by the Boltzmann transport theories; moreover, in recent years, the thermoelectric properties of Heusler compounds have been investigated via experimental studies.38–41 In this context, Chauhan et al. produced Zr1−xHfxCoSb0.9Sn0.1 Heusler alloys by employing high-energy ball-milling processes and investigated the thermoelectric properties of these alloys.38 Their method led to the production of nanoparticles, with low thermal conductivity and high figure of merit, suitable for thermoelectric applications. The thermoelectric properties of the Zr0.5Hf0.5Co0.4Rh0.6Sb1−xSnx (0.15 ≤ x ≤ 0.5) half-Heusler alloys synthesized using a hardened steel jar and balls have been investigated by Maji et al.40 Their team found materials with a high power factor (800 μW K−2) and a low thermal conductivity (2.2 W m−1). An n-type half Heusler compound (HfZrCoSnSb) has been synthesized experimentally by Poon et al.41 They succeeded in achieving a high figure of merit (1.05) at 900 °C. This material was tested for application in p–n couple devices, and it showed good power generation efficiencies reaching 8.7% for the hot-side temperatures of about 700 °C.
A recent study based on the density functional theory and semi-classical Boltzmann transport theory was aimed at providing more detailed information about the electrical, optical, phononic and thermoelectric behaviors of the Fe2ZrP half-metallic ferromagnetic full-Heusler compounds. Due to the novelty of this material, only one theoretical study has been conducted on this compound by Canko et al.42 The electrical and magnetic properties of this material were studied by them. They have concluded that due to its high Curie temperature and sufficient chemical stability, this compound can be a suitable magnetic intermetallic material;42 moreover, although the spin-up electronic band structure is metallic, the spin-down band structure has a semiconductor behavior with the gap of 0.593 eV, and the spin-flip gap is 0.129 eV; due to this property, this compound exists in nature as well as can be synthesized experimentally. Their theoretical study indicates that the Fe2ZrP compound may exhibit significant promise for application in spintronic devices. To complete their study, the thermoelectric and optical properties of this material were examined for the first time in the present study.
2. Computational details
In this study, calculations were performed using density functional theory plane waves and pseudopotentials via the Quantum ESPRESSO package.43 The exchange–correlation term was considered by the Perdew–Burke–Ernzerhof (PBE) functional.44 Moreover, generalized gradient approximation (GGA) and ultrasoft pseudopotentials (US PPs) were utilized. The energy cut-off for the expansion of the wave-functions was set to 30 Ry (due to ultrasoft pseudopotentials and lattice symmetry, this energy was suitable for achieving base-state energy). The electronic wave function was expanded with the energy cutoff value of 300 Ry for charge density. Brillouin zone integration was performed over the Monkhorst–Pack45 10 × 10 × 10 meshes. The lattice constant of the Fe2ZrP compound was optimized until the total energy converged to at least 10−8 Ry. Structure optimization was performed based on variable-cell (vc-relax) calculations. Considering the symmetry structure of this compound, four atoms were used in the simulation, which has been discussed in more detail in the next section. The TE properties of the Fe2ZrP compound were investigated with the BoltzTraP code.46 The denser k-mesh of 24 × 24 × 24 was used for the calculations of the TE properties such as Seebeck coefficient, electrical conductivity, thermal conductivity, specific heat and magnetic susceptibility. The Seebeck coefficient S is related to carrier concentration via the Mott formula as follows:47
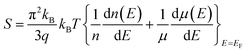 | (1) |
Electrical conductivity is related to carrier concentration as follows:48
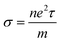 | (2) |
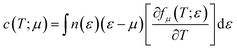 | (3) |
Pauli magnetic susceptibility is related to carrier concentration and chemical potentials as follows:49
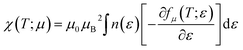 | (4) |
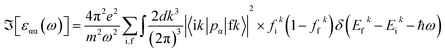 | (5) |
The real part of the complex dielectric function was expanded from the imaginary part using the Kramers–Kronig relations as follows:51–54
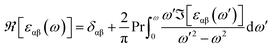 | (6) |
3. Results and discussion
3.1. Structural properties
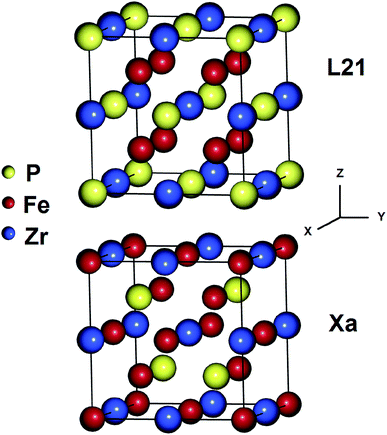
The Heusler alloys crystallize in the L21 and Xa structures, which belong to the Fm3m (no. 225) and F43m (no. 216) space groups, respectively.56 The L21 structure is represented by the general formula X2YZ, where X and Y are transition metals and Z is a main group element. The X atoms occupy the Wyckoff positions 4a (0, 0, 0) and 4c (1/2, 1/2, 1/2), and the Y and the Z atoms are located at 4b (1/4, 1/4, 1/4) and 4d (3/4, 3/4, 3/4), respectively.57 In the Xa structure, the X atoms are placed at the two Wyckoff positions (0, 0, 0) and (0.25, 0.25, 0.25), whereas the Y and Z atoms are located at (0.5, 0.5, 0.5) and (0.75, 0.75, 0.75), respectively. The differences between both the abovementioned structures are shown in Fig. 1.Total energies versus lattice constant were calculated for both the L21 and the Xa structures, and the results for the ferromagnetic (FM) and non-magnetic (NM) states are shown in Fig. 2. According to this figure, ferromagnetic order configuration in the L21 structure was found to be the most stable ground state phase as compared to other phases. The calculated values of lattice parameter (a0), bulk modulus (B0 in GPa) and the pressure derivative of bulk modulus 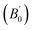 at the equilibrium lattice constant are presented in Table 1. In the previous study, the total energies were plotted in terms of the lattice volume, and it was concluded that the ferromagnetic order configuration in the L21 structure was the most stable phase; this confirmed the results of the present study.42
at the equilibrium lattice constant are presented in Table 1. In the previous study, the total energies were plotted in terms of the lattice volume, and it was concluded that the ferromagnetic order configuration in the L21 structure was the most stable phase; this confirmed the results of the present study.42
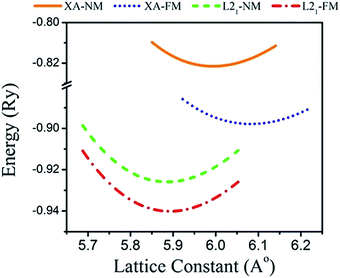 | ||
| Fig. 2 Calculated total energy as a function of the lattice constant of the Fe2ZrP compound in L21- and Xa-type structures. | ||
3.2. Vibrational properties
The thermoelectric properties of materials are often due to the movement of phonons. Materials that have a positive phonon frequency are thermally stable. In previous theoretical studies, to ensure thermoelectric properties, phonon properties were investigated first.58–62 The calculated phonon dispersion curve along the W–L–Γ–X–W–K directions and phonon density of states (PhDOS) are shown in Fig. 3. The calculated results show that the Fe2ZrP crystal is dynamically stable at zero pressure as no negative frequencies (imaginary modes) exist in the entire Brillouin zone. As observed from Fig. 3a, three vibrational modes below 0.5 THz are acoustic branches, and the remaining vibrational modes are optical modes. The number of optical modes is 3N-3. Therefore, the Fe2ZrP crystal with N = 4 atoms in the primitive cell exhibits three acoustic and nine optical modes. The acoustic bands are contributed by the Zr element due to its larger atomic mass.63 The highest frequency at Γ point is about 1.4 THz. According to Fig. 3b, there is no phonon anomaly in the phonon density of states. The heavier atoms are at low frequencies in the range of 0–0.5 THz.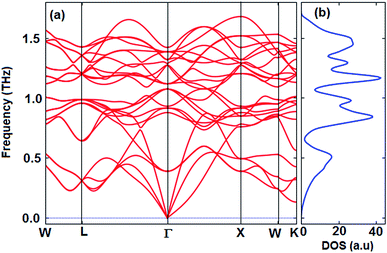 | ||
| Fig. 3 The calculated (a) phonon dispersion and (b) phonon density of states of the Fe2ZrP compound. | ||
3.3. Electronic band structure and density of states
In this subsection, the band structure and density of states of the Fe2ZrP compound have been discussed. Fig. 4 illustrates the spin-resolved band structures of the Fe2ZrP compound along the higher symmetry direction of the Brillouin zone in the majority (Fig. 4a) and minority (Fig. 4b) spin channels. The zero of the energy scale shows the position of the Fermi level. According to Fig. 4a, the spin-up band structure crosses the Fermi level, clearly showing a strong metallic nature. The Fe2ZrP compound exhibits a direct semiconductor behavior in the spin-down channel, with the top of the valence band and the bottom of the conduction band located at ΓV → ΓC (Fig. 4b). We found the direct band gap of about 0.485 eV near the high symmetry direction Γ point. It is obvious that Fe2ZrP is metallic and semiconductive in the majority and minority spin channels, respectively. This suggests that the Fe2ZrP compound exhibits half-metallic ferromagnetic properties. In addition, Canko et al. have shown that the Fermi level is located within the band gap of the spin-down channel but crosses the valence band of the spin-up channel; this is in accordance with the findings of the present study. They found a direct band gap near the high symmetry direction Γ.42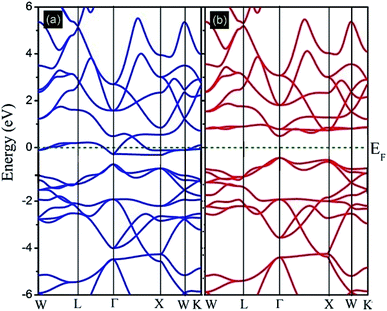 | ||
| Fig. 4 Calculated spin-polarized band structures of the Fe2ZrP compound for (a) spin-up and (b) spin-down electrons. | ||
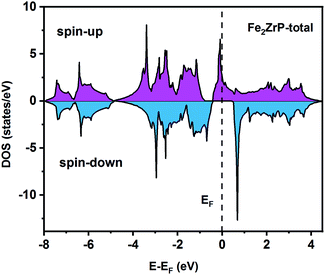
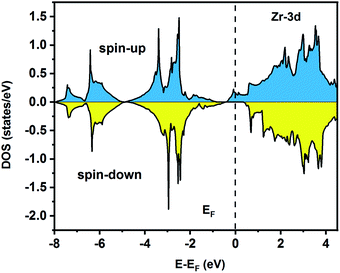
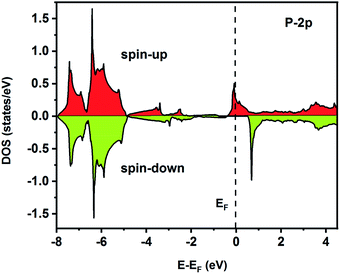
To understand the nature of the electronic states of the Fe2ZrP compound at its equilibrium lattice constant, the spin-polarized total density of states (DOS) and partial density of states (PDOS) are displayed in Fig. 5–8. In the previous study on this material, only DOS was examined; on the other hand, in the present theoretical study, in addition to DOS, PDOS was studied in more detail for the better understanding of the electronic structure of this compound.42 The energy with respect to the Fermi level is signified by a dashed line. As shown in Fig. 5, in the valence band near the Fermi level, the minority (spin-down) and majority (spin-up) spins are semiconductor and metallic, respectively. This confirms that the compound has a half-metallic behavior. According to Fig. 6a, both spin channels mainly originate from the Fe-3d states, with a small contribution from the Zr and P atoms with s and p orbitals. The Fe-4s, Zr-5p, Zr-4s and P-1s states have a slight effect on the formation of the half-metallic band gap. The transition metal Fe and Zr-3d-states make the main contributions to both spin configurations in the energy range from −4 eV to 4 eV. The electrons at EF are fully polarized as the density of spin-up or spin-down channels equals zero. For the Fe2ZrP compound, the energy gap located at EF leads to a 100% spin polarization.
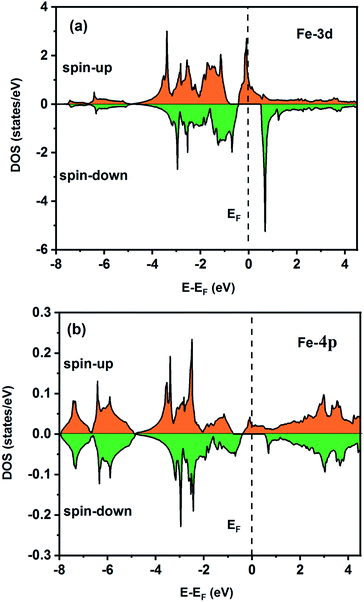 | ||
| Fig. 6 Spin-polarized partial density of states for the Fe atom in the Fe2ZrP compound: (a) 3d and (b) 4p orbitals. | ||
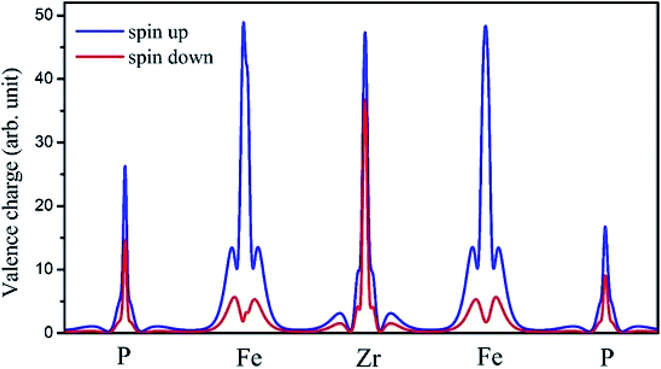
The on-site spin-polarized valence charge density was calculated and is illustrated in Fig. 9 to discuss the origin of magnetic properties in more details. In addition, we selected a crystal direction and made all atoms to lie in this direction to compare charge accumulation between different atoms. As can be observed from Fig. 9, there is an exchange splitting in the valence charge density for all atoms. However, the main difference between spin-up and -down channels is related to the Fe atom. Therefore, similar to other full Heusler alloys X2YZ, the main contribution to the magnetic properties is provided by the X (herein, Fe) atoms. The spin-polarized total and atom-projected DOS of the Fe2ZrP compound are in agreement with a previous study.42
3.4. Thermoelectric properties
The TE properties were calculated in the constant relaxation time approximation within the semi-classical Boltzmann theory using the Boltztrap package.46 The calculated properties were plotted for three considered temperatures: 300, 600, and 800 K.Fig. 10 presents the S of the Fe2ZrP compound as a function of chemical potential (μ) in the range from −2 eV to 2 eV (Fig. 10a) and carrier concentration (Fig. 10b). Fig. 10a shows two peaks, which are located at the chemical potentials of −0.65 and −0.55 eV. The Seebeck coefficient inclined rapidly to zero outside this range. As the temperature increased, S decreased because of the increase in thermal energy. This indicates that this material has a good thermoelectric performance. The maximum value of S is 512 μV K−1 at 300 K. For a higher temperature (800 K), S is slightly decreased to 260 μV K−1. The negative and positive S peaks are −606 and 512 μV K−1 at 300 K, −324, and 301 μV/K at 600 K and −253 and 260 μV K−1 at 800 K, respectively. The positive and negative values of the chemical potential μ indicate that the dopants are electrons (n-type) and holes (p-type), respectively. According to Fig. 10b, the maximum value of S is obtained for p-type doping, and the optimum carrier concentration is 0.22 × 1023 cm−3.
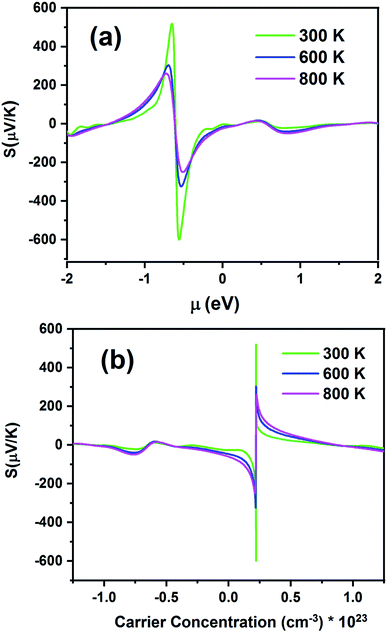 | ||
| Fig. 10 Seebeck coefficients of the Fe2ZrP compound as a function of (a) chemical potential and (b) carrier concentration. | ||
According to eqn (1), S at different temperatures is higher for smaller concentrations. In Table 2, a comparison between the present theoretical study and previous studies is made.64–67 According to this table, as the temperature increases, S decreases, and the Fe2ZrP compound has suitable values for thermoelectric application. The experimental results of other studies related to the Seebeck coefficient of Heusler compounds are presented in Table 3.38,39,41 By comparing the Tables 2 and 3, we concluded that the Fe2ZrP compound had good potential for experimental production.
Fig. 11 shows electrical conductivity (σ/τ) as a function of chemical potential (Fig. 11a) and carrier concentration (Fig. 11b) at different temperatures. Unlike the Seebeck coefficient, the electrical conductivity displays similar behavior at all temperatures.
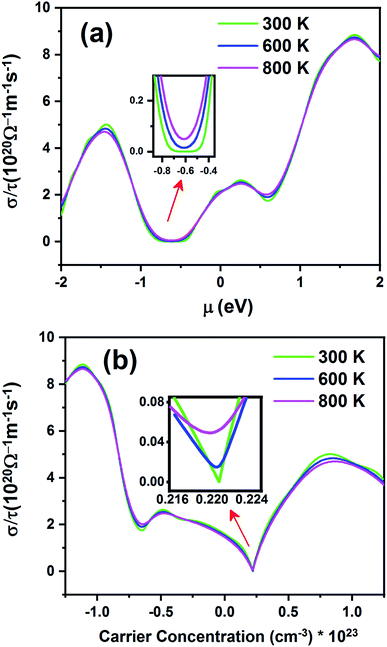 | ||
| Fig. 11 The electrical conductivity of the Fe2ZrP compound as a function of (a) chemical potential and (b) carrier concentration. | ||
According to Fig. 11a, the electrical conductivity increases with an increase in chemical potential. With an increase in chemical potential, the carrier concentration increases, and an increase in mobility increases the conductivity. The inset image in Fig. 11a shows that electrical conductivity is zero in the range from −0.49 to −0.73 at 300 K. As shown in Fig. 11b, the n-type doped compound has higher electrical conductivity than the p-type doped compound. According to eqn (2), the electrical conductivity increases with an increase in carrier concentration. The inset image in Fig. 11b shows that σ/τ is zero at 300 K in the p-type doping area, where the carrier concentration is about 0.22 × 1023 cm−3.
Fig. 12 displays the electronic power factor values (S2σ) as a function of chemical potential relative to the Fermi level (Fig. 12a) and carrier concentration (Fig. 12b) at different temperatures. This quantity investigates the efficiency of the thermoelectric materials. According to Fig. 12a, as the temperature increases, power factor also increases. The maximum value of power factor is 19.21 × 1011 W m−1 K−2 s−1 for negative chemical potential at 800 K. At room temperature, the power factor is slightly decreased to 4.43 × 1011 W m−1 K−2 s−1. As shown in Fig. 12b, the maximum value of power factor is located in the p-type doping area (0.22 × 1023 cm−3), which is higher than that of the n-type doping area (8.61 × 1011 W m−1 K−2 s−1).
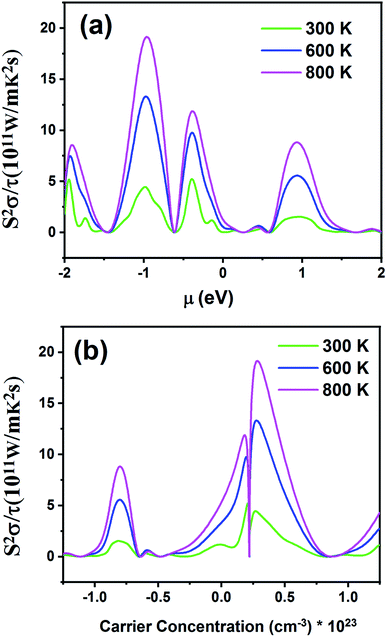 | ||
| Fig. 12 The power factor of the Fe2ZrP material as a function of (a) chemical potential and (b) carrier concentration. | ||
Fig. 13 displays the electronic thermal conductivity (κ/τ) as a function of chemical potential (Fig. 13a) and carrier concentration (Fig. 13b) at three constant temperatures (300, 600 and 800 K). According to this figure, as the temperature increases, thermal conductivity also increases. To increase the thermoelectric properties, the materials must have large S, high electrical conductivity, and low thermal conductivity.68 Therefore, the optimum temperature to obtain lower κe/τ is 300 K. According to Fig. 13a, the thermal conductivity increases with an increase in chemical potential. The thermal conductivity is zero in the range from −0.68 to −0.55 at 300 K. As shown in Fig. 13b, the n-type doped compound has higher thermal conductivity than the p-type doped compound. Moreover, the electrical conductivity increases with an increase in carrier concentration. The inset image in Fig. 13b shows that κ/τ is zero at 300 K in the p-type doping area where the carrier concentration is about 0.22 × 1023 cm−3.
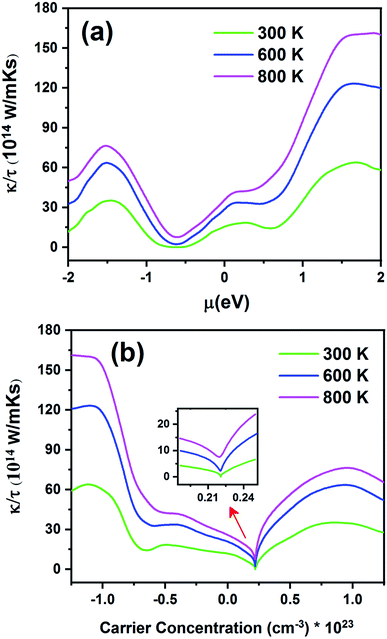 | ||
| Fig. 13 The electronic thermal conductivity of the Fe2ZrP compound as a function of (a) chemical potential and (b) carrier concentration. | ||
Fig. 14 displays the electronic specific heat (c) as a function of chemical potential (Fig. 14a) and carrier concentration (Fig. 14b) at different temperatures. According to this figure, as the temperature increases, specific heat also increases. According to eqn (3), the specific heat increases with an increase in carrier concentration and chemical potential. According to Fig. 14a, the maximum value of the specific heat is 11.22 J (mol K)−1 for negative chemical potential at 800 K. At room temperature, the specific heat is decreased to 4.81 J mol−1 K−1. As shown in Fig. 14b, the maximum value of specific heat is obtained in the p-type doping area (11.19 × 1023 cm−3), which is higher than that of the n-type doping area (8.7 J mol−1 K−1). The inset image in Fig. 14b shows that the specific heat is zero at 300 K in the p-type doping area where the carrier concentration is about 0.22 × 1023 cm−3.
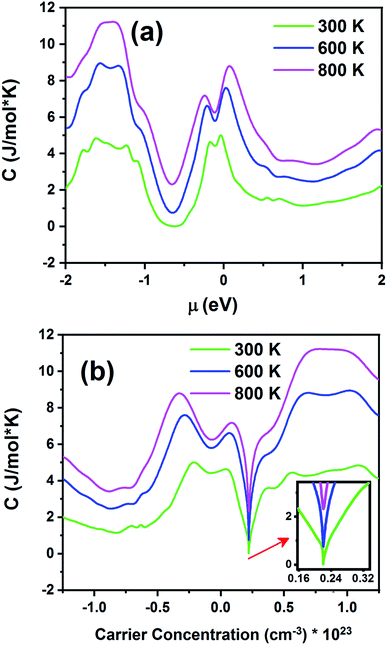 | ||
| Fig. 14 The electronic specific heat of the Fe2ZrP material as a function of (a) chemical potential and (b) carrier concentration. | ||
Fig. 15 exhibits the Pauli magnetic susceptibility (χ) as a function of chemical potential (Fig. 15a) and carrier concentration (Fig. 15b) at different temperatures. According to Fig. 15a, the Pauli magnetic susceptibility displays an almost similar behavior at all temperatures except near the Fermi level. At this point, as the temperature increases, χ decreases. The maximum value of χ is 38.65 × 10−10 m3 mol−1 at 300 K. For a higher temperature (800 K), χ is slightly decreased to 27.12 × 10−10 m3 mol−1. As observed from the inset image shown in Fig. 15a, the Pauli magnetic susceptibility is zero in the range from −0.68 to −0.55 at 300 K. According to eqn (4) and Fig. 15b, the Pauli magnetic susceptibility increases with an increase in carrier concentration. As shown in Fig. 15b, the maximum value of specific heat is obtained in the n-type doping area (−0.08 × 1023 cm−3). The inset image in Fig. 15b shows that the Pauli magnetic susceptibility is zero at 300 K in the p-type doping area where the carrier concentration is about 0.22 × 1023 cm−3.
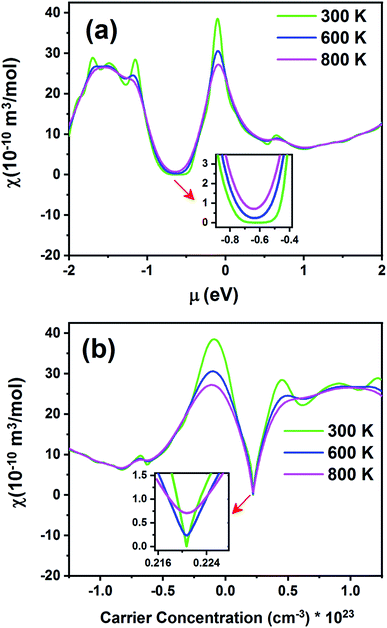 | ||
| Fig. 15 The Pauli magnetic susceptibility of the Fe2ZrP material as a function of (a) chemical potential and (b) carrier concentration. | ||
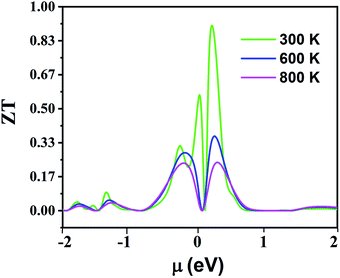
Fig. 16 displays the electronic figure of merit (ZT) values of the Fe2ZrP compound as a function of chemical potential at three constant temperatures (300, 600 and 800 K). This quantity investigates the efficiency of the thermoelectric materials. According to this figure, as the temperature increases, ZT decreases. At all temperatures, ZT is low where chemical potential is negative. According to this figure, the best temperature for thermoelectric applications is 300 K because ZT has a good value in the negative and positive fields of chemical potential. In Table 4, a comparison between the present theoretical study and previous studies is shown.64–66,69 According to the table, the Fe2ZrP compounds are good thermoelectric materials. The experimental results of other studies on Heusler compounds based on the figure of merit are also presented in Table 5.38,39,41 By comparing the Tables 4 and 5, we conclude that the Fe2ZrP compounds have a suitable figure of merit.
3.5. Optical properties
Herein, the optical properties of the Fe2ZrP compound have been studied using a random phase approximation (RPA) method. To investigate the optical properties of a half-metallic material, it was necessary to consider both intraband and interband contributions in our calculations; due to their transitional nature, the intraband transitions affected only the infra-red and visible ranges of light in the optical spectra.70The spin-dependent imaginary and real parts of the dielectric function are illustrated in Fig. 17. The electronic band structure exhibits that the spin-up channel has a metallic behavior, whereas the spin-down channel has a semiconductive behavior. Therefore, intraband transitions occur only for the free electrons of the spin-up channel. As a result, the intraband, interband and total contributions have been plotted only for the spin-up channel. As can be observed, the intraband transitions have the main role in the range of 0–2 eV in the real and imaginary parts of the spin-up channel. This trend refers to the free electron effect in the spin-up channel. For metallic materials in low frequency range, the refractive index n(ω) is lower than the extinction coefficient k(ω); thus, the real part of dielectric function has a negative value, ε1 = n2 − k2 < 0. The imaginary part of the dielectric function refers to optical absorption from the occupied states to the unoccupied states. In Fig. 17c, we can see a high value of absorption from zero energy to 2 eV (free electron absorption), whereas there is an absorption threshold in the spin-down imaginary part spectrum (Fig. 17d) that is according to the half-metallic band gap structure of the spin-down channel.
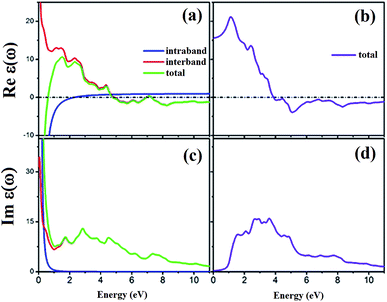 | ||
| Fig. 17 Calculated spin-dependent real part of dielectric function for (a) spin-up and (b) spin-down channels and the imaginary part for (c) spin-up and (d) spin-down channels. | ||
Furthermore, the total spectra, i.e. spin up plus spin down spectra, of optical conductivity and reflectivity were calculated and are plotted in Fig. 18 with and without intraband transitions. The results indicate that due to the partially occupied states in the spin-up band structure of Fe2ZrP around the Fermi level, the intraband contribution has the main role in the infra-red range of optical spectra. This phenomenon leads to a high reflectivity spectrum in the infra-red range of incident light.
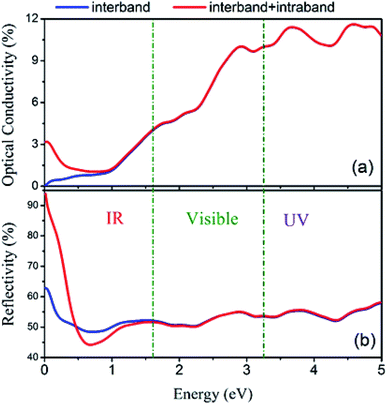 | ||
| Fig. 18 (a) Optical conductivity and (b) reflectivity spectra with and without considering intraband transitions. | ||
4. Conclusion
Herein, the electronic, phononic and thermoelectric properties of the Fe2ZrP compound were calculated using the DFT and Boltzmann transport theory calculations. It was found that this material was half-metallic with the indirect band gap of 0.485 eV along the ΓV–ΓC symmetry line. The phonon density of states and phonon dispersion curves confirm that the Fe2ZrP compound is dynamically stable. The results of Boltzmann calculations showed that the Fe2ZrP compound exhibited better thermoelectric properties after p-type doping than after n-type doping; the highest S value was obtained at the temperature of 300 K upon p-type doping. The thermoelectric and phononic properties of the Fe2ZrP compound were considered for the first time in this study. The maximum value of the power factor reaches 19.21 × 1011 W m−1 K−2 at the hole concentration of 0.22 × 1023 cm−3 and about 8.61 × 1011 W m−1 K−2 s−1 at the electron concentration at 800 K. The electrical and thermal conductivity increase with the increasing chemical potential. This study shows that the Fe2ZrP compound has a good potential for application in the thermoelectric field. The optical calculations confirm that the intraband contribution has the main role in the low energy ranges (infra-red and visible) of optical spectra.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computing resources were supported by the Dena High-Performance Computing (HPC) of Yasouj University.References
- A. M. Adam, et al., Ultra thin bismuth selenide-bismuth telluride layers for thermoelectric applications, Mater. Chem. Phys., 2019, 224, 264–270 CrossRef CAS.
- S. Anwar, et al., Spray pyrolysis deposited tin selenide thin films for thermoelectric applications, Mater. Chem. Phys., 2015, 153, 236–242 CrossRef CAS.
- Y. Lee, et al., Microstructural evolution of laser-brazed joint of Mg2Si and HMS on DBC substrate for thermoelectric generator, Mater. Chem. Phys., 2019, 227, 352–357 CrossRef CAS.
- I. Terasaki, 13 - Introduction to thermoelectricity, in Materials for Energy Conversion Devices, ed. C. C. Sorrell, S. Sugihara and J. Nowotny, Woodhead Publishing, 2005, pp. 339–357 Search PubMed.
- G. Sansone, A. Ferretti and L. Maschio, Ab initio electronic transport and thermoelectric properties of solids from full and range-separated hybrid functionals, J. Chem. Phys., 2017, 147(11), 114101 CrossRef PubMed.
- G. Yumnam, T. Pandey and A. K. Singh, High temperature thermoelectric properties of Zr and Hf based transition metal dichalcogenides: A first principles study, J. Chem. Phys., 2015, 143(23), 234704 CrossRef PubMed.
- H. Zhang, et al., A new type of thermoelectric material, EuZn2Sb2, J. Chem. Phys., 2008, 129(16), 164713 CrossRef PubMed.
- D. Wang, et al., First-principles investigation of organic semiconductors for thermoelectric applications, J. Chem. Phys., 2009, 131(22), 224704 CrossRef PubMed.
- H. Kara, M. U. Kahaly and K. Özdoğan, Thermoelectric response of quaternary Heusler compound CrVNbZn, J. Alloys Compd., 2018, 735, 950–958 CrossRef CAS.
- S. Singh, Assessing the thermoelectric properties of ScRhTe half-heusler compound, Comput. Condens. Matter, 2017, 13, 120–126 CrossRef.
- T. M. Bhat and D. C. Gupta, First-principles study of high spin-polarization and thermoelectric efficiency of ferromagnetic CoFeCrAs quaternary Heusler alloy, J. Magn. Magn. Mater., 2018, 449, 493–499 CrossRef CAS.
- B. G. Yalcin, Ground state properties and thermoelectric behavior of Ru2VZ (Z= Si, ge, sn) half-metallic ferromagnetic full-Heusler compounds, J. Magn. Magn. Mater., 2016, 408, 137–146 CrossRef CAS.
- A. H. Reshak, Fe 2 MnSi x Ge 1− x: influence thermoelectric properties of varying the germanium content, RSC Adv., 2014, 4(74), 39565–39571 RSC.
- D. Comtesse, et al., First-principles study of spin-dependent thermoelectric properties of half-metallic Heusler thin films between platinum leads, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(9), 094410 CrossRef.
- L. Chen, et al., High thermoelectric figure of merit by resonant dopant in half-Heusler alloys, AIP Adv., 2017, 7(6), 065208 CrossRef.
- D. P. Rai, et al., Electronic, optical, and thermoelectric properties of Fe2+xV1−xAl, AIP Adv., 2017, 7(4), 045118 CrossRef.
- T. M. Bhat, M. Nabi and D. C. Gupta, Structural, elastic, thermodynamic and thermoelectric properties of Fe2TiSn Heusler alloy: High pressure study, Results Phys., 2019, 12, 15–20 CrossRef.
- F. Heusler and E. Take, The nature of the Heusler alloys, Trans. Faraday Soc., 1912, 8(October), 169–184 RSC.
- C. J. Palmstrøm, Heusler compounds and spintronics, Prog. Cryst. Growth Charact. Mater., 2016, 62(2), 371–397 CrossRef.
- M. Jourdan, Revival of Heusler compounds for spintronics, Mater. Today, 2014, 17(8), 362–363 CrossRef.
- L. Bainsla, et al., CoRuFeX (X= Si and Ge) Heusler alloys: High TC materials for spintronic applications, J. Alloys Compd., 2015, 651, 631–635 CrossRef CAS.
- A. Hirohata, et al., Heusler-alloy films for spintronic devices, Appl. Phys. A: Mater. Sci. Process., 2013, 111(2), 423–430 CrossRef CAS.
- T. Graf, C. Felser and S. S. P. Parkin, Heusler Compounds: Applications in Spintronics, in Handbook of Spintronics, ed. Y. Xu, D. D. Awschalom, and J. Nitta, Springer Netherlands, Dordrecht, 2014, pp. 1–24 Search PubMed.
- S. Qi, J. Shen and C.-H. Zhang, First-principles study on the structural, electronic and magnetic properties of the Ti2VZ (Z = Si, Ge, Sn) full-Heusler compounds, Mater. Chem. Phys., 2015, 164, 177–182 CrossRef CAS.
- T. Bae, et al., Effects of magnetic seed-layers on the structural and magnetic properties of Co2MnSi Heusler alloy, Mater. Chem. Phys., 2012, 136(2), 577–581 CrossRef CAS.
- S. Yousuf and D. C. Gupta, Investigation of electronic, magnetic and thermoelectric properties of Zr2NiZ (Z = Al,Ga) ferromagnets, Mater. Chem. Phys., 2017, 192, 33–40 CrossRef CAS.
- D. Betto, et al., The zero-moment half metal: How could it change spin electronics, AIP Adv., 2016, 6(5), 055601 CrossRef.
- A. Tavana and L. Mikaeilzadeh, A first principles study of iron doping in Ni2CoGa magnetic shape memory alloy, AIP Adv., 2015, 5(11), 117210 CrossRef.
- M. Zipporah, et al., First-principle investigation of structural, electronic and magnetic properties of Co2VIn and CoVIn Heusler compounds, AIP Adv., 2017, 7(5), 055705 CrossRef.
- A. Hamidani, B. Bennecer and B. Boutarfa, Structural and elastic properties of the half-Heusler compounds IrMnZ (Z=Al, Sn and Sb), Mater. Chem. Phys., 2009, 114(2), 732–735 CrossRef CAS.
- W. Huang, et al., Structural and electronic properties of half-Heusler alloy PdMnBi calculated from first principles, Mater. Chem. Phys., 2014, 148(1), 32–38 CrossRef CAS.
- Z.-Y. Feng and J.-M. Zhang, Structural, electronic, magnetic and optical properties of semiconductor Zn1− xMoxTe compound, J. Phys. Chem. Solids, 2018, 114, 240–245 CrossRef CAS.
- N. Mehmood and R. Ahmad, Structural, electronic, magnetic and optical investigations of half-Heusler compounds YZSb (Z= Cr, Mn): FP-LAPW method, J. Supercond. Novel Magn., 2018, 31(3), 879–888 CrossRef CAS.
- X.-H. Kang and J.-M. Zhang, A comparison study of the structural, electronic, magnetic and optical properties of yttrium-based Heusler alloys Y3Si, Y2CrSi and ScYCrSi, Mater. Chem. Phys., 2018, 211, 283–294 CrossRef CAS.
- J.-J. He, et al., Electronic, magnetic and transport properties of transition metal-doped holely C2N-h2D nanoribbons, Phys. B, 2018, 528, 1–8 CrossRef CAS.
- Y. Nie, et al., Room-temperature half-metallicity in monolayer honeycomb structures of group-V binary compounds with carrier doping, Phys. Rev. B, 2017, 96(7), 075401 CrossRef.
- Z. Xu, et al., Electronic and magnetic behaviors of B, N, and 3d transition metal substitutions in germanium carbide monolayer, J. Magn. Magn. Mater., 2018, 451, 799–807 CrossRef CAS.
- N. S. Chauhan, et al., Enhanced thermoelectric performance in p-type ZrCoSb based half-Heusler alloys employing nanostructuring and compositional modulation, J. Materiomics, 2019, 5(1), 94–102 CrossRef.
- N. S. Chauhan, et al., Facile fabrication of p- and n-type half-Heusler alloys with enhanced thermoelectric performance and low specific contact resistance employing spark plasma sintering, Mater. Lett., 2018, 228, 250–253 CrossRef CAS.
- P. Maji, et al., Thermoelectric performance of nanostructured p-type Zr0.5Hf0.5Co0.4Rh0.6Sb1−xSnx half-Heusler alloys, J. Solid State Chem., 2013, 202, 70–76 CrossRef CAS.
- S. J. Poon, et al., Half-Heusler phases and nanocomposites as emerging high-ZT thermoelectric materials, J. Mater. Res., 2011, 26(22), 2795–2802 CrossRef CAS.
- O. Canko, et al., Magnetism and Half-Metallicity in the Fe2ZrP Heusler Alloy, J. Supercond. Novel Magn., 2016, 29(10), 2573–2578 CrossRef CAS.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- M. Cutler and N. F. Mott, Observation of Anderson localization in an electron gas, Phys. Rev., 1969, 181(3), 1336 CrossRef CAS.
- P. Drude, Zur elektronentheorie der metalle, Ann. Phys., 1900, 306(3), 566–613 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid state physics, Saunders college, Philadelphia, Pa, 1976 Search PubMed.
- R. Abt, C. Ambrosch-Draxl and P. Knoll, Optical response of high temperature superconductors by full potential LAPW band structure calculations, Phys. B, 1994, 194, 1451–1452 CrossRef.
- M. Gajdoš, et al., Linear optical properties in the projector-augmented wave methodology, Phys. Rev. B, 2006, 73(4), 045112 CrossRef.
- F. Behzadi, E. Saievar-Iranizad and E. Pakizeh, Optical study on single-layer photoluminescent graphene oxide nanosheets through a simple and green hydrothermal method, J. Photochem. Photobiol., A, 2018, 364, 595–601 CrossRef CAS.
- E. Pakizeh and M. Moradi, Kramers–Kronig method for determination of optical properties of PZT nanotubes fabricated by sol–gel method and porous anodic alumina with high aspect ratio, Int. J. Mod. Phys. B, 2018, 32(08), 1850096 CrossRef CAS.
- E. Pakizeh and M. Moradi, Effect of particle size on the optical properties of lead zirconate titanate nanopowders, J. Am. Ceram. Soc., 2018, 101(12), 5335–5345 CrossRef CAS.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175(1), 1–14 CrossRef CAS.
- S. Ouardi, et al., Realization of spin gapless semiconductors: the Heusler compound Mn 2 CoAl, Phys. Rev. Lett., 2013, 110(10), 100401 CrossRef PubMed.
- M. Katsnelson, et al., Half-metallic ferromagnets: From band structure to many-body effects, Rev. Mod. Phys., 2008, 80(2), 315 CrossRef CAS.
- P. D. Patel, et al., Electronic, magnetic, thermoelectric and lattice dynamical properties of full heusler alloy Mn2RhSi: DFT study, Phys. B, 2018, 550, 376–382 CrossRef CAS.
- X. Wang, et al., Phonon spectrum and thermodynamic properties of LaCoO3 based on first-principles theory, Comput. Mater. Sci., 2017, 136, 191–197 CrossRef CAS.
- B. Sabir, et al., First principle study of electronic, mechanical, optical and thermoelectric properties of CsMO3 (M = Ta, Nb) compounds for optoelectronic devices, J. Mol. Graphics Modell., 2019, 86, 19–26 CrossRef CAS PubMed.
- P. D. Patel, et al., The first principle calculation of structural, electronic, magnetic, elastic, thermal and lattice dynamical properties of fully compensated ferrimagnetic spin-gapless heusler alloy Zr2MnGa, Comput. Condens. Matter, 2018, 15, 61–68 CrossRef.
- V. Kanchana, et al., Density functional study of elastic and vibrational properties of the Heusler-type alloys Fe 2 VAl and Fe 2 VGa, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(12), 125108 CrossRef.
- W. Li and N. Mingo, Lattice dynamics and thermal conductivity of skutterudites CoSb 3 and IrSb 3 from first principles: Why IrSb 3 is a better thermal conductor than CoSb 3, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(9), 094302 CrossRef.
- M. Gürth, et al., Thermoelectric high ZT half-Heusler alloys Ti1−x−yZrxHfyNiSn (0 ≤ x ≤ 1; 0 ≤ y ≤ 1), Acta Mater., 2016, 104, 210–222 CrossRef.
- H. Joshi, et al., Thermoelectric properties of tetragonal half-Heusler compounds, TiXSb (X = Ge, Si): A probe from Density Functional Theory (DFT), J. Alloys Compd., 2017, 726, 1155–1160 CrossRef CAS.
- S. Yousuf and D. C. Gupta, Thermoelectric and mechanical properties of gapless Zr2MnAl compound, Indian J. Phys., 2017, 91(1), 33–41 CrossRef CAS.
- J. Li, et al., Electronic and thermoelectric properties of nonmagnetic inverse Heusler semiconductors Sc2FeSi and Sc2FeGe, J. Magn. Magn. Mater., 2017, 442, 371–376 CrossRef CAS.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7(2), 105 CrossRef CAS PubMed.
- H. A. Rahnamaye Aliabad, et al., Thermoelectric and phononic properties of (Gd, Tb) MnO3 compounds: DFT calculations, J. Alloys Compd., 2017, 690, 942–952 CrossRef CAS.
- J. Jalilian, S. Fakhri and A. Zolfaghari, Comment on “DFT investigation of structural, electronic and optical properties of pure and Er-doped ZnO: Modified Becke-Johnson exchange potential”, Optik, 2018, 156, 99–103 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |