Computational design of enhanced detoxification activity of a zearalenone lactonase from Clonostachys rosea in acidic medium

Abstract

Computational design of pH-activity profiles for enzymes is of great importance in industrial applications. In this research, a computational strategy was developed to engineer the pH-activity profile of a zearalenone lactonase (ZHD101) from Clonostachys rosea to promote its activity in acidic medium. The active site pK_a values of ZHD101 were computationally designed by introducing positively charged lysine mutations on the enzyme surface, and the experimental results showed that two variants, M2(D157K) and M9(E171K), increased the catalytic efficiencies of ZHD101 modestly under acidic conditions. Moreover, two variants, M8(D133K) and M9(E171K), were shown to increase the turnover numbers by 2.73 and 2.06-fold with respect to wild type, respectively, though their apparent Michaelis constants were concomitantly increased. These results imply that the active site pK_a value change might affect the pH-activity profile of the enzyme. Our computational strategy for pH-activity profile engineering considers protein stability; therefore, limited experimental validation is needed to discover beneficial mutations under shifted pH conditions.

---

1 Introduction

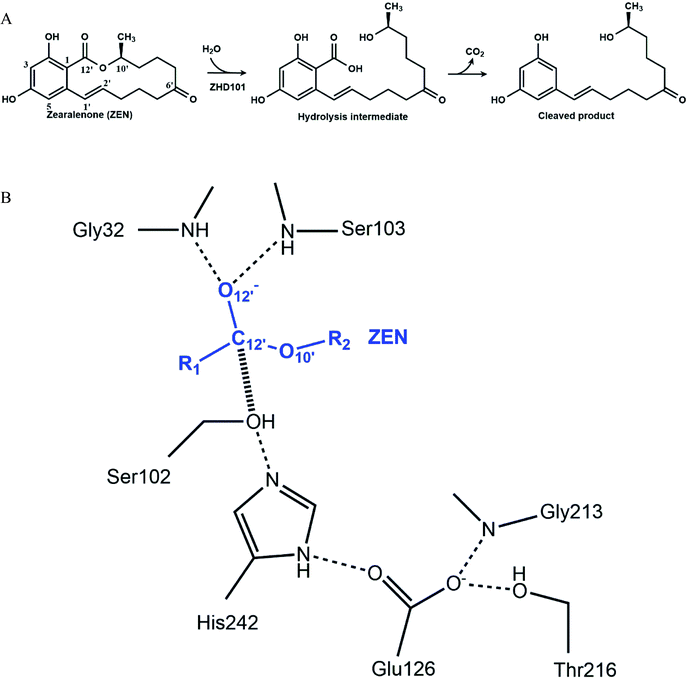
Enzymes are efficient biological catalysts that achieve chemical transformations under mild conditions such as neutral pH values. Industrial reaction conditions generally lie outside of enzymes' optimal pH range, and this leads to marked decreases in their activity. Modifying reaction conditions to accommodate enzymes' optimal working range may be infeasible, because this may come with high costs, generate considerable waste, or render the desired product unstable under the adjusted pH values. Protein engineering is needed to overcome these limitations and generate enzymatic activity in acidic or basic environments.^1–4 To retain enzymatic activity at reaction pH values that deviate from the optimal range, the pH-activity profile needs to be changed. Various strategies can be employed to shift an enzyme's pH-activity. The first strategy is to modify the surface charge of the enzyme to alter long-range charge–charge interactions. Making the enzyme surface more positively charged lowers the pK_a values of ionizable groups, while making the enzymatic surface more negatively charged raises them.⁵ Three decades ago, Fersht and colleagues demonstrated that changing the surface charge of enzymes could generate a significant pH-activity shift: removal of surface charge through site-directed mutagenesis lowered the pK_a of an active-site histidine in hydrolase.^5–7 Change of charge affects pH-activity profile through electrostatic shielding and field effects on catalysis. Recently, acidic or basic residues have been introduced to the enzyme to shift the pH-activity profiles of Aspergillus niger phyA phytase⁸ and Bacillus circulans xylanase.⁹ Replacing residues that directly contact with catalytic residues (e.g., residues forming a hydrophobic environment around or hydrogen bonds/salt bridges with catalytic residues) can also generate a pH-activity shift. Such molecular interactions can affect an enzyme's pH-activity profile.^10–12 A straightforward strategy is to change the catalytic motif into the one that performs better under the desired pH conditions. Gordon et al. studied an enzyme using the Ser–Glu–Asp triad. Unlike the Ser–His–Asp/Glu catalytic triad, which is active at neutral pH values, Ser–Glu–Asp can catalyze reactions under acidic conditions.¹³ The glutamic acid residue replaces the role of histidine to capture the proton from the serine. Its pK_a is much lower than histidine; therefore, it is active at low pH.

Although rational design approaches to generate pH-activity shift in enzymes have achieved a few modest successes, computational design of highly active mutants in acidic or basic environments is still a great challenge in enzyme engineering. In this paper, computational strategies were applied to redesign a lactonase, thus it would catalyze the hydrolysis of zearalenone (ZEN) efficiently in acidic medium. ZEN, a lactone derived from 2,4-dihydroxybenzoic acid, is an oestrogenic mycotoxin produced by various Fusarium species in corn and other cereals.^14–16 The carcinogenicity, genotoxicity, immunotoxicity, and estrogenic activity of ZEN makes it the most important mycotoxin worldwide,¹⁷ and its decontamination is a thorny problem in the feed and breeding industry. Among various detoxifying strategies, enzymatic detoxification seems to be practical and promising.^18–35 A lactonase named ZHD101 from Clonostachys rosea IFO 7063 was reported to cleave the ester bond of ZEN efficiently (Fig. 1A), thereby reducing its toxicity.^22–24 The optimal pH-activity profile of ZHD101 facilitates activity at neutral or slightly basic conditions, and its catalytic activity to facilitate ZEN hydrolysis declines abruptly with decreased pH value.²⁴ In the ethanol fuel industry, grains are fermented to produce ethanol, generating large amounts of waste mash, which is further processed with acid and transformed into dried distillers' grains and solubles (DDGS).³⁶ Because grain crops are susceptible to ZEN, the concentration of ZEN in DDGS can be relatively high. Therefore, the waste mash requires detoxification prior to processing. However, the waste mash is acidic, and ZEN cannot be hydrolyzed by ZHD101 directly in such an environment. Therefore, ZHD101 needs to be rationally designed to work efficiently in acidic environments.

Fig. 1 Mechanism of zearalenone hydrolysis catalyzed by ZHD101. (A) Reaction scheme. (B) Tetrahedral intermediate at the acylation step. The dashed lines indicate hydrogen bonds, and the hashed line represents the covalent bond generated in the nucleophilic attack by S102.

The catalytic machinery used by the lactonase ZHD101 is the classical catalytic triad (Ser102–His242–Glu126, Fig. 1B), where His242 acts as a general base assisting the nucleophile Ser102 to attack the carbonyl group of ZEN.^37,38 The problem is that the histidine residue His242 has a pK_a value of about 6.04 (for free amino acids³⁹), which means that it is mostly protonated at pH values lower than 6. Consequently, its role as a general base is greatly weakened by this protonation that undermines its ability to capture the HG proton of Ser102. In this research, we employ a rational design strategy to shift the pH-activity profile of ZHD101 into the acidic range. We do this by modifying the electrostatic environment of His242 to reduce its pK_a value and render it less inclined to protonation in acidic solutions, so that it will maintain its hydrogen-capturing ability. Here, two strategies are applied to change the electrostatic environment of His242: one is the introduction of an additional positively charged lysine on the protein surface of ZHD101,^5–7 and the other is a redesign of the surrounding environment of His242 to change its hydrophobicity.^11,40 A requirement was that the introduced mutations must not cause destructive change to the protein structure.⁴¹ The pK_a values of the polar and charged residues of ZHD101 were calculated by DelPhiPKa,^42,43 an efficient program for pK_a calculations of proteins that allows for energetic and structural analysis of pK_a shifts. The mutations to ZHD101 were predicted by our computational enzyme design program PRODA.^44–48 The predicted mutations that decrease the calculated pK_a value of His242 and cause no significant folding energy increase were further verified by enzymatic activity assay in acidic medium.

2 Materials and methods

2.1 Structure data

The crystal structure of the lactonase ZHD101 from Clonostachys rosea IFO 7063 (PDB ID: 3WZL) was taken directly from the Protein Data Bank.³⁷ Water molecules were stripped from the crystal structure, and the hydrogen atoms were added by PRODA using the topological parameters of the CHARMM 22 all-atom force field.⁴⁹ The atomic coordinates of ZEN were taken from the Cambridge Structure Database (CSD),⁵⁰ and its hydrogen atoms were added using the Discovery Studio molecular modeling software package.

2.2 Computational enzyme design

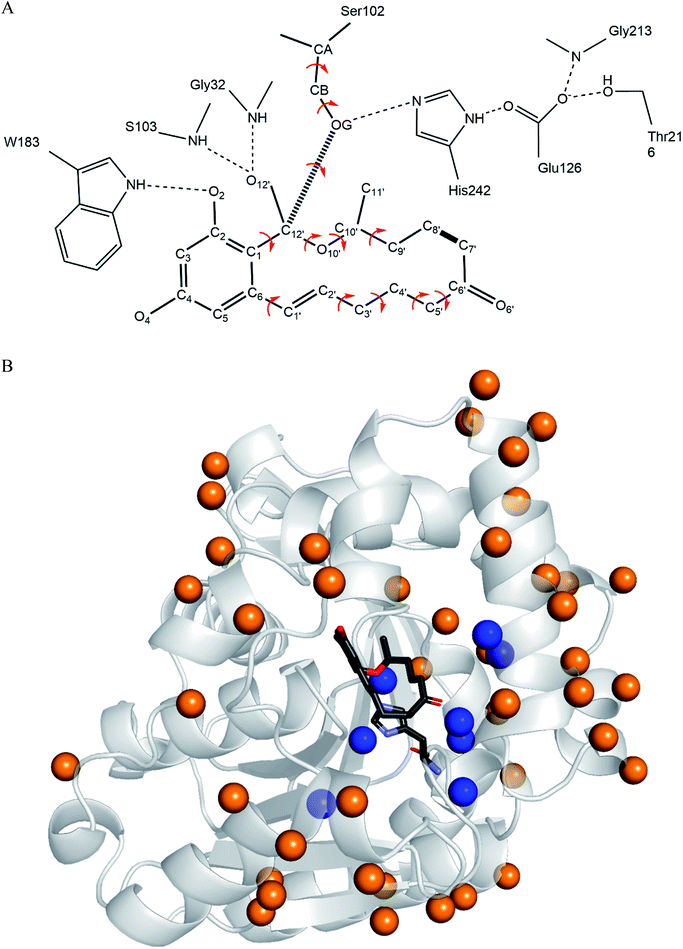
The computational redesign of lactonase ZHD101 to improve its catalytic activity towards ZEN hydrolysis in acidic medium was conducted using the PRODA computational enzyme design program starting with the Protein Data Bank structure 3WZL. The design principle was to modify the electrostatic environment of His242 and decrease its pK_a. Two design schemes were applied: one was the introduction of additional positive charges on the surface of ZHD101. Variations to lysine were allowed at positions neither too close to nor too far away from the active site. Specifically, residues on the protein surface and 8–20 Å from His242 were allowed to mutate to lysine; the list of those residues is shown in Table S1.† Gly and Pro were excluded from this list because of their critical role in protein structure, and Lys, Arg, and His were ruled out because they are positively charged in acidic medium. The other scheme was the introduction of weak positive charge in the active pocket. In total, 8 positions (D31, C101, V153, M154, V158, F221, M241, and F243) lying around His242 were allowed to be assumed to take on a polar amino acid H in acidic environments (in addition to existing as their native types). The residues in the vicinity of the type-changing residues, including those lying in the active site, were subjected to side chain conformation optimization (Tables S1 and S2†). The backbone atoms at the design positions and all atoms at other positions were kept rigid and referenced as the template of the scaffold. A backbone-independent rotamer library compiled by Xiang and Honig,⁵¹ which contains 11 810 original rotamers, was used to model the side chain conformations of the design sites. Moreover, the crystal conformation of the native amino acid at each design position was included in the rotamer library. The atomic and internal coordination parameters for amino acids were taken from the CHARMM 22 all-atom force field.⁴⁹ To represent the translational, rotational, and conformational freedom of the transition state (TS) of ZEN at the active site, a rotamer library of the TS with 276 conformers was generated based on the catalytic geometrical constraints (Table S3†) and placing rules (Table S4†) using the targeted small molecule placement approach developed in our earlier work. As ZEN is a cyclic molecule, the systematic strategy to search its conformational space is to break the lactone ring, yielding a pseudo-acyclic molecule that can be treated by our small molecule placement approach. When searching the conformational space of ZEN, three intramolecular parameters (including the bond length between atoms C_7′ and C_8′; Fig. 2B) and two bond angles (∠C_6′–C_7′–C_8′ and ∠C_7′–C_8′–C_9′) at these two atoms should be checked. The atomic parameters of ZEN were obtained from CHARMM 22 force field model compounds, and the atomic partial charges were assigned based on the PARSE model. The protein-ligand interactions of the enzyme-TS complex system in PRODA were calculated using the Molecular Mechanics-Generalized Born/Surface Area free energy function, with a reference state of both the scaffold template and isolated ligand in solvent. The amino acid sequences of the mutants corresponding to the global or near-global minimum energy conformations of the enzyme-TS complex system were obtained using the Dead-End Elimination/Linear Programming/Mixed-Integer Linear Programming-based deterministic combinatorial optimization algorithm.

Fig. 2 ZEN rotamer generation and design sites on ZHD101. (A) Targeted ZEN placement. The dashed lines indicate hydrogen bonds, the hashed line represents the acylation covalent bond, and the bold line between atoms C_7′ and C_8′ of ZEN denotes the closure position of the lactone loop. The red arrows show the torsion angles that are variated during placing. (B) Locations of sequence selection positions and ZEN on ZHD101. The secondary structure of ZHD101 is shown in cartoon and colored in gray. ZEN and His242 are shown as stick model. The O, N, C atoms are colored in red, slate and gray, respectively. Design positions on enzyme surface are presented as orange spheres, while design positions in active pocket are shown as blue spheres.

The pK_a values of the ionizable residues (Glu, Asp, His, Lys, and Arg) of ZHD101 and its mutants were calculated by the DelPhi-based program DelPhiPKa, which is a Poisson–Boltzmann based approach that uses a Gaussian-based smoothing function to mimic conformational changes associated with ionization changes and calculates electrostatic energy without defining a molecular surface.^42,43 For our calculations, the Smooth Gaussian dielectric model was chosen to calculate electrostatic potentials, and the variance of the Gaussian surface was set to 0.70. The dielectric constants were set to 10.0 and 80.0 for the protein interior and external environment, respectively, and the pH value was set to 5.5. The proteins' atomic charge and radius parameters were set in accordance with the CHARMM 22 force field.⁵² The mutants that generated a pK_a drop of His242 with decreased or modestly increased folding energy were subjected to further experimental evaluation.

2.3 Gene cloning, plasmid construction, and site-directed mutagenesis

The original gene was obtained from the nucleotide sequence for ZHD101 from Clonostachys rosea IFO 7063 (gene zhd101). Codon optimization was carried out for expression in Escherichia coli (E. coli), and the gene was chemically synthesized by Takara Biotechnology Co. (Dalian, China). The synthesized gene was then subcloned into the pET30a(+) vector, which carries resistance to kanamycin, and the gene fragment coding ZHD101 (795 bp) was ligated between the NdeI and XhoI sites of the pET30a(+) vector. A hexa-histidine tag was added at the 3′-end of the zhd101 gene. Mutations of zhd101 were generated by site-directed mutagenesis using polymerase chain reaction, and the introduced mutations were further confirmed by automated DNA sequencing.

2.4 Enzyme expression and purification

The recombinant pET30a(+)-zhd101 plasmids encoding the zhd101 mutants were first transferred to the host BL21(DE3) E. coli chain. Cells harboring the recombinant plasmids were grown overnight at 37 °C in LB medium containing 50 μg mL⁻¹ kanamycin. The culture was inoculated into 500 mL LB medium with 50 μg mL⁻¹ kanamycin and incubated at 37 °C until the OD_{600 nm} of the cell suspension reached 0.6. Protein expression was then induced by adding isopropyl-β-D-thiogalactopyranoside to a final concentration of 1.0 mM and incubating at 20 °C for another 14 h. Cell were harvested by centrifugation at 10 000g for 10 min at 4 °C.

Tris–HCl buffer (100 mM Tris, pH 8.0) was applied to resuspend the cells, and the resuspension was lysed by sonication. After sonication, the insoluble fraction was removed by centrifugation, while the supernatant was loaded onto a Ni-NTA column equilibrated with binding buffer A (100 mM Tris, pH 8.0, containing 500 mM NaCl and 20 mM imidazole). The column was then washed with binding buffer B (100 mM Tris, pH 8.0, containing 500 mM NaCl and 50 mM imidazole) to remove cell proteins. The target enzyme was then eluted with elution buffer (100 mM Tris, pH 8.0, containing 500 mM NaCl and 200 mM imidazole). Subsequently, the fractions containing the purified enzyme were desalted twice to remove the imidazole and NaCl. The purity of the target enzyme was >90%, as determined by SDS-PAGE analysis. The concentrations of the purified enzymes were predetermined by the Bradford method⁵³ using bovine serum albumin (BSA) as a standard reagent. The absorbance from each enzyme sample with the addition of the Bradford reagent was measured at 595 nm.

2.5 Enzyme activity and kinetic assay

Catalytic activities and kinetic parameters were determined by HPLC analysis (LC-20AT, Shimadzu, Japan). For the reaction, 100 μL of the enzyme (in 0.1 M Tris buffer, diluted to about 100 μg mL⁻¹, pH 8.0) was incubated with 4850 μL acetate sodium-HCl buffer (0.1 M NaAc, pH 5.5) and 50 μL substrate ZEN solution (in acetonitrile, a linear gradient with the maximum 2 mg mL⁻¹) for 10 min at 37 °C. The reaction was terminated by boiling for 1 min. After cooling down, 5 mL of acetonitrile was added to the reaction solution for the following HPLC assay. Then, 10 μL of this mixture was analyzed by HPLC at 254 nm with a flow rate of 1.0 mL min⁻¹. The column temperature was maintained at 30 °C. The elution buffer contained 60% acetonitrile and 40% trifluoroacetic acid solution (1‰) (v/v). The kinetic parameters (V_max, K_M, and V_max/K_M) were obtained by fitting data to the Michaelis–Menten equation using the Lineweaver–Burk method. The time course of bioconversion was determined by HPLC. 100 μL of the diluted enzyme (in 0.1 M Tris buffer, pH 8.0) was incubated with 4850 μL acetate sodium-HCl buffer (0.1 M NaAc, pH 5.5) and 50 μL substrate ZEN solution (in acetonitrile). The experimental conditions corresponded to a maximum of 20 mg L⁻¹ ZEN and 2 mg L⁻¹ purified enzyme variants. The reaction temperature was set at 37 °C in a water bath.

3 Results and discussion

3.1 Charge redesign on protein surface

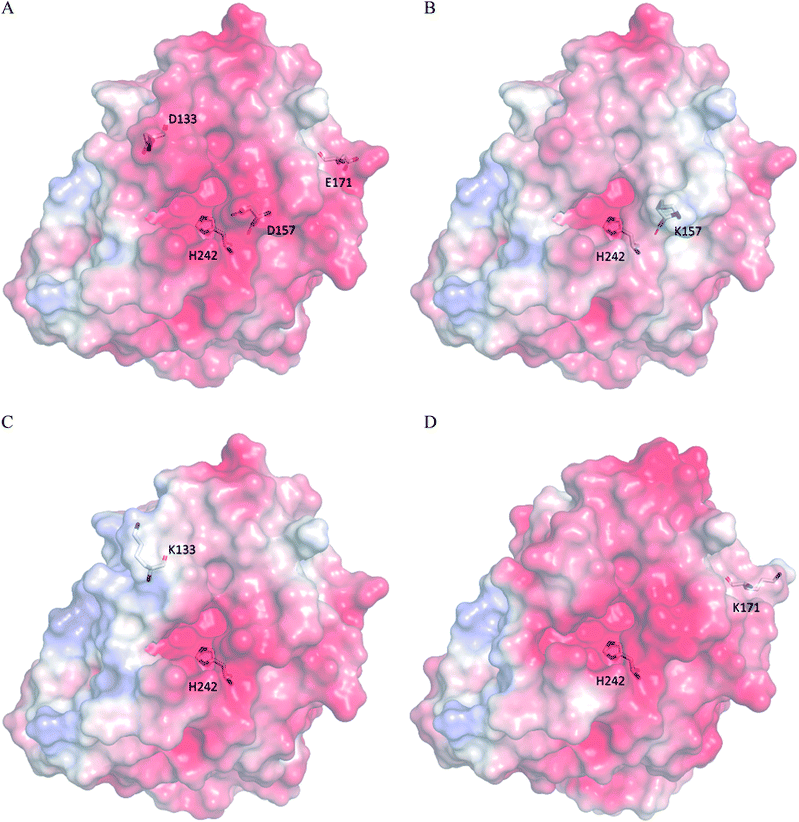
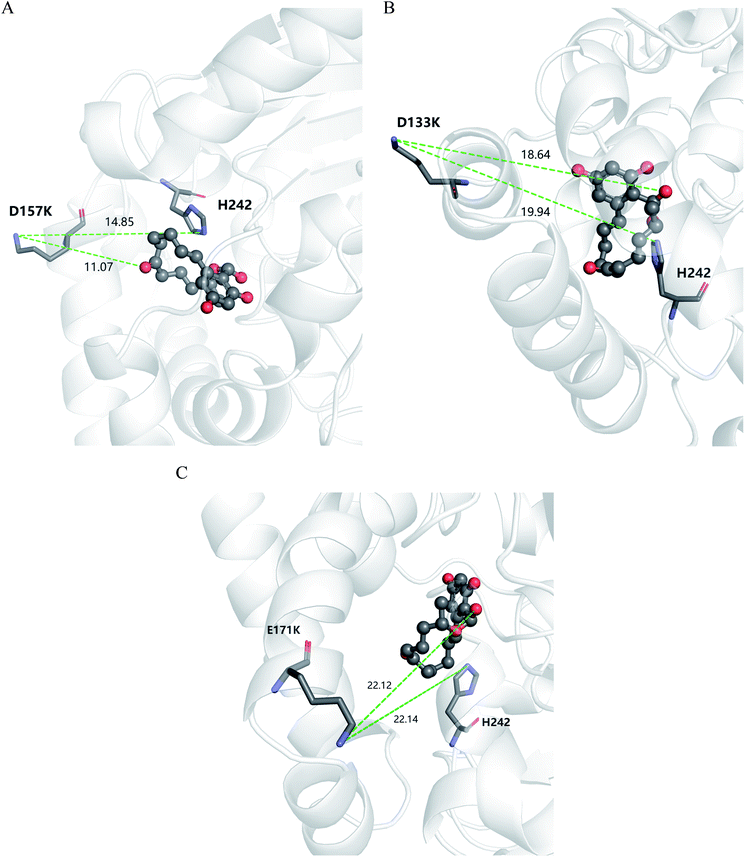
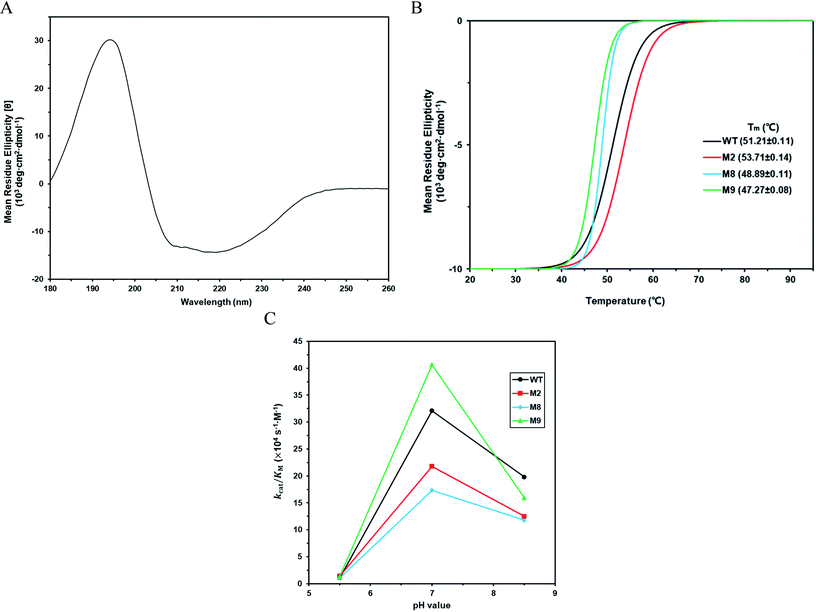
According to the classical Linderstøm-Lang theory,⁵⁴ increasing the surface charge lowers the pK_a values of acidic groups in proteins because they lose a proton upon ionization. We postulate that introducing additional positively charged residues such as lysine on the surface of ZHD101 would help to lower the pK_a value of His242 at the active site and hence improve its hydrolytic activity towards ZEN in acidic media. The design scheme for surface charge redesign of ZHD101 was shown in Table S1.† Specifically, 50 chosen surface positions (shown in Fig. 2B) were allowed to mutate to lysine, and 74 positions in the vicinity of the selected positions and those in the active site and TS of ZEN were subjected to side-chain conformational optimization. In total, 50 variants – each with a single lysine mutation compared with the wild type – were computationally generated by PRODA, and the calculated folding free energy changes, binding free energy changes, and pK_a drops of His242 are shown in Table S5.† The calculated binding free energies of the 50 variants were very close to those of the wild type. Therefore, the potentially beneficial mutations were selected based on the calculated pK_a drops of His242 and the folding free energy changes. In total, 9 variants predicted with explicitly dropped pK_a values of His242 and reduced or slightly increased folding free energies compared with the wild type were subjected to experimental validation.

The kinetic parameters of wild type ZHD101 and 9 single-point variants for the hydrolysis of ZEN at pH 5.5 were shown in Table 1. Among all variants, only M2 (D157K) and M9 (E171K) had better promoted catalytic efficiencies than the wild type in acidic medium. Fig. 3A, B, and C show the changes of the electrostatic potential of His242 in the active site after mutations D157K for M2 and E171K for M9 were introduced at the surface of ZHD101; these results were consistent with the calculated pK_a drops presented in Table 1. Moreover, we observed that the promotion of catalytic efficiency by M2 (D157K) in acidic medium was attributed to the decreased Michaelis binding constant, as its turnover number (k_cat) remained almost constant. Fig. 4A shows the computed binding geometry between M2 (D157K) and the substrate ZEN. The mutated residue K157 was in the vicinity of the active pocket, and the distance between the NE atom of K157 and the carbonyl oxygen O6′ of ZEN was 6.86 Å. We speculate that the favorable interaction between the introduced positively charged amino group of M2 (D157K) and the carbonyl oxygen O6′ of ZEN might have enhanced the binding between enzyme and substrate, considering that the electrostatic interaction was effective even at long range. The promoted catalytic efficiency of variant M9 (E171K) in acidic medium can be attributed to its increased turnover number (k_cat), as its Michaelis binding constant (K_M) was increased compared with that of the wild type (Table 1). Specifically, the computed binding geometry between variant M9 (E171K) and the transition state of ZEN is shown in Fig. 4B, and the distances between atom NE of K171 on the one hand and the oxyanion atom O12′ of ZEN and the NE atom of His242 on the other hand were 22.12 Å and 22.50 Å, respectively. This reveals that the introduced positive charge K171 was located closer to the negative charge on the oxyanion than the positive charge on His242. Therefore, mutation E171K should stabilize the oxyanion more than it destabilized the His242. Here, we assumed that the same effective dielectric constants could apply for the two interactions, as design site 171 was separated by protein (Fig. 4B). This could explain why the turnover number of variant M9 (E171K) increased by 2.06-fold (Table 1) with respect to the wild type in acidic medium. This reason can be further corroborated by variant M8(D133K), whose turnover number increased by 2.73-folds with respect to the wild type. The change in electrostatic potential of His242 variant M8(D133K) was shown in Fig. 3D, and the results were in accordance with the pK_a drop given in Table 1. The computed binding geometry between variant M8(D133K) and the transition state of ZEN is shown in Fig. 4C, and the distances between atom NE of K133 on the one hand and the oxyanion atom O12′ of ZEN and the NE atom of His242 on the other hand were 18.64 Å and 19.94 Å, respectively. Therefore, the greatly improved turnover number of M8(D133K) could be ascribed to the closer distance between the added positive charge K133 and the negative charge on the oxyanion than the distance from the positive charge on His242. The catalytic efficiency (k_cat/K_M = 10 430.8 s⁻¹ M⁻¹) of M8 was not improved compared with that of the wild type, as its Michaelis binding constant (K_M = 78.41 mM) increased simultaneously with its turnover number (k_cat). Fig. 4C shows that the mutated residue K133 was located on the rim of the active pocket but away from the carbonyl oxygen O6′ of ZEN. This might affect the productive binding between enzyme and the substrate, and resulted in the increased apparent Michaelis binding constant of variant M8. Circular dichroism and thermal denaturation measurements confirmed that the wild-type ZHD101 and variants M2, M8, and M9 were folded and exhibited similar stabilities (Fig. 5A and B). This indicated that the increased catalytic activities of the mutants were due to computational design. Moreover, the designed variants M2, M8, and M9 with increased activities at pH 5.5 all showed decreased activities at pH 8.5 (Fig. 5C), and these results corroborated that the apparent pK_a of His242 should be consistent with the calculated pK_a shifts. In contrary, the variants with a predicted activity shift towards more basic conditions are less active in acidic condition, and this prediction was confirmed by the control variant M17(R63E) as it lost activity completely at pH 5.5.

Table 1 Calculated free energy changes, predicted pK_a drops of His242, and kinetic parameters of wild type ZHD101 and its single variants M1–M9. Reaction conditions: pH 5.5, 37 °C

Variants	Mutations	pKa drop of H242	PRODA ΔΔG^bind (kcal mol^−1)	PRODA ΔΔG^fold (kcal mol^−1)	k cat (s^−1)	K M (mM)	k cat/KM (s^−1 M^−1)
WT	—	—	—	—	0.299 ± 0.013	28.25 ± 3.18	10 574.4
M1	E219K	0.095	−0.44	0.90	0.207 ± 0.023	28.62 ± 2.50	7228.2
M2	D157K	0.079	−0.42	−5.75	0.296 ± 0.009	20.83 ± 1.77	14 188.6
M3	D57K	0.068	−0.45	5.96	0.011 ± 0.001	11.17 ± 0.98	1026.5
M4	E145K	0.061	−0.39	−3.66	0.308 ± 0.019	33.95 ± 3.53	9072.0
M5	F222K	0.054	−0.23	−23.83	0.002 ± 0.001	28.97 ± 3.11	57.0
M6	L155K	0.052	−0.19	−4.30	0.167 ± 0.006	28.96 ± 3.10	5783.2
M7	N152K	0.045	−0.22	−1.84	0.204 ± 0.017	23.09 ± 1.77	8829.4
M8	D133K	0.044	−0.40	−2.17	0.818 ± 0.032	78.41 ± 4.90	10 430.8
M9	E171K	0.037	−0.36	−3.01	0.618 ± 0.022	45.32 ± 1.24	13 640.8

---

Fig. 3 Electrostatic potential surface of (A) wild type ZHD101; (B) M2(D157K); (C) M8(D133K); (D) M9(E171K). Positive, negative, and neutral potentials are colored in blue, red, and white, respectively. His242 and residues at mutation sites 133, 157, and 171 are shown as stick models.

Fig. 4 Stereochemical relationship between charges on mutated lysines, ZEN and His242 for (A) M2(D157K); (B) M8(D133K); (C) M9(E171K). ZEN is shown as ball-stick model while the mutated lysines and H242 are shown as stick models. The distances between designated atoms are shown as yellow dashed lines and values are given in angstrom.

Fig. 5 (A) Circular dichroism spectroscopy measurement of wild type ZHD101 at 25 °C. (B) Thermo unfolding curves of wild type ZHD101 and variants M2, M8, and M9, which are determined at 220 nm from 20 to 95 °C. (C) Catalytic efficiencies of wild type ZHD101 and variants M2, M8, M9 at different pH values (pH 5.5, 7.0, and 8.5).

3.2 Charge redesign in active pocket

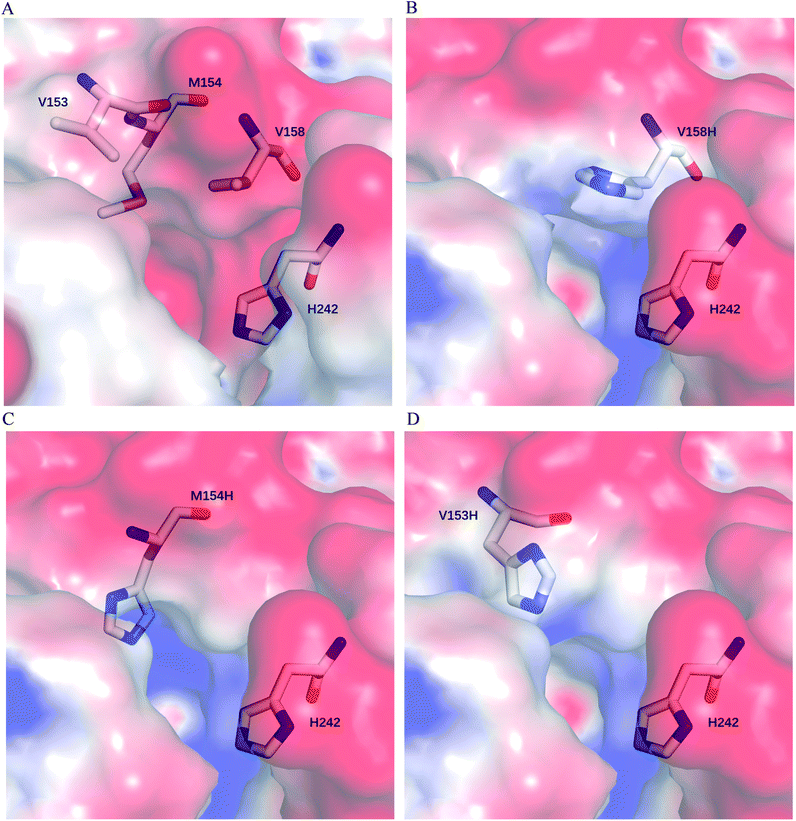
We postulate that introducing an additional weakly positive charge such as His in the active pocket may help to lower the pK_a value of His242 directly. This design scheme for charge redesign in the active pocket of ZHD101 is shown in Table S2.† Specifically, 8 positions (Fig. 2B) were mutated to histidine, and 31 positions in the vicinity of the selected positions and those in the active site and TS of ZEN were subjected to side-chain conformational optimization. In total, 8 variants, each with a single histidine mutation compared with the wild type, were computationally generated by PRODA, and the calculated folding free energy changes, binding free energy changes, and pK_a drops of His242 are shown in Table S6.† The top six calculated variants (Table S6†) showed obvious pK_a drops of His242, but variants D31H and F243H had largely increased free energies, and variant F221H had largely increased binding energy. Therefore, these three variants were ruled out, and the other three variants (V158H, M154H, and V153H) were selected for experimental evaluation. The kinetic parameters of three single-point variants – M10(V158H), M11(M154H), and M12(V153H) – for the hydrolysis of ZEN at pH 5.5 are shown in Table 2. Unfortunately, all three variants showed greatly decreased catalytic efficiency with respect to the wild type in acidic medium. Fig. 6A–D shows the changes in the electrostatic potential of His242 after mutations V158H, M154H, and V153H were introduced at the active site of ZHD101, and the results were consistent with the calculated pK_a drops of His242 shown in Table 2. Moreover, the previous experimental results stated that mutation V153H did not change hydrolytic activity at neutral pH and that mutation V158H retained 64% hydrolytic activity of the wild type ZHD101.³¹ The kinetic parameters shown in Table 2 imply that the decrease of the catalytic efficiencies of variants V158H, M154H, and V153H were ascribed to the abrupt drops in turnover number under acidic conditions (pH = 5.5). This might be explained by the concentrated chloride anions (from the acetate–HCl buffer) around the newly introduced positive charge for neutralization in H158, H154, and H153, as the concentrated counter anions in the active site would interact with protonated His242 more strongly and destroy its deprotonation ability alongside S102.

Table 2 Calculated free energy changes, predicted pK_a drops of His242, and kinetic parameters of wild type ZHD101 and its single variants M10–M12. Reaction conditions: pH 5.5, 37 °C

Variants	Mutations	pKa drop of H242	PRODA ΔΔG^bind (kcal mol^−1)	PRODA ΔΔG^fold (kcal mol^−1)	k cat (s^−1)	K M (mM)	k cat/KM (s^−1 M^−1)
WT	—	—	—	—	0.299 ± 0.013	28.25 ± 3.18	10 574.4
M10	V158H	0.265	−0.350	0.335	0.038 ± 0.004	17.04 ± 1.16	2215.6
M11	M154H	0.201	−1.730	5.119	0.009 ± 0.001	11.69 ± 1.23	757.5
M12	V153H	0.179	1.374	−6.088	0.064 ± 0.005	58.60 ± 2.05	1099.7

---

Fig. 6 Electrostatic potential surface at active site of (A) wild type ZHD101; (B) M10(V158H); (C) M11(M154H); (D) M12(V153H). Positive, negative, and neutral potentials are colored in blue, red, and white, respectively. His242 and residues at mutation sites 153, 154, and 158 are shown as stick models.

3.3 Multi-site combination of surface charges

Coulombic interactions are always additive; thus, we speculate that the changes in coulombic interactions caused by the single lysine mutations on the surface of ZHD101 may be cumulative for the pK_a drops of His242 in the active site. Therefore, the single mutations D157K, D133K, and E171K, which improved either the turnover number (k_cat), the Michaelis binding constant (K_M), or the catalytic efficiency (k_cat/K_M) of wild type ZHD101, were combined to obtain double or triple variants. The pK_a drops calculated by the DelPhiPKa program for the multisite variants (Table 3) were consistent with our speculation, and the folding free energies of the multisite variants calculated by PRODA were all decreased, indicating that the scaffold structures of these multisite mutants remained. However, the kinetic parameters shown in Table 3 imply that no multisite variants expressed improved catalytic efficiency (k_cat/K_M) in actual experiments. Moreover, both the turnover numbers (k_cat) and the Michaelis binding constants (K_M) of the multisite variants were deteriorated compared with those of the wild type ZHD101. These results imply that the effect of positive charges designed on the surface of enzyme was non-additive, and non-additivity is still a great challenge for protein engineering.⁵⁵ The non-additive characteristics of the coulombic interaction during enzyme catalysis may be caused by the proteins' heterogeneous structure, and pK_a calculation programs (here DelPhiPKa) based on classic macroscopic electrostatic interactions cannot adapt to this case. Besides, with multiple mutations, there may be changes in microscopic environment or interactions between charges caused by the orientation of solvent molecules.

Table 3 Calculated free energy changes, predicted pK_a drops of His242, and kinetic parameters of wild type ZHD101 and its multi-site variants M13–M16. Reaction conditions: pH 5.5, 37 °C

Variants	Mutations	pKa drop of H242	PRODA ΔΔG^bind (kcal mol^−1)	PRODA ΔΔG^fold (kcal mol^−1)	k cat (s^−1)	K M (mM)	k cat/KM (s^−1 M^−1)
WT	—	—	—	—	0.299 ± 0.013	28.25 ± 3.18	10 574.4
M13	D157K/E171K	0.125	−0.40	−7.221	0.265 ± 0.029	83.19 ± 5.46	3186.3
M14	D133K/E171K	0.117	−0.38	−7.391	0.235 ± 0.019	47.14 ± 4.37	4976.4
M15	D133K/D157K	0.086	−0.41	−4.809	0.132 ± 0.008	32.91 ± 2.97	4001.4
M16	D133K/D157K/E171K	0.162	−0.37	−8.454	0.128 ± 0.008	33.77 ± 0.69	3788.6

---

4 Conclusion

In this research, a computational strategy to design the pH-activity profiles of hydrolases was developed based on our enzyme design program PRODA and the pK_a value calculation tool DelPhiPKa. This strategy was tested by the computational design of the active site pK_a values of the zearalenone lactonase ZHD101 from Clonostachys rosea under acidic conditions by introducing additional positive charges on the enzyme surface or in the active pocket. Variants M2(D157K) and M9(E171K), which contain additional positive charges on the enzyme surface, achieved modest success in promoting catalytic efficiency (k_cat/K_M) towards ZEN hydrolysis in acidic medium, although the introduction of weakly positive charges in the active pocket failed to generate beneficial mutations. The advantage of our computational strategy is that protein stability is taken into account while the pH-activity profiles are engineered. Therefore, this computational strategy combined with limited experimental validation is promising to facilitate the discovery of effective enzyme variants that function under unphysiological pH conditions.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge the financial support from the National Natural Science Foundation of China (Grant Numbers: 21476123, 21878170) and the Ministry of Science and Technology of China (2017YFC1600900).

References

1. S. Ito, T. Kobayashi, K. Ara, K. Ozaki, S. Kawai and Y. Hatada, Extremophiles, 1998, 2, 185–190.
2. A. Shaw, R. Bott and A. G. Day, Curr. Opin. Biotechnol., 1999, 10, 349–352.
3. J. R. Cherry, M. H. Lamsa, P. Schneider, J. Vind, A. Svendsen, A. Jones and A. H. Pedersen, Nat. Biotechnol., 1999, 17, 379–384.
4. B. M. Tynan-Connolly and J. E. Nielsen, Protein Sci., 2007, 16, 239–249.
5. A. J. Russell and A. R. Fersht, Nature, 1987, 328, 496–500.
6. P. G. Thomas, A. J. Russell and A. R. Fersht, Nature, 1985, 318, 375.
7. A. J. Russell, P. G. Thomas and A. R. Fersht, J. Mol. Biol., 1987, 193, 803–813.
8. T. Kim, E. J. Mullaney, J. M. Porres, K. R. Roneker, S. Crowe, S. Rice, T. Ko, A. H. J. Ullah, C. B. Daly, R. Welch and X. G. Lei, Appl. Environ. Microbiol., 2006, 72, 4397–4403.
9. S. Pokhrel, J. C. Joo, Y. H. Kim and Y. J. Yoo, Process Biochem., 2012, 47, 2487–2493.
10. M. D. Joshi, G. Sidhu, I. Pot, G. D. Brayer, S. G. Withers and L. P. McIntosh, J. Mol. Biol., 2000, 299, 255–279.
11. J. E. Nielsen, T. V. Borchert and G. Vriend, Protein Eng., Des. Sel., 2001, 14, 505–512.
12. A. Hirata, M. Adachi, S. Utsumi and B. Mikami, Biochemistry, 2004, 43, 12523–12531.
13. S. R. Gordon, E. J. Stanley, S. Wolf, A. Toland, S. J. Wu, D. Hadidi, J. H. Mills, D. Baker, I. S. Pultz and J. B. Siegel, J. Am. Chem. Soc., 2012, 134, 20513–20520.
14. C. M. Placinta, J. P. F. D'Mello and A. M. C. Macdonald, Anim. Feed Sci. Technol., 1999, 78, 21–37.
15. B. Kabak, A. D. W. Dobson and I. Var, Crit. Rev. Food Sci. Nutr., 2006, 46, 593–619.
16. N. Winssinger and S. Barluenga, Chem. Commun., 2007, 22–36.
17. A. Zinedine, J. M. Soriano, J. C. Moltó and J. Mañes, Food Chem. Toxicol., 2007, 45, 1–18.
18. K. S. McKenzie, A. B. Sarr, K. Mayura, R. H. Bailey, D. R. Miller, T. D. Rogers, W. P. Norred, K. A. Voss, R. D. Plattner, L. F. Kubena and T. D. Phillips, Food Chem. Toxicol., 1997, 35, 807–820.
19. M. Megharaj, I. Garthwaite and J. H. Thiele, Lett. Appl. Microbiol., 1997, 24, 329–333.
20. E.-S. A. M. A. Alla, Food Nahr., 1997, 41, 362–365.
21. A. K. Alegakis, A. M. Tsatsakis, M. I. Shtilman, D. L. Lysovenko and I. G. Vlachonikolis, J. Environ. Sci. Health, Part B, 1999, 34, 633–644.
22. N. Takahashi-Ando, M. Kimura, H. Kakeya, H. Osada and I. Yamaguchi, Biochem. J., 2002, 365, 1–6.
23. H. Kakeya, N. Takahashi-Ando, M. Kimura, R. Onose, I. Yamaguchi and H. Osada, Biosci., Biotechnol., Biochem., 2002, 66, 2723–2726.
24. N. Takahashi-Ando, S. Ohsato, T. Shibata, H. Hamamoto, I. Yamaguchi and M. Kimura, Appl. Environ. Microbiol., 2004, 70, 3239–3245.
25. O. Molnar, G. Schatzmayr, E. Fuchs and H. Prillinger, Syst. Appl. Microbiol., 2004, 27, 661–671.
26. M. P. Mokoena, P. K. Chelule and N. Gqaleni, J. Food Prot., 2005, 68, 2095–2099.
27. A. D. Altalhi and B. El-Deeb, J. Hazard. Mater., 2009, 161, 1166–1172.
28. K. J. Cho, J. S. Kang, W. T. Cho, C. H. Lee, J. K. Ha and K. B. Song, Biotechnol. Lett., 2010, 32, 1921–1924.
29. P.-J. Yi, C.-K. Pai and J.-R. Liu, World J. Microbiol. Biotechnol., 2011, 27, 1035–1043.
30. D. Popiel, G. Koczyk, A. Dawidziuk, K. Gromadzka, L. Blaszczyk and J. Chelkowski, BMC Microbiol., 2014, 14, 82.
31. Z. Xu, W. Liu, C.-C. Chen, Q. Li, J.-W. Huang, T.-P. Ko, G. Liu, W. Liu, W. Peng, Y.-S. Cheng, Y. Chen, J. Jin, H. Li, Y. Zheng and R.-T. Guo, ACS Catal., 2016, 6, 7657–7663.
32. R. Hui, X. Hu, W. Liu, W. Liu, Y. Zheng, Y. Chen, R.-T. Guo, J. Jin and C.-C. Chen, Acta Crystallogr., Sect. F: Struct. Biol. Commun., 2017, 73, 515–519.
33. A. Lee, K.-C. Cheng and J.-R. Liu, PLoS One, 2017, 12, e0182220.
34. Q. Qi, W.-J. Yang, H.-J. Zhou, D.-M. Ming, K.-L. Sun, T.-Y. Xu, X.-J. Hu and H. Lv, Acta Crystallogr., Sect. F: Struct. Biol. Commun., 2017, 73, 376–381.
35. Y. Zheng, W. Liu, C.-C. Chen, X. Hu, W. Liu, T.-P. Ko, X. Tang, H. Wei, J.-W. Huang and R.-T. Guo, ACS Catal., 2018, 8, 4294–4298.
36. T. Ezeji and H. P. Blaschek, Bioresour. Technol., 2008, 99, 5232–5242.
37. W. Peng, T.-P. Ko, Y. Yang, Y. Zheng, C.-C. Chen, Z. Zhu, C.-H. Huang, Y.-F. Zeng, J.-W. Huang, A. H.-J. Wang, J.-R. Liu and R.-T. Guo, RSC Adv., 2014, 4, 62321–62325.
38. L. Hedstrom, Chem. Rev., 2002, 102, 4501–4524.
39. D. Voet and J. G. Voet, Biochemistry, Wiley, 2004.
40. H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2005, 61, 704–721.
41. B. Kuhlman and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 10383–10388.
42. L. Wang, L. Li and E. Alexov, Proteins: Struct., Funct., Bioinf., 2015, 83, 2186–2197.
43. L. Wang, M. Zhang and E. Alexov, Bioinformatics, 2016, 32, 614–615.
44. Y. Zhu, Ind. Eng. Chem. Res., 2007, 46, 839–845.
45. Y. Lei, W. Luo and Y. Zhu, Protein Sci., 2011, 20, 1566–1575.
46. X. Huang, K. Han and Y. Zhu, Protein Sci., 2013, 22, 929–941.
47. X. Huang, J. Xue and Y. Zhu, Chem. Commun., 2017, 53, 7604–7607.
48. J. He, X. Huang, J. Xue and Y. Zhu, Green Chem., 2018, 20, 5484–5490.
49. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
50. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
51. Z. Xiang and B. Honig, J. Mol. Biol., 2001, 311, 421–430.
52. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217.
53. M. M. Bradford, Anal. Biochem., 1976, 72, 248–254.
54. K. Linderstrøm-Lang, CR Trav Lab Carlsberg, 1924, 15, 70–95.
55. M. T. Reetz, Angew. Chem., Int. Ed., 2013, 52, 2658–2666.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra04964a

---