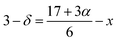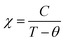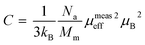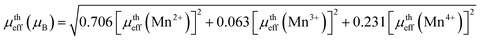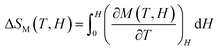Observation of enhanced magnetic entropy change near room temperature in Sr-site deficient La_0.67Sr_0.33MnO₃ manganite

Abstract

The effect of Sr-site deficiency on the structural, magnetic and magnetic entropy change of La_0.67Sr_0.33−yMnO_3−δ (y = 0.18 and 0.27) compounds was investigated. The compounds were prepared by the conventional solid-state route and powder X-ray diffraction technique along with Rietveld refinement was carried out to confirm the structure and phase purity. Lattice parameters and unit cell volumes are found to increase with the increase in Sr-deficiency due to the electrostatic repulsion from the neighbouring oxygen ions. A mixed valence state of Mn²⁺/Mn³⁺/Mn⁴⁺ was confirmed using the X-ray photoelectron spectroscopy technique and it was observed that the change of state from Mn³⁺ + Mn³⁺ pairs to Mn²⁺ + Mn⁴⁺ pairs is different for both the studied compounds. A second order ferromagnetic–paramagnetic transition with an enhancement in magnetization in comparison to the pristine compound (La_0.67Sr_0.33MnO₃) was observed due to multiple double exchange interactions. The La_0.67Sr_0.15□_0.18MnO_3−δ compound exhibits a magnetic entropy change (ΔS_M) of 4.61 J kg⁻¹ K⁻¹ at 310 K, and the La_0.67Sr_0.06□_0.27MnO_3−δ compound exhibits a ΔS_M of 4.11 J kg⁻¹ K⁻¹ at 276 K under a field of 50 kOe. In our previous work, we reported a large value of ΔS_M but at higher temperatures, around 350 K. However, in the present case, we have achieved a near room temperature (310 K) MCE with a significant ΔS_M value (4.61 J kg⁻¹ K⁻¹) which is larger than that reported for numerous perovskite manganites. Thus, the studied material could be a potential candidate for room temperature magnetic refrigeration applications.

---

Introduction

Magnetic refrigeration is a green and energy efficient technology based on the principle of the magnetocaloric effect (MCE). The recent trends in magnetic refrigeration confirm that it is a cost-effective and environmentally sound alternative to the conventional vapour compression refrigeration system.^1–3 In comparison to the conventional technique, the magnetic refrigeration system has better energy efficiency, adaptability and does not release any greenhouse gases. In the entire process, the magnetocaloric material is subjected to repeated magnetization and demagnetization cycles, and as a result, the magnetic material heats up and cools down respectively due to the magneto-thermodynamic effect.^4,5 However, the figure of merit of magnetocaloric materials is reported in terms of magnetic entropy change (ΔS_M) and adiabatic temperature change (ΔT_ad).^6,7 From the literature, it could be seen that intermetallic compounds (Gd₅(Si₂Ge₂), La(Fe_1−xSi_x), MnAs_1−xSb_x, Ni–Mn–X (X = Ga, In, Sn), MnFe(P_1−xSi_x) etc.) and oxide compounds (mixed valence manganites, ErCo₂, Ho₂O₃, etc.) are reported as potential candidates for magnetic refrigeration applications.^8–18 Even though the intermetallic compounds show significant ΔS_M values, they are detrimental to magnetic refrigeration applications due to their high cost, complicated synthesis routes, large thermal and field hysteresis etc. On the other hand, oxide materials especially perovskite manganites having an ABO₃ structure are reported to be potential candidates for magnetic refrigeration applications due to their low cost, simple synthesis route, high chemical stability and low eddy current heating.¹⁹

Doped manganites having a formula of 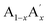MnO₃ are important candidates due to the correlation between charge, spin and orbital orders and their significant contribution towards the MCE. In doped manganites, rare Earth ions occupy the A-site, and alkaline rare Earth ions occupy the A′- site.^20,21 The different oxidation state of rare Earth and alkaline rare Earth ions create a mixed valence state of manganese (Mn²⁺/Mn³⁺/Mn⁴⁺ etc.) and eventually determine the strength of the exchange interactions. Moreover, different rare Earth ions having the same oxidation state such as 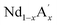MnO₃, 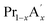MnO₃ and 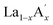MnO₃ also exhibit different exchange interactions as well as different magnetic and electrical transport properties due to the difference in the average A-site ionic radius.^22–27 It is understood that, in doped manganites, the double exchange (DE) interaction via the Mn³⁺–O²⁻–Mn⁴⁺ ions is responsible for the ferromagnetic (FM) behaviour and the superexchange (SE) interaction through Mn³⁺–O²⁻–Mn³⁺ and Mn⁴⁺–O²⁻–Mn⁴⁺ ions are responsible for the antiferromagnetic (AFM) behaviour. This indicates that the strength of the competing exchange interactions and magnetic properties are eventually affected by different factors such as rare Earth substitution at the A-site, replacement of manganese by other transition elements, the introduction of deficiency at A and A′- sites, etc.^28–37 Recently, many reports have demonstrated that the creation of deficiency at the rare Earth and alkaline rare Earth sites alter the Mn²⁺/Mn³⁺/Mn⁴⁺ ratio which severely affect the magnetic and magnetocaloric properties.^37–49 The structure of manganites is imperfect and contain vacancy type point defects, called Schottky defects due to the cyclic temperature changes during synthesis and sintering process.^50,51 The presence of cation (V^(c)) and anion (V^(a)) vacancies strongly influence the properties of the manganites and causing a change in the stability of the perovskite structure.⁵² The change in the valence state and coordination number of cations due to defect formation affects the magnetic phase transition temperature and magnetic ordering of the manganites. Moreover, a change in the bond length affects the packing of MnO₆ octahedral and leads to a change in the structure and stability of the compounds. The interstitial point defects, called Frenkel defects is not formed in these compounds and only vacancy type point defects are exist due to elevated synthesis and sintering temperature conditions.⁵⁰ The anion vacancies are formed during heating process due to the thermal dissociation of oxygen and that leads to the reduction of oxygen content to O_3−δ.⁵¹ Moreover, the presence of vacancies at the oxygen site is compensated by a reduction in the average valence of manganese ions.⁵² On the other hand, the cation vacancies are formed during cooling process due to high mobility of cation sub lattices, and the formation of vacancies at the A-site leads to a decrease in the average valence of Mn-ions. The defectiveness and the stability in the perovskite structure can be controlled by changing the cooling conditions and the sintering temperature.⁵¹ Moreover, researchers have tried to tune the transition temperature (T_C) and ΔS_M by varying the vacancy content to a certain extent. Boujelben et al. reported the effect of Pr and Sr-deficiency in Pr_0.7Sr_0.3MnO₃ compound and found that Pr-deficiency and Sr-deficiency have different effects on the magnetic properties.⁵³ The effect of La deficiency in (La_1−x)_0.8Ca_0.2MnO₃ was reported by Phan et al. and found that the La-deficient compound exhibits a large ΔS_M value than that of the pristine compound.⁵⁴ Na-deficient La_0.8Na_0.05□_0.15MnO₃ and Sr-deficient La_0.65Eu_0.05Sr_0.15MnO₃ exhibit ΔS_M values of 3.48 J kg⁻¹ K⁻¹ at 260 K and 4.96 J kg⁻¹ K⁻¹ at 280 K under a field change of 20 kOe.^43,44 A tunable transition temperature with a ΔS_M value of 3.42 J kg⁻¹ K⁻¹ (300 K) under 50 kOe field was reported by Skini et al. in K-deficient La_0.8K_0.1□_0.1MnO₃ compound.⁴⁵

Recently, our group has reported the effect of La and Sr-deficiency on the magnetocaloric properties in La_0.67Sr_0.33MnO₃ (LSMO) compound. La_0.67−xSr_0.33MnO_3−δ (x = 0.09) and La_0.67Sr_0.33−yMnO_3−δ (y = 0.09) termed as La-0.09 and Sr-0.09 compounds, were prepared by solid-state route and it was found that Sr-deficient compound has better magnetocaloric properties than that of the pristine as well as La-deficient compounds.³⁷ Compound with a deficiency of y = 0.09 i.e., La_0.67Sr_0.24□_0.09MnO_3−δ displayed a ΔS_M of 5.08 J kg⁻¹ K⁻¹ at 352 K and a adiabatic temperature change of 3.48 K for 50 kOe field. Thus the creation of Sr-deficiency in LSMO exhibits a promising MCE behaviour with an increase in magnetocaloric properties value and a decrease in T_C towards room temperature from 365 K of the pristine compound. In the present study, as a continuing effort, we have further increased the Sr-deficiency content in La_0.67Sr_0.33−yMnO_3−δ by a factor of y = 0.18 and 0.27 to further tune the T_C towards room temperature. Thus we have synthesized La_0.67Sr_0.33−yMnO_3−δ (y = 0.18 and 0.27) compounds using solid-state method and explored their structural, magnetic and magnetocaloric properties and compared the results with that of the pristine compound, reported in our previous study.³⁷

Experimental

La_0.67Sr_0.15□_0.18MnO_3−δ and La_0.67Sr_0.06□_0.27MnO_3−δ are termed as Sr-0.18 and Sr-0.27 compounds and were prepared by conventional solid-state method using La₂O₃ (Alfa Aesar, 99%), SrCO₃ (Sigma-Aldrich, 98%) and MnCO₃ (Sigma-Aldrich, 99.9+ %) as starting materials. The raw materials were weighed according to the stoichiometry and mixed in an agate mortar using distilled water as solvent medium for 6 h. The homogenous mixture was dried and calcined at 1000 °C and 1200 °C for 12 h with intermediate grinding. The grounded powders were pelletized into cylindrical shape of 12 mm diameter, which was then sintered at 1350 °C for 12 h. The pellets were then powdered and then structural analysis was carried out by powder X-ray diffraction (XRD) technique using PANalytical X'Pert Pro diffractometer having Ni-filtered Cu Kα radiation. Rietveld refinement was done using GSAS-EXPGUI software to analyze the crystal structure and phase purity of the compounds. Iodometric titration was performed to check the oxygen stoichiometry. X-ray photoelectron spectroscopy (XPS) was done to study the surface elemental composition and oxidation states using a PHY 5000 Versa Probe II, ULVAC-PHI, Inc. Instrument having Al Kα as the X-ray source. Initially, a wide scan was done, and a pressure of 5 × 10⁻¹⁰ mbar was maintained in the XPS chamber during the measurement. The binding energy of the high resolution scans were corrected using C 1s = 284.8 eV as the reference. Magnetic properties were measured using the vibrating sample magnetometer attached to the physical property measurement system (Quantum Design Inc., USA).

Results and discussion

From the Rietveld refinement of the powder XRD patterns, it is confirmed that both the studied compounds belong to rhombohedral structure with R3̄c space group. The refined parameters obtained from the Rietveld analysis are shown in Table 1 and the refined XRD patterns are shown in Fig. 1. The experimental XRD patterns are in good agreement with the patterns calculated by the software, and shows better goodness of fit. In our previous study, it was confirmed that the pristine compound LSMO was phase pure, and no impurity peaks were detected.³⁷ On the other hand, La-0.09 and Sr-0.09 compounds show an additional peak at 36.1° due to the presence of Mn₃O₄ as a secondary phase as reported in our previous work.^37,48,49 However, in the present case, Sr-0.18 and Sr-0.27 compounds show some additional secondary peaks at 28.9°, 36.1°, 25.9° etc. due to the prominent presence of Mn₃O₄ secondary phases. Moreover, with increase in Sr-deficiency, the intensity of the secondary peaks also increases. It indicates that, with increase in Sr-deficiency content, the percentage of rhombohedral ferrimagnetic Mn₃O₄ secondary phase also increases.⁴⁹ Even though the formation of Mn₃O₄ depends on the amount of deficiency, some reports show that the preparation conditions such as manual grinding sometimes does not ensure perfect homogeneity and produces Mn₃O₄ secondary phase.⁵⁵ In La and Sr-deficient compounds, three oxidation states are possible for manganese ions (Mn²⁺/Mn³⁺/Mn⁴⁺).^37,56,57 Out of these ions, Mn²⁺ ions (ionic radius of 1.13 Å) occupy the A-site along with La³⁺ (ionic radius of 1.36 Å) and Sr²⁺ (ionic radius of 1.44 Å).^37,56 However, Mn³⁺ (0.645 Å) and Mn⁴⁺ (0.53 Å) occupy the B-site forming a MnO₆ octahedral coordinated system. Recently, Hundley et al. suggested a charge disproportionation model in deficient manganites based on the stability of manganese pairs.⁵⁸ According to the charge disproportionation model, in octahedrally coordinated systems, Mn²⁺–Mn⁴⁺ pair is the more stable than Mn³⁺–Mn³⁺ pair.⁵⁸ Thus in deficient compounds, a change of state from Mn³⁺ + Mn³⁺ pair to Mn²⁺ + Mn⁴⁺ pair is possible because of the more stable nature of the later pair. Thus the presence of Mn²⁺ ions in Sr-0.18 and Sr-0.27 compounds can be attributed to the stable nature of Mn²⁺ + Mn⁴⁺ pairs as suggested by the charge disproportionation model and this indicates that a portion of the manganese ions form Mn₃O₄ secondary phase, and the other portion occupies the A-site as Mn²⁺ ions along with La³⁺ and Sr²⁺ ions. From Table 1, it can be seen that Sr-0.18 and Sr-0.27 compounds have greater unit cell volume (354.377 ų and 355.388 ų respectively) than that of the pristine (349.468 ų) and Sr-0.09 (351.686 ų) compounds.³⁷ The increase in the unit cell volume of the Sr-deficient compounds cannot be explained on the basis of the ionic radius of Mn²⁺/Mn³⁺/Mn⁴⁺ ions or the amount of Mn₃O₄ impurity phase present in the compound. The increase in unit cell volume of Sr-site deficient compounds can be related to the decreasing concentration of oxygen due to the formation of anionic vacancies and the increase in radius of the deficient Sr-site.^37,48,49,59 The presence of oxygen vacancies is compensated by a reduction in the average valence of manganese ions. This leads to the reduction of some Mn⁴⁺ to Mn³⁺and Mn³⁺ to Mn²⁺. Hence, due to defectiveness, the charge compensation is taking place and the average ionic radius and the unit cell volume increases. Moreover, the anion (V^(a)) vacancies at the oxygen sites reduces bonding electrostatic force and eventually leads to the increase of unit cell volume.⁵² Due to the electrostatic repulsion from the neighbour oxygen ions, the radius of the deficient Sr-site (1.547 Å) is increased by 7% than the actual ionic radius of Sr-site (1.44 Å).^37,49,60 This will eventually affect the unit cell volume of the Sr-deficient compounds and hence Sr-0.18 and Sr-0.27 compounds exhibit greater unit cell volume than that of the pristine and Sr-0.09 compounds. As the unit cell volume changes with Sr-deficiency, distortion occurs in the MnO₆ octahedra due to the changes in the Mn– O bond lengths and the Mn–O–Mn bond angles. The Jahn–Teller active ion, Mn³⁺ distorts the MnO₆ octahedra due to the strong Jahn–Teller effect, while Mn²⁺ and Mn⁴⁺ are Jahn–Teller inactive and do not tend to distort the octahedrally coordinated system. The iodometric titration method was performed to estimate the oxidation state of manganese and hence the stoichiometry of the oxygen ion.^48,61 Powders of Sr-deficient compounds are weighed and dissolved in a mixture of 10 ml of 10 mass% KI aqueous solution and 2.5 ml of 2 M HCl. The liberated iodine is titrated against 0.1 N sodium thiosulphate standard volumetric solution using 1 mass% starch solution as an indicator. It is assumed that the oxidation state of manganese is compensated due to the creation of vacancy and the Sr-deficient compounds can be written as La_0.67³⁺Sr_0.33−y²⁺Mn_1−α³⁺Mn_α⁴⁺O_3−δ (y = 0.18 and 0.27). The value of α was determined from the titration and the amount of oxygen content was calculated for 5 titrations using the equation as

Table 1 Structural parameters of La_0.67Sr_0.15□_0.18MnO_3−δ and La_0.67Sr_0.06□_0.27MnO_3−δ compounds obtained from the Rietveld refinement of XRD

	Sr-0.18	Sr-0.27
Cell parameters
a (Å)	5.4309 (1)	5.5379 (1)
b (Å)	5.5309 (1)	5.5379 (1)
c (Å)	13.3767 (2)	13.3805 (2)
V (Å^3)	354.377 (8)	355.388 (7)
Positional parameters
La/Sr x	0	0
La/Sr y	0	0
La/Sr z	0.25	0.25
Mn x	0	0
Mn y	0	0
Mn z	0	0
O x	0.546	0.550
O y	0	0
O z	0.25	0.25
Bond distance (Å)
〈d Mn–O〉	1.963 (2)	1.968 (2)
Bond angle (°)
Mn–O1–Mn	165.1 (0)	163.8 (0)
Agreement factors
RWP	5.20	4.77
RP	3.85	3.59
χ^2	1.84	1.51

---

Fig. 1 Rietveld refined XRD patterns of (a) La_0.67Sr_0.15□_0.18MnO_3−δ and (b) La_0.67Sr_0.06□_0.27MnO_3−δ compounds. Black colour indicates the experimental data. Red lines are theoretical fits to the XRD data; pink corresponds to the Bragg reflection, and blue lines correspond to the difference between the experimental and the calculated fits.

The oxygen content decreases with increase in deficiency and it is found to be 2.74 and 2.69 for Sr-0.18 and Sr-0.27 compounds respectively with an accuracy of ± 0.03.

To determine the oxidation state of manganese and to identify the elemental composition on the surface, a detailed XPS analysis was performed. The Mn–2P_3/2 spectra of Sr-0.18 and Sr-0.27 compounds were curve fitted using MultiPak spectrum: ESCA and are shown in Fig. 2(a) and (b) respectively. The fitting was done using a standard Shirley background, and the Mn–2P_3/2 spectra was decomposed into three components for both Sr-0.18 and Sr-0.27 compounds. In Sr-0.18 compound, the three peak centers at 640.9, 642.4 and 643.4 eV corresponds to Mn²⁺, Mn³⁺ and Mn⁴⁺ oxidation states respectively.^37,62–66 In Sr-0.27 compound, the peak centers of Mn²⁺, Mn³⁺ and Mn⁴⁺ are at 640.8, 642.3 and 643.2 eV respectively.^37,62–66 It was confirmed in our previous report that in deficient compounds, three oxidation states (Mn²⁺/Mn³⁺/Mn⁴⁺) are possible for manganese while only two oxidation states (Mn³⁺ and Mn⁴⁺) exist in the pristine compound.³⁷ The ratio of Mn²⁺/Mn³⁺/Mn⁴⁺ is calculated from the area of each component obtained from the peak fitting. For the pristine compound, the Mn³⁺/Mn⁴⁺ ratio is about 67.9 : 32.1, which is near to the expected ratio (67 : 33).³⁷ However, in the present case, the ratio of Mn²⁺/Mn³⁺/Mn⁴⁺ is found to be 70.6/6.3/23.1 and 64.7/10.4/24.9 for Sr-0.18 and Sr-0.27 compounds respectively. Hence it is to be noted that the change of state from Mn³⁺ + Mn³⁺ pairs to Mn²⁺ + Mn⁴⁺ pairs under charge disproportionation phenomena are different for Sr-deficient compounds, and this has been confirmed from XPS analysis. Thus the ratio of Mn²⁺/Mn³⁺/Mn⁴⁺ ions alter with the Sr-deficiency content, which inturn severely affects the DE interactions and thereby the magnetic properties.

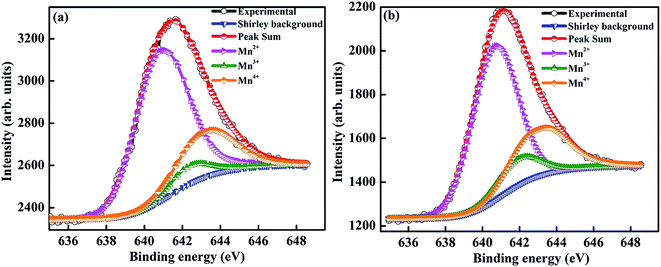Fig. 2 Mn–2P_3/2 X-ray photo electron spectra of (a) La_0.67Sr_0.15□_0.18MnO_3−δ and (b) La_0.67Sr_0.06□_0.27MnO_3−δ compounds.

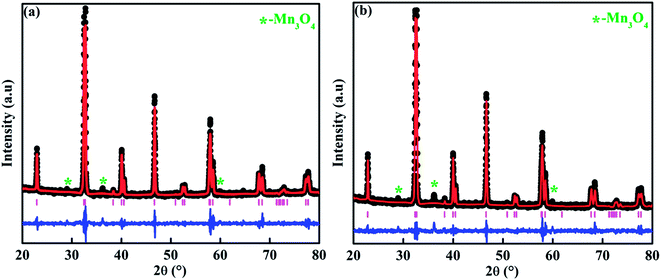
Fig. 3 shows the magnetization as a function of temperature from 2–380 K for both the compounds. The measurement was carried out under 100 Oe field in zero-field-cooled (ZFC) and field cooled (FC) modes. Large thermo-magnetic irreversibility is witnessed in both the compounds due to the competing interaction between different magnetic states. Both the compounds show a hump like feature below 50 K, which was not seen in the magnetization curves of La-0.09 and Sr-0.09 compounds, reported in our earlier work.³⁷ This low-temperature anomaly is due to the ordering of the ferrimagnetic Mn₃O₄ phase, which is very prominent with the increase in Sr-deficiency, this result corroborates with that obtained from the Rietveld refinement analysis.⁴⁹ From our previous report, it can be seen that the magnetization of La-0.09 and Sr-0.09 compounds are greater than that of the pristine compound due to the increase in DE interaction.³⁷ In the present case, the magnetization increases further for Sr-0.18 and then decreases for Sr-0.27, which means that Sr-0.18 compound shows maximum magnetization among all the Sr-deficient compounds. Thus the DE interaction and FM nature of Sr-0.18 and Sr-0.27 compounds do not merely destroy by Sr-deficiency. In the pristine compound, the exchange coupling is between Mn³⁺ ions having the electronic configuration of 3d⁴ (t^3↑_2g e^↑_g with S = 2) and Mn⁴⁺ ions having the electronic configuration of 3d³ (t^3↑_2g with S = 3/2). However, in deficient compounds, the exchange coupling is enhanced by the presence of Mn²⁺ ions due to its electronic configuration (t^3↑_2g e^2↑_g with S = 5/2) and spin only magnetic moment (5μ_B) compared to Mn³⁺ (4μ_B) and Mn₄⁺ (3μ_B). In addition to the traditional DE mechanism, some additional charge hopping mechanisms take place in the deficient compounds due to the presence of Mn²⁺ ions.⁵⁶ The Mn²⁺ ions at the A-site favour an additional hopping via Mn³⁺–O²⁻–Mn²⁺–O²⁻–Mn⁴⁺ path, called the multiple DE interactions and eventually the ferromagnetism and conductivity increases.^37,56 Thus it can be understood that the high magnetization value of Sr-0.18 and Sr-0.27 compounds compared to that of the pristine compound is due to the multiple DE interaction through intervening Mn²⁺ ions at the A-site. It suggests that the coexistence of Mn²⁺/Mn³⁺/Mn⁴⁺ ions in Sr-0.18 and Sr-0.27 compounds can be corroborated with the result obtained from XPS analysis. However, the unconventional charge hopping mechanism completely depends on the ratio of Mn²⁺/Mn³⁺/Mn⁴⁺ ions, the Sr-0.18 compound shows maximum magnetization, and after that decreases for Sr-0.27 compound. It suggests that the existence of Mn²⁺ ions in deficient compounds is responsible for the increase in the DE interaction, which is in agreement with the coexistence of the mixed valence state of Mn²⁺/Mn³⁺/Mn⁴⁺ in deficient compounds as obtained from XPS analysis. Again, the paramagnetic (PM) to FM transition temperature was calculated from the derivative of M versus T graph (not shown), and found significant changes with the increase in Sr-content. It is to be noted that in our previous work, we have tuned the T_C from 365 K (pristine) to 355 K for Sr-0.09 compound, however, in the present case, the same is further tuned down to 314 K and 277 K for Sr-0.18 and Sr-0.27 compounds respectively. The significant reduction in T_C towards room temperature in both the compounds is due to the changes in the average ionic radius and the changes in the Goldschmidt tolerance factor.^37,49 From the Rietveld refinement analysis, it is evident that the average A-site ionic radius and unit cell volume of both the compounds increases with increase in Sr-deficiency. As the tolerance factor of the compounds is directly proportional to the average A-site cationic radius, the decrease in T_C with Sr-deficiency can be related to the increase in tolerance factor.^37,49 The variation of inverse magnetic susceptibility χ⁻¹ with temperature was analyzed and shown in Fig. 3. The magnetic susceptibility obey the Curie–Weiss law at T > T_C, according to the relation

where θ is known as Curie–Weiss temperature and is determined from the point at which χ⁻¹ intercepts the temperature axis and C is the Curie constant. Then the experimental effective magnetic moment (μ^meas_eff) is calculated from the equation as follows
where, k_B is the Boltzmann constant, μ_B is the Bohr magneton, N_a is the Avogadro number and M_m is the molecular formula weight. The μ^meas_eff is found to be 5.83 μ_B 5.81 μ_B for Sr-0.18 and Sr-0.27 compounds. The theoretical effective magnetic moment μ^th_eff of Sr-0.18 compound is calculated as follows

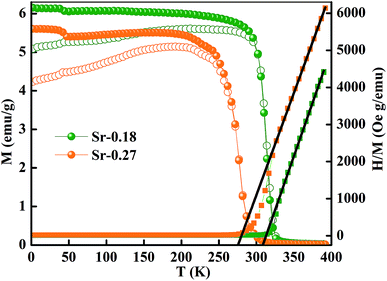Fig. 3 Temperature dependence of magnetization of La_0.67Sr_0.15□_0.18MnO_3−δ and La_0.67Sr_0.06□_0.27MnO_3−δ compounds under 100 Oe field.

With μ^th_eff(Mn²⁺) − 5.92μ_B, μ^th_eff(Mn³⁺) − 4.90μ_B and μ^th_eff(Mn⁴⁺) − 3.87μ_B and the ratio of Mn²⁺/Mn³⁺/Mn⁴⁺ is taken from the XPS analysis. The μ^th_eff is found to be 5.45 μ_B 5.37 μ_B for Sr-0.18 and Sr-0.27 compounds.

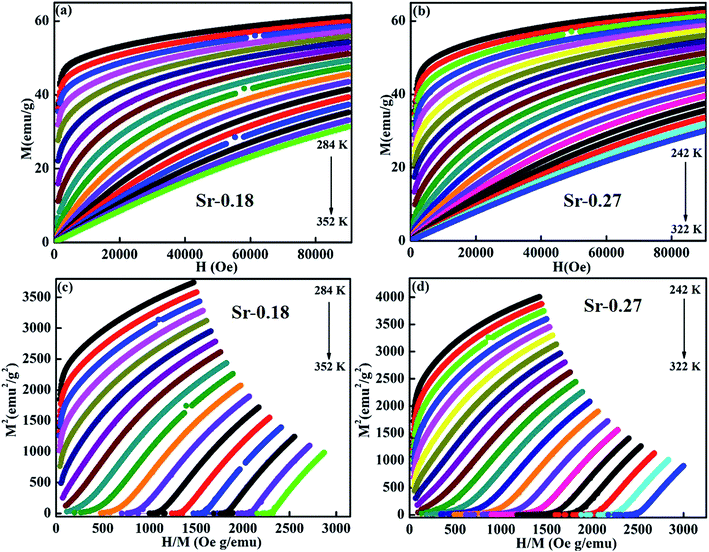
Further, the isothermal magnetization measurement was carried out at 2 K and 300 K and are shown in Fig. 4(a) and (b) respectively. Both the compounds show a small coercive field with soft ferromagnetic nature. It can be seen that magnetization increases rapidly at low field and does not saturate even at a field of 90 kOe. The hysteresis loops at 2 K confirm the high FM nature of the compounds, and it is evident that the FM nature is not merely destroyed by the increase in Sr-deficiency. From the hysteresis loop at 300 K, it can be understood that Sr-0.18 compound shows more FM character than that of Sr-0.27 compound, which confirm the room temperature FM behaviour of the former. The competing exchange interaction between DE and SE due to the FM/AFM components vary with the Mn²⁺/Mn³⁺/Mn⁴⁺ ratio, which in turn severely affects the isothermal magnetization behaviour of the deficient compounds at 2 K and 300 K. Furthermore, the isothermal magnetization measurements around the respective T_C was measured and are shown in Fig. 5(a) and (b). The magnetization was measured from 284 K to 354 K for Sr-0.18, and 242 K to 322 K for Sr-0.27 with an interval of 4 K. For T < T_C, a FM nature with a non-saturating behaviour at higher fields is seen for both the compounds. However, for T > T_C, a PM behaviour with a reduction in magnetization was observed. To further understand the nature of the magnetic transition, M² versus H/M called Arrott plots were plotted and are shown in Fig. 5(c) and (d). The regular Arrott plot between M² and H/M indicates that the transition governing the mean field model and the curve that pass through the origin should represent the T_C. Moreover, based on the Banerjee's criterion, a positive slope in the Arrott plot confirm that both the compounds undergo second order transition.⁶⁷

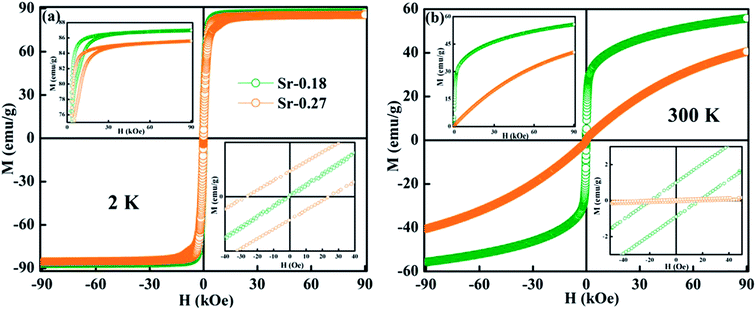Fig. 4 M–H loops at 2 K and 300 K of (a) La_0.67Sr_0.15□_0.18MnO_3−δ and (b) La_0.67Sr_0.06□_0.27MnO_3−δ compounds. The inset shows the enlarged view of the coercive field.

Fig. 5 Isothermal field dependence magnetization of (a) La_0.67Sr_0.15□_0.18MnO_3−δ and (b) La_0.67Sr_0.06□_0.27MnO_3−δ and Arrott plot of (c) La_0.67Sr_0.15□_0.18MnO_3−δ and (d) La_0.67Sr_0.06□_0.27MnO_3−δ compounds.

The magnetic entropy change is calculated from the isothermal magnetization curve based on the Maxwell relation as:⁶⁸

The ΔS_M as a function of temperature for 10–50 kOe field is shown in Fig. 6. Both the compounds show a maximum ΔS_M around T_C, and a reduction is seen on either side of the curve. For a field of 10 kOe, the Sr-0.18 compound exhibit a maximum ΔS_M value of 1.40 J kg⁻¹ K⁻¹ at 306 K, and for Sr-0.27 compound, the ΔS_M reaches a maximum value of 1.17 J kg⁻¹ K⁻¹ at 272 K. It can be seen that with increase in the magnetic field, the maximum ΔS_M value is slightly shifts to the high temperature region for both the compounds. For a field of 50 kOe, the Sr-0.18 compound exhibit a ΔS_M value of 4.61 J kg⁻¹ K⁻¹ at 310 K, and for Sr-0.27 compound, the ΔS_M reaches a maximum value of 4.11 J kg⁻¹ K⁻¹ at 276 K. In our previous work, we reported a ΔS_M value of 4.78 J kg⁻¹ K⁻¹ at 364 K for the pristine compound and 5.08 J kg⁻¹ K⁻¹ at 352 K for Sr-0.09 compound for a field change of 50 kOe.³⁷ However, in the present case, we have achieved a near room temperature (310 K) MCE with a significant ΔS_M value (4.61 J kg⁻¹ K⁻¹) for Sr-0.18 compound which is larger than that reported for numerous perovskite manganites^{29,31,35,45,47} Apart from the spin, charge and orbital ordering, the conventional DE interaction is the only favourable mechanism behind the entropy change in the pristine compound.³⁷ However, from the magnetization and magnetocaloric properties, it can be understood that the presence of Mn²⁺ ions in deficient compounds enhances the ferromagnetism and ΔS_M due to the multiple DE interaction via Mn³⁺–O²⁻–Mn²⁺–O²⁻–Mn⁴⁺ path. In addition to that, the Mn²⁺/Mn³⁺/Mn⁴⁺ ratio is the key parameter that determines the strength of the multiple DE interactions and hence, the ΔS_M of the deficient compounds. For practical applications at room temperature, the magnetocaloric materials should have a maximum ΔS_M value within the range of 300 K ≤ T ≤ 310 K. Hence Sr-0.18 compound is found to be an ideal candidate for room temperature magnetocaloric applications. Thus, the present investigation reveals that a significant magnetic entropy change near room temperature can be achieved by the creation of deficiency at the Sr-site in La_0.67Sr_0.33−yMnO_3−δ compound and the composition with a deficiency of y = 0.18, i.e., La_0.67Sr_0.15□_0.18MnO_3−δ could be a potential material for room temperature magnetic refrigeration applications.

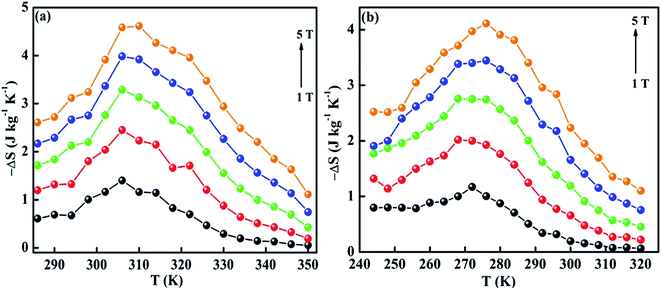Fig. 6 Magnetic entropy change of (a) La_0.67Sr_0.15□_0.18MnO_3−δ and (b) La_0.67Sr_0.06□_0.27MnO_3−δ compounds.

Conclusion

The effect of Sr-site deficiency on La_0.67Sr_0.33−yMnO_3−δ (y = 0.18 and 0.27) compounds and a detailed investigation on their structural, magnetic and magnetocaloric properties were carried out. The Rietveld refinement of the X-ray patterns confirms that both the compounds belong to rhombohedral crystal symmetry with R3̄c space group. Deficiency at the Sr-site compels to form Mn²⁺ states in addition to Mn³⁺/Mn⁴⁺, and the Mn²⁺ ions at the A-site favor multiple DE interactions via Mn³⁺–O²⁻–Mn²⁺–O²⁻–Mn⁴⁺ path and hence the ferromagnetic nature and magnetization enhanced. La_0.67Sr_0.15□_0.18MnO_3−δ was found to be ferromagnetic at 300 K and exhibit a ΔS_M of 4.61 J kg⁻¹ K⁻¹ at 310 K for a 50 kOe field. The present study indicates that the creation of deficiency at the Sr-site of La_0.67Sr_0.33MnO₃ helps to tune the T_C towards room temperature with a significant magnetic entropy change and the compound could be a potential candidate for room temperature magnetic refrigeration applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the financial support received from the Council of Scientific and Industrial Research (CSIR), Govt. of India, sponsored project MLP0031 and Department of Science and Technology sponsored project number, GAP232339. B. Arun and V. R. Akshay are thankful to the Council of Scientific and Industrial Research (CSIR), Government of India for granting the Senior Research Fellowship and also grateful to the Academy of Scientific and Innovative Research (AcSIR), CSIR.

References

1. K. A. Gschneidner Jr and V. K. Pecharsky, Annu. Rev. Mater. Res., 2000, 30, 387–429.
2. V. Franco, J. S. Blazquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342.
3. P. Sande, L. E. Hueso, D. R. Miguens, J. Rivas, F. Rivadulla and M. A. Lopez-Quintela, Appl. Phys. Lett., 2001, 79, 2040–2042.
4. A. M. Tishin and I. Spichkin, The Magnetocaloric Effect and Its Applications, Institute of Physics Publishing, Bristol, 2003.
5. M. H. Phan and S. C. Yu, J. Magn. Magn. Mater., 2007, 308, 325–340.
6. K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479–1539.
7. K. A. Gschneidner Jr and V. K. Pecharsky, Int. J. Refrig., 2008, 31, 945–961.
8. V. K. Pecharsky and K. A. Gschneidner Jr, Phys. Rev. Lett., 1997, 78, 4494–4497.
9. H. Wada and Y. Tanabe, Appl. Phys. Lett., 2001, 79, 3302–3304.
10. F. X. Hu, B. G. Shen, J. R. Sun, Z. H. Cheng, G. H. Rao and X. X. Zhang, Appl. Phys. Lett., 2001, 78, 3675–3677.
11. J. Shen, B. Gao, Q. Y. Dong, Y. X. Li, F. X. Hu, J. R. Sun and B. G. Shen, J. Phys. D: Appl. Phys., 2008, 41, 245005.
12. O. Tegus, E. Bruck, K. H. J. Buschow and F. R. deBoer, Nature, 2002, 415, 150–152.
13. Q. Y. Dong, B. G. Shen, J. Chen, J. Shen, F. Wang, H. W. Zhang and J. R. Sun, J. Appl. Phys., 2009, 105, 053908.
14. A. Giguere, M. Foldeaki, W. Shcnelle and E. Gmelin, J. Phys.: Condens. Matter, 1999, 11, 6969–6981.
15. T. Krenke, E. Duman, M. Acet, E. Wassermann, X. Moya, L. Manosa and A. Planes, Nat. Mater., 2005, 4, 450–454.
16. L. W. Li, G. Hu, Y. Qi and I. Umehara, Sci. Rep., 2017, 7, 42908.
17. Y. Yalin, L. W. Li, S. Kunpeng, Q. Yang and H. Dexuan, Intermetallics, 2017, 80, 22–25.
18. A. Boutahar, R. Moubah, E. K. Hlil, H. Lassri and E. Lorenzo, Sci. Rep., 2017, 7, 13904.
19. B. Arun, M. V. Suneesh and M. Vasundhara, J. Magn. Magn. Mater., 2016, 418, 265–272.
20. B. Arun, V. R. Akshay, G. R. Mutta, Ch. Venkatesh and M. Vasundhara, Mater. Res. Bull., 2017, 94, 537–543.
21. B. Sudakshina, B. Arun, K. D. Chandrasekhar, H. D. Yang and M. Vasundhara, Phys. B, 2018, 539, 14–20.
22. K. McBride, S. Bennington-Gray, J. Cook, L. Stella, S. Felton and D. Poulidi, CrystEngComm, 2017, 19, 3776–3791.
23. M. Abassi, Za. Mohamed, J. Dhahri and E. K. Hlil, Dalton Trans., 2016, 45, 4736–4746.
24. M. Jeddi, H. Gharsallah, M. Bejar, M. Bekri, E. Dhahri and E. K. Hlil, RSC Adv., 2018, 8, 9430–9439.
25. B. Arun, M. Athira, V. R. Akshay, B. Sudakshina, G. R. Mutta and M. Vasundhara, J. Magn. Magn. Mater., 2018, 448, 322–331.
26. B. Sudakshina, K. D. Chandrasekhar, H. D. Yang and M. Vasundhara, J. Phys. D Appl. Phys., 2017, 50, 065004.
27. B. Sudakshina, B. Arun and M. Vasundhara, J. Magn. Magn. Mater., 2018, 448, 250–256.
28. M. Oumezzine, A. C. Galca, I. Pasuk, C. F. Chiril, A. Leca, V. Kuncser, L. C. Tanase, A. Kuncser, C. Ghica and M. Oumezzine, Dalton Trans., 2016, 45, 15034–15040.
29. N. Kallel, S. Kallel, A. Hagaza and M. Oumezzine, Phys. B, 2009, 404, 285–288.
30. C. P. Reshmi, S. Savitha Pillai, K. G. Suresh and M. R. Varma, Solid State Sci., 2013, 19, 130–135.
31. S. Hcini, M. Boudard, S. Zemni and M. Oumezzine, Ceram. Int., 2014, 40, 16041–16050.
32. M. A. Zaidi, J. Dhahri, I. Zeydi, T. Alharbi and H. Belmabrouk, RSC Adv., 2017, 7, 43590–43599.
33. A. B. Hassine, A. Dhahri, M. L. Bouazizi, M. Oumezzine and E. K. Hlil, Ceram. Int., 2017, 43, 1390–1393.
34. I. Sfifir, A. Ezaami, W. Cheikhrouhou-Koubaa and A. Cheikhrouhou, J. Alloys Compd., 2017, 696, 760–767.
35. M. Chebaane, R. Bellouz, Ma. Oumezzine, E. K. Hlil and A. Fouzri, RSC Adv., 2018, 8, 7186–7195.
36. B. Arun, M. V. Suneesh, B. Sudakshina, V. R. Akshay, K. D. Chandrasekhar and M. Vasundhara, J. Phys. Chem. Solids, 2018, 123, 327–335.
37. B. Arun, V. R. Akshay and M. Vasundhara, Dalton Trans., 2018, 47, 15512–15522.
38. W. Boujelben, A. Cheikh-Rouhou, J. Pierre and J. C. Joubert, Phys. B, 2002, 321, 37–44.
39. M. Ellouze, W. Boujelben, A. Cheikhrouhou, H. Fuess and R. Madar, J. Alloys Compd., 2003, 352, 41–47.
40. L. Malavasi, J. Mater. Chem., 2008, 18, 3295–3308.
41. W. Cheikh-Rouhou Koubaa, M. Koubaa, A. Cheikh-Rouhou, W. Boujelben and A. M. Haghiri-Gosnet, J. Alloys Compd., 2008, 455, 67–72.
42. M. Khlifi, A. Tozri, M. Bejar, E. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2012, 324, 2142–2146.
43. R. Bellouz, M. Oumezzine, A. Dinia, G. Schmerber, E. K. Hlil and M. Oumezzine, RSC Adv., 2015, 5, 64557–64565.
44. M. Wali, R. Skini, M. Khlifi, E. Dhahri and E. K. Hlil, Dalton Trans., 2015, 44, 12796–12803.
45. R. Skini, M. Khlifi and E. K. Hlil, RSC Adv., 2016, 6, 34271–34279.
46. J. Makni-Chakroun, I. Sfifir, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, J. Magn. Magn. Mater., 2017, 432, 484–493.
47. S. Choura-Maatar, R. M’nassri, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Cheikhrouhou and E. K. Hlil, RSC Adv., 2017, 7, 50347–50357.
48. B. Arun, V. R. Akshay, K. D. Chandrasekhar, G. R. Mutta and M. Vasundhara, J. Magn. Magn. Mater., 2019, 472, 74–85.
49. B. Arun, V. R. Akshay, D. C. Kakarla and M. Vasundhara, J. Magn. Magn. Mater., 2019, 489, 165418.
50. A. V. Pashchenko, V. P. Pashchenko, N. A. Liedienov, V. K. Prokopenko, Yu. F. Revenko, N. E. Pismenova, V. V. Burhovetskii, V. Y. Sycheva, A. V. Voznyak, G. G. Levchenko, V. P. Dyakonov and H. Szymczak, J. Alloys Compd., 2017, 709, 779–788.
51. A. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, V. A. Turchenko, Yu. F. Revenko, A. S. Mazur, V. Ya. Sycheva, N. A. Liedienov, V. G. Pitsyuga and G. G. Levchenko, J. Exp. Theor. Phys., 2017, 124, 100–113.
52. K. Guidara, N. Abdelmoula, J. Dhahri and E. Dhahri, Phase Transitions, 2000, 70, 243–252.
53. W. Boujelben, A. Cheikh-Rouhou and J. C. Joubert, Eur. Phys. J. B, 2001, 24, 419–423.
54. M.-H. Phan, S. C. Yu and N. H. Hur, J. Magn. Magn. Mater., 2003, 262, 407–411.
55. R. Skini, A. Omri, M. Khlifi, E. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2014, 364, 5–10.
56. P. Orgiani, A. Galdi, C. Aruta, V. Cataudella, G. De Filippis, C. A. Perroni, V. Marigliano Ramaglia, R. Ciancio, N. B. Brookes, M. Moretti Sala, G. Ghiringhelli and L. Maritato, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205122.
57. D. Abou-Ras, W. Boujelben, A. Cheikh-Rouhou, J. Pierre, J.-P. Renard, L. Reversat and K. Shimizu, J. Magn. Magn. Mater., 2001, 233, 147–154.
58. M. F. Hundley and J. J. Neumeier, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11511–11515.
59. A. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, Yu. F. Revenko, Yu. S. Prylipko, N. A. Ledenev, G. G. Levchenko, V. P. Dyakonov and H. Szymczak, Acta Mater., 2014, 70, 218–227.
60. A. Tkach, A. Almeida, J. Agostinho Moreira, T. M. Correia, M. R. Chaves, O. Okhay, P. M. Vilarinho, I. Gregora and J. Petzelt, Appl. Phys. Lett., 2011, 98, 052903.
61. N. A. Liedienov, A. V. Pashchenko, V. A. Turchenko, V. Ya. Sycheva, A. V. Voznyak, V. P. Kladko, A. I. Gudimenko, D. D. Tatarchuk, Y. V. Didenko, I. V. Fesych, I. I. Makoed, A. T. Kozakov and G. G. Levchenko, Ceram. Int., 2019, 45, 14873–14879.
62. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson, R. St and C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
63. D. R. Baer, D. L. Blanchard, M. H. Engelhard and J. M. Zachara, Surf. Interface Anal., 1991, 17, 25–30.
64. C. Doroftei and L. Leontie, RSC Adv., 2017, 7, 27863–27871.
65. X. Xie, M. Chen, T. Liu, H. Jiang, H. Zhang and A. Chang, J. Mater. Sci.: Mater. Electron., 2017, 28, 8655–8661.
66. R. Natarajan, N. Palaniswamy, M. Natesan and V. S. Muralidharan, Open Corros. J., 2009, 2, 114–124.
67. B. K. Banerjee, Phys. Lett., 1964, 12, 16–17.
68. M. H. Phan, S. B. Tian, S. C. Yu and A. N. Ulyanov, J. Magn. Magn. Mater., 2003, 256, 306–310.

---