Open Access Article
Open Access ArticleFirst molecular electronic hyperpolarizability of series of π-conjugated oxazole dyes in solution: an experimental and theoretical study†
Luis M. G. Abegão *ab,
Ruben D. Fonsecacd,
Francisco A. Santosa,
José J. Rodrigues Jr
*ab,
Ruben D. Fonsecacd,
Francisco A. Santosa,
José J. Rodrigues Jr a,
Kenji Kamada
a,
Kenji Kamada e,
Cleber R. Mendonça
e,
Cleber R. Mendonça c,
Sandrine Piguelfg and
Leonardo De Boni*c
c,
Sandrine Piguelfg and
Leonardo De Boni*c
aDepartamento de Física, Universidade Federal de Sergipe, São Cristovão, SE 49100-000, Brazil
bDepartment of Radiology and Bioimaging, School of Medicine, Yale University, 300 Cedar Street, New Haven, Connecticut 06520, USA
cInstituto de Física de São Carlos, Universidade de São Paulo, CP 369, 13560-970 São Carlos, SP, Brazil. E-mail: deboni@ifsc.usp.br
dDepartamento de Fisica, Universidad Popular del Cesar, Barrio Sabana, Valledupar, Cesar 2000004, Colombia
eNational Institute of Advanced Industrial Science and Technology, Ikeda, Osaka 563-8577, Japan
fInstitut Curie, PSL Research University, CNRS, INSERM, UMR9187-U1196, Orsay, F-91405, France
gUniversité Paris Sud, Université Paris-Saclay, Orsay, F-91405, France
First published on 23rd August 2019
Abstract
In this work, we report the experimental and theoretical first molecular electronic hyperpolarizability (βHRS) of eleven π-conjugated oxazoles compounds in toluene medium. The Hyper-Rayleigh Scattering (HRS) technique allowed the determination of the experimental dynamic βHRS values, by exciting the compounds with a picosecond pulse trains from a Q-switched and mode-locked Nd:YAG laser tuned at 1064 nm. Theoretical predictions based on time-dependent density functional theory level using the Gaussian 09 program package were performed with three different functionals (B3LYP, CAM-B3LYP, and M06-2X), to calculate both static and dynamic theoretical βHRS values. Good accordance was found between the experimental and theoretical values, in particular for the CAM-B3LYP and M06-2X functionals.
Introduction
Organic compounds with the ability to convert the frequency of incident light in its double, i.e., second harmonic generation (SHG), nowadays have vital importance in the optoelectronics field.1–3 The significance of that role has been highly competed for by both organic and inorganic compounds that possess nonlinear optical (NLO) responses, in particular, the first molecular hyperpolarizability, which is the NLO response studied in this work.4,5 Such a response can be measured in a liquid medium by the hyper-Rayleigh scattering (HRS)6 technique. In general, inorganic compounds present a higher laser damage threshold than organic ones. On the other hand, the latter usually have a faster electronic response, making them more suitable, for example, for optical communications.7A π-conjugated system helps to promote the first electronic molecular hyperpolarizability, making dipolar organic compounds with a donor–bridge–acceptor (D–Br–A) configuration one of the most studied compounds in this field,8–10 although quadrupolar and octupolar configurations have also been explored.11–13 Regardless of the multipole configuration shape, two fundamental aspects enhance the NLO response: the high degree of π-conjugation and the non-symmetric nature of the compounds.14,15 The latter is an effect associated only to even-orders of NLO responses, while the first effect influences all NLO responses.16,17 Moreover, organic molecules tend to crystallize in the non-centrosymmetric form, which could amplify the SHG effect with the change of phase from liquid to solid, enhancing their potential as nonlinear optical switches.18,19
The series of π-conjugated molecular structures studied in this work belong to the oxazole family, in the particular case of oxazole dyes. This type of molecular structures, which possesses 2,5-diaryloxazole as its building block unit, has shown excellent transparency for wavelengths longer than 400 nm,20 making them extremely suitable to perform HRS measurements with a fixed excitation wavelength at the NIR region. Moreover, if the crystallization process of these type of compounds is successful, then their use as SHG organic crystals in the VIS-NIR region, which is the adequate region for optical communications,21–23 will be a real and concrete photonics application.
The fundamental principle of the HRS technique is to focus a laser beam with a certain frequency ω on a liquid sample and check whether the response of this light–matter interaction generates a light scattering with twice the frequency (2ω) of the incident radiation, in order to determine the first molecular electronic hyperpolarizability (βHRS) in an isotropic material. HRS is not the only available method to determine the βHRS value. The traditional approach to achieve this quantity is known as the EFISH (Electric-Field Induced Second Harmonic Generation).24,25 There are some advantages of using HRS instead of EFISH, such as the non-requirement to identify the permanent dipole moment and the second molecular hyperpolarizability, nor to estimate the local fields, thus eliminating the need to apply a high static electric field in the studied sample.
In this work, we report for the first time experimental βHRS values of eleven π-conjugated oxazole dyes in a solution of toluene, by using the HRS technique. Theoretical values of βHRS, calculated by using three different functionals (B3LYP, CAM-B3LYP, and M06-2X) with basis sets 6-311G++(d,p) and 6-311G+(d,p) are also reported, to best of our knowledge, for the first time, used to check accordance between experimental and theoretical data.
Experimental
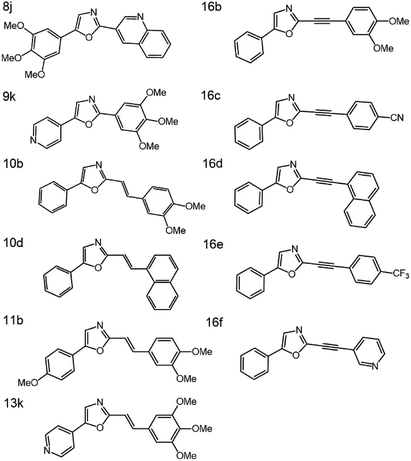
The molecular structures of the eleven oxazoles dyes studied, are shown in Fig. 1 and are designated henceforth as 8j (C21H18N2O4), 9k (C17H16N2O4), 10b (C19H17NO3), 10d (C21H15NO), 11b (C20H19NO4), 13k (C19H18N2O4), 16b (C19H15NO3), 16c (C18H10N2O), 16d (C21H13NO), 16e (C18H10F3NO) and 16f (C16H10N2O). The information about the synthesis and preparation of these compounds can be found elsewhere.20 Each compound was diluted in five different concentrations, ranging from 1 × 1017 to 3 × 1018 molecules per cm3, in toluene, and kept in a fused quartz cuvette with 10 mm long optical path. Toluene was used as a solvent due to its excellent solubility presented at the higher samples concentrations also, because it is from the family of hydrocarbon solvents belonging, which usually are inert to reagents of all kinds, besides being neither acid nor basic, under the Lewis or Brønsted perspective.The classical 90 degrees optical geometry was used in the HRS experimental setup (Fig. 2), which has the same optical configuration presented by Clays and Persoons,6 with some variations introduced by Franzen et al.26 to take advantage of the experimental optoelectronic setup described in the next paragraph.
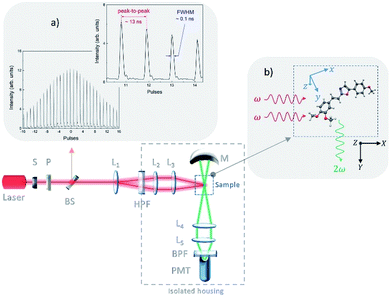 | ||
| Fig. 2 HRS experimental setup, with the (a) intrinsic intensity distribution of the pulse train at 1064 nm; and (b) the laboratory and molecular coordinates system of references. | ||
The excitation light source used was Q-switched and mode-locked solid-state laser (Nd:YAG), with a variable repetition rate from 3 Hz to 800 Hz, which produces a train with about 30 laser pulses separated from each other of approximately 13 ns. Each pulse of the pulse train has 100 ps of pulse width. The onset, depicted in Fig. 2a, shows the intrinsic intensity distribution of the pulse train at 1064 nm, corresponding to the laser's fundamental frequency (ω).
The laboratory and molecular coordinates system of references were defined as (X, Y, Z) and (x, y, z), respectively, as illustrated in Fig. 2b. The propagation of the laser beam is along the X-axis, defined as the laboratory system of reference, in which the first element is a computer-controlled shutter (S), set up closed during the dark count rate (DCR) and opened only during the measurements of the sample, i.e., when acquiring the HRS signal. The second element consists of a set of cross polarizers (P) to control two optical parameters: the maximum average power and to fix the linear polarization of the laser beam, which is always in the Z-axis. The third element is a beam splitter (BS), used to deviate a small portion of the laser beam into a fast-amplified photodetector (APD), which has a rise time around one nanosecond. The APD acquired signal is used as the reference pulse train intensities, as shown on Fig. 2a. After the BS, the laser beam is first expanded then collimated and finally focused on the sample by L1, L2, and L3 lenses respectively. This procedure avoids damaging the cuvette wall. The scattered signal (2ω), i.e., the HRS signal, is collected perpendicularly (Y-axis) to the excitation beam by a photomultiplier tube (PMT). A bandpass filter with 10 nm band at 532 nm was placed in front of the PMT window, to minimize any possible scattered excitation light. Also, a spherical mirror (M) is used to improve the PMT signal-to-noise ratio. More details about the experimental setup can be found elsewhere.11,27,28
HRS experiment is performed by measuring the intensity of the incoherently scattered frequency-doubled light, generated by the interaction of an intense laser beam with an isotropic solution. If the solution presents negligible molar absorptivity at harmonic wavelength, the relation between scattered intensity at double-frequency (I2ω) and intensity of the excitation beam (Iω) is given by eqn (1).29 G is a parameter that includes experimental factors such as the scattering geometry, local field factors at ω and 2ω, and photon collection efficiency. N represents the molar concentration of the used samples and 〈βHRS〉 is the orientational average first molecular electronic hyperpolarizability squared. The subscripts s and c refer to the solvent and chromophore respectively.
| I2ω = G(Ns〈βHRS2〉s + Nc〈βHRS2〉c)Iω2 | (1) |
By considering a plane-polarized incident light beam, while the observation of the scattered signal on a frequency doubled light is made perpendicular to the propagation plane, the full HRS intensity could be described by eqn 2. 〈βZZZ2〉 and 〈βZXX2〉 correspond to the orientationally averaged tensor components, here we adopted the laboratory coordinate system of reference.
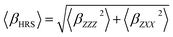 | (2) |
Eqn (3a) and (3b) show the relationship between those molecular averages and the molecular first-order hyperpolarizability tensor components, given by the molecular system of reference (x, y, z), without assuming Kleinman's conditions of symmetry.30–32
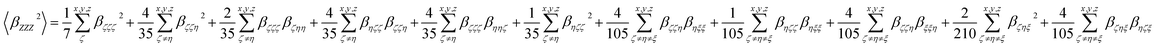 | (3a) |
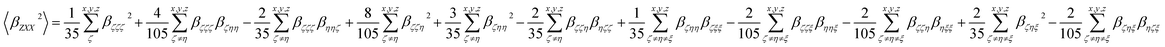 | (3b) |
Theoretical details
Quantum-chemical calculations (QCC) were performed at the density functional theory33 by using the well-known exchange–correlation functional Becke, three-parameter, Lee–Yang–Parr (B3LYP),34 as well its long-range corrected version which includes the Coulomb-attenuating method (CAM-B3LYP).35 Also, a variation of a hybrid functional by Truhlar and Zhao (M06-2X),36 which is one of the suitable functionals to study non-covalent interactions, was used. A split-valence basis set with one additional polarization function for non-hydrogen atoms, one additional polarization function on hydrogen atoms, and diffuse functions on non-hydrogen atoms were used associated with families of methods described previously. Geometry optimization calculations were performed in toluene medium employing a polarizable continuum model (PCM), using the integral equation formalism variant (IEF-PCM),37 to obtain the geometrical structure input used for the simulation of the static (ω = 0 a.u.) and dynamic (ω = 0.04282 a.u.) components of the first-order hyperpolarizability tensor (βijk) in solvent medium. Gaussian 09 program package38 was used to perform all the calculations mentioned above. The optimized geometries are shown in ESI (Tables S1 to S6†).When studying systems with a low-symmetry molecular structure, the hyperpolarizability tensor could be estimated more accurately by using the rotational invariance concept,39 combined with the use of the mixed spherical–Cartesian formalism.40 Eqn (4) expresses, under this formalism, the orientational averaged first-order hyperpolarizability squared 〈βHRS〉, in which the molecular βHRS tensor (symmetric 3rd rank tensor) is decomposed as the sum of a dipolar (J = 1) and an octupolar (J = 3) tensorial form. The relationships between the dipolar and octupolar components and the Cartesian components of β are described in eqn (5). The combination between eqn (4) and (5) allows the final theoretical values estimation regarding the static and dynamic first-order hyperpolarizabilities.
For the study of systems with very low-symmetry, it is convenient to explore the concept of rotational invariance to represent of the hyperpolarizability tensor and to use the mixed spherical–Cartesian formalism to discuss HRS measurements in terms of multipolar components.39 In this formalism,40 the orientational averaged first-order hyperpolarizability squared 〈βHRS〉 is expressed by eqn (4), in which the molecular βHRS tensor (symmetric 3rd rank tensor) is decomposed as the sum of a dipolar (J = 1) and an octupolar (J = 3) tensorial form. The relationships between the dipolar and octupolar components and the Cartesian components of β are described in eqn (5). The combination between eqn (4), 5(a) and 5(b) allows estimate the final theoretical values for the static and dynamic first-order hyperpolarizabilities.
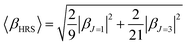 | (4) |
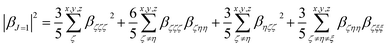 | (5a) |
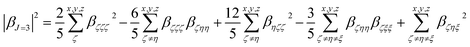 | (5b) |
Results and discussion
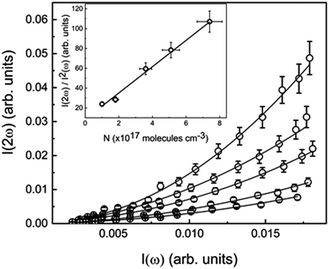
The absorbance spectra presented in the ESI (Fig. S1 to S11†) of all the studied samples in toluene medium showed that there is not any absorption at 532 nm. Therefore, an induced two-photon absorption process is also neglected when exciting the samples with 1064 nm. In fact, the absorbance spectra show that all samples present a transparency window that starts at approximately 425 nm, going to NIR region, indicating no absorption of the HRS signal by the samples. Moreover, the two-photon absorption spectra of some compounds have already been reported elsewhere,41 revealing that for excitation wavelengths longer than 900 nm the two-photon absorption cross-section is null. The probability of a three-photon excitation, which is a fifth-order NLO process, has significantly lower efficiency than its homolog third-order NLO phenomenon; thus, the fluorescence emission of the samples triggered by multi-photon excitation is completely ruled out. The optical signal acquired on the PMT, under this experimental setup, is considered a SHG effect at 532 nm, which is confirmed by the quadratic dependence of the HRS signal (I(2ω)) as a function of the excitation intensity (I(ω)), as can be observed in Fig. 3 for compound 8j.The data analysis of the compound 8j dissolved in toluene is shown in Fig. 3, as an example of how to interpret a typical experimental HRS result. The open circles are the experimental points acquired at 90 degrees by the PMT when the sample is shined by the intense pulsed laser at 1064 nm. The five solid lines represent the second order polynomial best fits for five different concentrations, which are in accordance with the fundamental HRS physical principle described in the literature.6 It is also possible to observe, in the inset of Fig. 3, the linear behaviour between the intensity of the first-order hyperpolarizability signal (I(2ω)/I2(ω)) and the sample concentration, allowing the comparison with the external reference compound, that, in this particular study, was the para-nitroaniline (PNA). The evaluation of the dynamic first-order hyperpolarizability, for this respective sample (8j), was made by calculating the ratio between the angular coefficients (α) of the sample with the one obtained from the reference molecule (PNA), by using eqn (6). The complete set of data analysis for all compounds is presented in the ESI (Fig. S12–S21†).
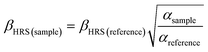 | (6) |
As mentioned before, the chosen compound to use as an external reference was PNA, with a β2ω value of 18 × 10−30 cm4 statvolt−1 in toluene medium.42 The highest HRS signal recorded corresponds to the compound 16c which is three times higher than the reference compound, while the lowest signal belongs to compound 10c, which has approximately the same value of the reference compound. All the theoretical results obtained by using the functionals B3LYP, M06-2X and CAM-B3LYP, with the basis sets 6-311+G(d,p) and 6-311++G(d,p), as well the experimental ones are presented in the ESI (Tables S7 and S8†).
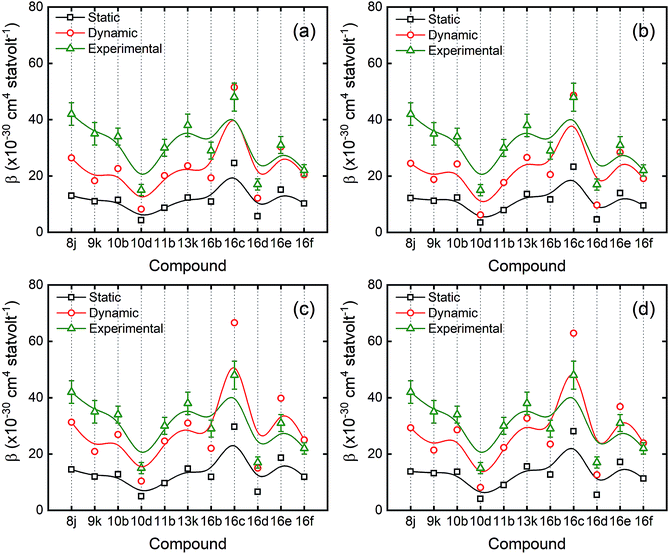
Fig. 4(a) and (b) compare the theoretical results with the previous mentioned functionals by using a basis set with diffuse functions only on heavy atoms (non-H atoms), while Fig. 4(c) and (d) show the comparison by using the same functionals, but now applying a basis set with both diffuse functions on H and non-H atoms. The theoretical results were considerably underestimated for every compound when compared to experimental ones, calculated with the B3LYP (data shown in Tables S7 and S8†). However, when calculated with M06-2X and CAM-B3LYP, the results are less underestimated when compared to experimental ones, in particular when using with the basis set which includes both diffuse functions on H and non-H atoms (6-311++G(d,p)).
As one can see in Fig. 4, the tendency is very similar between experimental and theoretical values, for both plotted methods as a function of the molecules. In other words, when the experimental value increases for some molecule, the theoretical one follows the same tendency. In fact, by applying the basis set 6-311++G(d,p), each theoretical value shows a small increment on their value when compared to 6-311+G(d,p). However, it still below to the experimental ones, except for compounds 16c and 16e. This behaviour suggests that by using 6-311++G(d,p) basis set, which takes into account diffuse functions on both non-H and H atoms, helps to improve the simulation on molecular hyperpolarizabilities. The contrast of performance between the functionals B3LYP and CAM-B3LYP is entirely accepted since CAM-B3LYP is the B3LYP corrected version taking into account the Coulomb-attenuating method.
When comparing the values of the experimental first hyperpolarizability with the theoretical values of the electric dipole moment, a similar trend to the one depicted in Fig. 4 is obtained, as one can see in the ESI (Fig. S22†).
Conclusions
In summary, we reported the first-order hyperpolarizability of a new class of chromophores based on the oxazole scaffold substituted with styryl or alkynyl groups. All compounds showed values for the first molecular hyperpolarizability higher than the standard sample. As mentioned elsewhere,43–45 centrosymmetrical molecular structures should have an extremely low second-order nonlinear optical signal. Consequently, it was expected that the compounds investigated in this work, which have a low centrosymmetric structure nature, present significant HRS signal, such as the compound 16c which presented a value three times higher than the reference compound.The samples were pumped with a pulsed laser at 1064 nm, which is a wavelength far away from the absorption region. In this condition, we excluded any contribution from the one- and two-photon absorption process to populate any excited states. Therefore, all βHRS experimental values presented in this work are due to pure electronic effects from the SHG in solution, suggesting that these compounds can be used as raw materials for developing nonlinear second-order photonics devices.
The theoretical values obtained by the QCC performed at the density functional theory by using the Gaussian 09 program package showed reasonable accordance with the experimental ones. In particular, when the calculations were performed with the functionals CAM-B3LYP and M06-2X.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brazil (CAPES) – Finance Code 001, CNPq/MCT, FAPITEC, Nanofoton Network, INCT-FOTÔNICA, FAPESP 2016/20886-1 and 2018/11283-7, Army Research Laboratory W911NF-17-1-0123 and Air Force Office of Scientific Research (FA9550-12-1-0028).References
- F. Castet, V. Rodriguez, J.-L. Pozzo, L. Ducasse, A. Plaquet and B. Champagne, Acc. Chem. Res., 2013, 46, 2656–2665 CrossRef CAS PubMed.
- H. Zhang, Q. Liao, X. Wang, Z. Xu and H. Fu, Nanoscale, 2015, 7, 10186–10192 RSC.
- X.-S. Xing, R.-J. Sa, P.-X. Li, N.-N. Zhang, Z.-Y. Zhou, B.-W. Liu, J. Liu, M.-S. Wang and G.-C. Guo, Chem. Sci., 2017, 8, 7751–7757 RSC.
- G. Ulrich, A. Barsella, A. Boeglin, S. Niu and R. Ziessel, ChemPhysChem, 2014, 15, 2693–2700 CrossRef CAS PubMed.
- J. Butet, P.-F. Brevet and O. J. Martin, ACS Nano, 2015, 9, 10545–10562 CrossRef CAS PubMed.
- K. Clays and A. Persoons, Phys. Rev. Lett., 1991, 66, 2980 CrossRef CAS PubMed.
- M. Li, Y. Li, H. Zhang, S. Wang, Y. Ao and Z. Cui, J. Mater. Chem. C, 2017, 5, 4111–4122 RSC.
- F. Meyers, S. Marder, B. Pierce and J. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- T.-G. Zhang, Y. Zhao, I. Asselberghs, A. Persoons, K. Clays and M. J. Therien, J. Am. Chem. Soc., 2005, 127, 9710–9720 CrossRef CAS PubMed.
- L. R. Dalton, P. A. Sullivan and D. H. Bale, Chem. Rev., 2009, 110, 25–55 CrossRef PubMed.
- R. D. Fonseca, M. G. Vivas, D. L. Silva, G. Eucat, Y. Bretonnière, C. Andraud, L. De Boni and C. R. Mendonça, J. Phys. Chem. C, 2018, 122, 1770–1778 CrossRef CAS.
- F. Castet, M. Blanchard-Desce, F. Adamietz, Y. M. Poronik, D. T. Gryko and V. Rodriguez, ChemPhysChem, 2014, 15, 2575–2581 CrossRef CAS PubMed.
- W. Li, Y. Hu, C. Zhong, X. Zhou, Q. Wang, W. Q. Tian and J. D. Goddard, J. Mater. Chem. C, 2016, 4, 6054–6062 RSC.
- S. R. Marder, L.-T. Cheng, B. G. Tiemann, A. C. Friedli, M. Blanchard-Desce, J. W. Perry and J. Skindhøj, Science, 1994, 263, 511–514 CrossRef CAS PubMed.
- R. Andreu, M. J. Blesa, L. Carrasquer, J. Garín, J. Orduna, B. Villacampa, R. Alcalá, J. Casado, M. C. Ruiz Delgado and J. T. López Navarrete, J. Am. Chem. Soc., 2005, 127, 8835–8845 CrossRef CAS PubMed.
- A. Plaquet, B. Champagne, J. Kulhánek, F. Bureš, E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, ChemPhysChem, 2011, 12, 3245–3252 CrossRef CAS PubMed.
- O. Ostroverkhova, Handbook of Organic Materials for Electronic and Photonic Devices, Elsevier Science, 2018 Search PubMed.
- B. Gu, C. Zhao, A. Baev, K.-T. Yong, S. Wen and P. N. Prasad, Adv. Opt. Photonics, 2016, 8, 328–369 CrossRef.
- P. G. Lacroix, I. Malfant and C. Lepetit, Coord. Chem. Rev., 2016, 308, 381–394 CrossRef CAS.
- F. Mahuteau-Betzer and S. Piguel, Tetrahedron Lett., 2013, 54, 3188–3193 CrossRef CAS.
- R. Surekha, R. Gunaseelan, P. Sagayaraj and K. Ambujam, CrystEngComm, 2014, 16, 7979–7989 RSC.
- M. Anis, S. Ramteke, M. Shirsat, G. Muley and M. Baig, Opt. Mater., 2017, 72, 590–595 CrossRef CAS.
- M. Kajamuhideen, K. Sethuraman, K. Ramamurthi and P. Ramasamy, Opt. Laser Technol., 2017, 91, 159–165 CrossRef CAS.
- C. Bosshard, G. Knöpfle, P. Pretre and P. Günter, J. Appl. Phys., 1992, 71, 1594–1605 CrossRef CAS.
- D. Burland, C. Walsh, F. Kajzar and C. Sentein, J. Opt. Soc. Am. B, 1991, 8, 2269–2281 CrossRef CAS.
- P. L. Franzen, L. Misoguti and S. C. Zilio, Appl. Opt., 2008, 47, 1443–1446 CrossRef PubMed.
- L. M. Abegão, R. D. Fonseca, F. A. Santos, G. B. Souza, A. L. B. Barreiros, M. L. Barreiros, M. Alencar, C. R. Mendonça, D. L. Silva and L. De Boni, Chem. Phys. Lett., 2016, 648, 91–96 CrossRef.
- M. G. Vivas, D. L. Silva, R. D. Rodriguez, S. Canuto, J. r. m. Malinge, E. n. Ishow, C. R. Mendonca and L. De Boni, J. Phys. Chem. C, 2015, 119, 12589–12597 CrossRef CAS.
- E. Hendrickx, K. Clays and A. Persoons, Acc. Chem. Res., 1998, 31, 675–683 CrossRef CAS.
- R. Bersohn, Y. H. Pao and H. Frisch, J. Chem. Phys., 1966, 45, 3184–3198 CrossRef CAS.
- E. Bogdan, A. Plaquet, L. Antonov, V. Rodriguez, L. Ducasse, B. t. Champagne and F. Castet, J. Phys. Chem. C, 2010, 114, 12760–12768 CrossRef CAS.
- M. de Wergifosse and S. Grimme, J. Chem. Phys., 2018, 149, 024108 CrossRef PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. Tomasi, B. Mennucci and E. Cances, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09 Rev. D01, Gaussian, Inc., Wallingford, 2012 Search PubMed.
- S. Brasselet and J. Zyss, J. Opt. Soc. Am. B, 1998, 15, 257–288 CrossRef CAS.
- K. Pielak, F. Bondu, L. Sanguinet, V. Rodriguez, B. Champagne and F. d. r. Castet, J. Phys. Chem. C, 2017, 121, 1851–1860 CrossRef CAS.
- L. M. Abegão, R. D. Fonseca, T. N. Ramos, F. Mahuteau-Betzer, S. Piguel, R. José Joatan Jr, C. R. Mendonça, S. Canuto, D. L. Silva and L. De Boni, J. Phys. Chem. C, 2018, 122, 10526–10534 CrossRef.
- D. L. Silva, R. D. Fonseca, M. G. Vivas, E. Ishow, S. Canuto, C. R. Mendonca and L. De Boni, J. Chem. Phys., 2015, 142, 064312 CrossRef PubMed.
- G. de la Torre, T. Torres and F. Agulló-López, Adv. Mater., 1997, 9, 265–269 CrossRef CAS.
- X. Liu, Z. Yang, D. Wang and H. Cao, Crystals, 2016, 6, 158 CrossRef.
- F. A. Santos, L. M. Abegão, R. D. Fonseca, A. M. Alcântara, C. R. Mendonça, M. S. Valle, M. Alencar, K. Kamada, L. De Boni and J. Rodrigues Jr, J. Photochem. Photobiol., A, 2019, 369, 70–76 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05246a |
| This journal is © The Royal Society of Chemistry 2019 |