DOI:
10.1039/C9RA06323D
(Paper)
RSC Adv., 2019,
9, 29429-29432
A formation model of superoxide radicals photogenerated in nano-TiO2 suspensions†
Received
14th August 2019
, Accepted 23rd August 2019
First published on 17th September 2019
Abstract
A formation model of O2˙− produced in TiO2 photocatalysis was established, and then a custom built continuous flow chemiluminescence (CFCL) system was used to confirm the model's reliability by monitoring the O2˙− formation process. This model may give deeper insights into O2˙− formation for TiO2 and other photocatalysts.
In photocatalytic reactions, such as TiO2, it is generally accepted that O2˙− is produced from the reduction of adsorbed oxygen by photogenerated electrons on the TiO2 surface.1–5 O2˙− formation is a rate-limiting process in TiO2 photocatalytic reactions,6 and thus determines the efficiency of TiO2 photocatalytic reactions by promoting the separation of photogenerated electrons and holes. Moreover, O2˙− is an intriguing active species, attracting a great deal of attention in recent years due to its unique role. Previous studies have confirmed that O2˙− plays an essential role in the photodegradation of pollutants.7,8 Therefore, probing the dynamic formation of O2˙− over the course of time under UV irradiation is conducive to better understanding TiO2 photocatalytic reactions. We have successfully identified surface long-lived O2˙− photogenerated on TiO2 surface,9 however, the dynamic details of O2˙− formation in TiO2 photocatalytic reactions still remain to be solved.
In photocatalytic reactions, O2˙− is continuously undergoing the processes of formation and deactivation simultaneously. Many methods have been developed to determine the O2˙−, including electron spin resonance (ESR),10 spectrophotometric assays,11–13 and fluorescence assays,14,15 but the O2˙− could only be detected at discrete times, and thus the total quantity could only be given within the irradiation duration. Given these limitations, O2˙− dynamic monitoring is a great challenge. Chemiluminescence (CL) is inherently sensitive and rapid due to the relative ease with which light emission is instantly generated through a chemical reaction when two or more reactants are mixed. These qualities of CL make it suitable for the dynamic study of O2˙−, despite its characteristic instability. In a previous study, we were able to successfully develop a continuous flow chemiluminescence (CFCL) method for dynamic monitoring of the formation process of O2˙− in TiO2 photocatalytic reactions.16
For the formation mechanism of O2˙− in TiO2 photocatalytic reactions, it is generally accepted that O2˙− formation occurs on TiO2 surfaces by the following scheme:
where O
2 denotes the dissolved oxygen (DO) in solution, S denotes the oxygen adsorption site on TiO
2 surface,
k1 and
k−1 denote the adsorption/desorption rate constant of O
2 respectively, O
2,
s denotes the adsorbed oxygen on TiO
2 surface,
kf denotes the formation rate constant of O
2˙
−, O
2,s˙
− denotes the O
2˙
− formed on TiO
2 surface, and
kd denotes the rate constant of O
2˙
− decomposition. It was reported that DO was first adsorbed on the site of TiO
2 surface following the Langmuir isotherm,
6 and then the adsorbed O
2 was reduced to O
2˙
− by photogenerated electrons under UV irradiation. Meanwhile, the formed O
2˙
− was transformed into other species by side reactions, such as H
2O
2 or
1O
2 which deactivated to O
2 quickly. Specifically, it is suggested by some research that O
2˙
− could be produced from the oxidation of H
2O
2 by valence-band hole (h
+) or hydroxyl radical (·OH) in solution, where H
2O
2 is produced by the two-step oxidation of water or the two-electron reduction of O
2.
17 It is insignificant in this study because the O
2˙
− detected by CFCL method is the long-lived superoxide adsorbed on TiO
2 surface which is produced from the reduction of O
2 by photogenerated electrons, not in solution according to our previous study.
9 The process of O
2˙
− formation was illustrated concretely as follows: when TiO
2 semiconductor is irradiated, the photogenerated electrons transferring to the TiO
2 surface are captured by five-coordinated surface Ti
4+ to form the Ti
3+ (
eqn (1)). Then the O
2 adsorbed on TiO
2 surface react with Ti
3+ to form O
2˙
− (
eqn (2)).
1,2,18| | |
–Ti4+–OH + e → –Ti3+ + OH−
| (1) |
| | |
–Ti3+ + O2,s → –Ti4+⋯OO˙−
| (2) |
| | |
O2˙− + O2˙− + H+ → H2O2 + O2
| (5) |
Meanwhile, O2˙− formed also undergoes a decaying process possibly via the following three pathways (eqn (3)–(5)): (1) oxidation by h+ or ·OH, (2) further reduction by e, or (3) self-disproportionation in solution. Therefore, the number of O2˙− determined in photocatalytic reactions at any irradiation time (t) is what the total quantity of formed O2˙− subtract those decomposed via the aforementioned side reactions from t0 s to t s upon irradiation. The formula can be expressed as follows:
| |
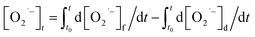 | (6) |
In this equation, the
t0 and
t of the lower and upper limit of the definite integral represent the starting and ending time of UV irradiation respectively. Based on the formation process of O
2˙
− mentioned above, the net rate of O
2˙
− formation at any time in photocatalytic reactions can be obtained as shown in
eqn (7.1). The first term of the right side of the
eqn (7.1) represents the formation rate of O
2˙
−, and it is a second-order reaction with respect to the concentration of –Ti
3+([Ti
3+]) and adsorbed oxygen (O
2,s).
kf is a second-order formation rate constant. The second term (
eqn (7.1)) represents the decay rate of O
2˙
−, among which
kd is a second-order decay rate constant, [X] represents the concentration of e, h
+, ·OH or O
2˙
− in terms of
eqn (3)–(5). It is generally believed to contain the aforementioned three pathways. We have previously confirmed that the O
2˙
− adsorbed on TiO
2 surface is thermodynamically favored.
9 Therefore, the two former pathways (
eqn (3) and
(4)) dominated the decay process under UV irradiation. These processes were considered to be pseudo-first-order due to the constant of h
+, ·OH and e under steady-state irradiation. So
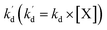
is the pseudo-first-order apparent rate constant (
eqn (7.2)). [O
2]
s is equal to oxygen coverage on TiO
2 surface (
θ) by the number of adsorption sites ([S]) according to Langmuir isotherm (
eqn (7.2)), in which
θ is related to the DO concentration in solution ([O
2]), adsorption constant (
k1), desorption constant (
k−1), and formation rate constant of O
2˙
− (
kf) (
eqn (7.3)).
| |
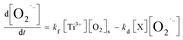 | (7.1) |
| |
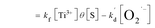 | (7.2) |
| |
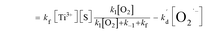 | (7.3) |
It has been reported that the electron transfer from TiO2 to O2 is the rate-limiting step in TiO2 photocatalytic reaction.6,19–21 Upon this, kf is far less than k1[O2] and k−1. Furthermore, the [O2] in solution is low, and thus k1[O2] is far less than k−1. If such speculation is true, the eqn (7.3) can be eventually transformed into the following:
| |
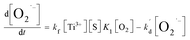 | (8) |
where
K1 (
K1 =
k1/
k−1) is the adsorption equilibrium constant of [O
2]. Assuming that [O
2˙
−] =
mCL +
n, which is a linear relationship between O
2˙
− concentration and CL intensity, the
eqn (8) can then be converted into the following:
| |
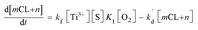 | (9) |
Finally, the eqn (10) representing the formation model of O2˙−, with respect to time as the independent variable and CL intensity as the dependent variable, would be obtained by integrating these variables with the eqn (9) from t0 to t:
| |
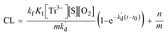 | (10) |
In eqn (10), kf, K1, 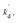 [S], [O2], m, and n are constants under certain conditions. The coefficient
[S], [O2], m, and n are constants under certain conditions. The coefficient 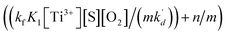 represents the theoretical maximum CL intensity (CL0) corresponding to the steady-state concentration of O2˙− when t is infinite in irradiated TiO2 suspensions. Herein t0 is the time when irradiation starts for 50 s, due to the disturbance of background signal within the first 50 s of irradiation. According to eqn (10), given that kf, K1, and kd are determined by the intrinsic property of TiO2 photocatalyst regardless of experimental conditions, CL0 is dependent on [Ti3+], [S], [O2] and [X], which are closely related to experimental conditions. In photocatalytic reactions, [Ti3+] relies on the number of photogenerated electrons highly dependent on I; [S] is the total surface area of TiO2 in suspension, closely related to [TiO2]; [O2] is dependent on [DO] in TiO2 suspensions; [X], the aforementioned concentration of h+, ·OH and e, is also dependent on I.
represents the theoretical maximum CL intensity (CL0) corresponding to the steady-state concentration of O2˙− when t is infinite in irradiated TiO2 suspensions. Herein t0 is the time when irradiation starts for 50 s, due to the disturbance of background signal within the first 50 s of irradiation. According to eqn (10), given that kf, K1, and kd are determined by the intrinsic property of TiO2 photocatalyst regardless of experimental conditions, CL0 is dependent on [Ti3+], [S], [O2] and [X], which are closely related to experimental conditions. In photocatalytic reactions, [Ti3+] relies on the number of photogenerated electrons highly dependent on I; [S] is the total surface area of TiO2 in suspension, closely related to [TiO2]; [O2] is dependent on [DO] in TiO2 suspensions; [X], the aforementioned concentration of h+, ·OH and e, is also dependent on I.
In order to verify the formation model of O2˙−, we fit the different CL curves with eqn (10) by changing [TiO2], I, and [DO]. As shown in Fig. 1(a–i), the CL curves from different [TiO2], I and [DO] were well-fit by eqn (10) with high correlation coefficients (R2 > 0.99), indicating that the model could simulate dynamic process of O2˙− formation. Furthermore, according to the O2˙− formation model (eqn (10)), CL intensity is linearly correlated to [S], [Ti3+], and [O2], indicating that CL intensity could increase linearly with the increase of [TiO2], I and [DO] within set limits. In order to verify this assumption, CL intensity at 300 s, 600 s, 900 s, 1200 s and +∞ under different [TiO2], I and [DO] conditions in TiO2 suspensions was calculated by eqn (10) (Table S1†). Then the CL intensity from different [TiO2], I and [DO] at different time points were linearly fit (Fig. S1–3†), and the R square values were calculated and summarized in Table 1. For instance, the CL intensity with TiO2 concentration of 0.02 mg mL−1, 0.05 mg mL−1 and 0.1 mg mL−1 at 300 s, 600 s, 900 s, 1200 s and +∞, respectively, had good linear fit with high correlation coefficients (R2 > 0.99), except at +∞ (R2 = 0.903), confirming that CL intensity increased linearly with the increase of [S] as indicated by eqn (10). There was also a good linear relationship between CL intensity and I with high correlation coefficients (R2 > 0.9), except at +∞ (R2 = 0.821), indicating that CL intensity increased linearly with the increase of [Ti3+]. At different [DO], the corresponding R2 values were also high (R2 > 0.95), indicating that CL intensity was also linearly dependent on [O2]. Overall, the formation model of O2˙− could adequately describe the dynamic process of O2˙− formation in photo-irradiated TiO2 suspensions.
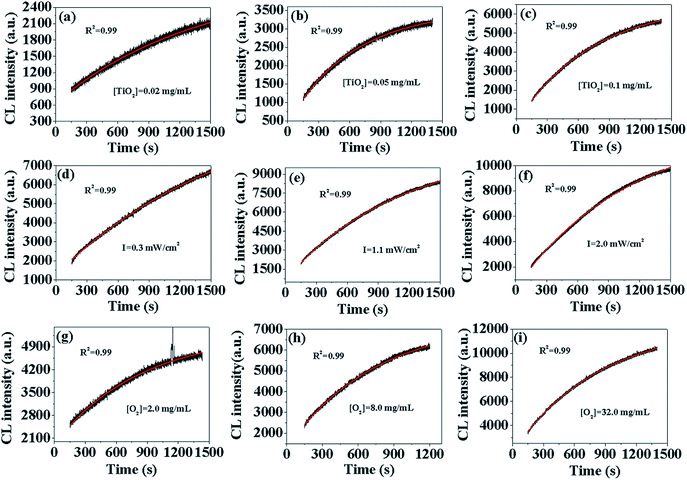 |
| | Fig. 1 CL curves of luminol (50 μM) with photo-irradiated TiO2 suspensions (pH = 11) under different experimental conditions: TiO2 concentration (a–c), irradiation intensity (d–f), DO concentration (g–i). The black lines represent experimentally measured values and the red lines are the fitted values. | |
Table 1 The calculated value of R square upon different experimental conditions at different irradiation time
| Time (s) |
TiO2 concentration (mg mL−1) |
Irradiation intensity (mW cm−2) |
DO concentration (mg mL−1) |
| 300 |
0.998 |
0.921 |
0.999 |
| 600 |
0.999 |
0.946 |
0.982 |
| 900 |
0.998 |
0.960 |
0.971 |
| 1200 |
0.994 |
0.972 |
0.968 |
| +∞ |
0.903 |
0.821 |
0.977 |
In the present work, a formation model of O2˙− in TiO2 photocatalytic reactions was established. According to the model, the O2˙− formation was closely related with [TiO2], [DO] and I, under which the dynamic process of O2˙− formation was successfully simulated by the model with high correlation coefficients (R2 > 0.9), thereby confirming the model validity. This model can explicitly provide details on O2˙− formation which determines the photocatalytic efficiency in TiO2 photocatalytic reactions, and give deeper insights into designing high-efficiency TiO2 photocatalysts. In accordance with this model, Feng et al. reported the self-doped Ti3+ enhanced TiO2 photocatalyst for hydrogen production through the reduction of the TiO2 surface using a one-step combustion method.22 Furthermore, this model may have significant implications for other photocatalysts with respect to O2˙− formation.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge financial support from the Agricultural Science and Technology Innovation Program (ASTIP-TRIC06), National Key Research and Development Program of China (2016YFA0203102), National Natural Science Foundation of China (31601483, 31801646, 21876184, 21677152), Fundamental Research Funds for Central Non-profit Scientific Institution (1610232017011, 1610232016008, 1610232017010, 1610232018002).
Notes and references
- Y. Nakaoka and Y. Nosaka, J. Photochem. Photobiol., A, 1997, 110, 299–305 CrossRef CAS.
- A. L. Attwood, D. M. Murphy, J. L. Edwards, T. A. Egerton and R. W. Harrion, Res. Chem. Intermed., 2003, 29, 449–465 CrossRef CAS.
- M. A. Henderson, W. S. Epling, C. H. F. Peden and C. L. Perkins, J. Phys. Chem. B, 2003, 107, 534–545 CrossRef CAS.
- E. Carter, A. F. Carley and D. M. Murphy, J. Phys. Chem. C, 2007, 111, 10630–10638 CrossRef CAS.
- J. Green, E. Carter and D. M. Murphy, Chem. Phys. Lett., 2009, 477, 340–344 CrossRef CAS.
- M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96 CrossRef CAS.
- C. Chen, P. Lei, H. Ji, W. Ma and J. Zhao, Environ. Sci. Technol., 2004, 38, 329–337 CrossRef CAS PubMed.
- J. Yang, C. C. Chen, H. W. Ji, W. H. Ma and J. C. Zhao, J. Phys. Chem. B, 2005, 109, 21900–21907 CrossRef CAS PubMed.
- D. Wang, L. Zhao, D. Wang, L. Yan, C. Jing, H. Zhang, L.-H. Guo and N. Tang, Phys. Chem. Chem. Phys., 2018, 20, 18978–18985 RSC.
- J. Sun, H. Zhang, L.-H. Guo and L. Zhao, ACS Appl. Mater. Interfaces, 2013, 5, 13035–13041 CrossRef CAS PubMed.
- M. W. Sutherland and B. A. Learmonth, Free Radical Res., 1997, 27, 283–289 CrossRef CAS PubMed.
- B. H. J. Blelski, G. G. Shiue and S. Bajuk, J. Phys. Chem., 1980, 84, 830–833 CrossRef.
- Y. Li, W. Zhang, J. Niu and Y. Chen, ACS Nano, 2012, 6, 5164–5173 CrossRef CAS PubMed.
- S. T. Wang, N. G. Zhegalova, T. P. Gustafson, A. Zhou, J. Sher, S. Achilefu, O. Y. Berezin and M. Y. Berezin, Analyst, 2013, 138, 4363–4369 RSC.
- K.-I. Ishibashi, A. Fujishima, T. Watanabe, K. Hashimoto, K. Ishibashi, A. Fujishima and T. Watanabe, J. Photochem. Photobiol., A, 2000, 134, 139–142 CrossRef CAS.
- D. Wang, L. Zhao, L. H. Guo and H. Zhang, Anal. Chem., 2014, 86, 10535–10539 CrossRef CAS PubMed.
- Y. Nosaka and A. Y. Nosaka, Chem. Rev., 2017, 117, 11302–11336 CrossRef CAS PubMed.
- T. Daimon, T. Hirakawa, M. Kiazawa, J. Suetake and Y. Nosaka, Appl. Catal., A, 2008, 340, 169–175 CrossRef CAS.
- C. M. Wang, A. Heller and H. Gerischer, J. Am. Chem. Soc., 1992, 114, 5230–5234 CrossRef CAS.
- H. Gerischer and A. Heller, J. Electrochem. Soc., 1992, 139, 113–118 CrossRef CAS.
- A. M. Peiró, C. Colombo, G. Doyle, J. Nelson, A. Mills and J. R. Durrant, J. Phys. Chem. B, 2006, 110, 23255–23263 CrossRef PubMed.
- F. Zuo, L. Wang, T. Wu, Z. Zhang, D. Borchardt and P. Feng, J. Am. Chem. Soc., 2010, 132, 11856–11857 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06323d |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Lixia Zhao
a,
Lixia Zhao *b,
Dean Song
*b,
Dean Song a,
Jun Qiua,
Fanyu Kong*a and
Liang-Hong Guo
a,
Jun Qiua,
Fanyu Kong*a and
Liang-Hong Guo b
b
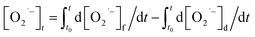
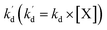 is the pseudo-first-order apparent rate constant (eqn (7.2)). [O2]s is equal to oxygen coverage on TiO2 surface (θ) by the number of adsorption sites ([S]) according to Langmuir isotherm (eqn (7.2)), in which θ is related to the DO concentration in solution ([O2]), adsorption constant (k1), desorption constant (k−1), and formation rate constant of O2˙− (kf) (eqn (7.3)).
is the pseudo-first-order apparent rate constant (eqn (7.2)). [O2]s is equal to oxygen coverage on TiO2 surface (θ) by the number of adsorption sites ([S]) according to Langmuir isotherm (eqn (7.2)), in which θ is related to the DO concentration in solution ([O2]), adsorption constant (k1), desorption constant (k−1), and formation rate constant of O2˙− (kf) (eqn (7.3)).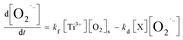
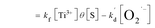
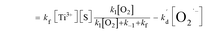
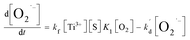
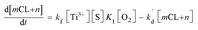
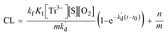
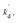 [S], [O2], m, and n are constants under certain conditions. The coefficient
[S], [O2], m, and n are constants under certain conditions. The coefficient 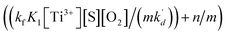 represents the theoretical maximum CL intensity (CL0) corresponding to the steady-state concentration of O2˙− when t is infinite in irradiated TiO2 suspensions. Herein t0 is the time when irradiation starts for 50 s, due to the disturbance of background signal within the first 50 s of irradiation. According to eqn (10), given that kf, K1, and kd are determined by the intrinsic property of TiO2 photocatalyst regardless of experimental conditions, CL0 is dependent on [Ti3+], [S], [O2] and [X], which are closely related to experimental conditions. In photocatalytic reactions, [Ti3+] relies on the number of photogenerated electrons highly dependent on I; [S] is the total surface area of TiO2 in suspension, closely related to [TiO2]; [O2] is dependent on [DO] in TiO2 suspensions; [X], the aforementioned concentration of h+, ·OH and e, is also dependent on I.
represents the theoretical maximum CL intensity (CL0) corresponding to the steady-state concentration of O2˙− when t is infinite in irradiated TiO2 suspensions. Herein t0 is the time when irradiation starts for 50 s, due to the disturbance of background signal within the first 50 s of irradiation. According to eqn (10), given that kf, K1, and kd are determined by the intrinsic property of TiO2 photocatalyst regardless of experimental conditions, CL0 is dependent on [Ti3+], [S], [O2] and [X], which are closely related to experimental conditions. In photocatalytic reactions, [Ti3+] relies on the number of photogenerated electrons highly dependent on I; [S] is the total surface area of TiO2 in suspension, closely related to [TiO2]; [O2] is dependent on [DO] in TiO2 suspensions; [X], the aforementioned concentration of h+, ·OH and e, is also dependent on I.

