Lanthanide chains containing the naphthalenyl nitronyl nitroxide radical

Abstract

In this contribution we report the synthesis, structure and magnetic properties of a family of lanthanide-based one dimensional compounds [Ln(hfac)₃(NaphNN)]_n, where Ln^III = Gd (1), Dy(2), Tb(3) and NaphNN is the nitronyl nitroxide (NN) radical 2-(1′-naphthalenyl)-4,4,5,5-tetramethyl-4,5-dihydro-1H-Imidazole-3-oxide-1-oxyl. The crystal structure reveals well isolated chains with a twofold helical axis. Magnetic investigation of the gadolinium(III) chains showed relevant intrachain interactions between Gd–NN nearest neighbors and also Gd–Gd and NN–NN next nearest neighbors. The magnetic interaction parameters were obtained by fitting the data with a six membered ring model. The stronger antiferromagnetic interaction between NN radicals was confirmed by investigation of the mononuclear complex [Y(hfac)₃(NaphNN)₂] (4) with a similar coordination environment. The dynamic magnetic properties of 2 and 3 were investigated by using the temperature and frequency dependence of the magnetic susceptibility evidencing single chain magnet dynamics under a zero dc field.

---

Introduction

Single molecule magnets (SMM), single chain magnets (SCM) and single ion magnets (SIM) present similar slow relaxation of the magnetization without long range magnetic ordering. The interest in these families of molecular nanomagnets arises from their potential application to build ultra small information storage and more recently spintronic devices, as well as the interest in understanding their magnetic behavior.¹ Many efforts have been made in order to increase the blocking temperature,² which is defined as the highest temperature that magnetic hysteresis can be observed in quasi static conditions, now reaching liquid nitrogen temperatures as recently reported for a dysprosium(III) mononuclear system,³ with small coercive fields.

The first example of SCM behavior was reported in 2001: a one dimensional compound [Co(hfac)₂{NIT(C₆H₄OMe)}]_n (hfac = hexafluoroacetylacetonate); NITPhOMe = 2-(4′-methoxyphenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide) presenting slow magnetic relaxation and hysteresis around 4 K from one dimensional character rather than long range ordering.⁴ Since then, many efforts have been devoted to the synthesis of new chains with strong intrachain interaction and large Ising anisotropy avoiding interchain interactions, issues essential to obtain the aimed so called SCM behavior.⁵ In fact, using NN radicals containing large pendant polyaromatic substituents such as naphthalenyl or pyrenyl the interchain magnetic interactions were effectively reduced and a strong intrachain exchange interaction, high anisotropy and parallel local easy axis lead to high blocking temperatures around 14 K and very high coercive field for cobalt(II)-based ferrimagnetic chains.⁶ In SCMs, quantum tunneling of magnetization existent in many SMM/SIM is avoided leading to larger coercive fields for SCMs. More recently a new surge of interest in magnetic chains emerged with the observation of strong magneto-chiral effect⁷ in a non-centrosymmetric three-fold helical cobalt(II)–NN and a magneto-electric effect in the analogue manganese(II)–NN.⁸

Lanthanide ions are attractive building blocks for molecular magnetic materials because of their large magnetic moment and/or anisotropy as well as the possibility to explore additional luminescent properties.⁹ Early reports on lanthanide–NN based molecular chains were published by Gatteschi and co-workers.¹⁰ For the [Dy(hfac)₃{NIT(Et)}]_n the intrachain and the non negligible interchain interactions resulted in a 3D magnetic order at 4.3 K.^10d In 2005 the same group showed that it was possible to increase the distances between chains by using as ligand a radical containing two aromatic rings linked by an ether group, avoiding the 3D order.¹¹ The compound [Dy(hfac)₃(NIT(C₆H₄OPh))] presented slow relaxation of magnetization as well as a magnetic hysteresis below 3 K typical of SCM behavior.

In this contribution we report a family of lanthanide-based one dimensional compounds [Ln(hfac)₃(NaphNN)]_n, where Ln^III = Gd (1), Dy(2) and Tb(3) and NaphNN = 2-(1′-naphthalenyl)-4,4,5,5-tetramethyl-4,5-dihydro-1H-imidazole-3-oxide-1-oxyl is a NN radical substituted with rigid and large pendant polyaromatic group. This substituent contributed to increasing the interchain distance between lanthanide ions being among the largest known for Ln–NN chain. Magnetic investigation of the gadolinium(III)-NN chain showed the relevance of intrachain next-nearest neighbour between NaphNN radicals as well as between gadolinium(III) ions. Additionally, a mononuclear complex containing a diamagnetic ion, [Y(hfac)₃(NaphNN)₂] (4), is described to elucidate the relevant next nearest neighbour interactions (between the radicals) in the chain systems. The dynamic magnetic properties of 2 and 3 were investigated using temperature and frequency dependence of the magnetic susceptibility revealing evidences of SCM behavior under a zero dc field.

Experimental

General

The solvents n-heptane and chloroform were distilled over sodium and phosphor pentoxide, respectively. Elemental analyses were performed on a PerkinElmer 2400 series II. Infrared spectra (IR) were obtained using a Bruker ALPHA FTIR-ATR spectrophotometer.

Synthesis

General synthetic procedure for [Ln(hfac)₃(NaphNN)]_n(1–3). The complexes¹² [Ln(hfac)₃(H₂O)₂], where Ln^III = Gd, Dy or Tb and the radical¹³ NaphNN were synthesized according to a previously described procedure. Complexes 1–3 were synthesized using a similar procedure. To a solution of 24 mg (0.03 mmol) of [Gd(hfac)₃(H₂O)₂] in 15 mL of boiling n-heptane was added 8 mg (0.03 mmol) of NaphNN dissolved in 2 mL of chloroform. After a couple of days at 15 °C in a dry atmosphere containing silica gel as dehydrating agent, purple needle-shape single crystals were obtained. Elemental analyses calculated for C₃₂H₂₂F₁₈GdN₂O₈ (1) C = 36.20, H = 2.09, N = 2.64, found C = 35.06, H = 1.86, N = 2.38; for C₃₂H₂₂F₁₈DyN₂O₈ (2) C = 36.02, H = 2.08, N = 2.63, found C = 35.69, H = 1.78, N = 2.53; for C₃₂H₂₂F₁₈TbN₂O₈ (3) C = 36.14, H = 2.08, N = 2.63, found C = 36.50, H = 1.98, N = 2.71. IR 1 (cm⁻¹): 3139 (w), 3101 (w), 3003 (w), 2998 (w), 2979 (w), 2947 (w), 1646 (s), 1598 (w), 1555 (w), 1527 (m), 1499 (m), 1480 (m), 1463 (m), 1397 (m), 1375 (w), 1354 (m), 1333 (m), 1250 (s), 1193 (s), 1133 (s), 1096 (s), 1009 (w), 976 (w), 949 (w), 874 (w), 851 (w), 794 (s), 767 (s), 740 (m), 659 (s), 640 (m), 585 (s), 549 (w), 525 (m), 464 (m), 416 (w); 2 3142 (w), 3009 (w), 2964 (w), 2963 (w), 2941 (w), 1683 (w), 1648 (s), 1616 (w), 1598 (w), 1582 (w), 1557 (m), 1529 (m), 1503 (m), 1480 (m), 1462 (m), 1396 (m), 1376 (w), 1352 (m), 1333 (m), 1250 (s), 1194 (s), 1133 (s), 1098 (s), 1006 (w), 970 (w), 951 (w), 874 (w), 853 (w), 794 (s), 769 (s), 741 (m), 722 (m), 659 (s), 640 (w), 584 (s), 547 (w), 529 (m), 466 (m), 451 (w), 418 (w), 409 (w); 3 3144 (w), 2994 (w), 2945 (w), 1685 (w), 1649 (s), 1598 (w), 1582 (w), 1556 (m), 1525 (m), 1501 (m), 1483 (m), 1462 (m), 1395 (m), 1378 (w), 1367 (w), 1354 (m), 1334 (m), 1395 (w), 1378 (w), 1367 (w), 1354 (m), 1334 (m), 1251 (s), 1194 (s), 1133 (s), 1098 (s), 1006 (w), 970 (w), 949 (w), 874 (w), 853 (w), 795 (s), 769 (s), 740 (m), 724 (w), 659 (s), 640 (w), 584 (s), 547 (w), 530 (m), 466 (m), 452 (w), 419 (w), 412 (w).

[Y(hfac)₃(NaphNN)₂].4H₂O (4). To a solution of 78 mg (1.1 mmol) of [Y(hfac)₃(H₂O)₂] in 10 mL of boiling n-heptane, a solution of 24 mg (0.8 mmol) of the NaphNN radical dissolved in 2 mL of chloroform was added. The final solution was kept at 4 °C for 2 days giving purple block-shape single crystals suitable for X-ray analysis. IR 4 (cm⁻¹): 3144 (w), 2994 (w), 2961 (w), 2930 (w), 2859 (w), 1679 (w), 1650 (s), 1587 (w), 1553 (w), 1517 (m), 1480 (m), 1461 (m), 1398 (w), 1360 (m), 1337 (m), 1250 (s), 1190 (s), 1139 (s), 1101 (s), 1040 (w), 972 (w), 948 (w), 915 (w), 874 (w), 851 (w), 792 (m), 764 (s), 659 (m), 628 (w), 582 (m), 530 (m), 470 (w), 449 (w).

Crystallographic studies

Single crystal X-ray data for complexes 1–4 were collected on a Bruker D8 Venture diffractometer using monochromatic MoK_α radiation (λ = 0.71073 Å). Data collection and cell refinement were performed with APEX3 software.¹⁴ Data reduction was carried out using SAINT.¹⁵ Empirical multiscan absorption correction using equivalent reflections was performed using SADABS software.¹⁶ The structure solution was performed using SHELXS-2014 while the refinement was performed using SHELXL-2014 based on F² through the full-matrix least-squares routine.¹⁷ All non-hydrogen atoms were refined using anisotropic displacement parameters. The hydrogen atom positions were calculated using a riding model.¹⁸ Some of the CF₃ groups are disordered and fluorine atom occupancies were refined freely. Large thermal displacement parameters were found for fluorine atoms. The C–F bond length and F⋯F distances were restrained to be equivalent. The displacement parameters of disordered fluorine atoms were constrained to be the same using the EADP constrain. Compound 4 presented loss of crystallinity at 150 K so the data was collected at room temperature, but crystals did not diffract to high resolution angles. Summary of crystallographic data collection and refinement are gathered in Table S1.† Powder X-ray diffraction data for 1–4 were collected on a Bruker D8 Advance equipped with a LynxEye detector using CuK_α radiation at room temperature. Powder X-ray diffraction (PXRD) patterns were simulated from the structures determined by using single crystal X-ray diffraction data. The experimental and simulated PXRD patterns corresponded well in peak positions and relative intensity, confirming the crystalline phase purity of the compounds (see the ESI for details, Fig. S1 and S2†).

Magnetic measurements

Magnetic measurements were performed on a Physical Property Measurement System (PPMS) from Quantum Design. All the samples were mounted in a Teflon tape and the anisotropic compounds were pressed into a pellet manually. DC magnetic measurements were carried out using vibrating sample magnetometer (VSM) option. The sample's diamagnetism correction was estimated from Pascal's constants. AC magnetic measurements were performed using the ACMS mode. The DC magnetic data was fitted and simulated using Software Phi.¹⁹

Results and discussions

All complexes were obtained by reactions between [Ln(hfac)₃] or [Y(hfac)₃] complexes and NaphNN radical using 1 : 1 molar ratio between the complex and radical. Compounds 1–3 were crystallized in dry atmosphere while 4 was obtained after opening the reaction medium to the air. The contact of the solution with the air was important for the formation of the crystals of 4 that contains lattice water molecules. Even using the same reaction condition of 1–3 (including dry atmosphere) and a slight excess of yttrium(III) complex, it was not possible to obtain the isostructural chain containing the yttrium(III) ion.

Crystal structure

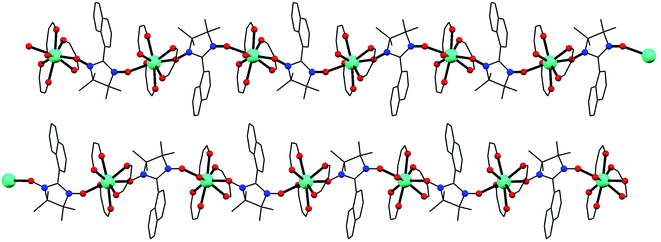
Compounds 1–3 are isostructural and crystallize in the P2₁/n space group with the lanthanide ions octacoordinated by six oxygen atoms from three bidentated hfac ligands and two oxygen atoms from two NaphNN radicals (Fig. S3†). The lanthanide ion is bridge-coordinated by NaphNN radical generating 2-fold helical chains parallel to the crystallographic b axis (Fig. 1). There are two crystallographically independent lanthanide ions per unit cell, each one belongs to one chain (Fig. S4†). The coordination environment of the lanthanide ions were calculated using the SHAPE program (Table S2†) and the geometries for Ln1 and Ln2 are better described as triangular dodecahedron. The bond lengths are in the range 2.336(6)–2.389(7) Å, 2.351(7)–2.387(7) Å, 2.316(4)-2.387(4) Å, 2.334(4)–2.366(4) Å, 2.319(5)–2.380(6) Å and 2.344(5)–2.376(5) Å for Gd1–O, Gd2–O, Dy1–O, Dy2–O, Tb1–O, Tb2–O, respectively. The coordination environments of both lanthanide ions are very similar with slightly longer bond lengths for Ln1–O when compared with Ln2–O. Selected bond lengths and bond angles are gathered in Table S3.† The two radicals coordinated to the lanthanide ions have bond angles O7–Ln–O8 and O15–Ln–O16 equals to 138.7(3), 138.85(16), 139.9(2), 138.5(2), 138.25(15) and 139.7(2)° for 1, 2 and 3, respectively. The intrachain distances between lanthanide ions are nearly the same for the two crystallographically independent chains being 8.456(6) Å for Gd1⋯Gd1, 8.466(6) Å for Gd2⋯Gd2, 8.4379(6) Å for Dy1⋯Dy1 and 8.4488(6) Å for Dy2⋯Dy2, 8.5769(6) Å for Tb1⋯Tb1 and 8.5844(6) Å Tb2⋯Tb2. The shortest interchain distances between lanthanide ions are 11.768(1), 11.436(2) and 11.5773(8) Å for 1, 2 and 3 respectively, being among the largest known for Ln–NN chains.^11,20

Fig. 1 View of the two crystallographically independent chains. The hydrogen atoms and CF₃ groups were omitted for clarity. Color code: cyan, black, blue and red stand for lanthanide(III) ion, carbon, nitrogen and oxygen atoms.

Compound 4 crystallizes in centrosymmetric P1̄ space group and contains one crystallographically independent molecule per unit cell. The yttrium(III) ion is also coordinated by six oxygen atoms from three bidentated hfac ligands and two oxygen atoms from two NaphNN radicals (Fig. S5†). The calculated coordination environment for Y^III was also triangular dodecahedron as observed for 1–3 (Table S2†). Differently than observed for the chains 1–3, two NaphNN radicals are monocoordinated to Y^III ion through only one of the two equivalent oxygen atoms from nitroxide group leading to a mononuclear complex. The Y–O bond lengths are in the range 2.299(6)-2.383(6) Å and the bond angle O7–Y–O8 between the coordinated oxygen atoms from nitroxide is 139.3(2)°, close to the values observed for 1–3. The shortest intermolecular distance between non-coordinated O atoms from nitroxide group is 5.14(2). This compound crystallizes with lattice water molecules located in the channels between [Y(hfac)₃(NaphNN)₂] molecules along the crystallographic direction b (Fig. S6†). These water molecules are involved in hydrogen bonds. Short distances between carbon atoms from adjacent naphthalenyl moiety are compatible with π⋯π intermolecular interaction. These intermolecular interactions contribute to stabilize the crystal lattice.

Magnetic properties

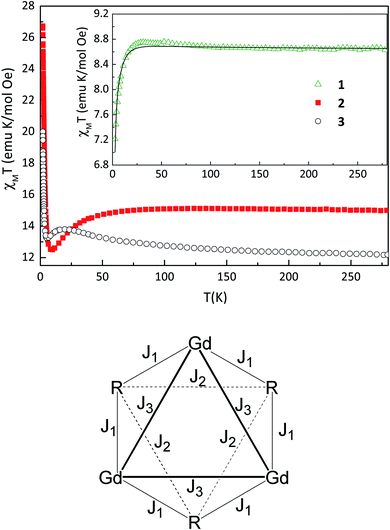
The temperature dependence of the product of magnetic susceptibility and temperature (χT vs. T) for 1–3 is reported in Fig. 2. At the highest temperature, the χT value is 8.6, 15.0 and 12.2 emu mol⁻¹ K for 1, 2 and 3, respectively. These values are slightly higher than expected considering a sum of one NaphNN radical (S = 1/2 with g = 2.00) and one Gd^III ion (S = 7/2, g = 2.00) 8.3 emu mol⁻¹ K for 1 and 14.6 emu mol⁻¹ K for Dy^III (J = 15/2, g_J = 4/3) for 2, without magnetic interactions. For 3, the obtained χT value at the highest temperature is equal to the calculated one considering non-interacting Tb^III (J = 6, g_J = 3/2) and NN radical. As the temperature is decreased for 1, χT increases slowly and reach a maximum of 8.8 emu mol⁻¹ K at 31.2 K followed by a decrease to 7.2 emu mol⁻¹ K at 2.7 K. This behavior indicates a coexistence of ferro- and antiferromagnetic interactions. Intrachain Ln-radical, radical–radical and also Gd–Gd magnetic interactions can be expected. Since the interchain distances between paramagnetic centers are large, the magnetic interactions between them are expected to be very small and were neglected in the magnetic analysis. In order to quantify the magnetic interactions we used a model of six-member ring (three pairs Ln-Rad) to simulate an infinite chain. This ring contains S_Gd = 7/2 for gadolinium(III) ion and S_R = 1/2 for NaphNN radical with the spin topology shown in Fig. 2 (bottom) and described by the Hamiltonian in eqn (1). The parameters J₁ and J₂ are intrachain Gd-radical and radical–radical exchange interactions and J₃ represents approximately the Gd–Gd dipolar interaction.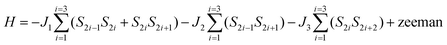Being S_odd = S_R, S_even = S_Gd, S₇ = S₁ and S₈ = S₂

Fig. 2 Temperature dependence of χT for 1 at 1 kOe (inset), 2 and 3 at 200 Oe (Top). Solid line represents the best fit curve using the model described in the text. Spin topology used to fit magnetic data (bottom).

The best fit parameters obtained using g_R = 2.00 were g_Gd = 2.05, J₁ = 1.2 cm⁻¹, J₂ = −12.4 cm⁻¹ and J₃ = −0.06 cm⁻¹. The intrachain ferromagnetic Gd–NN exchange interaction (J₁) is in the range observed for other gadolinium(III)–nitronyl nitroxide chains reported in the literature.^10b,20b,21 This weak interaction is due to the deep and localized nature of f magnetic orbitals of gadolinium(III) ion. In fact, the ferromagnetic exchange interaction J₁ is approximately one order of magnitude smaller than the antiferromagnetic intrachain interaction between NN radicals J₂. This stronger AFM between NN radicals was confirmed by the results obtained for the analogous compound containing the diamagnetic yttrium(III) ion (see below) and is in agreement with other gadolinium–NN radicals described in the literature.^10b,21a,22 The obtained magnetic interaction J₃ is close to the calculated dipolar magnetic energy −0.035 cm⁻¹ through the expression E = μ_B²S_Gd²g_Gd²/4πr_Gd–Gd³ considering the shortest intrachain distance between Gd^III ions. In addition, we also performed a fit neglecting the intrachain dipolar magnetic interaction between gadolinium(III) ions. Despite its small value, no reasonable fit could be obtained in the whole temperature range and in particular at low temperatures with J₃ = 0.

The field dependence of the magnetization curves were fitted to the same Hamiltonian (eqn (1)) independently of the χT fit, but simultaneously for three isotherms (see Fig. S7†). The obtained results with J₁ = 1.0 cm⁻¹, J₂ = −9.2 cm⁻¹, J₃ = −0.06 cm⁻¹ are in agreement with the above reported χT.

The temperature dependence of χT for 2–3 shows a slow increase of χT as temperature decreases reaching a maximum (as seen for 1) followed by a decrease to a minimum of 12.5 emu mol⁻¹ K at 9.8 K and 13.2 emu mol⁻¹ K at 5.3 K for 2 and 3 respectively. Below these temperatures, χT increases to 26.7 for 2 and 19.9 emu mol⁻¹ K for 3 at 2 K, a behavior different from the one observed for 1. The magnetic behavior of these compounds is suggestive of a chain due to relatively strong intrachain radical–radical interaction, and non negligible dipolar Ln–Ln interactions (as observed for 1) as well as magnetic anisotropy of Dy^III or Tb^III ions. Any trial to fit the magnetic data to estimate magnetic interactions and anisotropy with models of a ring with up to 4 magnetic centers, 2 radicals and 2 Ln ions resulted in overparametrization and unphysical values of the parameters. Furthermore, any model with more magnetic centers is unfeasible for our computing facilities. The same difficulty applies for the magnetization versus field results shown in Fig. S8.†

The temperature dependence of χT for compound 4 is shown in Fig. 3. At 283 K, the χT value of 0.81 emu mol⁻¹ K is slightly larger than the value expected (0.75 emu mol⁻¹ K) for two non-interacting magnetic radicals with S_R = 1/2 and g = 2.00. As temperature decreases, χT value is nearly constant, followed by a decrease of χT below about 100 K down to 0.13 emu mol⁻¹ K at 3.3 K, indicating antiferromagnetic interactions. Below 3.3 K, a plateau is observed down to 2.0 K, suggesting a paramagnetic radical. Since intermolecular distances between paramagnetic centers are large, the expected magnetic interaction occurs only between two NaphNN radicals coordinated to Y^III ion. In order to determine intramolecular interaction in 4, the magnetic data was fitted considering a magnetic dimer (H = −JS_RS_R) using the Bleaney and Bowers expression²³ (eqn (2)) and isolated paramagnetic centers presumably from traces of radical that did not react fully.

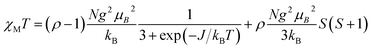where S = 1/2, N is Avogadro's number, μ_B is the Bohr magneton, k_B is the Boltzmann's constant, g is Landè factor and ρ is the relative concentration of paramagnetic centers.

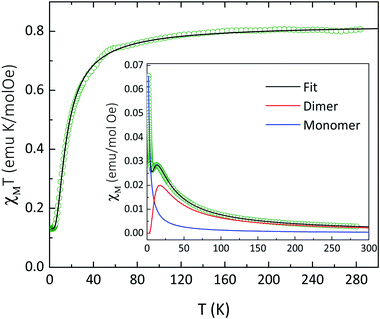Fig. 3 Temperature dependence of χT for 4 at 1 kOe. Solid line represents a fit curve obtained using eqn (2) with parameters described in the text. Inset: temperature dependence of χ evidencing the magnetic contribution of the dimer and paramagnetic contribution.

The best fit was obtained with g = 2.00 (fixed), the magnetic coupling constant J = −20 cm⁻¹ and 7.5% of paramagnetic radical contribution. Similar magnetic coupling constant were observed for one dimensional and also mononuclear yttrium(III)-based compounds coordinated by NN radicals.²⁴ Inset of Fig. 3 presents the contribution of the magnetic dimer and paramagnetic contribution. In fact, the obtained intramolecular magnetic coupling constant between NN radicals for 4 is stronger than the analogous found for compound 1, and in agreement with dominant intrachain radical–radical magnetic interaction when compared with the Gd-radical interaction. The magnetization versus field results corroborate with the above findings considering a paramagnetic contribution (ρ = 6.5%) and an antiferromagnetic dimer with J = −20 cm⁻¹ (see Fig. S9†).

In order to probe the magnetic relaxation of these compounds, the dynamic magnetic properties of 2–3 were investigated using temperature and frequency dependence of the magnetic susceptibility under a zero dc field. Both real and imaginary magnetic susceptibilities of 2 show frequency dependent maxima (T_max) (Fig. S10†) with a small temperature spread. These T_max were used to estimate the parameter φ = ΔT_max/(T_maxΔ(log ν)) = 0.18, a value between spin glass (φ < 0.01) and superparamagnetic (φ = 0.28) type behaviors.^25,26 In addition, the τ₀ (see below) value is very small, indicating substantial interaction among the relaxing pieces of chain. Note that the obtained value for 2 is close to the value found (φ = 0.1) for the SCM CoPhOMe.²⁶

The relaxation times were determined from fits of the frequency dependence of the real and imaginary magnetic susceptibilities at fixed temperatures using the generalized Debye model²⁷ (Fig. 4). The relaxation times were fitted according to an Arrhenius law τ = τ₀ exp(Δτ/k_BT) giving an activation barrier Δτ = 35 ± 2 cm⁻¹ and pre-exponential factor τ₀ ≈ 10⁻¹⁴ s (Fig. S11†). This small pre-exponential factor was also observed in other Dysprosium(III)–NN chains reported as SCM in literature.^20a The α values obtained from a Cole–Cole analysis are in the range 0.72–0.80 indicating a wide distribution of relaxation times (see Fig. S12 and Table S4† for details). In one dimensional compounds the correlation length (ξ) is related to χT, and increases when the temperature decreases following the expression χT = C_eff exp(Δξ/k_BT), where C_eff is the effective Curie constant of the repeat units in the chain and Δξ is the energy to create a domain wall. This expression is valid in both Ising-like as well as anisotropic Heisenberg regimes.²⁸ We have found Δξ = 2.9 K (2.0 cm⁻¹) for 2 and 1.9 K (1.3 cm⁻¹) for 3, from the slope of a ln(χT) versus 1/T plots (see Fig. S13 and S14†).

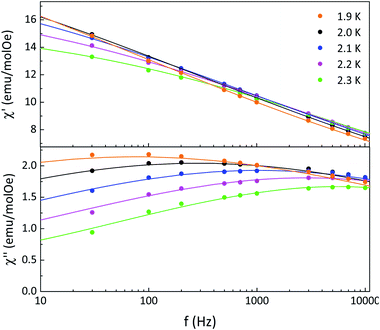Fig. 4 Frequency dependence of real (χ′) and imaginary (χ′) magnetic susceptibilities at different temperatures for 2 where the solid lines are the best fits obtained with a generalized Debye model.

For compound 3, a maximum of χ′′(T) could not be observed within the available temperature and frequency range (Fig. S15†), we used the procedure described by Bartolomé et al.,²⁹ also used for Ln-chains³⁰ to estimate the relaxation parameters. Assuming only one relaxation process, the expression ln(χ′′/χ′) = ln(ωτ₀)+ Δτ/k_BT was used to evaluate Δτ and τ₀. In Fig. 5 the ln(χ′′/χ′) vs. 1/T graph is presented and linear fits give an activation barrier Δτ = 6.7 cm⁻¹ and pre-exponential factor τ₀ ≈ 10⁻⁷ s. Such high values of τ₀ were already observed in other Tb-nitronyl nitroxide chains.³¹

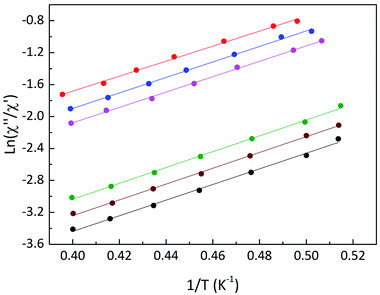Fig. 5 Plot of ln(χ′′/χ′) as a function of the reciprocal temperature. Lines represent best linear fits.

Conclusions

A family of lanthanide-based one dimensional compounds containing a nitronyl nitroxide radical was synthesized and characterized. The large separation between lanthanide ions caused by large pendant substituent in nitronyl nitroxide radical afforded a one dimensional magnetic behavior. The investigation of the gadolinium(III) derivative evidenced the relevance of intrachain next near neighbor between NaphNN radicals as well as between gadolinium(III) ions to the magnetic behavior. Magnetization results could be modeled by a six member ring model resulting in J_NN–NN = −12.4 cm⁻¹, J_Gd–NN = 1.2 cm⁻¹ and J_Gd–Gd = −0.06 cm⁻¹. The strong antiferromagnetic interaction between NaphNN radicals was confirmed by investigation of the mononuclear complex [Y(hfac)₃(NaphNN)₂] where J_NN–NN was found to be −20 cm⁻¹ from magnetization data versus temperature and field. The anisotropic Dy and Tb chains presented dynamic magnetic properties typical of single chain magnets with blocking temperatures below 2 K.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge FAPERJ and CNPq for the financial support. CVC acknowledges CAPES for the fellowship. We also thank LDRX-UFF for using its laboratory facilities.

References

1. (a) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138; (b) M. Gobbi, M. A. Novak and E. Del Barco, J. Appl. Phys., 2019, 125, 240401; (c) A. Caneschi, D. Gatteschi, C. Sangregorio, R. Sessoli, L. Sorace, A. Cornia, M. A. Novak, C. Paulsen and W. Wernsdorfer, J. Magn. Magn. Mater., 1999, 200, 182–201.
2. (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442; (b) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449; (c) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239; (d) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
3. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
4. A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760–1763.
5. (a) L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758; (b) K. S. Pedersen, A. Vindigni, R. Sessoli, C. Coulon and R. Clérac, Molecular Magnetic Materials: Concepts and Applications, Wiley-VCH, 2017, ch. 6; (c) S. Dhers, H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2015, 296, 24–44; (d) H.-L. Sun, Z.-M. Wang and S. Gao, Coord. Chem. Rev., 2010, 254, 1081–1100; (e) X. Meng, W. Shi and P. Cheng, Coord. Chem. Rev., 2019, 378, 134–150.
6. (a) M. G. F. Vaz, R. A. A. Cassaro, H. Akpinar, J. A. Schlueter, P. M. Lahti and M. A. Novak, Chem.–Eur. J., 2014, 20, 5460–5467; (b) R. A. A. Cassaro, S. G. Reis, T. S. Araujo, P. M. Lahti, M. A. Novak and M. G. F. Vaz, Inorg. Chem., 2015, 54, 9381–9383.
7. R. Sessoli, M. E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69–74.
8. M. Fittipaldi, A. Cini, G. Annino, A. Vindigni, A. Caneschi and R. Sessoli, Nat. Phys., 2019, 18, 329–334.
9. (a) F. Pointillart, T. Cauchy, O. Maury, Y. Le Gal, S. Golhen, O. Cador and L. Ouahab, Chem.–Eur. J., 2010, 16, 11926–11941; (b) A. Lannes, M. Intissar, Y. Suffren, C. Reber and D. Luneau, Inorg. Chem., 2014, 53, 9548–9560; (c) X.-L. Li, C.-L. Chen, H.-P. Xiao, A.-L. Wang, C.-M. Liu, X. Zheng, L.-J. Gao, X.-G. Yanga and S.-M. Fang, Dalton Trans., 2013, 42, 15317–15325.
10. (a) C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1989, 28, 275–280; (b) C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1990, 29, 4223–4228; (c) C. Benelli, A. Caneschi, D. Gatteschi and R. Sessoli, Inorg. Chem., 1993, 32, 4797–4801; (d) C. Benelli, A. Caneschi, D. Gatteschi and R. Sessoli, Adv. Mater., 1992, 4, 504–505.
11. L. Bogani, C. Sangregorio, R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2005, 44, 5817–5821.
12. K. Bernot, L. Bogani, R. Sessoli and D. Gatteschi, Inorg. Chim. Acta, 2007, 360, 3807–3812.
13. T. Sugano, M. Kurmoo, H. Uekusa, Y. Ohashi and P. Day, J. Solid State Chem., 1999, 145, 427–442.
14. APEX3 v2016.1-0, Bruker AXS.
15. SAINT V8.34A, Bruker AXS Inc., 2013.
16. G. M. Sheldrick, SADABS, Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Germany, 1996.
17. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
18. C. K. Johnson, in Crystallographic Computing, ed. F. R. Ahmed, Munksgaard, Copenhagen, Denmark, 1970, pp. 207–219.
19. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
20. (a) X. Wang, Y. Li, P. Hu, J. Wanga and L. Li, Dalton Trans., 2015, 44, 4560–4567; (b) C. Li, J. Sun, M. Yang, G. Sun, J. Guo, Y. Ma and L. Li, Cryst. Growth Des., 2016, 16, 7155–7162; (c) K. Bernot, L. Bogani, A. Caneschi, D. Gatteschi and R. Sessoli, J. Am. Chem. Soc., 2006, 128, 7947–7956.
21. (a) C. Benelli, D. Gatteschi, R. Sessoli, A. Rettori, M. G. Pini, F. Bartolomé and J. Bartolomé, J. Magn. Magn. Mater., 1995, 140–144, 1649–1650; (b) N. Zhou, Y. Ma, C. Wang, G.-F. Xu, J. Tang, S.-P. Yan and D.-Z. Liao, J. Solid State Chem., 2010, 183, 927–932.
22. C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2388 and references therein.
23. B. Bleaney and K. D. Bowers, Proc. R. Soc. London, Ser. A, 1952, 214, 451–465.
24. (a) T. Nakamura and T. Ishida, Polyhedron, 2015, 87, 302–306; (b) R. Murakami, T. Nakamura and T. Ishida, Dalton Trans., 2014, 43, 5893–5898; (c) J. Jung, M. Puget, O. Cador, K. Bernot, C. J. Calzado and B. Le Guennic, Inorg. Chem., 2017, 56, 6788–6801.
25. J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993.
26. M. A. Novak, J. Magn. Magn. Mater., 2004, 272–276, E707–E713.
27. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
28. (a) C. Coulon, H. Miyasaka and R. Clerac, Struct. Bonding (Berlin), 2006, 122, 163–206; (b) H. Miyasaka, M. Julve, M. Yamashita and R. Clerac, Inorg. Chem., 2009, 48, 3420–3437.
29. J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014430.
30. P. Hu, C. Zhang, Y. Gao, Y. Li, Y. Ma, L. Li and D. Liao, Inorg. Chim. Acta, 2013, 398, 136–140.
31. P. Hu, X. Wang, Y. Ma, Q. Wang, L. Li and D. Liao, Dalton Trans., 2014, 43, 2234–2243.

---

Footnote

† Electronic supplementary information (ESI) available: Details about crystallographic data collection, refinement and additional figures, tables containing selected bond lengths and bond angles, additional magnetic analysis and X-ray crystallographic files in CIF format. CCDC 1937302–1937304 and 1937770. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra06506g

---