DOI:
10.1039/C9RA06735C
(Paper)
RSC Adv., 2019,
9, 31398-31405
Theoretical prediction of some layered Pa2O5 phases: structure and properties†
Received
26th August 2019
, Accepted 19th September 2019
First published on 2nd October 2019
Abstract
Density functional theory (DFT) was used to predict and study protactinium pentoxide (Pa2O5), which presents a fluorite and layered protactinium oxide-type structure. Although the layered structure has been observed with the isostructural transition Nb and Ta metal pentoxides experimentally, the detailed structure and properties of the layered Pa2O5 are not clear and understandable. Our theoretical prediction explored some possible stable structures of the Pa2O5 stoichiometry according to the existing M2O5 structures (where M is an actinide Np or transition Nb, Ta, and V metal) and replacing the M ions with protactinium ions. The structural, mechanical, thermodynamic and electronic properties including lattice parameters, bulk moduli, elastic constants, entropy and band gaps were predicted for all the simulated structures. Pa2O5 in the β-V2O5 structure was found to be a competitive structure in terms of stability, whereas Pa2O5 in the ζ-Nb2O5 structure was found to be the most stable overall. This is consistent with Sellers's experimental observations. In particular, Pa2O5 in the ζ-Nb2O5 structure is predicted to be charge-transfer insulators. Furthermore, we predict that ζ-Nb2O5-structured Pa2O5 is the most thermodynamically stable under ambient conditions and pressure.
1. Introduction
The structure and properties of actinide-based oxides have been extensively studied using many theoretical1–5 and experimental approaches6–17 due to their technological importance in the nuclear material cycle. However, protactinium pentoxide (Pa2O5) is an underexplored area of the protactinium–oxygen phase diagram, and its practical applications have received little attention owing to its instability relative to the fluorite and layered protactinium oxides.18,19 One of its intriguing features is that it represents the composition of a transition point between the fluorite and layered protactinium oxides, with reports of it forming in both types of structures. Since reports about the structure and properties of Pa2O5 are extremely limited in the literature, most likely owing to its scarcity, high radioactivity and toxicity, theoretical prediction provides a way to predict and study the structure and properties of this material.
In the actinide elements, uranium (U) exhibits rich oxide phases, such as UO2, U2O3, U2O5, and U3O8,20–27 and its two prominent oxidation states are U4+ and U6+. Plutonium (Pu) has stable Pu4+, Pu5+, and Pu6+ oxidation states in aqueous solutions. Neptunium (Np) has two stable oxides, NpO2 and Np2O5, corresponding to stoichiometric Np4+ and Np5+, respectively. Protactinium (Pa), like actinide Np and the transition niobium (Nb), tantalum (Ta), and vanadium (V) metals, has the predominant oxidation state of Pa5+. In particular, protactinium pentoxide is isostructural with the transition metals Nb and Ta, sharing a closed shell pentavalent oxidation state.28 In addition, a study on Pa is considered to be a unique opportunity for studying the potential periodic properties of the actinide elements and their compounds with respect to their physics and chemistry, including structure and bonding. Wilson recently reported about protactinium as a potential intersection between the d-transition metals (Nb and Ta) and the 5f actinide elements U, Np and Pu owing to the participation of 5f and 6d orbitals cross in energy.28 Although U, Np and Pu oxide systems are known, a detailed structural study of the layered protactinium pentoxide (Pa2O5) has not been systematically reported to date.
To develop new nuclear materials and understand their basic physical and chemical properties, a systematic study about the structure and properties of protactinium oxides is critical from a theoretical perspective. Pa2O5 is used for the preparation of metal Pa and other oxides (PaO and PaO2), high temperature dielectrics for ceramic capacitors, in nuclear industry, etc.19,29 Sellers et al.19 experimentally showed that protactinium pentoxide has a fluorite structure and an orthorhombic structure. The fluorite Pa2O5 was prepared by heating the hydrated oxide in air (500 °C). Also, density data for fluorite Pa2O5 is not available, which suggests that it is more likely to be a defective fluorite PaO2.19 The orthorhombic Pa2O5, which is isostructural with Nb2O5 and Ta2O5, was obtained in the course of an attempt to prepare a fluoride by action of CuF5 on the oxide (500 °C). Sellers' diffraction experiment suggested that Pa2O5 is a layered phase. Our theoretical work explores some possible structures of Pa2O5 by replacing the metal ions with protactinium ions from existing metal pentoxide structures. To study the potential structure and properties of layered Pa2O5, we report the structural, elastic, thermodynamic and electronic properties of some possible layered Pa2O5 phases using the Perdew–Burke–Ernzerhof generalized gradient approximation+U implemented in density functional theory (DFT). Our aim is to develop reliable structural models to aid the identification of possible phases and give a quantitative description of their relative stability.
2. Methodology
Theoretical calculations were performed using the projector augmented wave (PAW) method, as implemented in the Vienna Ab Initio Simulation Package (VASP).30,31 The generalized gradient approximation (GGA) functional in the Perdew–Burke–Ernzerhof (PBE)32 parametrization was adopted for structural optimization. The crystal structures of all systems concerned were relaxed using a Γ-centered k-mesh determined by requiring the product of the number of k points and the length of the lattice vectors to be ∼30 Å and a large kinetic energy cutoff of 550 eV for plane waves. The energy convergence criterion was 10−6 eV, and the force convergence criterion was 10−4 eV Å−1. After relaxation, the electronic structures were calculated with a kinetic energy cutoff of 500 eV.
The Dudarev approach33 to the Perdew–Burke–Ernzerhof generalized gradient approximation GGA (PBE)+U implementation34–38 was employed to enforce localization of the Pa 5f electrons. The effective Ueff (U–J) parameter of 4.0 eV (ref. 39) was used. This value was tested for PaO2 and all simulated Pa2O5 structures, where the actinide (U, Np, and Pu) oxides in the literature6,16,17,27,40–43 predicted good calculated structural properties. Spin–orbit coupling was not included in any of the calculations described herein since it has been previously demonstrated on actinide dioxides10,44 that its effects on the structural properties and relative stabilities are inconsequential. The cutoff energy of 550 eV was reached for the convergence of the energy and the Γ-centered Monkhorst–Pack k-meshes of ζ-Nb2O5 4 × 6 × 6; Nb2O5 4 × 6 × 4; R-Nb2O5 6 × 6 × 4; B-Ta2O5 4 × 6 × 6; Z-Ta2O5 6 × 6 × 6; β-Ta2O5 6 × 6 × 6; β-V2O5 3 × 6 × 4; α-V2O5 2 × 6 × 2; and Np2O5 4 × 6 × 4 were automatically generated. The enthalpies of formation as a function of pressure and thermodynamic properties are presented in Fig. S1–S5.†
3. Results and discussion
3.1 Structural properties
The different structures of the layered Pa2O5 composition were simulated. Nb2O5,45–47 Ta2O5,48,49 V2O5,50,51 Np2O5 (ref. 52) structured M2O5 (where M is an actinide or transition metal) structures were investigated by replacing the metal ion with protactinium. All the relaxed simulated structures retained the coordination environments of the original M2O5 structures. We report the experimental structures of ζ-Nb2O5 and Np2O5 in comparison to our calculated structure of Pa2O5 in the ζ-Nb2O5 and Np2O5 structures. For Pa2O5 in the Np2O5 structure, the calculated lattice parameters (Table 1) are in good agreement with the experimental results of Np2O5, most likely because of the similarity between the protactinium and neptunium atomic radii (0.78 and 0.75 Å, respectively). Although the large protactinium cation (0.78 Å) substitutes the transition metal ions V (0.54 Å), Nb (0.69 Å) and Ta (0.69 Å), PBE+U demonstrates that the cell volume for Pa2O5 in the ζ-Nb2O5 structure is excellent compared to the experimental value of the original ζ-Nb2O5. An important reason for this is the change from transition metal ions to protactinium ions in the coordinate environment of the substitute position. The original ζ-Nb2O5 structure has an alternating MO6-rich perovskite structure, and the replaced Pa2O5 in ζ-Nb2O5 phase was transformed into alternating MO9 distorted hexahedron and quadrangular pyramid layers. The structural and mechanical properties of all the simulated systems are shown in Tables 1 and 2 and their relaxed structures are presented in Fig. 1–5.
Table 1 Predicted properties of some layered Pa2O5 phasesa
| Phase |
Method |
Lattice parameters (Å) |
Lattice parameters (deg) |
Vol. (Å3) |
Space group |
E
gap (eV) |
B (GPa) |
E
form (eV) |
|
a
|
b
|
c
|
α
|
β
|
γ
|
|
The enthalpy of formation (Eform = E(Pa2O5) − 2E(Pa) − 5E(O)) was calculated with respect to the energy of the Pa metal (8.72 eV per Pa) and the O2 molecule (−4.90 eV per O). The energy of an O atom was predicted to be −4.90 eV, as calculated from an O2 molecule in a 25 Å box using the Γ point.
|
| Pa2O5 |
Expt19 |
13.84 |
4.02 |
4.18 |
90.0 |
90.0 |
90.0 |
|
|
|
|
|
| ζ-Nb2O5 |
Expt47 |
12.740 |
4.883 |
5.561 |
90.0 |
105.02 |
90.0 |
334.12 |
C2/c (15) |
|
|
|
| PBE+U |
12.620 |
5.387 |
5.387 |
90.0 |
114.68 |
90.0 |
332.72 |
C2/c (15) |
2.67 |
198.33 |
−27.92 |
| Nb2O5 |
PBE+U |
14.446 |
4.282 |
15.035 |
90.0 |
163.64 |
90.0 |
262.02 |
P1 (1) |
3.05 |
170.67 |
−26.41 |
| R-Nb2O5 |
PBE+U |
4.235 |
4.283 |
14.445 |
90.0 |
90.29 |
90.0 |
262.00 |
C2/m (12) |
3.49 |
170.61 |
−26.40 |
| Z-Ta2O5 |
PBE+U |
6.302 |
4.077 |
6.517 |
90.0 |
107.37 |
90.0 |
159.82 |
C2/m (12) |
2.21 |
282.70 |
−26.16 |
| β-Ta2O5 |
PBE+U |
6.991 |
4.048 |
8.474 |
90.0 |
90.0 |
90.0 |
239.84 |
Pccm (49) |
1.93 |
178.87 |
−24.13 |
| β-V2O5 |
PBE+U |
6.645 |
3.937 |
7.412 |
90.0 |
78.57 |
90.0 |
190.05 |
P21/m (11) |
3.28 |
198.91 |
−27.89 |
| α-V2O5 |
PBE+U |
11.576 |
4.220 |
10.664 |
90.0 |
90.0 |
90.0 |
520.93 |
Cmcm (63) |
3.05 |
120.63 |
−25.01 |
| Np2O5 |
Expt52 |
8.17 |
6.58 |
9.31 |
90.0 |
116.01 |
90.0 |
449.81 |
P2/c (13) |
|
|
|
| PBE+U |
8.150 |
6.887 |
9.404 |
90.0 |
115.69 |
90.0 |
470.35 |
P2/c (13) |
3.29 |
166.76 |
−26.95 |
Table 2 Coordination and charges of protactinium in the simulated Pa2O5 structures
| Pa environment |
No. of Pa environments per simulated unit cell |
| ζ-Nb2O5 |
Nb2O5 |
R-Nb2O5 |
Z-Ta2O5 |
β-Ta2O5 |
β-V2O5 |
α-V2O5 |
Np2O5 |
| Pa5+ distorted octahedron |
|
4 |
4 |
|
|
|
8 |
|
| Pa5+ octahedron |
|
|
|
|
2 |
|
|
4 |
| Pa5+ pentagonal bipyramid |
|
|
|
|
2 |
|
|
4 |
| Pa5+ distorted hexahedron and quadrangular pyramid |
8 |
|
|
4 |
|
|
|
|
| Pa5+ 7-fold |
|
|
|
|
|
2 |
|
|
| Pa4+ 7-fold |
|
|
|
|
|
2 |
|
|
Pa2O5 in Nb2O5 structure.
The ζ-,45 R-46 and Nb2O5 (ref. 47) polymorphs were simulated. The ζ-Nb2O5 and Pa2O5 in the ζ-Nb2O5 structure are shown in Fig. 1a and b, respectively. Although the ζ-Nb2O5 structure is a skutterudite-like structure, the optimized Pa2O5 in the ζ-Nb2O5 phase can be considered a diamond-like (for 4 protactinium ions) structure, which has alternating MO9 distorted hexahedron and quadrangular pyramid layers. As shown in Fig. 2a and b, the Nb2O5 and R-Nb2O5 phases are anatase-like structures and have layers of edge-sharing MO6 octahedra, respectively. For the R-Nb2O5 structure, the layers are continuous in the c direction, while they are separated by 2 layers of a skutterudite-like structure for the Nb2O5 structure. All the protactinium ions for the R- and Nb2O5 phases are Pa5+ in the distorted octahedral coordination (Table 2).
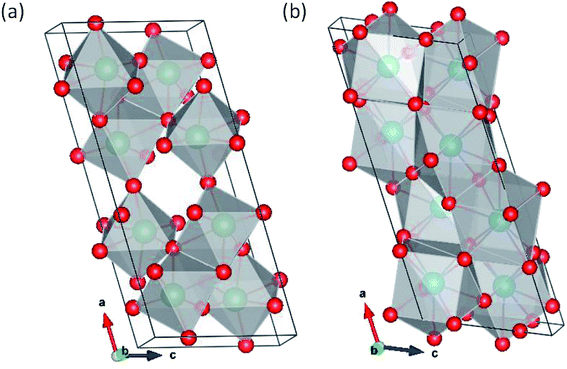 |
| | Fig. 1 (a) Original ζ-Nb2O5 structure and (b) Pa2O5 in the ζ-Nb2O5 structures. | |
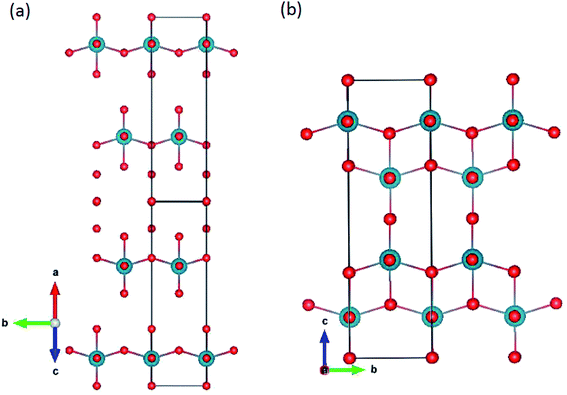 |
| | Fig. 2 Pa2O5 in (a) Nb2O5 and (b) R-Nb2O5 structures. | |
Pa2O5 in Ta2O5 structure.
We simulated the Z-48 and β-Ta2O5 (ref. 49) polymorphs (Fig. 3a and b, respectively). Although many polymorphs exist for this oxide, they are generally very similar to Nb2O5. In particular, the structure of B-Ta2O5 is very similar to ζ-Nb2O5. β-Ta2O5 is a typical two-layer orthogonal structure. Z-Ta2O5 does not resemble the anatase structure and is more comparable to a distorted brookite structure (Fig. 2b). For the β-Ta2O5 and ζ-Nb2O5 structures, all the protactinium ions are Pa5+ in the distorted octahedral coordination (Table 2). In contrast, all the protactinium ions for the β-Ta2O5 structure are in the octahedral coordination.
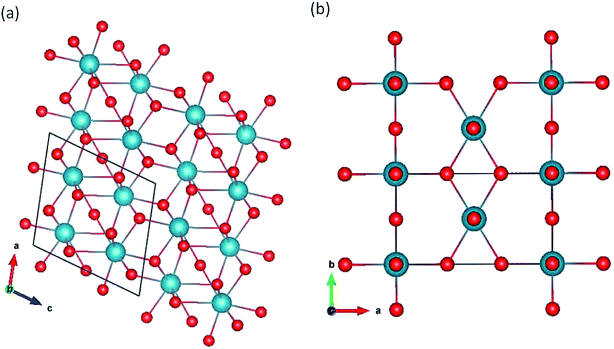 |
| | Fig. 3 Pa2O5 in (a) Z-Ta2O5 and (b) β-Ta2O5 structures. | |
Pa2O5 in V2O5 structure.
Two polymorphs, α-50 and β-V2O5,51 are presented in Fig. 4. The β-V2O5 structure is built of infinite chains made of quadruple units of edge-sharing PaO6 octahedra along the b axis. The chains are linked by sharing corners of two octahedra along the c axis. The α-V2O5 structure has a layered structure with orthorhombic symmetry consisting of PaO5 square pyramids sharing edges and corners.
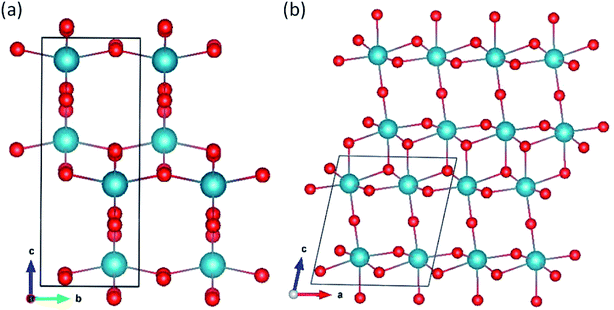 |
| | Fig. 4 Pa2O5 in (a) α-V2O5 and (b) β-V2O5 structures. | |
Pa2O5 in Np2O5 structure.
The simulated Np2O5 structure consists of 8 protactinium environments,52 4 with pentagonal bipyramidal coordination and 4 with octahedral coordination (Fig. 5 and Table 2). All the protactinium ions are predicted to be Pa5+.
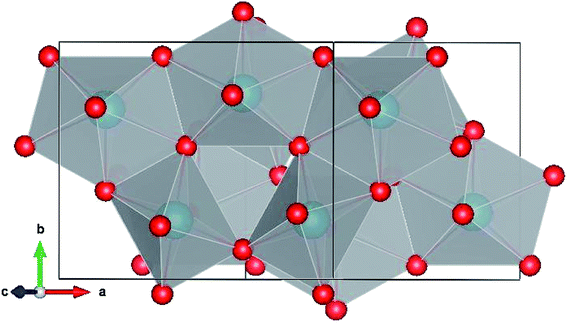 |
| | Fig. 5 Pa2O5 in the Np2O5 structure. | |
3.2 Stability
To confirm the thermodynamic stabilities of the predicted structures, the enthalpy of formation (Eform) for the simulated Pa2O5 structures are listed in Table 1. The relative enthalpy of formation Eform was calculated for each stoichiometry with respect to all the simulated Pa2O5 structures and gas O2, as follows:| | | Eform = E(Pa2O5) − 2E(Pa) − 5E(O) | (1) |
For clarity, the energies against the volume per Pa2O5 unit are plotted in Fig. 6. There is a clear dependence of the formation energy on the volume, with a decrease in stability for volumes smaller or larger than the most stable phases (ζ-Nb2O5).
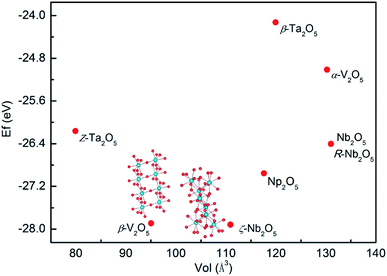 |
| | Fig. 6 Stability plot of the formation energy per Pa2O5 in electronvolt vs. volume per Pa2O5 unit. Phases are named with the original M2O5 structures for clarity. | |
The distribution of protactinium charges and protactinium coordination influence the stability. The ζ-Nb2O5-structured Pa2O5 is the most stable overall, although this structure contains all the Pa in a distorted hexahedron and quadrangular pyramid coordination. β-V2O5 was found to be just slightly less stable than ζ-Nb2O5 (0.03 eV) in terms of formation energy. The stability of the other phases follows the order of Np2O5 > Nb2O5 > R-Nb2O5 > Z-Ta2O5 > α-V2O5 > β-Ta2O5. Since Pa5+ prefers higher coordination numbers compared to the 6-fold distorted octahedral coordination, all the structures featuring protactinium ions entirely in the 6-fold coordination are consequently less stable. The V2O5-structured oxides are the least stable with the β-polymorph less stable than the α-V2O5 structure due to the presence of Pa in mixed oxidation states (Pa4+ and Pa5+) compared to α-V2O5, which is comprised of only Pa5+ ions.
The DFT work from Molinari et al.25 predicted that the Np2O5-structured U2O5 is the most stable among those considered under ambient conditions. However, the observed δ-U2O5 structure is found to be the second most stable. In particular, Pa2O5 in the β-V2O5 structure, given that it contains only octahedrally coordinated Pa, is closely followed by β-V2O5. The higher coordination numbers are also very similar to U2O5 since U is closely followed by R-Nb2O5.
These energetics show that Pa2O5 can crystallize in the ζ-Nb2O5 structure, but due to the relative instability of the Pa2O5 stoichiometry compared to the other protactinium oxides, it has not been synthesized or reported experimentally. The difficulty in synthesizing layered Pa2O5 is likely to stem from the fact that Pa5+ is more stable in the pentagonal bipyramidal coordination. One can also consider the formation of the studied Pa2O5 phases as a function of pressure, representing a range of conditions from low pressure to high pressure. The formation enthalpies as a function of pressure are presented in Fig. S1† and are normalized with respect to the most stable Pa2O5 (i.e., the ζ-Nb2O5 structure) such that
| | | δHf = ΔH(x) − ΔH(ζ-Nb2O5) | (2) |
where
x is the phase in question and Δ
H(
x) corresponds to
Eform in
Table 1. Interestingly, we predicted that at high pressure (above 100 kbar), Pa
2O
5 will be more thermodynamically stable in the ζ-Nb
2O
5 structure.
Using the density functional perturbation theory (DFPT)53,54 calculated for each unit cell, the Helmholtz free energy, Fvib (Fig. S2†), vibrational entropy, Svib (Fig. S3†), vibrational energy, Evib (Fig. S4†), Helmholtz free energy, Ftot = Eform + Fvib (Fig. S5†), and the heat capacity, Cv (Table 3), were evaluated. The Helmholtz free energy, F, entropy, S, internal energy, E, and constant volume specific heat capacity, Cv, can be directly calculated as a function of temperature using the following equations:
| | 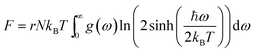 | (3) |
| | 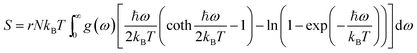 | (4) |
| | 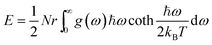 | (5) |
| | 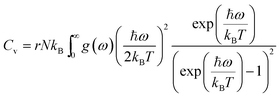 | (6) |
where the indices
ω is the phonon frequency,
g(
ω) is the normalized phonon density of states
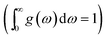
,
r is the number of degrees of freedom in the primitive unit cell, and
N is the number of primitive unit cells.
ħ is Planck's constant,
kB is the Boltzmann constant, and
T is the temperature in kelvin [K]. All these properties are expressed per Pa
2O
5 unit, and a sample of their values at 300 K is presented in
Table 3. A full calculation of the phase stability for the Pa
2O
5 phases is beyond the scope of this work; however, our calculations show that the energy-minimized ζ-Nb
2O
5 phase has a lower enthalpy of formation (
Eform) and vibrational entropy (
Svib) than the other phases. Hence, using our calculated values, ζ-Nb
2O
5 is predicted to be the preferred structure at around 300 K and 0 bar (Fig. S5
†).
Table 3 Predicted thermodynamic properties of some layered Pa2O5 phases at 300 K
| Phase |
F
vib (meV) |
S
vib (meV K−1) |
C
V (meV) |
E
vib (meV) |
F
tot (eV) |
| ζ-Nb2O5 |
214.2 |
1.43 |
135.5 |
612.0 |
−27.71 |
| Nb2O5 |
18.9 |
2.03 |
145.3 |
628.7 |
−26.40 |
| R-Nb2O5 |
45.3 |
1.95 |
145.4 |
629.3 |
−26.35 |
| Z-Ta2O5 |
218.3 |
1.49 |
123.5 |
606.7 |
−25.94 |
| β-Ta2O5 |
56.6 |
1.46 |
105.3 |
494.2 |
−24.07 |
| β-V2O5 |
212.5 |
1.46 |
137.2 |
650.9 |
−27.68 |
| α-V2O5 |
47.0 |
1.46 |
85.1 |
395.2 |
−24.96 |
| Np2O5 |
107.6 |
1.72 |
140.7 |
622.8 |
−26.84 |
3.3 Elastic properties
To evaluate the mechanical stability of all the simulated structures at ambient pressure, the calculated elastic constants are shown in Table S1,† which were calculated using the strain–stress relationship. The key criterion for the mechanical stability of a crystal is that the strain energy must be positive, which implies that the elastic constants should satisfy the generalized elastic stability criteria. In all the simulated structures, the Pccm phase (β-Ta2O5) is the only orthorhombic structure, and the others are monoclinic structures. For the orthorhombic structure, the nine independent elastic constants are C11, C22, C33, C44, C55, C66, C12, C13 and C23, and the corresponding mechanical stability criteria are given as55
| C11 > 0, C11C12 > C122, C44 > 0, C55 > 0, C66 > 0, C11C22C33 + 2C12C13C23 − C11C232 − C22C132 − C33C122 > 0. |
Meanwhile, the monoclinic structure has thirteen independent elastic constants (C11, C22, C33, C44, C55, C66, C12, C13, C23, C15, C25, C35, C46) and the corresponding mechanical stability criteria are given as55
| C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0, [C11 + C22 + C33 + 2(C12 + C13 + C23)] > 0, (C33C55 − C352) > 0, (C44C66 − C462) > 0, (C22 + C33 − 2C23) > 0, [C22(C33C55 − C352) + 2C23C25C35 − C232C35 − C252C33] > 0, {2[C15C25(C33C12 − C13C23) + C15C35(C22C13 − C22C23) + C25C35(C11C23 − C12C13)] − [C152(C22C33 − C232) + C252(C11C33 − C132) + C352(C11C22 − C122)] + C55(C11C22C33 − C11C232 − C22C132 − C33C122 + 2C12C13C23)} > 0. |
From the elastic constants listed in Table S1,† we find that the monoclinic phase of Pa2O5 in the ζ-Nb2O5 structures satisfies their respective mechanical stability criteria at ambient pressure, thus confirming their mechanical stability. However, the Pccm phase of Pa2O5 in the β-Ta2O5 structure is not the ground-state structure because this orthorhombic phase does not satisfy its mechanical stability criteria. Combining the thermodynamic and mechanical stability results, we conclude that the monoclinic phase is the ground-state structure for ζ-Nb2O5-structured Pa2O5 at ambient pressure. In addition, there is no evident correlation between the bulk moduli B and the volume (Vol.) or formation energy (Eform) of the layered Pa2O5 phases. Our work gives a high bulk modulus, B, for the ζ-Nb2O5-structured Pa2O5, but the bulk modulus of the Z-Ta2O5 structure is the largest.
3.4 Electronic properties
The experimental band gaps of the layered Pa2O5 phase are not currently available. In accordance with the higher layered oxide M2O5, all the structures are predicted to be ligand-to-metal charge-transfer (LMCT) insulators (O-2p to Pa-5f), with a conductance band composed of Pa 5f states and valence band comprised of O 2p states, with higher energy Pa 5f states at the core. To clearly describe the electronic properties of the most stable structure, the densities of states (DOS), projected density of states (PDOS) and band structure of Pa2O5 in the ζ-Nb2O5 and β-V2O5 structures are provided in Fig. 7 and S6.† These characteristics of Pa are attributed to its partially occupied 5f orbitals, which favors itinerancy for the early actinides. The appearance of significant Pa-5f/O-2p mixing arises from the increasing stabilization of the Pa 5f band due to incomplete shielding of the nuclear charge as one proceeds across the actinide series. There is a great variation in the predicted band gaps, with Pa2O5 in the ζ-Nb2O5 structure predicted to be 2.67 eV, which is more than the PaO2 band gap of 1.40 eV.56 As a comparison, the DOS and PDOS of Pa2O5 in the β-V2O5 structure are shown in Fig. 7b. Our PBE+U calculation predicts Pa2O5 in the β-V2O5 structure as a charge-transfer insulator with a band gap of 3.28 eV, which is bigger than the Pa2O5 in the ζ-Nb2O5 structure with a predicted gap of 0.61 eV. The presence of Pa 5f states in the valence band suggests a degree of covalent mixing with O 2p (fully ionic bonding would feature no overlapping states).
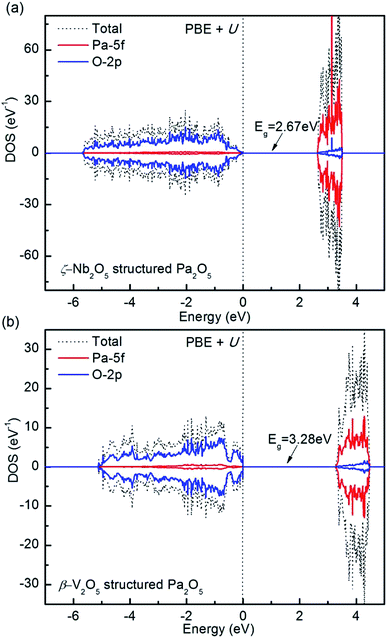 |
| | Fig. 7 Total and projected density of states of Pa2O5 in the ζ-Nb2O5 (a) and β-V2O5 (b) structures computed for the ground states in PBE+U. The Fermi energy stands at 0 eV. | |
4. Conclusions
In this work, we presented some possible structures of the Pa2O5 stoichiometry starting from existing actinide and transition metal pentoxides based on density functional theory. Our calculations showed that the Pa2O5 structures prefer the Pa ions in homogeneous Pa5+ oxidation states and that all are in distorted hexahedron and quadrangular pyramid coordination. Our simulations predict that the ζ-Nb2O5-structured Pa2O5 is the most stable under zero temperature and ambient conditions. The observed β-V2O5 structure was found to be the second most stable structure. Thus, it is expected that protactinium can crystallize with the ζ-Nb2O5 structure; however, this has not been observed experimentally. ζ-Nb2O5-structured Pa2O5 is a charge-transfer insulator and its calculated band gap is 2.67 eV. Thus, this stoichiometry is clearly worthy of synthetic investigation since the ζ-Nb2O5 structure is found to be a stable phase. To better understand the fluorite to layered transformation, we will focus on using a more pragmatic approach to model fluorite-based Pa2O5 phases in future simulation work.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Project supported by the National Natural Science Foundation of China (No. 21771167).
References
- T. Mark McCleskey, E. Bauer, Q. Jia, A. K. Burrell, B. L. Scott, S. D. Conradson, A. Mueller, L. Roy, X. Wen and G. E. Scuseria, J. Appl. Phys., 2013, 113, 013515 CrossRef.
- T. Yaashita, N. Nitani, T. Tsuji and H. Inagaki, J. Nucl. Mater., 1997, 245, 72–78 CrossRef.
- S. Kern, R. Robinson, H. Nakotte, G. Lander, B. Cort, P. Watson and F. Vigil, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 104 CrossRef CAS.
- L. Asprey, F. Ellinger, S. Fried and W. Zachariasen, J. Am. Chem. Soc., 1955, 77, 1707–1708 CrossRef CAS.
- P. Santini, S. Carretta, G. Amoretti, R. Caciuffo, N. Magnani and G. H. Lander, Rev. Mod. Phys., 2009, 81, 807 CrossRef CAS.
- B. T. Wang, H. Shi, W. Li and P. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 045119 CrossRef.
- Q. Yin and S. Y. Savrasov, Phys. Rev. Lett., 2008, 100, 225504 CrossRef.
- P. Zhang, B. T. Wang and X. G. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144110 CrossRef.
- I. D. Prodan, G. E. Scuseria, J. A. Sordo, K. N. Kudin and R. L. Martin, J. Chem. Phys., 2005, 123, 014703 CrossRef.
- X. D. Wen, R. L. Martin, T. M. Henderson and G. E. Scuseria, Chem. Rev., 2012, 113, 1063–1096 CrossRef.
- X. D. Wen, R. L. Martin, L. E. Roy, G. E. Scuseria, S. P. Rudin, E. R. Batista, T. M. McCleskey, B. L. Scott, E. Bauer and J. J. Joyce, J. Chem. Phys., 2012, 137, 154707 CrossRef.
- A. Bouasria, A. Zaoui, S. Ait Abderrahmane, S. Kacimi, A. Boukortt, M. Bejar and E. Dhahri, Int. J. Comput. Mater. Sci. Eng., 2017, 6, 1750006 CAS.
- K. N. Kudin, G. E. Scuseria and R. L. Martin, Phys. Rev. Lett., 2002, 89, 266402 CrossRef.
- I. D. Prodan, G. E. Scuseria and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033101 CrossRef.
- D. Andersson, J. Lezama, B. Uberuaga, C. Deo and S. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 024110 CrossRef.
- G. Jomard, B. Amadon, F. Bottin and M. Torrent, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075125 CrossRef.
- B. Sun, P. Zhang and X. G. Zhao, J. Chem. Phys., 2008, 128, 084705 CrossRef PubMed.
- K. T. Moore and G. van der Laan, Rev. Mod. Phys., 2009, 81, 235 CrossRef CAS.
- P. A. Sellers, S. Fried, R. E. Elson and W. Zachariasen, J. Am. Chem. Soc., 1954, 76, 5935–5938 CrossRef CAS.
- H. R. Hoekstra, S. Siegel and F. X. Gallagher, J. Inorg. Nucl. Chem., 1970, 32, 3237–3248 CrossRef CAS.
- N. A. Brincat, S. C. Parker, M. Molinari, G. C. Allen and M. T. Storr, Dalton Trans., 2015, 44, 2613–2622 RSC.
- D. Andersson, G. Baldinozzi, L. Desgranges, D. Conradson and S. Conradson, Inorg. Chem., 2013, 52, 2769–2778 CrossRef CAS.
- C. Guéneau, M. Baichi, D. A. A. Labroche, C. Chatillon and B. Sundman, J. Nucl. Mater., 2002, 304, 161–175 CrossRef.
- R. J. McEachern and P. Taylor, J. Nucl. Mater., 1998, 254, 87–121 CrossRef CAS.
- M. Molinari, N. A. Brincat, G. C. Allen and S. C. Parker, Inorg. Chem., 2017, 56, 4468–4473 CrossRef.
- N. A. Brincat, S. C. Parker, M. Molinari, G. C. Allen and M. T. Storr, Inorg. Chem., 2014, 53(23), 12253–12264 CrossRef CAS.
- N. A. Brincat, M. Molinari, S. C. Parker, G. C. Allen and M. T. Storr, J. Nucl. Mater., 2015, 456, 329–333 CrossRef CAS.
- R. E. Wilson, S. Sio and V. Vallet, Nat. Commun., 2018, 9, 622 CrossRef.
-
L. R. Morss, N. M. Edelstein and J. Fuger, The Chemistry of the Actinide and Transactinide Elements, Springer, The Netherlands, 2010 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- A. Liechtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467 CrossRef CAS.
- M. T. Czyżyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14211 CrossRef.
- T. Yamazaki and A. Kotani, J. Phys. Soc. Jpn., 1991, 60, 49–52 CrossRef CAS.
- V. I. Anisimov, A. I. Poteryaev, M. A. Korotin, A. O. Anokhin and G. Kotliar, J. Phys.: Condens. Matter, 1997, 9, 7359 CrossRef CAS.
- Y. Yun, J. Rusz, M. T. Suzuki and P. Oppeneer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075109 CrossRef.
- K. O. Obodo and N. Chetty, J. Phys.: Condens. Matter, 2013, 25, 145603 CrossRef CAS PubMed.
- X. D. Wen, R. L. Martin, G. E. Scuseria, S. P. Rudin, E. R. Batista and A. K. Burrell, J. Phys.: Condens. Matter, 2012, 25, 025501 CrossRef.
- J. Flitcroft, M. Molinari, N. Brincat, M. Storr and S. Parker, Chem. Commun., 2015, 51, 16209–16212 RSC.
- T. S. Ercit, Mineral. Petrol., 1991, 43, 217–223 CrossRef CAS.
- B. O. Marinder, Acta Chem. Scand., 1990, 44, 123–134 CrossRef CAS.
- J. Spyridelis, P. Delavignette and S. Amelinckx, Phys. Status Solidi B, 1967, 19, 683–704 CrossRef CAS.
- I. Zibrov, V. Filonenko, M. Sundberg and P. E. Werner, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 659–665 CrossRef CAS PubMed.
- L. Aleshina and S. Loginova, Crystallogr. Rep., 2002, 47, 415–419 CrossRef CAS.
- J. Cocciantelli, P. Gravereau, J. Doumerc, M. Pouchard and P. Hagenmuller, J. Solid State Chem., 1991, 93, 497–502 CrossRef CAS.
- V. Filonenko, M. Sundberg, P. E. Werner and I. Zibrov, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 375–381 CrossRef CAS.
- T. Z. Forbes, P. C. Burns, S. Skanthakumar and L. Soderholm, J. Am. Chem. Soc., 2007, 129, 2760–2761 CrossRef CAS.
- S. Baroni, S. De Gironcoli and A. D. Corso, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- X. Gonze, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 1096–1114 CrossRef CAS.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- I. D. Prodan, G. E. Scuseria and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033101 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Density functional theory optimized some layered Pa2O5 in the fractional format, enthalpies of formation, independent elastic constants, and thermodynamic properties (PDF). See DOI: 10.1039/c9ra06735c |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Shichang
Li
ab,
Shichang
Li
 a,
Tao
Gao
*a and
Bingyun
Ao
a,
Tao
Gao
*a and
Bingyun
Ao
 *c
*c

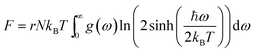
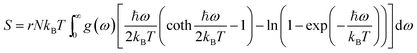
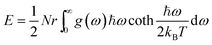
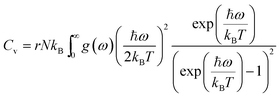
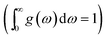 , r is the number of degrees of freedom in the primitive unit cell, and N is the number of primitive unit cells. ħ is Planck's constant, kB is the Boltzmann constant, and T is the temperature in kelvin [K]. All these properties are expressed per Pa2O5 unit, and a sample of their values at 300 K is presented in Table 3. A full calculation of the phase stability for the Pa2O5 phases is beyond the scope of this work; however, our calculations show that the energy-minimized ζ-Nb2O5 phase has a lower enthalpy of formation (Eform) and vibrational entropy (Svib) than the other phases. Hence, using our calculated values, ζ-Nb2O5 is predicted to be the preferred structure at around 300 K and 0 bar (Fig. S5†).
, r is the number of degrees of freedom in the primitive unit cell, and N is the number of primitive unit cells. ħ is Planck's constant, kB is the Boltzmann constant, and T is the temperature in kelvin [K]. All these properties are expressed per Pa2O5 unit, and a sample of their values at 300 K is presented in Table 3. A full calculation of the phase stability for the Pa2O5 phases is beyond the scope of this work; however, our calculations show that the energy-minimized ζ-Nb2O5 phase has a lower enthalpy of formation (Eform) and vibrational entropy (Svib) than the other phases. Hence, using our calculated values, ζ-Nb2O5 is predicted to be the preferred structure at around 300 K and 0 bar (Fig. S5†).






