Open Access Article
Open Access ArticleBiomimetic heterobimetallic architecture of Ni(II) and Fe(II) for CO2 hydrogenation in aqueous media. A DFT study†
Bilal Ahmad Shiekh *
*
Department of Chemistry, UGC Sponsored Centre of Advanced Studies-II, Guru Nanak Dev University, Amritsar-143005, India. E-mail: bilal.ahmad459@gmail.com
First published on 16th October 2019
Abstract
In this work, density functional theory has been employed to design a heterobimetallic catalyst of Ni(II) and Fe(II) for the effective CO2 hydrogenation to HCOOH. Based on computational results, our newly designed catalyst is found to be effective for such conversion reactions with free energy as low as 14.13 kcal mol−1 for the rate determining step. Such a low value of free energy indicates that the NiFe heterobimetallic catalyst can prove to be very efficient for the above said conversion. Moreover, the effects of ligand substitutions at the active metal center and the effects due to various spin states are also explored, and can serve as a great tool for the rational design of NiFe catalyst for CO2 hydrogenation.
1 Introduction
Carbon dioxide, being a detrimental component of the atmosphere in higher concentrations, has reached freakish levels and continues to build up; this has become a cause of concern to the present day scientific community.1,2 The continued dependence on non-renewable fossils fuels for energy, high standards of living, and population explosion are exacerbating this situation even more.3,4 In this perspective, a possible way out of this problem is to convert CO2 into formic acid, which holds great promise in reversible hydrogen storage.5–8 Since, being an abundant, cheaper, and freely available chemical reservoir, recycling of CO2 forms a clean technology with zero carbon footprint for the synthesis of value added chemicals.9 Thus, hydrogenation of CO2 to HCOOH can address both the atmospheric as well as economic crisis concomitantly.7,10–12 Therefore, over the last few decades steady progress has been achieved for hydrogenation of CO2 to formic acid using homogenous metal catalysis. However, most of the effective homogenous catalysts proposed to date for such conversion utilize costly and toxic noble metals.13–25 For example, Nozaki and co-workers reported an iridium based pincer catalyst IrH3(P) (P represents 2,6-bis(diisopropylphosphinomethyl)pyridine) with TON 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and TOF 150
000 and TOF 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1.26 Subsequently after this, Hazari et al. also reported another Ir-based reported catalyst Ir(H3)(P) (P represents (diisopropylphosphinoethyl)amine) in which hydride from secondary coordination sphere N–H is transferred to CO2 and is very efficient catalyst with TON 348
000 h−1.26 Subsequently after this, Hazari et al. also reported another Ir-based reported catalyst Ir(H3)(P) (P represents (diisopropylphosphinoethyl)amine) in which hydride from secondary coordination sphere N–H is transferred to CO2 and is very efficient catalyst with TON 348![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and TOF 18
000 and TOF 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 h−1.20 Pidko and co-workers reported a Ru-based catalyst with TOF equal to 1
780 h−1.20 Pidko and co-workers reported a Ru-based catalyst with TOF equal to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 892
892![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1.27,28 Therefore, in quest of cheaper and nontoxic alternatives, researchers have shifted themselves towards earth abundant metal catalysts.29–35 Although significant number of earth abundant catalysts have been reported but almost all of them either require an external base or vigorous reaction conditions for the reaction to accomplish. Moreover, the catalytic activity of these reported catalysts is quite low and thus the design of efficient and highly active earth abundant metal catalysts remains elusive.
000 h−1.27,28 Therefore, in quest of cheaper and nontoxic alternatives, researchers have shifted themselves towards earth abundant metal catalysts.29–35 Although significant number of earth abundant catalysts have been reported but almost all of them either require an external base or vigorous reaction conditions for the reaction to accomplish. Moreover, the catalytic activity of these reported catalysts is quite low and thus the design of efficient and highly active earth abundant metal catalysts remains elusive.
Nature's remarkable design, evolved over a long period for different reactions to accomplish, is an inspiration for rational design of catalysts by biomimicking active site of these architectures. However, such an approach of catalytic design requires in-depth understanding mechanism of action and structure of the active center of the enzyme. The remarkable structural information available for enzymes has led to design of various models for hydrogenation of CO2.36–41 The mechanistic studies of CO2 hydrogenation through DFT studies has revealed that either abstraction of hydride from the metal center or heterolytic cleavage of coordinated H2 over the metal center is usually the rate-determining step of entire catalytic cycle.36–39 The barrier height for H2 heterolytic cleavage can be significantly reduced by introducing a base in catalyst and one of such example is hydrogen oxidation catalyst reported by Bullock and co-workers containing pendant amine as base.42 Likewise, the significant role of base in heterolytic cleavage of coordinated H2 has also been reported in other studies as well.43,44 Moreover, MN2S2 metallodithiolate frameworks have been reported to be the best donors than phosphines and these ligands have been found in so many natural enzymes such as nitrile and thiocyanate hydratases.45,46 Such an architecture adopt square planar geometry and serve as bidentate ligand through two cis-configured S-donors.47
In previous study, we computationally designed biomimetic Mo and W based catalysts for hydrogenation of CO2.48 In this present work, inspired by the active site of [NiFe]-hydrogenase, Bullock's catalyst, and MN2S2 metallodithiolate framework, our aim here is to examine the catalytic activity of heterobimetallic Ni(II) and Fe(II) architecture shown in Scheme 1, for the hydrogenation of CO2 to HCOOH in aqueous media using various computational tools. We will also understand the various mechanistic aspects of CO2 hydrogenation involving various species such as carbonic acid, bicarbonate and carbonate ions formed by the reaction of CO2 with water.49 Moreover, the effects of various ligand substitutions and alteration of spin state of the metal atoms on catalytic activity will also be explored.
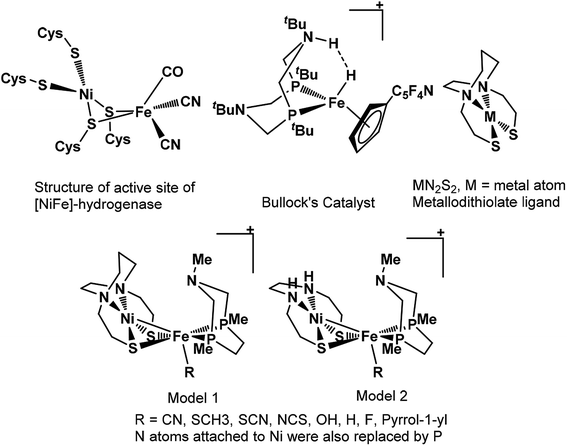 | ||
| Scheme 1 The structural representation of active site of [NiFe]-hydrogenase, Bullock's catalyst, MN2S2 metallodithiolate ligand and our modelled structures used in present work. | ||
2 Computational details
The geometrical calculations of all the complexes were optimized at PBE-D3 (ref. 50 and 51) level of theory in conjunction with 6-31+G(d,p)52 basis set for all atoms except for nickel and iron for which LANL2DZ53 basis set and ECP were employed. We tested the other functionals like M06-L,54 M06,55 PBE0-D3,56 and B3LYP,57,58 for computing the barrier heights for the addition of H2 over the metal center using PBE-D3 optimized geometries (refer to ESI for more details†). B3LYP and M06 procreated high results while as the best functionals for computing thermochemistry of transition metal complexes59–61 M06-L, PBE0-D3 and PBE-D3 produced almost similar results and thus PBE-D3 functional was chosen for our studies. In addition to LANL2DZ,53 the results were also gauged with Stuttgart-Dresden (SDD) basis-set, ECP10MDF including the ECP's augmented with d-polarization functions from Frenking.62 The computed results are almost same with both the basis sets (for details refer to ESI†). The solvent effects were incorporated employing integral equation formalism polarizable continuum model (IEFPCM)63 with SMD64 atomic radii corrections using water as solvent. All the calculations were performed using ultrafine numerical integration grid as defined in ‘G09’.65 The nature of all the stationary states along the reaction coordinate were confirmed by analyzing harmonic frequency data computed at the above said method. The transition states were confirmed by a single imaginary frequency along the reaction coordinate and the intermediates were without any imaginary frequency. The former were also confirmed by intrinsic reaction coordinate (IRC) calculations performed at the above level of theory. Thermal corrections within the rigid rotor and harmonic approximations were employed at 298.15 K temperature and 1 atm pressure. All the reported energies are Gibbs free energies unless mentioned otherwise. The free energy of Gaq(H+) equal to −264.0 kcal mol−1 has been taken from the literature66 and has been employed in other computational studies as well.67 Number of corrections to Gibbs free energies reported in the text were employed. First, the free energy of complexes were corrected by 1.89 kcal mol−1 considering the 1 atm to 1 M standard state conversion (added in those cases in which number of moles increases or vice versa). Second, correction equal to 2.38 kcal mol−1 for 55.4 to 1 molar standard state conversion and −6.32 kcal mol−1 correction for self-solvation were added for water molecules as well.68All the above said calculations have been performed using Gaussian 09 software suite.65
3 Results and discussions
3.1 Mechanistic aspects of CO2 hydrogenation
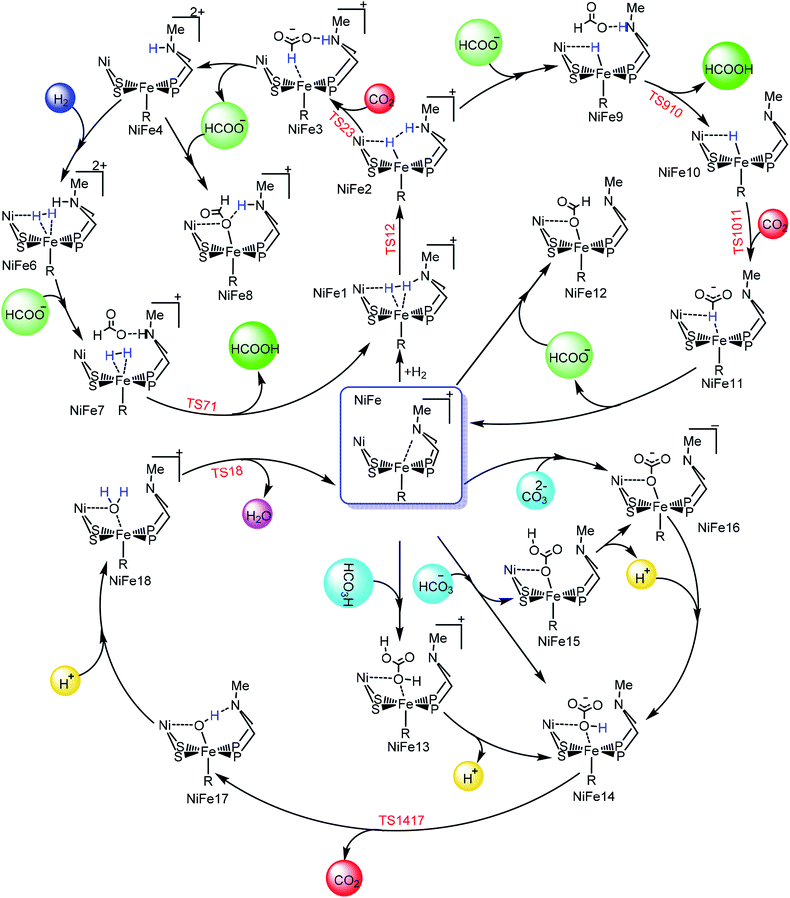
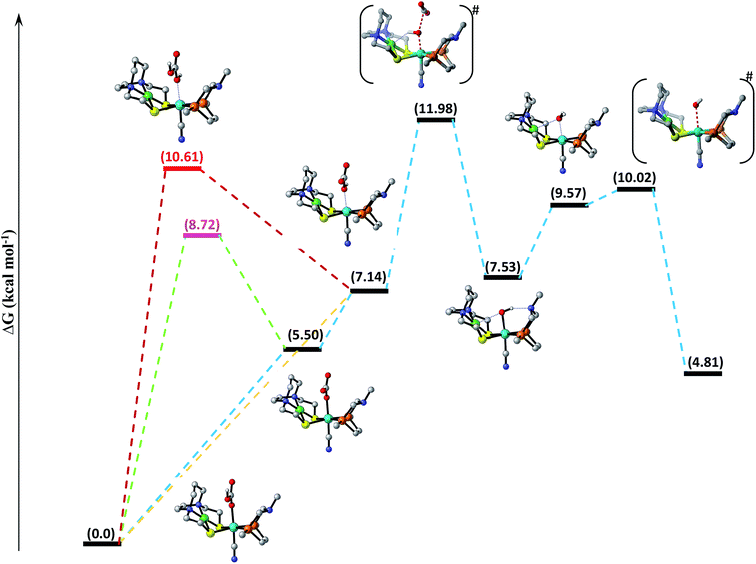
The entire mechanistic cycle of CO2 hydrogenation in aqueous media catalyzed by our NiFe-heterobimetallic catalyst has been divided into two sections, one in which HCOOH is formed and the second in which catalytic decomposition of carbonic acid, bicarbonate and carbonate ions takes place. Both these mechanistic cycles have been briefly described separately in the following two sections.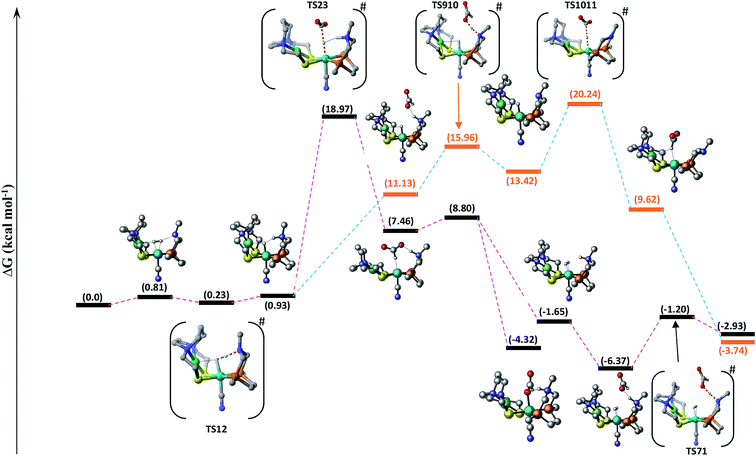 | ||
| Fig. 1 Free energy profile of CO2 hydrogenation catalyzed by [NiFe] heterobimetallic catalyst along the reaction coordinate. Non-essential hydrogen atoms have been omitted for the sake of clarity. | ||
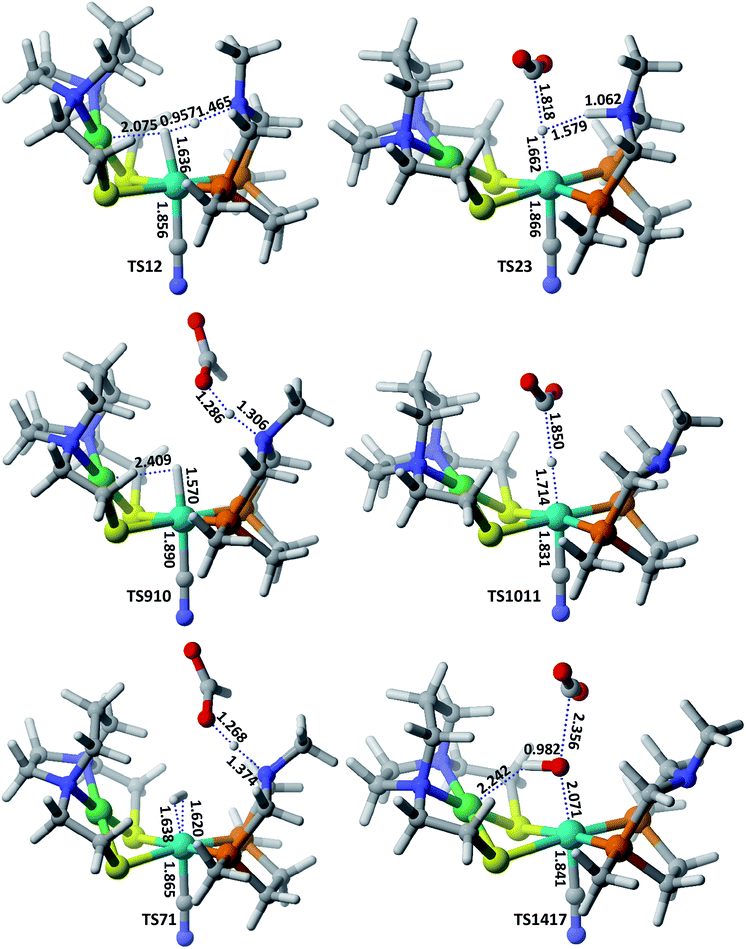 | ||
| Fig. 2 Optimized geometrical parameters of some of the important transition states involved in CO2 hydrogenation catalyzed by model 2 complex. All the bond distances are given in Å. | ||
In route second, instead of reacting with CO2, NiFe2 can interact with HCOO− anion to form NiFe9 with 10.2 kcal mol−1 uphill energy. In the next elementary step, the NiFe9 subsequently undergoes HCOOH elimination via TS910 transition state with an uphill barrier height equal to 4.83 kcal mol−1 (NiFe9 → TS910). Next, NiFe10 thus formed from NiFe9 interacts with CO2 through metal-hydride bond via TS1011 to form NiFe11 having an uphill barrier height equal to 6.82 kcal mol−1 (NiFe10 → TS1011). The transfer of hydride from NiFe10 to CO2, which proceeds through the transition state TS1011, is the rate-determining step of pathway 2 with total free energy of activation equal to 20.24 kcal mol−1. Finally, the loss of HCOO− anion from NiFe11 regenerates the initial catalyst.
The first route is less energy demanding compared to route second with abstraction of hydride from Fe-metal center by CO2 being the rate determining step of both the mechanistic pathways. As far as the catalysis of CO2 by model 2 is concerned, the free energy of various intermediates and transition states is almost similar to model 1. For example, free energy of H2 addition over the Fe(II)-metal center is 1.93 kcal mol−1 (NiFe1), the heterolytic cleavage of coordinated H2 is 0.59 kcal mol−1 while as the transfer of hydride from metal center to CO2 is 19.03 kcal mol−1.
3.2 Effect of ligand substitution
In order to design a catalyst with higher efficiency, we examined the effects of replacing CN ligand with other substituent ligands like SCH3, SCN, NCS, OH, H, F, and pyrrol-1-yl including metallodithiolate analogous variant in which N-atoms attached with Ni(II) were replaced with P. In total nine complexes were examined and after computational assessment, it was found that the activity of [NiFe] heterobimetallic catalyst is highly sensitive to these positions. The free energy of activation for TS23 in these newly proposed complexes decreased by almost 5 kcal mol−1 with lowest value obtained for OH group equal to 14.13 kcal mol−1 as shown in Table 1. The ligands SCH3, SCN, NCS, and H decrease the free energy of activation within 1–2 kcal mol−1 range. These effects of ligand substitution can be explained based on NBO analysis, according to which the ligands with low free energy of activation increase the negative charge at the Fe(II) metal center as listed in Table 1. The ligands with strong sigma donating ability like OH and pyrrol-1-yl increase the electron density at the metal center as depicted by their high negative charges at Fe(II) (−1.673 and −1.597). The C-atom of CO2 is electrophilic in nature as predicted by its NBO charge equal to 0.987 and thus higher negative charge at metal center will favors the hydride transfer. Likewise, F destabilizes TS23 by lowering electron density at the metal center (−1.365), which increases the activation energy of hydride transfer step. Moreover, replacement of N in metallodithiolate ligand with P also decreases the free energy of activation of TS23 transition state significantly. Thus, we recommend complex with metallodiothiolate ligand containing P instead of N and strong sigma donating ligands at Fe(II) metal center for the effective hydrogenation of CO2.| R | ΔG#TS (kcal mol−1) | Energy gap (eV) | NBO Charges (e) |
|---|---|---|---|
| Fe | |||
| a The atom of the ligand written first are the donor atoms with Fe(II) center. | |||
| SCH3 | 17.09 | 4.01 | −1.495 |
| SCN | 17.83 | 4.11 | −1.443 |
| NCS | 16.19 | 3.89 | −1.546 |
| OH | 14.13 | 3.61 | −1.673 |
| H | 17.12 | 4.02 | −1.483 |
| F | 20.78 | 4.51 | −1.365 |
| Pyrrol-1-yl | 14.92 | 3.72 | −1.597 |
| CN | 18.97 | 4.27 | −1.398 |
| N is replaced by P | |||
| P | 14.29 | 3.63 | −1.622 |
The above said effects of ligand substitution can further be explained based on energy gap between Fe–H σ-bonding orbital and the π*-antibonding orbital of CO2. According to NBO analysis Fe–H σ-bonding orbital populates the π*-antibonding orbital of CO2, which is the driving force for hydride abstraction step. The molecular orbital analysis of substituted complexes predict that HOMO and HOMO-1 represent the Fe–H σ-bonding orbital and LUMO+1 which represent π*-antibonding orbital for CO2. The LUMO+1 of CO2 is having energy equal to −0.44 eV while as the energy of other complexes falls in the range −4.048 to −4.953 eV with total difference of entire range almost equal to 1 eV as shown in Fig. 4. It is quite interesting to see that the complexes with lowest free energy of activation are having lowest energy difference between Fe–H σ-bonding orbital and π*-antibonding orbital of CO2. For example, OH and P ligands with low free energy of activation equal to 14.13 and 14.29 kcal mol−1 are having lowest energy gaps 3.61 and 3.63 eV, respectively. Similarly, F ligand with high free energy of activation 20.73 kcal mol−1 is having high-energy gap 4.51 eV as listed in Table 1. Thus, our computed free energy barriers are consistent with molecular orbital analysis.
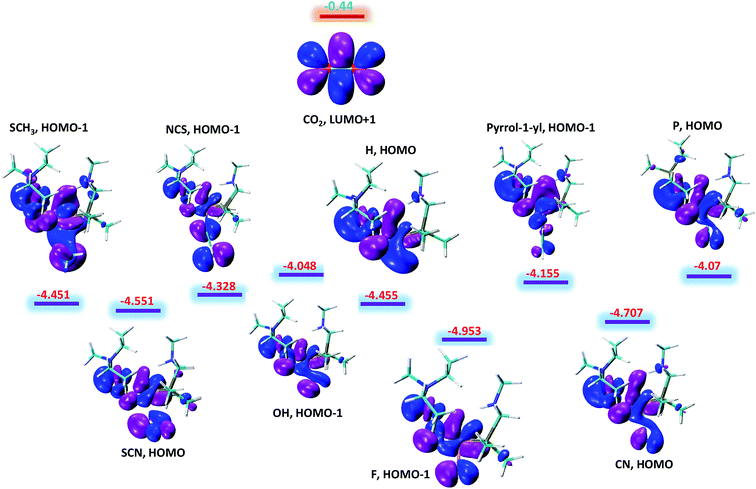 | ||
| Fig. 4 The energy difference between Fe–H σ-bonding orbitals of substituted NiFe2 complexes and π*-antibonding orbital of CO2. All the given values are in eV. | ||
3.3 Electronic effects
| Complex | Spin state | TS12 | TS23 |
|---|---|---|---|
| NiFe | Ni, singlet: Fe, singlet | 0.22 | 18.97 |
| NiFeT | Ni, singlet: Fe, triplet | 0.59 | 24.25 |
| NiTFe | Ni, triplet: Fe, singlet | 0.59 | 24.25 |
| NiTFeT | Ni, triplet: Fe, triplet | 8.95 | 37.22 |
The spin densities of some of the important transition states and intermediates located in catalytic cycle of CO2 hydrogenation has been computed using Mulliken method. The higher free energy of transition states as well as the stability of various arrangements of complexes relative to one another with increasing spin density over the metal centers can be explained based on their spin densities. As shown in Table 3, with increase in Mulliken spin density on both the metal centers the free energy of transition states (Table 2) increases, which explains the lower stability of these complexes with increasing spin density. Moreover, the higher stability of transition states with Fe being the active metal center is explained by its low spin density compared to Ni. The protonated complex, NiFe10 has much lower spin density in either of the spin combinations (NiFeT/NiTFeT) from initial value 1.831/2.383 (NiFe complex). The low spin density of Fe center and negative ESP charge over hydride ligand explains the higher stability of the arrangement NiII⋯−H–FeII over other possible combinations like NiIII–−H⋯FeII etc.
| Atom | TS12 | TS23 | NiFe10 | NiFe11 | ||||
|---|---|---|---|---|---|---|---|---|
| NiFeT | NiTFeT | NiFeT | NiTFeT | NiFeT | NiTFeT | NiFeT | NiTFeT | |
| a H represents the hydrogen atom attached with Fe-center. | ||||||||
| Fe | 0.326 | 1.864 | 0.324 | 1.905 | 0.403 | 1.992 | 0.327 | 2.195 |
| Ni | 1.153 | 1.186 | 1.145 | 1.106 | 1.103 | 1.120 | 1.141 | 0.997 |
| Ha | — | — | 0.005 | −0.007 | 0.024 | −0.048 | −0.001 | −0.030 |
| S | 0.171 | 0.272 | 0.189 | 0.159 | 0.163 | 0.261 | 0.186 | 0.168 |
| N | 0.082 | 0.093 | 0.078 | 0.077 | 0.074 | 0.077 | 0.080 | 0.072 |
| P | −0.007 | 0.110 | −0.004 | 0.116 | −0.012 | 0.089 | 0.000 | 0.004 |
4 Conclusions
In present work, two heterobimetallic Ni(II) and Fe(II) catalysts, model 1 and model 2 were computationally designed inspired by the active site of [NiFe] hydrogenase using density functional theory. The assessment of DFT results demonstrated that free energy of activation for both the models were almost identical. The abstraction of hydride at Fe(II)-center (TS23) is the rate-determining step of entire catalytic cycle with total free energy equal to 18.97 kcal mol−1. Such a low free energy of activation indicates that [NiFe] heterobimetallic architecture is a promising catalyst for CO2 hydrogenation. Moreover, the carbonic acid, bicarbonate and carbonate ions formed by CO2 with water are decomposed back to CO2 by the catalyst with free energy of activation for the rate-determining step equal to 11.98 kcal mol−1. In order to design a catalyst with higher activity, we examined the free energy of activation for TS23 by substituting the CN-group with SCH3, SCN, NCS, OH, H, F, and pyrrol-1-yl in our model 1 complex including the metallodithiolate analogous variant in which N-atoms attached with Ni(II) were replaced with P. After analysis of their results, the strong sigma donating ligands like OH, pyrrol-1-yl, and P analogous variant of metallodithiolate were found have lowest free energies of activation for TS23 equal to 14.13, 14.92, and 14.29 kcal mol−1. These results were further supported by the energy difference between Fe–H σ-bonding orbital of complexes and π*-antibonding orbital of CO2. In addition to this, variation of spin states of the metal centers has great influence on the catalytic activity of the catalyst. With increase in spin density of metal centers, the free energy of transition states as well as the instability of the various complexes increases. Thus, our DFT results not only provide a complete overview of mechanistic insights of CO2 hydrogenation by [NiFe] heterobimetallic architecture in aqueous media but also provide deep insights regarding effects of changing chemical environment around the metal center and spin states on the catalytic activity of the catalyst.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was financially supported by University Grants Commission (UGC), Govt. of India under UGC-BSR scheme as SRF (Senior Research Fellow) vide notification number, No. F.25-1/2013-14(BSR)/5-27/2007(BSR).References
- A. M. Appel, J. E. Bercaw and A. B. Bocarsly, et al., Chem. Rev., 2013, 113, 6621–6658 CrossRef CAS.
- H. Arakawa, M. Aresta and J. N. Armor, et al., Chem. Rev., 2001, 101, 953–996 CrossRef CAS.
- J. Bongaarts, Pop. Devel. Rev., 1992, 18, 299–319 CrossRef.
- D. Archer, J. Geophys. Res., 2005, 110, C09S05, DOI:10.1029/2004jc002625.
- M. Aresta, A. Dibenedetto and A. Angelini, Chem. Rev., 2014, 114, 1709–1742 CrossRef CAS.
- G. A. Olah, G. K. S. Prakash and A. Goeppert, J. Am. Chem. Soc., 2011, 133, 12881–12898 CrossRef CAS.
- J. Qiao, Y. Liu, F. Hong and J. Zhang, Chem. Soc. Rev., 2014, 43, 631–675 RSC.
- J. Eppinger and K. W. Huang, ACS Energy Lett., 2017, 2, 188–195 CrossRef CAS.
- E. A. Quadrelli, G. Centi, J. L. Duplan and S. Perathoner, ChemSusChem, 2011, 4, 1194–1215 CrossRef CAS.
- M. Aresta and A. Dibenedetto, Dalton Trans., 2007, 2975–2992 RSC.
- A. K. Singh, S. Singh and A. Kumar, Catal. Sci. Technol., 2016, 6, 12–40 RSC.
- D. Mellmann, P. Sponholz, H. Junge and M. Beller, Chem. Soc. Rev., 2016, 45, 3954–3988 RSC.
- E. Fujita, J. T. Muckerman and Y. Himeda, Biochim. Biophys. Acta, 2013, 1827, 1031–1038 CrossRef CAS.
- K. W. Huang, J. H. Han, C. B. Musgrave and E. Fujita, Organometallics, 2007, 26, 508–513 CrossRef CAS.
- N. Onishi, S. Xu, Y. Manaka, Y. Suna, W. H. Wang, J. T. Muckerman, E. Fujita and Y. Himeda, Inorg. Chem., 2015, 54, 5114–5123 CrossRef CAS PubMed.
- R. Tanaka, M. Yamashita and K. Nozaki, J. Am. Chem. Soc., 2009, 131, 14168–14169 CrossRef CAS.
- K. Mori, T. Taga and H. Yamashita, ACS Catal., 2017, 7, 3147–3151 CrossRef CAS.
- C. A. Huff and M. S. Sanford, ACS Catal., 2013, 3, 2412–2416 CrossRef CAS.
- J. A. Therrien, M. O. Wolf and B. O. Patrick, Inorg. Chem., 2014, 53, 12962–12972 CrossRef CAS.
- T. J. Schmeier, G. E. Dobereiner, R. H. Crabtree and N. Hazari, J. Am. Chem. Soc., 2011, 133, 9274–9277 CrossRef CAS.
- W. H. Wang, Y. Himeda, J. T. Muckerman, G. F. Manbeck and E. Fujita, Chem. Rev., 2015, 115, 12936–12973 CrossRef CAS.
- S. Sato, T. Morikawa, T. Kajino and O. Ishitani, Angew. Chem., Int. Ed., 2013, 52, 988–992 CrossRef CAS PubMed.
- R. Lalrempuia, M. Iglesias, V. Polo, P. J. S. Miguel, F. J. F. Alvarez, J. J. P. Torrente and L. A. Oro, Angew. Chem., Int. Ed., 2012, 51, 12824–12827 CrossRef CAS.
- J. F. Hull, Y. Himeda, W. H. Wang, B. Hashiguchi, R. Periana, D. J. Szalda, J. T. Muckerman and E. Fujita, Nat. Chem., 2012, 4, 383–388 CrossRef CAS PubMed.
- Y. Himeda, S. Miyazawa and T. Hirose, ChemSusChem, 2011, 4, 487–493 CrossRef CAS PubMed.
- R. Tanaka, M. Yamashita and K. Nozaki, J. Am. Chem. Soc., 2009, 131, 14168–14169 CrossRef CAS.
- G. A. Filonenko, M. P. Conley, C. Coperet, M. Lutz, E. J. M. Hensen and E. A. Pidko, ACS Catal., 2013, 3, 2522–2526 CrossRef CAS.
- G. A. Filonenko, R. V. Putten, E. N. Schulpen, E. J. M. Hensen and E. A. Pidko, ChemCatChem, 2014, 6, 1526–1530 CrossRef CAS.
- A. Z. Spentzos, C. L. Barnes and W. H. Bernskoetter, Inorg. Chem., 2016, 55, 8225–8233 CrossRef CAS PubMed.
- M. S. Jeletic, M. L. Helm, E. B. Hulley, M. T. Mock, A. M. Appel and J. C. Linehan, ACS Catal., 2014, 4, 3755–3762 CrossRef CAS.
- F. Bertini, N. Gorgas, B. Stöger, M. Peruzzini, L. F. Veiros, K. Kirchner and L. Gonsalvi, ACS Catal., 2016, 6, 2889–2893 CrossRef CAS.
- S. A. Burgess, A. J. Kendall, D. R. Tyler, J. C. Linehan and A. M. Appel, ACS Catal., 2017, 7, 3089–3096 CrossRef CAS.
- J. M. Smieja, M. D. Sampson, K. A. Grice, E. E. Benson, J. D. Froehlich and C. P. Kubiak, Inorg. Chem., 2013, 52, 2484–2491 CrossRef CAS.
- R. Langer, Y. Diskin-Posner, G. Leitus, L. J. W. Shimon, Y. Ben-David and D. Milstein, Angew. Chem., Int. Ed., 2011, 50, 9948–9952 CrossRef CAS.
- A. Dubey, L. Nencini, R. R. Fayzullin, C. Nervi and J. R. Khusnutdinova, ACS Catal., 2017, 7, 3864–3868 CrossRef CAS.
- X. Chen and X. Yang, J. Phys. Chem. Lett., 2016, 7, 1035–1041 CrossRef CAS PubMed.
- X. Yang, Chem. Commun., 2015, 51, 13098–13101 RSC.
- M. G. Mingot, J. P. Porcher, T. K. Todorova, T. Fogeron, C. M. Draznieks, Y. Li and M. Fontecave, J. Phys. Chem. B, 2015, 119, 13524–13533 CrossRef PubMed.
- X. Chen, Y. Jing and X. Yang, Chem.–Eur. J., 2016, 22, 8897–8902 CrossRef CAS.
- C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245–2274 CrossRef CAS.
- C. Wombwell and E. Reisner, Chem.–Eur. J., 2015, 21, 8096–8104 CrossRef CAS.
- T. Liu, D. L. DuBois and R. M. Bullock, Nat. Chem., 2013, 5, 228–233 CrossRef CAS.
- K. A. Murray, M. D. Wodrich, X. Hu and C. Corminboeuf, Chem.–Eur. J., 2015, 21, 3987–3996 CrossRef CAS.
- K. S. Rawat, A. Mahata and B. Pathak, J. Phys. Chem. C, 2016, 120, 26652–26662 CrossRef CAS.
- T. Arakawa, Y. Kawano, S. Kataoka, Y. Katayama, N. Kamiya, M. Yohda and M. Odaka, J. Mol. Biol., 2007, 366, 1497–1509 CrossRef CAS PubMed.
- S. Nagashima, M. Nakasako, N. Dohmae, M. Tsujimura, K. Takio, M. Odaka, M. Yohda, N. Kamiya and I. Endo, Nat. Struct. Mol. Biol., 1998, 5, 347–351 CrossRef CAS.
- J. A. Denny and M. Y. Darensbourg, Chem. Rev., 2015, 115, 5248–5273 CrossRef CAS.
- B. A. Shiekh, D. Kaur and S. Kumar, Phys. Chem. Chem. Phys., 2019, 21, 21370–21380 RSC.
- K. P. Zeller, P. Schuler and P. Haiss, Eur. J. Inorg. Chem., 2005, 2005, 168–172 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- EMSL Basis Set Exchange, http://bse.pnl.gov/bse/portal.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- D. G. Gusev, Organometallics, 2013, 32, 4239–4243 CrossRef CAS.
- K. H. Hopmann, Organometallics, 2016, 35, 3795–3807 CrossRef CAS.
- B. B. Averkiev and D. G. Truhlar, Catal. Sci. Technol., 2011, 1, 1526–1529 RSC.
- A. Höllwarth, M. Böhme, S. Dapprich, A. W. Ehlers, A. Gobbi, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 237–240 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, et al., Gaussian 09; Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- M. Z. Ertem, Y. Himeda, E. Fujita and J. T. Muckerman, ACS Catal., 2016, 6, 600–609 CrossRef CAS.
- M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794 CrossRef CAS.
- R. Fu, W. A. Goddard, M. J. Cheng and R. J. Nielsen, ACS Catal., 2017, 7, 356–364 CrossRef CAS.
- T. Liu, X. Wang, C. Hoffmann, D. L. DuBois and R. M. Bullock, Angew. Chem., Int. Ed., 2014, 53, 5300–5304 CrossRef CAS.
- R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980 CrossRef CAS.
- X. Yang, ACS Catal., 2011, 1, 849–854 CrossRef CAS.
- H. Ge, X. Chen and X. Yang, Chem. Commun., 2016, 52, 12422–12425 RSC.
- C. Hou, J. Jiang, S. Zhang, G. Wang, Z. Zhang, Z. Ke and C. Zhao, ACS Catal., 2014, 4, 2990–2997 CrossRef CAS.
- B. Mondal, F. Neese and S. Ye, Inorg. Chem., 2016, 55, 5438–5444 CrossRef CAS.
- P. G. Jessop, T. Ikariya and R. Noyori, Chem. Rev., 1995, 95, 259–272 CrossRef CAS.
- G. Dong, Q. M. Phung, S. D. Hallaert, K. Pierloot and U. Ryde, Phys. Chem. Chem. Phys., 2017, 19, 10590–10601 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07139c |
| This journal is © The Royal Society of Chemistry 2019 |