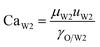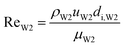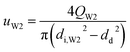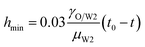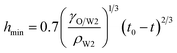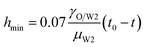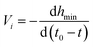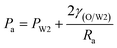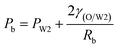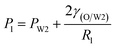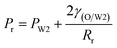DOI:
10.1039/C9RA07141E
(Paper)
RSC Adv., 2019,
9, 41943-41954
Effects of surfactant adsorption on the formation of compound droplets in microfluidic devices
Received
5th September 2019
, Accepted 2nd December 2019
First published on 17th December 2019
Abstract
Driven by the need to prepare monodisperse compound droplets, the formation mechanism of compound droplets was comprehensively investigated. With increasing poly(vinyl alcohol) (PVA) concentration in the W2 phase, the formation mechanism of inner W1 droplet is not affected while the behavior of the O phase in the W2 phase is different. The W1/O compound droplets can form stably in an inner squeezing – outer dripping regime, but the structure of the W1/O compound droplets are affected by the formation time matching between inner W1 droplet and W1/O compound droplets, which influences the stability of the compound droplets. Moreover, the formation process of the W1/O compound droplet is composed of cone recoiling, neck formation, neck developing, neck thinning and neck pinch-off. The formation time of the W1/O compound droplet is mainly determined the neck formation stage. The higher interfacial tension is unfavorable to the neck formation at the initial stages, but it makes the Laplace pressure difference increasing, which promotes the thinning of the neck in the neck pinch-off stage. The results provide more in-depth insights of the effects of surfactants on the formation of compound droplets, benefiting for preparing monodisperse and stable compound droplets.
1. Introduction
With the advantages of protecting important components by encapsulation, polymer shells have found applications such as drug delivery, food additives and bioreactors.1 Especially, polymer shells such as polystyrene (PS), deuterated polystyrene (DPS), and poly(a-methylstyrene) (PAMS) shells have been used for preparing targets for laser-driven inertial confined fusion (ICF), laboratory astrophysics, high field physics and so on.2–4 Generally, these polymer shells are made by the microfluidic technique, in which water-in-oil-in-water (W1/O) compound droplets, consisting of three phases and two interfaces, are formed first and then the solvent in the O phase is removed by evaporation during the solidifying process.5–7 There are stringent specifications on the size of these shells since they contain deuterium and tritium fuels.8–10 Therefore, it is important to precisely control their corresponding compound droplets, the precursor of polymer shells.11,12
Compound droplets are successfully prepared by kinds of microfluidic devices with different structures including cross-flow, co-flow and flow-focusing, but the formation mechanism is not clear enough, unfavorable to precise controllability of their structure and size.13–16 Especially, the formation process is significantly affected by surfactants, which are an important part of the components in the preparation of compound droplets.17,18 Fresh interface between dispersed and continuous phases is formed during the droplet formation, so the adsorption of the surfactant on the interface is important.19 The dynamic interfacial tension depends strongly on the adsorption of the surfactant, affecting the formation process.20,21 Roché et al. showed that the dynamic interfacial tension controlled by the surfactant led to the changes of the neck thinning rate.22 Kovalchuk et al. pointed out that the dynamic interfacial tension during the formation process depended on the adsorption kinetics of the surfactant at the surface of the droplet23–26 and the effect of the surfactant on the transition between flow regimes correlated with the dynamic surface tension. Kamat et al. demonstrated by the simulation and experiment that Marangoni stresses resulting from the nonuniformity of surfactant concentration on the interface led to reduced thread thinning rate and formation of multiple satellites.27
From the literature, it is clearly seen that the processes of both neck thinning and pinch-off have been paid attentions during the formation of single droplet, but the whole formation process of the droplet, especially initial stage of neck formation, is little studied. On the other hand, the surfactants studied in the literature are always surfactants with low molecular weight such as cetyltrimethylammonium bromide (CTAB), and sodium dodecyl sulfate (SDS). In fact, polymers such as partially hydrolyzed poly(vinyl alcohol) (PVA) and poly(acrylic acid) (PAA) are widely used to prepare stable droplets due to its non-toxicity and biodegradability.8,28–30 Moreover, the formation of compound droplets is more complicated than that of single droplet since both the formation processes of inner and outer interfaces in the compound droplets are probably affected by the introduction of surfactants in any phase. However, as far as we know, there are a few reports about the effects of surfactants on compound droplet formation.2 Therefore, it is necessary to investigate the effects of these macromolecule surfactants on the formation of compound droplets.
In the paper, to avoid surfactants adsorbing on both inner and outer interfaces, aqueous solutions with different PVA mass fractions were used as the outer phase (W2) while there were no surfactants in both inner and oil phases. The adsorption of surfactants at oil/water interface on the whole formation process of compound droplets in a coflow microfluidic device was comprehensively investigated, and the effect of the interfacial tension on the formation mechanism of compound droplets were also discussed.
2. Experimental
2.1 Materials
Polystyrene (PS, Mw= 250 kg mol−1, ρs = 1.05 g cm−3, Acros Organics Inc.), and PVA (Mw = 13–23 kg mol−1, 87–89% hydrolysis degree, Sigma-Aldrich Company) were all used as received without further purification. Fluorobenzene (FB) (Shanghai Aladdin Bio-Chem Technology Co., Ltd) was purified by the distillation. Distilled, deionized water was used in the preparation of all aqueous phases.
2.2 Preparation of W1/O compound droplets
As shown in Fig. 1, W1/O compound droplets were prepared by a coflow microfluidic device. The device was composed of a steel needle (di,W1 = 330 μm, dO, W1 = 500 μm), a plastic tube (di,O = D, dO,O = 1588 μm) and a transparent glass tube with 1800 μm inner diameter (di,W2 = 1800 μm), which were used as the inner, middle and outer channels, respectively. The microfluidic device used in the study was a “two-step” device, in which the end of steel needle was located upstream to the end of the plastic tube.31 Pure water and PS/FB solution with 8.2% PS mass fractions were used as the inner phase (W1) and oil phase (O), respectively. Aqueous solutions with different PVA mass fractions (0.002%, 0.04%, 0.1%, 0.5% and 2.0%) were used as the outer phase. The flow rates of the W1, O and W2 phases (QW1, QO and QW2) are 1.5 ml h−1, 3.0 ml h−1 and 500 ml h−1, respectively, which are controlled by three separate syringe pumps (PHD ULTRA™ Advanced Syringe Pumps). Details of the preparation process were described in the ref. 8. The formation of compound droplets was monitored at 1000 fps using a high speed videocamera (Optronis) equipped with a Navitar objective (Fig. 1). Image processing was carried out using Image J free software created by the National Institutes of Health (NIH).
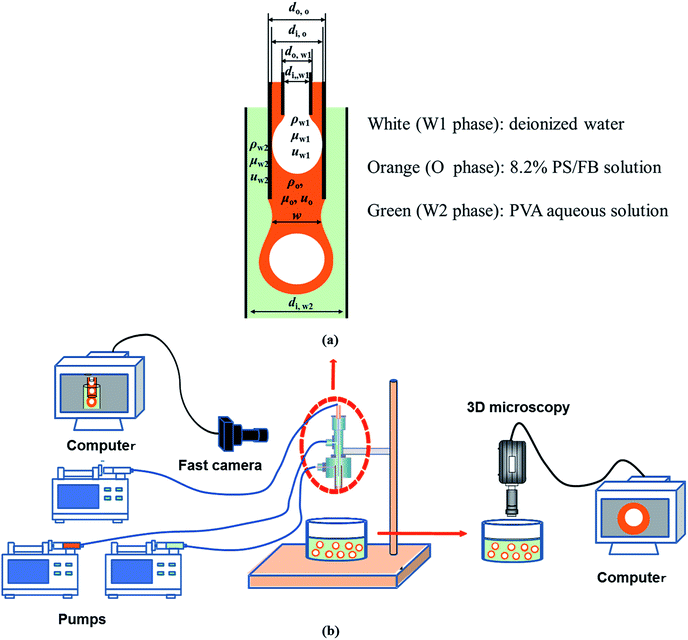 |
| | Fig. 1 Schematic of compound droplet formation in a “two-step” microfluidic device: (a) key parameters during the formation and (b) experimental setup. | |
2.3 Characterization
The densities of the phases were measured precisely by a densitometer (Anton Paar®, DMA 5000) at 25 °C. The densitometer accuracy is 10−6 g cm−3. The viscosities of the phases were measured precisely by a microviscometer (Anton Paar®, Lovis 2000M) at 25 °C. The microviscometer accuracy is 10−3 mPa s. The dynamic interfacial tensions (IFT) were measured by an interfacial tensiometer (Krüss, DSA25) via the pendant drop method.32,33
3. Results and discussion
3.1 Density, viscosity and dynamic interfacial tension
The results of the density and viscosity measurement are listed in Table 1. When the PVA mass fraction increases from 0.002% to 2.0%, the increase of the density is only about 0.004496 g cm−3 while that of the viscosity is 0.781 mPa s. Moreover, it is interesting to note that the viscosity of the O phase is much higher than that of both the W1 and W2 phases, since there are more PS with higher molecular weight in the solution (compared with PVA). Compared with the density and viscosity, PVA concentration shows more significant effect on the dynamic interfacial tension. As shown in Fig. 2, with increasing the PVA mass fraction from 0.002% to 2.0%, the dynamic interfacial tension decreases obviously for a fixed time, which indicates that there are more PVA molecules migrating to the O/W2 interface. Therefore, PVA makes the dynamic interfacial tension decrease sharply by increasing its concentration, but have little effect on the density and viscosity.
Table 1 W1, O and W2 phases and their physical properties at 25 °C
| Phases |
Components |
Density (g cm−3) |
Viscosity (mPa s) |
| W1 |
Distilled water |
0.997053 |
0.887 |
| O |
8.2% PS/FB |
1.024433 |
23.57 |
| W2 |
0.002% PVA |
0.997014 |
0.889 |
| 0.01% PVA |
0.997091 |
0.894 |
| 0.04% PVA |
0.997175 |
0.903 |
| 0.1% PVA |
0.997298 |
0.922 |
| 0.5% PVA |
0.998333 |
1.047 |
| 2.0% PVA |
1.001510 |
1.670 |
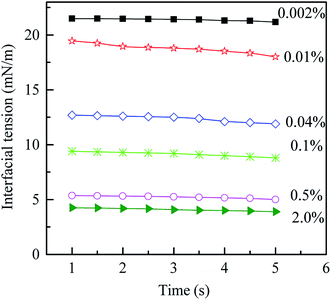 |
| | Fig. 2 Dynamic interfacial tension between O and W2 phases with different PVA mass fractions vs. time at 25 °C. | |
3.2 Formation of W1/O compound droplet in W2 phase with different PVA concentrations
Since the “two-step” microfluidic device is used to produce the W1/O compound droplet, the W1 droplet is firstly formed and flows with the O phase (Fig. 1(a)). Then, the O phase containing the W1 droplet is stripped off by the W2 phase, forming a W1/O compound droplet in the W2 phase. Therefore, the formation of W1/O compound droplet can be divided into two processes including the formation of inner W1 droplet and the formation of the O droplet with inner W1 droplets.
3.2.1 Formation of the W1 droplet in the O phase. For the W2 phases with different PVA concentrations, the formations of the W1 droplet in the O phase are almost the same, as shown in Fig. 3 (t0 is the time at the pinch-off of the filament). When the W1 phase flows out from the W1 tube, it expands and forms a bulb-shaped droplet. With more W1 phase flowing out, the droplet grows to almost occupy the whole space of the O tube, so it deviates from spherical shape to pear-shaped shape, forming a pendent droplet. Then, a cylindrical fluid filament is formed to connect the droplet with the cone of the W2 phase. Finally, the filament breaks up symmetrical, accompanying with the formation of a W1 droplet and a very tiny satellite droplet in the O phase. The “symmetrical rupture process” is also observed by Du et al.34,35 The part of the filament close to the W1 droplet retracts, merging into the W1 droplet, while another part also recoils, merging into the cone. A very tiny satellite droplet is also formed, probably due to large viscosity ratio of the O phase and the W1 phase.34
 |
| | Fig. 3 Snapshots of W1 droplets formation in O phase (762 μm inner diameter of the O tube): (a) formation of neck and (b) pinch-off of neck. | |
From the formation process, it is clearly seen that the W1 droplet is formed in squeezing regime, in which the growing droplet occupy the whole space of the O tube.23 PVA concentrations show no significant effect on the formation mechanism of the W1 droplet, but affect the formation time of W1 droplets, which is defined as the interval time between the break of the filament and that of the next. As shown in Table 2, the formation time increases firstly and then decreases with increasing PVA concentration.
Table 2 Effect of PVA concentration on the formation time of W1 droplets
| Sample |
Formation time of W1 droplets (ms) |
| 0.002% PVA |
822 ± 105 |
| 0.04% PVA |
964 ± 10 |
| 0.1% PVA |
1077 ± 11 |
| 0.5% PVA |
1022 ± 12 |
| 2.0% PVA |
996 ± 15 |
3.2.2 Formation of the O droplet with inner W1 droplets in the W2 phase. Compared with the formation of the W1 droplet, PVA concentrations have more significant effect on the formation of the O droplet. For the W2 phases with 0.002% PVA and 0.04% PVA (Fig. 4), the initial stages of the O phase flowing out from the O tube are almost the same. It becomes wider, almost completely blocking the W2 tube at the end of the O phase. With more O phase flowing out, it adheres to some parts of the W2 tube probably due to that the inner surface of the W2 tube is not completely hydrophilic and smooth. So, the O phase flows slower and the W2 flows faster. The flow rates of the O and W2 phase in their tube calculated from the fluid volumes are 0.002 m s−1 and 0.05 m s−1, respectively. With more O phase entering into the W2 phase, more than half of the W2 tube space is occupied by the O phase, and the velocity difference increases. It has been reported that the Kelvin–Helmholtz (KH) instability probably occurs when the velocity difference is higher than 0.1 m s−1 for liquid–liquid fluids with similar densities.36,37 With the increase of the velocity difference, a wave-like interface between the O and W2 phases appears, indicating that the KH instability occurs. Finally, the head of the O phase narrows, but it is very difficult to obtain W1/O compound droplets in the W2 phase with 0.002% PVA even with increasing the W2 flow rate. For the W2 phase with 0.04% PVA (Fig. 4(b)), a wave trough deepens at the adjacent head, which is far from the end of the O tube, forming a neck region. Then the neck becomes thinner, forming a cylindrical fluid filament. Finally, the filament breaks up symmetrical, forming either a W1/O compound droplet or a O droplet, and a satellite droplet due to the Plateau–Rayleigh (PR) instability (Fig. 4(c)).38
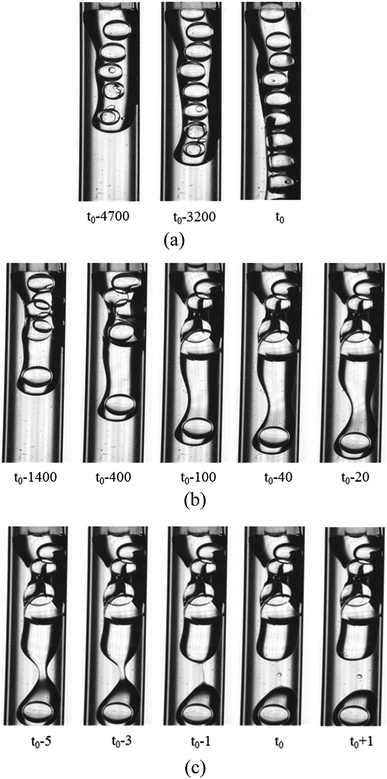 |
| | Fig. 4 Behaviors of the O phase in the W2 phases (1800 μm inner diameter of the W2 tube) with 0.002% PVA and 0.04% PVA: (a) 0.002% PVA, (b) formation of neck in 0.04% PVA and (c) pinch-off of neck in 0.04% PVA. | |
For the W2 phases with 0.1% PVA, 0.5% PVA and 2.0% PVA, the formation process of the O droplet containing inner W1 droplets in W2 phase are similar. They are formed in the dripping regime. As shown in Fig. 5, with the O phase flowing out from the O tube, it becomes a little wider, forming a cylindrical shape. The width of the cylinder is almost the same as the outer diameter of the O tube. Then, waves are formed on the sides of the cylindrical O phase at the adjacent end of the O tube and the W1 droplets move to the head of the O phase. The waves become deeper over time, forming a neck. The neck becomes thinner over time, forming a cylindrical fluid filament connecting a pear-shaped head with inner W1 droplets and a cone near the O tube. Wave-like interfaces appear on the cylinder sides of the filament, leading to two necks formed between the middle of the filament and the cone, and between that and the droplet due to the PR instability. Finally, the two necks break up, forming a satellite droplet in the middle of the filament. The part of the filament close to the W1/O compound droplet retracts, merging into the O shell, while another part also recoils, merging into the cone. It seems that the breakup type of the filament is also symmetrical rupture.
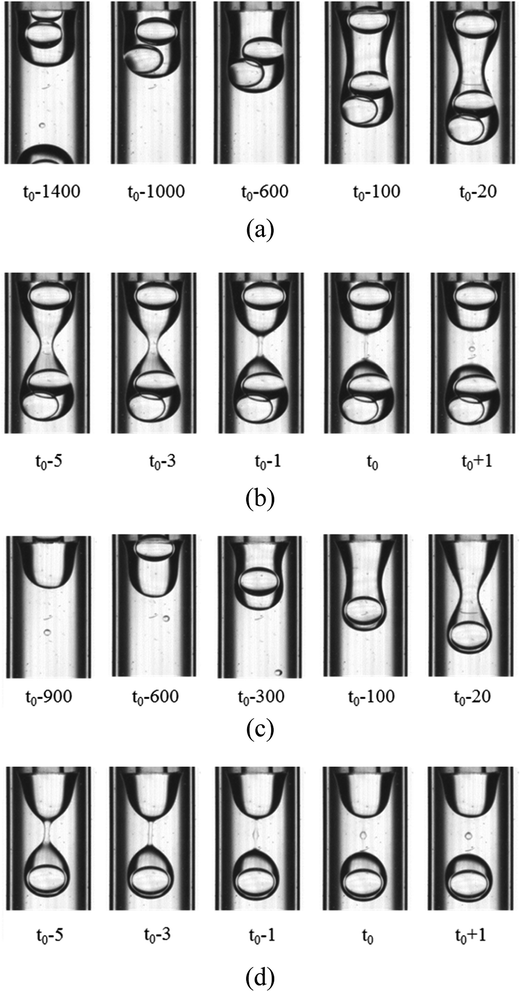 |
| | Fig. 5 Snapshots of compound droplets formation in the W2 phases with 0.1% PVA and 2.0% PVA (1800 μm inner diameter of the W2 tube): (a) formation of neck in 0.1% PVA, (b) pinch-off of neck in 0.1% PVA, (c) formation of neck in 2.0% PVA, and (d) pinch-off of neck in 2.0% PVA. | |
However, the number of the W1 droplets in the O droplet is different though the formation mechanisms of the O droplet in W2 phase with 0.1% PVA, 0.5% PVA and 2.0% PVA are the same. For 0.1% PVA, there is one O droplet containing one W1 droplet inside formed after two O droplets containing two W1 droplets inside formed. For 0.5% PVA, one O droplet containing one W1 droplet inside is formed after one O droplet containing two W1 droplets inside formed. For 2.0% PVA, there is only one W1 droplet in all O droplets. Moreover, the formation time of a W1/O compound droplet containing one W1 droplet decreases with increasing PVA concentration (Table 3). Therefore, the formation period of W1/O compound droplets prepared from 2.0% PVA is shorter than that of W1/O compound droplets prepared from 0.1% PVA and 0.5% PVA. Compared with Tables 2 and 3, it is clearly seen that W1/O compound droplets with only one W1 droplet inside can be obtained when the formation time of W1 droplet is almost the same as that of the O droplet.
Table 3 Effect of PVA concentration on the formation time of compound droplets
| Sample |
Formation time of W1/O compound droplets (ms) |
| Containing one W1 droplet |
Containing two W1 droplets |
Period |
| 0.1% PVA |
2168 ± 69 |
1656 ± 197 |
5736 ± 413 |
| 0.5% PVA |
1564 ± 99 |
1717 ± 129 |
3271 ± 263 |
| 2.0% PVA |
992 ± 16 |
— |
992 ± 16 |
3.3 Formation mechanism of W1/O compound droplets in W2 phases with different PVA concentrations
As mentioned above, PVA concentrations show no significant effect on the formation mechanism of the W1 droplets, but affect their formation time. Since PVA is in the W2 phase, it does not affect the properties of W1 and O phases including the density, viscosity and dynamic interfacial tension. Therefore, most of the forces acting on the W1 phase in the O phase such as the gravity, shear force and interfacial force are not significantly affected by PVA concentrations in the W2 phase. In the squeezing regime, the pressure jump (ΔP) across the droplet is the dominant force for the neck thinning while the interfacial tension resists it.35 The pressure jump can be calculated bywhere Pa and Pb are the pressures above and below the droplet, respectively (Fig. 3(b)). Pb are different for the W2 phases with different PVA concentrations, since it is affected by the behavior of the O phase in the W2 phase. Therefore, the formation time of W1 droplets is affected by PVA concentration in the W2 phases, which leads to different sizes of the W1 droplet.
With increasing PVA concentrations, the behavior of the O phase in the W2 phase are different. To study the transition, the dimensionless numbers including the capillary number (CaW2) and Reynolds number (ReW2) are calculated by eqn (2) and (3), respectively23,39
| |
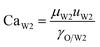 | (2) |
| |
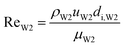 | (3) |
where
ρW2,
μW2 and
uW2 are the density, viscosity and flow velocity of the W2 phase, respectively.
γo/W2 and
di,W2 are the dynamic interfacial tension between the O and W2 phases, and the inner diameter of the W2 tube, respectively. It is difficult to obtain the dynamic interfacial tension during the formation time of W1/O compound droplets. To investigate the effect of the interfacial tension on the formation of W1/O compound droplets, the dynamic interfacial tension measured at
t = 1 s was used to calculate the values of the capillary number. The flow velocity of the W2 phase in the W2 tube is calculated by the following equation.
| |
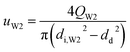 | (4) |
where
QW2 are flow rate of the W2 phase controlled by the syringe pumps.
di,W2, and
dd are the diameter of the W2 tube and the droplet, respectively. From the properties of the W2 phase, compared with the density and viscosity, the dynamic interfacial tension increases more quickly with increasing PVA concentrations (
Table 1). Moreover, the Re
W2 is in the same order of magnitude, while the capillary number increases from 0.002 to 0.02 indicating that the dynamic interfacial tension plays an important role on the transition (
Table 4).
Table 4 Dimensionless number values for the W2 phase
| Samples |
ReW2 (W2) |
CaW2 (W2) |
| 0.002% PVA |
55.1 |
0.002 |
| 0.04% PVA |
54.3 |
0.004 |
| 0.1% PVA |
53.2 |
0.006 |
| 0.5% PVA |
46.9 |
0.015 |
| 2.0% PVA |
29.5 |
0.02 |
As shown in Fig. 6, on the vertical direction, the interfacial force (F2) prevents the cylindric-like liquid from being elongated and thinned, while the shear force (F1) makes the liquid become long and thin. With increasing the dynamic interfacial tension, the interfacial force increases, unfavorable to the neck formation. On the horizontal direction, the Laplace pressures (P) are different due to different radii of the liquid. The Laplace pressure in the neck (P1) is the highest, while the Laplace pressure far from the neck is low. The Laplace pressure difference make the liquid flow from the neck. Therefore, the neck becomes thinning. With increasing the dynamic interfacial tension, the Laplace pressure difference increases, benefiting the thinning of the neck.
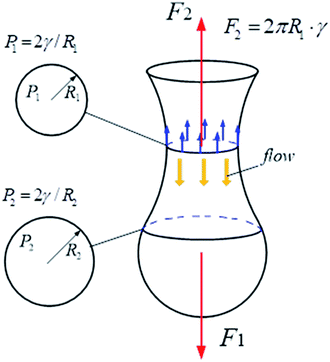 |
| | Fig. 6 Effect of interfacial tension on the vertical and horizontal direction of the compound droplet formation. | |
At the initial of the droplet formation in our study, the radius is large and the interfacial force plays a major role. When the PVA concentration is low (0.002% PVA and 0.01% PVA), the interfacial tension is also high. All make it is difficult to form the neck near the end of the O tube. The O phase flowing out from the O tube becomes wider. With more O phase flowing out, it adheres to some parts of the W2 tube probably due to that the inner surface of the W2 tube is not completely hydrophilic and smooth, which makes that it is more difficult to form the neck near the end of the O tube. If the inner surface of the W2 tube is completely hydrophilic and smooth, the O phase can not adhere to the tube. It is deduced that the O phase would almost occupy the whole space of the W2 tube. A squeezing regime probably occurs when the pressure jump across the droplet is high enough. With decreasing the interfacial tension (0.1% PVA, 0.5% PVA and 2.0% PVA), the interfacial force decreases, which makes that it is easy to form the neck, leading to the occurrence of the dripping regime in our study.
In the dripping regime, W1/O droplets form stably. To investigate the droplet formation quantitatively, the evolution of liquid–liquid interface is analyzed by measuring the neck width (w). As shown in Fig. 7(a), according to the thinning rate of the width, the formation process of the W1/O droplet can be divided five stages including cone recoiling, neck formation, neck developing, neck thinning and neck pinch-off. Both recoiling and neck pinch-off stages are very short, less than 5 ms. The cone firstly recoils due to the pinch-off of former droplet, while the Plateau–Rayleigh instability occurs in the cylindrical fluid filament, making it breaking in the neck pinch-off stage. Compared with those of the neck developing and neck thinning stages, the neck formation process is much slower due to its large radius. Therefore, the formation time of W1/O droplets is mainly determined the neck formation stage. Moreover, the formation time decreases with increasing the PVA concentration due to the decrease of the interfacial tension. The shear force is the dominant factor making the neck becoming narrower in the stage. With the W1 droplet being pushed through the wave trough into the head, the head expands, leading to the increase of the shear force acting on the head, which making the wave trough developing into the neck.
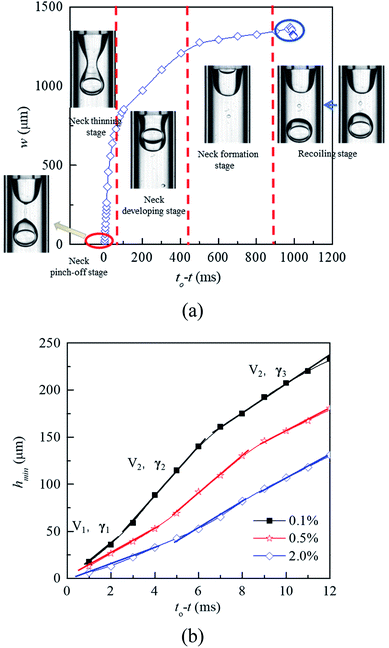 |
| | Fig. 7 Profile of neck width versus the relative time during the formation process of W1/O droplets: (a) formation process, and (b) short time kinetic of the neck thinning in 0.1% PVA, 0.5% PVA and 2.0% PVA. | |
In the vicinity of the pinch-off stage, whether in 0.1% PVA, 0.5% PVA or 2.0% PVA, it seems that the neck thinning processes are almost the same. It has been shown to proceed in three different regimes (Fig. 7(b)), which is similar to that of a single droplet.22,40 For Newtonian fluids, the scaling theories of pinch-off have been developed to describe the dynamics of the pinch-off process. The visco-inertial (VI) regime predicted by Eggers describes the dynamics of the vicinity of the pinch-off singularity, in which the minimum neck radius (hmin) decreases linearly with the time (t0 − t).20,41,42
| |
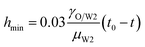 | (5) |
The inertial (I) regime predicted by Keller is used to explain the neck evolution close to the pinch-off when the viscous force can be neglected, in which the hmin is the following.20,43,44
| |
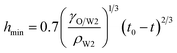 | (6) |
When viscous effects are strong, the viscous (V) regime described by Papageorgiou is given as45
| |
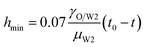 | (7) |
Here, it seems that the pinch-off process undergoes the transition from the V regime to VI regime, and two different slopes appears in the V regime due to the change of the interfacial tension. Eqn (5) and (7) are used to correlate the minimum neck radius with the time in each regime and the effective interfacial tensions are calculated (Table 5). With the neck thinning, the interfacial tension increases due to the depletion of the surfactant.22,46 Moreover, the trend shows more significant in low PVA concentration.
Table 5 Effective interfacial tension in the vicinity of the pinch-off stage
| Sample |
γ1 (mN m−1) |
γ2 (mN m−1) |
γ3 (mN m−1) |
| 0.1% PVA |
14.5 |
9.3 |
5.5 |
| 0.5% PVA |
10.3 |
6.8 |
4.5 |
| 2.0% PVA |
7.0 |
5.0 |
4.2 |
The neck thinning rates (V1, V2 and V3) in the regimes are also calculated by the slope of their linear fits, and the results are listed in Table 6.
| |
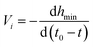 | (8) |
where
t0 is the times at the pinch-off of the neck and
t is the time at the image taken before the pinch-off. For the same PVA concentration, with approaching the pinch-off, the neck thinning rate increases firstly, and then decreases when the neck evolves into a cylindrical filament, which is combination role of the effective interfacial tension and Marangoni stress. The interfacial tension increases with the neck thinning, benefiting the acceleration of the pinch-off, so the neck thinning rate increases firstly. On the other hand, the nonuniform surfactant distribution along the surface of the filament results in Marangoni stress. It has been proved that Marangoni stress acting near the pinch point plays more important role, which not only reduces the thinning rate, but also leads to formation of satellites.
27 Moreover, for the same regime, the pinch-off process is delayed with increasing PVA concentrations (
Fig. 7(b) and
Table 6), probably due to the combination role of the effective interfacial tension and Marangoni stress.
Table 6 Neck thinning rate in the vicinity of the pinch-off stage
| Sample |
V1 (cm s−1) |
V2 (cm s−1) |
V3 (cm s−1) |
| 0.1% PVA |
1.8 |
2.6 |
1.5 |
| 0.5% PVA |
1.3 |
2.0 |
1.3 |
| 2.0% PVA |
0.9 |
1.5 |
1.2 |
3.4 Unstable behaviors of W1 droplets in microfluidic device
Two types of unstable behaviors of the W1 droplets are observed in the W2 tube (Fig. 8). There are more and more W1 droplets in the O phase since it is difficult to form W1/O compound droplets in the W2 phases with 0.002% PVA and 0.04% PVA. There are some W1 droplets pushed by other droplets close to the W1/O interface. With the role of the shear force of the W2 phase and the Laplace pressure of the interface, the interface becomes thinner and thinner. Finally, the interface breaks up and the W1 droplet merges into the W2 phase (Fig. 8(a)). Moreover, the coalescence also occurs to form a bigger W1 droplets when two W1 droplets are close enough whereby the van der Waals forces is strong enough to make the dissepiment film rupture, since there are no surfactant in both W1 and O phases (Fig. 8(b)).47 Therefore, both coalescence and rupture can happen in the O phase. For the W2 phases with 0.1% PVA, 0.5% PVA and 2.0% PVA, W1/O compound droplets are formed stably and W1 droplets does not accumulate in the O phase. They do not push each other and there is a distance between W1 droplets in the O phase, so the W1 droplets are stable in the channel.
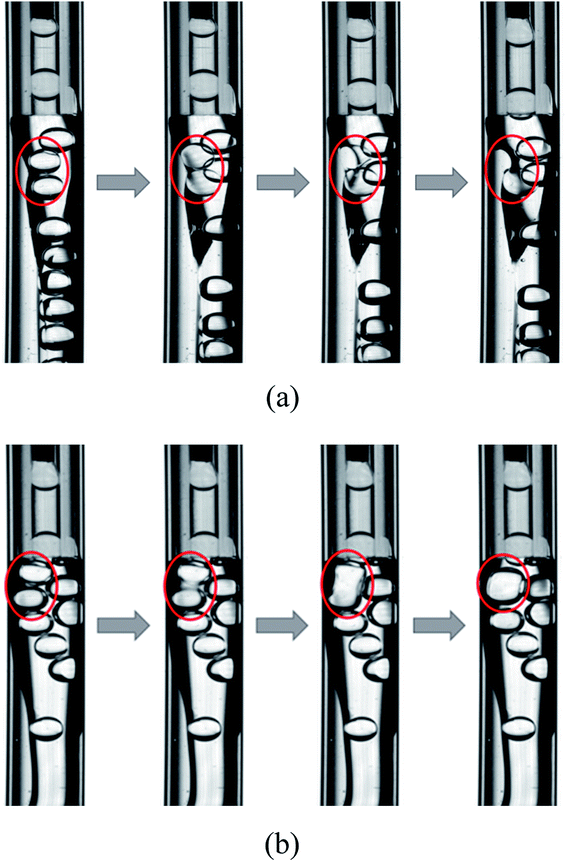 |
| | Fig. 8 Unstable behaviors of W1 droplet in microfluidic device: (a) rupture and (b) coalescence. | |
3.5 Unstable behaviors of collected W/O compound droplets
Fig. 9 shows the morphologies of collected droplets prepared from 0.1% PVA and 2.0% PVA. Though only W/O compound droplets with one W1 droplet and W/O compound droplets with two W1 droplets are formed in the microfluidic device, there are four kinds of collected droplets in 0.1% PVA including W/O compound droplets with either a W1 droplet inside, a larger W1 droplet inside, two W1 droplets inside or without inner droplet, due to the structure evolution of W1/O compound droplets containing two W1 droplets (Fig. 10). As shown in Fig. 10(a), the W1/O compound droplet containing two W1 droplets is ellipsoid and the radii of the arcs at the end of longer axis of the W1/O compound droplet (Rl and Rr) are usually shorter than those at the end of the shorter axis (Ra and Rb). The corresponding pressures (Pa, Pb, Pl and Pr) in the O phase are calculated by the following equations.2,48| |
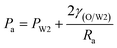 | (9) |
| |
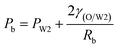 | (10) |
| |
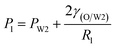 | (11) |
| |
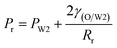 | (12) |
 |
| | Fig. 9 Effects of PVA concentrations on the structure of the W1/O compound droplets: (a) 0.1% PVA, and (b) 2.0% PVA. | |
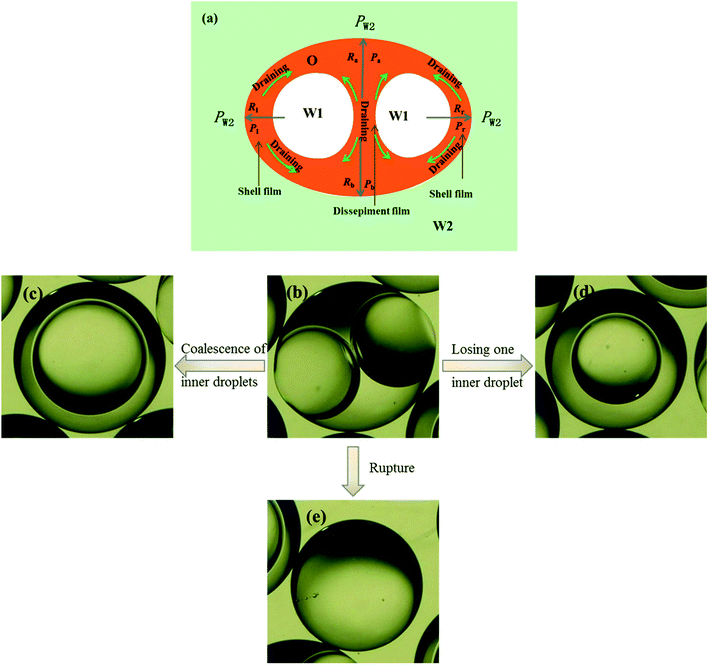 |
| | Fig. 10 Structure evolutions of W1/O compound droplets containing two W1 droplets: (a) Schematic of the drainage, (b) a W1/O compound droplet containing two W1 droplets, (c) a W1/O compound droplet containing a large W1 droplets from the coalescence, (d) a W1/O compound droplet containing a W1 droplets and (e) a single droplet. | |
Therefore, the pressure at the end of the longer axis (Pl and Pr) is higher than those at the end of the shorter axis ((Pa and Pb), making the O phase moving from the former to the latter. The shell films at the end of the longer axis becomes thinner and thinner. When the Pl and Pr increases to an extent that the interfacial film cannot resists it, the interfacial film at the highest-pressure ruptures, which leads to the transfer of the W1 droplets to the W2 phase, making the droplets losing either one W1 droplet or all W1 droplets to form droplets with a W1 droplet inside or O single droplets (Fig. 10(d) and (e)).49 Moreover, the Laplace pressure (2γ/R) tends to make the compound droplets become spherical, which would push the W1 droplets move close, making the dissepiment film become thinner.49 The van der Waals forces become significant when the W1 droplets approach close enough, which leads to local rupture of the thin film, forming a W1/O compound droplet with a larger W1 droplet inside (Fig. 10(c)).47 From Fig. 9(b), it is clearly seen that the structures of collected W1/O compound droplets from 2.0% PVA are the same and they are stable, since each compound droplet contains only one W1 droplet inside and there are more surfactants at the O/W2 interface. Therefore, to obtain the compound droplets with good monodispersity, it is important to prepare the compound droplet with one W1 droplet inside.
4. Conclusions
Monodisperse and stable compound droplets were successfully prepared by adjusting PVA concentrations in the W2 phase and the adsorption of surfactants at oil/water interface on the formation of compound droplets was comprehensively investigated by measuring the dynamic interfacial tension and analyzing the W1/O and O/W2 interface evolution. Some useful insights are obtained. (I) With increasing PVA concentration in W2 phase, the formation mechanism of inner W1 droplet does not be affected but the formation time of W1 droplets does, since the pressures below the W1 droplet are affected by the behavior of the O phase in the W2 phase. (II) W1/O compound droplets can form stably in inner squeezing – outer dripping regime, but the structure of the W1/O compound droplets are affected by the formation time matching between inner W1 droplet and compound droplet. (III) The dynamic interfacial tension plays a different effect on different stages of the W1/O compound droplet formation. The higher interfacial tension is unfavorable to the neck formation at the initial stages, but it makes the Laplace pressure difference increasing, which promotes the thinning of the neck in the neck pinch-off stage. (IV) The formation time of W1/O droplets decreases, but the pinch-off process is delayed with increasing PVA concentration in W2 phase, due to the decrease of the interfacial tension and the increase of the Marangoni stress. (V) Both coalescence and rupture occur in the microfluidic device when the O phase adheres to some parts of the W2 tube, due to the accumulation of W1 droplets and no surfactant in both W1 and O phases. Similar phenomenon also takes place in collected W1/O compound droplets with two inner W1 droplets, leading to four different droplets either with a smaller W1 droplet inside, a larger W1 droplet inside, two inner W1 droplets or without inner droplet. Therefore, preparing the compound droplet with one W1 droplet inside benefits improving the monodispersity and stability.
Conflicts of interest
There is no conflicts of interest.
Acknowledgements
We gratefully acknowledge the funding from the National Natural Science Foundation of China (51703212) and the Open Project of State Key Laboratory of Environment-friendly Energy Materials (No. 2018kfhg03).
References
- J. Zhang, R. J. Coulston, S. T. Jones, J. Geng, O. A. Scherman and C. Abell, Science, 2012, 335, 690–694 CrossRef CAS PubMed.
- L. Mei Fang, Z. Yue Qing, L. Jie, C. Su Fen, L. Yi Yang, L. Jing, L. Bo and Z. Zhan Wen, Nucl. Fusion, 2017, 57, 016018 CrossRef.
- K. Du, M. F. Liu, T. Wang, X. S. He, Z. W. Wang and J. Zhang, Matter Radiat. Extremes, 2018, 3, 135–144 CrossRef.
- M. Liu, Y. Liu, J. Li, S. Chen, J. Li, L. Su, X. b. Qi, B. Li and Z. Zhang, Colloids Surf., A, 2015, 484, 463–470 CrossRef CAS.
- M. Takagi, T. Norimatsu, T. Yamanaka and S. Nakai, J. Vac. Sci. Technol., A, 1991, 9, 2145–2148 CrossRef CAS.
- P. R. Paguio, S. P. Paguio, C. A. Frederick, A. Nikroo and O. Acenas, Fusion Sci. Technol., 2006, 49, 743–749 CrossRef.
- K. Nagai, H. Yang, T. Norimatsu, H. Azechi, F. Belkada, Y. Fujimoto, T. Fujimura, K. Fujioka, S. Fujioka and H. Homma, Nucl. Fusion, 2009, 49, 095028 CrossRef.
- M. F. Liu, S. F. Chen, X. B. Qi, B. Li, R. T. Shi, Y. Y. Liu, Y. P. Chen and Z. W. Zhang, Chem. Eng. J., 2014, 241, 466–476 CrossRef CAS.
- M. F. Liu, Y. W. Huang, S. F. Chen, D. W. Pan, M. Chen, Q. M. Chu, Y. Y. Liu, Q. Yin and Z. W. Zhang, Matter Radiat. Extremes, 2019, 4, 018401 CrossRef.
- M. F. Liu, L. Su, J. Li, S. F. Chen, Y. Y. Liu, J. Li, B. Li, Y. P. Chen and Z. W. Zhang, Matter Radiat. Extremes, 2016, 1, 213–223 CrossRef.
- G. Randall and B. Blue, Bull. Am. Phys. Soc., 2012, 57, 17 Search PubMed.
- X. Qu and Y. Wang, Phys. Fluids, 2012, 24, 123302–123321 CrossRef.
- A. S. Utada, E. Lorenceau, D. R. Link, P. D. Kaplan, H. A. Stone and D. A. Weitz, Science, 2005, 308, 537 CrossRef CAS PubMed.
- J. W. Kim, A. S. Utada, A. Fernández-Nieves, Z. Hu and D. A. Weitz, Angew. Chem., 2007, 119, 1851–1854 CrossRef.
- A. R. Abate, J. Thiele and D. A. Weitz, Lab Chip, 2011, 11, 253–258 RSC.
- L. R. Shang, Y. Cheng and Y. J. Zhao, Chem. Rev., 2017, 117, 7964–8040 CrossRef CAS PubMed.
- D. Guzey and D. J. McClements, Adv. Colloid Interface Sci., 2006, 128–130, 227–248 CrossRef CAS PubMed.
- T. Tadros, Adv. Colloid Interface Sci., 2015, 222, 692–708 CrossRef CAS PubMed.
- Y. Chen, J.-H. Xu and G.-S. Luo, Chem. Eng. Sci., 2015, 138, 655–662 CrossRef CAS.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- X. Zhang and O. A. Basaran, Phys. Fluids, 1995, 7, 1184–1203 CrossRef CAS.
- M. Roché, M. Aytouna, D. Bonn and H. Kellay, Phys. Rev. Lett., 2009, 103, 264501 CrossRef PubMed.
- N. M. Kovalchuk, E. Roumpea, E. Nowak, M. Chinaud, P. Angeli and M. J. H. Simmons, Chem. Eng. Sci., 2018, 176, 139–152 CrossRef CAS.
- N. M. Kovalchuk and M. J. H. Simmons, Colloids Surf., A, 2018, 545, 1–7 CrossRef CAS.
- N. M. Kovalchuk, H. Jenkinson, R. Miller and M. J. H. Simmons, J. Colloid Interface Sci., 2018, 516, 182–191 CrossRef CAS PubMed.
- N. M. Kovalchuk, E. Nowak and M. J. H. Simmons, Langmuir, 2016, 32, 5069–5077 CrossRef CAS PubMed.
- P. M. Kamat, B. W. Wagoner, S. S. Thete and O. A. Basaran, Phys. Rev. Fluids, 2018, 3, 043602 CrossRef.
- C. X. Zhao, D. Chen, Y. Hui, D. A. Weitz and A. P. J. Middelberg, ChemPhysChem, 2016, 17, 1553–1556 CrossRef CAS PubMed.
- V. Tirtaatmadja, G. H. McKinley and J. J. Cooper-White, Phys. Fluids, 2006, 18, 043101 CrossRef.
- G. T. Vladisavljević, E. E. Ekanem, Z. Zhang, N. Khalid, I. Kobayashi and M. Nakajima, Chem. Eng. J., 2018, 333, 380–391 CrossRef.
- T. Shao, X. L. Feng, Y. Jin and Y. Cheng, Chem. Eng. Sci., 2013, 104, 55–63 CrossRef CAS.
- B. H. Song and J. Springer, J. Colloid Interface Sci., 1996, 184, 64–76 CAS.
- B. Song and J. Springer, J. Colloid Interface Sci., 1996, 184, 77–91 CAS.
- P. Doshi, I. Cohen, W. W. Zhang, M. Siegel, P. Howell, O. A. Basaran and S. R. Nagel, Science, 2003, 302, 1185–1188 CrossRef CAS PubMed.
- W. Du, T. T. Fu, C. Y. Zhu, Y. G. Ma and H. Z. Li, AIChE J., 2016, 62, 325–337 CrossRef CAS.
- Q. Peng, H. Shao, X. Hu and Y. Zhang, Macromol. Mater. Eng., 2017, 302, 1700102 CrossRef.
- X. Y. Hu and T. Cubaud, Phys. Rev. Lett., 2018, 121, 044502 CrossRef PubMed.
- S. D. Geschiere, I. Ziemecka, V. van Steijn, G. J. M. Koper, J. H. v. Esch and M. T. Kreutzer, Biomicrofluidics, 2012, 6, 022007 CrossRef PubMed.
- D. W. Pan, M. F. Liu, F. Li, Q. Chen, X. D. Liu, Y. Y. Liu, Z. W. Zhang, W. X. Huang and B. Li, Chem. Eng. Sci., 2018, 176, 254–263 CrossRef CAS.
- J. R. Castrejón-Pita, A. A. Castrejón-Pita, S. S. Thete, K. Sambath, I. M. Hutchings, J. Hinch, J. R. Lister and O. A. Basaran, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4582–4587 CrossRef PubMed.
- J. Eggers, Phys. Rev. Lett., 1993, 71, 3458–3460 CrossRef PubMed.
- J. Eggers, Rev. Mod. Phys., 1997, 69, 865–930 CrossRef CAS.
- J. B. Keller and M. J. Miksis, SIAM J. Appl. Math., 1983, 43, 268–277 CrossRef.
- Y. Li and J. E. Sprittles, J. Fluid Mech., 2016, 797, 29–59 CrossRef CAS.
- D. T. Papageorgiou, Phys. Fluids, 1995, 7, 1529–1544 CrossRef CAS.
- N. M. Kovalchuk, E. Nowak and M. J. H. Simmons, Colloids Surf., A, 2017, 521, 193–203 CrossRef CAS.
- K. Sambath, V. Garg, S. S. Thete, H. J. Subramani and O. A. Basaran, J. Fluid Mech., 2019, 876, 449–480 CrossRef.
- C.-H. Choi, J.-M. Jeong, S.-M. Kang, C.-S. Lee and J. Lee, Adv. Mater., 2012, 24, 5078–5082 CrossRef CAS PubMed.
- L. K. Hou, Y. K. Ren, Y. K. Jia, X. M. Chen, X. K. Deng, Z. Tang, Q. M. Hu, Y. Tao and H. Y. Jiang, Microfluid. Nanofluid., 2017, 21, 60 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Jing Lia,
Jie Lia,
Yawen Huangc and
Qiang Yin
a,
Jing Lia,
Jie Lia,
Yawen Huangc and
Qiang Yin *a
*a