Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of dihydrogen bonding on lattice energies and sublimation enthalpies of crystalline [H2GaNH2]3, [H2BNH2]3 and [H2GeCH2]3†
Wayne L. Gladfelter *a and
Christopher J. Cramer
*a and
Christopher J. Cramer b
b
aDepartment of Chemistry, University of Minnesota, 207 Pleasant St., SE, Minneapolis, MN 55455, USA. E-mail: wlg@umn.edu
bDepartment of Chemistry, Chemical Theory Center, Minnesota Supercomputing Institute, University of Minnesota, 207 Pleasant St., SE, Minneapolis, MN 55455, USA
First published on 17th September 2019
Abstract
The lattice energies of [H2GaNH2]3, [H2BNH2]3 and [H2GeCH2]3 in their experimentally determined space groups, P21/m, Pmn21 and Pbcm, respectively, were calculated using density functional methods for periodic structures with the ab initio periodic code CRYSTAL17. Using the basis set pob-TZVP for all calculations, B3LYP including Grimme's D3 dispersion correction was found to reproduce experimental bond distances and angles most accurately. CRYSTAL17 was also used to optimize geometries and calculate energies of the molecular structures in the gas phase. While the chair conformation of the six-membered rings is found in all of the crystals, only [H2GeCH2]3 retains this as the preferred conformation in the gas phase. By contrast, a twist-boat conformation is preferred for both [H2GaNH2]3 and [H2BNH2]3 in the gas phase, and thus a correction for this change in conformation must be included in corresponding sublimation enthalpy calculations. In addition to the D3 dispersion correction, all lattice energies included a correction for basis set superposition error. The lattice energies for [H2GaNH2]3, [H2BNH2]3 and [H2GeCH2]3 were 153.5, 120.8 and 84.9 kJ mol−1, respectively. These values were used to calculate the sublimation enthalpies, which exhibited good agreement for the single case where an experimental measurement is available, namely [H2BNH2]3 (exp ΔHsub(298), 119 ± 12 kJ mol−1; calcd, 119.4 kJ mol−1). The energetic impact of the crystal structure was assessed by minimizing the structures of each molecule in each of the three space groups spanned by them experimentally and calculating their respective lattice energies. In every case, the experimentally observed space group was the one computed to be the most stable.
Introduction
Volatility is a necessary property for molecules to function as precursors in chemical vapor deposition and related processes. In the case involving solid precursors, the heat of sublimation is useful for predicting the equilibrium gas-phase concentration of a precursor. For molecular solids, lattice energy, the energy per molecule required to separate the molecules to gas-phase species, is the major contributor to the value of
is useful for predicting the equilibrium gas-phase concentration of a precursor. For molecular solids, lattice energy, the energy per molecule required to separate the molecules to gas-phase species, is the major contributor to the value of 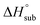 , and there has been much effort focused on using computational methods to predict
, and there has been much effort focused on using computational methods to predict 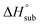 .1–10
.1–10
Lattice energy depends on the strength of intermolecular bonds present in the crystalline phase and there has been great interest in structures exhibiting dihydrogen bonds. Ammonia–borane and related compounds, including [H2BNH2]3, exhibit intermolecular dihydrogen bonds and have been the focus of study due to their potential application in hydrogen storage systems.11–13 Numerous other main group metal compounds with hydrido ligands have been found to exhibit short intra- or intermolecular contacts with protic hydrogens.1,11,14–22 Dihydrogen bonds can also be important in the reactivity of the compounds.11–13,16,17 Structural studies of both cyclotrigallazane, [H2GaNH2]3,16 and cyclotriborazane, [H2BNH2]3,22 have revealed short intermolecular contacts between the hydridic hydrogens bound to the gallium or boron and the protic hydrogens bound to the nitrogens. A previous computational study of the gas phase dimers of [H2BNH2]3 and of [H2GaNH2]3 connected via dihydrogen bonds suggested a H⋯H bond energy of 13 kJ mol−1.16
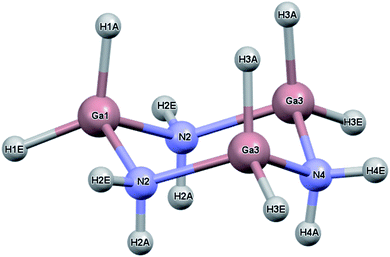
While the previous study modeled the dihydrogen bond strength computationally based on the difference in energy between gas phase monomers and dimers, the current study includes all intermolecular interactions and reports heats of sublimation that in one case, [H2BNH2]3, can be compared to an experimental value.23 The current study expands on earlier work by calculating the lattice energy of crystalline [H2BNH2]3, [H2GaNH2]3 and [H2GeCH2]3. In the solid state, each of these molecules exist as a six-membered ring in a chair conformation. For convenience, the atomic labelling scheme was unified for all three molecules and is shown in Fig. 1 using [H2GaNH2]3 as an example. In their respective space groups, atoms 1 and 4 and their attached hydrogens of all three compounds reside on a crystallographic mirror plane. In this study, the lattice energy of each of the compounds in their native (experimentally determined) space group as well as in the space groups native to the other compounds was calculated. In each case the native space group was found to have the largest lattice energy, illustrating the manner in which the varying strengths of different intermolecular interactions can influence preferred packing arrangements.
Computational methods
For calculations of crystalline [H2BNH2]3 (ref. 22) and [H2GeCH2]3 (ref. 24) the experimental crystal parameters and atomic coordinates obtained from single crystal X-ray diffraction results were used as the starting point. For [H2GaNH2]3 the crystal parameters and atomic coordinates resulting from Rietveld refinement of the neutron powder diffraction of the corresponding perdeutero compound were used.16 All calculations were made using the CRYSTAL17 code.25 The pob-TZVP basis set26 was used in all DFT calculations, and a shrinking factor of 4 was used to generate a grid of k points in reciprocal space. Four density functionals, B3LYP, PBE, PBE0 and M06-2x, were evaluated by comparing their results to the experimental structure of [H2GaNH2]3. For calculations using B3LYP, PBE and PBE0, Grimme's D3 dispersion correction,27–29 including Becke–Johnson damping,30 was employed by use of the keyword DFT-D3. Table 1 shows that the B3LYP and PBE functionals most closely reproduced the experimental results. B3LYP, which more closely reproduced the molecular structure, was chosen for all remaining calculations. Using the keyword MOLEBSSE invoked the counterpoise method to determine the basis set superposition error (BSSE).| Method | ||||||
|---|---|---|---|---|---|---|
| XRD (EXP) | ND (EXP) | B3LYP | M06-2X | PBE | PBE0 | |
| a Based on the formula [H2GaNH2]3. | ||||||
| Temp. (K) | 106 | 298 | 0 | 0 | 0 | 0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Lattice parameters | ||||||
| a (Å) | 5.7615 | 5.7893 | 5.6471 | 5.6861 | 5.6607 | 5.6572 |
| b (Å) | 8.5079 | 8.5635 | 8.3703 | 8.3289 | 8.4648 | 8.3929 |
| c (Å) | 8.0848 | 8.1617 | 7.8564 | 7.7462 | 7.8960 | 7.8331 |
| β (°) | 110.843 | 111.038 | 110.347 | 110.095 | 110.846 | 110.987 |
| Volume (Å3) | 370.37 | 377.66 | 348.18 | 344.53 | 353.58 | 347.25 |
| Density (g cm−3) | 2.36 | 2.31a | 2.49 | 2.52 | 2.45 | 2.50 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Average absolute errors | ||||||
| Cell axis dimensions (Å) | 0.214 | 0.251 | 0.164 | 0.210 | ||
| Bond lengths (Å) | 0.026 | 0.037 | 0.087 | 0.115 | ||
| Bond angles (°) | 4.383 | 4.689 | 5.446 | 5.646 | ||
Determination of the lattice energies required calculation of the energies of the isolated molecules in the chair conformation observed in the crystal structures. These calculations also used B3LYP and the same basis set used for the solid state calculations. For [H2GeCH2]3 the chair conformation was preferred in the gas phase, however, the twist-boat conformation was more stable for both [H2GaNH2]3 and [H2BNH2]3. The energy associated with this conformational change was included in the determination of the sublimation enthalpy. Vibrational frequency calculations were performed on both the gas phase and solid state structures in their native space groups using the keyword FREQCALC. From these calculations, zero point vibrational energies (ZPVE) and vibrational contributions to the sublimation enthalpy of each species at 298 K were determined.
Analysis of the Hirshfeld surfaces for each of the crystals used CrystalExplorer17.31,32
Results and discussion
As reported previously the crystal and molecular structures of [H2GaNH2]3 and [D2GaND2]3 were solved by single crystal X-ray diffraction and Rietveld refinement of the powder neutron diffraction, respectively.16 For two reasons, the neutron diffraction results for [D2GaND2]3 were chosen as the source for comparison with the computational results. First, bond distances between heavy atoms and hydrogen determined using X-ray methods are known to be the shortened relative to those obtained using neutron methods. Because the calculated structures will report distances between nuclei positions, results from the neutron diffraction were considered more appropriate. Second, the twinning present in the single crystals affected the accuracy of the distances and angles in [H2GaNH2]3. Another difference between the two structural studies is the data collection temperature; 106 K for the X-ray diffraction experiment and 298 K for the neutron diffraction one. This led to a unit cell volume expansion of 1.97% for the higher temperature structure. As shown in Table 1, the calculated unit cell volumes at 0 K were 4–6% smaller regardless of the density functional used. At least part of this contraction can be assigned to the effect of temperature. In addition, part of the underestimation of the computed volumes could be ascribed to BSSE due to the finite basis set used for the calculations.33The choice of density functional used for the calculations was based on how well it reproduced the experimental neutron diffraction results. One functional (PBE) and three hybrid functionals (PBE0, B3LYP and M06-2X) were tested using the same basis set (pob-TZVP). For calculations using the PBE, B3LYP and PBE0 functionals, Grimme's D3 dispersion correction was applied. In all calculations, both the atomic positional and unit cell parameters were allowed to refine to convergence within the chosen space group. Although the cell parameters (a, b, c and β for the native space P21/m of [D2GaND2]3) were reproduced best using the PBE-D3 functional, B3LYP-D3 led to the smallest differences in bond lengths and angles of the molecular unit. The latter was chosen for all subsequent calculations. For purposes of comparison to the computational results, the density reported in Tables 1 and 2 for [D2GaND2]3 was calculated using the neutron diffraction cell volume for the protio formula. Tables 3 and 4 list the experimental and calculated metrical parameters for [H2GeCH2]3 and [H2BNH2]3, respectively.
| Method | |||||
|---|---|---|---|---|---|
| XRD (EXP) | ND (EXP) | B3LYP | B3LYP | B3LYP | |
| a Based on the formula [H2GaNH2]3. | |||||
| Temp. (K) | 106 | 298 | 0 | 0 | 0 |
| Crystal system | Monoclinic | Monoclinic | Monoclinic | Orthorhombic | Orthorhombic |
| Space group | P21/m | P21/m | P21/m | Pmn21 | Pbcm |
| Z | 2 | 2 | 2 | 2 | 4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Lattice parameters | |||||
| a (Å) | 5.7615 | 5.7893 | 5.6471 | 8.4203 | 4.7423 |
| b (Å) | 8.5079 | 8.5635 | 8.3703 | 7.4080 | 13.7297 |
| c (Å) | 8.0848 | 8.1617 | 7.8564 | 5.6075 | 11.7629 |
| β (°) | 110.843 | 111.038 | 110.347 | ||
| Volume (Å3) | 370.37 | 377.66 | 348.18 | 349.78 | 765.89 |
| Density (g cm−3) | 2.36 | 2.31a | 2.49 | 2.48 | 2.26 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Average bond distances (Å) | |||||
| Ga–N | 1.978 | 1.976 | 1.995 | 1.995 | 1.993 |
| Ga–HA | 1.577 | 1.568 | 1.567 | 1.575 | |
| Ga–HE | 1.537 | 1.570 | 1.571 | 1.562 | |
| N–HA | 1.046 | 1.019 | 1.019 | 1.019 | |
| N–HE | 1.026 | 1.018 | 1.018 | 1.018 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Close H–H nonbonded contacts (Å) | |||||
| H2A–H3A | 1.972 | 1.964 | 1.914 | 2.265 | |
| H2A–H1A | 2.082 | ||||
| H1E–H4A | 2.025 | ||||
| Method | ||||
|---|---|---|---|---|
| XRD (EXP) | B3LYP | B3LYP | B3LYP | |
| Temp. (K) | 213 | 0 | 0 | 0 |
| Crystal system | Orthorhombic | Orthorhombic | Monoclinic | Orthorhombic |
| Space group | Pmn21 | Pmn21 | P21/m | Pbcm |
| Z | 2 | 2 | 2 | 4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Lattice parameters | ||||
| a (Å) | 8.663 | 8.431 | 5.847 | 5.068 |
| b (Å) | 7.783 | 7.365 | 8.336 | 14.019 |
| c (Å) | 6.124 | 5.836 | 7.833 | 10.730 |
| β (°) | 110.49 | |||
| Volume (Å3) | 412.91 | 362.39 | 357.64 | 762.32 |
| Density (g cm−3) | 2.14 | 2.47 | 2.51 | 2.35 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Average bond distances (Å) | ||||
| Ge–C | 1.951 | 1.956 | 1.957 | 1.957 |
| Ge–HA | 1.572 | 1.531 | 1.536 | 1.537 |
| Ge–HE | 1.548 | 1.536 | 1.532 | 1.532 |
| C–HA | 1.107 | 1.088 | 1.088 | 1.089 |
| C–HE | 0.972 | 1.088 | 1.087 | 1.087 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Close H–H nonbonded contacts (Å) | ||||
| H2A–H3A | 2.200 | 2.101 | 2.143 | |
| H2A–H1A | 2.186 | |||
| Method | ||||
|---|---|---|---|---|
| XRD | B3LYP | B3LYP | B3LYP | |
| Temp. (K) | 180 | 0 | 0 | 0 |
| Crystal system | Orthorhombic | Orthorhombic | Monoclinic | Orthorhombic |
| Space group | Pbcm | Pbcm | P21/m | Pmn21 |
| Z | 4 | 4 | 2 | 2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Lattice parameters | ||||
| a (Å) | 4.383 | 4.248 | 5.004 | 7.358 |
| b (Å) | 12.193 | 11.914 | 7.343 | 6.635 |
| c (Å) | 11.180 | 10.917 | 7.225 | 5.025 |
| β (°) | 112.39 | |||
| Volume (cm3) | 597.50 | 552.53 | 245.48 | 245.31 |
| Density (g cm−3) | 0.96 | 1.05 | 1.18 | 1.18 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Average bond distances (Å) | ||||
| B–N | 1.574 | 1.576 | 1.578 | 1.578 |
| B–HA | 1.133 | 1.208 | 1.201 | 1.203 |
| B–HE | 1.168 | 1.206 | 1.207 | 1.205 |
| N–HA | 0.863 | 1.020 | 1.021 | 1.021 |
| N–HE | 0.895 | 1.020 | 1.019 | 1.019 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Close H–H nonbonded contacts (Å) | ||||
| H2A–H3A | 1.882 | 1.912 | ||
| H4E–H1E | 2.275 | 2.022 | ||
| H4E–H1A | 2.217 | 1.984 | ||
| H2E–H3A | 2.259 | 2.009 | ||
| H2E–H3E | 2.351 | 2.173 | ||
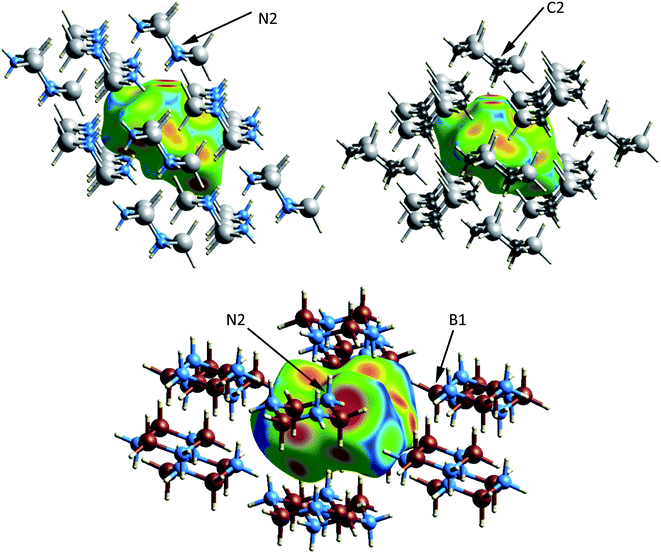
The crystal and molecular structures of each of the compounds have been reported and compared elsewhere, and no further discussion of the molecular structure will be included here.16,22,24 An appreciation of the intermolecular interactions can be gleaned through the use of Hirshfeld surfaces as developed by Spackman and coworkers.31,32 Based on the calculated structures, the Hirshfeld surfaces are shown in Fig. 2. In each case the Hirshfeld surface is displayed for one molecule surrounded by 14 neighbors. The color code assesses the distance between the Hirshfeld surface and the neighboring atoms with red indicating the shortest distance, green intermediate and blue the longest. Despite their different space groups, the Hirshfeld surfaces of [H2GaNH2]3 and [H2GeCH2]3 and the corresponding contacts with neighboring molecules (as indicated by the red to yellow regions) are remarkably similar. In both cases all contacts result from Ga–H⋯H–N or Ge–H⋯H–C interactions. For both compounds the closest approach to the Hirshfeld surface can be seen at the top of the figure between the axial hydrogens attached to the nitrogen (labelled N2) in [H2GaNH2]3 and the carbon (C2) in [H2GeCH2]3.
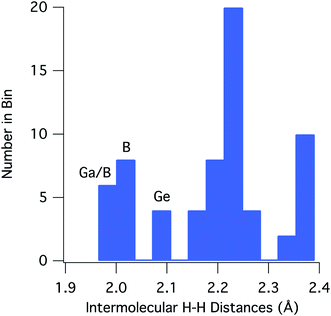
For [H2GaNH2]3 and [H2BNH2]3, there are 22 and 30 intermolecular H⋯H contacts between 1.9 and 2.4 Å, respectively. In this same range, [H2GeCH2]3 has 14 contacts among which only 4 shorter, symmetry equivalent contacts of 2.100 Å are found. All contacts below 2.4 Å occur between hydrides on a B, Ga or Ge and a hydrogen bound to a N or C. For the 66 H⋯H contacts in the three compounds, Fig. 3 shows a histogram of contact distances. Based on Bondi's van der Waal radius for hydrogen of 1.2 Å (ref. 34) previous reports suggest H⋯H distances below 2.4 Å constitute dihydrogen bonds. More recent studies of van der Waals radii suggest that a value of 1.1 Å is more appropriate for the hydrogen radius.35,36 Consistent with this shorter radius, the mode for the distribution in Fig. 3 includes contacts between 2.21 and 2.25 Å. All three compounds exhibit contacts shorter that 2.2 Å that can be reasonably considered as dihydrogen bonds. The shortest, and presumably the strongest, occur in [H2GaNH2]3 and [H2BNH2]3.
The number of H⋯H contacts per hydrogen differs in the three structures. In [H2BNH2]3 each of the axial hydrogens has three H⋯H contacts to neighboring molecules, whereas each of the equatorial hydrogens has two. The equatorial NH groups contact both hydrogens of an adjacent BH2 moiety to form an unsymmetrical, bifurcated dihydrogen bond. The equatorial hydrogen H4E that lies within the crystallographic mirror plane exhibits the shortest H⋯H contact of 1.984 Å (to H1A) and the second short contact (2.021 Å) is to H1E; both H1A and H1E are bonded to B1 (Fig. 2). Close inspection of the Hirshfeld surface in the region adjacent to B1 reveals two red spots corresponding to the bifurcated interaction with H4E. This interaction generates a chain of molecules connected by dihydrogen bonds parallel to the crystallographic b-axis in the bc plane. A second set of close contacts exists between the equatorial N–H (see N2 on Fig. 2) and the hydrides (H3A and H3E located within the Hirshfeld surface) attached to B3. The chain resulting from this interaction also lies in the bc plane but runs parallel to the c-axis. Longer H⋯H interactions connect molecules in the ab plane with the layers above and below. In contrast to [H2BNH2]3, most of the hydrogens in [H2GaNH2]3 and [H2GeCH2]3 exhibit two and one H⋯H contacts, respectively. The predominance of bifurcated dihydrogen bonds in cyclotriborazane compared to the complete lack of such interactions in cyclotrigallazane is likely attributable to the longer Ga–H bonds (1.57 Å) vs. the B–H distance of 1.21 Å and the wider H–Ga–H angle (119.7°) vs. H–B–H (111.6°). These metrical parameters would require the H–N proton to span a much larger distance between the two hydrogens on an HGaH group (2.71 Å) compared to 2.00 Å for an HBH group.
The Mulliken charges on each of the atoms (Table 5) confirm the hydridic nature of hydrogens attached to gallium, germanium and boron and the protic nature of those bound to nitrogen. The small positive charges on the carbon-bound hydrogens in [H2GeCH2]3 are undoubtedly a factor leading to the nonexistence of dihydrogen bonding in this compound.
| Atom | [H2BNH2]3 | [H2GaNH2]3 | [H2GeCH2]3 |
|---|---|---|---|
| X = B, Y = N | X = Ga, Y = N | X = Ge, Y = C | |
| X1 | 0.96 | 0.99 | 1.05 |
| X3 | 0.95 | 1.00 | 1.03 |
| Y2 | −0.60 | −0.89 | −0.59 |
| Y4 | −0.58 | −0.85 | −0.59 |
| H1A | −0.30 | −0.27 | −0.32 |
| H1E | −0.31 | −0.26 | −0.28 |
| H2A | 0.12 | 0.22 | 0.07 |
| H2E | 0.13 | 0.20 | 0.07 |
| H3A | −0.30 | −0.28 | −0.31 |
| H3E | −0.30 | −0.24 | −0.27 |
| H4A | 0.13 | 0.18 | 0.07 |
| H4E | 0.11 | 0.22 | 0.07 |
Calculated structures in non-native space groups
Considering the similar chair conformation of the molecular unit among these structures, we were curious to calculate each of the crystal and molecular structures in the alternative space groups. This was readily accomplished using the original atomic coordinates and lattice parameters as the starting point and changing the appropriate atoms for each calculation. All possibilities converged successfully. Table 2 compares the [H2GaNH2]3 experimental and calculated structures in both the native space group (P21/m) and in the space groups for [H2GeCH2]3 (Pmn21) and [H2BNH2]3 (Pbcm). The space group choice has little impact on the intramolecular distances and parameters, but it is interesting that the closest calculated intermolecular contact for [H2GaNH2]3 is slightly shorter (1.914 vs. 1.964 Å) in the non-native Pmn21 space group. All calculated intermolecular contacts in Pbcm were longer than those found in P21/m and Pmn21. The intermolecular H⋯H contacts in [H2GeCH2]3 (Table 3) are longer than those calculated for [H2GaNH2]3 but the shortest contact occurs in the native space group. In the native space group for [H2BNH2]3 the intermolecular H⋯H contacts are longer than those calculated for either of the non-native space groups, which may reflect the impact of bifurcated bonding in determining the structure.Lattice energies
In an attempt to quantify the energetic impact of the crystal structure, lattice energies, E(lattice), were calculated for the three molecules in both their native and non-native space groups. Lattice energy is defined as the energy required to separate a mole of the crystalline solid into isolated gas phase molecules having the same conformation as in the solid state. In addition, the atom-centered calculations of CRYSTAL mandate correction for basis set superposition error, E(BSSE). In eqn (1), E(crystal) equals the crystal energy, Z equals the number of molecules in the unit cell, E(Cs) equals the energy of a gaseous molecule having the same chair conformation (Cs point group) as observed in the solid. Density functional calculations for the gas phase molecules were conducted using the same functional and basis set (B3LYP-D3/pobTZVP) used for the solid-state structures.
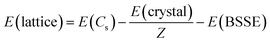 | (1) |
Table 6 lists each of the energies for the three compounds in each of the space groups. For each, the lattice energy calculated using CRYSTAL was largest for that compound's native space group. In each of the current compounds, the energy difference was less than 3 kJ mol−1 between P21/m and Pmn21. For [H2GaNH2]3 and [H2GeCH2]3, the lattice energy of the Pbcm space group was smaller by 13 to 19 kJ mol−1. For [H2BNH2]3, the Pbcm space was only 2.5 kJ mol−1 more stable that either of the others. Although the energy differences among the three space groups is small, there are no experimental results establishing the existence of polymorphs for these compounds.
| Compound | P21/m | Pmn21 | Pbcm |
|---|---|---|---|
| [H2GaNH2]3 | |||
| E(crystal) | −31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293.41 293.41 |
−31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290.63 290.63 |
−62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 444![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488.70 488.70 |
| Z | 2 | 2 | 4 |
| E(Cs) | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951.15 951.15 |
−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951.15 951.15 |
−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951.15 951.15 |
| E(BSSE) | 42.06 | 42.52 | 36.24 |
| E(lattice) | 153.49 | 151.65 | 134.79 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| [H2GeCH2]3 | |||
| E(crystal) | −33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028.40 028.40 |
−33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025.40 025.40 |
−66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711 711![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984.15 984.15 |
| Z | 2 | 2 | 4 |
| E(Cs) | −16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 677![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867.31 867.31 |
−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 677![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867.31 867.31 |
−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 677![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867.31 867.31 |
| E(BSSE) | 64.7 | 60.52 | 60.11 |
| E(lattice) | 82.19 | 84.87 | 68.62 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| [H2BNH2]3 | |||
| E(crystal) | −1292![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625.17 625.17 |
−1292![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624.28 624.28 |
−2585![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245.45 245.45 |
| Z | 2 | 2 | 4 |
| E(Cs) | −646157.94 | −646157.94 | −646157.94 |
| E(BSSE) | 36.33 | 35.91 | 32.66 |
| E(lattice) | 118.32 | 118.29 | 120.77 |
Sublimation enthalpies
Eqn (2) was used to calculate the sublimation energy for each compound in their native space group (vibrational frequencies were not computed for the higher energy polymorphs). For [H2GaNH2]3 and [H2BNH2]3, the lowest energy conformation of the gas phase molecule differed from the molecular conformation in the solid state, thus requiring an additional term, ΔE(conf), in the calculation. For [H2GaNH2]3 and [H2BNH2]3 the twist-boat was preferred over the chair conformation by −16.8 and −5.0 kJ mol−1, respectively. These values compare to −10.9 and −3.8 kJ mol−1, respectively, based on the earlier calculations at the MP2/VDZ level of theory.16 For [H2GeCH2]3, the chair was calculated to be more stable than the twist-boat conformation by 4.4 kJ mol−1, and thus no conformation correction was needed.| ΔHsub(T) = E(lattice) + ΔEconf + ΔEZPVE + ΔEvib(T) + 4RT | (2) |
The next two terms in eqn (2) are the difference in zero point vibrational energy between the crystalline and gaseous states, ΔEZPVE, and the difference in the vibrational contributions at temperature T of the crystalline and gaseous states, ΔEvib(T). The 4RT term accounts for the rotational, translational and pV work contributions to the energy of the gaseous product. Table 7 summarizes all contributions and the final ΔHsub for each molecule at 298 K.
| Compound | [H2GaNH2]3 | [H2GeCH2]3 | [H2BNH2]3 |
|---|---|---|---|
| Space group | P21/m | Pmn21 | Pbcm |
| Z | 2 | 2 | 4 |
| T (K) | 298.15 | 298.15 | 298.15 |
| E(lattice) | 153.49 | 84.87 | 120.77 |
| ΔE(conf) | −16.83 | 0.00 | −4.95 |
| ZPVE(crystal)/Z | 341.06 | 347.41 | 427.74 |
| ZPVE(gas) | 334.31 | 343.04 | 422.61 |
| Evib(crystal)/Z at T | 29.76 | 26.83 | 18.51 |
| Evib(gas) at T | 30.11 | 26.29 | 17.89 |
| 4RT(gas) | 9.92 | 9.92 | 9.92 |
| ΔHsub(T, calcd) | 140.18 | 89.89 | 119.43 |
| ΔHsub(T, exp) | na | na | 119 ± 12 |
Experimentally, neither [H2BNH2]3 nor [H2GaNH2]3 exhibited a detectable melting point prior to decomposing at 150 °C.16,23 Both sublimed under high vacuum above temperatures of 80–90 °C, whereas [H2GeCH2]3 had a melting point of −14 °C and was purified by distillation at 65 °C under reduced pressure (11 mbar).24 Using a Knudson cell, Shore and coworkers measured the vapor pressure of [H2BNH2]3 in the range from 47.5 to 75.5 °C to establish its heat of sublimation as 105 ± 13 kJ mol−1.23 Using the center of their temperature range, the ΔHsub was converted to the value at 298.15 K using the method described by Chickos and Acree and the calculated heat capacities for the crystalline and molecular states.37 The agreement was good between the experimental (119 ± 12 kJ mol−1) and calculated (119.4 kJ mol−1) values.
Conclusions
The crystal and molecular structures of [H2BNH2]3, [H2GaNH2]3 and [H2GeCH2]3 were successfully modeled using periodic DFT calculations in their native space groups of (Pbcm, P21/m and Pmn21, respectively). The calculated structures provided a basis for a more uniform comparisons among the structures. In each compound, all intermolecular H⋯H contacts occur between hydridic and protic hydrogens, and the majority of the H⋯H distances occur at or slightly above the expected van der Waals distance (2.2 Å). Both [H2BNH2]3 and [H2GaNH2]3 exhibit several contacts that are ∼0.2 Å shorter than the van der Waals contact distance, which places them in the range of typical dihydrogen bonds. The shortest H⋯H contacts in [H2GeCH2]3 (2.1 Å) are intermediate between the van der Waals and dihydrogen bonding distances. Comparison of the crystal energies to the energy of the gas phase molecules having the same chair conformation found in the solid state yielded lattice energies of 120.77, 153.49 and 84.87 kJ mol−1, respectively. For comparison, the crystal and molecular structure of each compound were also calculated in the two non-native space groups (e.g. P21/m and Pmn21 for [H2BNH2]3). In each case the largest lattice energy corresponded to the experimentally observed (native) space group. For the gas phase molecules and the compounds in their native space group, vibrational frequency calculations allowed calculation of their sublimation enthalpies. For [H2BNH2]3 and [H2GaNH2]3 the sublimation enthalpy calculation included a contribution associated with the conformational difference between the solid state and gas phase conformations. Good agreement was found between the calculated sublimation energy of [H2BNH2]3 (119.4 kJ mol−1) and the published experimental value (119 ± 12 kJ mol−1).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded in part by a grant from the National Science Foundation (DMR 1607318). The authors acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the research results reported within this paper.References
- C. A. Morrison and M. M. Siddick, Chem.–Eur. J., 2003, 9, 628–634 CrossRef CAS.
- C. A. Morrison and M. M. Siddick, Angew. Chem., Int. Ed., 2004, 43, 4780–4782 CrossRef CAS.
- B. Civalleri, K. Doll and C. M. Zicovich-Wilson, J. Phys. Chem. B, 2007, 111, 26–33 CrossRef CAS.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 1693 RSC.
- A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS.
- A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705 CrossRef.
- J. G. Brandenburg, M. Alessio, B. Civalleri, M. F. Peintinger, T. Bredow and S. Grimme, J. Phys. Chem. A, 2013, 117, 9282–9292 CrossRef CAS.
- J. Yang, W. F. Hu, D. Usvyat, D. Matthews, M. Schutz and G. K. L. Chan, Science, 2014, 345, 640–643 CrossRef CAS PubMed.
- G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613 CrossRef CAS PubMed.
- C. Cervinka and M. Fulem, J. Chem. Theory Comput., 2017, 13, 2840–2850 CrossRef CAS PubMed.
- X. N. Chen, J. C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675 CrossRef CAS PubMed.
- A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed.
- F. H. Stephens, V. Pons and R. T. Baker, Dalton Trans., 2007, 2613–2626 RSC.
- T. B. Richardson, S. deGala, R. H. Crabtree and P. E. M. Siegbahn, J. Am. Chem. Soc., 1995, 117, 12875–12876 CrossRef CAS.
- C. J. Cramer and W. L. Gladfelter, Inorg. Chem., 1997, 36, 5358–5362 CrossRef CAS.
- J. P. Campbell, J. W. Hwang, V. G. Young, R. B. Von Dreele, C. J. Cramer and W. L. Gladfelter, J. Am. Chem. Soc., 1998, 120, 521–531 CrossRef CAS.
- R. Custelcean and J. E. Jackson, J. Am. Chem. Soc., 1998, 120, 12935–12941 CrossRef CAS.
- L. M. Epstein, E. S. Shubina, E. V. Bakhmutova, L. N. Saitkulova, V. I. Bakhmutov, A. L. Chistyakov and I. V. Stankevich, Inorg. Chem., 1998, 37, 3013–3017 CrossRef CAS.
- W. T. Klooster, T. F. Koetzle, P. E. M. Siegbahn, T. B. Richardson and R. H. Crabtree, J. Am. Chem. Soc., 1999, 121, 6337–6343 CrossRef CAS.
- N. V. Belkova, L. M. Epstein, O. A. Filippov and E. S. Shubina, Chem. Rev., 2016, 116, 8545–8587 CrossRef CAS.
- J. Echeverria, Cryst. Growth Des., 2017, 17, 2097–2103 CrossRef CAS.
- H. K. Lingam, C. Wang, J. C. Gallucci, X. N. Chen and S. G. Shore, Inorg. Chem., 2012, 51, 13430–13436 CrossRef CAS.
- D. R. Leavers, J. R. Long, S. G. Shore and W. J. Taylor, J. Chem. Soc. A, 1969, 1580–1581 RSC.
- H. Schmidbaur, J. Rott, G. Reber and G. Mueller, Z. Naturforsch., B: J. Chem. Sci., 1988, 43, 727–732 CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, e1360 Search PubMed.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- M. A. Spackman and P. G. Byrom, Chem. Phys. Lett., 1997, 267, 215–220 CrossRef CAS.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- D. V. Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376 CrossRef.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS.
- R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2002, 31, 537–698 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07144j |
| This journal is © The Royal Society of Chemistry 2019 |