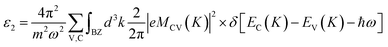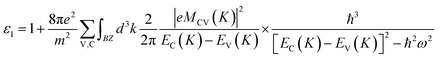A first-principles study of strain tuned optical properties in monolayer tellurium

Abstract

First-principles calculations are employed to study the optical properties of monolayer Te tuned by biaxial strain. Our results demonstrate that monolayer Te has strong absorption in the visible and ultraviolet regions, and that a structural transition occurs between the α-phase and the β-phase under certain strain. In addition, there is significant optical anisotropy in α- and β-Te, while γ-Te shows isotropic characteristics due to their different structural properties. Furthermore, strain has a significant impact on the optical properties. With increasing strain, the real and imaginary parts of the dielectric function exhibit redshift. In addition, the absorption spectrum is more likely to be excited under compressive strain rather than tensile strain in α- and β-Te, while only slight differences are induced in γ-Te. These findings can not only enhance the understanding of two-dimensional tellurium, but also provide an effective way to tune the optical properties for potential application in optoelectronic devices.

---

1. Introduction

In 2017, two-dimensional (2D) tellurium (Te) was predicted to exist stably and its structural, electronic and optical properties have been studied theoretically.¹ According to this paper, monolayer Te possesses strong optical absorption and owns higher carrier mobility than MoS₂ at room temperature, suggesting that 2D Te can be a promising material for electronic and optoelectronic devices. Hence, its outstanding electronic, optical and related properties have attracted significant attention.^2–11 Besides these theoretical investigations, experimental studies on the synthesis of 2D Te have also been reported.^12,13 By using molecular beam epitaxy, both monolayer and few-layer α-Te films have been obtained on a graphene/6H-SiC(0001) substrate,¹² while β-Te has been fabricated on highly oriented pyrolytic graphite.¹³

It is well acknowledged that property modulation is a hot issue, especially for 2D materials.^14–23 Among those, it can be seen that strain is one of the most used methods and an effective and promising way to modify the physical properties of 2D materials. For example, local strain can modulate the optical gap and enhance light emission in ReSe_2, as well as increase visible light absorption of ScNbCO₂.^17,18 It was also reported that optical properties in monolayer black phosphorus can be readily controlled by applying external stress.²⁰ Accordingly, it is likely that the physical properties of monolayer Te can be successfully tuned with strain, though such related reports are still lacking. Therefore, we adopted three phases of monolayer Te and calculated their optical properties under external biaxial strain using first-principles calculations.

In this work, a systematic study of the optical properties under external strain of monolayer Te is presented as follows: first, the computational methods are given in detail in section 2; second, the optical properties of monolayer Te with and without strain are discussed in section 3; finally, conclusions are given in section 4.

2. Computational details

First-principles calculations within density functional theory (DFT) were performed with the Vienna ab initio simulation package (VASP).^24–26 The Perdew–Burke–Ernzerhof (PBE) functional for the generalized gradient approximation (GGA) was applied to describe the exchange-correlation potential.²⁷ In our calculations, the DFT-D2 method from Grimme was employed to take the van der Waals interactions into account.²⁸ The effect of spin–orbit-coupling (SOC) was also considered because of the heavy metal nature of Te. To maintain the discontinuity of monolayer Te in the perpendicular direction, the thickness of the vacuum is set to ∼16 Å. During the structural relaxation and optical property calculations, energy cutoff is set to 500 eV and k-point meshes of 15 × 15 × 1 and 15 × 11 × 1 were used for the γ- and α-phases (or β-phase), respectively. For the fully relaxed structures, the convergence threshold for total energy and atomic force components were set to 10⁻⁶ eV per atom and 0.01 eV Å⁻¹, respectively.

Based on the theory of electromagnetic fields, the optical response function can be expressed as ε = ε₁ + iε₂. The terms ε₁ and ε₂ are the real and imaginary parts of the dielectric function respectively and can be obtained by following formulas:²⁹

where m is the free electron mass, BZ is the first Brillouin zone, k is the extinction coefficient, |eM_CV(K)|² is the momentum transition matrix element, K is the inverted lattice vector and E_C(K) and E_V(K) are the intrinsic levels of conduction and valence bands, respectively. During our calculations, calculated optical constants are reprocessed with the effect of the vacuum layer taken into account. All other optical constants on the energy dependence including refractive index, extinction coefficient and absorption coefficient can be derived from the dielectric function.

3. Results and discussion

3.1 Geometric structure and optical properties of monolayer Te

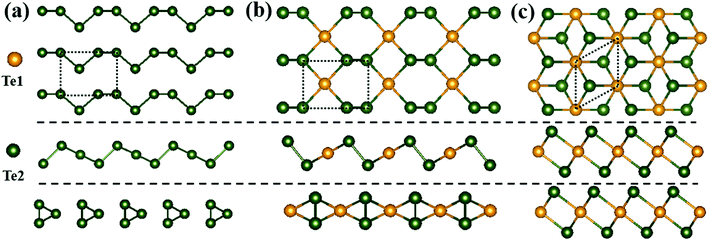
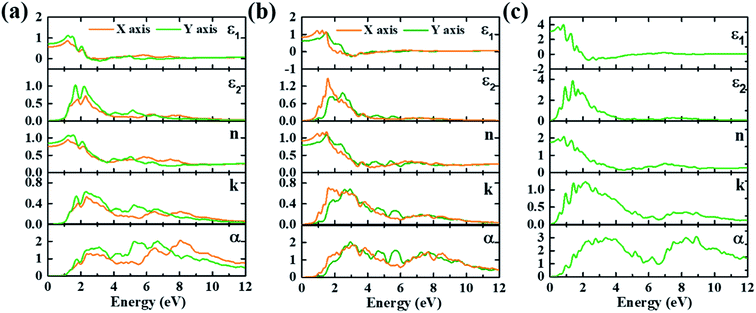
Three different monolayer Te configurations, denoted by α-, β- and γ-Te, are investigated in this paper, as presented in Fig. 1(a)–(c). In Fig. 1(a), α-Te can be considered as parallel Te chains with lattice constant a = 5.99 Å and b = 4.48 Å, which is in good agreement with previous research.¹² Meanwhile, β-Te is constructed by alternating a planar hexagon and four-membered rings with a = 5.54 Å and b = 4.14 Å. The optimized unit cell contains two types of Te atoms based on different coordination atoms (n_c), including one central atom Te1 bonded to four neighboring atoms and two outer atoms Te2 with n_c = 3. As for γ-Te, it has a structure similar to 1T-MoS₂, which consists of one Mo atom and two S atoms per unit cell. As a result, its optimized unit cell contains three atoms: a central atom occupying the Mo site with n_c = 6 and two outer atoms occupying the S site with n_c = 3. In addition, γ-Te is the only one with isotropic properties among these three structures, with a = b = 4.15 Å.

Fig. 1 Top and side views of atomic configurations for (a) α-Te, (b) β-Te and (c) γ-Te. Projections on the xy-, xz- and yz-planes of each structure are presented from top to bottom. Orange and green spheres represent Te1 and Te2 atoms, respectively. The dotted lines indicate the optimized unit cells of each structure.

Optical properties of three monolayer Te configurations have been calculated. The imaginary (ε₂) and real parts (ε₁) of the dielectric function, refractive index (n), extinction coefficient (k) and absorption spectra (α) are depicted in Fig. 2. Table 1 gives the corresponding optical parameters obtained from Fig. 2. Clearly, γ-Te has same optical properties along the k_x and k_y directions, while α-Te and β-Te are anisotropic. In α- and β-Te, the peak positions between the k_x and k_y directions are basically the same and the peak values are distinct, which is the major difference between the k_x and k_y directions. In Fig. 2, it can be observed that overall intensity along the k_y direction in α-Te are larger than those along the k_x direction, while it is just the opposite in β-Te. From Table 1, it can be seen that monolayer Te (ε₀ ∼ 0.57–3.08) can be considered as a low dielectric constant material, which suggests that monolayer Te may have potential application in microelectronics. In addition, the static refractive index n₀ in γ-Te is 1.76, larger than that of α-Te and β-Te. Further, all structures show strong absorption characteristics in visible and ultraviolet regions, where magnitude is 10⁵ cm⁻¹. It can be seen that the absorption spectra mainly contains two groups of peaks in all three configurations: one covers light ranging from visible to near ultraviolet regions and the other one appears in the far ultraviolet region where the peak is located at around 8 eV. Moreover, it can be clearly observed that γ-Te exhibits stronger absorption and a broader absorption band than α- and β-Te. Therefore, its superior absorption characteristics may enable monolayer Te to be used as a saturated absorber for laser devices.

Fig. 2 Calculated imaginary (ε₂) and real parts (ε₁) of the dielectric function, refractive index (n), extinction coefficient (k) and absorption spectra (α/10⁵ cm⁻¹) of (a) α-Te, (b) β-Te and (c) γ-Te.

Table 1 Optical parameters for α-, β- and γ-Te. The energy values (in eV) in the parenthesis are the corresponding peak energies

	α-Te		β-Te		γ-Te
Polarization	kx	ky	kx	ky	kx and ky
Static dielectric constant	0.57	0.72	0.84	0.63	3.08
Static refractive index	0.75	0.85	0.92	0.79	1.76
Refractive index maximum (energy in eV)	0.94 (1.22)	1.08 (1.54)	1.15 (1.25)	1.09 (1.52)	2.07 (0.83)
Extinction coefficient maximum (energy in eV)	0.53 (2.35)	0.63 (2.30)	1.50 (0.93)	2.10 (5.21)	1.23 (2.16)
Absorption maximum (10^5 cm^−1) (energy in eV)	2.06 (8.06)	1.99 (5.25)	1.85 (3.18)	2.03 (2.95)	3.09 (8.88)

---

3.2 Tunable optical properties under strain

Previous investigations suggest that structural transition may occur under a strong external force field.^30,31 Our recent work showed that α- and β-Te can transform into each other under certain strains.³² In α-Te, one atom in the helical chain moves towards the adjacent chain, leading to the bonding status between adjacent chains changing from non-bonding to bonding. In consequence, the structural transition from α-Te to β-Te occurs at strain ε = −0.06. In addition, α-Te under ε = −0.06 has approximately equal structural parameters with those of strainless β-Te. The structure of β-Te at ε = 0.08 transforms approximately into strainless α-Te by losing its symmetry.

Optical properties of monolayer Te under biaxial strain have been calculated, and optical properties including the imaginary and real parts of the dielectric function and absorption spectra are presented in Fig. 3–5. There is a significant optical anisotropy in α- and β-Te, while γ-Te shows isotropic characteristics due to the different structural features of their configurations. On account of the structural transition between α- and β-Te, we will compare their optical properties with each other to better understand the variations of their optical properties under strains.

Fig. 3 The imaginary part of the dielectric function ε₂ for (a) α-, (b) β- and (c) γ-Te under different strains.

Fig. 4 The real part of the dielectric function ε₁ for (a) α-, (b) β- and (c) γ-Te under different strains.

Fig. 5 The absorption spectrum of (a) α-, (b) β- and (c) γ-Te under different strains.

The real and imaginary parts of the dielectric function of monolayer Te are calculated and shown in Fig. 3–4. Two obvious effects of strain on the dielectric function can be seen. On one hand, the first peak appears redshifted with strain value increasing along both directions in all structures until structural transition occurs. This can be explained by the effect of strain on the band gap. As indicated in our previous study,³² the band gap is decreased under strains for all systems. In addition, the anisotropy between the k_x and k_y directions is enhanced with the increase of strain in α- and β-Te. This stems from the fact that the overall intensities along the k_x direction are gradually reduced for strains ranging from −0.14 (−0.08) to 0.08 (0.16), while only slight differences occur with strain changing from −0.14 (−0.08) to 0.08 (0.16) along the k_y direction in α-Te (β-Te). Furthermore, it can be inferred from Fig. 3 that monolayer Te will show strong absorption characteristics in the visible region.

Fig. 5 displays the evolution of absorption spectrum with biaxial strain applied in α-, β- and γ-Te. We can see from Fig. 5 that the absorption band is mainly located at the visible and ultraviolet regions for all structures. As is shown in Fig. 5(a), the overall absorption intensities decrease with strains ranging from −0.06 eV to 0.08 eV. As for the width of the absorption band, it reaches its minimum with ε = 0 and expands towards the lower energy with increasing tensile strain. Meanwhile, the absorption band becomes wider with strain increasing from 0 to −0.06, and then α-Te changes into β-Te at levels under ε = −0.06. A similar trend occurs in the other two structures. As a result, it can be demonstrated that the overall absorption intensities decrease with strain changing from −0.06 to 0.08, −0.08 to 0.08 and −0.08 to 0.10 in α-, β- and γ-Te, respectively. Furthermore, the system is more likely to be excited under compressive strain rather than tensile strain in α- and β-Te. The increase in width as well as intensity can be observed with increasing compressive strain applied to α- and β-Te. In consequence, materials with strong absorption and a wide absorption band can be obtained with this application of compressive strain. In the case of γ-Te, no notable increase of the absorption intensity occurs as in α- and β-Te, which may imply that γ-Te has better strain resistance than the other two.

4. Conclusions

To summarize, strain-engineering optical properties of three monolayer Te configurations have been investigated using first-principles calculations. All three phases have strong absorption in visible and ultraviolet regions at zero strain. Further, a structural transition occurs between α- and β-Te with certain strain applied. Optical anisotropy is found in α- and β-Te while γ-Te shows an isotropic characteristic, due to the structural features of their configurations. With increasing strain, the real and imaginary parts of the dielectric function exhibit redshift in all three structures, and there is a sizable anisotropy between the k_x and k_y directions under large strains in α- and β-Te. Moreover, the absorption spectra in α- and β-Te can be excited under compressive strain. When applied compressive strain increases, the absorption band width broadens and the absorption intensity increases. As for γ-Te, no notable increase of the absorption intensity occurs as it does in α- and β-Te, which may imply that γ-Te has better strain resistance than the other two. Our work can not only enhance the understanding of the optical properties of monolayer Te, but also support its potential use in the field of optoelectronics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

W.-S. Su would like to thank the Ministry of Science and Technology for financially supporting this research under contract no. MOST-108-2112-M-979-001 and MOST-108-2623-E-979-001-NU. Support from the National Centers for Theoretical Sciences and High-performance Computing of Taiwan in providing significant computing resources to facilitate this research is also gratefully acknowledged. Work at the Fudan University was supported by the key projects of basic research of Shanghai Municipal Science and Technology Commission (no. 18JC1411500), the National Natural Science Foundation of China (grant no. 11374055 and 61427815), CIOMP-Fudan University joint fund (no. FC2017-001), and the Fudan High-end Computing Center.

References

1. Z. Zhu, X. Cai, S. Yi, J. Chen, Y. Dai, C. Niu, Z. Guo, M. Xie, F. Liu, J. H. Cho, Y. Jia and Z. Zhang, Phys. Rev. Lett., 2017, 119, 106101.
2. S. Sharma, N. Singh and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2018, 1, 1950–1954.
3. W. Wu, G. Qiu, Y. Wang, R. Wang and P. Ye, Chem. Soc. Rev., 2018, 47, 7203–7212.
4. Y. Wang, C. Xiao, M. Chen, C. Hua, J. Zou, C. Wu, J. Jiang, S. A. Yang, Y. Lu and W. Ji, Mater. Horiz., 2018, 5, 521–528.
5. Y. Wang, G. Qiu, R. Wang, S. Huang, Q. Wang, Y. Liu, Y. Du, W. A. Goddard, M. J. Kim, X. Xu, P. D. Ye and W. Wu, Nat. Electron., 2018, 1, 228–236.
6. Y. Liu, W. Wu and W. A. Goddard, J. Am. Chem. Soc., 2018, 140, 550–553.
7. S. Guo, Z. Zhu, X. Hu, W. Zhou, X. Song, S. Zhang, K. Zhang and H. Zeng, Nanoscale, 2018, 10, 8397–8403.
8. Z. Gao, G. Liu and J. Ren, ACS Appl. Mater. Interfaces, 2018, 10, 40702–40709.
9. L. Xian, A. Pérez Paz, E. Bianco, P. M. Ajayan and A. Rubio, 2D Mater., 2017, 4, 041003.
10. Y. Du, G. Qiu, Y. Wang, M. Si, X. Xu, W. Wu and P. D. Ye, Nano Lett., 2017, 17, 3965–3973.
11. S. Lin, W. Li, Z. Chen, J. Shen, B. Ge and Y. Pei, Nat. Commun., 2016, 7, 10287.
12. X. Huang, J. Guan, Z. Lin, B. Liu, S. Xing, W. Wang and J. Guo, Nano Lett., 2017, 17, 4619–4623.
13. J. Chen, Y. Dai, Y. Ma, X. Dai, W. Ho and M. Xie, Nanoscale, 2017, 9, 15945–15948.
14. W. Zhou, S. Guo, S. Zhang, Z. Zhu, S. A. Yang, M. Chen, B. Cai, H. Qu and H. Zeng, Phys. Rev. Appl., 2019, 11, 064045.
15. S. Zhang, W. Zhou, Y. Ma, J. Ji, B. Cai, S. A. Yang, Z. Zhu, Z. Chen and H. Zeng, Nano Lett., 2017, 17, 3434–3440.
16. Z. Guan, S. Ni and S. Hu, J. Phys. Chem. C, 2018, 122, 6209–6216.
17. S. Yang, C. Wang, H. Sahin, H. Chen, Y. Li, S. S. Li, A. Suslu, F. M. Peeters, Q. Liu, J. Li and S. Tongay, Nano Lett., 2015, 15, 1660–1666.
18. J. Guo, Y. Sun, B. Liu, Q. Zhang and Q. Peng, J. Alloys Compd., 2017, 712, 752–759.
19. A. M. Smith, A. M. Mohs and S. Nie, Nat. Nanotechnol., 2009, 4, 56–63.
20. Z. Xie, L. Hui, J. Wang, G. a. Zhu, Z. Chen and C. Li, Comput. Mater. Sci., 2018, 144, 304–314.
21. K. A. Mengle, G. S. Shi, D. Bayerl and E. Kioupakis, Appl. Phys. Lett., 2016, 109, 212104.
22. X. Liang, J. L. Xie, L. J. Deng and L. Bi, Appl. Phys. Lett., 2015, 106, 052401.
23. G. G. Naumis, S. Barraza-Lopez, M. Oliva-Leyva and H. Terrones, Rep. Prog. Phys., 2017, 80, 096501.
24. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
25. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
29. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
30. W. Zhang, Q. Wu, O. V. Yazyev, H. Weng, Z. Guo, W.-D. Cheng and G.-L. Chai, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 115411.
31. Z. Wang, X. Cao, C. Qiao, R. J. Zhang, Y. X. Zheng, L. Y. Chen, S. Y. Wang, C. Z. Wang, K. M. Ho, Y. J. Fan, B. Y. Jin and W. S. Su, Nanoscale, 2017, 9, 19310–19317.
32. J. Wang, Y. Guo, C. Qiao, H. Shen, R. Zhang, Y. Zheng, L. Chen, S. Wang, Y. Jia and W.-S. Su, Chin. J. Phys., 2019, 62, 172–178.

---