Open Access Article
Open Access ArticleThe nature of G⋯E–Y σ(3c–4e) in o-MenGCH2C6H4EY (MenG = Me2N and MeE; E = O, S, Se and Te; Y = F, Cl, Br, EMe and Me) with contributions from CT and compliance constants in noncovalent G⋯E interactions†
Satoko Hayashi *a,
Taro Nishidea,
Waro Nakanishi
*a,
Taro Nishidea,
Waro Nakanishi *a,
Luca Sancineto
*a,
Luca Sancineto bc and
Claudio Santi*c
bc and
Claudio Santi*c
aFaculty of Systems Engineering, Wakayama University, 930 Sakaedani, Wakayama 640-8510, Japan. E-mail: hayashi3@sys.wakayama-u.ac.jp; nakanisi@sys.wakayama-u.ac.jp; Tel: +81 73 457 8252
bOrganic Chemistry Section, Center of Molecular and Macromolecular Studies, Polish Academy of Sciences, Sienkiewicza 112, 90-363, Lódz, Poland
cDipartimento di Chimica e Tecnologia del Farmaco, Università degli Studi di Perugia, Via del Liceo 1, 06123 Perugia, Italy. E-mail: claudio.santi@unipg.it; Tel: +39 075 5855102
First published on 29th November 2019
Abstract
The intrinsic dynamic and static nature of G–*–E–*–Y σ(3c–4e) interactions was elucidated with the quantum theory of atoms in molecules dual functional analysis (QTAIM-DFA), employing o-MenGCH2C6H4EY (MenG = Me2N and MeE; E = O, S, Se and Te; Y = F, Cl, Br, I, EMe and Me). Asterisks (*) are employed to emphasize the existence of bond critical points (BCPs) on the bond paths (BPs), corresponding to the interactions in question. Data from the fully optimized structure correspond to the static nature of interactions. The dynamic nature is called the intrinsic dynamic nature if the perturbed structures are generated using the coordinates derived from the compliance constants. Basis sets of the Sapporo-TZP type with diffusion functions are employed for the heteroatoms at the MP2 level. The noncovalent G–*–E interactions in GEY σ(3c–4e) are predicted to demonstrate van der Waals bonding to CT-TBP (trigonal bipyramidal adduct formation through charge transfer) nature, while the E–*–Y bonds have the covalent nature. Some E–F bonds show strong ionic character when G–*–E is predicted to be stronger than E–*–Y. The contributions of the CT terms to the G–*–E interactions, evaluated with NBO, are discussed in relation to the predicted nature. The E(2) values based on NBO are strongly correlated to the compliance constants for the G–*–E interactions if suitably treated separately.
Introduction
Weak interactions in chemistry, such as van der Waals (vdW), hydrogen bonds (HB) and charge transfer (CT) interactions, determine the fine details of the structure of molecules and create the functionalities of materials; strong interactions, such as classical chemical bonds, construct the framework of molecules. Weak interactions play a crucial role in the modulation of biological properties of selenium and sulfur containing compounds, driving their activity towards a protective antioxidant effect or a toxic pro-oxidant effect.1 Three-centre four-electron interactions of the σ-type (σ(3c–4e)) are typical in cases of such weak interactions, which determine fine details of these structures.2–4 The concept of σ(3c–4e) was first proposed by Musher, Pimentel, and Rundle.2a–2d It was developed through the preparation and characterization of such compounds and theoretical investigations mainly by Martin,2e Akiba,4a Schleyer3e and others.3a–3d,4b,4c Lots of sulfuranes of the symmetric and unsymmetric types were prepared by Martin and coworkers.2e They clarified the behaviour of unsymmetric σ(3c–4e) in sulfuranes, through the careful investigations of the interactions.2eThe CT interactions between nonbonded orbitals of G (n(G)) and the σ*-orbitals of E–Y (σ*(E–Y)) are also typically described as G⋯E–Y σ(3c–4e). The interactions should be denoted by unsymmetric GEY σ(3c–4e), since they must be (very) unsymmetric. Nevertheless, they will be described as GEY σ(3c–4e), here, for the simplification of notation. Scheme 1 illustrates the structures of the target species in this work 1–5 and the related ones I and 6, together with the approximate MO model for GEY σ(3c–4e) and the simplified interaction model for GEY σ(3c–4e). While the models may evoke the image of symmetric GEY σ(3c–4e), the contributions from the p-AOs on GEY σ(3c–4e) will change depending on the unsymmetric nature of GEY σ(3c–4e). The system will be energetically stabilized most effectively through GEY σ(3c–4e) when the three GEY atoms align linearly, allowing the orbital between n(G) and σ*(E–Y) to overlap most effectively. As a result, the formation of GEY σ(3c–4e) makes the three atoms align linearly. Such linear alignment of the three atoms is typically observed in conventional HBs of the shared proton interaction type (cv-HBs: B⋯H–X). The unsymmetric B⋯H–X σ(3c–4e) is formed through the reaction between electron donor B and acceptor H–X. Energies in the formation of cv-HBs are typically 10–40 kJ mol−1 for the neutral form,5–8 although HBs spread over a wide range from vdW to covalent bonds. The nature of BHX σ(3c–4e) have been reported recently.9,10
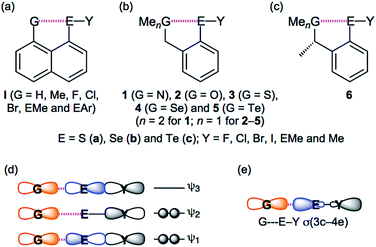 | ||
| Scheme 1 Structures of I (a) and 1–6 (b and c), together with the approximate MO model of GEY σ(3c–4e) (d) and the simplified interaction model for GEY σ(3c–4e) (e). | ||
There has been much interest in the weak interactions of GEY σ(3c–4e), rather than BHX σ(3c–4e), in cv-HBs. The chemistry originating from GEY σ(3c–4e) in the naphthalene 1,8-positions of 8-G–C10H6–EY-1 (I) has been studied thoroughly by Wakayama group.11 The linear alignment of the three GEY atoms was called “G-dependence”, especially for Y = C, and the donor ability for G = F is demonstrated. The nature of G⋯E–Y in I is clarified, which is discussed elsewhere.11a,11c,11d,11f,11h The benzyl type species of o-MeGCH2C6H4EY (1–5) are also important candidates to investigate the chemistry originating from GEY σ(3c–4e). Structure analysis, spectroscopic analysis and reactivity in asymmetric synthesis for GEY σ(3c–4e) were investigated by employing the methyl derivatives of 1–5 (6) in Perugia.12 Surprisingly, short Se⋯S distances were observed in 6 (2.344(2) Å for (G, E, Y) = (S, Se, Cl) and 2.497(7) Å for (S, Se, Br)). Iwaoka and Tomoda also investigated the GEY σ(3c–4e) type interactions, employing 1–5 or similar.13 They reported the negative values of the total electron energy densities at bond critical points (Hb(rc)) for O⋯Se in 2 (EY = SeCl and SeBr), benzyl alcohols and 2-formyl derivatives. As shown in Scheme 1, GEY σ(3c–4e) in 1–5 seem closely related to X–H⋯F–Y investigated by Espinosa and co-workers,14 although some of the latter interactions should be analyzed by the σ(4c–6e) model.
What is the behaviour of GEY σ(3c–4e)? The nature of the noncovalent G⋯E interactions and the (covalent) E–Y bonds in G⋯E–Y σ(3c–4e) is elucidated by employing 1–5, rather than I, where the noncovalent G⋯E interactions are synonymous with the closed shell (CS) interactions, in this work. Indeed, stronger G⋯E interactions are expected to be detected in I, but the framework around the naphthalene 1,8-positions in I seems too rigid to detect the delicate behaviour of the GEY interactions. Instead, the framework around GEY σ(3c–4e) in 1–5 seems suitably flexible, which would be more advantageous for elucidating the fine details of the GEY σ(3c–4e) nature originating from the delicate properties of G, E and Y, relative to the case of I.15
How can the nature of GEY σ(3c–4e) be clarified? The quantum theory of atoms in molecules (QTAIM) approach, introduced by Bader,16,17 enables us to analyze the nature of chemical bonds and interactions.18–22 A bond critical point (BCP, *) is an important concept in QTAIM approach in which ρ(r) (charge density) reaches a minimum along the interatomic (bond) path and a maximum on the interatomic surface separating the atomic basins. The ρ(r) at the BCP is described by ρb(rc), as well as other QTAIM functions, such as Hb(rc), potential energy densities Vb(rc) and kinetic energy densities Gb(rc). A chemical bond or interaction between atoms A and B is denoted by A–B, which corresponds to the bond path (BP) in QTAIM. We will use A–*–B for BP, where the asterisk emphasizes the existence of a BCP in A–B.16,17,23 Eqn (1), (2) and (2′) represent the relations between Gb(rc), Vb(rc), Hb(rc) and ∇2ρb(rc). Hb(rc) must be negative when ∇2ρb(rc) < 0 since Vb(rc) are negative at all BCPs (cf.: eqn (2)).
| Hb(rc) = Gb(rc) + Vb(rc) | (1) |
| (ℏ2/8m)∇2ρb(rc) = Hb(rc) − Vb(rc)/2 | (2) |
| = Gb(rc) + Vb(rc)/2 | (2′) |
Interactions are classified by the signs of ∇2ρb(rc) and Hb(rc). They are called shard shell (SS) interactions for those with ∇2ρb(rc) < 0 (and Hb(rc) < 0) and CS interactions for those with ∇2ρb(rc) > 0.14 The CS interactions are especially called pure CS (p-CS) interactions when Hb(rc) > 0 with ∇2ρb(rc) > 0. We call such interactions regular CS (r-CS) interactions that have the QTAIM values of Hb(rc) < 0 and ∇2ρb(rc) > 0, which distinguish the interactions clearly from the p-CS interactions. The signs of ∇2ρb(rc) can be replaced by those of Hb(rc) − Vb(rc)/2 in the discussion, since (ℏ2/8m)∇2ρb(rc) = Hb(rc) − Vb(rc)/2 (see, eqn (2)). Details are explained later, again.
Recently, the QTAIM dual functional analysis (QTAIM-DFA) was formulated based on the QTAIM approach, allowing experimental chemists to analyse their own chemical bond and interaction results based on their own expectations.24–28 In QTAIM-DFA, we proposed to use the signs of the first derivatives of Hb(rc) − Vb(rc)/2 and Hb(rc)((Hb(rc) − Vb(rc)/2)/dr and Hb(rc)/dr, respectively), in addition to the signs of Hb(rc) − Vb(rc)/2 and Hb(rc), to classify (and characterize) the interactions. Hb(rc) are plotted versus Hb(rc) − Vb(rc)/2 (= (ℏ2/8m)∇2ρb(rc)) (cf.: eqn (2)) at BCPs in QTAIM-DFA. Data from the fully optimized structures are analysed using the polar coordinate (R, θ) representation,29 which correspond to the static natures of the interactions.24a,25–28 Data from the perturbed structures around the fully optimized structures are employed, in addition to those from the fully optimized structures, in our treatment. Each interaction plot, which contains data from both the perturbed and fully optimized structures, includes a specific curve that provides important information about the interaction. This plot is expressed by (θp, κp), where θp corresponds to the tangent line of the plot and κp is the curvature. The dynamic nature of interactions was proposed based on (θp, κp).29 We call (R, θ) and (θp, κp) the QTAIM-DFA parameters, which are illustrated in Fig. 3 and exemplified by the intramolecular S–*–SF interaction in 3a.
It is necessary to establish a reliable method to generate the perturbed structures for the effective analysis with QTAIM-DFA. We recently proposed a highly reliable method to generate the perturbed structures for QTAIM-DFA.30 The method is called CIV and employs the coordinates derived from the compliance constants Cii for the internal vibrations. Eqn (3) defines Cij, as the partial second derivatives of the potential energy due to an external force, where i and j refer to internal coordinates, and the force constants fi and fj correspond to i and j, respectively. While the off-diagonal elements Cij (i ≠ j) in eqn (3) correspond to the compliance coupling constants, the diagonal elements Cii represent the compliance constants for an internal coordinate i. The Cii values and coordinates corresponding to Cii were calculated using the Compliance 3.0.2 program31 released by Grunenberg and Brandhorst.32 The dynamic nature of interactions based on the perturbed structures with CIV is described as the “intrinsic dynamic nature of interactions,” as the coordinates are invariant to the choice of the coordinate system.
| Cij = ∂2E/∂fi∂fj | (3) |
QTAIM-DFA is applied to standard interactions, and rough criteria to distinguish the interaction in question from others are obtained. The applications of CIV to the CS interactions are substantially more effective than those to the SS interactions in QTAIM-DFA.30 QTAIM-DFA has excellent potential for evaluating, classifying, characterizing and understanding weak to strong interactions according to a unified form.24a,25–28,30 The basis sets and levels for the calculations must also be important when the calculated nature is discussed in relation to the observed results.33 Therefore, higher basis set systems are used for the calculations. QTAIM-DFA and the criteria are explained in the ESI using Schemes S1–S3, Fig. S1, S2, Table S1 and eqn (S1)–(S7).† The basic concept of the QTAIM approach is also explained.
The negative values of Hb(rc), reported for O⋯Se in 2 (EY = SeCl and SeBr), predict the covalent contribution in these interactions, which correspond to the static nature, although Hb(rc) for O⋯Se in 2 (EY = SeBr) is positive in our calculations. The nature of the interactions will be discussed latter again. However, the dynamic nature is to be elucidated for GEY σ(3c–4e) for better understanding of the interactions. QTAIM-DFA employing the perturbed structures generated with CIV is well-suited to elucidate the intrinsic dynamic and static nature of GEY σ(3c–4e) of 1–5. Herein, we present the results of calculations on the intrinsic dynamic and static nature of the interactions. The interactions are classified and characterized by employing the criteria as a reference. NBO analysis is applied to the interactions in question in 1–5. The nature of the interactions will also be discussed in relation to the interaction energies calculated with NBO (E(2)) and the structural features. A proportional relationship is detected between E(2) and Cii.
Methodological details in calculations
Gaussian 09 programs34 were employed for the calculations, containing the NBO analysis.35 The basis sets of the (6211/311/21/2 + 1s1p), (63211/6111/31/2 + 1s1p1d1f), (743211/74111/721/2 + 1s1p1d1f) and (7433111/743111/7411/2 + 1s1p1d1f) types were employed for (O, F), (S, Cl), (Se, Br) and (Te, I), respectively, as implemented from the Sapporo Basis Set Factory,36 with the 6-311G(d) basis set for C and H. The basis set system is called A (BSS-A). The Møller–Plesset second order energy correlation (MP2) level37 was applied to the calculations (MP2/BSS-A). The results of the frequency analysis were used to obtain the compliance constants (Cij) and the coordinates corresponding to Cij.31 The optimizations were not corrected with the BSSE method.Eqn (4) explains the method to generate the perturbed structures with CIV.30 A i-th perturbed structure in question (Siw) is generated by the addition of the coordinates corresponding to Cii in eqn (3) (Ci) to the standard orientation of a fully optimized structure (So) in the matrix representation. The coefficient giw in eqn (4) controls the structural difference between Siw and So:38 giw is determined to satisfy eqn (5) for r. The Ci values of five digits are used to predict Siw.
| Siw = So + giwCi | (4) |
| r = ro + wao (w = (0), ±0.025 and ±0.05; ao = 0.52918 Å) | (5) |
| y = co + c1x + c2x2 + c3x3 (Rc2: square of correlation coefficient.) | (6) |
QTAIM functions were calculated with the same method as the optimizations at the MP2 level, unless otherwise noted. The calculated values were analysed with the AIM2000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 and AIMAll40 programs. Hb(rc) are plotted versus Hb(rc) − Vb(rc)/2 for data of five points of w = 0, ±0.05 and ±0.1 in eqn (5) in QTAIM-DFA. Each plot is analysed using a regression curve of the cubic function, shown in eqn (6), where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)) (Rc2 > 0.99999 is typical).27
39 and AIMAll40 programs. Hb(rc) are plotted versus Hb(rc) − Vb(rc)/2 for data of five points of w = 0, ±0.05 and ±0.1 in eqn (5) in QTAIM-DFA. Each plot is analysed using a regression curve of the cubic function, shown in eqn (6), where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)) (Rc2 > 0.99999 is typical).27
Results and discussion
Optimizations of species, 1–5
Selected structural parameters, r(G, E), r(E, Y) and ∠GEY, of 1a, 1b, 2a, 2b, 3a, 3b, 4a, 4b and 5c (1–5), optimized with MP2/BSS-A, are collected in Table S2 of the ESI,† with the Δr(G, E) and Δr(E, Y) values. Eqn (7) defines the Δr(G, E) values as the differences from the sum of the van der Waals radii of G and E, while eqn (8) produces the Δr(E, Y) values as the differences from the sum of the covalent radii of E and Y.| Δr(G, E) = r(G, E) − (rvdW(G) + rvdW(E)) | (7) |
| Δr(E, Y) = r(E, Y) − (rco(E) + rco(Y)) | (8) |
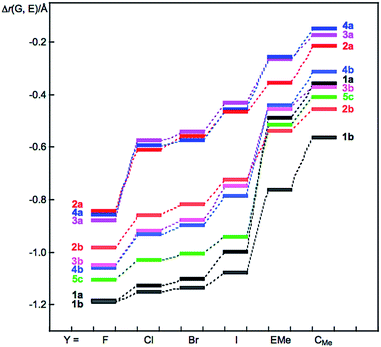
Fig. 1 shows the plot of Δr(G, E) versus Y for 1–5. The Δr(G, E) values change depending on G, E and Y, as shown in Fig. 1. The Δr(E, Y) values are plotted versus Δr(G, E), although that of 1 is tentative. The plot is shown in Fig. S5 of the ESI.† The Δr(E, Y) values are expected to change in a manner that is inversely proportional to Δr(G, E). The inverse proportionality between Δr(G, E) and Δr(E, Y) is well recognized if the plots are analysed separately by 2 and 3–5, with the exceptions of Y = F and EMe in G⋯E–Y of 2–5. The exceptions correlate well, although the data for O⋯E–F (E = S and Se) and Te⋯Te–F are neglected. Fortunately, the neglected three data points also showed good correlation. As a result, the plot is finally analysed as five correlations.
The results can be explained by assuming that the total covalency of the central atom E in GEY σ(3c–4e) is almost constant when G and Y are changed. A valence atomic p-orbital of E, in the linear GEY direction, is employed to connect G and Y to E to form GEY σ(3c–4e) in the species (see Scheme 1c). Specifically, E–Y will be weaker if G⋯E becomes stronger in GEY σ(3c–4e). The ∠GEY values must be 180° or larger than 150° for G⋯E–Y interactions to be analysed as linear σ(3c–4e), where ∠GEY of 150° is the tentative value, which we proposed as a lower limit for the linear interactions. The ∠GEY values drop in the range of 165° to 175°, which satisfy the above explanation.
Before a discussion of the nature of GEY σ(3c–4e), it is necessary to examine the molecular graphs with contour plots.
Molecular graphs with contour plots for 1–5
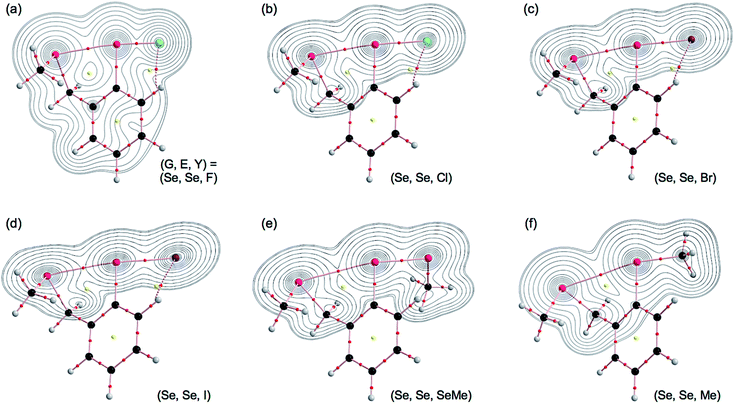
The molecular graphs with the contour plots are drawn for 1–5. Fig. 2 illustrates the contour exemplified by 4b with Y = F, Cl, Br, I, SeMe and Me. All BCPs are clearly detected, containing those for the noncovalent G–*–E interactions and the E–*–Y bonds. The BCPs are well located at the (three-dimensional) saddle points of ρ(r). Similar results are obtained for 1–5, other than 4b in Fig. 2, although the BP with BCP corresponding to the Se⋯SCMe in 4a is not detected.BPs, corresponding to the noncovalent G⋯E interactions, appear straight, as shown in Fig. 2. To examine the linearity of the noncovalent interactions further, the lengths of the BPs (rBP) in question and the corresponding straight-line distances (RSL) are calculated for G⋯E in 1–5. The values calculated with MP2/BSS-A are collected in Table S3 of the ESI,† with the differences between the two (ΔrBP = rBP − RSL). The magnitudes of ΔrBP are 0.001–0.022 Å for the BPs. Consequently, the noncovalent G⋯E interactions in 1–5 can be approximated as straight.
QTAIM-DFA treatment of the G⋯E and E–Y interactions in 1–5
QTAIM functions of ρb(rc), Hb(rc) − Vb(rc)/2 and Hb(rc) are calculated for the noncovalent G⋯E interactions and the E–Y bonds at BCPs in noncovalent G⋯E interactions, while those for the E–Y bonds are collected in Table S4 of the ESI.† Fig. 3 shows the plots of Hb(rc) 1–5 with MP2/BSS-A. Table 1 summarizes the values for the versus Hb(rc) − Vb(rc)/2 for the data in Table 1 and those from the perturbed structures, generated with CIV, as shown for G⋯E in 3a, 4b and 5c. Fig. 3 shows that the noncovalent G⋯E interactions become stronger in the order of G⋯E = S⋯S < Se⋯Se < Te⋯Te. The Hb(rc) values are negative for all Te–*–Te in 5c, indicating that the interactions contain covalent nature appeared in the regular CS region. The QTAIM-DFA parameters of (R, θ) and (θp, κp) for G–*–E in GEY σ(3c–4e) were obtained for 3a, 4b and 5c by analysing the plots in Fig. 3, according to eqn (S1)–(S6) of the ESI.† The values for G–*–E in 1–5, but not 3a, 4b and 5c, were similarly obtained, with the exception of Se⋯SCMe in 4a. Table 1 shows the values for G–*–E in 1–5. The (R, θ) and (θp, κp) values for E–*–Y are similarly calculated, and these values are presented in Table S4 of the ESI.† The Cii values, corresponding to CIV employed to generate the perturbed structures, are also given in the tables. The noncovalent G⋯E interactions and the E–Y bonds of GEY σ(3c–4e) in 1–5 are classified and characterized based on the (R, θ, θp) values, employing the standard values as a reference. The results evaluated with MP2/BSS-A are summarized in Table 2.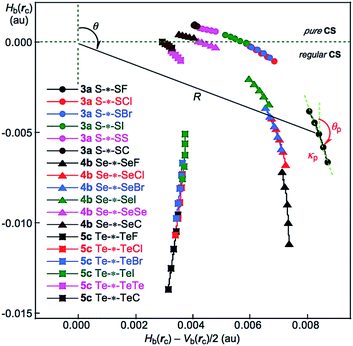 | ||
| Fig. 3 Plots of Hb(rc) versus Hb(rc) − Vb(rc)/2 for G–*–E in GEY σ(3c–4e), as shown for 3a, 4b and 5c. Perturbed structures are generated with CIV. | ||
| Species: G–*–EY | ρb(rc) (eao−3) | c∇2ρb(rc)b (au) | Hb(rc) (au) | Rc (au) | θd (°) | Ciie (Å mdyn−1) | θpf (°) | κpg (au−1) |
|---|---|---|---|---|---|---|---|---|
| a See text for MP2/BSS-A.b c∇2ρb(rc) = Hb(rc) − Vb(rc)/2, where c = ℏ2/8m.c R = (x2 + y2)1/2, where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)).d θ = 90° − tan−1 (y/x).e Defined in eqn (3) in the text.f θp = 90° − tan−1 (dy/dx).g κp = |d2y/dx2|/[1 + (dy/dx)2]3/2.h Data from w = ±0.0125, ±0.025, ±0.050 being employed for the evaluation.i The bond path corresponding to the interaction not detected. | ||||||||
| 1a: N–*–SF | 0.0815 | 0.0094 | −0.0289 | 0.0303 | 162.0 | 1.505 | 189.9 | 5.2 |
| 1a: N–*–SCl | 0.0738 | 0.0108 | −0.0216 | 0.0241 | 153.4 | 2.331 | 187.7 | 9.1 |
| 1a: N–*–SBr | 0.0713 | 0.0112 | −0.0195 | 0.0225 | 150.2 | 2.510 | 186.4 | 11.6 |
| 1a: N–*–SI | 0.0573 | 0.0121 | −0.0109 | 0.0163 | 132.0 | 5.172 | 179.2 | 23.4 |
| 1a: N–*–SSMe | 0.0198 | 0.0074 | 0.0008 | 0.0074 | 84.1 | 8.174 | 106.0 | 117 |
| 1a: N–*–SCMe | 0.0152 | 0.006 | 0.0011 | 0.0061 | 79.7 | 7.757 | 96.1 | 76.2 |
| 1b: N–*–SeF | 0.0713 | 0.0106 | −0.0235 | 0.0258 | 155.6 | 1.318 | 182.4 | 3.1 |
| 1b: N–*–SeCl | 0.0680 | 0.0107 | −0.0202 | 0.0228 | 152.1 | 1.659 | 183.1 | 7.1 |
| 1b: N–*–SeBr | 0.0662 | 0.0108 | −0.0187 | 0.0216 | 150.0 | 1.763 | 182.6 | 9.9 |
| 1b: N–*–SeI | 0.0597 | 0.0112 | −0.0141 | 0.0180 | 141.5 | 2.244 | 180.5 | 12.8 |
| 1b: N–*–SeSeMe | 0.0314 | 0.0098 | −0.0014 | 0.0099 | 98.2 | 5.408 | 140.3 | 140 |
| 1b: N–*–SeCMe | 0.0209 | 0.0075 | 0.0006 | 0.0075 | 85.3 | 6.266 | 107.5 | 137 |
| 2a: O–*–SF | 0.0330 | 0.0134 | −0.0001 | 0.0134 | 90.3 | 5.337 | 124.6 | 132 |
| 2a: O–*–SCl | 0.0212 | 0.0093 | 0.0015 | 0.0094 | 80.8 | 8.067 | 95.0 | 76.8 |
| 2a: O–*–SBr | 0.0196 | 0.0086 | 0.0015 | 0.0088 | 79.9 | 8.546 | 92.5 | 68.0 |
| 2a: O–*–SI | 0.0165 | 0.0074 | 0.0016 | 0.0075 | 78.1 | 9.674 | 88.2 | 51.4 |
| 2a: O–*–SSMe | 0.0133 | 0.0061 | 0.0015 | 0.0063 | 76.5 | 9.033 | 84.9 | 14.2 |
| 2a: O–*–SCMe | 0.0120 | 0.0056 | 0.0014 | 0.0058 | 75.7 | 8.770 | 84.4 | 45.9 |
| 2b: O–*–SeF | 0.0399 | 0.0146 | −0.0029 | 0.0149 | 101.4 | 2.904 | 147.4 | 79.4 |
| 2b: O–*–SeCl | 0.0320 | 0.0126 | −0.0003 | 0.0126 | 91.1 | 4.307 | 125.9 | 125 |
| 2b: O–*–SeBr | 0.0299 | 0.0119 | 0.0002 | 0.0119 | 88.9 | 4.791 | 119.2 | 127 |
| 2b: O–*–SeI | 0.0250 | 0.0102 | 0.0010 | 0.0103 | 84.4 | 5.925 | 105.3 | 112 |
| 2b: O–*–SeSeMe | 0.0176 | 0.0075 | 0.0014 | 0.0076 | 79.4 | 7.396 | 89.0 | 67.3 |
| 2b: O–*–SeCMe | 0.0149 | 0.0065 | 0.0014 | 0.0066 | 77.6 | 7.557 | 84.2 | 48.3 |
| 3a: S–*–SF | 0.0389 | 0.0084 | −0.0051 | 0.0098 | 121.2 | 7.613 | 167.1 | 68.8 |
| 3a: S–*–SCl | 0.0220 | 0.0064 | −0.0006 | 0.0064 | 95.4 | 9.525 | 133.8 | 162 |
| 3a: S–*–SBr | 0.0210 | 0.0063 | −0.0004 | 0.0063 | 93.9 | 10.027 | 131.4 | 167 |
| 3a: S–*–SI | 0.0169 | 0.0055 | 0.0002 | 0.0055 | 87.9 | 12.043 | 121.5 | 174 |
| 3a: S–*–SSMe | 0.0121 | 0.0045 | 0.0007 | 0.0045 | 81.0 | 9.477 | 109.4 | 30.8 |
| 3a: S–*–SCMeh | 0.0101 | 0.0041 | 0.0009 | 0.0042 | 77.3 | 10.252 | 127.2 | 6195 |
| 3b: Se–*–SF | 0.0498 | 0.0084 | −0.0104 | 0.0134 | 141.3 | 2.704 | 177.4 | 21.8 |
| 3b: S–*–SeCl | 0.0396 | 0.0080 | −0.0057 | 0.0098 | 125.3 | 4.685 | 168.7 | 56.0 |
| 3b: S–*–SeBr | 0.0369 | 0.0078 | −0.0047 | 0.0091 | 120.9 | 5.190 | 165.0 | 67.8 |
| 3b: S–*–SeI | 0.0291 | 0.0071 | −0.0023 | 0.0074 | 108.1 | 6.640 | 151.7 | 117 |
| 3b: S–*–SeSeMe | 0.0163 | 0.0051 | 0.0002 | 0.0051 | 88.2 | 8.297 | 116.7 | 167 |
| 3b: S–*–SeCMe | 0.0127 | 0.0044 | 0.0006 | 0.0044 | 82.4 | 8.548 | 105.9 | 116 |
| 4a: Se–*–SF | 0.0350 | 0.0072 | −0.004 | 0.0082 | 118.8 | 7.601 | 163.1 | 91.7 |
| 4a: Se–*–SCl | 0.0218 | 0.0057 | −0.0008 | 0.0057 | 98.3 | 9.732 | 135.3 | 167 |
| 4a: Se–*–SBr | 0.0213 | 0.0056 | −0.0007 | 0.0057 | 97.5 | 10.162 | 134.2 | 170 |
| 4a: Se–*–SI | 0.0173 | 0.0050 | −0.0001 | 0.0050 | 91.3 | 12.191 | 124.8 | 182 |
| 4a: Se–*–SSMe | 0.0119 | 0.0040 | 0.0005 | 0.0040 | 83.2 | 9.983 | 112.2 | 142 |
| 4a: Se–*–SCMe | i | i | i | i | i | i | i | i |
| 4b: Se–*–SeF | 0.0470 | 0.0073 | −0.009 | 0.0116 | 140.9 | 2.766 | 176.7 | 29.1 |
| 4b: Se–*–SeCl | 0.0386 | 0.007 | −0.0054 | 0.0089 | 127.5 | 4.565 | 168.9 | 62.4 |
| 4b: Se–*–SeBr | 0.0366 | 0.0068 | −0.0047 | 0.0083 | 124.3 | 4.943 | 165.8 | 71.5 |
| 4b: Se–*–SeI | 0.0296 | 0.0063 | −0.0026 | 0.0068 | 112.7 | 6.399 | 154.1 | 115 |
| 4b: Se–*–SeSeMe | 0.0160 | 0.0045 | −0.0001 | 0.0045 | 91.1 | 8.731 | 118.5 | 1154 |
| 4b: Se–*–SeCMe | 0.0120 | 0.0038 | 0.0004 | 0.0038 | 84.5 | 9.347 | 108.5 | 47.1 |
| 5c: Te–*–TeF | 0.0448 | 0.0033 | −0.0115 | 0.0119 | 163.8 | 2.232 | 184.8 | 7.5 |
| 5c: Te–*–TeCl | 0.0402 | 0.0035 | −0.0089 | 0.0096 | 158.2 | 3.087 | 184.3 | 15.1 |
| 5c: Te–*–TeBr | 0.0387 | 0.0036 | −0.0081 | 0.0089 | 156.3 | 3.350 | 183.9 | 19 |
| 5c: Te–*–TeI | 0.0347 | 0.0037 | −0.0062 | 0.0073 | 149.3 | 4.204 | 182.0 | 25.1 |
| 5c: Te–*–TeTeMe | 0.0169 | 0.0034 | −0.0007 | 0.0035 | 102.0 | 8.359 | 148.7 | 271 |
| 5c: Te–*–TeCMe | 0.0136 | 0.0031 | −0.0001 | 0.0031 | 92.7 | 8.869 | 133.7 | 335 |
| Species: GE–*–Y | R (au) | θ (°) | θp (°) | Predicted nature | Species: G–*–EY | θ (°) | θp (°) | Predicted nature |
|---|---|---|---|---|---|---|---|---|
| a The (R, θ, θp) values are shown for the E–*–Y interactions, while the (θ, θp) values for the G–*–E interactions.b The bond path corresponding to the interaction not detected.c Data from w = ±0.0125, ±0.025 and ±0.050 being employed for the evaluation. | ||||||||
| 1a: NS–*–F | 0.1556 | 183.0 | 175.2 | SS/Cov | 1a: N–*–SF | 162.0 | 189.9 | r-CS/CT-TBP |
| 1a: NS–*–Cl | 0.0536 | 180.5 | 195.6 | SS/Cov-w | 1a: N–*–SCl | 153.4 | 187.7 | r-CS/CT-TBP |
| 1a: NS–*–Br | 0.0375 | 176.7 | 193.9 | r-CS/CT-TBP | 1a: N–*–SBr | 150.2 | 186.4 | r-CS/CT-TBP |
| 1a: NS–*–I | 0.0340 | 180.3 | 192.8 | SS/Cov-w | 1a: N–*–SI | 132.0 | 179.2 | r-CS/CT-MC |
| 1a: NS–*–SMe | 0.0936 | 191.1 | 197.6 | SS/Cov-w | 1a: N–*–SSMe | 84.1 | 106.0 | p-CS/t-HBnc |
| 1a: NS–*–CMe | 0.1309 | 196.0 | 199.7 | SS/Cov-w | 1a: N–*–SCMe | 79.7 | 96.1 | p-CS/t-HBnc |
| 1b: NSe–*–F | 0.0830 | 155.0 | 146.9 | r-CS/t-HBwc | 1b: N–*–SeF | 155.6 | 182.4 | r-CS/CT-TBP |
| 1b: NSe–*–Cl | 0.0417 | 174.7 | 187.3 | r-CS/CT-TBP | 1b: N–*–SeCl | 152.1 | 183.1 | r CS/CT-TBP |
| 1b: NSe–*–Br | 0.0307 | 173.3 | 189.5 | r-CS/CT-TBP | 1b: N–*–SeBr | 150.0 | 182.6 | r-CS/CT-TBP |
| 1b: NSe–*–I | 0.0260 | 177.3 | 191.7 | r-CS/CT-TBP | 1b: N–*–SeI | 141.5 | 180.5 | r-CS/CT-TBP |
| 1b: NSe–*–SeMe | 0.0485 | 185.6 | 194.2 | SS/Cov-w | 1b: N–*–SeSeMe | 98.2 | 140.3 | r-CS/t-HBwc |
| 1b: NSe–*–CMe | 0.0998 | 193.0 | 192.7 | SS/Cov-w | 1b: N–*–SeCMe | 85.3 | 107.5 | p-CS/t-HBnc |
| 2a: OS–*–F | 0.1964 | 177.0 | 136.3 | r-CS/t-HBwc | 2a: O–*–SF | 90.3 | 124.6 | r-CS/t-HBwc |
| 2a: OS–*–Cl | 0.0890 | 188.1 | 196.4 | SS/Cov-w | 2a: O–*–SCl | 80.8 | 95.0 | p-CS/t-HBnc |
| 2a: OS–*–Br | 0.0611 | 185.3 | 195.2 | SS/Cov-w | 2a: O–*–SBr | 79.9 | 92.5 | p-CS/t-HBnc |
| 2a: OS–*–I | 0.0483 | 183.9 | 187.9 | SS/Cov-w | 2a: O–*–SI | 78.1 | 88.2 | p-CS/vdW |
| 2a: OS–*–SMe | 0.0971 | 191.4 | 197.5 | SS/Cov-w | 2a: O–*–SSMe | 76.5 | 84.9 | p-CS/vdW |
| 2a: OS–*–CMe | 0.1320 | 196.0 | 199.7 | SS/Cov-w | 2a: O–*–SCMe | 75.7 | 84.4 | p-CS/vdW |
| 2b: OSe–*–F | 0.1018 | 153.7 | 141.8 | r-CS/t-HBwc | 2b: O–*–SeF | 101.4 | 147.4 | r-CS/t-HBwc |
| 2b: OSe–*–Cl | 0.0603 | 180.4 | 184.4 | SS/Cov-w | 2b: O–*–SeCl | 91.1 | 125.9 | r-CS/t-HBwc |
| 2b: OSe–*–Br | 0.0448 | 181.1 | 190.8 | SS/Cov-w | 2b: O–*–SeBr | 88.9 | 119.2 | p-CS/t-HBnc |
| 2b: OSe–*–I | 0.0367 | 183.3 | 191.7 | SS/Cov-w | 2b: O–*–SeI | 84.4 | 105.3 | p-CS/t-HBnc |
| 2b: OSe–*–SeMe | 0.0533 | 186.7 | 194.0 | SS/Cov-w | 2b: O–*–SeSeMe | 79.4 | 89.0 | p-CS/vdW |
| 2b: OSe–*–CMe | 0.1016 | 193.2 | 192.7 | SS/Cov-w | 2b: O–*–SeCMe | 77.6 | 84.2 | p-CS/vdW |
| 3a: SS–*–F | 0.1840 | 180.2 | 150.0 | SS/Cov | 3a: S–*–SF | 121.2 | 167.1 | r-CS/CT-MC |
| 3a: SS–*–Cl | 0.0825 | 187.2 | 196.8 | SS/Cov-w | 3a: S–*–SCl | 95.4 | 133.8 | r-CS/t-HBwc |
| 3a: SS–*–Br | 0.0569 | 184.2 | 195.5 | SS/Cov-w | 3a: S–*–SBr | 93.9 | 131.4 | r-CS/t-HBwc |
| 3a: SS–*–I | 0.0461 | 183.6 | 188.7 | SS/Cov-w | 3a: S–*–SI | 87.9 | 121.5 | p-CS/t-HBnc |
| 3a: SS–*–SMe | 0.0949 | 191.2 | 197.5 | SS/Cov-w | 3a: S–*–SSMe | 81.0 | 109.4 | p-CS/t-HBnc |
| 3a: SS–*–CMe | 0.1305 | 196.0 | 199.7 | SS/Cov-w | 3a: S–*–SCMe | 77.3 | 127.2 | p-CS/t-HBnc |
| 3b: SSe–*–F | 0.0888 | 155.1 | 145.3 | r-CS/t-HBwc | 3b: S–*–SeF | 141.3 | 177.4 | r-CS/CT-MC |
| 3b: SSe–*–Cl | 0.0503 | 178.0 | 188.0 | r-CS/CT-TBP | 3b: S–*–SeCl | 125.3 | 168.7 | r-CS/CT-MC |
| 3b: SSe–*–Br | 0.0375 | 177.7 | 191.9 | r-CS/CT-TBP | 3b: S–*–SeBr | 120.9 | 165.0 | r-CS/CT-MC |
| 3b: SSe–*–I | 0.0327 | 181.4 | 192.7 | SS/Cov-w | 3b: S–*–SeI | 108.1 | 151.7 | r-CS/CT-MC |
| 3b: SSe–*–SeMe | 0.0515 | 186.3 | 194.0 | SS/Cov-w | 3b: S–*–SeSeMe | 88.2 | 116.7 | p-CS/t-HBnc |
| 3b: SSe–*–CMe | 0.0994 | 193.3 | 193.2 | SS/Cov-w | 3b: S–*–SeCMe | 82.4 | 105.9 | p-CS/t-HBnc |
| 4a: SeS–*–F | 0.1831 | 180.4 | 151.3 | SS/Cov | 4a: Se–*–SF | 118.8 | 163.1 | r-CS/CT-MC |
| 4a: SeS–*–Cl | 0.0807 | 186.8 | 196.9 | SS/Cov-w | 4a: Se–*–SCl | 98.3 | 135.3 | r-CS/t-HBwc |
| 4a: SeS–*–Br | 0.0554 | 183.9 | 195.7 | SS/Cov-w | 4a: Se–*–SBr | 97.5 | 134.2 | r-CS/t-HBwc |
| 4a: SeS–*–I | 0.0454 | 183.5 | 189.0 | SS/Cov-w | 4a: Se–*–SI | 91.3 | 124.8 | r-CS/t-HBwc |
| 4a: SeS–*–SMe | 0.0944 | 191.2 | 197.5 | SS/Cov-w | 4a: Se–*–SSMe | 83.2 | 112.2 | p-CS/t-HBnc |
| 4a: SeS–*–CMec | 0.1308 | 195.9 | 199.7 | SS/Cov-w | 4a: Se–*–SCMe | b | b | b |
| 4b: SeSe–*–F | 0.0869 | 155.4 | 146.0 | r-CS/t-HBwc | 4b: Se–*–SeF | 140.9 | 176.7 | r-CS/CT-MC |
| 4b: SeSe–*–Cl | 0.0482 | 177.4 | 188.5 | r-CS/CT-TBP | 4b: Se–*–SeCl | 127.5 | 168.9 | r-CS/CT-MC |
| 4b: SeSe–*–Br | 0.0357 | 176.7 | 192.0 | r-CS/CT-TBP | 4b: Se–*–SeBr | 124.3 | 165.8 | r-CS/CT-MC |
| 4b: SeSe–*–I | 0.0313 | 180.7 | 192.9 | SS/Cov-w | 4b: Se–*–SeI | 112.7 | 154.1 | r-CS/CT-MC |
| 4b: SeSe–*–SeMe | 0.0510 | 186.2 | 194.0 | SS/Cov-w | 4b: Se–*–SeSeMe | 91.1 | 118.5 | r-CS/t-HBwc |
| 4b: SeSe–*–CMe | 0.0993 | 193.1 | 193.2 | SS/Cov-w | 4b: Se–*–SeCMe | 84.5 | 108.5 | p-CS/t-HBnc |
| 5c: TeTe–*–F | 0.0655 | 121.1 | 115.8 | r-CS/t-HBwc | 5c: Te–*–TeF | 163.8 | 184.8 | r-CS/CT-TBP |
| 5c: TeTe–*–Cl | 0.0331 | 163.6 | 154.9 | r-CS/CT-MC | 5c: Te–*–TeCl | 158.2 | 184.3 | r-CS/CT-TBP |
| 5c: TeTe–*–Br | 0.0274 | 170.7 | 173.0 | r-CS/CT-MC | 5c: Te–*–TeBr | 156.3 | 183.9 | r-CS/CT-TBP |
| 5c: TeTe–*–I | 0.0236 | 178.5 | 188.3 | r-CS/CT-TBP | 5c: Te–*–TeI | 149.3 | 182.0 | r-CS/CT-TBP |
| 5c: TeTe–*–TeMe | 0.0332 | 186.9 | 190.8 | SS/Cov-w | 5c: Te–*–TeTeMe | 102.0 | 148.7 | r-CS/t-HBwc |
| 5c: TeTe–*–CMe | 0.0615 | 180.6 | 163.8 | SS/Cov-w | 5c: Te–*–TeCMe | 92.7 | 133.7 | r-CS/t-HBwc |
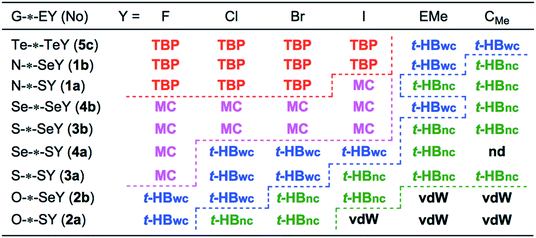
Nature of the G⋯E and E–Y interactions in 1–5
The criteria to classify the interactions in question is formulated based on the signs of Hb(rc) − Vb(rc)/2 and Hb(rc), similarly to those by Espinosa and coworkers.14,41 In this classification, we employ regular CS interactions for those with 0 < Hb(rc) − Vb(rc)/2 and 0 > Hb(rc) to distinguish the CS interactions of the region from pure CS interactions of 0 < Hb(rc) − Vb(rc)/2 and 0 < Hb(rc). The criteria also characterize the interactions in question by using the signs of d(Hb(rc) − Vb(rc)/2)/dr and dHb(rc)/dr, although dHb(rc)/(Hb(rc) − Vb(rc)/2) is employed in QTAIM-DFA, as aforementioned. Interactions in question will be classified and characterized by θ and θp, respectively, after the treatment of the interactions in question with QTAIM-DFA.It is instructive to survey the criteria shown in Scheme S3 and Table S1 of the ESI,† before detailed discussion. The criteria tell us that 45° < θ < 180° (0 < Hb(rc) − Vb(rc)/2) for the CS interactions and 180° < θ < 206.6° (Hb(rc) − Vb(rc)/2 < 0) for the SS interactions.28 The CS interactions are sub-divided into 45°< θ < 90° (Hb(rc) > 0) for the pure CS (p-CS) interactions and 90° < θ < 180° (Hb(rc) < 0) for the regular CS (r-CS) interactions.14,16,17,24,25 In the p-CS region of 45° < θ < 90°, the character of interactions will be the vdW type for 45° < θp < 90° (45° < θ < 75°), whereas it will be t-HBnc (the typical hydrogen bonds type with no covalency) for 90° < θp < 125° (75° < θ < 90°), where θ = 75° and θp = 125° are tentatively given to satisfy θp = 90° and θ = 90°, respectively. The CT interactions will appear in the r-CS region of 90° < θ < 180°. The t-HB interactions with covalency (t-HBwc) appear in the range of 125° < θp < 150° (90° < θ < 115°), where (θ, θp) = (115°, 150°) are tentatively borderline between the nature of t-HBwc and CT-MC (molecular complex formation through CT). The borderline interactions between CT-MC and CT-TBP (trigonal bipyramidal adduct formation through CT) is defined by (θ, θp) = (150°, 180°), where θ = 150° is tentatively given corresponding to θp = 180°. As a result, the (θ, θp) values of (75°, 90°), (90°, 125°), (115°, 150°), (150°, 180°) and (180°, 190°) correspond to the borderlines between the nature of interactions for vdW/t-HBnc, t-HBnc/t-HBwc, t-HBwc/CT-MC, CT-MC/CT-TBP and CT-TBP/Cov-w (weak covalent bonds), respectively. The covalent bonds (Cov) will be strong (Cov-s) if R > 0.15 au, but they will be weak for R < 0.15 au (Cov-w). θp = 190° is tentatively given for θ = 180°, the border for CT-TBP/Cov-w. The parameters, described in bold, are superior to the tentatively given parameters, described in plane, in the classification and/or characterization of interactions. However, the rule should be carefully applied to the E–F bonds since the values of Hb(rc) − Vb(rc)/2 and Hb(rc) will be greater for the bonds containing F.42
The nature of the E–*–Y bonds is discussed first. The (R, θ, θp) values are (0.034–0.132 au, 180.3–196.0°, 187.9–199.7°) for E = S of the S–*–Cl, S–*–Br, S–*–I, S–*–SMe and/or S–*–CMe interactions with G = N, O, S and Se, except for GE–*–Y = NS–*–Br, of which (R, θ, θp) are (0.038 au, 176.7°, 193.9°). Therefore, the interactions of the former are typically classified as the SS interactions and characterized to be the Cov-w nature (SS/Cov-w), while the latter is predicted to have the r-CS/CT-TBP nature. In the case of E = Se, the nature of GSe–*–Y is affected by the change of G and Y. The OSe–*–Cl, OSe–*–Br and OSe–*–I interactions are predicted to have the SS/Cov-w nature with (R, θ, θp) of (0.037–0.060 au, 180.4–183.3°, 184.4–191.7°), while NSe–*–Cl, NSe–*–Br and NSe–*–I are predicted to have the r-CS/CT-TBP nature with (R, θ, θp) of (0.026–0.042 au, 173.3–177.3°, 187.3–191.7°). The Se–*–Cl and Se–*–Br interactions with G = S and Se are predicted to have the r-CS/CT-TBP nature with (R, θ, θp) of (0.036–0.050 au, 176.7–178.0°, 188.0–192.0°), whereas the SS/Cov-w nature is predicted for Se–*–I, Se–*–SeMe and Se–*–CMe with G = S and Se, as (R, θ, θp) are (0.031–0.099 au, 180.7–193.3°, 192.7–194.0°).
In the case of Y = F in GE–*–Y, the E–*–F interactions show a specific and complex nature due to the highly electronegative character of F. The (R, θ, θp) values are (0.156–0.184 au, 180.2–183.0°, 150.0–175.2°) for GS–*–F with G = N, S and Se. As a result, the bonds could be characterized as Cov-s based on the values of R and θ; however, the θp values do not satisfy the requirements for Cov-s (or Cov). Therefore, they are characterized as “Cov” in this work, where θ is superior to θp, in this case. The (R, θ, θp) values are (0.196 au, 177.0°, 136.3°) for S–*–F with G = O, which is classified as r-CS and characterized as t-HBwc (r-CS/t-HBwc), irrespective of the R value. The observed results must be the reflection of the specific and complex nature of S–*–F, where the R values are much larger than those expected based on the (θ, θp) values. The R values of S–*–F are about two times larger than those corresponding S–*–Cl, respectively, although the (θ, θp) values for S–*–F are (much) smaller than those corresponding S–*–Cl, respectively. For the Se–*–F interactions, the (R, θ, θp) values are (0.083–0.102 au, 153.7–155.4°, 141.8–146.9°) for G = N, O, S and Se; therefore, the interactions are predicted to have the r-CS/t-HBwc nature. The nature of r-CS/t-HBwc predicted for the Se–*–F interactions seems rather curious, which may come from the QTAIM-DFA parameters of θ > θp, although the values are θ < θp for the usual interactions. The (R, θ, θp) values for Te–*–F with G = Te are (0.066 au, 121.1°, 115.8°), which is also predicted to have the r-CS/t-HBwc nature. The R values of Se–*–F are also about two times larger than those corresponding Se–*–Cl, respectively, although the (θ, θp) values for Se–*–F are (much) smaller than those corresponding Se–*–Cl.
The nature of the G–*–E interactions of GEY σ(3c–4e) in 1–5 is discussed next. BP with BCP was detected for all G–*–E interactions of 1–5, except for 4a (Y = CMe). The Se–*–SCMe interaction in 4a (Y = CMe) would not satisfy the conditions for the appearance of BP with BCP.43 Therefore, the nature of the G–*–E interactions in 1–5 is discussed without considering the interaction in 4a (Y = CMe). The R values in Table 1 are less than 0.031 au, therefore, the nature of the G–*–E interactions in 1–5 can be discussed using the (θ, θp) values, except for that of 4a (Y = CMe). The θ values for G–*–E in 1–5 are in the range of 75.7° ≤ θ ≤ 163.8°; therefore, the G–*–E interactions in 1–5 are classified as p-CS or r-CS interactions.
The nature is discussed on an individual basis. The (θ, θp) values for N–*–SY (1a: Y = F, Cl and Br), N–*–SeY (1b: Y = F, Cl, Br and I) and Te–*–TeY (5c: Y = F, Cl, Br and I) are (141.5–163.8°, 180.5–189.9°). Therefore, the interactions are predicted to have the r-CS/CT-TBP nature. The r-CS/CT-MC nature is similarly predicted for N–*–SY (1a: Y = I), S–*–SY (3a: Y = F), S–*–SeY (3b: Y = F, Cl, Br and I), Se–*–SY (4a: Y = F) and Se–*–SeY (4b) (Y = F, Cl, Br and I), as the (θ, θp) values are (108.1–141.3°, 151.7–179.2°). Alternatively, the p-CS/vdW nature is predicted for O–*–SY (2a: Y = I, SMe and Me) and O–*–SeY (2b: Y = SeMe and Me) with (θ, θp) = (75.7–79.4°, 84.2–89.0°), while the p-CS/t-HBnc nature is predicted for N–*–SY (1a: Y = SMe and Me), N–*–SeY (1b: Y = Me), O–*–SY (2a: Y = Cl and Br), O–*–SeY (2b: Y = Br and I), S–*–SY (3a: Y = I, SMe and Me), S–*–SeY (3b: Y = SeMe and Me), Se–*–SY (4a: Y = SMe) and Se–*–SeY (4b: Y = Me) with (θ, θp) = (77.3–88.9°, 92.5–127.2°). The (θ, θp) values are (90.3–102.0°, 118.5–148.7°) for N–*–SeY (1b: Y = SeMe), O–*–SeY (2a: Y = F), O–*–SeY (2b: Y = F and Cl), S–*–SY (3a: Y = Cl and Br), Se–*–SY (4a: Y = Cl, Br and I), Se–*–SeY (4b: Y = SeMe) and Te–*–TeY (5c: Y = TeMe and Me); therefore, the p-CS/t-HBwc nature is predicted for the interactions.
The values of (Hb(rc) − Vb(rc)/2, Hb(rc)) for O–*–SeCl (2b) and O–*–SeBr (2b) are (0.0126 au, −0.0003 au) and (0.0119 au, 0.0002 au), respectively, as shown in Table 1, although the values have been reported as (0.0106 au, −0.0013 au) and (0.0099 au, −0.0011 au), respectively.13c The Hb(rc) − Vb(rc)/2 values for O–*–SeCl (2b) and O–*–SeBr (2b) in literature are approximately 0.002 au smaller than those in Table 1, while the Hb(rc) values in the literature are more than 0.001 au smaller than those in Table 1. The differences seem small, however, the values are just on the borderline between the t-HBnc and t-HBwc natures. Specifically, the positive values of Hb(rc) correspond to the pure CS nature with no covalency (p-CS/t-HBnc), whereas the negative values represent the regular CS nature with covalency (r-CS/t-HBwc). Therefore, it is necessary to select the basis sets and levels for the calculations very carefully.33 We believe that MP2/6-311+(3df, 3pd) or greater methods, such as MP2/BSS-A, would be necessary if the results are discussed in relation to the observed structural parameters.
The predicted nature for G–*–EY in 1a–5c is summarized in Fig. 4. The strength of the G–*–E interactions seems weakest for O–*–S and becomes stronger in the order shown in eqn (9). As shown in Fig. 4, the E–Y bonds in 1a–5c affect the strength of the G–*–E interaction. The effect seems smallest for CMe and becomes larger in the order shown in eqn (10).
| G–*–EY = O–*–SY < O–*–SeY < S–*–SY < Se–*–SY < S–*–SeY < Se–*–SeY < N–*–SY < N–*–SeY ≈ Te–*–TeY | (9) |
| GE–*–Y = GE–*–CMe < GE–*–EMe < GE–*–I < GE–*–Br < GE–*–Cl < GE–*–F | (10) |
The strength of G–*–EY in GEY σ(3c–4e) of 1a–5c can also be evaluated by the NBO analysis, where donor NBO and acceptor NBO must be related to n(G) and σ*(E–Y), respectively. The results are discussed in relation to those of the NBO analysis.
NBO analysis for G–*–EY in GEY σ(3c–4e) of 1a–5c
The stabilization energy E(2) in NBO analysis44 is calculated for each donor NBO(i) and acceptor NBO(j) based on the second-order perturbation theory according to eqn (11). The qi value in eqn (11) is the donor orbital occupancy, Ei, Ej are diagonal elements (orbital energies) and F(i,j) is the off-diagonal NBO Fock matrix element. The treatments evaluate the CT terms of the intramolecular interactions.| E(2) = qiF(i,j)2/(Ej − Ei) | (11) |
NBO is applied to 1a–5c (see, Scheme 1d for the simplified interaction model of G–*–EY in GEY σ(3c–4e)). The E(2) values were successfully obtained under the threshold of 0.5 kcal mol−1 (2.1 kJ mol−1). The results of NBO analysis, calculated with MP2/BSS-A, are shown in Table S5 of the ESI.† No data were detected for the np(N) → σ*(E–Y) interactions in 1a and 1b, as the only one nonbonded orbital of N is characterized as s-type (ns(N)) (see Table S5 of the ESI†). In the case of 1a, 1b, 2b, 3a, 3b, 4b and 5c, the E–F bonds (E = S, Se and Te) are described as the ionic E+–F− bonds in the NBO framework, since the valence orbitals of F are almost fully filled with electrons. The orbitals for the ionic E+–F− bonds are described as np(E+: E = S, Se and Te) and np(F−) in Table S5 of the ESI.† Instead, the S–F bonds in 2a and 4a are denoted as S–F bonds. Very large values of E(2) were predicted for ns(N) → np(E+: E = S and Se) in 1a and 1b and np(E) → np(E+) for (E, E+) = (O, Se+) in 2a, (S, S+) in 3a, (S, Se+) in 3b, (Se, Se+) in 4b and (Te, Te+) in 5c. The E(2) values are larger than 20 kcal mol−1 and up to 126 kcal mol−1 in 5c. Very large values of E(2) were also predicted for ns(N) → σ*(S–Y) in 1a, ns(N) → σ*(Se–Y) in 1b, np(S) → σ*(Se–Y) in 3b, np(Se) → σ*(Se–Y) in 4b and np(Te) → σ*(Te–Y) in 5c, where Y = Cl, Br and/or I. As shown in Table S5 of the ESI,† the predicted E(2) values for G–*–EY in 1a–5c will be stronger in an order similar to that shown in eqn (9). The order for E(2) evaluated with NBO shown in eqn (12) is in accordance with that estimated with QTAIM-DFA shown in eqn (9).
| G–*–EY = O–*–SY ≪ O–*–SeY ≈ S–*–SY ≈ Se–*–SY ≪ S–*–SeY < Se–*–SeY < N–*–SY < N–*–SeY ≪ Te–*–TeY | (12) |
The E(2) values are also larger than 20 kcal mol−1, and this value is greater than 60 kcal mol−1 in 5c. The E(2) values for np(G) → σ*(E–Y), other than those given above, are less than 12 kcal mol−1, while those for ns(E) → np(E′+) and ns(G) → σ*(E–Y) in 2a–5c are less than approximately 5 kcal mol−1. Some E(2) values were not detected for ns(G) → σ*(E–Y), which would be smaller than the threshold values of 0.5 kcal mol−1 (see Table S5 of the ESI†).
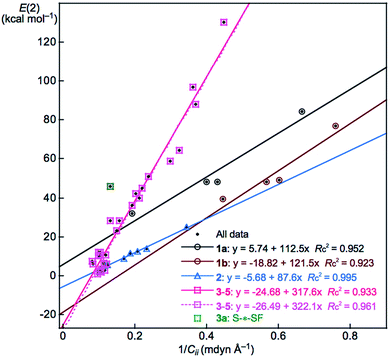
It is noteworthy that the E(2) values for ns(N) → np(E+: E = S and Se) in 1a and 1b and the combined values of ns(G) → σ*(E–Y) and np(G) → σ*(E–Y) seem to increase proportionally to the inverse values of Cii, the diagonal elements of the compliance constants for an internal coordinate i, (Cii−1). To confirm the proportionality, the E(2) values are plotted versus Cii−1, separately by 1a, 1b, 2 (2a and 2b) and 3–5 (3a, 3b, 4a, 4b and 5c). Fig. 5 shows the plot and the correlations are very good. The correlation for 3–5 (y = −24.68 + 317.6x: Rc2 = 0.933) will be better if the data point of 3a (S–*–SF) is omitted from the correlation (y = −26.49 + 322.1x: Rc2 = 0.961). As also shown in Fig. 5, the tangent lines for the correlations (a in y = ax + b) become larger in the order of 2 (a = 88) < 1a (113) ≈ 1b (122) ≪ 3–5 (318). It is noteworthy that the CT contributions in G–*–EY of GEY σ(3c–4e) in 1a–5c can also be estimated based of the Cii (or Cii−1) values. Very good proportionality will be observed if the E(2) values are plotted versus Cii−1 and are analysed suitably separated by G.
Conclusions
Weak interactions in chemistry determine the fine details of structures and create fine properties in materials, while strong interactions construct the framework of molecules. Three centre four electron interactions of the σ-type (σ(3c–4e)) are typical cases of such weak interactions. The noncovalent G⋯E interactions and the (covalent) E–Y bonds in GEY σ(3c–4e) of o-MenGCH2C6H4EY are elucidated with the QTAIM dual functional analysis (QTAIM-DFA) and QC calculations. The system detects delicate interactions by considering the suitable rigidity. The dynamic nature of the interactions can be discussed by applying QTAIM-DFA in addition to the static nature. The dynamic nature is called the intrinsic dynamic nature if the perturbed structures are generated using the coordinates derived from the compliance constants in QTAIM-DFA, as the coordinates are invariant to the choice of coordinate system. The E–*–Y bonds are typically classified as the SS interactions for G = N, O, S and Se, although there are some exceptions. The E–F bonds are described as ionic E+–F− bonds for all GE–F, except for OS–F (2a), in the NBO framework. In the case of the noncovalent G–*–E interactions of GEY σ(3c–4e), these interactions are predicted to have vdW to CT-TBP natures. The strength of G–*–E seems weakest for O–*–S and becomes stronger in the order show in eqn (9). The G–*–E interactions apparently inversely affect the strength of the E–Y bonds.The strength of G–*–EY in GEY σ(3c–4e) is also evaluated with NBO. Very large values of E(2) were predicted for ns(N) → np(E+: E = S and Se) and np(E) → np(E+) for (E, E+) = (O, Se+), (S, S+), (S, Se+), (Se, Se+) and (Te, Te+) (Y− = F−). The E(2) value results in 126 kcal mol−1 in 5c. The predicted E(2) values for G–*–EY in 1a–5c will be stronger in the similar order shown in eqn (12). The order for E(2) determined with NBO seems to be in accordance with that estimated with the QTAIM approach. It is noteworthy that E(2) increases in a manner inversely proportional to Cii (Cii−1). The proportionality is demonstrated by the plot of E(2) versus Cii−1. The results show that the contributions from the CT interactions in G–*–EY of 1a–5c can be estimated by the Cii (Cii−1) values. Very good proportionality will be observed if the E(2) values are plotted versus Cii−1 and are analysed suitably separated by G (and E). As a result, Cii (or Cii−1) will be a good tool to elucidate the complex energy profiles of species.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was partially supported by a Grant-in-Aid for Scientific Research (No. 17K05785) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. L. S. acknowledges the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 665778 – POLONEZ funding programme, National Science Centre, Poland – project registration number 2016/21/P/ST5/03512. This work was performed under the umbrella of the network Selenium Sulfur and Redox Catalysis (SeSRedCat).Notes and references
- A. J. Pacuła, F. Mangiavacchi, L. Sancineto, J. L. Eder, J. Ścianowski and C. Santi, Curr. Chem. Biol., 2015, 9, 97–112 CrossRef.
- (a) G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448 CrossRef CAS; (b) J. I. Musher, Angew. Chem., Int. Ed. Engl., 1969, 8, 54–68 CrossRef CAS; (c) R. J. Hatch and R. E. Rundle, J. Am. Chem. Soc., 1951, 73, 4321–4324 CrossRef; (d) R. E. Rundle, J. Am. Chem. Soc., 1963, 85, 112–113 CrossRef CAS; (e) R. A. Hayes and J. C. Martin, Sulfurane Chemistry in Organic Sulfur Chemistry: Theoretical and Experimental Advances, ed. F. Bernardi, I. G. Csizmadia and A. Mangini, Elsevier, Amsterdam, 1985; ch. 8 Search PubMed.
- (a) M. M. L. Chen and R. J. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1647–1653 CrossRef CAS; (b) P. J. Hay, J. Am. Chem. Soc., 1977, 99, 1003–1012 CrossRef CAS; (c) W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295 CrossRef; (d) A. E. Reed and F. Weinhold, J. Am. Chem. Soc., 1986, 108, 3586–3593 CrossRef CAS; (e) A. E Reed and P. R. Schleyer, J. Am. Chem. Soc., 1990, 112, 1434–1445 CrossRef.
- (a) Chemistry of Hypervalent Compounds, ed. K.-y. Akiba, Wiley-VCH, New York, 1999 Search PubMed; (b) W. Nakanishi, Hypervalent Chalcogen Compounds In Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova, Royal Society of Chemistry, Cambridge, 2006, ch. 10.3, pp. 644–668 Search PubMed; (c) A. J. Mukherjee, S. S. Zade, H. B. Singh and R. B. Sunoj, Chem. Rev., 2010, 110, 4357–4416 CrossRef CAS PubMed.
- G. Buemi, Intramolecular Hydrogen Bonds. Methodologies and Strategies for Their Strength Evaluation, in Hydrogen Bonding – New Insights, Vol. 3, Challenges and Advances in Computational Chemistry and Physics, ed. S. J. Grabowski, Springer, New York, 2006, ch. 2 Search PubMed.
- G. Gilli and P. Gilli, The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory (IUCr Monographs on Crystallography), Oxford University Press, Oxford, 2009 Search PubMed.
- M. Meot-Ner (Mautner), Chem. Rev., 2005, 105, 213–284 CrossRef PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- S. Hayashi, K. Matsuiwa, M. Kitamoto and W. Nakanishi, J. Phys. Chem. A, 2013, 117, 1804–1816 CrossRef CAS PubMed.
- T. Nishide, S. Hayashi and W. Nakanishi, ChemistryOpen, 2018, 7, 565–575 CrossRef CAS PubMed.
- (a) W. Nakanishi, S. Hayashi, A. Sakaue, G. Ono and Y. Kawada, J. Am. Chem. Soc., 1998, 120, 3635–3640 CrossRef CAS; (b) W. Nakanishi, S. Hayashi and T. Uehara, J. Phys. Chem. A, 1999, 103, 9906–9912 CrossRef CAS; (c) W. Nakanishi and S. Hayashi, J. Org. Chem., 2002, 67, 38–48 CrossRef CAS PubMed; (d) K. Yamane, S. Hayashi, W. Nakanishi, T. Sasamori and N. Tokitoh, Polyhedron, 2008, 27, 3557–3566 CrossRef CAS; (e) S. Hayashi and W. Nakanishi, Bull. Chem. Soc. Jpn., 2008, 81, 1605–1615 CrossRef CAS; (f) S. Hayashi and W. Nakanishi, Bull. Chem. Soc. Jpn., 2009, 82, 712–722 CrossRef CAS; (g) T. Nakai, M. Nishino, S. Hayashi, M. Hashimoto and W. Nakanishi, Dalton Trans., 2012, 41, 7485–7497 RSC; (h) S. Hayashi, M. Uegaito, T. Nishide, E. Tanaka, W. Nakanishi, T. Sasamori, N. Tokitoh and M. Minoura, New J. Chem., 2019, 43, 14224–14237 RSC.
- M. Tiecco, L. Testaferri, C. Santi, C. Tomassini, S. Santoro, F. Marini, L. Bagnoli, A. Temperini and F. Costantino, Eur. J. Org. Chem., 2006, 4867–4873 CrossRef CAS.
- (a) M. Iwaoka and S. Tomoda, J. Am. Chem. Soc., 1996, 118, 8077–8084 CrossRef CAS; (b) M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 1902–1909 CrossRef CAS PubMed; (c) M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2004, 126, 5309–5317 CrossRef CAS PubMed; (d) M. Iwaoka, T. Katsuda, H. Komatsu and S. Tomoda, J. Org. Chem., 2005, 70, 321–327 CrossRef CAS PubMed.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529 CrossRef CAS See also R. Bianchi, G. Gervasio and D. Marabello, C. R. Chim., 2005, 8, 1392 CrossRef.
- The natures of G–*–E in I with various (G, E–Y) were also elucidated.11h,45,46.
- Atoms in Molecules. A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- C. F. Matta and R. J. Boyd, in An Introduction to the Quantum Theory of Atoms in Molecules In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007, ch. 1 Search PubMed.
- (a) R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061 CrossRef CAS; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS; (c) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314 CrossRef CAS; (d) F. Biegler-könig, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317 CrossRef; (e) R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9 CrossRef CAS; (f) T. H. Tang, R. F. W. Bader and P. MacDougall, Inorg. Chem., 1985, 24, 2047 CrossRef CAS; (g) F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545 CrossRef; (h) F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489 CrossRef PubMed.
- J. A. Dobado, H. Martínez-García and M. R. Sundberg, J. Am. Chem. Soc., 2000, 122, 1144 CrossRef CAS.
- J. M. Molina and J. A. Dobado, Theor. Chem. Acc., 2001, 105, 328 Search PubMed.
- S. K. Ignatov, N. H. Rees, B. R. Tyrrell, S. R. Dubberley, A. G. Razuvaev, P. Mountford and G. I. Nikonov, Chem.–Eur. J., 2004, 10, 4991 CrossRef CAS PubMed.
- W. Nakanishi, T. Nakamoto, S. Hayashi, T. Sasamori and N. Tokitoh, Chem.–Eur. J., 2007, 13, 255 CrossRef CAS PubMed.
- Dots are usually employed to show BCPs in molecular graphs. Therefore, A–•–B would be more suitable to describe the BP with the BCP. Nevertheless, A–*–B is employed to emphasize the existence of the BCP on the BP, in question, in our case..
- (a) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057 CrossRef CAS PubMed; (b) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2008, 112, 13593–13599 CrossRef CAS PubMed.
- W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197 CrossRef CAS.
- W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423–7430 CrossRef CAS PubMed.
- W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293–1305 CrossRef CAS.
- W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2013, 117, 1795–1803 CrossRef CAS PubMed.
- QTAIM-DFA parameters of (R, θ) and (θp, κp) are defined as: R = (x2 + y2)1/2, where (x,y) = (Hb(rc) − Vb(rc)/2, Hb(rc)), θ = 90° − tan−1 (y/x), θp = 90° − tan−1 (dy/dx), and κp = |d2y/dx2|/[1 + (dy/dx)2]3/2. (See, eqn. (S3)–(S6) of the ESI.†).
- W. Nakanishi and S. Hayashi, Int. J. Quantum Chem., 2018, 118, e25590 CrossRef.
- The Cii values and the coordinates corresponding to Cii were calculated by using the Compliance 3.0.2 program released by Grunenberg and Brandhorst, http://www.oc.tu-bs.de/Grunenberg/compliance.html.
- (a) K. Brandhorst and J. Grunenberg, J. Chem. Phys., 2010, 132, 184101–184107 CrossRef; (b) K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558–1567 RSC; (c) J. Grunenberg, Chem. Sci., 2015, 6, 4086–4088 RSC.
- S. Hayashi, T. Nishide, K. Ueda, K. Hayama and W. Nakanishi, ChemistrySelect, 2019, 4, 6198–6208 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels,Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural bond orbital analysis program, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124 Search PubMed.
- (a) C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef; (b) J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643 CrossRef CAS; (c) J. Gauss, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1001–1008 CrossRef CAS.
- The perturbed structures with CIV correspond to the improved ones of the vibrational mode for each zero-point internal vibration. Therefore, each perturbed structure with CIV can be imaged based on the vibrational mode of the zero-point internal vibration. The perturbed structures with CIV are very close to those obtained with POM, so are the relative energies..
- The AIM2000 program (Version 2.0) is employed to analyze and visualize atoms-in-molecules: F. Biegler-König, J. Comput. Chem., 2000, 21, 1040–1048 CrossRef . See also ref. 16..
- T. A. Keith, AIMAll (Version 17.11.14), TK Gristmill Software, Overland Park KS, USA, 2017, aim.tkgristmill.com Search PubMed.
- E. Espinosa and coworkers discussed the behaviour of the interactions in the wide view based on the QTAIM functions at BCPs on H⋯F of the fully optimized various X–H⋯F–Y and those on the partially optimized [F–H–F]−.14 On the other hand, we employed the standard interactions in the typical species and the wide range of perturbed structures of [Cl–Cl–Cl]− for the purpose. QTAIM-DFA parameters, instead of the QTAIM functions, are employed for the classification and characterization of interactions, after treatment of Q TAIM-DFA.24a,30.
- The (R, θ, θp:CIV) values are evaluated to be (0.354 au, 180.3°, 154.5°), (0.152 au, 194.4°, 198.4°), and (0.102 au, 192.8°, 195.9°) for the C–*–F, C–*–Cl, and C–*–Cl bonds, respectively, in CH3X (X = F, Cl and Br) of which R value of C–*–F is predicted to be very large. See also the ESI of ref. 27 for the QTAIM parameters of the fluorine containing interactions..
- The bond path corresponding to the interaction being not detected..
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO 3.0 Program Manual, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 1990 Search PubMed.
- The (θ, θp) values are determined for (G, EY) = (MeO, SMe), (MeO, SeMe), (MeS, SeMe), (MeS, SMe), (MeSe, SeMe) and (MeTe, TeMe) in I to be (83.4, 96.0), (85.1, 101.2), (100.9, 133.4), (98.0, 126.2), (101.2, 130.5), and (122.3, 165.8), respectively. The (θ, θp) values for I are larger than the corresponding values in 2–5, respectively.11h,46.
- The (θ and θp) values of I were plotted versus the corresponding values of 2–5, which gave a very good correlation (y = 1.36x − 13.89: Rc2 = 0.954, although the data for (MeS, SMe) being omitted from the correlation). The plot is shown in Fig. S6 of the ESI.†.
Footnote |
| † Electronic supplementary information (ESI) available: QTAIM-DFA approach, computational data, and the fully optimized structures given by Cartesian coordinates, together with total energies of 1–5. See DOI: 10.1039/c9ra09022c |
| This journal is © The Royal Society of Chemistry 2019 |