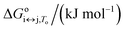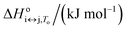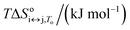Open Access Article
Open Access ArticleProof of concept web application for understanding the energetic basis of oligonucleotide unfolding†
Iztok Prislan *a,
Sara Sajko
*a,
Sara Sajko b,
Nataša Poklar Ulriha and
Luka Fürst*c
b,
Nataša Poklar Ulriha and
Luka Fürst*c
aBiotechnical Faculty, University of Ljubljana, Ljubljana, 1000, Slovenia. E-mail: iztok.prislan@bf.uni-lj.si
bMax Perutz Labs Vienna, Medical University of Vienna, 1030 Vienna, Austria
cFaculty of Computer and Information Science, University of Ljubljana, Ljubljana, 1000, Slovenia. E-mail: luka.fuerst@fri.uni-lj.si
First published on 16th December 2019
Abstract
Measuring and quantifying thermodynamic parameters that determine both the stability of and interactions between biological macromolecules are an essential and necessary complement to structural studies. Although basic thermodynamic parameters for an observed process can be readily obtained, the data interpretation is often slow and analysis quality can be extremely variable. We have started to develop a web application that will help users to perform thermodynamic characterizations of oligonucleotide unfolding. The application can perform global fitting of calorimetric and spectroscopic data, and uses a three-state equilibrium model to obtain thermodynamic parameters for each transition step – namely, the Gibbs energy, the enthalpy, and the heat capacity. In addition, the application can define the number of K+ ions and the number of water molecules being released or taken up during unfolding. To test our application, we used UV spectroscopy, circular dichroism, and differential scanning calorimetry to monitor folding and unfolding of a model 22-nucleotide-long sequence of a human 3′-telomeric overhang, known as Tel22. The obtained data were uploaded to the web application and the global fit revealed that unfolding of Tel22 involves at least one intermediate state, and that K+ ions are released during the unfolding, whereas water molecules are taken up.
1. Introduction
The laws of thermodynamics provide tools for the mathematical description of the stabilities and interactions of biological macromolecules. Although a specialist discipline, thermodynamic studies have become an essential and necessary complement to structural studies, so as to fully define the forces driving folding and binding interactions.1 The increased accessibility of calorimetry hardware means that more laboratories have the potential to measure enthalpy values for binding reactions and conformational transitions of biomolecules. Complete thermodynamic profiles of simple transitions (e.g. two-state) can now be obtained in a relatively straightforward manner using software solutions provided by instrument manufacturers. If thermodynamic analysis requires implementation of complex/multistep transitions or global analysis of experimental data obtained from several experimental techniques however,2 researchers have no other option but to develop their own solutions. As the skills required to build custom software are fairly rare, commercial programs tend to be used indiscriminately for different systems. This can prevent meaningful in-depth thermodynamic analyses, and sometimes result in wrong conclusions.Based on our experience of thermodynamic analysis of biological systems,3–6 we are developing a web application that will be accessible to everyone, and that will allow easy thermodynamic analysis of calorimetric and spectroscopic data. This application can be used as a research and/or teaching tool, and allows comparisons of the thermodynamic parameters obtained between different laboratories. In addition, good quality thermodynamic data are needed for predicting the secondary structure of DNA or RNA molecules. These thermodynamic data can be incorporated into software packages such as UNAFold,7 Freiburg RNA tools,8 RNAsoft,9 ViennaRNA,10 RNAstructure,11 Rtools,12 Bielefeld RNA tools,13 Galaxy RNA workbench14 and others. We have tested our web application with experimental data obtained from monitoring thermal folding/unfolding of the 5′-AG3T2AG3T2AG3T2AG3-3′ (Tel22) DNA sequence.
Tel22 represents a model sequence for human telomeric repeats of d(TTAGGG), and is rich in guanines. Sequences that are rich in guanines can form four-stranded structures known as G-quadruplexes. These are composed of several layers of G-quartets, where four guanines are associated in planar tetrads. G-quadruplexes are not held together by classic Watson–Crick base pairing, but by Hoogsteen base pairing.15,16 Although the configuration of G-quadruplexes might be intramolecular or intermolecular (e.g., bimolecular, tetramolecular),17 it has been proposed that intramolecular G-quadruplexes are more relevant in vivo.18
Blackburn and Gall studied the macronucleus DNA of the ciliate Tetrahymena thermophila, and showed that chromosome ends consist of tandem repeats of guanine-rich sequences.19 This ultimately led to the discovery of telomerase20 and the sequence of the human telomere, which consists of tandem repeats of d(TTAGGG).21,22 The formation of stable G-quadruplexes in the region of telomeric single-stranded overhangs has been shown to inhibit telomerase activity,23–25 and this has increased interest in telomeric G-quadruplexes as promising targets for anticancer agents.26–29 Such agents should have exquisite specificity for G-quadruplexes, but defining them requires an understanding of the forces that are responsible for the structural interconversions of several G-quadruplex structures. These forces are strictly connected to the solution conditions, i.e. temperature, cation type, and water activity, which have major roles in the formation of G-quadruplexes and in their physicochemical properties.30–34
G-quadruplex structures can fold into a variety of topologies.35 Nuclear magnetic resonance and some biophysical techniques have been used to show that at room temperature and in the presence of K+ ions, Tel22 can adopt different structures.36,37 Indeed, it has been suggested that in K+ solutions, Tel22 appears as a mixture of two different intramolecular (3 + 1) G-quadruplexes (Hybrid-1, Hybrid-2).38,39 While the Tel22 structures have been well characterized, their folding pathways are not yet fully understood. On the basis of in silico studies,40–42 it has been suggested that triplex intermediates can participate in the folding of the human telomeric quadruplex, which has been confirmed to a certain extent by in vitro studies.3,43 Studying and understanding the thermodynamics of quadruplex unfolding can contribute to the better design of quadruplex-interactive compounds, and improve the algorithms used to evaluate quadruplex formation and stability.44
Water needs to be taken into account as a ligand for complete physical understanding of the macromolecule stability and conformation.45 The particular conformation of duplex, triplex, or quadruplex DNA depends directly on the degree of hydration, so changes in the water activity can shift the equilibrium to favor one conformation over the others.44,46,47 It has also been shown that small osmolytes (e.g. ethylene glycol, glycerol, acetamide, sucrose) can decrease the water activity and destabilize duplex and triplex DNA.48 On the other hand, decreased water activity stabilizes quadruplexes,34,49,50 which indicates that quadruplexes are less hydrated in their folded form, and that water is taken up during their unfolding. Also, conformational changes of G-quadruplexes can be observed when the water activity is decreased, as shown for the human telomeric quadruplex in potassium solutions.51
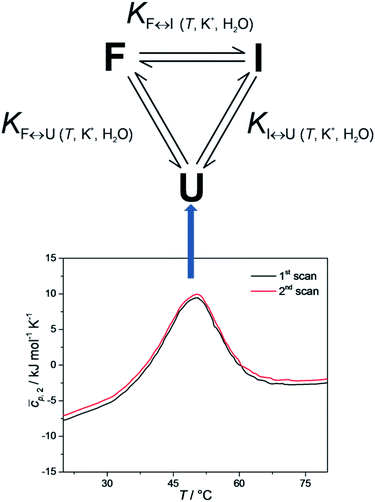
It has been shown that the folding of Tel22 can be described as an equilibrium of a three-state process, which suggests the formation of a stable intermediate triplex structure in the pathway between the fully unfolded structure and the intramolecular G-quadruplex structure.3 The goal of the present study was to develop a web application that could be used to perform thermodynamic characterizations of G-quadruplex unfolding and test it by describing the thermodynamic behavior of Tel22 unfolding. The web application uses spectroscopic and calorimetric data at different salt and co-solute concentrations as an input to calculate thermodynamic parameters of the unfolding mechanism of Tel22. Our results show that the unfolding mechanism of Tel22 can be explained by a three-state equilibrium model (Fig. 1) and that K+ ions are released during the unfolding, whereas water molecules are taken up.
2. Materials and methods
Sample preparation
Tel22 is the oligonucleotide 5′-AGGGTTAGGGTTAGGGTTAGGG-3′, and was obtained at HPLC-grade from Midland Certified Reagent Company (USA). This DNA was first dissolved in water, and then extensively dialyzed (three buffer changes in 24 h) against 10 mM cacodylate buffer with 1 mM EDTA (pH 6.9) using dialysis tubing (Float-A-Lyser; Spectrum Laboratories, USA; Mw cut-off, 500–1000 Da). The DNA concentration in the buffer was determined spectrophotometrically at 25 °C. For the extinction coefficient of the single-stranded forms at 25 °C, an ε260 value of 228.500 M−1 cm−1 was used, which was obtained by extrapolation of the tabulated values52 at 25 °C to 90 °C using procedures reported previously.53 The starting solution of the oligonucleotide was initially heated to 90 °C in an outer thermostat for 5 min, to make sure that all of the DNA was converted into an unfolded form. This was then cooled to 5 °C (cooling rate, 0.5 °C min−1), to allow the DNA to adopt quadruplex structure(s). This was then used in the study.Solution conditions
The buffers used consisted of 10 mM cacodylic acid (DSC, CD, UV) with 1 mM EDTA, with the addition of various concentrations of K+ ions and ethylene glycol. KOH was added to cacodylic acid to pH 6.9, and then KCl was added to obtain the desired K+ ion concentrations (15, 55, 110 mM). To determine the effects of water activity on Tel22 stability, ethylene glycol was added to the buffer with the lowest K+ ion concentration, to provide 3 M ethylene glycol.UV melting
The absorbance versus temperature profiles of the DNA samples were measured in a spectrophotometer (Cary 100 BIO UV/visible; Varian Inc.) that was equipped with a thermoelectric temperature controller, using cells of 1.0 cm path length. The melting of Tel22 at a heating rate of 1.0 °C min−1, followed by its formation at the cooling rate of 1.0 °C min−1, were monitored at 260 nm and 293 nm, between 5 °C and 90 °C. Accurate concentrations were obtained at 25 °C from the melting curves recorded at 260 nm.Circular dichroism spectroscopy
The circular dichroism (CD) spectra of the G-quadruplexes were determined as a function of temperature in a CD spectropolarimeter (62A DS; AVIV) equipped with a thermoelectric temperature controller. The CD spectra of the samples (cDNA ≈ 0.15 mM, in single strands) were collected between 215 nm and 320 nm in a 0.25 mm cuvette with a signal averaging time of 3 s and a bandwidth of 5 nm. The CD spectra were measured in the 5 °C to 90 °C temperature range, and at temperature intervals of 3 °C.Differential scanning calorimetry
Differential scanning calorimetry was performed using a Nano DSC instrument (TA Instruments, USA). The Tel22 concentration used in the DSC studies was cDNA ≈ 0.15 mM, in single strands. Cyclic DSC measurements were performed at heating and cooling rates of 0.5, 1.0, and 2.0 °C min−1. The measured temperature interval was between 1 °C and 90 °C. The corresponding baseline (buffer–buffer) scans were subtracted from the unfolding/folding scans of the samples, and normalized to 1 mole of G-quadruplex in single strands, to obtain the partial molar heat capacity of the DNA,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) p,2, as a function of temperature. These data were analyzed in a model-dependent way by fitting the model function based on the reversible monomolecular three-state model (Fig. 1) to the corresponding experimental thermodynamic functions (see below).
p,2, as a function of temperature. These data were analyzed in a model-dependent way by fitting the model function based on the reversible monomolecular three-state model (Fig. 1) to the corresponding experimental thermodynamic functions (see below).
Thermodynamics of Tel22 folding/unfolding
For each transition step i ↔ j (i ↔ j = F ↔ I, I ↔ U, F ↔ U) in the proposed folding/unfolding mechanism (Fig. 1), the temperature-, cation-concentration-, and water-activity-dependent apparent equilibrium constant was calculated as given in eqn (1):| Ki↔j,T,K+,H2O = [i]/[j]. | (1) |
The real equilibrium constant is cation and water independent, and can be calculated as in eqn (2):
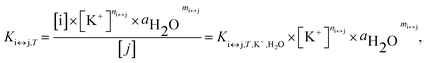 | (2) |
 | (3) |
| Osm = 0.042 + 0.912 × [EG]. | (4) |
Each conformational transition of i↔j can be described in terms of the Gibbs energy by rearranging eqn (2) to eqn (5):
 | (5) |
 is the apparent, and ΔGoi↔j,T the true, thermodynamic Gibbs energy. Using the Gibbs–Helmholtz relationship, Kirchhoff's law, and the reference temperature To of 298.15 K, the apparent Gibbs energy can be expressed as in eqn (6):
is the apparent, and ΔGoi↔j,T the true, thermodynamic Gibbs energy. Using the Gibbs–Helmholtz relationship, Kirchhoff's law, and the reference temperature To of 298.15 K, the apparent Gibbs energy can be expressed as in eqn (6):
 | (6) |
Each equilibrium constant that appears in the proposed model (see Fig. 1) can be expressed as in eqn (7):
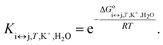 | (7) |
It can be seen from eqn (2), (6) and (7) that to specify the population of any species in a single i ↔ j transition step, five parameters need to be calculated: 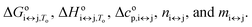 As all of these parameters are state dependent, only 10 parameters (rather than 15) are needed to calculate the population of species F, I, and U in the solution at any T, K+, and ethylene glycol concentration. The calculated population of species i can be expressed as the molar ratio given in eqn (8):
As all of these parameters are state dependent, only 10 parameters (rather than 15) are needed to calculate the population of species F, I, and U in the solution at any T, K+, and ethylene glycol concentration. The calculated population of species i can be expressed as the molar ratio given in eqn (8):
| αi = (moles of species i)/(total moles of Tel22) | (8) |
The calculated values of αF, αI, and αU can be used to express the normalized CD signal, f, thus obtaining the CD model function shown in eqn (9):3,54
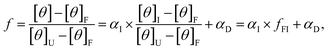 | (9) |
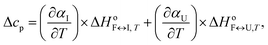 | (10) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) p,int, approximated by the second-order polynomial on T from the measured partial molar heat capacity of the DNA,
p,int, approximated by the second-order polynomial on T from the measured partial molar heat capacity of the DNA, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) p,2. The global fitting of the DSC-based and CD-based model functions to the experimental DSC and CD data measured at different K+ concentrations and water activities was based on the nonlinear Levenberg–Marquardt χ2 regression procedure.
p,2. The global fitting of the DSC-based and CD-based model functions to the experimental DSC and CD data measured at different K+ concentrations and water activities was based on the nonlinear Levenberg–Marquardt χ2 regression procedure.
Web application to calculate and fine-tune the model parameters
We developed a web application that enables the user to calculate and fine-tune the model parameters in an interactive and visual fashion. The web application is accessible through the following link: http://ltpo2.fri1.uni-lj.si/dna/. Sample screenshots of the application are shown in the ESI.† A typical case-use scenario is as follows:• The user selects a model (two-state or three-state) uploads an arbitrary number of DSC datasets in the form of a CSV file. For each dataset, the file should specify the concentration of K+ ions, the concentration of ethylene glycol, and a series of temperature–Δcp pairs (Fig. S1†).
• Optionally, the user can upload an arbitrary number of spectroscopic datasets in a form similar to the DSC data (Fig. S2†).
• The user then provides the initial values of the thermodynamic parameters and begins the automated optimization procedure. The procedure computes the optimized values of the parameters using the Levenberg–Marquardt algorithm, then plots the calculated model function and the measurement function for each DSC dataset and spectroscopic dataset, and optionally calculates the error interval for each parameter using the bootstrapping technique. The user can save the optimized values of the parameters, revert to the old values if desired (either collectively or for each parameter individually), or fine-tune the parameters and continuously monitor the model and measurement function plots (Fig. S3 and S4†).
• The user can control the optimization process by providing the optional upper and lower limits for the individual thermodynamic parameters, and by specifying which, if any, of the parameters should be kept intact during the optimization procedure. At the same time, the application makes it possible to specify the number of function evaluations in the Levenberg–Marquardt algorithm, and the number of iterations in the error estimation procedure (Fig. S5†).
The back-end of our web application was programmed in Python, using the Flask framework and the NumPy and SciPy libraries. The front-end was developed using a combination of various web technologies, including jQuery, Bootstrap, Highcharts, and MathJax.
3. Results and discussion
Building an application for the thermodynamic characterization of oligonucleotide unfolding is a challenging task, primarily because of the variety of mathematical models that can be used. As a first step, a proof of concept was created to test the technical viability of an application. Thus, the web application currently only offers a non-customizable two-state and three-state equilibrium models. The two-state model was selected because it is most often used for calculating model-dependent van't Hoff enthalpies, and the three-state model was selected because it can be used to describe thermally induced conformational transitions of Tel22.3 To obtain the data feed for our web application, several experiments were performed.Equilibrium model of Tel22 unfolding
To check whether equilibrium models can be used to describe thermally-induced conformational transitions of Tel22, CD spectra and DSC thermograms were recorded at different heating and cooling rates. These data were reproducible, which confirmed that the folding and unfolding processes of Tel22 in the presence of K+ ions can be described as an equilibrium process. Furthermore, the melting profile of the Tel22 thermal unfolding monitored by DSC, CD and UV showed biphasic behavior. The simplest model that can be used to describe the biphasic behavior of this Tel22 thermal unfolding is illustrated in Fig. 1. The model incorporates three resolvable structural forms and transitions of Tel22 that are dependent on temperature and K+ and ethylene glycol concentrations. The model also allows the thermally induced unfolding of Tel22 to follow two paths – the transition of structure F into structure I, followed by the transition into the unfolded structure U, and the direct transition from structure F to the unfolded structure U.Using CD spectroscopy to probe Tel22 structure
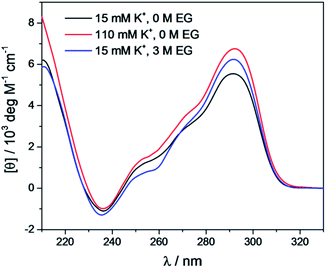
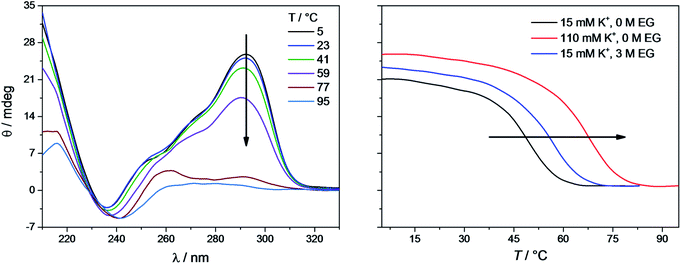
The CD spectra of Tel22 in 15 mM and 110 mM K+ solutions and in 15 mM K+ solutions with 3 M ethylene glycol are shown in Fig. 2. CD is a very useful experimental technique for characterization of G-quadruplexes. The shape of the CD spectra allowed us to predict the DNA strand orientation, and to distinguish between parallel-stranded G-quadruplexes (positive peak at 260 nm; negative peak at 240 nm) and antiparallel-stranded G-quadruplexes (positive peak at 295 nm; negative peak at 265 nm). The CD spectra of Tel22 showed a negative band at ∼240 nm, a plateau at ∼250 nm, a shoulder at ∼270 nm, and a strong positive band at ∼290 nm. This shape of the CD spectra is characteristic of hybrid type G-quadruplexes.36,55 Furthermore, the complex shapes of these CD spectra suggest that Tel22 in K+ solution is a mixture of at least two hybrid-type G-quadruplex structures.44 As it can be seen from Fig. 2, the position and height of these peaks depend on the K+ and ethylene glycol concentrations. Increased K+ ions concentration resulted in stronger CD spectra at an unchanged Tel22 concentration, which suggests more densely packed G-quadruplexes due to a stronger K+ electrostatic screening of the negatively charged phosphate groups. Decreased water activity resulted in a stronger negative peak at 240 nm, a drop in the signal at 250 nm, an unchanged shoulder at 270 nm, and a stronger positive peak at 290 nm. These changes are subtle, and they might reflect a shift in the population of the hybrid Tel22 conformations upon addition of ethylene glycol.44,56The melting profile of the Tel22 quadruplex (c = 0.15 mM) was characterized in the presence of different K+ and ethylene glycol concentrations by monitoring the changes in ellipticity with increased temperature. Fig. 3 shows a representative recording of the CD spectra at different temperatures ([K+] = 15 mM). The plot of ellipticity at 292 nm versus temperature yielded melting curves with melting temperatures, Tm, that depended on the K+ and ethylene glycol concentrations. Increased K+ and ethylene glycol concentrations shifted Tm to higher values, thus demonstrating the stabilizing effects of K+ ions and ethylene glycol on these G-quadruplexes (Fig. 3). This effect was also confirmed by the UV-melting curves (data not shown), and demonstrated the importance of the electrostatic interactions between the cationic metal ion and the anionic phosphate group for the stability of these G-quadruplexes. Additionally, quadruplex formation involves the specific binding of certain metal ions, and their coordination with the guanine carbonyl oxygen atoms. For this coordination to take place, the metal ions must shed their water of hydration. As ethylene glycol not only decreases the water activity, but also the bulk dielectric constant, this allows the metal ions to shed their waters of hydration more easily, and thus increases the stability of the cation–quadruplex complex.56,57
Global fitting of DSC and CD data
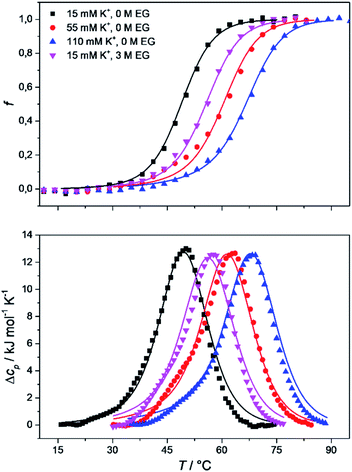
To obtain the complete thermodynamic profile of the thermally induced Tel22 unfolding, the DSC melting curves were measured at different salt and ethylene glycol concentrations. On the basis of several specific examples of DNA and protein unfolding, it has been shown that the global thermodynamic analysis of experimental data obtained from several experimental techniques is essential for the critical evaluation of model mechanisms.54 Thus, we uploaded experimental CD and DSC data to the web application to perform global fitting of the model functions (eqn (9) and (10)). NanoAnalyse was used to subtract the baselines before uploading the DSC curves to the web application. Although it is recommended to allow baseline correction for each species involved in the unfolding process during a fitting process,44 this option is not yet available for the web application, but will be added in future versions. The CD melting curves were also normalized prior to being uploaded, but manual/automatic adjustments of the normalization procedures will be implemented in future versions of the web application. Next, the thermodynamic parameters obtained by Bončina et al.3 were uploaded and used as initial values in fitting procedure and bootstrapping was used to calculate the errors.Fig. 4 shows the comparison of model-based and measured CD melting and DSC heating curves. The thermodynamic parameters obtained by web application are shown in Table 1. Although some differences can be found when comparing these results to values obtained by Bončina et al.,3 the main conclusions for the overall unfolding process F ↔ U of Tel22 remain the same: (i) 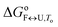 was positive and relatively small due to the enthalpy–entropy compensation; (ii) the enthalpy change was ∼200 kJ mol−1, which is comparable to the literature data;6,58 (iii) the heat capacity change was positive and substantial (Δcop,F↔U = 1200 J mol−1 K−1); (iv) K+ ions were released upon unfolding of Tel22.
was positive and relatively small due to the enthalpy–entropy compensation; (ii) the enthalpy change was ∼200 kJ mol−1, which is comparable to the literature data;6,58 (iii) the heat capacity change was positive and substantial (Δcop,F↔U = 1200 J mol−1 K−1); (iv) K+ ions were released upon unfolding of Tel22.
Water behavior during thermally induced unfolding of Tel22
The proposed model allowed us to study the effects of water activity on the thermally induced unfolding, and to calculate the number of water molecules that were released or taken up during unfolding. Fig. 4 shows that addition of ethylene glycol (i.e., a decrease in the water activity) resulted in an increased Tm, which is in favor of stabilizing effects of ethylene glycol on these Tel22 quadruplexes. We obtained negative mi↔j values for the unfolding of the G-quadruplexes (Table 1), which shows the uptake of water molecules. Specifically, per molecule of Tel22, we determined a water uptake of three molecules of H2O during the F ↔ I transition, and a water uptake of 33 molecules of H2O during the I ↔ U transition. According to Olsen et al.,34 these values can be attributed to several contributions to the unfolding of a quadruplex: (i) uptake of structural water by the unfolded state; (ii) release of electrostricted water by the quadruplex due to its lower charge density in the unfolded state; (iii) uptake of electrostricted water by the K+ ions upon their release from the G-quadruplex core. All three of these contributions will influence the heat capacity change – the uptake of structural water and the release of electrostricted water by the unfolded state will increase the heat capacity, while the uptake of electrostricted water by K+ will decrease the heat capacity. As the overall unfolding process F ↔ U is accompanied by a positive heat capacity change (Δcop,F↔U = 1270 J mol−1 K−1) and a net uptake of water molecules (mF↔U = −36 molecules of H2O/molecule of Tel22), we can speculate that the main event responsible for the redistribution of water molecules during the F ↔ U transition is the exposure of a large number of thymines and other hydrophobic groups to the water. This is consistent with the calculated hydration heat capacity of nucleic-acid constituents, which shows that the melting of duplex DNA is accompanied by an increase in heat capacity.59 The number of water molecules that are taken up during the unfolding of the K+-stabilized Tel22 (36 molecules of H2O/molecule of Tel22) is of the same order of magnitude as the number of water molecules that have been reported to be taken up during the unfolding of Na+-stabilized Tel22 (100 molecules of H2O/molecule of Tel22).60 The difference between the number of water molecules being taken up during this unfolding of K+- and Na+-stabilized Tel22 (i.e., 36 vs. 100 water molecules) can be in part attributed to the different types of loops present in the hybrid (e.g., propeller-type, lateral, diagonal) and in the antiparallel (e.g., lateral, diagonal) structures. Specifically, different types of loops can lead to greater exposure of nonpolar nucleotides to the surrounding water, which will in turn decrease the number of water molecules taken up during the unfolding of Tel22. The difference in the water behaviors between K+- and Na+-stabilized Tel22 can also be attributed to the different free energies of K+ and Na+ hydration.61 As the Na+ cation has more negative hydration free energy, it is more effective at disrupting the water structure than K+. The number of water molecules taken up in the first and second transitions are significantly different, and correlate with the corresponding heat capacity changes. Table 1 shows that the uptake of the four molecules of water during the F ↔ I transition is associated with a lower heat capacity change (Δcop,F↔I = −326 J mol−1 K−1) than the uptake of the 33 molecules of water during the I ↔ U transition, which is accompanied by a higher heat capacity change (Δcop,I↔U = 1600 J mol−1 K−1). The differences between the first and second transitions are not limited to the water uptake and heat capacity change, but also extend to the other thermodynamic parameters that are characteristic for such individual transition steps (Table 1). Overall, we conclude that the second transition is accompanied by greater changes in the thermodynamic parameters, which suggests that this involves more dramatic structural changes than the first transition. These results support the previously described Tel22 unfolding mechanism, where intermediate state was believed to be a triplex.3,44 Partial unfolding of Tel22 to triplex structure exposes only one G-quadruplex strand to the water, whereas the unfolding of the triplex structures itself exposes the remaining three G-quadruplex strands to water, which provides a large number of thymines and other hydrophobic groups. Consequently, the first transition (F ↔ I) is accompanied by a smaller heat capacity change than the second transition (I ↔ U).Temperature, potassium and ethylene glycol dependence of Tel22 quadruplex species
The model analysis described here also provides the speciation diagrams at different K+ and ethylene glycol concentrations, as shown in Fig. 5. Comparisons of these curves that were calculated for all of the quadruplex species in the solutions with the corresponding measured DSC thermograms (Fig. 4) shows that the interconversion (F ↔ I) starts at relatively low temperatures (∼15 °C for 15 mM K+, ∼30 °C for 110 mM K+). It also shows that higher concentrations of potassium ions and addition of ethylene glycol not only shifts unfolding temperatures of Tel22 to higher values but also increases intermediate concentration. The observed increase in concentration shows that intermediates are stabilized by higher K+ and EG concentration. This behavior suggests that intermediates must exhibit several structural similarities with G-quadruplexes and thus supports our previous conclusion based on calculated thermodynamic parameters (Table 1) which describe intermediate state as a G-triplex structure.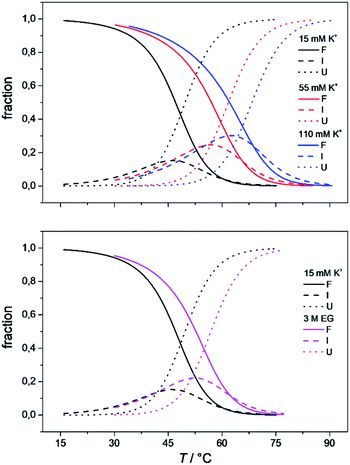 | ||
| Fig. 5 The model-based fractions of species F, I, and U as a function of T at the different concentrations of K+ ions (top) and ethylene glycol (bottom), determined using the best fit parameters reported in Table 1. | ||
4. Conclusions
The importance of thermodynamic parameters that determine the stabilities and interactions of biological macromolecules has contributed to an increase in the number of laboratories that are now equipped with sensitive microcalorimeters. Nowadays, thermodynamic data collection is comprehensive and routine, although thermodynamic data interpretation is still suboptimal. This is partially because the general-purpose commercial software fails to provide tools to describe the behaviors of several unique biological systems, which leaves scientists with no other options but to develop their own software solutions.As the skills to build tailor-made analysis software are still fairly rare, we are developing an Open Access web application that will allow relatively easy thermodynamic analysis of calorimetric and spectroscopic data. This application can be used as a research and/or teaching tool and will allow comparisons to be made of thermodynamic parameters obtained in different laboratories. As a proof of concept, we have tested the web application with experimental data obtained from monitoring thermal folding and unfolding of Tel22 in the presence of different concentrations of K+ ions and ethylene glycol. We have thus described the unfolding of Tel22 according to a three-state equilibrium model (Fig. 1), and obtained the thermodynamic profile. The unfolding of Tel22 was associated with positive changes in the free energy 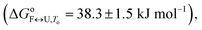 the enthalpy
the enthalpy 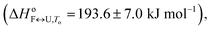 and the heat capacity (Δcop,F↔U = 1270 ± 140 J mol−1 K−1), along with the release of K+ ions (nF↔U = 2.2 ± 0.1) and the uptake of water molecules (mF↔U = −35.5 ± 5.8).
and the heat capacity (Δcop,F↔U = 1270 ± 140 J mol−1 K−1), along with the release of K+ ions (nF↔U = 2.2 ± 0.1) and the uptake of water molecules (mF↔U = −35.5 ± 5.8).
Incorporating the effect of water activity in Tel22 thermal unfolding model allowed our web application to calculate the number of water molecules taken up during transition of Tel22 from the folded to the unfolded state. Comparing the number of water molecules taken up to changes in heat capacity led us to conclude that the main event responsible for the redistribution of water molecules during Tel22 unfolding is exposure of a large number of thymines and other hydrophobic groups to solvent. In addition, the comparison of thermodynamic parameters used to describe Tel22 unfolding (Table 1) revealed big differences between the first (F ↔ I) and second transitions (I ↔ U). Specifically, the second transition is accompanied by higher numbers suggesting that it involves more dramatic structural changes. This suggests that the intermediate is structurally more similar to the folded than the unfolded state. Speciation diagrams (Fig. 5) also revealed that the addition of ethylene glycol increases the intermediate concentration during thermal unfolding. This behavior supports the classification of intermediates as G-quadruplex related structures since stabilization of DNA sequences with decreased water activity is characteristic of G-quadruplexes. One possibility of such G-quadruplex related structure is a G-triplex which was described in several publications as an important step in Tel22 folding/unfolding mechanism.
The present study demonstrates the possibilities of performing thermodynamic analysis with specialized online tools. Our web application could be used to provide better understanding of the forces responsible for the structural interconversion of macromolecular structures. These forces play a major role in the formation of biological macromolecules and their physicochemical properties and are related to the solution conditions (temperature, cation concentration/type and water activity). In the near future, we are planning to add several more models that can be used to describe folding and unfolding of biological macromolecules, the possibility to include experimental data from pressure perturbation calorimetry into this global fitting procedure, the possibility to draw a phase diagram and possibility to upload other types of data such as binding data from spectroscopy and ITC experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Jurij Lah for his helpful comments and suggestions, Chris Berrie and Brooke C. Morriswood for English language input. This work was supported in part by the Ministry of Higher Education, Science and Technology through the Slovenian Research Agency [grant numbers L7-8277, J4-8225, P4-0121].References
- J. B. Chaires, Annu. Rev. Biophys., 2008, 37, 135–151 CrossRef CAS PubMed.
- I. Drobnak, G. Vesnaver and J. Lah, J. Phys. Chem. B, 2010, 114, 8713–8722 CrossRef CAS PubMed.
- M. Bončina, J. Lah, I. Prislan and G. Vesnaver, J. Am. Chem. Soc., 2012, 134, 9657–9663 CrossRef PubMed.
- I. Prislan, J. Lah, M. Milanic and G. Vesnaver, Nucleic Acids Res., 2011, 39, 1933–1942 CrossRef CAS PubMed.
- I. Prislan, H. T. Lee, C. Lee and L. A. Marky, J. Phys. Chem. B, 2015, 119, 96–104 CrossRef CAS PubMed.
- I. Prislan, J. Lah and G. Vesnaver, J. Am. Chem. Soc., 2008, 130, 14161–14169 CrossRef CAS PubMed.
- N. R. Markham and M. Zuker, Methods Mol. Biol., 2008, 453, 3–31 CrossRef CAS PubMed.
- C. Smith, S. Heyne, A. S. Richter, S. Will and R. Backofen, Nucleic Acids Res., 2010, 38, W373–W377 CrossRef CAS PubMed.
- M. Andronescu, R. Aguirre-Hernández, A. Condon and H. H. Hoos, Nucleic Acids Res., 2003, 31, 3416–3422 CrossRef CAS PubMed.
- R. Lorenz, S. H. Bernhart, C. Höner zu Siederdissen, H. Tafer, C. Flamm, P. F. Stadler and I. L. Hofacker, Algorithms Mol. Biol., 2011, 6, 26 CrossRef PubMed.
- J. S. Reuter and D. H. Mathews, BMC Bioinf., 2010, 11, 129 CrossRef PubMed.
- M. Hamada, Y. Ono, H. Kiryu, K. Sato, Y. Kato, T. Fukunaga, R. Mori and K. Asai, Nucleic Acids Res., 2016, 44, W302–W307 CrossRef CAS PubMed.
- S. Janssen and R. Giegerich, Bioinformatics, 2014, 31, 423–425 CrossRef PubMed.
- B. A. Grüning, J. Fallmann, D. Yusuf, S. Will, A. Erxleben, F. Eggenhofer, T. Houwaart, B. Batut, P. Videm, A. Bagnacani, M. Wolfien, S. C. Lott, Y. Hoogstrate, W. R. Hess, O. Wolkenhauer, S. Hoffmann, A. Akalin, U. Ohler, P. F. Stadler and R. Backofen, Nucleic Acids Res., 2017, 45, W560–W566 CrossRef PubMed.
- M. Gellert, M. N. Lipsett and D. R. Davies, Proc. Natl. Acad. Sci. U. S. A., 1962, 48, 2013–2018 CrossRef CAS PubMed.
- W. I. Sundquist and A. Klug, Nature, 1989, 342, 825–829 CrossRef CAS PubMed.
- E. Kejnovsky, V. Tokan and M. Lexa, Chromosome Res., 2015, 23, 615–623 CrossRef CAS PubMed.
- D. Rhodes and H. J. Lipps, Nucleic Acids Res., 2015, 43, 8627–8637 CrossRef CAS PubMed.
- E. H. Blackburn and J. G. Gall, J. Mol. Biol., 1978, 120, 33–53 CrossRef CAS PubMed.
- C. W. Greider and E. H. Blackburn, Cell, 1985, 43, 405–413 CrossRef CAS PubMed.
- R. K. Moyzis, J. M. Buckingham, L. S. Cram, M. Dani, L. L. Deaven, M. D. Jones, J. Meyne, R. L. Ratliff and J. R. Wu, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 6622–6626 CrossRef CAS PubMed.
- R. C. Allshire, J. R. Gosden, S. H. Cross, G. Cranston, D. Rout, N. Sugawara, J. W. Szostak, P. A. Fantes and N. D. Hastie, Nature, 1988, 332, 656–659 CrossRef CAS PubMed.
- A. M. Zahler, J. R. Williamson, T. R. Cech and D. M. Prescott, Nature, 1991, 350, 718–720 CrossRef CAS PubMed.
- S. Neidle, FEBS J., 2010, 277, 1118–1125 CrossRef CAS PubMed.
- Q. Wang, J.-q. Liu, Z. Chen, K.-w. Zheng, C.-y. Chen, Y.-h. Hao and Z. Tan, Nucleic Acids Res., 2011, 39, 6229–6237 CrossRef CAS PubMed.
- M. Ruden and N. Puri, Cancer Treat. Rev., 2013, 39, 444–456 CrossRef CAS PubMed.
- S. Balasubramanian, L. H. Hurley and S. Neidle, Nat. Rev. Drug Discovery, 2011, 10, 261–275 CrossRef CAS PubMed.
- M. Düchler, J. Drug Targeting, 2012, 20, 389–400 CrossRef PubMed.
- W. Zhang, M. Chen, Y. Ling Wu, Y. Tanaka, Y. Juan Ji, S. Lin Zhang, C. He Wei and Y. Xu, Sci. Rep., 2015, 5, 13693 CrossRef PubMed.
- C. Antonacci, J. B. Chaires and R. D. Sheardy, Biochemistry, 2007, 46, 4654–4660 CrossRef CAS PubMed.
- R. D. Gray, R. Buscaglia and J. B. Chaires, J. Am. Chem. Soc., 2012, 134, 16834–16844 CrossRef CAS PubMed.
- D. Yang and K. Okamoto, Future Med. Chem., 2010, 2, 619–646 CrossRef CAS PubMed.
- L. Petraccone, B. Pagano and C. Giancola, Methods, 2012, 57, 76–83 CrossRef CAS PubMed.
- C. M. Olsen, H.-T. Lee and L. A. Marky, J. Phys. Chem. B, 2009, 113, 2587–2595 CrossRef CAS PubMed.
- A. I. Karsisiotis, C. O'Kane and M. Webba da Silva, Methods, 2013, 64, 28–35 CrossRef CAS PubMed.
- A. Ambrus, D. Chen, J. Dai, T. Bialis, R. A. Jones and D. Yang, Nucleic Acids Res., 2006, 34, 2723–2735 CrossRef CAS PubMed.
- Y. Xu, Y. Noguchi and H. Sugiyama, Bioorg. Med. Chem., 2006, 14, 5584–5591 CrossRef CAS PubMed.
- A. T. Phan, V. Kuryavyi, K. N. Luu and D. J. Patel, Nucleic Acids Res., 2007, 35, 6517–6525 CrossRef CAS PubMed.
- R. D. Gray, L. Petraccone, J. O. Trent and J. B. Chaires, Biochemistry, 2010, 49, 179–194 CrossRef CAS PubMed.
- P. Stadlbauer, L. Trantírek, T. E. Cheatham III, J. Koča and J. Šponer, Biochimie, 2014, 105, 22–35 CrossRef CAS PubMed.
- D. Luo and Y. Mu, J. Phys. Chem. B, 2016, 120, 4912–4926 CrossRef CAS PubMed.
- T. Mashimo, H. Yagi, Y. Sannohe, A. Rajendran and H. Sugiyama, J. Am. Chem. Soc., 2010, 132, 14910–14918 CrossRef CAS PubMed.
- R. D. Gray, J. O. Trent and J. B. Chaires, J. Mol. Biol., 2014, 426, 1629–1650 CrossRef CAS PubMed.
- R. Buscaglia, R. D. Gray and J. B. Chaires, Biopolymers, 2013, 99, 1006–1018 CAS.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- W. Saenger, in Principles of Nucleic Acid Structure, Springer, New York, NY, 1984, pp. 368–384 Search PubMed.
- C. H. Spink and J. B. Chaires, J. Am. Chem. Soc., 1995, 117, 12887–12888 CrossRef CAS.
- C. H. Spink and J. B. Chaires, Biochemistry, 1999, 38, 496–508 CrossRef CAS PubMed.
- C. M. Olsen, W. H. Gmeiner and L. A. Marky, J. Phys. Chem. B, 2006, 110, 6962–6969 CrossRef CAS PubMed.
- D. Miyoshi, H. Karimata and N. Sugimoto, J. Am. Chem. Soc., 2006, 128, 7957–7963 CrossRef CAS PubMed.
- B. Heddi and A. T. Phan, J. Am. Chem. Soc., 2011, 133, 9824–9833 CrossRef CAS PubMed.
- C. R. Cantor, M. M. Warshaw and H. Shapiro, Biopolymers, 1970, 9, 1059–1077 CrossRef CAS.
- L. A. Marky, K. S. Blumenfeld, S. Kozlowski and K. J. Breslauer, Biopolymers, 1983, 22, 1247–1257 CrossRef CAS PubMed.
- I. Drobnak, G. Vesnaver and J. Lah, J. Phys. Chem. B, 2010, 114, 8713–8722 CrossRef CAS PubMed.
- D. Renčiuk, I. Kejnovská, P. Školáková, K. Bednářová, J. Motlová and M. Vorlíčková, Nucleic Acids Res., 2009, 37, 6625–6634 CrossRef PubMed.
- I. V. Smirnov and R. H. Shafer, Biopolymers, 2007, 85, 91–101 CrossRef CAS PubMed.
- A. N. Lane, J. B. Chaires, R. D. Gray and J. O. Trent, Nucleic Acids Res., 2008, 36, 5482–5515 CrossRef CAS PubMed.
- J. S. Hudson, L. Ding, V. Le, E. Lewis and D. Graves, Biochemistry, 2014, 53, 3347–3356 CrossRef CAS PubMed.
- B. Madan and K. A. Sharp, Biophys. J., 2001, 81, 1881–1887 CrossRef CAS.
- H. Y. Fan, Y. L. Shek, A. Amiri, D. N. Dubins, H. Heerklotz, R. B. Macgregor and T. V. Chalikian, J. Am. Chem. Soc., 2011, 133, 4518–4526 CrossRef CAS PubMed.
- N. V. Hud, F. W. Smith, F. A. L. Anet and J. Feigon, Biochemistry, 1996, 35, 15383–15390 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra09800c |
| This journal is © The Royal Society of Chemistry 2019 |