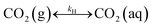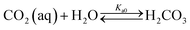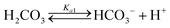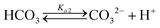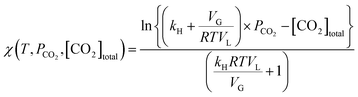Towards efficient calcium extraction from steel slag and carbon dioxide utilisation via pressure-swing mineral carbonation†
Raghavendra
Ragipani
 abc,
Sankar
Bhattacharya
abc,
Sankar
Bhattacharya
 b and
Akkihebbal K.
Suresh
b and
Akkihebbal K.
Suresh
 *c
*c
aIITB-Monash Research Academy, Indian Institute of Technology Bombay, Mumbai, India
bDepartment of Chemical Engineering, Monash University, Clayton, Victoria 3800, Australia. E-mail: sankar.bhattacharya@monash.edu
cDepartment of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai, India. E-mail: aksuresh@iitb.ac.in
First published on 14th November 2018
Abstract
Production of precipitated calcium carbonate (PCC) via carbon dioxide (CO2) pressure-swing mineral carbonation is a potential way to utilise calcium-rich steel slag and carbon dioxide. Calcium supersaturation and slag surface passivation are two aspects of the calcium extraction step that strongly influence the choice of operating conditions necessary for rapid and complete calcium leaching, which are investigated in the present work. To investigate these aspects, slag dissolution characteristics were studied in a closed high-pressure batch-reactor taking care to eliminate gas–liquid mass transport limitations. This experimental design has two distinct advantages: (1) rapid CO2 absorption necessary for dissolution under acidic conditions and to gain insights into calcium dissolution kinetics and (2) the closed system allowing measurement of the drop in reactor pressure, which along with elemental analysis of leachate is sufficient to determine the ionic species concentration and solution saturation state. The results provide evidence against surface passivation of residual slag by silica or calcium carbonate layers. Further, the experiments confirm high supersaturation with respect to calcite during the dissolution step, which we hypothesise to be a consequence of unfavourable calcite precipitation kinetics due to the low pH and high calcium to carbonate ion ratio. The results show scope for further enhancement in calcium solubility, up to the solubility limit of amorphous calcium carbonate, which can substantially reduce the water volume and CO2 pressure required for dissolution. Pressure-swing to atmospheric pressure led to spontaneous co-precipitation of rhombohedral calcite and amorphous silica, also a paper-filler with similar optical properties to PCC, with impurities less than 1.5 wt%.
1 Introduction
The use of steel slag, the calcium-rich industrial waste from the steel industry, by mineral carbonation to sequester the carbon dioxide emitted by the process of steel making, has attracted considerable attention for carbon dioxide capture and better solid waste management.1 Recently, the focus has been on producing precipitated calcium carbonate (PCC) by indirect mineral carbonation, a multi-step process which consists of selective calcium extraction and carbonate precipitation steps.2 PCC is used as a filler material in writing and printing paper for better optical properties and has a high market value.3 The indirect route, in the case of steel slag, further yields Fe enriched residual slag, which can be recycled within the iron & steel industry4 and has a prospective use in production of cathode precursor materials.5Slow calcium extraction rates from silicates and low extraction efficiency,6 especially in the case of coarser feedstock particle sizes,7 are serious impediments to commercialisation of the process. The calcium extraction rate and overall efficiency have been shown to increase with particle size reduction.7,8 This behaviour, along with parabolic kinetics, led to the speculation that the reactive surface is passivated by silica and calcium carbonate layers.1,7,9,10 To accelerate the calcium extraction, dissolution is typically carried out in mineral11,12 or organic acids,13–15 which are difficult to regenerate and require additional pH-swing, wherein the Ca-rich aqueous solution pH is increased by addition of alkaline media to facilitate CO2 absorption and carbonate precipitation. Similarly, recycling and regeneration of the leaching agent (ammonium chloride solution) is a problem with spontaneous pH-swing methods.16 Alternatively, the carbon dioxide pressure-swing technique proposed by Iizuka et al.17 is promising for PCC production, as it does not involve the use of any acids or bases except carbon dioxide itself. Pressure-swing carbonation has been devised to take advantage of the increase in calcium carbonate solubility at high CO2 partial pressure. The dissolution stage of the process involves leaching of Ca in aqueous solution under high-pressure of carbon dioxide. Post dissolution, Ca rich aqueous solution is filtered and precipitated at low partial pressure of CO2. Studies on waste cement17,18 showed potential for high Ca extraction rates and Ca extraction efficiency. The purity of calcium carbonate, however, was found to be 80% in unseeded precipitation; synthesis of high-purity (98 wt%) PCC required a large amount (2.5 wt%) of calcium carbonate seed material, an amount which was comparable to the expected precipitate weight. The nature of impurities and influence of dissolution conditions on carbonate characteristics have also not been reported. Further, in the case of Ca extraction from waste cement, the process required either high water volume (liquid-to-solid ratio of 350 ml g−1) or large recycle of residual waste cement at a low liquid-to-solid ratio (L/S of 40 ml g−1), which resulted in a significant process cost.18
In terms of the mechanisms involved, multi-oxide/silicate dissolution and carbonate precipitation under CO2 pressure appear to be complex and not clearly understood. For instance, precipitation of carbonate and silica preferentially occurs on the surface of the slag1 leading to speculation about surface passivation. However, such passivation has not been conclusively established.19 Iizuka et al.17 reported supersaturation of calcium during the dissolution step. However, reasons for the same are not clear. Calcium extraction beyond the calcite solubility limit can significantly reduce the water volume required for complete calcium extraction, an aspect which has not yet been explored. Also, some direct mineral carbonation experiments1,20,21 showed better overall conversion at very low liquid-to-solid ratios, which was deduced as an enhancement in Ca dissolution efficiency. However, these studies were in contradiction to a few other studies17,22 where better Ca dissolution efficiency was obtained at high L/S. To a large extent, the problem of not being able to understand the dissolution and precipitation mechanisms is due to limited data,9 inconsistency in methodology and incomplete evidence. In most high-pressure mineral dissolution and carbonation studies, researchers relied upon either inductively coupled plasma (ICP) analysis of filtered liquid samples or carbonate quantification of solid samples obtained after de-pressurisation of the system to interpret the kinetics. It must be noted that the precipitation of carbonate is spontaneous when the system is de-pressurised and the estimated carbonate content in the residues after filtration and drying does not therefore reflect the true process efficiency. Thus, it is impossible to resolve the true rate of dissolution from apparent rates without the knowledge of in situ carbonation. In addition to these shortcomings in existing data, there are specific complexities arising due to the nature of feedstock. For instance, in the case of mineral carbonation of steel slag, the influence of Mg and Fe which can potentially affect the carbonate morphology23–25 and form secondary precipitates is yet to be explored.
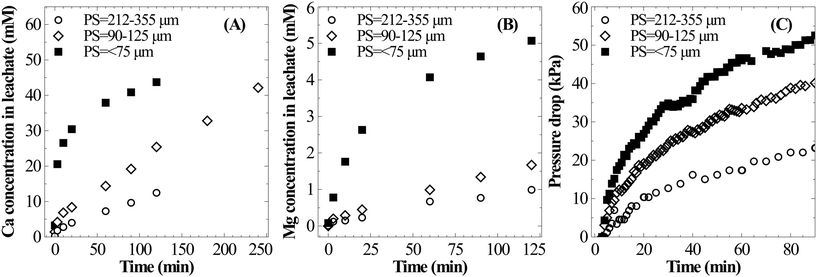
This work attempts to address the above-mentioned gaps in experimentation and determine true calcium dissolution rates. High-pressure batch dissolution experiments have been carried out in a closed system after eliminating CO2 mass transfer limitations (described in sections 2 and 3.2.1). Calcium leaching characteristics from steel slag under CO2 pressure have been studied to probe surface passivation and its influence on dissolution kinetics. This study further attempts to understand the mechanism behind calcium supersaturation and the possibility of reducing the water requirement. To investigate these aspects, dissolution experiments were performed at moderate CO2 pressures, temperatures and liquid-to-solid ratios (0.6–1.25 MPa, 25–60 °C, and 50–100 ml g−1, respectively) using steel slag with fine (<75 μm) and coarse particle size fractions (90–125 μm, and 212–355 μm). A study has also been carried out on carbonate precipitation characteristics at atmospheric pressure by pressure-swing and PCC characterisation to determine the PCC purity and overall calcium conversion.
2 Methodology of the study
The present methodology involves the use of a closed system to study the existence and extent of calcium supersaturation in the liquid and surface passivation of slag particles by calcium carbonate precipitation. The rationale behind the choice of a closed system is to monitor the CO2 pressure change with time, in addition to the elemental concentration in the aqueous solution by ICP analysis. As shown below, based on these measurements in a closed system, wherein the CO2 moles, gas phase volume, and temperature are constant (constant NVT), it is possible to determine the state of the solution (pH, supersaturation). We base this on a calculation, from the experimental data, of the moles of CO2 fixed as bicarbonate and carbonate per unit mole change of M2+ ions in solution (ΔCs/Δ[M]). Relationships between ΔCs/Δ[M] and the solution state are obtained using an overall carbon balance (equation given below) and the condition that the aqueous solution is saturated with CO2.‡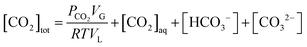 | (1) |
Under CO2 saturated conditions (using Henry's law [CO2]aq = kH × PCO2), the change in the concentration of CO2 fixed as carbonate and bicarbonate in aqueous solution is, from eqn (1),
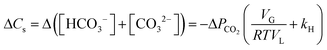 | (2) |
Table 1 shows the reactions involved. Based on the reaction chemistry and charge balance equation, depending on the solution state, different conditions for ΔCs/Δ[M] exist (as shown below). Based on the saturation state of the solution, these conditions are categorised into two cases.
Case I: ionic activity product (IAP) less than solubility product (Ksp) for CaCO3
During the dissolution step (under acidic and circumneutral pH conditions, where [CO32−] ≪ [HCO3−]),| ΔCs/Δ[M] ≈ 2 | (3) |
On the other hand, when dissolution takes place in a mildly basic environment (8 < pH < 10) where [CO32−] and [HCO3−] are comparable,
| 1 < ΔCs/Δ[M] < 2 | (4) |
In the case of dissolution under very basic conditions (pH > 10) where [CO32−] ≫ [HCO3−],
| ΔCs/Δ[M] ≈ 1 | (5) |
Case II: IAP greater than Ksp for CaCO3
Here, three possibilities exist—(a) the solution may remain supersaturated with respect to CaCO3, or (b) the supersaturation may be discharged as a precipitate that remains suspended and does not show up in the liquid samples, or (c) the supersaturation is discharged as a colloidal precipitate that passes through the sampling filter and shows up in the liquid sample. These cases may be distinguished by defining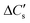 , the moles of CO2 consumed to dissolve Ca2+ in the solution,§eqn (6)
, the moles of CO2 consumed to dissolve Ca2+ in the solution,§eqn (6)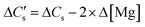 | (6) |
(a) In the case of acidic pH (eqn (3)) and true solution saturation with respect to CaCO3, we have,
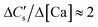 | (7) |
(b) In the case where supersaturation is discharged as a CaCO3 precipitate and the precipitate is not passed into the liquid sample (precipitate size > filter pore size),
| Δ[Ca] ≤ 0 | (8) |
(c) In the case where the CaCO3 precipitate exists in the colloidal form, which passes through the sampling filter and dissolves upon acidification of the sample,¶ if the calcium dissolution rate from the slag is negligible,
| Δ[Ca] = 0 | (9) |
On the other hand, when the calcium dissolution and CaCO3 precipitation rates are comparable,
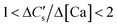 | (10) |
Thus, by measuring the ΔPCO2 under CO2 saturated conditions, it is possible to distinguish the Ca dissolution reaction from the carbonate precipitation reaction, and a true supersaturated solution from a colloidal precipitate.
Though the above methodology is limited by the sensitivity of pressure loss measurement and ability to maintain the system at constant temperature, the concept is useful to gain insights into various regimes of dissolution and precipitation. A detailed discussion on such limitations and numerical methods to overcome them is presented in the Results and discussion section 4.2.
3 Materials and methods
3.1 Materials
Basic oxygen furnace slag was kindly provided by M/s JSW Ltd, India, from their steel-making plant. The as-received slag was washed in acetone to remove surface impurities. The washed slag was dried and crushed in a Herzog pulverizing mill (HSM100) for 60 seconds. The crushed sample was carefully sieved to separate 212–355, 150–212, 90–125 and <75 μm fractions using standard test sieves, and the fractions were stored in airtight containers. The chemical and mineral composition of the slag was characterized by X-ray fluorescence (XRF) and X-ray diffraction (XRD). The slag was found to be rich in elements such as Ca (30.7%), Fe (16.9%), Si (8.0%), and Mg (5.5%) which were mainly concentrated in C2S (36.2 wt%), C3S (9.1 wt%), the RO phase containing FeO and MgO (20.4 wt%), and dicalcium ferrite (23.5 wt%) mineral phases. CO2 gas (99.99% purity) was obtained from BOC. Deionized water from a Milli-Q® dispenser was used in all experiments. 0.01 M nitric acid prepared from 65% concentrate (analytical reagent grade) was used to measure the alkalinity of slag leachate samples by potentiometric titration. Standard buffers (pH 4 and 7) received from Horiba Scientific along with a LAQUAtwin pH meter were used for pH meter calibration. Multi-element standard solution 6 for ICP (TraceCERT® grade) obtained from Sigma-Aldrich was used to prepare standard calibration solutions for elemental analysis.3.2 High-pressure experiments
All high-pressure experiments were performed in a 600 ml bench top Parr autoclave (4568) equipped with a Parr 4848 reaction controller (shown in Fig. 1). The reactor temperature is maintained using an electrically heated mantle and circulating cooling water. The reactor stirrer has two 4-blade impellers and has a maximum stirring speed of 800 rpm in water. Details of the setup with inlet and outlet ports are shown in Fig. 1.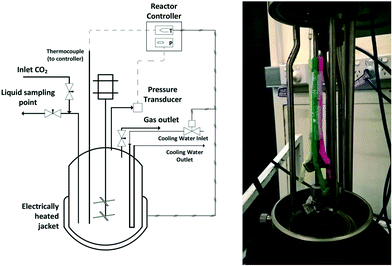 | ||
| Fig. 1 Schematic of the high-pressure autoclave and modified stirrer which acts as a self-inducing impeller. | ||
4 Results and discussion
4.1 Elimination of gas–liquid mass transfer limitations
To understand the rate of CO2 absorption in the autoclave, absorption experiments were performed in a closed system with 250 ml of distilled water and a gas volume of 350 ml of at 25 °C. As described in the experimental section, the experiment was stopped when the CO2 pressure remained constant. Since, the absorption is performed in a constant NVT and variable pressure system, the following equation is used to determine the mass transfer coefficient (kLa),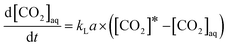 | (11) |
Using eqn (1), Henry's law ([CO2]* = kH × PCO2), and neglecting [HCO3−] + [CO32−] which is ≪[CO2]aq under CO2 pressure greater than 1 bar in distilled water, the following equation was arrived at.
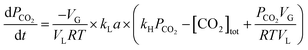 | (12) |
Integrating the above equation, we obtain
χ(T,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCO2, PCO2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CO2]total) = −kLa × t + C [CO2]total) = −kLa × t + C | (13) |
Using eqn (13), the mass transfer coefficient (kLa) is estimated as the slope of the linear fit as illustrated in Fig. 2B.
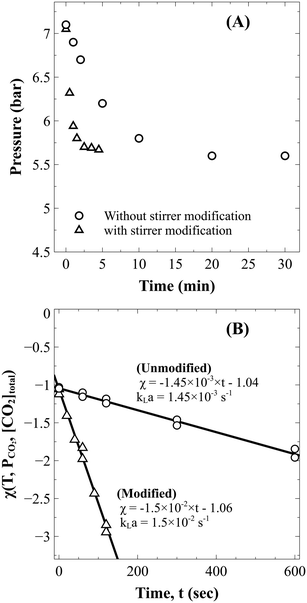 | ||
| Fig. 2 (A) Drop in the reactor pressure during absorption in distilled water without (○) and with (△) stirrer modification and (B) the corresponding kLa estimation. | ||
Absorption experiments showed that the time required to reach constant pressure (CO2 saturation time) with the existing reactor configuration was about 25 min (Fig. 2A). Since this time was comparable to the estimated dissolution time of 1–2 hours,1,17 it was anticipated that external mass transfer limitations would influence the reaction rate. To overcome the problem, as described in section 3.2.1, the reactor stirrer was modified to act like a self-inducing impeller. As demonstrated in Fig. 2, the mass transfer coefficient improved by an order of magnitude from 1.45 ± 0.07 ×10−3 s−1 to 1.50 ± 0.01 × 10−2 s−1, reducing the saturation time to three minutes. The pressure data in slag carbonation experiments (to be discussed later) showed that the fall in pressure in the post saturation phase was much more gradual than that in the initial saturation phase. Thus, it can be stated that the rate of CO2 absorption is much faster than those of slag dissolution reactions and does not influence the dissolution kinetics.
4.2 Temperature sensitivity of pressure loss measurement
In a closed system, the reactor pressure is expected to be influenced by fluctuation in reactor temperature, mainly due to changes in CO2 solubility, and in turn influence the pressure loss measurements. An analysis has therefore been carried out to understand the influence of temperature fluctuations on the observed reactor pressure.A total CO2 balance in the slag carbonation system with a solid phase gives,
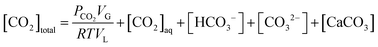 | (14) |
In pure water, under CO2 pressure, the concentrations of [HCO3−] and [CO32−] are insignificant compared to [CO2]aq. On the other hand, in the case of slag carbonation, the concentration of these species is strongly dependent on the concentration of metal ions (for charge balance) and is expected to show negligible influence with small temperature changes. Hence, eqn (15) can be used for further analysis under saturated conditions, where [CO2]aq can be described by Henry's law.
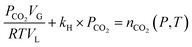 | (15) |
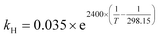 mol L−1 bar−1.26
mol L−1 bar−1.26
Differentiating the above equation with respect to P and T, we obtain dnCO2 = 0 and
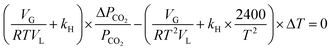 | (16) |
Eqn (16) is rearranged as follows to estimate the changes in reactor pressure due to a small magnitude of change in reactor temperature,
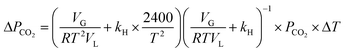 | (17) |
Under typical experimental conditions of VG = 0.35 L, VL = 0.25 L, T = 298.5 K and P(CO2) = 800 kPa, a change in reaction temperature of 1 °C influences the pressure measurement by ∼10 kPa (Fig. 3A). Though this temperature change induced error in pressure is insignificant when compared to the total reactor pressure, it is large enough to introduce noise into reaction induced pressure loss estimates. Ideally, temperature fluctuation less than 0.1 °C is desired to contain errors in pressure measurement less than 1 kPa. However, the reactor used for the current study was electrically heated and the PID controller often resulted in fluctuations of about 1–2 °C due to the reaction exothermicity and changes in cooling water temperature. As the observed accuracy in the pressure loss measurement was lower than the desired value, recorded pressure was corrected based on the temperature changes using eqn (17). Changes in reactor pressure observed with a change in reactor temperature in a closed system were experimentally determined under typical experimental conditions of VG = 0.35 L, VL = 0.25 L, T = 298.15 K and P(CO2) = 885 kPa and compared with the predictions of eqn (17). As shown in Fig. 3A, corrections in pressure predicted by eqn (17) are in excellent match with experimental observations. Further, as shown in Fig. 3B and C, corrections using eqn (17) significantly reduced the noise in pressure loss measurements, which allowed to accurately determine the relationship between ΔCs and Δ[M].
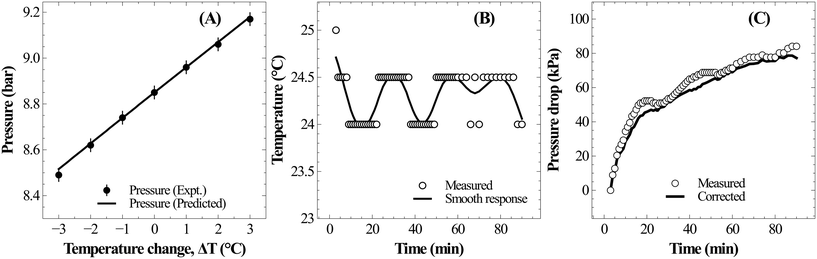 | ||
| Fig. 3 (A) Sensitivity of pressure with temperature change during CO2 absorption in distilled water at 25 °C; (B) typical temperature fluctuation during slag carbonation experiment, and (C) fluctuations in the corresponding pressure loss measurement during slag dissolution and the numerically corrected response using eqn (17). | ||
4.3 Calcium leaching characteristics from slag—parametric study
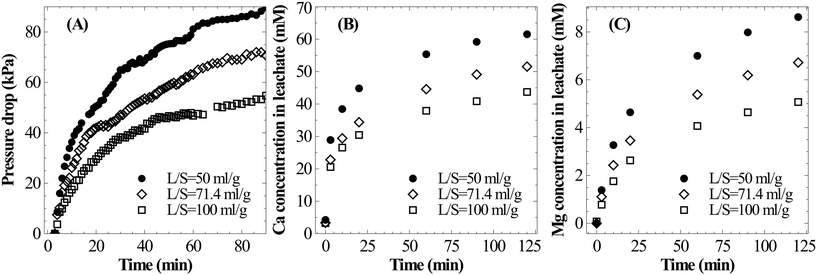
A parametric study was conducted to understand the influence of various operating parameters such as the liquid-to-solid ratio, particle size, temperature and carbon dioxide pressure on the dissolution characteristics of slag. Based on these results, an attempt has been made to identify the optimal conditions for mineral carbonation.The current experimental observations on the influence of L/S on calcium dissolution rates are in contrast with previously reported work. For instance, Huijgen et al.1 reported that the overall calcium carbonate yield monotonically increased with the decrease in the liquid-to-solid ratio. It was hypothesised that ionic strength improved the dissolution of Ca. Also, some studies20,21 reported the presence of an optimal L/S ratio for unstirred systems and rather weakly stirred systems.27 These studies hypothesised that too much water hindered CO2 permeability into the material. Together, these hypotheses that the dissolution step accelerates when L/S is reduced contradict current experimental results and those reported by a few others.17 Further, all these studies determined the extent of carbonation by measuring the weight gain of the carbonated residue which did not provide direct insights into Ca dissolution characteristics. Possible reasons for these contradicting observations are i) varying liquid volume reduced the liquid surface-area-to-volume ratio which in turn reduced gas–liquid absorption rates and ii) incomplete carbonation precipitation at a higher L/S ratio (due to low supersaturation) led to low overall efficiency. Under CO2 saturated conditions, it is clear from the current experimental observations that higher L/S improves the calcium extraction efficiency.
Similar to Ca leaching behaviour, the initial rate of Mg dissolution was observed to proportionally increase with increasing mass of slag owing to the higher surface area (Fig. 4C). However, the deceleration in dissolution of Mg with progression of leaching at a low L/S ratio is comparatively lower than that of Ca. This resulted in a marginal increase in the Mg/Ca ratio from 0.11 to 0.14 when L/S was varied from 100 to 50 ml g−1.
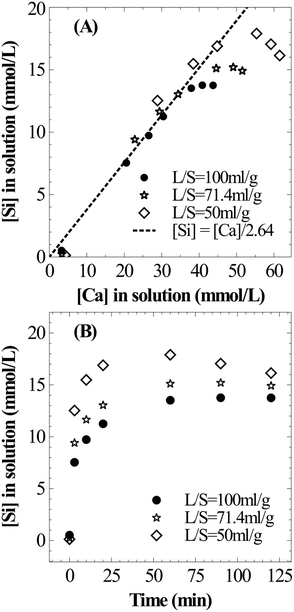
The influence of L/S on Si dissolution characteristics is very similar to that on Ca dissolution behaviour. As shown in Fig. 5A, a stoichiometric relationship exists between the temporal evolution of dissolved Si and Ca. This can be explained by the mineralogy of the slag where extractable Ca and Si are present in dicalcium silicate and tricalcium silicate phases (calcium present in the dicalcium ferrite phase is not susceptible for leaching28). These phases belong to the orthosilicate group containing no bridging oxygen (Si–O–Si) and dissolution is expected to occur in two-steps where the breaking of Ca–O bonds is followed by liberation of SiO4 tetrahedra without any need to break Si–O bonds.9 The overall dissolution step from the calcium silicate phase present in the slag can be considered as follows with soluble silica (present as silicic acid) as a stable intermediate which is further expected to undergo polymerization to form silica particles.
In all three cases, the Si concentration reached a plateau within the two hour period of dissolution (Fig. 5B). And the maximum Si concentration (18 mmol L−1) was significantly higher than its expected solubility (1.9 mmol L−1) under prevailing reaction conditions. Given the extremely high apparent supersaturation, it is highly likely that silica exists as colloidal particles of size less than 0.2 μm (filter pore size) instead of a true solution. At the prevailing pH (4–6), nanocolloid silica demonstrates uncharacteristic stability with a lifetime ranging from a few hours to days.29 This behaviour is expected due to strong repulsion among nanocolloid silica particles due to their negative surface charge. However, the increase in ionic strength30 and the presence of divalent cations31 could accelerate the growth of particles, possibly due to reduction or cancellation of the negative surface charge.32 As observed by Iler,33 a critical calcium ion concentration is necessary for coagulation of colloidal silica where the critical concentration is higher for smaller colloidal silica particles. Thus, silica precipitation is induced with further Ca dissolution as shown in Fig. 5B. As the slag loading was increased, understandably, the rate of Si precipitation increased because of higher Ca concentration in the solution.
From the current investigation, it may thus be concluded that higher L/S is desirable for maximum utility of calcium in the slag. Further, slower polymerisation of silica at high L/S allows easy filtration as polymerised silica from orthosilicates is gelatinous and makes filtration difficult.34
Surface passivation by the Si rich layer or precipitated calcium carbonate layer has been widely suspected as the reason for the reduction in the overall Ca leaching/carbonation efficiency when the particle size is increased.1,7 Extended dissolution experiments with 90–125 μm particles for 240 min showed that the Ca extraction efficiency can reach as high as that for finer particles without showing any sign of surface passivation. These results suggest that high Ca extraction efficiency from coarser particles can be achieved, which can bring down the need for energy-intensive particle-size reduction.
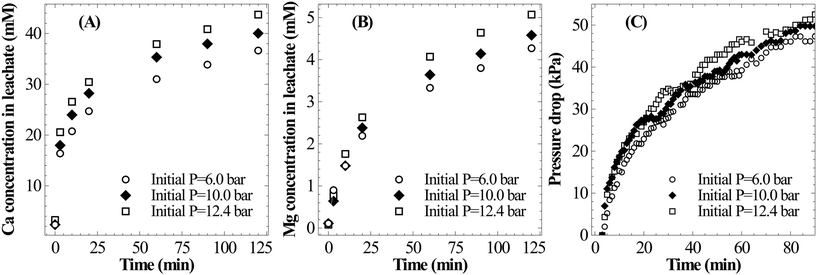
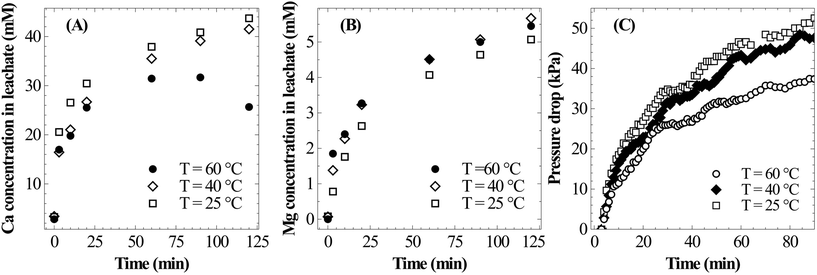
As shown in Fig. 8B, the temperature has only a marginal influence on dissolution of Mg. It appears that the rate of Mg dissolution increases with the increase in temperature, however, due to very small changes and low concentration it could not be clearly resolved. The drop in reaction pressure, which is shown in Fig. 8C, was found to be higher at 25 °C as compared to those at higher temperatures; this is due to the higher overall extraction of calcium at low temperature. Thus, in view of complete extraction of Ca from slag, lower temperature appears to be optimal for mineral carbonation through the pressure-swing route.
4.4 Supersaturation of calcite
Iizuka et al.17 reported up to three times supersaturation of calcium in dissolution experiments with waste cement. As shown in Table 2, similar observations were made in the current study where all the fine particle experiments, depending on the L/S ratio, showed an ionic activity product (IAP) 4–10 times higher than the solubility product of calcite. Since such an observation has implications to obtain high Ca dissolution at lower CO2 (reaction) pressure than thermodynamically predicted, it is worth exploring the reasons for the same. Further, understanding reasons for the observed remarkable solution stability for long time periods can pave the way for complete extraction of calcium without surface passivation posing a limitation as posited by many researchers. Also, even if the apparent supersaturation is due to the colloidal nature of precipitated calcium carbonate formed in solution (which passed through a syringe filter during sampling), it is worth understanding the reason behind nucleation in bulk solution so that surface precipitation can be avoided.| Experimental conditions | [Ca]total | [Mg]total | P CO2 | pH | [Ca2+] | [CO32−] | IAP | Ω calcite | Ω aragonite | Ω vaterite | Ω ACC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mM | mM | bar | — | mM | mM | — | M2 | — | — | — | — | |
| IAP: ionic activity product; Ω: saturation index (IAP/Ksp); ACC: amorphous calcium carbonate.a Precipitation was noticed during dissolution; Ksp values for various polymorphs reported in ref. 37 were used; the Davies equation37 was used for estimation of the activity coefficient for ionic species. | ||||||||||||
| L/S = 100 ml g−1, 120 min | 43.7 | 5.1 | 8.05 | 5.71 | 31.6 | 4.5 × 10−3 | 7022 | 1.7 × 10−8 | 4.5 | 3.8 | 1.4 | 0.04 |
| L/S = 71.4 ml g−1, 120 min | 51.5 | 6.7 | 7.85 | 5.78 | 36.0 | 6.5 × 10−3 | 5538 | 2.6 × 10−8 | 6.8 | 5.7 | 2.2 | 0.07 |
| L/S = 50 ml g−1, 120 min | 61.5 | 8.6 | 7.38 | 5.88 | 41.2 | 9.9 × 10−3 | 4162 | 4.2 × 10−8 | 10.9 | 9.2 | 3.5 | 0.11 |
| T = 60 °C, 60 mina | 31.4 | 4.5 | 9.31 | 5.82 | 22.9 | 6.3 × 10−3 | 3635 | 1.8 × 10−8 | 9.4 | 7.1 | 3.0 | 0.15 |
Firstly, to determine whether the apparent supersaturation is a true solution or a colloidal suspension, the moles of CO2 consumed per mole of metal ions released into the solution are estimated. Theoretical formulation based on which solution state could be interpreted is presented in section 2. Since the observed supersaturation levels are as high as 4–10 times ([Ca]total − [Ca]saturated > 20 mM), the sensitivity of pressure loss measurement was found to be suitable to distinguish a true solution from a saturated colloidal suspension. For all the datasets where supersaturation was evident (Ωcalcite > 1) and Ca concentration monotonously increased, an excellent prediction of total metal ion concentration could be made from the pressure loss data when the ratio of CO2 moles consumed per moles of metal ions was assumed to be 2 (Fig. 9). This shows that the solution is a true solution and disproves formation of any measurable colloidal precipitation or formation of a non-recoverable precipitate. Further, in the case of the coarse particle size (90–125 μm) experiment, where rapid filtration was possible to avoid further CaCO3 precipitation on residual slag after reactor de-pressurisation, the thermogravimetric analysis (TGA) on the slag residue obtained after 240 min dissolution (Ωcalcite = 4.5) showed no weight loss corresponding to carbonate decomposition (Fig. S2 in the ESI†). This corroborates that there is no precipitation of calcium carbonate on the slag surface.
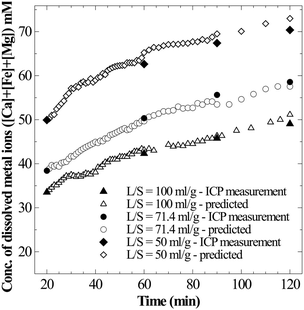 | ||
| Fig. 9 Total concentration of metal ions in super saturated solutions – measured (solid symbols) and predicted (open symbols) assuming true solution (Δ[M] = ΔCs/2). | ||
High supersaturation compared to calcite appears to be a consequence of calcite precipitation being kinetically unfavourable compared to other less-stable polymorphs such as amorphous calcium carbonate (ACC) or vaterite which subsequently transform to calcite. As the more stable calcite grows, the solution becomes undersaturated with respect to less-stable polymorphs leading to their dissolution and complete transformation to calcite. Multiple studies38,39 agree that amorphous calcium carbonate is the preferred nucleating polymorph when the supersaturation is sufficient to produce ACC. However, in the current study all the solutions, including where precipitation occurred, were undersaturated with respect to ACC (Table 2). Under circumstances where ACC cannot be produced, several studies38,40,41 agree that the first formed solid is metastable vaterite with the exception of the study of Clarkson et al.42 who reported it to be calcite when there are no calcite inhibiting species. Vaterite also appears to be the kinetically preferred polymorph because of its very high [Ca2+]/[CO32−],41 a parameter which significantly affects the calcite growth rate.43 Also, condensation of supersaturated silica (>10 mM) on carbonate particles especially under acidic conditions can potentially stabilize the growth and transformation of carbonate particles to calcite.44 Though it is difficult to precisely conclude the reason for the remarkable stability of supersaturated solution, low pH and very high [Ca2+]/[CO32−] appear to be important factors.
4.5 Surface passivation
Several previous studies1,7 reported passivation of the residual slag surface due to precipitation of silica and calcium carbonate. In the current study calcium carbonate precipitated during the dissolution step only at high temperature and very high supersaturation. Accordingly, as shown in Fig. 10, no calcium carbonate precipitate was observed on the surface where supersaturated aqueous solution was determined to be a true solution. Thus, it can be concluded that calcium carbonate does not passivate the surface under current experimental conditions. As reported in section 4.3.1, Si releases as monomeric units of silica and does not polymerise even at high supersaturation. For instance, in the case of coarse particle dissolution, Si was found to remain stable in solution for a dissolution time of 240 minutes. Overall, about 57% of the calcium could be extracted from fine and coarse particles in 120 minutes and 240 minutes, respectively, without any sign of surface passivation.In the case where precipitation occurred (60 °C), as shown in Fig. 11, micron-sized calcite crystals were observed as agglomerates along with silica, with the slag surface still being exposed. In contrast, Huijgen et al.1 reported that the precipitation occurred exclusively on the surface and no carbonate crystals were observed in the bulk. The study also reported the presence of a silica rich layer on the surface of residual slag. Based on the current experimental results, it appears that calcite and silica co-precipitated as agglomerates in the bulk rather than precipitating as individual layers on the slag surface. This may be because of the acidic slurry pH, under which conditions, the calcium silicate surface and calcite nuclei are generally expected to be positively charged and more so because of their high Ca2+/CO32− ratio (>4000).45 Thus, calcite is expected to co-precipitate with negatively charged silica. Smaller calcite crystals which appear to partly cover the slag surface might have precipitated after depressurisation when the saturation index increases multi-fold along with slurry pH.
Based on these results, it can be concluded that surface passivation is not significant with steel slag as the feedstock under current experimental conditions.
4.6 Precipitation
Unseeded precipitation of CaCO3 was carried out under atmospheric CO2 pressure using the filtrate (through 0.2 μm filter) from dissolution experiments, using <75 μm particles at 25 °C, an initial pressure of 12.41 bar and varying L/S in the range of 50–100 ml g−1. A reduction in CO2 pressure from 7.38–8.05 bar to atmospheric conditions increased the supersaturation by more than an order of magnitude (even after considering that the solution is not completely free of dissolved CO2). After 2–5 minutes of stirring, the clear solution turned turbid indicating the onset of precipitation. During this induction period, a rapid increase in pH to 7.5 was noticed (Fig. 12A). This probably indicates degassing of excess dissolved CO2. After 60 minutes of precipitation, the solution pH reached 8.45 and turbidity was completely lost with a suspension of calcium carbonate particles in a clear solution. Beyond this point, the solution pH continued to increase at a slower rate until it stabilized in the range of 8.5–8.6.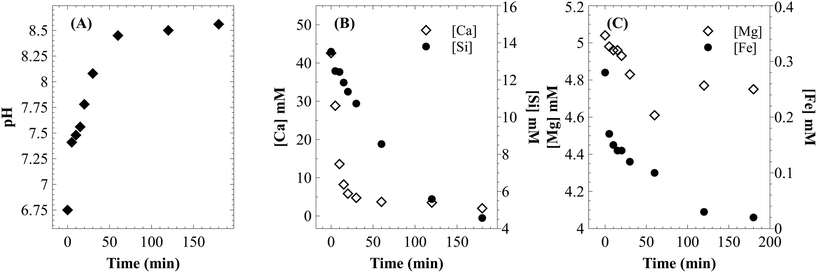 | ||
| Fig. 12 (A) Change in pH during the precipitation step; change in concentration of (B) Ca and Si, and (C) Mg and Fe during the precipitation step. | ||
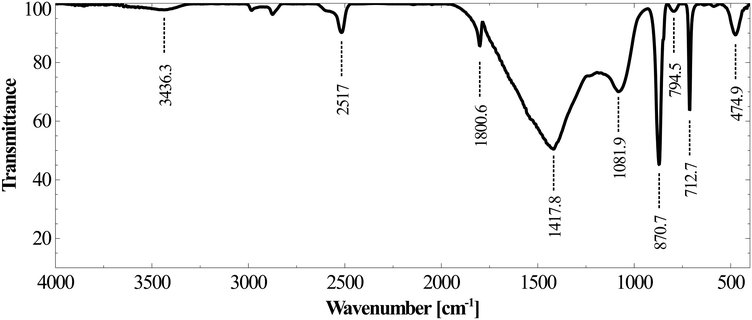
As shown in Fig. 12B, the calcium concentration reached a plateau after rapidly decreasing for the first 30 minutes. The silicon concentration, however, continued to decrease at the same rate for 120 minutes. These results suggest that while very high calcium recovery as carbonate is possible, the amount of silicon in PCC increases exponentially with calcium recovery. Mg remained in the mother liquor and only a small fraction precipitated along with PCC (Fig. 12C). The combined maximum concentration of Mg and Fe as impurities (determined based on elemental concentrations in the mother liquor) was found to be less than 1.5 wt% as magnesium carbonate and Fe(III) hydroxide. Silicon is the major secondary constituent with a maximum concentration of 16.6 wt% as SiO2, as estimated based on the Si concentration change in the mother liquor. The calcium carbonate content determined by thermal decomposition of PCC samples up to 900 °C showed a weight loss of 36%, which was equivalent to 81.5 wt% purity. This is in close agreement with the elemental analysis where other constituents were estimated to be ∼18 wt%. Si is known to co-precipitate as silica along with calcium carbonate without formation of silicate.46 As shown in Fig. 13, the morphology of precipitated calcium carbonate under all experimental conditions was found to be rhombohedral indicating the calcite polymorph. Additionally, a globular amorphous phase rich in silicon was also observed in SEM-EDS analysis (Fig. 13B). FT-IR analysis was performed to investigate the chemical form of Si in the PCC sample. The FT-IR spectra shown in Fig. 14, show peaks corresponding to symmetric (794 cm−1), anti-symmetric (1082 cm−1), and bending vibrations (475 cm−1) of the Si–O–Si group. Additionally, peaks corresponding to anti-symmetric (1418 cm−1), out-of-plane bending (871 cm−1), and planar bending (713 cm−1) vibrations of the CO3 group were noticed. No shoulders or peaks corresponding to Si–O–Ca which were expected at 950 cm−1 (ref. 47) were noticed. This result suggests the absence of silicate and existence of Si as silica. Silica is also a paper-filler with similar optical and ink adsorption properties to PCC.48 These observations suggest that further purification of PCC is not required for its use as a filler in writing and printing paper.
4.7 Outlook for pressure-swing carbonation
In the current study, about 57% of calcium from steel slag could be extracted in 120 minutes under mild operating conditions of 12.4 bar and 25 °C. Under these conditions, the quantity of PCC generated including silica is 535 kg per tonne of steel slag. Considering the complete extraction of calcium from silicates with extended dissolution time (assuming dicalcium ferrite is inert), the maximum potential for PCC generation is as high as 720 kg per tonne of steel slag. The corresponding potential for CO2 sequestration is 260 kg per tonne of steel slag.In the current study, very high solubility of calcium (2465 mg L−1) could be obtained at an initial CO2 pressure of 12.4 bar (actual pressure after CO2 absorption was <10 bar) and L/S of 50 ml g−1 while a previous study49 reported a maximum concentration of 1200 mg L−1 under similar conditions for waste cement. Rapid CO2 absorption allowed dissolution under acidic conditions, which in turn facilitated high supersaturation and potential to reduce the water volume. The remarkable stability of supersaturated solution suggests that calcium extraction up to the solubility limit of amorphous calcium carbonate (ACC) may be achieved by further process intensification. Steel slag is found to be very reactive as calcium is mainly present in orthosilicates, a class of silicates which dissolve by breaking weaker Ca–O bonds (instead of stronger Si–O–Si bonds) and dissolve as fast as calcium oxide in aqueous solutions.34,50 Further, congruent dissolution of Si from orthosilicates does not leave leached layers which can potentially passivate the reactive surface. Overall, pressure-swing carbonation appears to be very attractive for steel slag and CO2 utilisation.
5 Conclusions
In this study we have investigated the pressure-swing route as a potential route for production of PCC using steel slag to capture CO2. Simple stirrer modification allowed us to increase the gas–liquid mass transfer coefficient and perform studies on mineral carbonation under CO2 saturated conditions, which in turn permitted us to perform carbon balance and determine that the solution is truly supersaturated during the dissolution stage. Precipitation of calcite is not kinetically favoured possibly due to the low slurry pH and high calcium to carbonate ion ratio. Precipitation of silica or calcium carbonate on the residual slag surface which could lead to surface passivation was not observed in this study. Thus, the overall recovery of Ca as calcium carbonate is an order of magnitude higher than the equilibrium estimate based on calcite solubility. Within the investigated parametric space, dissolution at low temperature, high-pressure and high liquid-to-solid ratios are favourable conditions for PCC production. Silica which has similar optical and ink adsorption characteristics to PCC co-precipitated with calcite, wherein further purification may not be required for its use as a filler in the paper industry. Under all conditions investigated, rhombohedral calcite was the product. The overall extraction efficiency obtained after 120 minutes of dissolution was 57% leading to a production of 535 kg of PCC per tonne of steel slag. Further extension of dissolution time can enhance the PCC production and CO2 sequestration to 720 kg and 260 kg per tonne of steel slag, respectively.This study shows significant scope for process-intensification of pressure-swing carbonation, especially to reduce the water requirement. Further investigations on the dissolution step to achieve high and stable calcium concentration in the leachate, up to the solubility limit of amorphous calcium carbonate, are necessary. Also, investigations to obtain various morphologies of PCC and to control the particle size distribution are necessary for taking the process a step closer to commercialisation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the JSW Foundation, India for funding the project. The authors also thank Dr. Suman Majumdar of the JSW Foundation for providing the steel slag sample and for suggestions during collegial discussions.Notes and references
- W. J. J. Huijgen, G.-J. Witkamp and R. N. J. Comans, Environ. Sci. Technol., 2005, 39, 9676–9682 CrossRef CAS PubMed.
- A. Sanna, M. Uibu, G. Caramanna, R. Kuusik and M. M. Maroto-Valer, Chem. Soc. Rev., 2014, 43, 8049–8080 RSC.
- S. Teir, S. Eloneva and R. Zevenhoven, Energy Convers. Manage., 2005, 46, 2954–2979 CrossRef CAS.
- H. Shen and E. Forssberg, Waste Manage., 2003, 23, 933–949 CrossRef CAS PubMed.
- Z. J. Wu, B. F. Jiang, W. M. Liu, F. B. Cao, X. R. Wu and L. S. Li, Ind. Eng. Chem. Res., 2011, 50, 13778–13788 CrossRef CAS.
- K. S. Lackner, D. P. Butt and C. H. Wendt, Energy Convers. Manage., 1997, 38, S259–S264 CrossRef CAS.
- S. N. Lekakh, C. H. Rawlins, D. G. C. Robertson, V. L. Richards and K. D. Peaslee, Metall. Mater. Trans. B, 2008, 39, 125–134 CrossRef.
- R. M. Santos, D. François, G. Mertens, J. Elsen, T. V. Gerven and T. Van Gerven, Appl. Therm. Eng., 2013, 57, 154–163 CrossRef CAS.
- L. Marini, Geological Sequestration of Carbon Dioxide - Thermodynamics, Kinetics, and Reaction Path Modeling, Elsevier, 2006, vol. 11, pp. 27–51 Search PubMed.
- R. M. Santos, M. Bodor, P. N. Dragomir, A. G. Vraciu, M. Vlad, T. V. Gerven and T. Van Gerven, Miner. Eng., 2014, 59, 71–81 CrossRef CAS.
- J. Mulopo, M. Mashego and J. N. Zvimba, Water Sci. Technol., 2012, 65, 2236 CrossRef CAS PubMed.
- S. Van der Zee and F. Zeman, J. Cleaner Prod., 2017, 174, 718–727 CrossRef.
- S. Eloneva, S. Teir, J. Salminen, C.-J. Fogelholm and R. Zevenhoven, Energy, 2008, 33, 1461–1467 CrossRef CAS.
- J. Baldyga, M. Henczka and K. Sokolnicka, Chem. Eng. Res. Des., 2011, 89, 1841–1854 CrossRef CAS.
- H. Zhao, Y. Park, D. H. Lee and A.-H. A. Park, Phys. Chem. Chem. Phys., 2013, 15, 15185–15192 RSC.
- S. Kodama, T. Nishimoto, N. Yamamoto, K. Yogo and K. Yamada, Energy, 2008, 33, 776–784 CrossRef.
- A. Iizuka, M. Fujii, A. Yamasaki and Y. Yanagisawa, Ind. Eng. Chem. Res., 2004, 43, 7880–7887 CrossRef CAS.
- Y. Katsuyama, A. Yamasaki, A. Iizuka, M. Fujii, K. Kumagai and Y. Yanagisawa, Environ. Prog., 2005, 24, 162–170 CrossRef CAS.
- D. Daval, I. Martinez, J. Corvisier, N. Findling, B. Goffé and F. Guyot, Chem. Geol., 2009, 265, 63–78 CrossRef CAS.
- M. F. Bertos, X. Li, S. J. R. Simons, C. D. Hills and P. J. Carey, Green Chem., 2004, 6, 428–436 RSC.
- N. L. Ukwattage, P. G. Ranjith and S. H. Wang, Energy, 2013, 52, 230–236 CrossRef CAS.
- N. L. Ukwattage, P. G. Ranjith and X. Li, Measurement, 2017, 97, 15–22 CrossRef.
- J. D. Rodriguez-Blanco, S. Shaw, P. Bots, T. Roncal-Herrero and L. G. Benning, J. Alloys Compd., 2012, 536, S477–S479 CrossRef CAS.
- M. M. Reddy and G. H. Nancollas, J. Cryst. Growth, 1976, 35, 33–38 CrossRef CAS.
- T. Chen, A. Neville and M. Yuan, Chem. Eng. Sci., 2006, 61, 5318–5327 CrossRef CAS.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS.
- R. R. Tamilselvi Dananjayan, P. Kandasamy and R. Andimuthu, J. Cleaner Prod., 2015, 112, 4173–4182 CrossRef.
- M. Bodor, R. M. Santos, L. Kriskova, J. Elsen, M. Vlad and T. Van Gerven, Eur. J. Mineral., 2013, 25, 533–549 CrossRef CAS.
- C. F. Conrad, G. A. Icopini, H. Yasuhara, J. Z. Bandstra, S. L. Brantley and P. J. Heaney, Geochim. Cosmochim. Acta, 2007, 71, 531–542 CrossRef CAS.
- E. A. Gorrepati, P. Wongthahan, S. Raha and H. S. Fogler, Langmuir, 2010, 26, 10467–10474 CrossRef CAS PubMed.
- D. A. Crerar, E. V. Axtmann and R. C. Axtmann, Geochim. Cosmochim. Acta, 1981, 45, 1259–1266 CrossRef CAS.
- D. J. Belton, O. Deschaume and C. C. Perry, FEBS J., 2012, 279, 1710–1720 CrossRef CAS PubMed.
- R. K. Iler, J. Colloid Interface Sci., 1975, 53, 476–488 CrossRef CAS.
- B. Terry, Hydrometallurgy, 1983, 10, 135–150 CrossRef CAS.
- G. R. Holdren and R. A. Berner, Geochim. Cosmochim. Acta, 1979, 43, 1161–1171 CrossRef CAS.
- K. Lívanský, Folia Microbiol., 1982, 27, 55–59 CrossRef.
- L. Brečević and A. E. Nielsen, J. Cryst. Growth, 1989, 98, 504–510 CrossRef.
- T. Ogino, T. Suzuki and K. Sawada, Geochim. Cosmochim. Acta, 1987, 51, 2757–2767 CrossRef CAS.
- J. Rieger, T. Frechen, G. Cox, W. Heckmann, C. Schmidt and J. Thieme, Faraday Discuss., 2007, 136, 265 RSC.
- N. Spanos and P. G. Koutsoukos, J. Phys. Chem. B, 1998, 102, 6679–6684 CrossRef CAS.
- L. Z. Lakshtanov and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 2655–2664 CrossRef CAS.
- J. R. Clarkson, T. J. Price and C. J. Adams, J. Chem. Soc., Faraday Trans., 1992, 88, 243 RSC.
- K. Larsen, K. Bechgaard and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 2099–2109 CrossRef CAS.
- M. Kellermeier, F. Glaab, R. Klein, E. Melero-García, W. Kunz and J. M. García-Ruiz, Nanoscale, 2013, 5, 7054 RSC.
- E. Chibowski, L. Hotysz and A. Szcze's, Colloids Surf., A, 2003, 222, 41–54 CrossRef CAS.
- Y. Kitano, M. Okumura and M. Idogaki, Geochem. J., 1979, 13, 253–260 CrossRef CAS.
- G. S. Pappas, P. Liatsi, I. A. Kartsonakis, I. Danilidis and G. Kordas, J. Non-Cryst. Solids, 2008, 354, 755–760 CrossRef CAS.
- R. Gill, Paper Chemistry, Springer Netherlands, Dordrecht, 1st edn, 1995, ch. Fillers, pp. 1–8 Search PubMed.
- Y. Abe, A. Iizuka, H. Nagasawa, A. Yamasaki and Y. Yanagisawa, Chem. Eng. Res. Des., 2013, 91, 933–941 CrossRef CAS.
- W. H. Casey, J. Colloid Interface Sci., 1991, 146, 586–589 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8re00167g |
| ‡ Experimental design to achieve rapid CO2 saturation is presented in section 3.2.1. |
| § In the current study, the reaction slurry is undersaturated with respect to MgCO3 and Fe2+ leaching is negligible at the operating CO2 pressure. |
| ¶ Standard practice to store the sample for ICP analysis. |
| This journal is © The Royal Society of Chemistry 2019 |