Pushing the limits of concertedness. A waltz of wandering carbocations

Abstract

Among the array of complex terpene-forming carbocation cyclization/rearrangement reactions, the so-called “triple shift” reactions are among the most unexpected. Such reactions involve the asynchronous combination of three 1,n-shifts into a concerted process, e.g., a 1,2-alkyl shift followed by a 1,3-hydride shift followed by a second 1,2-alkyl shift. This type of reaction so far has been proposed to occur during the biosynthesis of diterpenes and the sidechains of sterols. Here we describe efforts to push the limits of concertedness in this type of carbocation reaction by designing, and characterizing with quantum chemical computations, systems that could couple additional 1,n-shift events to a triple shift leading, in principle to quadruple, pentuple, etc. shifts. While our designs did not lead to clear-cut examples of quadruple, etc. shifts, they did lead to reactions with surprisingly flat energy surfaces where more than five chemical events connect reactants and plausible products. Ab initio molecular dynamics simulations demonstrate that the formal minima on these surfaces interchange on short timescales, both with each other and with additional unexpected structures, allowing us a glimpse into a very complex manifold that allows ready access to great structural diversity.

---

Introduction

Terpenoids comprise the largest class of natural products, with more than 80 000 compounds reported to date.¹ Compounds in this family of secondary metabolites often contain complex carbon skeletons,^1–7 and they have captivated the interest of researchers in many branches of the scientific community, not only because of their complex structures, but also because many display significant biological activities.^2,8–12 The intrinsic complexity of these molecules, however, has made their laboratory synthesis particularly challenging, a situation that has led to some spectacular advances in synthetic methods,^13–16 but has also led to some terpenoid drugs being produced via semisynthetic routes that rely upon biocatalysis.¹⁷ In nature, terpenoids are derived from terpene hydrocarbons via oxidation (and sometimes other) reactions.^18–20 These terpene precursors, which generally contain the complex carbon backbones in the terpenoids derived from them, are produced by terpene synthases (also sometimes called cyclases) that promote the (poly)cyclization/rearrangement of acyclic, (usually) achiral precursors.^1,21,22 While many terpene synthases produce a single product with high selectivity (of hundreds or thousands of possible isomers), some are promiscuous in their cyclization chemistry; an extreme example of the latter is γ-humulene synthase, which generates >50 terpene products.²³

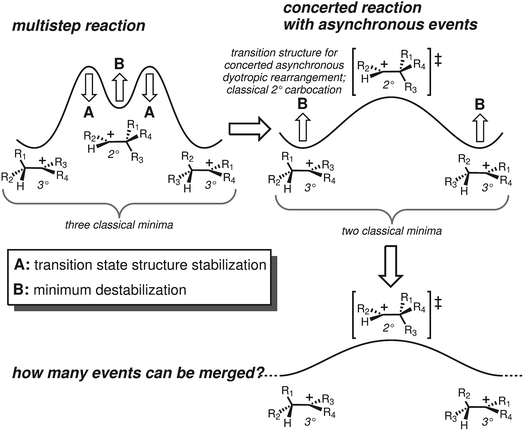
Terpene synthase promoted reactions universally involve carbocations as intermediates. Although their inherent reactivity tendencies are often expressed,²⁴ these can be modulated by steric/shape effects (preorganization/conformational restriction), noncovalent interactions (e.g., CH–π, CH–O interactions)^25–28 and positioning of active site bases (or, occassionally, nucleophiles) for site-selective termination of carbocationic cascades.^1,2,29,30 These conclusions have arisen from both experimental and theoretical studies.⁵ In addition, theoretical studies have highlighted the fact that many proposed carbocation intermediates are not minima on the potential energy surfaces (PESs) involved, particularly primary and secondary carbocations.^5,31–34 As a consequence, what would conventionally be proposed as multistep reaction pathways are better described (at least in the absence of enzymes) as processes in which different chemical events take place asynchronously along a single (often long) reaction path featuring only one transition state structure (TSS): i.e., concerted reactions with asynchronous events^35–39 (see Fig. 1-right).

Fig. 1 Top left: a two-step reaction. Top right: conversion of a 2-step reaction into a concerted reaction with 2 asynchronous chemical events. Bottom: potential extension to a concerted reaction with even more asynchronous events.

We focus here on concerted carbocation rearrangements involving the asynchronous combination of a 1,2-alkyl shift, a 1,3-hydride shift and a second 1,2-alkyl shift – a so-called “triple shift”. This type of reaction was proposed to occur during the biosynthesis of kaurene, atiserene and related diterpenes as well as sterol sidechains.^40–43 The specific triple shift of interest here is shown in Fig. 2, a reaction with a predicted barrier of only 15 kcal mol⁻¹.^42,43 The intrinsic reaction coordinate (IRC)^44–46 for this reaction visits structures resembling the secondary cations shown in the scheme (i.e., “hidden intermediates”),^47–49 but these occur as shoulders on the IRC rather than minima. After analyzing this system, we postulated that the number of concatenated shifts could be increased beyond three – an exercise in pushing the limits of concertedness – by replacing the methyl group at carbon 8 in Fig. 2 with hydrogen. This change would convert the minima (1 and 4) from tertiary to secondary carbocations, increasingly the likelihood that they would not be minima. Below we discuss the results of implementing this change not only on the potential energy surface but also on the dynamics of passage over it through the use of ab initio molecular dynamics (AIMD) simulations.^50–53 AIMD calculations provide a view of reactions involving PESs containing unusual features such as post-transition state bifurcations, anomalous branching, unusual topographies, etc. that accounts for kinetic as well as potential energy.^50–58

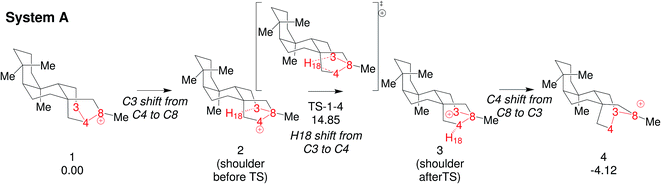Fig. 2 Triple shift reaction reported by Hong and Tantillo⁴² (System-A). Relative free energies (in kcal mol⁻¹ computed at 298 K and 1 atm) are calculated with respect to 1 at the B3LYP/6-31+G(d,p) level (see Fig. 1 in ref. 42 for more details).

Computational methods

Geometries of stationary points were fully optimized by using B3LYP/6-31+G(d,p)^59–65 in the gas phase with the Gaussian 09 package.⁶⁶ This level of theory has been used previously to investigate many carbocation reactions and its performance compares favorably to that of other methods.^5,67

B3LYP is known to have issues in correctly capturing the relative energies of cyclic and acyclic structures.⁶⁸ In addition, while not always the case, B3LYP has been shown in related carbocation rearrangements to find shallow minima that are not present at other levels of theory (e.g., mPWPW91 and MPWB1K).^33,41,69 As a result, using B3LYP rather than other functionals (or non-DFT methods) likely intensifies the challenge of increasing the number of events that can be combined into concerted processes.

Quassiclassical molecular dynamic calculations were used to follow trajectories; these made use of the Gaussian 09 package⁶⁶ for quantum chemical computations coupled with the PROGDYN scripts (first version)^55,70,71 for propagating trajectories. Trajectories were initiated at the TSS (0 fs). Starting from the TSS a Maxwell–Boltzman distribution of energies is considered. A specific total energy value is assigned stochastically, using a random number generator. For this total energy, each vibrational mode is given its zero point energy plus additional excitations. Those trajectories for which the energy criteria is met⁷² are allowed to evolve during 2000 fs (using 1 fs time steps), in both the reactant and product directions. A second set of 4000 fs trajectories was also acquired starting at the TSS (0 fs) and using the same conditions. The trajectories were run using B3LYP/6-31+G(d,p), in the gas phase at 298 K. Analysis of geometry optimizations, IRCs and trajectories was performed using the Molden program.⁷³

Different functionals (and non-DFT methods) will give different quantitative results because they lead to (at least slightly) different stationary point structures, energies and vibrational frequencies, as well as differences in PES curvature away from stationary points (e.g., see pioneering work on S_N2 reactions).^74–78 However, here we are after qualitative pictures of reactivity.

Zero point vibrational energy leakage during quasiclassical trajectories (especially given the long trajectory lengths considered here)^79–81 may diminish the accuracy of our results, e.g., in terms of recrossing percentage and absolute rates, but given the flatness of the PESs involved, i.e., the ease of moving onward rather than getting trapped in a particular region, unphysical ZPE flow is unlikely to be a major issue.

General protocols

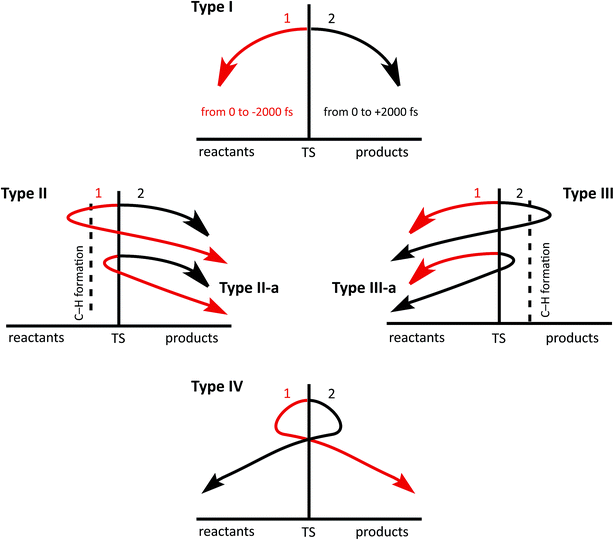
To simplify the analysis of trajectories, we apply the following classification, based on the existence and/or the type of recrossing found (see Fig. 3). We define the “product region” as the region of coordinate space where the C4–H18 bond is formed and C3–H18 is broken and the “reactant region” as the region where C3–H18 is formed while C4–H18 is broken (vide infra).

Fig. 3 Top: regular trajectory, starting from the TS towards reactants and then from the TS towards products (type I). Middle: trajectories that recross in one direction (types II–III). Bottom: trajectories that recross in both directions (type IV). Numbering (1 and 2) is used to distinguish halves of a complete trajectory.

(1) Type I. Trajectories following the expected path starting from the transition state (TS) and evolving to reactants in one direction (1) and to products in the other (2) (Fig. 3, top).

(2) Type II. Trajectories that, during their time in the reactant well (1) recross⁸² and evolve towards the product region (Fig. 3, middle-left); the half-trajectory from the TS to products (2) evolves as expected. Type II-a. Both halves of the trajectory (1 and 2) start from the TS and evolve towards the product well without visiting the reactant region, i.e., with C–H bond formation.

(3) Type III. Trajectories that during their time in the product well (2) recross and evolve towards the reactant region (Fig. 3, middle-right). Type III-a. Both half-trajectories start from the TS and evolve towards the reactant well without visiting the product region (Fig. 3, middle-right).

(4) Type IV. Trajectories that, after having followed the expected behaviour for a while, eventually re-visit the TS from both regions and cross to the other basins, once or several times (Fig. 3, bottom).

To simplify the analysis of the structures that appear along trajectories, we use inter-atom connectivity to classify them. Many of the structures described below are not minima on the PES, but clearly correspond to particular types of carbocations familiar to organic chemists; they meet neither a topographical (they do not constitute a stationary point on the PES) nor a kinetic criterion, as defined by the IUPAC,⁸³ to be considered a minimum. We consider two structures to be equivalent if they present the same bonding pattern, using the criteria implemented in Molden to define the existence of a bond: C_i − C_f < 1.8 Å and C_k − H_l < 1.3 Å. While this classification is admittedly arbitrary, it is useful.

Results and discussion

Dynamics of a biologically relevant triple shift

To start this study, we decided to analyze the dynamics of an already-known biologically relevant triple shift, see Fig. 2.⁴³ As has been done in other studies on dynamics of diterpene-forming carbocation rearrangements,^58,69,84,85 we simplified the diterpenes in system A (Fig. 2) by replacing two of the fused cyclohexanes by methyl groups, arriving at system B (Fig. 4; for details about the appropriateness of this simplification see ESI†). After having optimized 1-Me, 4-Me and TS1-4-Me and calculated the IRC connecting them (see Fig. 4) we ran 500 quasiclassical trajectories for System B using PROGDYN.^55,70 Trajectories were initiated from (TS-1-4-Me) and allowed to evolve towards the reactant and product wells for 2000 fs each.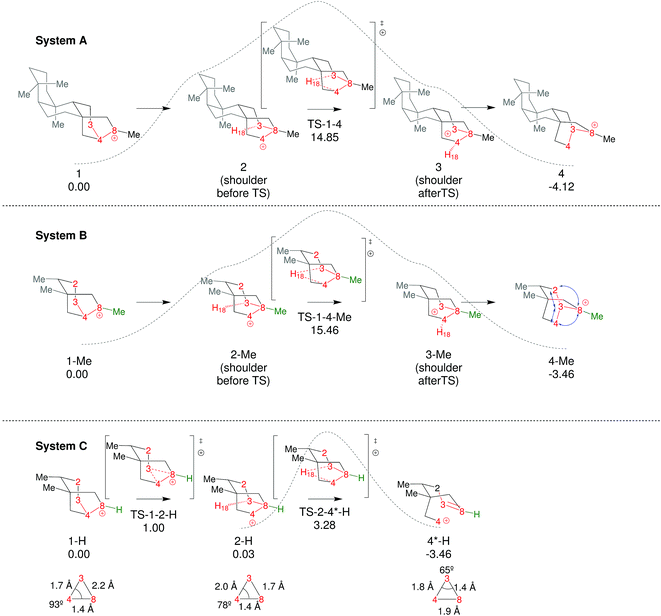

Fig. 4 Comparison of the three systems examined. Relative free energies of the stationary points (B3LYP/6-31+G(d,p)) are noted in kcal mol⁻¹. Dashed lines are qualitative representations of the IRCs generated from TS-1-4-Me and TS-2-4*-H. For system C we have included a representation of the plane formed by C3, C4 and C8 in 1-H, 2-H and 4*-H with selected distances and angles, with the purpose of highlighting their geometric features, which are characteristic of non-classical carbocations (for further discussion on this topic see ESI†).^86–91

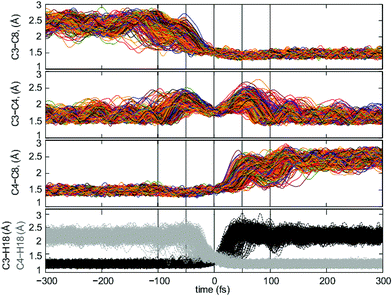
When analyzing the trajectories, we found that the chemical events were mostly concentrated in a time window of −100–100 fs. We first examined the evolution of five key bond distances in the transformation of 1-Me into 4-Me (C3–C8, C3–C4, C3–H18, C4–H18 and C4–C8) in this time window, and then extended the analysis to a wider frame, between −300 and 300 fs, to ensure that no further chemical events occur at longer times (see ESI† for the full time frame).

As can be seen from Fig. 5, the analysis of the bond distances along trajectories is quite indicative of the asynchronicity – in time – of C3–C8 bond formation and C4–C8 bond breaking with respect to C3–H18 bond breaking and C4–H18 bond formation events, and with the breaking and formation of the C3–C4 bond. The C3–C8 distance shortens to bonding distance in the −100 fs to 0 fs interval, approximately 50 fs ahead of the formation of C4–H18, a phase which corresponds to the pre-TSS shoulder. In parallel, C4–C8 starts breaking approximately 20 fs after the TSS and increases its bond distance until it breaks approximately 30 fs later. This corresponds to a time frame where the breaking of the C3–H18 bond has already occurred, thus corresponding to the region around 3-Me. Once both the C4–C8 and C4–H18 bonds are formed, at ∼100 fs, the 4-Me basin is reached.

Fig. 5 Top: evolution of the C3–C8 bond distance from −300 fs to 300 fs. Middle-up: evolution of the C3–C4 bond distance from −300 fs to 300 fs. Middle-down: evolution of the C4–C8 bond distance from −300 fs to 300 fs. Bottom: evolution of the C3–H18 (black) and C4–H18 (grey) bond distances from −300 fs to 300 fs. In all cases, only data from those trajectories that did not recross is shown.

The variation of the C3–C4 distance with time is revealing (Fig. 5, middle-up), as these two atoms are involved in the three key events in the reaction mechanism. The C3–C4 bond starts to lengthen significantly at around −100 fs and reaches its maximum length around −50 fs. This is consistent with the breaking of the C3–C8 bond associated with the initial C3 migration. After this time, a hydrogen shift, implying the formation of a C4–H18 bond, ensues, which brings C3 and C4 closer together again. A reverse type of process occurs after the TSS region, first with elongation of the C3–C4 bond due to the breaking of the C3–H18 bond, up until 50 fs, and then with regeneration of the C3–C4 bond upon migration of C4 from C8 to C3, 50 fs after the TSS has been visited. Variation in the C3–C4, C4–C8 and C3–C8 distances in the reactant and product regions reflects variations in the degree of hyperconjugation with the C8 carbocation as the molecule vibrates. A detailed analysis of other atomic motions occuring during trajectories can be found in the ESI.†

Of these four bond distances, C3–H18 and C4–H18 are the most representative of the regions delimited by the transition state structure, as their changes concentrate around a small time region around the TSS (−50–50 fs) and are rather clear cut (C3–H18 is formed between 0 and 50 fs and C4–H18 is broken between −50 and 0 fs). Consequently, their formation/breaking are considered from now on as the parameter defining whether we are located in the reactant or product region, and consequently to evaluate recrossing.

16% of the trajectories examined (79/500) were found to recross. Of these: (1) 23 trajectories belong to type II-a. (2) Two trajectories are type II (see ESI†). (3) 44 trajectories can be classified as type III-a. (4) 10 trajectories belong to type I, but their phases are inverted; they follow a (2) to (1) path. The fact that we have found a relatively large amount of recrossing is likely a result of a flat PES around the TSS for the reaction in question (it is unlikely that adding entropy contributions will change that significantly).^82,92 Up to this point, dynamics simulations have provided a clearer picture of the mechanism of the triple shift but one that does not diverge significantly from that obtained through examination of the PES.

Coupling triple shifts to additional chemical events

In an effort to extend the number of bond-making/breaking events that can be coupled into concerted processes, we modified system B with the hope of making other carbon and hydrogen migrations available to reactants and products. Our hypothesis was that further flattening of the PES by relative destabilization of reactants and products (Fig. 1) would open such reaction channels. Thus, we converted tertiary cation centers into secondary ones, arriving at system C (Fig. 4-bottom). Contrary to our expectations, we found that the triple shift rearrangement for system C is technically a stepwise process, i.e., the secondary carbocations (identified as shoulders on the IRC for systems A and B) were actual minima on the PES.⁹³ However, these minima are very shallow, (we calculate a barrier for the transformation of 1-H into 2-H of only 1 kcal mol⁻¹), and 1-H and 2-H are essentially isoenergetic (Fig. 4, bottom). In addition, the overall barrier for the transformation of 1-R into 4-R (R = H, Me) is much lower for system C than for system B or system A.

These very low barriers prompted us to analyze the dynamical behaviour of system C in order to evaluate any differences with the concerted triple shift previously described and to predict the fate of 4*-H, a non-classical carbocation.^86–91 Thus, dynamics calculations were run for system C, starting from TS-1-2-H following the same methodology as previously used for system B. For system C, 193/500 (39%) of these trajectories recrossed, consistent with an even flatter PES for this system. For non-recrossing trajectories, we found that the variation of C3–H18 distance with time (Fig. 6) is considerably larger than for system B (Fig. 5), indicating that additional transformations may indeed be present along some trajectories.

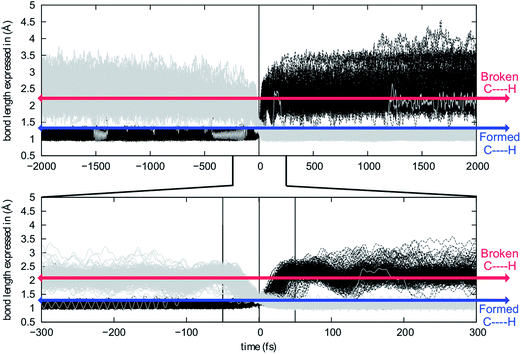Fig. 6 Evolution of C3–H18 (black) and C4–H18 (grey) distances along the analyzed trajectories. Top: full time-frame. Bottom: −300 to 300 fs time-frame.

As a result, we first examined (following the scheme described in the Computational section to characterize connectivity) the structures reached by each trajectory at 1000 and 2000 fs. If 1000 fs were enough time for the system to have reached its “product state”, we would expect (in the aggregate) a set of structures equivalent at the two time points.

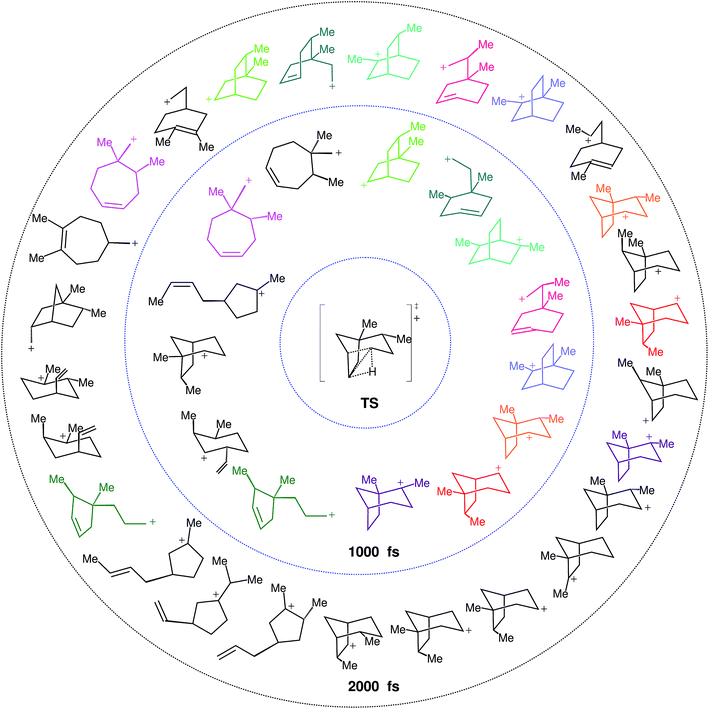
What we find instead is that 17 structures are reached at 1000 fs and 33 at 2000 fs, a striking difference. These structures are not necessarily minima on the PES, but each of them corresponds to a particular connectivity between atoms. If we take into account that some of the structures are equivalent but for the atom numbering, these 17 and 33 structures are reduced to 14 and 26 distinct structures, respectively (see Fig. 7). That equivalent structures with different atom numbering are formed indicates that they are being reached through different paths. Besides evidencing a much richer reactivity than expected from the IRC (see Fig. 4), these results clearly show that equilibrium has not been reached at 1000 fs, and might not have been reached at 2000 fs either.

Fig. 7 Product distribution at 1000 fs (inner circle) and 2000 fs (outer circle). Structures in black at the inner circle disappear in the larger trajectories (at 2000 fs) and structures in black in the outer circle are not found at 1000 fs. Structures in other colors are found in trajectories at both time steps. Structures shown are not necessarily PES minima.

Further analysis of the results of our dynamics simulations led us to organize all the structures visited by each of the trajectories in reaction paths. These paths are summarized in Fig. 8, which collects all structures formed in the product region. The scheme is complex and highly branched as a result of the diversity of trajectories, but there are some paths (or parts thereof) that seem to be favored. Structure 4 (relative potential energy: −4.9 kcal mol⁻¹) is generally the first structure to be formed, and in one of the most frequently followed paths it evolves towards 5 through the lengthening of the C4–C8 bond, (resulting in 4*), followed by formation of the C4–C3 bond. Then structure 5 further evolves towards 6 through lengthening of the C2–C3 bond. Subsequently, the formation of a C2–C8 bond can occur, leading to 7 (−6.0 kcal mol⁻¹), a secondary carbocation. Thus, in the most common path, the 4 → 7 transformation, we find a mechanism involving five distinct chemical events that occur after the TSS. Another frequently observed route for the evolution of 4 starts with the lengthening of the C7–C8 bond, which leads to primary carbocation 8, followed by formation of the C3–C7 bond to yield an alternative secondary carbocation, 9 (−6.0 kcal mol⁻¹).

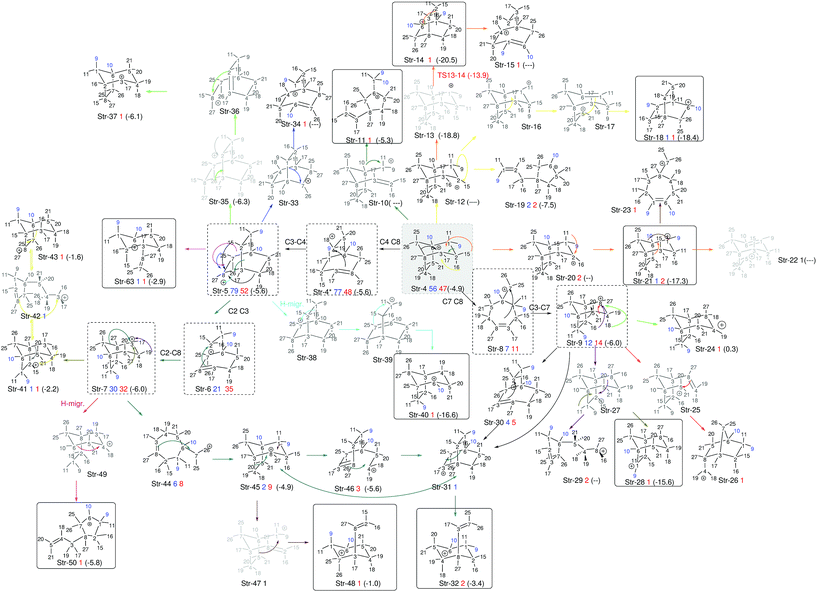Fig. 8 Reaction paths followed by trajectories, depicted as sequences of structures with a defined connectivity. Structures in black correspond to those that appear in Fig. 7 (we use the prefix Str on their names to avoid confusion with other numbers used in the representation). Below each of those, a number in blue indicates how many times this structure appears at exactly the 1000 fs time step of a trajectory, and a number in red how many times it does so at 2000 fs. With dashed squares, we have highlighted those structures most frequently encountered, while we have used solid squares to indicate tertiary carbocations (perhaps surprisingly, they are not among those structures most frequently encountered at either 1000 or 2000 fs). All black structures in the scheme were used as starting points of geometry optimizations. For those where the optimization preserved connectivity (they are actual minima on the potential energy surface), their energies relative to 1-H are noted between parentheses. The numbers in blue on the structures represent the methyl groups that keep their structural integrity along the trajectory.

At 1000 fs, only the 4*, 4, 5, 6, 7, 8 and 9 wells are visited frequently, but other C–C and C–H migrations do occassionally occur and furnish different structures. At 2000 fs, the same structures are visited most frequently, but in a lower proportion, as an additional set of carbocations has been formed in these longer trajectories. Of the 24 new structures formed at these longer times, only 10 are tertiary carbocations (highlighted in Fig. 8 through continuous line rectangles). In addition to these paths, structures 4, 5 and 9 can also spawn subsequent structures via multiple different paths, depending on which vibrational modes are activated as these parent structures are being formed.

When the geometry of the structures shown in Fig. 8 are optimized, only some of them preserve their connectivity, allowing us to characterize them as real minima in the potential energy surface of the system. As expected, tertiary carbocations are lower in energy than secondary or primary ones, however, the fact that so many of the latter are actual minima and relatively stable, highlights the fact that a large number of them are actually non-classical carbocations^86–91 (see the ESI† for a more detailed description of them).

As happened for system B, recrossing trajectories from system C came in a variety of flavors: (a) 41 (8%) recrossed from the product region towards reactants; 33 of these are type III-a while eight belong to type III. (b) 136 (27%) recrossed from the reactant region toward products; 50 of these belong to type II-a, while 86 are type II. (c) 23 (5%) recrossed multiple times; 15 belong to type IV, 8 belong to type I but the TS phase is inverted at them. Looking for additional new structures, we selected those recrossing trajectories that had reached the product region by 2000 fs and performed an analysis, analogous to that described above for non-recrossing trajectories. New structures are indeed found, e.g., two formal primary cations, three secondary cations and five tertiary cations (a more detailed description of these trajectories can be found on the ESI†). This appearance of new structures in the recrossing trajectories and the divergence in the set of structures found at 1000 and 2000 fs, together with the fact that the most stable tertiary carbocations were not among the most visited regions of the potential energy surface in the trajectories analyzed, led us to suspect that the system cannot be considered to have reached equilibrium at 2000 fs. To test this hypothesis, we ran a smaller set of 100 trajectories for 4000 fs (at a significant computational cost), whose detailed analysis is described in the ESI.† The main result is that while some of the primary and secondary carbocations in Fig. 8 are still appearing at the 4000 fs time point, some seem to have further progressed to new tertiary carbocations, and there is even interconversion between different tertiary carbocations.

Bird's eye view

The pathways connecting the structures encountered during dynamics simulations for system C can be viewed as a web, with a carbocation of different connectivity at each node. These nodes are interconnected through single hydride or alkyl migration events. Residence times in nodes corresponding to primary (but nonclassical)^86,94 and secondary carbocations are short (<20 fs). Given the flatness of the PES surrounding the TSS, i.e., most structures are within 5–10 kcal mol⁻¹ of each other, the system rapidly samples different nodes for a long time before falling into a comparatively deep well (e.g., a tertiary carbocation). During this time, the system can even visit a number of nodes that connect it from the product (C4–H18 bonded, C3–H18 broken) to the reactant region (C4–H18 broken, C3–H18 formed) blurring the limits of these two a priori differentiated regions. In other words, we observe fluxional behaviour involving an apparently unprecedented diversity of structures.^95–98

The subtle structural modification made to system B seems to have made these players (carbocations) lose their tempo and engage in a wandering melody. Such a PES could perhaps be modulated by solvent (although some solvents might lead to even flatter surfaces) or be controlled via geometric constraints imposed by a surrounding catalyst (biological or synthetic). In the biological context, one might wonder whether there would be (or has been) evolutionary pressure against utilization of reactions with exceedingly flats PESs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Centro de Supercomputación de Galicia (CESGA) for the allocation of computational resources. MCR is thankful to the Ministerio de Ministerio de Educación Cultura y Deporte of the Spain Goverment for her FPU fellowship and to the Fundación Pedro Barrié de la Maza for a fellowship to visit the Tantillo Lab. Funding for this work has been provided by the Spanish Ministerio de Economía y Competitividad (CTQ-2016-75023-C2-2-P) and the Xunta de Galicia (ED431C-2017/70). DJT gratefully acknowledges support from the US National Science foundation (CHE-1565933 and CHE-030089 [XSEDE]).

References

1. D. W. Christianson, Structural and Chemical Biology of Terpenoid Cyclases, Chem. Rev., 2017, 117, 11570–11648.
2. P. M. Dewick, The biosynthesis of C5–C25 terpenoid compounds, Nat. Prod. Rep., 2002, 19, 181–222.
3. D. W. Christianson, Structural Biology and Chemistry of the Terpenoid Cyclases, Chem. Rev., 2006, 106, 3412–3442.
4. B. Singh and R. A. Sharma, Plant terpenes: defense responses, phylogenetic analysis, regulation and clinical applications, 3 Biotech, 2015, 5, 129–151.
5. D. J. Tantillo, Biosynthesis via carbocations: Theoretical studies on terpene formation, Nat. Prod. Rep., 2011, 28, 1035–1053.
6. R. Xu, G. C. Fazio and S. P. Matsuda, On the origins of triterpenoid skeletal diversity, Phytochemistry, 2004, 65, 261–291.
7. R. Thimmappa, K. Geisler, T. Louveau, P. O'Maille and A. Osbourn, Triterpene Biosynthesis in Plants, Annu. Rev. Plant Biol., 2014, 65, 225–257.
8. N. F. Salakhutdinov, K. P. Volcho and O. I. Yarovaya, Monoterpenes as a renewable source of biologically active compounds, Pure Appl. Chem., 2017, 89, 1105–1117.
9. A. Ludwiczuk, K. Skalicka-Woniak and M. Georgiev, in Pharmacognosy, ed. S. Badal and R. Delgoda, Academic Press, Boston, 2017, ch. 11 – terpenoids, pp. 233–266.
10. C.-H. Li, X.-T. Yan, A.-L. Zhang and J.-M. Gao, Structural Diversity and Biological Activity of the Genus Pieris Terpenoids, J. Agric. Food Chem., 2017, 65, 9934–9949.
11. A. Pasdaran and A. Hamedi, The genus Scrophularia: a source of iridoids and terpenoids with a diverse biological activity, Pharm. Biol., 2017, 55, 2211–2233.
12. T. Zhao, S.-J. Li, Z.-X. Zhang, M.-L. Zhang, Q.-W. Shi, Y.-C. Gu, M. Dong and H. Kiyota, Chemical constituents from the genus Saussurea and their biological activities, Heterocycl. Commun., 2017, 23, 331–358.
13. T. J. Maimone and P. S. Baran, Modern synthetic efforts toward biologically active terpenes, Nat. Chem. Biol., 2007, 3, 396–407.
14. A. H. Trotta, Toward a Unified Total Synthesis of the Xiamycin and Oridamycin Families of Indolosesquiterpenes, J. Org. Chem., 2017, 82, 13500–13516.
15. A. Yilmaz, R. S. Crowley, A. M. Sherwood and T. E. Prisinzano, Semisynthesis and κ-Opioid Receptor Activity of Derivatives of Columbin, a Furanolactone Diterpene, J. Nat. Prod., 2017, 80, 2094–2100.
16. D. Urabe, T. Asaba and M. Inoue, Convergent Strategies in Total Syntheses of Complex Terpenoids, Chem. Rev., 2015, 115, 9207–9231.
17. B. Qin, Y. Li, L. Meng, J. Ouyang, D. Jin, L. Wu, X. Zhang, X. Jia and S. You, Mirror-Image Manipulation of Curdione Stereoisomer Scaffolds by Chemical and Biological Approaches: Development of a Sesquiterpenoid Library, J. Nat. Prod., 2015, 78, 272–278.
18. T. Kuzuyama and H. Seto, Diversity of the biosynthesis of the isoprene units, Nat. Prod. Rep., 2003, 20, 171–183.
19. T. Kuzuyama, Biosynthetic studies on terpenoids produced by Streptomyces, J. Antibiot., 2017, 70, 811–818.
20. B. Pattanaik and P. Lindberg, Terpenoids and Their Biosynthesis in Cyanobacteria, Life, 2015, 5, 269–293.
21. J. Bohlmann, G. Meyer-Gauen and R. Croteau, Plant terpenoid synthases: Molecular biology and phylogenetic analysis, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 4126–4133.
22. B. A. Hess and L. Smentek, Concerted Nature of AB Ring Formation in the Enzymatic Cyclization of Squalene to Hopenes, Org. Lett., 2004, 6, 1717–1720.
23. Y. Yoshikuni, T. E. Ferrin and J. D. Keasling, Designed divergent evolution of enzyme function, Nature, 2006, 440, 1078–1082.
24. D. J. Tantillo, Importance of Inherent Substrate Reactivity in Enzyme-Promoted Carbocation Cyclization/Rearrangements, Angew. Chem., Int. Ed., 2017, 56, 10040–10045.
25. Y. J. Hong and D. J. Tantillo, Tension between Internal and External Modes of Stabilization in Carbocations Relevant to Terpene Biosynthesis: Modulating Minima Depth via C–H⋯π Interactions, Org. Lett., 2015, 17, 5388–5391.
26. D. T. Major, Electrostatic Control of Chemistry in Terpene Cyclases, ACS Catal., 2017, 7, 5461–5465.
27. H. Sato, K. Narita, A. Minami, M. Yamazaki, C. Wang, H. Suemune, S. Nagano, T. Tomita, H. Oikawa and M. Uchiyama, Theoretical Study of Sesterfisherol Biosynthesis: Computational Prediction of Key Amino Acid Residue in Terpene Synthase, Sci. Rep., 2018, 8, 2473–2482.
28. Y. J. Hong and D. J. Tantillo, Quantum chemical dissection of the classic terpinyl/pinyl/bornyl/camphyl cation conundrum-the role of pyrophosphate in manipulating pathways to monoterpenes, Org. Biomol. Chem., 2010, 8, 4589–4600.
29. L.-Q. Zhang, Y.-y. Zhao, H. Cheng, K.-x. Chen, Y.-m. Li and F.-I. Scrodentoids, Four C19-norditerpenoids from Scrophularia dentata, Tetrahedron, 2016, 72, 8031–8035.
30. J. A. Faraldos, D. J. Miller, V. González, Z. Yoosuf-Aly, O. Cascón, A. Li and R. K. Allemann, A 1,6-Ring Closure Mechanism for (+)-Cadinene Synthase?, J. Am. Chem. Soc., 2012, 134, 5900–5908.
31. M. Isegawa, S. Maeda, D. J. Tantillo and K. Morokuma, Predicting pathways for terpene formation from first principles – routes to known and new sesquiterpenes, Chem. Sci., 2014, 5, 1555–1560.
32. Y. J. Hong and D. J. Tantillo, Branching Out from the Bisabolyl Cation. Unifying Mechanistic Pathways to Barbatene, Bazzanene, Chamigrene, Chamipinene, Cumacrene, Cuprenene, Dunniene, Isobazzanene, Iso-γ-bisabolene, Isochamigrene, Laurene, Microbiotene, Sesquithujene, Sesquisabinene, Thujopsene, Trichodiene, and Widdradiene Sesquiterpenes, J. Am. Chem. Soc., 2014, 136, 2450–2463.
33. Y. J. Hong and D. J. Tantillo, Consequences of Conformational Preorganization in Sesquiterpene Biosynthesis: Theoretical Studies on the Formation of the Bisabolene, Curcumene, Acoradiene, Zizaene, Cedrene, Duprezianene, and Sesquithuriferol Sesquiterpenes, J. Am. Chem. Soc., 2009, 131, 7999–8015.
34. D. J. Tantillo, Recent excursions to the borderlands between the realms of concerted and stepwise: carbocation cascades in natural products biosynthesis, J. Phys. Org. Chem., 2008, 21, 561–570.
35. A. Williams, in Concerted Organic and Bio-organic Mechanisms, ed. A. R. Katritzky, CRC Press LLC, USA, 2000, pp. 1–287.
36. B. A. Hess, Concomitant C-Ring Expansion and D-Ring Formation in Lanosterol Biosynthesis from Squalene without Violation of Markovnikov's Rule, J. Am. Chem. Soc., 2002, 124, 10286–10287.
37. M. J. S. Dewar and A. B. Pierini, Mechanism of the Diels-Alder reaction. Studies of the addition of maleic anhydride to furan and methylfurans, J. Am. Chem. Soc., 1984, 106, 203–208.
38. L. Smentek and B. A. Hess, Compelling Computational Evidence for the Concerted Cyclization of the ABC Rings of Hopene from Protonated Squalene, J. Am. Chem. Soc., 2010, 132, 17111–17117.
39. B. A. Hess and L. Smentek, The Concerted Nature of the Cyclization of Squalene Oxide to the Protosterol Cation, Angew. Chem., Int. Ed., 2013, 52, 11029–11033.
40. D. E. Ortega, S. Gutierrez-Oliva, D. J. Tantillo and A. Toro-Labbe, A detailed analysis of the mechanism of a carbocationic triple shift rearrangement, Phys. Chem. Chem. Phys., 2015, 17, 9771–9779.
41. Y. J. Hong, J.-L. Giner and D. J. Tantillo, Triple Shifts and Thioether Assistance in Rearrangements Associated with an Unusual Biomethylation of the Sterol Side Chain, J. Org. Chem., 2013, 78, 935–941.
42. Y. J. Hong, R. Ponec and D. J. Tantillo, Changes in Charge Distribution, Molecular Volume, Accessible Surface Area and Electronic Structure along the Reaction Coordinate for a Carbocationic Triple Shift Rearrangement of Relevance to Diterpene Biosynthesis, J. Phys. Chem. A, 2012, 116, 8902–8909.
43. Y. J. Hong and D. J. Tantillo, Formation of Beyerene, Kaurene, Trachylobane, and Atiserene Diterpenes by Rearrangements That Avoid Secondary Carbocations, J. Am. Chem. Soc., 2010, 132, 5375–5386.
44. C. González and H. B. Schlegel, Reaction path following in mass-weighted internal coordinates, J. Phys. Chem., 1990, 94, 5523–5527.
45. K. Fukui, The path of chemical reactions – the IRC approach, Acc. Chem. Res., 1981, 14, 363–368.
46. S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Intrinsic reaction coordinate: Calculation, bifurcation, and automated search, Int. J. Quantum Chem., 2015, 115, 258–269.
47. D. Cremer, A. Wu and E. Kraka, The mechanism of the reaction FH + H₂C=CH₂ → H₃C–CFH₂. Investigation of hidden intermediates with the unified reaction valley approach, Phys. Chem. Chem. Phys., 2001, 3, 674–687.
48. E. Kraka and D. Cremer, Computational Analysis of the Mechanism of Chemical Reactions in Terms of Reaction Phases: Hidden Intermediates and Hidden Transition States, Acc. Chem. Res., 2010, 43, 591–601.
49. H. Joo, E. Kraka, W. Quapp and D. Cremer, The mechanism of a barrierless reaction: hidden transition state and hidden intermediates in the reaction of methylene with ethene, Mol. Phys., 2007, 105, 2697–2717.
50. B. K. Carpenter, Intramolecular dynamics for the organic chemist, Acc. Chem. Res., 1992, 25, 520–528.
51. B. K. Carpenter, Nonstatistical Dynamics in thermal reactions of polyatomic molecules, Annu. Rev. Phys. Chem., 2005, 56, 57–89.
52. X. Ma and W. L. Hase, Perspective: chemical dynamics simulations of non-statistical reaction dynamics, Philos. Trans. R. Soc., A, 2017, 375, 20160204/1–20160224/20.
53. U. Lourderaj, K. Park and W. L. Hase, Classical trajectory simulations of post-transition state dynamics, Int. Rev. Phys. Chem., 2008, 27, 361–403.
54. B. R. Ussing, C. Hang and D. A. Singleton, Dynamic Effects on the Periselectivity, Rate, Isotope Effects, and Mechanism of Cycloadditions of Ketenes with Cyclopentadiene, J. Am. Chem. Soc., 2006, 128, 7594–7607.
55. B. Biswas and D. A. Singleton, Controlling Selectivity by Controlling the Path of Trajectories, J. Am. Chem. Soc., 2015, 137, 14244–14247.
56. R. Villar López, O. Faza and C. Silva López, Dynamic Effects Responsible for High Selectivity in a [3,3] Sigmatropic Rearrangement Featuring a Bispericyclic Transition State, J. Org. Chem., 2017, 82, 4758–4765.
57. R. P. Pemberton, Y. J. Hong and D. J. Tantillo, Inherent dynamical preferences in carbocation rearrangements leading to terpene natural products, Pure Appl. Chem., 2013, 85, 1949–1957.
58. S. R. Hare and D. J. Tantillo, Dynamic behavior of rearranging carbocations – implications for terpene biosynthesis, Beilstein J. Org. Chem., 2016, 12, 377–390.
59. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
60. A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
61. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
62. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627.
63. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269.
64. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301.
65. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, 6-31G* basis set for third-row atoms, J. Comput. Chem., 2001, 22, 976–984.
66. M. J. Frisch, et al., Gaussian Inc., Wallingford CT, 2009.
67. Y. J. Hong, J.-L. Giner and D. J. Tantillo, Bicyclobutonium Ions in Biosynthesis Interconversion of Cyclopropyl-Containing Sterols from Orchids, J. Am. Chem. Soc., 2015, 137, 2085–2088.
68. S. P. T. Matsuda, W. K. Wilson and Q. Xiong, Mechanistic insights into triterpene synthesis from quantum mechanical calculations. Detection of systematic errors in B3LYP cyclization energies, Org. Biomol. Chem., 2006, 4, 530–543.
69. Y. J. Hong and D. J. Tantillo, Biosynthetic consequences of multiple sequential post-transition-state bifurcations, Nat. Chem., 2014, 6, 104–111.
70. L. M. M. Quijano and D. A. Singleton, Competition between Reaction and Intramolecular Energy Redistribution in Solution: Observation and Nature of Nonstatistical Dynamics in the Ozonolysis of Vinyl Ethers, J. Am. Chem. Soc., 2011, 133, 13824–13827.
71. D. A. Singleton, C. Hang, M. J. Szymanski and E. E. Greenwald, A New Form of Kinetic Isotope Effect. Dynamic Effects on Isotopic Selectivity and Regioselectivity, J. Am. Chem. Soc., 2003, 125, 1176–1177.
72. As described in literature, after an energy/force calculation on the initial geometry, the total initial energy is randomly assigned from a Maxwell–Boltzmann distribution. The trajectory is thrown out if the energy resulting from the activation of the different vibrational modes (assumed to follow harmonic behaviour) does not agree satisfactorily (within 1 kcal mol⁻¹) with the desired starting total energy.
73. G. Schaftenaar and J. Noordik, Molden: a pre- and post-processing program for molecular and electronic structures, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
74. I. Szabó and G. Czakó, Dynamics and Novel Mechanisms of S_N2 Reactions on ab Initio Analytical Potential Energy Surfaces, J. Phys. Chem. A, 2017, 121, 9005–9019.
75. T. Györi, B. Olasz, G. Paragi and G. Czakó, Effects of the Level of Electronic Structure Theory on the Dynamics of the F⁻ + CH₃I Reaction, J. Phys. Chem. A, 2018, 122, 3353–3364.
76. J. Zhang, U. Lourderaj, R. Sun, J. Mikosch, R. Wester and W. L. Hase, Simulation studies of the Cl⁻ + CH₃I S_N2 nucleophilic substitution reaction: Comparison with ion imaging experiments, J. Chem. Phys., 2013, 138, 114309.
77. R. Sun, C. J. Davda, J. Zhang and W. L. Hase, Comparison of direct dynamics simulations with different electronic structure methods. F⁻ + CH₃I with MP2 and DFT/B97-1, Phys. Chem. Chem. Phys., 2015, 17, 2589–2597.
78. M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Density functional theory is straying from the path toward the exact functional, Science, 2017, 355, 49–52.
79. L. Bonnet and J. Rayez, Quasiclassical trajectory method for molecular scattering processes: necessity of a weighted binning approach, Chem. Phys. Lett., 1997, 277, 183–190.
80. C. Doubleday, M. Boguslav, C. Howell, S. D. Korotkin and D. Shaked, Trajectory Calculations for Bergman Cyclization Predict H/D Kinetic Isotope Effects Due to Nonstatistical Dynamics in the Product, J. Am. Chem. Soc., 2016, 138, 7476–7479.
81. M. Ben-Nun and R. D. Levine, Conservation of zero-point energy in classical trajectory computations by a simple semiclassical correspondence, J. Chem. Phys., 1994, 101, 8768–8783.
82. J. P. Bergsma, B. J. Gertner, K. R. Wilson and J. T. Hynes, Molecular dynamics of a model S_N2 reaction in water, J. Chem. Phys., 1987, 86, 1356–1376.
83. The lifetimes found for these species are generally less than 100 fs, so they do not match the IUPAC's definition of an intermediate as a “molecular entity with a lifetime appreciably longer than a molecular vibration (corresponding to a local potential energy minimum of depth greater than RT) that is formed (directly or indirectly) from the reactants and reacts further to give (either directly or indirectly) the products of a chemical reaction”.
84. M. R. Siebert, J. Zhang, S. V. Addepalli, D. J. Tantillo and W. L. Hase, The Need for Enzymatic Steering in Abietic Acid Biosynthesis: Gas-Phase Chemical Dynamics Simulations of Carbocation Rearrangements on a Bifurcating Potential Energy Surface, J. Am. Chem. Soc., 2011, 133, 8335–8343.
85. M. R. Siebert, P. Manikandan, R. Sun, D. J. Tantillo and W. L. Hase, Gas-Phase Chemical Dynamics Simulations on the Bifurcating Pathway of the Pimaradienyl Cation Rearrangement: Role of Enzymatic Steering in Abietic Acid Biosynthesis, J. Chem. Theory Comput., 2012, 8, 1212–1222.
86. R. P. Pemberton and D. J. Tantillo, Lifetimes of carbocations encountered along reaction coordinates for terpene formation, Chem. Sci., 2014, 5, 3301–3308.
87. C. A. Grob, Inductivity and bridging in carbocations, Acc. Chem. Res., 1983, 16, 426–431.
88. H. C. Brown, The energy of the transition states and the intermediate cation in the ionization of 2-norbornyl derivatives. Where is the nonclassical stabilization energy?, Acc. Chem. Res., 1983, 16, 432–440.
89. G. A. Olah, G. K. S. Prakash and M. Saunders, Conclusion of the classical-nonclassical ion controversy based on the structural study of the 2-norbornyl cation, Acc. Chem. Res., 1983, 16, 440–448.
90. C. Walling, An innocent bystander looks at the 2-norbornyl cation, Acc. Chem. Res., 1983, 16, 448–454.
91. H. C. Brown, The Nonclassical Ion Problem, Springer US, Boston, MA, 1977, pp. 283–289.
92. J. Pu, J. Gao and D. G. Truhlar, Multidimensional Tunneling, Recrossing, and the Transmission Coefficient for Enzymatic Reactions, Chem. Rev., 2006, 106, 3140–3169.
93. In this sense, what would be structures 4-H and 3-H coalesce into 4*-H due to the strong hyperconjugation between the C4–C8 and C4–C3 σ-bonds and the formal p-orbital of the carbocation located at C3 or C8 respectively.
94. D. J. Tantillo, The carbocation continuum in terpene biosynthesis-where are the secondary cations?, Chem. Soc. Rev., 2010, 39, 2847–2854.
95. T. Oka, Taming CH₅⁺, the enfant terrible of chemical structures, Science, 2015, 347, 1313–1314.
96. Z. Varga, About the structure of CH₅⁺ and structural variations in related systems, Struct. Chem., 2017, 28, 297–301.
97. S. Brackertz, S. Schlemmer and O. Asvany, Searching for new symmetry species of CH₅⁺ - From lines to states without a model, J. Mol. Spectrosc., 2017, 342, 73–82.
98. M. Heshmat and T. Privalov, Structurally Flexible Oxocarbenium/Borohydride Ion Pair: Dynamics of Hydride Transfer on the Background of Conformational Roaming, J. Phys. Chem. A, 2018, 122, 5098–5106.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates, electronic energies and the number of imaginary frequencies for all the structures reported in this work; also full ref. 66. See DOI: 10.1039/c8sc03567a

---