Open Access Article
Open Access ArticleF10BINOL-derived chiral phosphoric acid-catalyzed enantioselective carbonyl-ene reaction: theoretical elucidation of stereochemical outcomes†
Jun
Kikuchi
 ,
Hiromu
Aramaki
,
Hiroshi
Okamoto
and
Masahiro
Terada
,
Hiromu
Aramaki
,
Hiroshi
Okamoto
and
Masahiro
Terada
 *
*
Department of Chemistry, Graduate School of Science, Tohoku University, Aoba-ku, Sendai 980-8578, Japan. E-mail: mterada@m.tohoku.ac.jp; Fax: +81-22-795-6602; Tel: +81-22-795-6602
First published on 19th November 2018
Abstract
An F10BINOL-derived chiral phosphoric acid was shown to be an effective catalyst for an enantioselective carbonyl-ene reaction of 1,1-disubstituted olefins with ethyl glyoxylate as the common enophile. The perfluoro-binaphthyl skeleton is beneficial not only for adopting high catalytic activity but also for creating an effective chiral environment for enantioselective transformations. Indeed, the reaction afforded enantio-enriched homoallylic alcohols in high yields with high enantioselectivities. Theoretical studies identified that the multi-point C–H⋯O hydrogen bonds and the π interactions between the substrates and the 6-methoxy-2-naphthyl substituents at the 3,3′-positions of the F10BINOL skeleton play a crucial role in determining the stereochemical outcomes. The significance of the perfluoro-binaphthyl skeleton in achieving the high enantioselectivity was also evaluated through a structural analysis of the catalysts.
Introduction
The development of enantioselective catalysis using a chiral Brønsted acid has evolved into an active research field over the past decades.1 In particular, BINOL (1,1′-bi-2-naphthol)-derived chiral phosphoric acids 1, shown in Fig. 1a, have emerged as privileged organocatalysts2 for a broad range of enantioselective reactions.3 As the acidity of chiral Brønsted acids is the dominant factor for generating a range of reactive electrophilic species, the development of strong chiral Brønsted acids is crucial to expand the scope of electrophilic species. In general, the modification of the acidic functionality introduced at the 2,2′-positions of the binaphthyl skeleton has been demonstrated to enhance the acidity of chiral Brønsted acid catalysts.4 The most representative approach is the introduction of a triflyl group to the nitrogen atom of phosphoramide, namely, BINOL derivatives 24a shown in Fig. 1b, which exhibit higher acidity than parent phosphoric acids 1. Hence, N-triflylphosphoramides 2 have been widely utilized in the reaction of less reactive substrates, such as carbonyl compounds, which have been much less employed as an electrophile in the reaction using chiral phosphoric acids 1 than imine electrophiles, because of the insufficient acidity of parent phosphoric acids 1. In this context, we previously executed another approach to enhance the acidity of the parent phosphoric acid: we introduced a perfluoroaryl unit, namely, an F10BINOL moiety,5 as an axially chiral skeleton and developed F10BINOL-derived phosphoric acid catalyst (R)-3, shown in Fig. 1c, as a highly acidic chiral Brønsted acid catalyst.6 The efficient catalytic performance of (R)-3 was proved in the imino-ene reaction of N-acyl imines with 1,1-disubstituted olefins, a transformation with few enantioselective examples,7 affording enantio-enriched homoallylamine derivatives in good yields. The strong electron-withdrawing property of the perfluoro-binaphthyl backbone not only increased the acidity of the catalyst8 but also maintained the structural properties of the axially chiral binaphthyl skeleton originating from parent chiral phosphoric acid 1. We anticipated that this highly acidic catalyst 3 would function as an effective enantioselective catalyst even in the reaction of carbonyl compounds. Hence, to further validate the high performance of catalyst 3, we selected a carbonyl-ene reaction as a beneficial candidate.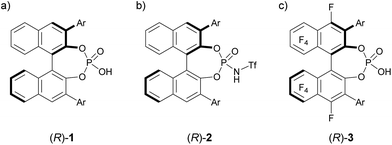 | ||
| Fig. 1 (a) BINOL-derived phosphoric acid 1 and its analogues (b) 2 and (c) 3, both of which have higher acidity than 1. | ||
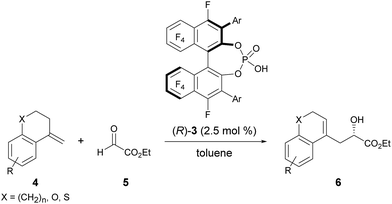
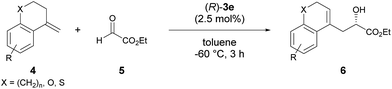
The enantioselective carbonyl-ene reaction is a powerful and atom-economical9 method for the preparation of enantio-enriched homoallylic alcohols and a number of successful examples using chiral Lewis acidic metal catalysts have been reported to date.10 However, organocatalytic enantioselective carbonyl-ene reactions are still rarely explored.11 In fact, successful examples using chiral phosphoric acid derivatives are quite limited. Rueping et al. reported an enantioselective carbonyl-ene reaction of 1,1-disubstituted olefins with highly reactive ethyl trifluoropyruvate as the dedicated enophile, using N-triflylphosphoramide catalyst 2.11a Meanwhile, List et al. recently achieved an enantioselective intramolecular carbonyl-ene cyclization.11b Although, in these reports, chiral phosphoric acid derivatives have been successfully employed as the catalyst in the carbonyl-ene reaction, a specific reaction system, such as a dedicated enophile or an intramolecular process, is requisite. In order to demonstrate the notable performance of F10BINOL-derived phosphoric acid (R)-3 as a highly acidic chiral Brønsted acid catalyst,8 we herein report an intermolecular carbonyl-ene reaction of 1,1-disubstituted olefins 4 with ethyl glyoxylate 5 as the common enophile in the presence of (R)-3 (Scheme 1). The reaction provided homoallylic alcohol products 6 in a highly enantioselective manner and the origin of the stereochemical outcome was elucidated by theoretical studies. Further detailed structural analysis of the phosphoric acid catalysts led to the identification of the specific properties of the F10BINOL skeleton crucial to achieving the high enantioselectivity.
Results and discussion
Optimization of catalyst structure and reaction conditions
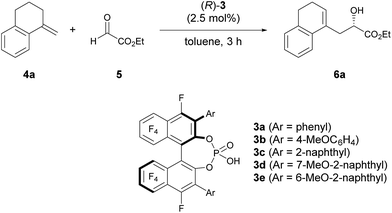
As an initial attempt, the reaction of α-methylenetetralin 4a with ethyl glyoxylate 5 was performed in the presence of (R)-3a (Ar = phenyl) in toluene at 0 °C (Table 1, entry 1). The carbonyl-ene reaction proceeded smoothly to afford product 6a in an acceptable yield albeit with moderate enantioselectivity. To improve the enantioselectivity, the effect of the substituents at the 3,3′-positions of 3 was investigated. The enantioselectivity was improved by using catalysts 3b and 3c, which have 4-methoxyphenyl and 2-naphthyl groups, respectively, as the substituents (entries 2 and 3). These results stimulated further screening for electron-rich aryl groups that would generate an efficient chiral environment to improve enantioselectivity. Two types of regio-isomeric methoxynaphthyl groups were examined as the more electron-rich aryl substituents than the 4- methoxyphenyl and 2-naphthyl groups. Whereas 3d with 7-methoxy-2-naphthyl groups resulted in the reduction of enantioselectivity (entry 4), the use of 3e with 6-methoxy-2-naphthyl groups, in which the position of the methoxy moiety was slightly changed from that in 3d (7-methoxy-), improved the enantioselectivity (entry 5). Having identified the optimal catalyst as (R)-3e, further improvement of enantioselectivity was pursued by reducing the reaction temperature (entries 6–8). Gratifyingly, when the temperature was decreased to −60 °C, 6a was obtained with an increase in enantioselectivity to 87% ee (entry 8), albeit in moderate yield. Further optimization by altering the 4a:5 ratio from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 improved the yield to 84% without any loss of enantioselectivity (entry 9).12
2 improved the yield to 84% without any loss of enantioselectivity (entry 9).12
| Entry | Catalyst | T (°C) | Yieldb (%) | eec (%) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Unless otherwise noted, all reactions were carried out using 0.005 mmol of (R)-3 (2.5 mol%), 0.6 mmol of 4a (3.0 eq.), and 0.2 mmol of 5 in toluene (1.0 mL). b Isolated yield. c ee was determined by chiral stationary phase HPLC analysis. d 0.2 mmol of 4a and 0.4 mmol of 5 were used. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | (R)-3a | 0 | 66 | 46 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | (R)-3b | 0 | 94 | 65 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | (R)-3c | 0 | 80 | 69 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | (R)-3d | 0 | 76 | 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | (R)-3e | 0 | 83 | 75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | (R)-3e | −20 | 62 | 83 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | (R)-3e | −40 | 43 | 85 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | (R)-3e | −60 | 51 | 87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9d | (R)-3e | −60 | 84 | 87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Comparison of catalysts
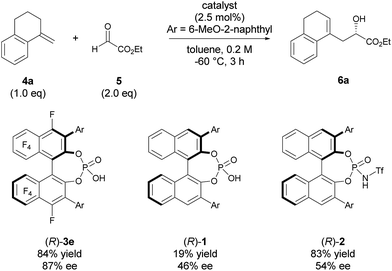
The high potential of F10BINOL-derived phosphoric acid (R)-3 was confirmed by comparing its catalytic efficiency with those of related BINOL-derived phosphoric acids, namely, parent phosphoric acid (R)-1 and its N-triflyl derivative (R)-2 (Scheme 2). Indeed, catalyst (R)-1, having the same 6-methoxy-2-naphthyl substituent, resulted in a considerable decrease in both yield and enantioselectivity. On the other hand, catalyst (R)-2 having the same substituent promoted the reaction smoothly to give 6a in 83% yield, which was comparable to that of (R)-3e (84% yield), however the enantioselectivity was moderate (54% ee) and comparable to that of (R)-1 having the same BINOL skeleton (46% ee). These results clearly indicate that the introduction of the perfluoro-binaphthyl skeleton leads to not only high catalytic activity but also an effective chiral environment for controlling the stereochemical outcome.Theoretical studies
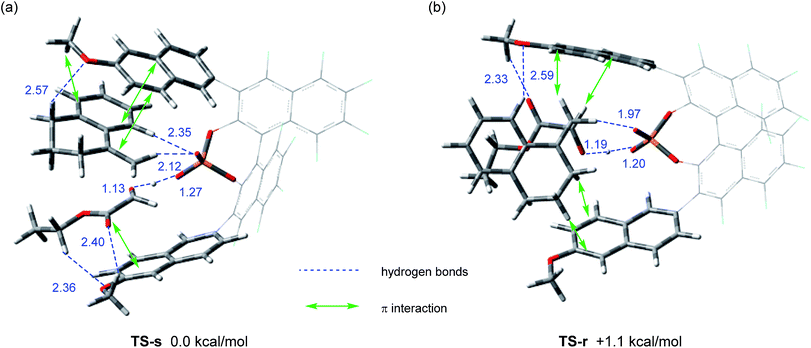
We next conducted DFT calculation to elucidate the origin of the stereochemical outcome.13 Geometry optimization and frequency analysis were performed by the M06-2X/6-31G(d,p) basis set using the Gaussian 16 program.14–16 Gibbs free energies in the solution phase were calculated using single-point energy calculations at the same level according to the CPCM solvation model (toluene: ε = 2.379) for the optimized structures.17 A variety of initial structures generated from a series of conformations of 6-methoxy-2-naphthyl substituents attached to the 3,3′-positions of the F10BINOL skeleton were thoroughly explored to identify the energetically favored transition states.18 The calculated transition states TS-s and TS-r, affording corresponding products (S)-6a and (R)-6a, respectively, are shown in Fig. 2. The Gibbs free energy difference (ΔG) between these two transition states is 1.1 kcal mol−1 with TS-s resulting in (S)-6a being energetically favored. The result of the calculation is consistent with the experimental finding that (S)-6a is obtained as the major enantiomer in the reaction of 4a with 5 catalyzed by (R)-3e (Table 1, entry 9).19Further structural analysis of TS-s and TS-r enabled the identification of the essential factors contributing to the efficient enantioselection. In both transition structures, chiral phosphoric acid 3e interacts not only with enophile 5 but also with ene-component 4a through hydrogen bonds: the carbonyl oxygen of enophile 5 interacts through the O⋯H⋯O hydrogen bond at the protonation site of the phosphoric acid (P–O![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ), whereas the vinylic hydrogen of ene-component 4a interacts through the C–H⋯O non-classical hydrogen bond at the phosphoryl oxygen (P
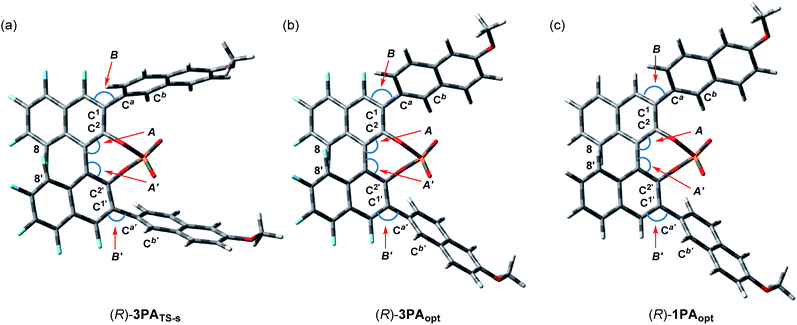
), whereas the vinylic hydrogen of ene-component 4a interacts through the C–H⋯O non-classical hydrogen bond at the phosphoryl oxygen (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O).20 In the energetically less favorable TS-r (Fig. 2b), both 4a and 5 are inserted perpendicularly between the two naphthyl planes of the catalyst substituents. In contrast, in the energetically more favorable TS-s (Fig. 2a), 4a and 5 are positioned nearly parallel to the two naphthyl planes. In TS-s and TS-r, the relative positions of the catalyst substituents and the transition structures of the carbonyl-ene reaction are completely different, while these transition states are further stabilized by several noncovalent bond interactions,21,22 such as C–H⋯O, C–H⋯π, and π–π stacking, between the naphthyl substituents and substrates 4a and 5. These interactions play crucial roles in determining the relative positions of the substrates and the catalyst accurately. In particular, the methoxy groups attached to the naphthyl substituents interact with both of the substrates through C–H⋯O hydrogen bonds and/or C–H⋯π interactions. It is considered that these interactions contribute to the high enantioselectivity, despite the fact that these methoxy groups are distant from the activation site, because the use of catalyst (R)-3d having methoxy groups attached to a different position (7-position) of the naphthyl substituents resulted in the marked reduction of enantioselectivity (Table 1, entry 4). It is concluded that the combination of not only the steric congestion between the substrates and the catalyst but also these noncovalent bond interactions,23 coupled with the structural distortion of the catalyst fragment (vide infra), is the key to differentiating the major and minor pathways. In order to gain an insight into the effectiveness of the perfluoro-binaphthyl skeleton, we next turned our attention to the structural properties of the catalysts by performing DFT calculations. For this purpose, we focused on the chiral phosphate anion (PA). The structural analysis of PAs was conducted as follows:24 (i) the structure of F10BINOL-derived phosphate anion (R)-3PATS-s was extracted from TS-s (Fig. 3a); (ii) the structure of F10BINOL-derived phosphate anion (R)-3PAopt was optimized from (R)-3PATS-s as the initial structure (Fig. 3b); and (iii) the structure of BINOL-derived phosphate anion (R)-1PAopt was optimized after replacing the fluorine atoms of (R)-3PAopt with hydrogen atoms (Fig. 3c). Then, we extracted the following key geometric parameters (Table 2): dihedral angles (C2–C1–Ca–Cb, C2′–C1′–Ca′–Cb′), interior bond angles (A and A′), and exterior bond angles (B and B′), which influence the distance between the 6-methoxy-2-naphthyl substituents of the catalyst and the substrates.25
O).20 In the energetically less favorable TS-r (Fig. 2b), both 4a and 5 are inserted perpendicularly between the two naphthyl planes of the catalyst substituents. In contrast, in the energetically more favorable TS-s (Fig. 2a), 4a and 5 are positioned nearly parallel to the two naphthyl planes. In TS-s and TS-r, the relative positions of the catalyst substituents and the transition structures of the carbonyl-ene reaction are completely different, while these transition states are further stabilized by several noncovalent bond interactions,21,22 such as C–H⋯O, C–H⋯π, and π–π stacking, between the naphthyl substituents and substrates 4a and 5. These interactions play crucial roles in determining the relative positions of the substrates and the catalyst accurately. In particular, the methoxy groups attached to the naphthyl substituents interact with both of the substrates through C–H⋯O hydrogen bonds and/or C–H⋯π interactions. It is considered that these interactions contribute to the high enantioselectivity, despite the fact that these methoxy groups are distant from the activation site, because the use of catalyst (R)-3d having methoxy groups attached to a different position (7-position) of the naphthyl substituents resulted in the marked reduction of enantioselectivity (Table 1, entry 4). It is concluded that the combination of not only the steric congestion between the substrates and the catalyst but also these noncovalent bond interactions,23 coupled with the structural distortion of the catalyst fragment (vide infra), is the key to differentiating the major and minor pathways. In order to gain an insight into the effectiveness of the perfluoro-binaphthyl skeleton, we next turned our attention to the structural properties of the catalysts by performing DFT calculations. For this purpose, we focused on the chiral phosphate anion (PA). The structural analysis of PAs was conducted as follows:24 (i) the structure of F10BINOL-derived phosphate anion (R)-3PATS-s was extracted from TS-s (Fig. 3a); (ii) the structure of F10BINOL-derived phosphate anion (R)-3PAopt was optimized from (R)-3PATS-s as the initial structure (Fig. 3b); and (iii) the structure of BINOL-derived phosphate anion (R)-1PAopt was optimized after replacing the fluorine atoms of (R)-3PAopt with hydrogen atoms (Fig. 3c). Then, we extracted the following key geometric parameters (Table 2): dihedral angles (C2–C1–Ca–Cb, C2′–C1′–Ca′–Cb′), interior bond angles (A and A′), and exterior bond angles (B and B′), which influence the distance between the 6-methoxy-2-naphthyl substituents of the catalyst and the substrates.25
| C2–C1–Ca–Cb | C2′–C1′–Ca′–Cb′ | A | A′ | B | B′ | |
|---|---|---|---|---|---|---|
| (R)-3PATS-s | 76.4° | 115.7° | 118.0° | 117.4° | 122.8° | 123.6° |
| (R)-3PAopt | 50.3° | 134.4° | 117.8° | 117.2° | 120.2° | 121.7° |
| (R)-1PAopt | 46.0° | 139.7° | 119.1° | 118.6° | 119.5° | 120.5° |
As shown in Table 2, the dihedral angles C2–C1–Ca–Cb and C2′–C1′–Ca′–Cb′ in (R)-3PATS-s are markedly different from those in (R)-3PAopt, whereas the dihedral angles in (R)-3PAopt and (R)-1PAopt show a little difference because of the influence of the substituted atoms at the 4,4′-positions. Considering these characteristics, the marked differences of the dihedral angles between (R)-3PATS-s and (R)-3PAopt clearly indicate that the 6-methoxy-2-naphthyl substituents rotate to meet the requirements for the noncovalent bond interactions and the steric exclusion with the substrates in the transition state. In contrast, the interior bond angles A and A′ in (R)-3PATS-s are almost identical to those in (R)-3PAopt and smaller than the ideal angle (120°). Hence, these bond angles are not affected by the substrates in the transition state but arise from the inherent structural characteristics of the perfluoro-binaphthyl skeleton. Indeed, the bond angles A and A′ of (R)-3PAopt are smaller than those of (R)-1PAopt of which angles are nearly ideal, probably due to the repulsion of fluorine atoms at the 8,8′-positions in (R)-3PAopt. On the other hand, the exterior bond angles B and B′ in (R)-3PAopt are slightly larger than those in (R)-1PAopt presumably because of the repulsion between fluorine atoms at the 4,4′-positions and the naphthyl substituents at the 3,3′-positions.
The bond angle differences (ΔA, ΔA′, ΔB, and ΔB′) between (R)-3PAopt and (R)-1PAopt are not significant. However, these bond angles markedly influence the direction of the naphthyl substituents and hence the location of the tail end of the naphthyl substituents should be entirely different between (R)-3PAopt and (R)-1PAopt. Thus, in the F10BINOL-derived catalyst having small A and A′ and large B and B′, the 6-methoxy-2-naphthyl substituents create a narrow reaction space inherently and hence approach the transition structure. Interestingly, further enlargement of the exterior bond angles B and B′ is observed in (R)-3PATS-s. This implies that the noncovalent bond interactions between the catalyst and the substrates, which stabilize the transition states, lead to structural distortion of the catalyst, although this distortion results in an energetic destabilization of the catalyst fragment. It is considered that F10BINOL-derived phosphoric acid having an intrinsic narrow reaction space is allowed to interact with the transition structure of the substrates while minimizing catalyst distortion, namely, structural destabilization. In contrast, the BINOL-derived phosphoric acid framework creates a wide reaction space and hence the distortion should be more significant than that of the F10BINOL-derived one, when a similar transition structure is formed through the noncovalent bond interactions between the substrates and the catalyst.25 Consequently, the structural distortion of the catalyst, which results in the destabilization of the transition states, is also considered one of the rational factors for determining the stereochemical outcome (Scheme 2).26
Confirmation of potential of F10BINOL-derived phosphoric acid
With the optimized catalyst and reaction conditions in hand, as shown in Table 1, the potential of F10BINOL-derived phosphoric acid was further confirmed in the reaction that used a series of 1,1-disubstituted olefins having a cyclic framework. As shown in Table 3, the reaction of α-methylenetetralin derivatives 4b–g having an electron-donating or -withdrawing group afforded the corresponding products 6 in moderate to good yields (entries 1–6). In addition, high enantioselectivities were observed in most cases, although 6c and 6g exhibited moderate enantioselectivities (entries 3 and 6). The decrease in enantioselectivity of 6g suggests that the C–H bond at the C8 position is important to achieve high enantioselectivity. Indeed, as shown in the transition structure of the more favorable TS-s (Fig. 2a), C–H⋯O hydrogen bond is formed between the hydrogen atom at the C8 position and the phosphoryl oxygen of the catalyst. Notably, oxygen and sulfur heterocycles 4h and 4i, respectively, were compatible, affording the corresponding chromene 6h and thiochromene 6i derivatives with high enantioselectivities (entries 7 and 8). α-Methylenindane 4j having a five-membered ring was also applicable to the reaction, although both yield and enantioselectivity were moderate (entry 9). The reaction of 4k having a seven-membered ring furnished 6k in an acceptable yield with the highest enantioselectivity among the olefins tested (entry 10). As shown in Table 1, entry 9 and Table 3, entries 9 and 10, an increase in the ring size of 1,1-disubstituted olefins from five to seven markedly enhanced the enantioselectivity from 62% ee (five) to 93% ee (seven) via 87% ee (six). This trend is also well rationalized on the basis of the transition structures of the present reaction (Fig. 2). In the more favorable TS-s, ene-component 4a and enophile 5 are nearly parallel to the naphthyl planes of the catalyst substituents and hence the ring size does not cause steric congestion between ene-component 4 and the naphthyl substituents. In contrast, in the less favorable TS-r, 4a and 5 are perpendicular to the two naphthyl substituents. Therefore, the increase in ring size enhances the repulsive interaction between ene-component 4 and the naphthyl substituents, which leads to further destabilization of the transition state in the minor pathway. The enhancement of enantioselectivity with increasing ring size is rationally understood on the basis of the above structural expectations in these transition states.| Entry | 4 | Yieldb (%) | eec (%) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Unless otherwise noted, all reactions were carried out using 0.005 mmol of (R)-3 (2.5 mol%), 0.2 mmol of 4, and 0.4 mmol of 5 (2.0 eq.) in toluene (1.0 mL) at −60 °C. b Isolated yield. c ee was determined by chiral stationary phase HPLC analysis. d Reaction was conducted at −40 °C. e 0.6 mmol of 5 was used. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 |
|
4b: R = 5-MeO | 77 | 86 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 4c: R = 6-MeO | 87 | 63 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 4d: R = 6-Cl | 66 | 86 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4e: R = 7-MeO | 86 | 92 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 4f: R = 7-Br | 64 | 88 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6d | 4g: R = 8-Br | 37 | 60 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 |
|
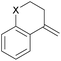
4h: X = O | 75 | 91 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 4i: X = S | 59 | 83 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 |
|
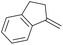
4j | 48 | 62 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10e |
|
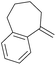
4k | 75 | 93 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Conclusions
We have demonstrated that F10BINOL-derived chiral phosphoric acid is an effective catalyst for the enantioselective carbonyl-ene reaction. This highly acidic catalyst efficiently activated ethyl glyoxylate as the common enophile and accelerated the reaction with 1,1-disubstituted olefins, affording the corresponding homoallylic alcohols in good yields with high enantioselectivities in most cases. Theoretical studies of the present catalytic reaction revealed that multi-point noncovalent bond interactions, such as O⋯H⋯O, C–H⋯O hydrogen bonds, C–H⋯π, and π–π stacking, determine the relative locations of the catalyst and the substrates, namely, the enophile and the ene-component, accurately. In fact, it was confirmed that the remote noncovalent bond interactions between the substrates and the methoxy groups introduced to the naphthyl substituents of the catalyst aid to stabilize the transition structures. Further structural analysis of F10BINOL-derived catalyst identified the specific properties of the F10BINOL skeleton. The introduction of fluorine atoms to the binaphthyl skeleton leads to bond angle distortion, which induces the 6-methoxy-2-naphthyl substituents to create a narrow reaction space for the transition structure. The higher enantioselectivity achieved by F10BINOL-derived phosphoric acid than by BINOL-derived ones originates from this narrow reaction space in which noncovalent bond interactions occur readily without marked distortion, namely, destabilization, of the catalyst framework and stabilize the transition states efficiently in the major pathway. Based on these theoretical studies of the transition states and the structural analysis of the catalyst frameworks, it is concluded that the major and minor pathways are differentiated by the total balance of the steric congestion between the substrates and the catalyst, the noncovalent bond interactions, and the structural distortion of the catalyst framework. Further studies of the development of enantioselective reactions using F10BINOL-derived chiral Brønsted acids will be conducted in due course.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by a Grant-in-Aid for Scientific Research on Innovative Areas “Advanced Molecular Transformations by Organocatalysts” from The MEXT, Japan (No. 23105002) and a Grant-in-Aid for Scientific Research on Innovative Areas “Hybrid Catalysis for Enabling Molecular Synthesis on Demand” from the MEXT, Japan (No. JP17H06447). We gratefully thank Professor Toshinobu Korenaga (Department of Chemistry and Biological Sciences, Faculty of Science and Engineering, Iwate University) for his helpful advice of the theoretical studies.Notes and references
- For selected reviews on chiral Brøsnted acid catalysis, see: (a) T. Akiyama, Chem. Rev., 2007, 107, 5744–5758 CrossRef CAS PubMed; (b) M. Terada, Synthesis, 2010, 1929–1982 CrossRef CAS; (c) D. Kampen, C. M. Reisinger and B. List, Top. Curr. Chem., 2010, 291, 395–456 CrossRef CAS PubMed; (d) D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047–9153 CrossRef CAS PubMed.
- For book and reviews on enantioselective organocatalysis, see: (a) P. I. Dalko and L. Moisan, Angew. Chem., Int. Ed., 2004, 43, 5138–5175 CrossRef CAS PubMed; (b) J. Seayad and B. List, Org. Biomol. Chem., 2005, 3, 719–724 RSC; (c) B. List, Chem. Commun., 2006, 819–824 RSC; (d) M. S. Taylor and E. N. Jacobsen, Angew. Chem., Int. Ed., 2006, 45, 1520–1543 CrossRef CAS PubMed; (e) Enantioselective Organocatalysis: Reactions and Experimental Procedures, ed. P. I. Dalko, Wiley-VCH, Weinheim, 2007 Search PubMed; (f) N. Marion, S. Díez-González and S. P. Nolan, Angew. Chem., Int. Ed., 2007, 46, 2988–3000 CrossRef CAS PubMed; (g) R. M. de Figueiredo and M. Christmann, Eur. J. Org. Chem., 2007, 2575–2600 CrossRef CAS; (h) H. Pellissier, Tetrahedron, 2007, 63, 9267–9331 CrossRef CAS; (i) A. G. Doyle and E. N. Jacobsen, Chem. Rev., 2007, 107, 5713–5743 CrossRef CAS PubMed.
- Seminal works of chiral phosphoric acid, see: (a) T. Akiyama, J. Itoh, K. Yokota and K. Fuchibe, Angew. Chem., Int. Ed., 2004, 43, 1566–1568 CrossRef CAS PubMed; (b) D. Uraguchi and M. Terada, J. Am. Chem. Soc., 2004, 126, 5356–5357 CrossRef CAS PubMed.
- (a) D. Nakashima and H. Yamamoto, J. Am. Chem. Soc., 2006, 128, 9226–9627 Search PubMed; (b) T. Hashimoto and K. Maruoka, J. Am. Chem. Soc., 2007, 129, 10054–10055 CrossRef CAS PubMed; (c) M. Hatano, T. Maki, K. Moriyama, M. Arinobe and K. Ishihara, J. Am. Chem. Soc., 2008, 130, 16858–16860 CrossRef CAS PubMed; (d) P. García-García, F. Lay, P. García-García, C. Rabalakos and B. List, Angew. Chem., Int. Ed., 2009, 48, 4363–4366 CrossRef PubMed; (e) I. Čorić and B. List, Nature, 2012, 483, 315–319 CrossRef PubMed.
- (a) D. J. Morrison, S. D. Riegel, W. E. Piers, M. Parvez and R. McDonald, Chem. Commun., 2006, 2875–2877 RSC; (b) N. Momiyama, H. Okamoto, M. Shimizu and M. Terada, Chirality, 2015, 27, 464–475 CrossRef CAS PubMed.
- N. Momiyama, H. Okamoto, J. Kikuchi, T. Korenaga and M. Terada, ACS Catal., 2016, 6, 1198–1204 CrossRef CAS.
- For enantioselective imino-ene reactions, see: (a) W. J. Drury III, D. Ferraris, C. Cox, B. Young and T. Lectka, J. Am. Chem. Soc., 1998, 120, 11006–11007 CrossRef; (b) S. Yao, X. Fang and K. A. Jørgensen, Chem. Commun., 1998, 2547–2548 RSC; (c) D. Ferraris, B. Young, C. Cox, T. Dudding, W. J. Drury III, L. Ryzhkov, A. W. Taggi and T. Lectka, J. Am. Chem. Soc., 2002, 124, 66–67 CrossRef; (d) N. A. Caplan, F. E. Hancock, P. C. B. Page and G. H. Hutchings, Angew. Chem., Int. Ed., 2004, 43, 1685–1688 CrossRef CAS PubMed; (e) M. Hatano, K. Nishikawa and K. Ishihara, J. Am. Chem. Soc., 2017, 139, 8424–8427 CrossRef CAS PubMed.
- In order to estimate the acidity of (R)-3a (Ar = Ph), we conducted the DFT-calculation in accordance with Cheng's methods. The calculated pKa value of (R)-3a (Ar = Ph) in DMSO: 1.24 (proton exchange method), 1.03 (direct method). See ESI† for details. Cheng et al. calculated the pKa value of (R)-1 (Ar = Ph) and (R)-2 (Ar = Ph) (a) pKa value of (R)-1 C. Yang, X.-S. Xue, J.-L. Jin, X. Li and J.-P. Cheng, J. Org. Chem., 2013, 78, 7076–7085 CrossRef CAS PubMed (Ar = Ph) in DMSO: 3.55 (proton exchange method), 3.33 (direct method), see: ; (b) pKa value of (R)-2 (Ar = Ph) in DMSO: −3.36 (direct method), see: C. Yang, X.-S. Xue, X. Li and J.-P. Cheng, J. Org. Chem., 2014, 79, 4340–4351 CrossRef CAS PubMed.
- B. M. Trost, Angew. Chem., Int. Ed. Engl., 1995, 34, 259–281 CrossRef CAS.
- For selected examples of enantioselective carbonyl-ene reactions, see: (a) K. Maruoka, Y. Hoshino, T. Shirasaka and H. Yamamoto, Tetrahedron Lett., 1988, 29, 3967–3970 CrossRef CAS; (b) K. Mikami, M. Terada and T. Nakai, J. Am. Chem. Soc., 1989, 111, 1940–1941 CrossRef CAS; (c) D. A. Evans, C. S. Burgey, N. A. Paras, T. Vojkovsky and S. W. Tregay, J. Am. Chem. Soc., 1998, 120, 5824–5825 CrossRef CAS; (d) C. Qian and L. Wang, Tetrahedron: Asymmetry, 2000, 11, 2347–2357 CrossRef CAS; (e) S. Kezuka, T. Ikeno and T. Yamada, Org. Lett., 2001, 3, 1937–1939 CrossRef CAS PubMed; (f) J. H. Koh, A. O. Larsen and M. R. Gagné, Org. Lett., 2001, 3, 1233–1236 CrossRef CAS PubMedY. Yuan, X. Zhang and K. L. Ding, Angew. Chem., Int. Ed., 2003, 42, 5478–5480 CrossRef CAS PubMed; (g) G. E. Hutson, A. H. Dave and V. H. Rawal, Org. Lett., 2007, 9, 3869–3872 CrossRef CAS PubMed; (h) M. L. Grachan, M. T. Tudge and E. N. Jacobsen, Angew. Chem., Int. Ed., 2008, 47, 1469–1472 CrossRef CAS PubMed; (i) K. Zheng, J. Shi, X. Liu and X. M. Feng, J. Am. Chem. Soc., 2008, 130, 15770–15771 CrossRef CAS PubMed; (j) P. M. Truong, P. Y. Zavalij and M. P. Doyle, Angew. Chem., Int. Ed., 2014, 53, 6468–6472 CrossRef CAS PubMed; (k) X. C. Xu, X. C. Wang, Y. Liu and M. P. Doyle, J. Org. Chem., 2014, 79, 12185–12190 CrossRef CAS PubMed; (l) X. Zhang, M. Wang, R. Ding, Y.-H. Xu and T.-P. Loh, Org. Lett., 2015, 17, 2736–2739 CrossRef CAS PubMed.
- (a) M. Rueping, T. Theissmann, A. Kuenkel and R. M. Koenigs, Angew. Chem., Int. Ed., 2008, 47, 6798–6801 CrossRef CAS PubMed; (b) L. Liu, M. Leutzsch, Y. Zheng, M. W. Alachraf, W. Thiel and B. List, J. Am. Chem. Soc., 2015, 137, 13268–13271 CrossRef CAS PubMed; (c) J. Lv, Q. Zhang, X. Zhong and S. Luo, J. Am. Chem. Soc., 2015, 137, 15576–15583 CrossRef CAS PubMed.
- The enantioselective carbonyl-ene reaction of α-methylstyrene was also attempted in the presence of 2.5 mol% (R)-3e. Although the reaction gave a product with excellent enantioselectivity, the yield was extremely low (5% yield, 90% ee). See ESI† for details.
- For selected recent reports of theoretical studies on stereochemical outcomes using chiral phosphoric acids, see: (a) Y. Y. Khomutnyk, A. J. Argüelles, G. A. Winschel, Z. Sun, P. M. Zimmerman and P. Nagorny, J. Am. Chem. Soc., 2016, 138, 444–456 CrossRef CAS PubMed; (b) J. P. Reid and J. M. Goodman, J. Am. Chem. Soc., 2016, 138, 7910–7917 CrossRef CAS PubMed; (c) R. Maji, P. A. Champagne, K. N. Houk and S. E. Wheeler, ACS Catal., 2017, 7, 7332–7339 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016, see ESI† for the full citation.
- For M06-2X, see: Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- For Gaussian basis sets, see: (a) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS; (b) W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, John Wiley, New York, USA, 1986, and references cited therein Search PubMed.
- For the CPCM model, see: (a) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS; (b) B. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef.
- In order to conduct rigorous conformational analysis of these transition states, initial structures of the transition states were systematically generated by changing the dihedral angles of C2–C1–Ca–Cb and C2′–C1′–Ca′–Cb′ (for each dihedral angle: −135°, −45°, 45°, and 135°) as well as the orientation of the methoxy group (dihedral angle: 0° and 180° to the naphthyl ring). This procedure generates eight conformers for each naphthyl ring and hence totally 64 conformers were considered for the initial structures of the catalyst. In addition, on the basis of the model studies of the transition states, conformationally different transition states of the real system were considered by changing the orientation of ene-component 4a and the conformation of the six-membered ring of 4a for each enantiomeric pathway. Thus, nearly 200 initial structures were calculated to identify the energetically favored transition states accurately.
- The ee value was calculated as follows:
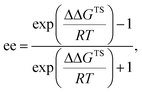 where ΔΔGTS is the energy gap between major and minor transition states, R is the gas constant, and T is the absolute temperature. The 1.1 kcal mol−1 energy gap at −60 °C corresponds to 86% ee.
where ΔΔGTS is the energy gap between major and minor transition states, R is the gas constant, and T is the absolute temperature. The 1.1 kcal mol−1 energy gap at −60 °C corresponds to 86% ee. - For representative and recent examples for C–H⋯O hydrogen bonds as the key interaction in asymmetric catalysis, see: (a) E. J. Corey and J. J. Rohde, Tetrahedron Lett., 1997, 38, 37–40 CrossRef CAS; (b) M. N. Grayson and J. M. Goodman, J. Am. Chem. Soc., 2013, 135, 6142–6148 CrossRef CAS PubMed; (c) P. Maity, R. P. Pemberton, D. J. Tantillo and U. K. Tambar, J. Am. Chem. Soc., 2013, 135, 16380–16383 CrossRef CAS PubMed; (d) H. Wang, P. Jain, J. C. Antilla and K. N. Houk, J. Org. Chem., 2013, 78, 1208–1215 CrossRef CAS PubMed; (e) T. Ishii, R. Watanabe, T. Moriya, H. Ohmiya, S. Mori and M. Sawamura, Chem.–Eur. J., 2013, 19, 13547–13553 CrossRef CAS PubMed; (f) K. Kanomata, Y. Toda, Y. Shibata, M. Yamanaka, S. Tsuzuki, I. D. Gridnev and M. Terada, Chem. Sci., 2014, 5, 3515–3523 RSC; (g) N. Grimblat, M. Sugiura and S. C. Pellegrinet, J. Org. Chem., 2014, 79, 6754–6758 CrossRef CAS PubMed; (h) Y. Xie, G.-J. Cheng, S. Lee, P. S. J. Kaib, W. Thiel and B. List, J. Am. Chem. Soc., 2016, 138, 14538–14541 CrossRef CAS PubMed; (i) M. N. Grayson, Z. Yang and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 7717–7720 CrossRef CAS PubMed; (j) Y. Takayama, T. Ishii, H. Ohmiya, T. Iwai, M. C. Schwarzer, S. Mori, T. Taniguchi, K. Monde and M. Sawamura, Chem.–Eur. J., 2017, 23, 8400–8404 CrossRef CAS PubMed; (k) F. Li, T. Korenaga, T. Nakanishi, J. Kikuchi and M. Terada, J. Am. Chem. Soc., 2018, 140, 2629–2642 CrossRef CAS PubMed.
- For π interactions, see: (a) E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979–989 CrossRef CAS PubMed; (b) A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Nature, 2017, 543, 637–646 CrossRef CAS PubMed.
- For representative and recent examples of π interaction as the key interaction in asymmetric catalysis, see: (a) M. Yamakawa, I. Yamada and R. Noyori, Angew. Chem., Int. Ed., 2001, 40, 2818–2821 CrossRef CAS; (b) H. Kawai, A. Kusuda, S. Nakamura, M. Shiro and N. Shibata, Angew. Chem., Int. Ed., 2009, 48, 6324–6327 CrossRef CAS PubMed; (c) J. Calleja, A. B. Gonzalez-Perez, A. R. de Lera, R. Alvarez, F. J. Fanan and F. Rodrıguez, Chem. Sci., 2014, 5, 996–1007 RSC; (d) G. Jindal and R. B. Sunoj, Angew. Chem., Int. Ed., 2014, 53, 4432–4436 CrossRef CAS PubMed; (e) S. S. Meng, Y. Liang, K. S. Cao, L. Zou, X. B. Lin, H. Yang, K. N. Houk and W. H. Zheng, J. Am. Chem. Soc., 2014, 136, 12249–12252 CrossRef CAS PubMed; (f) B. Bhaskararao and R. B. Sunoj, J. Am. Chem. Soc., 2015, 137, 15712–15722 CrossRef CAS PubMed; (g) A. C. Doney, B. J. Rooks, T. X. Lu and S. E. Wheeler, ACS Catal., 2016, 6, 7948–7955 CrossRef CAS; (h) M. Pareek and R. B. Sunoj, ACS Catal., 2016, 6, 3118–3126 CrossRef CAS; (i) J. Guo and M. W. Wong, J. Org. Chem., 2017, 82, 4362–4368 CrossRef CAS PubMed; (j) M. Li and X.-S. Xue, ACS Catal., 2017, 7, 7977–7986 CrossRef CAS; (k) T. Korenaga, R. Sasaki, T. Takemoto, T. Yasuda and M. Watanabe, Adv. Synth. Catal., 2018, 360, 322–333 CrossRef CAS.
- The second-order perturbative donor–acceptor interactions for the two transition states were also analyzed. See ESI† for details.
- The structures of the catalysts were optimized as phosphate anion because the acidic proton is located closer to enophile 5 than the catalyst fragment in TS-s. For the optimization of the catalyst structures as phosphoric acid, see ESI† for details.
- The same structural analysis of BINOL-derived phosphate anion (R)-1PATS-s, which was extracted from the transition state of the major pathway of the carbonyl-ene reaction catalyzed by (R)-1 (Ar = 6-methoxy-2-naphthyl), was also conducted. It has been confirmed that the structural distortion of the BINOL-derived phosphoric acid framework is more significant than that of the F10BINOL-derived one. See ESI† for details.
- For the distortion/interaction analysis of transition states, see: (a) K. Morokuma, and K. Kitaura, in Chemical Applications of Atomic and Molecular Electrostatic Potentials, ed. P. Politzer and D. G. Truhlar, Plenum press, New York, 1981, pp. 215−242 Search PubMed; (b) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS PubMed; (c) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed; (d) Y.-H. Lam, P. H.-Y. Cheong, J. M. Blasco Mata, S. J. Stanway, V. Gouverneur and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 1947–1957 CrossRef CAS PubMed; (e) R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366–10368 CrossRef CAS PubMed; (f) A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583 CrossRef CAS PubMed; (g) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03587c |
| This journal is © The Royal Society of Chemistry 2019 |