Open Access Article
Open Access ArticleCrystallographic characterization of Lu2C2n (2n = 76–90): cluster selection by cage size†
Wangqiang
Shen
a,
Lipiao
Bao
a,
Shuaifeng
Hu
a,
Le
Yang
b,
Peng
Jin
 *b,
Yunpeng
Xie
*b,
Yunpeng
Xie
 *a,
Takeshi
Akasaka
a and
Xing
Lu
*a,
Takeshi
Akasaka
a and
Xing
Lu
 *a
*a
aState Key Laboratory of Materials Processing and Die & Mould Technology, School of Materials Science and Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan, 430074, China. E-mail: lux@hust.edu.cn
bSchool of Materials Science and Engineering, Hebei University of Technology, Tianjin, 300130, China. E-mail: china.peng.jin@gmail.com
First published on 30th October 2018
Abstract
The successful isolation and unambiguous crystallographic assignment of a series of lutetium-containing endohedral metallofullerenes (EMFs), Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90), reveal an unrecognized decisive effect of the cage size on the configuration of the encapsulated clusters. The molecular structures of these compounds are unambiguously assigned as Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88, Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88. Specifically, when the cage is relatively small, Lu2@C2n (2n = 76–86) are all dimetallofullerenes (di-EMFs) and a Lu–Lu single bond could be formed between the two lutetium ions inside the cages. However, when the cage expands further, the valence electrons forming the possible Lu–Lu bond donate to a readily inserted C2-unit, resulting in the formation of carbide EMFs, Lu2C2@C2n (2n = 86, 88). Consistently, our theoretical results reveal that all these EMFs are thermodynamically favorable isomers. Thus the comprehensive characterization of the series of Lu2C76–90 isomers and the overall agreement between the experimental and theoretical results reveal for the first time that the exact configuration of the internal metallic cluster is determined by the cage size, taking a solid step towards the controlled synthesis of novel hybrid molecules which may have potential applications as building blocks of single molecule devices.
Introduction
Putting metal atoms or metallic clusters into fullerenes has generated a new class of novel hybrid molecules, defined as endohedral metallofullerenes (EMFs), possessing novel structures and fascinating properties which are different from those of empty fullerenes.1–4 During the last three decades, EMFs containing different metallic clusters, including metal nitride (M3N),5,6 metal carbide (M2C2/M3C2/M4C2),7–9 metal sulfide (M2S),10,11 metal oxide (M2O/M4O2/M4O3)12–14 and metal cyanide (M3CN/MCN)15–17 clusters, have been structurally characterized in addition to the conventional EMFs containing only metal atoms (M/M2/M3).18–20EMFs exhibit a variety of electronic and physicochemical properties which markedly depend on the nature of the encapsulated species.21,22 One of the most brilliant features of EMFs is the charge transfer from the internal metallic species to the surrounding cage which is revealed to play an important role in determining the stability of the formed molecules.2,3,23 For example, the C2v(9)-C82 cage is the most stable one after accepting three electrons, and the corresponding M@C2v(9)-C82 isomers have the highest production yield among all reported mono-EMFs for a variety of lanthanide elements regardless of the metal type.24,25 As for cluster EMFs, theoretical and experimental results have suggested that the hexa-anionic Ih(7)-C80 cage is the most suitable candidate for encapsulating an M3N (M = Sc, Y, Gd, Lu, etc.) cluster.26,27
In addition to the electronic interactions, the geometry of the cluster, especially the cluster size, also has a significant effect on the cage structure and symmetry. For instance, Dunsch and co-workers proposed theoretically that the small Sc3N cluster presents a planar geometry inside the D3h(5)-C78 cage, whereas the larger M3N (M = Y, Lu, Dy, Tm) clusters prefer the C2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010)-C78 cage that violates the isolated pentagon rule (IPR) to keep their planarity.28 And a subsequent experimental report confirmed that the large Gd3N unit prefers to adopt the planar geometry in the C2(22
010)-C78 cage that violates the isolated pentagon rule (IPR) to keep their planarity.28 And a subsequent experimental report confirmed that the large Gd3N unit prefers to adopt the planar geometry in the C2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010)-C78 cage.29 Another example demonstrated that M3N clusters containing metals with a relatively small radius (e.g. Sc, Y and Gd) are preferentially encapsulated inside a C80 cage. In comparison, larger metals like La and Nd prefer to template C88 or C96.30,31 Accordingly, it seems that the size, shape, and charge of the encapsulated cluster play important roles in the selection of the complementary carbon cages. However, there is still a lack of experimental evidence to confirm whether the cage size has any influence on the cluster configuration or not. For example, Dunsch et al. proposed that the number of Sc atoms in the internal GdxSc3−xN clusters decreases along with the cage expansion (C78 to C88), as demonstrated by absorption and vibrational spectroscopy, electrochemical studies and density functional theory (DFT) computations.32 Popov et al. reported a systematic computational study on the analysis of the distortions in three classes of EMFs with nitride, sulfide, and carbide clusters, indicating that the preferable shapes of the internal clusters can be altered by the cage size.33 Moreover, an interesting report from Dorn and co-workers theoretically revealed that the fullerene cage may compress the internal Y2C2 cluster to adopt different shapes, from butterfly-like configurations in small cages to nearly linear structures in large cages.34 Nonetheless, there are no crystallographic results showing that the composition of the metallic species is controllable by the cage size.
010)-C78 cage.29 Another example demonstrated that M3N clusters containing metals with a relatively small radius (e.g. Sc, Y and Gd) are preferentially encapsulated inside a C80 cage. In comparison, larger metals like La and Nd prefer to template C88 or C96.30,31 Accordingly, it seems that the size, shape, and charge of the encapsulated cluster play important roles in the selection of the complementary carbon cages. However, there is still a lack of experimental evidence to confirm whether the cage size has any influence on the cluster configuration or not. For example, Dunsch et al. proposed that the number of Sc atoms in the internal GdxSc3−xN clusters decreases along with the cage expansion (C78 to C88), as demonstrated by absorption and vibrational spectroscopy, electrochemical studies and density functional theory (DFT) computations.32 Popov et al. reported a systematic computational study on the analysis of the distortions in three classes of EMFs with nitride, sulfide, and carbide clusters, indicating that the preferable shapes of the internal clusters can be altered by the cage size.33 Moreover, an interesting report from Dorn and co-workers theoretically revealed that the fullerene cage may compress the internal Y2C2 cluster to adopt different shapes, from butterfly-like configurations in small cages to nearly linear structures in large cages.34 Nonetheless, there are no crystallographic results showing that the composition of the metallic species is controllable by the cage size.
We herein confirm for the first time that the exact form of the internal metallic cluster is determined by the cage size based on the concrete single-crystal X-ray crystallographic results of ten lutetium-containing endohedrals, namely, Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88, Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88. It is revealed that the Lu–Lu distance increases along with the cage expansion as a direct result of the preferential coordination of the Lu atoms with the cage carbon atoms. Accordingly, the small cages can only accommodate a Lu2 cluster because of the limited inner space, accompanied by the possible formation of a Lu–Lu bond. However, when the cage expands further, a C2-unit is inserted between the two Lu atoms, which takes over partially the charges from the metals and coordinates with them, making the whole system more stable. The systematic characterization of Lu2C76–90 isomers and the overall agreement between experimental and theoretical studies present concrete evidence for the decisive effect of the cage size on the composition of the encapsulated clusters of EMFs.
Results and discussion
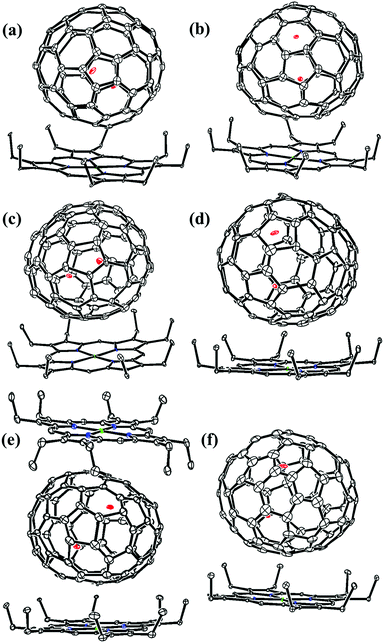
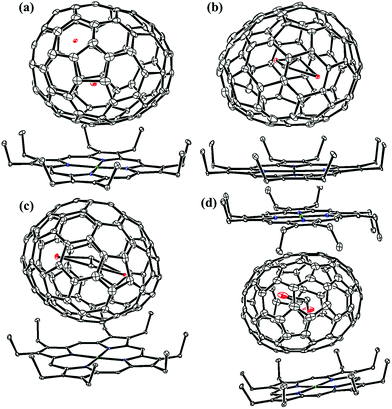
Lu-EMFs were synthesized by a direct-current arc discharge method and pure isomers of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) were obtained by multistage HPLC separation (see ESI, Fig. S1–S4 for details†). The analytical HPLC chromatograms (Fig. S5†) and the laser-desorption/ionization time-of-flight (LDI-TOF) mass spectra (Fig. S6†) of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers confirm their high purity. Fig. S7 and Table S1† show the visible-near-infrared (Vis-NIR) absorption spectra and the detailed characteristic bands of Lu2C76–90 isomers dissolved in carbon disulfide (CS2), respectively. The absorption spectra of Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88 and Lu2C2@Cs(32)-C88 are quite different from those of the corresponding EMFs possessing C84, C86 and C88 cages reported before,15,35–43 indicating their different structures.Finally, the molecular structures of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers were unambiguously determined by single-crystal X-ray diffraction (XRD) crystallography to be Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88, Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88, respectively, taking advantage of the high-quality of the co-crystals of Lu2C2n/NiII(OEP) (OEP = 2,3,7,8,12,13,17,18-octaethylporphyrin dianion). Although Lu2@Td(2)-C76 was first isolated and confirmed to have a Td-symmetric cage according to 13C NMR spectroscopic studies in combination with scanning tunneling microscopy results,44 and D3h(5)-C78, C2v(5)-C80, C2v(9)-C86 and D2(35)-C88 cages were obtained and crystallographically characterized for EMFs possessing the same cage symmetry, such as Sc2O@D3h(5)-C78,45 Sc2O@C2v(5)-C80,12 Sc2C2@C2v(9)-C86 (ref. 36) and Sm2@D2(35)-C88,40 it is noteworthy that the cages of C2v(7)-C84, Cs(8)-C86, Cs(15)-C86, C1(26)-C88 and Cs(32)-C88 have never been experimentally reported before in spite of the fact that Sc2O@C2v(7)-C84 was theoretically predicted without further experimental evidence.46
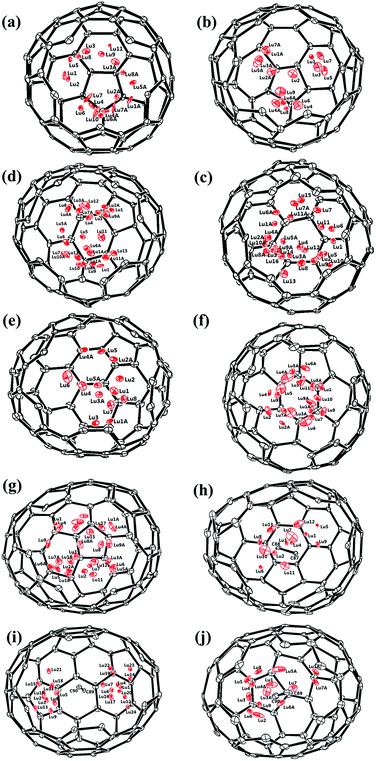
Fig. 1 and 2 portray the molecular structures of Lu2@C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers co-crystallized with the NiII(OEP) molecules. For Lu2@Cs(8)-C86 and Lu2C2@D2(35)-C88, each fullerene cage is surrounded by two NiII(OEP) molecules in a sandwich-like arrangement, and the ethyl groups of one of the NiII(OEP) molecules are arranged in such a way that they can embrace the fullerene cage from both sides whereas the other endohedrals adopt the normal one-EMF-one-Ni(OEP) fashion. The shortest Ni-cage distances in all the systems fall in the range of 2.631 Å–3.050 Å, suggesting substantial π–π interactions between the fullerene cage and the NiII(OEP) molecule(s).47–49 Inside these cages, the Lu atoms show severe disorder in all EMFs (Fig. 3, Tables S2 and S3, ESI†), indicating a motional behavior of the two Lu ions which may account for the strong Lu-cage interactions by fulfilling the coordination requirements of the Lu ions as much as possible. In detail, 19, 16 and 27 Lu positions are found for the two Lu atoms inside the Lu2@Td(2)-C76, Lu2@D3h(5)-C78 and Lu2@C2v(5)-C80 cages, respectively, whereas 26, 13 and 20 Lu sites are positioned for the two Lu atoms in the respective Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86 cage. In Lu2@C1(26)-C88, 27 Lu sites are positioned for the two Lu atoms. Moreover, 13, 24 and 16 Lu sites are found for the two Lu atoms in Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88, respectively.
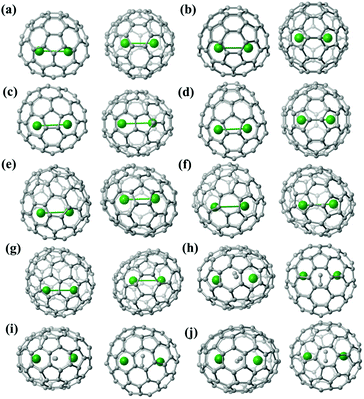
Furthermore, the representative structural data of Lu2@C76–90 isomers, such as the cage length/width ratio (L/W ratio), major Lu–Lu distance, Lu–Lu distance range and Lu-cage distance, are summarized in Table 1. The Lu–Lu distances between any two opposite Lu sites with comparable occupancy values are in the range of 3.31–3.53 Å, 3.27–3.67 Å, 3.22–3.73 Å, 3.33–3.84 Å, 3.49–3.73 Å, 3.34–3.84 Å and 3.57–3.62 Å for Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86 and Lu2@C1(26)-C88, respectively. In contrast, for Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88, which possess relatively large cages, the respective Lu–Lu distances are much longer and fall in 3.94–4.43 Å, 4.45–4.66 Å and 4.14–4.41 Å, respectively. Therefore, in these cages, a C2-unit is inserted between the two Lu atoms, which fulfills the coordination requirement of the Lu ions by taking over partially the charges from the metal ions. The shortest Lu-cage distances are consistently 2.108 Å, 2.263 Å, 2.065 Å, 2.106 Å, 2.086 Å, 2.103 Å, 2.291 Å, 2.269 Å, 2.319 Å and 2.166 Å for Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88, Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88, respectively, which are all shorter than the calculated values for Lu2@Td-C76 (2.37–2.42 Å),50,51 suggesting strong Lu-cage interactions.
| Compound | Cage length (Å) | Cage width (Å) | L/W ratio | Major Lu–Lu distance (Å)a | Calculated Lu–Lu distance (Å) | Lu–Lu distance range (Å)b | Shortest Lu-cage distancec |
|---|---|---|---|---|---|---|---|
| a Lu–Lu distance between the major Lu sites. b Lu–Lu distance between any two opposite Lu sites with comparable occupancy. c The shortest Lu-cage distance between the major Lu sites and the cage carbon atoms. | |||||||
| Lu2@Td(2)-C76 | 7.126 | 7.110 | 1.00 | 3.50 | 3.44 | 3.14–3.50 | 2.054 |
| Lu2@D3h(5)-C78 | 8.338 | 7.548 | 1.10 | 3.27 | 3.41 | 3.27–3.67 | 2.263 |
| Lu2@C2v(5)-C80 | 8.245 | 7.896 | 1.04 | 3.60 | 3.72 | 3.22–3.73 | 2.065 |
| Lu2@C3v(8)-C82 | 8.400 | 8.315 | 1.01 | 3.21 | 3.47 | 3.21–3.57 | 2.299 |
| Lu2@Cs(6)-C82 | 8.413 | 7.739 | 1.08 | 3.59 | 3.60 | 3.35–3.67 | 2.243 |
| Lu2@D2d(23)-C84 | 8.212 | 7.934 | 1.04 | 3.75 | 4.00 | 3.24–3.75 | 2.135 |
| Lu2@C2v(7)-C84 | 8.502 | 8.199 | 1.04 | 3.56 | 3.46 | 3.33–3.84 | 2.106 |
| Lu2@C2v(9)-C86 | 8.991 | 7.553 | 1.09 | 3.43 | 3.70 | 3.43–3.72 | 2.293 |
| Lu2@Cs(8)-C86 | 8.455 | 7.296 | 1.16 | 3.49 | 3.53 | 3.49–3.73 | 2.086 |
| Lu2@Cs(15)-C86 | 8.611 | 7.454 | 1.16 | 3.34 | 3.67 | 3.34–3.84 | 2.103 |
| Lu2@C1(26)-C88 | 9.018 | 7.501 | 1.20 | 3.57 | 3.65 | 3.57–3.62 | 2.291 |
| Lu2C2@C2v(9)-C86 | 8.986 | 7.502 | 1.18 | 4.41 | 4.37 | 3.94–4.43 | 2.269 |
| Lu2C2@Cs(32)-C88 | 8.883 | 7.124 | 1.25 | 4.66 | 4.64 | 4.45–4.66 | 2.319 |
| Lu2C2@D2(35)-C88 | 9.104 | 7.184 | 1.27 | 4.41 | 4.64 | 4.14–4.41 | 2.166 |
It is interesting to find that the small cages (C76–86) prefer to accommodate a Lu2 dimer to form di-EMFs whereas carbide cluster metallofullerenes (CCMFs) are formed for Lu2C88 or Lu2C90, which possess relatively large cages. We speculate that this phenomenon is caused by the different cage structure parameters, particularly the cage length and width. As clearly shown in Table 1, the cage length and L/W ratio increase in accordance with cage expansion, resulting in a substantial increase of the Lu–Lu distance. In particular, C86-based lutetium-containing EMFs have two different compositions: Cs(8)-C86 (L/W ratio = 1.16) and Cs(15)-C86 (L/W ratio = 1.16) possess relatively round cages and they choose to encapsulate a Lu2 dimer instead of a Lu2C2 cluster because of the limited inner space, whereas the elongated C2v(9)-C86 (L/W ratio = 1.20) causes the increased Lu–Lu distance because of strong Lu-cage interactions and easy C2 insertion, resulting in the formation of the CCMF Lu2C2@C2v(9)-C86. As a matter of fact, the cages smaller than C86 can only accommodate a Lu2 dimer and the larger ones always prefer the Lu2C2 composition to make the resultant EMFs more stable.49,52
Fig. S8† shows the location of the major Lu2/Lu2C2 cluster relative to the cage orientation in the ten EMFs under study. In Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@C1(26)-C88 and Lu2C2@Cs(32)-C88, one major Lu site is situated over a [5,6]-bond, whereas the other one is close to a hexagonal ring. In the other five endohedrals, each prominent Lu position is located over a [5,6]-bond. Moreover, the configurations of the Lu2C2 clusters inside the carbon cages are all shaped like a butterfly with two tightly bonded carbon atoms in the respective cage centers. The Lu–C–C–Lu dihedral angles are 132.13°, 145.46° and 142.83° in the C2v(9)-C86, Cs(32)-C88 and D2(35)-C88 cages, respectively. Furthermore, the C–C bond lengths of the C2 unit in Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88 are 1.11 Å, 1.20 Å and 1.00 Å, respectively, which represent typical C–C triple bonds (Fig. S8†).
The redox behaviors of the EMFs under study are characterized by cyclic voltammetry (CV) except for Lu2@D3h(5)-C78 and Lu2@C2v(5)-C80 due to their extremely low yields (Fig. S9 and S10†). In general, these compounds display one or two oxidation steps together with four reduction steps within the solvent window. It is noteworthy that the electrochemical gaps of Lu2C2n (2n = 76, 82, 84, 86, 88, 90) isomers are relatively large (1.19 eV–1.39 eV), indicating their high stability. Moreover, it appears that the CCMFs show better reversibility of the redox processes than the di-EMFs. For instance, several irreversible processes, either reduction or oxidation, are found for Lu2@Td(2)-C76, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86 and Lu2@C1(26)-C88, but all of the two oxidation and the four reduction processes are reversible for Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88. Table S6† lists the electrochemical potentials of the EMFs under study. In particular, the first and the second reduction potentials are mutually very close, as are the third and the fourth, but the gap between the third and the second is generally large. These results strongly corroborate their closed-shell electronic configuration with nondegenerate low-lying LUMO and accessible LUMO+1 orbitals. Consequently, such electrochemical behaviors can be regarded as characteristic properties of Lu2C2n-type EMFs.53 Accordingly, there are no EPR signals for all the EMFs reported here because of their closed-shell electronic configuration.
The unobserved decisive effect of the cage size on the configuration of the encapsulated clusters stimulates our interest to find a reasonable explanation. DFT calculations at the M06-2X/6-31G*∼SDD level were thus conducted to rationalize the formation of these Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers. Fig. 4 depicts their optimized geometries, which agree well with their respective X-ray structures. The lutetium element has a [Xe]4f146s25d1 electronic configuration and may keep its 6s electrons due to the relativistic contraction and large stabilization of the 6s atomic orbital. For Lu2@C76–88 isomers, the calculated Lu–Lu distances range from 3.41 Å to 3.72 Å, and are all comparable to those observed from our crystallographic data (Tables 1 and S7†). Actually, our results are perfectly consistent with the theoretical predictions reported by Popov and co-workers, who proposed that lutetium atoms are more inclined to adopt the +2 state, and accordingly, Lu–Lu bonding could be favorable in lutetium-containing EMFs.54,55 In comparison, the calculated Lu–Lu distances in Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88 are as long as 4.37 Å, 4.64 Å and 4.64 Å, respectively, indicating the insertion of a C2-unit.
Natural bond orbital (NBO) analysis demonstrates that the two Lu atoms in Lu2@C76–88 may form a Lu–Lu single bond with an electron occupancy of 1.97–1.98 e, which is supported by the calculated Wiberg bond orders (WBOs) ranging from 0.94 to 0.98 (Table S7†). Moreover, consistent with the low-lying (6s)σg2 molecular orbital of the free Lu2 dimer, the possible Lu–Lu bonds have an spd-hybrid character with the Lu-6s orbitals contributing the most to the metal bonding MOs, and each Lu atom donates one 5d electron and one 6s electron to the cage with the 4f electrons remaining intact. However, for Lu2C2@C86–88, the Lu–Lu single bond could not be formed in the corresponding cage because the valence electrons are partially donated to the C2-unit, as indicated by the calculated small WBO values ranging from 0.15 to 0.17 (Table S7†), resulting in the formation of the Lu2C2 units.
Furthermore, we optimized the structures of different Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers in either the Lu2@C2n or Lu2C2@C2n–2 form based on a series of low-energy C74–904− cages to differentiate their relative stability. Fig. S11–S17† and Table 2 show the optimized structures of the low-energy Lu2C76–90 isomers and relative energies as well as HOMO–LUMO gap energies. As clearly shown in Table 2, both Lu2@Td(2)-C76 and Lu2@D3h(5)-C78 are the lowest-energy ones among all the considered isomers. Moreover, Lu2@Ih(7)-C80 is 6.6 kcal mol−1 lower in energy than Lu2@C2v(5)-C80 when it has a triplet ground state. Therefore, it is highly possible that Lu2@Ih(7)-C80 is generated together with Lu2@C2v(5)-C80 during the arc-discharge process, but it may form insoluble products in the raw soot due to its radical character and thus is absent in the usual solvent extract (Table 2).56–58 As for Lu2C82, a previous report has revealed that Lu2@Cs(6)-C82 and Lu2@C3v(8)-C82 are both lower in energy than any of the Lu2C2@C80 isomers (Table 2).39 Accordingly, for a composition of Lu2C76–82, Lu2@C2n is always more stable than the corresponding carbide form Lu2C2@C2n–2, indicating that the formation of di-EMFs is energetically favorable within this cage size range.
| Compounds | Relative energies of the selected low-lying isomers | ||||
|---|---|---|---|---|---|
| Lu2C76 | Lu2@Td(2)-C76, 0.0 (2.95) | Lu2C2@C2(13333)-C74, 9.9 (2.98) | Lu2C2@C1(13334)-C74, 17.3 (3.08) | Lu2@C2v(19138)-C76, 19.5 (1.75) | Lu2C2@C1(13384)-C74, 22.7 (3.03) |
| Lu2C78 | Lu2@D3d(5)-C78, 0.0 (2.41) | Lu2@C2v(3)-C78, 5.2 (2.96) | Lu2@Cs(24099)-C78, 12.7 (2.74) | Lu2@C1(22595)-C78, 13.1 (2.89) | Lu2C2@Td(2)-C76, 16.4 (2.81) |
| Lu2C80 | Lu2@Ih(7)-C80, 0.0 (3.31/2.03) | Lu2@C2v(5)-C80, 6.6 (2.88) | Lu2@D5h(6)-C80, 8.0 (2.26) | Lu2@C1(31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891)-C80, 26.4 (2.51) 891)-C80, 26.4 (2.51) |
Lu2C2@D3d(5)-C78, 30.0 (2.60) |
| Lu2C82 | Lu2@C3v(8)-C82,39 0.0 (3.39) | Lu2@Cs(6)-C82,39 0.5 (3.03) | Lu2C2@C2v(5)-C80, 19.7 (2.94) | Lu2C2@D5h(6)-C80, 22.7 (2.37) | Lu2C2@Ih(7)-C80, 31.5 (2.16) |
| Lu2C84 | Lu2@D2d(23)-C84,39 0.0 (2.99) | Lu2C2@C3v(8)-C82, 6.2 (3.42) | Lu2@C2v(7)-C84, 6.4 (3.19) | Lu2C2@Cs(6)-C82, 6.6 (3.08) | Lu2C2@C2v(9)-C82, 8.7 (2.62) |
| Lu2C86 | Lu2@C2v(9)-C86,39 0.0 (3.10) | Lu2C2@D2d(23)-C84, 8.9 (3.02) | Lu2@Cs(8)-C86, 9.9 (3.37) | Lu2C2@C1(51383)-C84, 13.2 (3.04) | Lu2@Cs(15)-C86, 15.6 (2.77) |
| Lu2C88 | Lu2C2@C2v(9)-C86, 0.0 (3.02) | Lu2@C1(26)-C88, 2.9 (3.06) | Lu2C2@C1(13)-C86, 13.5 (2.91) | Lu2@C1(30)-C88, 14.4 (2.64) | Lu2C2@Cs(15)-C86, 14.4 (2.62) |
| Lu2C90 | Lu2C2@D2(35)-C88, 0.0 (2.86) | Lu2C2@Cs(32)-C88, 1.5 (2.85) | Lu2@D5h(41)-C90, 5.6 (2.73) | Lu2@C1(43)-C90, 6.5 (2.60) | Lu2@C1(21)-C90, 8.5 (3.00) |
However, Lu2C84–86, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, and Lu2@Cs(15)-C86 and their respective Lu2C2@C2n–2 isomers are mixed in energy, with the recently reported Lu2@D2d(23)-C84 and Lu2@C2v(9)-C86 being the most stable ones (Table 2).39 These results imply that the formation of CCMFs is gradually favored with increasing cage size. Indeed, as shown in Fig. S16 and S17,† Lu2C2@C2v(9)-C86, Lu2C2@D2(35)-C88 and Lu2C2@Cs(32)-C88 are the lowest-energy Lu2C88 and Lu2C90 isomers, respectively. Therefore, as the cage size increases to C88 and C90, the CCMFs are energetically more stable than the corresponding di-EMFs.
Overall, our experimental and theoretical results have unambiguously confirmed that the exact composition of the internal cluster is changed from Lu2 to Lu2C2 along with the cage expansion, which is a synergetic result of C2 insertion and the strong Lu-cage coordination of the Lu ions with the cage carbon atoms. It appears that the C86 cage is a threshold for Lu2C2n-type EMFs transforming from di-EMFs to CCMFs. If the transformation is a common phenomenon in other systems, it is expected that larger metals such as erbium, gallium and lanthanum may prefer a larger cage for the transformation from M2 to M2C2 (M = Er, Gd, La). Indeed, Balch. et al. have separated two Gd2C94 isomers, one of which is structurally confirmed to be a CCMF, namely Gd2C2@D3(85)-C92, while the other is theoretically proposed to be a conventional endohedral, Gd2@C2(121)-C94.59 A more recent study reported the isolation and crystallographic elucidation of an Er-based CCMF, i.e. Er2C2@D3(85)-C92, confirming again that larger cages tend to accommodate the carbide cluster.60 Moreover, for the even larger La3+ ions, although the structures of some di-EMFs, namely La2@D2(10611)-C72,61 La2@Cs(17490)-C76,62 La2@D3h(5)-C78,63 La2@Ih(7)-C80,64 and La2@D5(450)-C100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 have been confirmed by single crystal XRD crystallography, the La3+ ions are also more inclined to form carbide structures with some giant cages such as C90–104, which are rationalized by considering the synergistic effect of inserting a C2-unit on the stabilization of CCMFs both electronically and geometrically.47–49
65 have been confirmed by single crystal XRD crystallography, the La3+ ions are also more inclined to form carbide structures with some giant cages such as C90–104, which are rationalized by considering the synergistic effect of inserting a C2-unit on the stabilization of CCMFs both electronically and geometrically.47–49
Conclusions
In summary, a series of lutetium-containing EMFs, namely Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@Cs(8)-C86, Lu2@Cs(15)-C86, Lu2@C1(26)-C88, Lu2C2@C2v(9)-C86, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88, have been isolated and structurally determined. Based on our experimental and theoretical results, a clear correlation between the cage size and the configuration of the internal metallic cluster is revealed. Moreover, we also propose that the C86 cage is the threshold for Lu2C2n-type EMFs transforming from di-EMFs to CCMFs. Specifically, the relatively small cages, i.e. C76–86, choose to encapsulate a Lu2 cluster with the possible formation of a Lu–Lu bond because of the limited inner space. However, further cage expansion elongates the Lu–Lu distance due to the strong Lu-cage interactions and the insertion of a C2-unit, resulting in the formation of CCMFs, Lu2C2@C2n (2n = 86, 88). Accordingly, we confirm for the first time that the preferential formation of the Lu2@C2n/Lu2C2@C2n–2 composition is determined by the cage size, presenting a practical strategy for the templated synthesis of EMFs possessing desired internal clusters, which may facilitate the application of EMFs as building blocks for molecular devices/machines.Experimental
Synthesis and isolation of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90)
Soot containing Lu-EMFs was synthesized by a direct-current arc discharge method and was extracted using carbon disulfide (CS2). After the removal of CS2, the residue was dissolved in toluene and the solution was subjected to a multi-stage high-performance liquid chromatography (HPLC) separation. The experimental details are given in the ESI.†General characterization
High-performance liquid chromatography (HPLC) was conducted on an LC-9130 NEXT machine (Japan Analytical Industry Co., Ltd.) with toluene as the mobile phase. Matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometry was performed on a BIFLEX III spectrometer (Bruker Daltonics Inc., Germany). Vis-NIR spectra were obtained on a PE Lambda 750S spectrophotometer in CS2. Cyclic voltammograms (CV) were measured in 1,2-dichlorobenzene with 0.05 M n-Bu4NPF6 as the supporting electrolyte at a Pt working electrode with a CHI660E workstation.Single crystal XRD measurements of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90)
The crystallographic data are shown in Tables S4 and S5.† Crystalline blocks of Lu2C2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers were obtained by layering a benzene solution of NiII(OEP) over a CS2 solution of the corresponding metallofullerenes at room temperature. Over a 20-day period, the two solutions diffused together, and black crystals formed. Single-crystal XRD measurement of Lu2@Cs(8)-C86, Lu2@Cs(15)-C86 and Lu2C2@C2v(9)-C86 was performed at 173 K on a Bruker D8 QUEST machine equipped with a CMOS camera (Bruker AXS Inc., Germany). Crystallographic characterization of Lu2@Td(2)-C76, Lu2@D3h(5)-C78, Lu2@C2v(5)-C80, Lu2@C2v(7)-C84, Lu2@C1(26)-C88, Lu2C2@Cs(32)-C88 and Lu2C2@D2(35)-C88 was performed at 100 K at BL17B station of the Shanghai Synchrotron Radiation Facility. The multi-scan method was used for absorption corrections. The structures were solved by the direct method and were refined with SHELXL-2014/7.66 CCDC-1582214 (Lu2@Td(2)-C76), CCDC-1582215 (Lu2@D3h(5)-C78), CCDC-1582216 (Lu2@C2v(5)-C80), CCDC-1582217 (Lu2@C2v(7)-C84), CCDC-1582218 (Lu2@Cs(8)-C86), CCDC-1582219 (Lu2@Cs(15)-C86), CCDC-1836827 (Lu2@C1(26)-C88), CCDC-1836828 (Lu2C2@C2v(9)-C86), CCDC-1836829 (Lu2C2@Cs(32)-C88) and CCDC-1836830 (Lu2C2@D2(35)-C88) contain the supplementary crystallographic data for this paper.†Computational details
Density functional theory calculations were carried out by using the M06-2X67 functional in conjunction with the 6-31G* basis set for C68,69 and SDD basis set and corresponding effective core potential for Lu70 (denoted as 6-31G*∼SDD), as implemented in the Gaussian 09 software package.71Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the NSFC (No. 51472095, 51672093, 51602112, 51602097 and 21103224) is gratefully acknowledged. We thank the staff from BL17B beamline of the National Facility for Protein Science Shanghai (NFPS) at the Shanghai Synchrotron Radiation Facility for assistance during data collection. Also, we are grateful to the Analytical and Testing Center in Huazhong University of Science and Technology for all related measurements.Notes and references
- L. Bao, P. Peng and X. Lu, Acc. Chem. Res., 2018, 51, 810–815 CrossRef CAS PubMed.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760 RSC.
- X. Lu, T. Akasaka and S. Nagase, Acc. Chem. Res., 2013, 46, 1627–1635 CrossRef CAS PubMed.
- T. Cai, L. Xu, M. R. Anderson, Z. Ge, T. Zuo, X. Wang, M. M. Olmstead, A. L. Balch, H. W. Gibson and H. C. Dorn, J. Am. Chem. Soc., 2006, 128, 8581–8589 CrossRef CAS PubMed.
- S. Stevenson, H. M. Lee, M. M. Olmstead, C. Kozikowski, P. Stevenson and A. L. Balch, Chem.–Eur. J., 2002, 8, 4528–4535 CrossRef CAS.
- H. Kurihara, X. Lu, Y. Iiduka, N. Mizorogi, Z. Slanina, T. Tsuchiya, T. Akasaka and S. Nagase, J. Am. Chem. Soc., 2011, 133, 2382–2385 CrossRef CAS PubMed.
- H. Fang, H. Cong, M. Suzuki, L. Bao, B. Yu, Y. Xie, N. Mizorogi, M. M. Olmstead, A. L. Balch, S. Nagase, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2014, 136, 10534–10540 CrossRef CAS PubMed.
- T.-S. Wang, N. Chen, J.-F. Xiang, B. Li, J.-Y. Wu, W. Xu, L. Jiang, K. Tan, C.-Y. Shu, X. Lu and C.-R. Wang, J. Am. Chem. Soc., 2009, 131, 16646–16647 CrossRef CAS PubMed.
- L. Dunsch, S. Yang, L. Zhang, A. Svitova, S. Oswald and A. A. Popov, J. Am. Chem. Soc., 2010, 132, 5413–5421 CrossRef CAS PubMed.
- N. Chen, M. N. Chaur, C. Moore, J. R. Pinzón, R. Valencia, A. Rodríguez-Fortea, J. M. Poblet and L. Echegoyen, Chem. Commun., 2010, 46, 4818–4820 RSC.
- Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2015, 54, 9845–9852 CrossRef CAS PubMed.
- S. Stevenson, M. A. Mackey, M. A. Stuart, J. P. Phillips, M. L. Easterling, C. J. Chancellor, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 11844–11845 CrossRef CAS PubMed.
- B. Q. Mercado, M. M. Olmstead, C. M. Beavers, M. L. Easterling, S. Stevenson, M. A. Mackey, C. E. Coumbe, J. D. Phillips, J. Paige Phillips, J. M. Poblet and A. L. Balch, Chem. Commun., 2010, 46, 279–281 RSC.
- F. Jin, S. Wang, N. B. Tamm, S. Yang and S. I. Troyanov, Angew. Chem., Int. Ed., 2017, 129, 12152–12156 CrossRef.
- T.-S. Wang, L. Feng, J.-Y. Wu, W. Xu, J.-F. Xiang, K. Tan, Y.-H. Ma, J.-P. Zheng, L. Jiang, X. Lu, C.-Y. Shu and C.-R. Wang, J. Am. Chem. Soc., 2010, 132, 16362–16364 CrossRef CAS PubMed.
- F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771 CrossRef CAS PubMed.
- X. Zhang, Y. Wang, R. Morales-Martínez, J. Zhong, C. de Graaf, A. Rodríguez-Fortea, J. M. Poblet, L. Echegoyen, L. Feng and N. Chen, J. Am. Chem. Soc., 2018, 140, 3907–3915 CrossRef CAS PubMed.
- Y. Wang, R. Morales-Martínez, X. Zhang, W. Yang, Y. Wang, A. Rodriguez-Fortea, J. M. Poblet, L. Feng, S. Wang and N. Chen, J. Am. Chem. Soc., 2017, 139, 5110–5116 CrossRef CAS PubMed.
- W. Cai, R. Morales-Martínez, X. Zhang, D. Najera, E. L. Romero, A. Metta-Magaña, A. Rodríguez-Fortea, S. Fortier, N. Chen, J. M. Poblet and L. Echegoyen, Chem. Sci., 2017, 8, 5282–5290 RSC.
- A. Rodríguez-Fortea, A. L. Balch and J. M. Poblet, Chem. Soc. Rev., 2011, 40, 3551–3563 RSC.
- T. Wang and C. Wang, Acc. Chem. Res., 2014, 47, 450–458 CrossRef CAS PubMed.
- S. Yang, T. Wei and F. Jin, Chem. Soc. Rev., 2017, 46, 5005–5058 RSC.
- K. Kobayashi and S. Nagase, Chem. Phys. Lett., 1998, 282, 325–329 CrossRef CAS.
- L. Bao, C. Pan, Z. Slanina, F. Uhlik, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 55, 9234–9238 CrossRef CAS PubMed.
- S. Yang, S. I. Troyanov, A. A. Popov, M. Krause and L. Dunsch, J. Am. Chem. Soc., 2006, 128, 16733–16739 CrossRef CAS PubMed.
- M. Krause and L. Dunsch, ChemPhysChem, 2004, 5, 1445–1449 CrossRef CAS PubMed.
- A. A. Popov, M. Krause, S. Yang, J. Wong and L. Dunsch, J. Phys. Chem. B, 2007, 111, 3363–3369 CrossRef CAS PubMed.
- C. M. Beavers, M. N. Chaur, M. M. Olmstead, L. Echegoyen and A. L. Balch, J. Am. Chem. Soc., 2009, 131, 11519–11524 CrossRef CAS PubMed.
- F. Melin, M. N. Chaur, S. Engmann, B. Elliott, A. Kumbhar, A. J. Athans and L. Echegoyen, Angew. Chem., Int. Ed., 2007, 46, 9032–9035 CrossRef CAS PubMed.
- M. N. Chaur, F. Melin, J. Ashby, B. Elliott, A. Kumbhar, A. M. Rao and L. Echegoyen, Chem.–Eur. J., 2008, 14, 8213–8219 CrossRef CAS PubMed.
- A. L. Svitova, A. A. Popov and L. Dunsch, Inorg. Chem., 2013, 52, 3368–3380 CrossRef CAS PubMed.
- Q. Deng and A. A. Popov, J. Am. Chem. Soc., 2014, 136, 4257–4264 CrossRef CAS PubMed.
- J. Zhang, T. Fuhrer, W. Fu, J. Ge, D. W. Bearden, J. Dallas, J. Duchamp, K. Walker, H. Champion, H. Azurmendi, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2012, 134, 8487–8493 CrossRef CAS PubMed.
- H. Kurihara, X. Lu, Y. Iiduka, H. Nikawa, M. Hachiya, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, Inorg. Chem., 2012, 51, 746–750 CrossRef CAS PubMed.
- C.-H. Chen, K. B. Ghiassi, M. R. Cerón, M. A. Guerrero-Ayala, L. Echegoyen, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2015, 137, 10116–10119 CrossRef CAS PubMed.
- C.-H. Chen, L. Abella, M. R. Cerón, M. A. Guerrero-Ayala, A. Rodríguez-Fortea, M. M. Olmstead, X. B. Powers, A. L. Balch, J. M. Poblet and L. Echegoyen, J. Am. Chem. Soc., 2016, 138, 13030–13037 CrossRef CAS PubMed.
- J. Zhang, F. L. Bowles, D. W. Bearden, W. K. Ray, T. Fuhrer, Y. Ye, C. Dixon, K. Harich, R. F. Helm, M. M. Olmstead, A. L. Balch and H. C. Dorn, Nat. Chem., 2013, 5, 880–885 CrossRef CAS PubMed.
- W. Shen, L. Bao, Y. Wu, C. Pan, S. Zhao, H. Fang, Y. Xie, P. Jin, P. Peng, F.-F. Li and X. Lu, J. Am. Chem. Soc., 2017, 139, 9979–9984 CrossRef CAS PubMed.
- H. Yang, H. Jin, B. Hong, Z. Liu, C. M. Beavers, H. Zhen, Z. Wang, B. Q. Mercado, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 16911–16919 CrossRef CAS PubMed.
- C. M. Beavers, T. Zuo, J. C. Duchamp, K. Harich, H. C. Dorn, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2006, 128, 11352–11353 CrossRef CAS PubMed.
- H. Yang, M. Yu, H. Jin, Z. Liu, M. Yao, B. Liu, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2012, 134, 5331–5338 CrossRef CAS PubMed.
- T. Zuo, C. M. Beavers, J. C. Duchamp, A. Campbell, H. C. Dorn, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2007, 129, 2035–2043 CrossRef CAS PubMed.
- H. Umemoto, K. Ohashi, T. Inoue, N. Fukui, T. Sugai and H. Shinohara, Chem. Commun., 2010, 46, 5653–5655 RSC.
- Y. Hao, Q. Tang, X. Li, M. Zhang, Y. Wan, L. Feng, N. Chen, Z. Slanina, L. Adamowicz and F. Uhlík, Inorg. Chem., 2016, 55, 11354–11361 CrossRef CAS PubMed.
- Y.-J. Guo, X. Zhao, P. Zhao and T. Yang, J. Phys. Chem. A, 2015, 119, 10428–10439 CrossRef CAS PubMed.
- W. Cai, L. Bao, S. Zhao, Y. Xie, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2015, 137, 10292–10296 CrossRef CAS PubMed.
- W. Cai, F.-F. Li, L. Bao, Y. Xie and X. Lu, J. Am. Chem. Soc., 2016, 138, 6670–6675 CrossRef CAS PubMed.
- S. Zhao, P. Zhao, W. Cai, L. Bao, M. Chen, Y. Xie, X. Zhao and X. Lu, J. Am. Chem. Soc., 2017, 139, 4724–4728 CrossRef CAS PubMed.
- T. Yang, X. Zhao and E. Osawa, Chem.–Eur. J., 2011, 17, 10230–10234 CrossRef CAS PubMed.
- J. Hao, F. Li, H. Li, X. Chen, Y. Zhang, Z. Chen and C. Hao, RSC Adv., 2015, 5, 34383–34389 RSC.
- B. Christen, H. Christen and S. Xin, J. Am. Chem. Soc., 2017, 139, 3919 Search PubMed.
- X. Lu, Z. Slanina, T. Akasaka, T. Tsuchiya, N. Mizorogi and S. Nagase, J. Am. Chem. Soc., 2010, 132, 5896–5905 CrossRef CAS PubMed.
- A. A. Popov, S. M. Avdoshenko, A. M. Pendás and L. Dunsch, Chem. Commun., 2012, 48, 8031 RSC.
- N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. C. Kirkhorn, M. Rosenkranz, S. Schiemenz, F. Ziegs, A. U. B. Wolter, S. Yang, S. Stevenson and A. A. Popov, Nanoscale, 2017, 23, 7977–7990 RSC.
- A. Velloth, Y. Imamura, T. Kodama and M. Hada, J. Phys. Chem. C, 2017, 121, 18169–18177 CrossRef CAS.
- Z. Wang, R. Kitaura and H. Shinohara, J. Phys. Chem. C, 2014, 118, 13953–13958 CrossRef CAS.
- Y. Maeda, T. Tsuchiya, T. Kikuchi, H. Nikawa, T. Yang, X. Zhao, Z. Slanina, M. Suzuki, M. Yamada, Y. Lian, S. Nagase, X. Lu and T. Akasaka, Carbon, 2016, 98, 67–73 CrossRef CAS.
- H. Yang, C. Lu, Z. Liu, H. Jin, Y. Che, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 17296–17300 CrossRef CAS PubMed.
- A. L. Balch, M. M. Olmstead, X. Powers, C. M. Davison, S. Stevenson and K. R. Tepper, Chem.–Eur. J., 2018, 24, 13479–13484 CrossRef PubMed.
- M. Yamada, Y. Muto, H. Kurihara, Z. Slanina, M. Suzuki, Y. Maeda, Y. Rubin, M. M. Olmstead, A. L. Balch, S. Nagase, X. Lu and T. Akasaka, Angew. Chem., Int. Ed., 2015, 54, 2232–2235 CrossRef CAS PubMed.
- M. Suzuki, N. Mizorogi, T. Yang, F. Uhlik, Z. Slanina, X. Zhao, M. Yamada, Y. Maeda, T. Hasegawa, S. Nagase, X. Lu and T. Akasaka, Chem.–Eur. J., 2013, 19, 17125–17130 CrossRef CAS PubMed.
- B. Cao, H. Nikawa, T. Nakahodo, T. Tsuchiya, Y. Maeda, T. Akasaka, H. Sawa, Z. Slanina, N. Mizorogi and S. Nagase, J. Am. Chem. Soc., 2008, 130, 983–989 CrossRef CAS PubMed.
- L. Bao, M. Chen, C. Pan, T. Yamaguchi, T. Kato, M. M. Olmstead, A. L. Balch, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 55, 4242–4246 CrossRef CAS PubMed.
- C. M. Beavers, H. Jin, H. Yang, Z. Wang, X. Wang, H. Ge, Z. Liu, B. Q. Mercado, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 15338–15341 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1582214–1582219; 1836827–1836830. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc03886d |
| This journal is © The Royal Society of Chemistry 2019 |