Investigations on non-classical silylium ions leading to a cyclobutenyl cation

Abstract

Instead of yielding the desired non-classical silylium ions, the reactions of different alkenes/alkynes with several [Me₃Si]⁺ sources mostly led to oligomerization, or – in the presence of Me₃SiH – hydrosilylation of the alkenes/alkynes. Yet, from the reaction of 2-butyne with ion-like Me₃Si–F–Al(OR^F)₃ (R^F = C(CF₃)₃) the salt of the silylated tetramethyl cyclobutenyl cation [Me₄C₄–SiMe₃]⁺[al–f–al]⁻1 ([al–f–al]⁻ = [(R^FO)₃Al–F–Al(OR^F)₃]⁻) was obtained in good yield (NMR, scXRD, Raman, and IR). All the experimental and calculated evidence suggest a mechanism in which 1 was formed via a non-classical silylium ion as an intermediate. The removal of the [Me₃Si]⁺ moiety from the cation in 1 was investigated as a means to provide free tetramethyl cyclobutadiene (CBD). However, the addition of [NMe₄]F, in order to release Me₃SiF and form CBD, led to the unexpected deprotonation of the cation. The addition of 4-dimethylaminopyridine to remove the [Me₃Si]⁺ cation as a Lewis acid/base adduct, led to an adduct with the four-membered ring in the direct neighborhood of the Me₃Si group. By the addition of Et₂O to a solution of 1, the [F–Al(OR^F)₃]⁻ anion (and Et₂O–Al(OR^F)₃) was generated from the [al–f–al]⁻ counterion. Subsequently, the [F–Al(OR^F)₃]⁻ anion abstracted the [Me₃Si]⁺ moiety from [Me₄C₄–SiMe₃]⁺, probably releasing CBD. However, due to the immediate reaction of CBD with [Me₄C₄–SiMe₃]⁺ and subsequent oligomerization, it was not possible to use CBD in follow-up chemistry.

---

Introduction

Carbocations play an important role as intermediates, e.g. in S_N1 reactions or in Wagner–Meerwein rearrangements.¹ The classical carbenium ions, e.g. [C(CH₃)₃]⁺, feature a tricoordinate electron deficient carbon atom with 2e–2c bonds.² While their existence has long been accepted, there has been a long dispute about the existence of the (pentacoordinate) non-classical carbonium ions.³ Only in 2013 the final crystal structure evidence for the existence of non-classical carbocations was provided by our group.⁴ Motivated by this result, we were interested to see if analogous non-classical silylium ions also exist in the condensed phase, i.e. silylium ions stabilized by a 3c–2e bond (Scheme 1a and b). Although adducts of [Me₃Si]⁺ with ethylene and acetylene were detected in the gas phase by mass spectrometry, their structures in condensed phases hitherto remain unknown.^5–7 Yet, quantum-chemical calculations suggest a non-classical structure for adducts between [Me₃Si]⁺ and C₂H₄/C₂H₂. However, it appears that the latter are only intermediates and react further by a methyl shift and formation of a vinyl silylium ion (Scheme 1c).^6,7 By contrast, with substituted alkenes, classical carbenium ions as in Scheme 1b were calculated to be favored.⁶ Adducts of silylium ions with benzene or toluene could also be considered to possess non-classical structures, but crystallographic studies and also quantum-chemical calculations suggest a classical structure.^8,9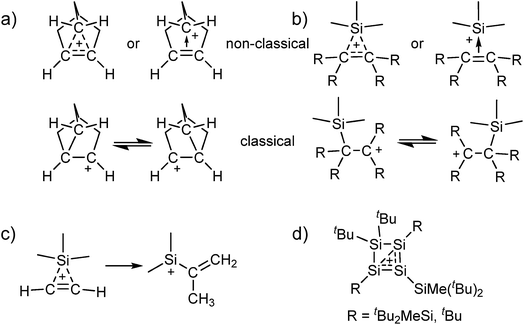

Scheme 1 Classical and non-classical structures of (a) the 2-norbornyl cation and (b) analogous silylium ions (although we refer to “classical silylium ions” here, these are rather to be seen as carbenium ions stabilized by the β-Si effect); (c) the calculated methyl shift for the [Me₃Si(C₂H₂)]⁺ cation;⁷ (d) the reaction products of silylium ions with di- and trisilenes.^10,11

The all-silicon analogue to the non-classical carbonium ions would be a silylium ion, which is coordinated by a disilene R₂Si=SiR₂ or by a (formal) disilyne RSi≡SiR. To the best of our knowledge, for the [Si₃R₅]⁺ cations no experimental data exist and computational analyses are limited to thermodynamics and do not discuss structural properties.¹² Reactions of silylium ions with di- and trisilenes yielded cyclotetrasilenylium ions [(RSi)₃SiR₂]⁺ as part of more complicated rearrangement reactions (Scheme 1d; R = ^tBu₂MeSi, ^tBu).^10,11 In any event, the stabilization of disilenes and disilynes against oligomerization requires large substituents R, which hinder their – classical or non-classical – coordination to a silylium ion.^10,11,13 Although calculations at the MP2/def2-TZVPP level suggest a non-classical adduct between [Me₃Si]⁺ and the sterically unhindered Me₂Si=SiMe₂, this disilene would not be isolable due to the discussed oligomerization. Therefore, we set out to synthesize non-classical silylium ions by reaction of sources of the small [Me₃Si]⁺ silylium ion with alkenes or alkynes. With small substituents, their π bond is more accessible than that in sterically hindered room temperature stable disilenes and disilynes. Additionally, alkenes and alkynes would allow for a homogeneous delocalization of the positive charge among the carbon atoms, which would require more reorganization for the disilenes/disilynes due to their trans-bent structure. However, the fluoride ion affinity (FIA), as a measure of Lewis acidity,¹⁴ of silylium ions is significantly higher than that of carbenium ions (FIA = 952 vs. 836 kJ mol⁻¹ for [Me₃E]⁺; E = Si, C; calculated like in ref. 15; BP86/def-SV(P)). As a result, the addition of an alkene or alkyne to a silylium ion may also result in the formation of a carbenium ion that is stabilized in the classical structure by the so-called β-Si effect. This implies a hyperconjugative stabilization due to electron density transfer from the occupied σ(Si–C) orbital into the empty p-orbital of the cationic C atom (Scheme 1b).

Results and discussion

Before turning to the experiments, we investigated the principle feasibility of the planned reactions by assessing the cations sought for with DFT and ab initio calculations and including solvation energies for the polar and weakly basic solvent ortho-difluorobenzene (o-DFB, ε_r = 13.4).¹⁶

Preliminary assessment of the stabilities of non-classical silylium ions

Calculations on the reaction of the free [Me₃Si]⁺ cation with different alkenes and alkynes were performed at the MP2/def2-TZVPP level of theory according to eqn (1) and (2) (Table 1).

[Me₃Si]⁺ + RC≡CR → [Me₃Si(RC≡CR)]⁺ (R = H, Me, Ph) (1)

[Me₃Si]⁺ + R₂C=CR₂ → [Me₃Si(R₂C=CR₂)]⁺ (R = H, Me, Ph) (2)

Table 1 Calculated Gibbs reaction energies ΔG⁰ in kJ mol⁻¹ and structures of the reaction [Me₃Si]⁺ + L → [Me₃Si(L)]⁺ calculated at the MP2/def2-TZVPP level of theory with thermal contributions from BP86-D3(BJ)/def-TZVP calculations. The Gibbs solvation energy in o-DFB was calculated using the COSMO model (ε_r = 13.4)¹⁶ at the BP86-D3(BJ)/def-TZVP level. Scheme: H (light gray), C (dark gray), Si (blue)

Ligand L	ΔrH^0gas/ΔrG^0gas	C–C–Si/°	Gas phase structure
	(ΔG^0o-DFB)	d SiC/pm
a Experimental data from ref. 8. b Cipso and Cortho were used for the measurements.
H2C=CH2	−109/−60	73.4
	(−38)	236.7
Me2C=CMe2	−174/−113	72.9
	(−56)	235.6
Ph2C=CPh2	−143/−67	93.8/54.6
	(+20)	221.6/271.4
HC≡CH	−98/−53	78.3/71.6
	(−28)	231.0/238.4
MeC≡CMe	−157/−103	74.3
	(−58)	228.3
PhC≡CPh	−188/−132	74.3
	(−52)	229.5
C6H6^a	−134/−86	98.3/51.3^b
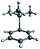
	(−39)	217.3/275.8^b

---

For comparison, the structure of the (classical) benzene complex [Me₃Si(C₆H₆)]⁺ is also included in Table 1. In order to evaluate whether the calculated molecules are non-classical silylium ions or classical carbenium ions, we analyzed both relevant C–C–Si bond angles. For a classical carbenium ion, one of these angles is expected to be larger than at least 90°, while for non-classical silylium ions both angles should be (almost) equal and smaller than 90°. The complex [Me₃Si(Ph₂C=CPh₂)]⁺ was calculated to be a classical carbenium ion stabilized by the β-Si effect with a C–C–Si angle of 93.8°, possibly due to the resonance of the phenyl moieties and also for steric reasons. The C–C–Si angles in the H₂C=CH₂ (73.4°), Me₂C=CMe₂ (72.9°), MeC≡Me (74.3°) and PhC≡CPh (74.3°) complexes combined with the symmetric C–Si distances suggest a non-classical structure for these cations. Regarding its structure, the [Me₃Si(HC≡CH)]⁺ cation is a special case with asymmetric C–C–Si angles of 78.3° and 71.6°, most likely induced by steric repulsion of the H-atom with one methyl group. Yet, we will refer to its structure as being non-classical. It should be noted that the non-classical structure of this cation with symmetric C–C–Si angles is disfavored by only ΔG⁰_gas = 0.01 kJ mol⁻¹ and therefore these two structures would be expected to be indistinguishable. The structures calculated at the simpler BP86-D3(BJ)/def-TZVP level of theory are similar, except for [Me₃Si(PhC≡CPh)]⁺. Here, the PhC≡CPh adduct is calculated to be a classical carbenium ion. It was not possible to calculate similar classical structures for the other adducts, as these are not even local minima or transition states on the respective energy hypersurface. This was exemplarily verified by calculating the energy of [Me₃Si(MeC≡CMe)]⁺ dependent on the C–C–Si angle in the range of 60 to 140° (see the ESI† for details). Therefore, classical starting structures also collapse to the non-classical structures. Thus no clear energy difference between a formally classical and a non-classical structure can be given.

The gas phase reaction enthalpies Δ_rH⁰_gas and Gibbs energies Δ_rG⁰_gas with alkynes become more favorable when replacing the H substituents of the parent alkyne HC≡CH with Me, and even more so with Ph (MP2/def2-TZVPP). This can be explained by an increased stabilization of the positive charge due to hyperconjugation and resonance, respectively (Δ_rH⁰_gas = −98 (H) vs. −157 (Me) and −188 kJ mol⁻¹ (Ph)). For alkenes, the same trend was expected. However, Δ_rH⁰_gas of the reaction with Ph₂C=CPh₂ (−143 kJ mol⁻¹) was calculated to be less favored than that with Me₂C=CMe₂ (−174 kJ mol⁻¹). We attribute this to steric reasons, as the phenyl groups cannot be coplanar as in the alkyne case. It should be noted that the non-classical structure of [Me₃Si(Ph₂C=CPh₂)]⁺ with equivalent Si–C distances was calculated to be a transition state for the [Me₃Si]⁺ migration between both carbon atoms. This transition state is higher in energy than the calculated minimum structure by only ΔG⁰_o-DFB = +7 kJ mol⁻¹ (ΔG⁰_gas = +11 kJ mol⁻¹). Therefore, it might not be possible to differentiate between the classical and non-classical structure by NMR spectroscopy (coalescence) or single crystal X-ray diffraction (dynamic disorder).

Including COSMO¹⁷ Gibbs solvation energies, all calculated reaction energies become less favored and the reaction of [Me₃Si]⁺ with the larger PhC≡CPh was also calculated to be less exergonic than that with the smaller MeC≡CMe. This is attributed to the fact that smaller ions are generally better solvated than larger ones. Since upon reaction with [Me₃Si]⁺ the product cation always increases in size, reactions (1) and (2) become less favored the larger the ligand. Due to this effect, the formation of [Me₃Si(Ph₂C=CPh₂)]⁺ was calculated to be endergonic in solution by ΔG⁰_o-DFB = +20 kJ mol⁻¹.

Reactions of Me₃Si–F–Al(OR^F)₃ with alkenes and alkynes

Since the calculations suggested that the formation of non-classical silylium ions should be possible, in part also in solution, we turned towards their synthesis. Ethylene and acetylene are gases and only weakly bound to [Me₃Si]⁺ (cf.Table 1). Therefore, we performed the reactions of Me₃Si–F–Al(OR^F)₃ with the substituted compounds R₂C=CR₂ and RC≡CR (R = Me, Ph). 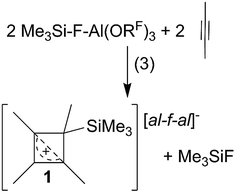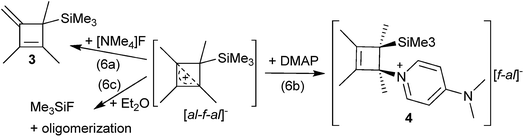However, the reactions with Me₂C=CMe₂, Ph₂C=CPh₂ and PhC≡CPh in o-DFB or CH₂Cl₂ and at r.t. or −40 °C did not yield any silylium ions, but only led to exergonic oligomerization of the alkenes and alkynes. However, this signals activation of the unsaturated hydrocarbons by Me₃Si–F–Al(OR^F)₃. By contrast, reactions with MeC≡CMe in o-DFB or CH₂Cl₂ at various temperatures (−40 °C to r.t.; eqn (3)), reproducibly gave a 28% yield of [Me₄C₄–SiMe₃]⁺[al–f–al]⁻1 ([al–f–al]⁻ = [(R^FO)₃Al–F–Al(OR^F)₃]⁻; NMR, scXRD, Raman, IR) after crystallization. This compound will be discussed later in more detail.

Reactions of [Ph₃C]⁺[al–f–al]⁻ with Me₃SiH and alkenes/alkynes

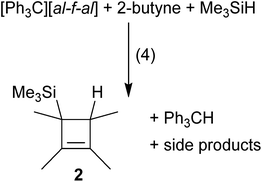
By exchanging Me₃Si–F–Al(OR^F)₃ for more reactive silylium ions, we hoped to form the desired products faster and thereby prevent oligomerization. In order to generate the [Me₃Si]⁺ cation as an intermediate, we mixed the starting materials (liquid alkenes or alkynes) with [Ph₃C]⁺[al–f–al]⁻ in the absence of solvent. An excess of Me₃SiH was condensed onto this mixture to generate silylium ions or their Me₃SiH adducts¹⁸in situ and allowed to warm to r.t. Although NMR spectra of these reaction mixtures in CD₂Cl₂ showed complete conversion of the starting materials, the non-classical silylium ions could not be detected. Instead, hydrosilylation of PhC≡CPh and Me₂C=CMe₂ (see the ESI† for details) and formation of neutral 2 for MeC≡CMe were observed (eqn (4)). Upon reaction of MeC≡CMe with [Ph₃C]⁺[al–f–al]⁻ and Me₃SiH, presumably 1 was formed, which then reacted with excess Me₃SiH to yield 2 and [Me₃Si(solv)]⁺ (solv = Me₃SiH, CH₂Cl₂). Only after complete conversion of the alkenes and alkynes, the anion was attacked and decomposed.¹⁹ It should be noted that the evolving [Me₃Si–H–SiMe₃]⁺[al–f–al]⁻ is not isolable as a pure material. Yet, the [al–f–al]⁻ anion was shown to be fairly stable against silylium ions in CH₂Cl₂.¹⁹

Reactions of bromo-ethyl/vinyl silanes with Ag⁺[al–f–al]⁻

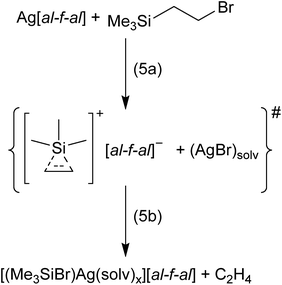
In order to prevent oligomerization of the alkenes and alkynes, we reacted bromo-ethyl and bromo-vinyl silanes with Ag⁺[al–f–al]⁻ in CH₂Cl₂ at −40 °C, respectively. The abstraction of Br⁻ from these silanes by Ag⁺ should result in the formation of ethylene/acetylene adducts of [Me₃Si]⁺ (cf. eqn (5a) for the bromo-ethyl example). Here the reaction with a second equivalent of an alkene/alkyne is not possible and the non-classical silylium ions should become isolable. Upon reaction, no solid AgBr visibly formed. Nevertheless, NMR spectra of these reactions did not show signals of the starting silanes, but of Me₃SiBr in both cases. This signal is slightly shifted to a lower field by 2 ppm and suggests a coordination of Me₃SiBr to Ag⁺.¹⁹ It seems likely that the non-classical silylium ions [Me₃Si(C₂H₄/C₂H₂)]⁺ were generated in situ (eqn (5a)). However, apparently these silylium ions then reacted further with the (solvated) AgBr under the formation of [(Me₃SiBr)Ag(solv)_x]⁺ and release of C₂H₄/C₂H₂ (see eqn (5b) for the ethene example; the evolving C₂H₄ could be identified by gas phase IR spectroscopy).²⁰ Similar silver–halosilane adducts were observed and structurally characterized upon reaction of ^tBu₃SiBr with Ag⁺[al–f–al]⁻ – although halide abstraction and AgBr formation were desired.¹⁹ Additionally, partial decomposition of the anion and formation of Me₃SiF and Me₃SiCl were observed, which is further evidence for the generation of silylium ions.

Formation of [Me₃Si(MeC≡CMe)]⁺vs. [Me₄C₄–SiMe₃]⁺

The reactions of 2-butyne with Me₃Si–F–Al(OR^F)₃ and silylium ions only yielded 1 and 2, respectively. Both compounds were formed from two 2-butyne units. This led to the question of whether it is at least theoretically possible to isolate the desired silylium ion [Me₃Si(MeC≡CMe)]⁺ by these routes, or if such non-classical ions reside in shallow potential wells that allow for a simple and low-barrier subsequent reaction with MeC≡CMe to give 1. Therefore, we calculated the reaction mechanism for the formation of [Me₄C₄–SiMe₃]⁺ (P-4) at the BP86-D3(BJ)/def-TZVP level of theory (Fig. 1). In order to reduce computational cost, we started from 2-butyne and [Me₃Si]⁺, instead of Me₃Si–F–Al(OR^F)₃.

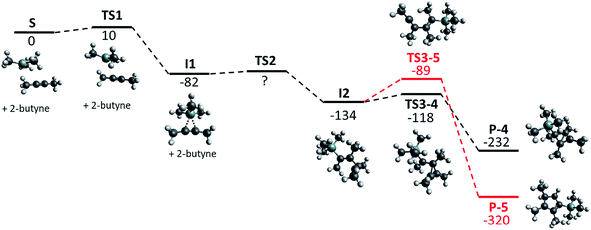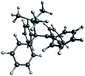
Fig. 1 Calculated reaction path, geometries and relative energies in kJ mol⁻¹ for the formation of [Me₄C₄–SiMe₃]⁺ (P-4, black) and the 5-membered ring (P-5, red); BP86-D3(BJ)/def-TZVP.

Since 2-butyne itself does not dimerize under standard conditions,²¹ the silylation of 2-butyne can be assumed to be the first step in the formation of [Me₄C₄–SiMe₃]⁺. The Gibbs activation energy ΔG^≠ (TS1) for this exothermic process was calculated to be only 10 kJ mol⁻¹. The silylated 2-butyne (I1) then reacts with a second equivalent of 2-butyne to exothermically form the intermediate I2. We were not able to determine the Gibbs activation energy (TS2) for this reaction with the method used. This indicates that this barrier is either very small or not existent at all. Based on thermodynamics, this intermediate should rearrange to yield a 5-membered ring (P-5). However, the barrier for this rearrangement (TS3-5) was calculated to be 45 kJ mol⁻¹ – which is almost triple the barrier (TS3-4) for the formation of the observed [Me₄C₄–SiMe₃]⁺ (P-4, 16 kJ mol⁻¹). Thus, the calculations are in agreement with the experimental observation and suggest that P-4 (=1) is the kinetic product.

When Me₃Si–F–Al(OR^F)₃ is used for the silylation of 2-butyne, the Gibbs activation energy (transition state similar to TS1) for this reaction is expected to be higher, due to its lower reactivity compared to [Me₃Si]⁺. However, this will not change the entire picture. In conclusion it seems impossible to isolate the silylated 2-butyne (I1) by use of Me₃Si–F–Al(OR^F)₃ or even (non-existent) free [Me₃Si]⁺, as the reaction with the second molecule of 2-butyne appears to be much faster than the silylation.

Properties of [Me₄C₄–SiMe₃]⁺[al–f–al]⁻

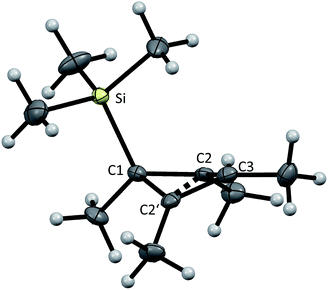
From the reaction solution in o-DFB at r.t. single crystals of 1 were obtained by the addition of less polar CH₂Cl₂. The molecular cation structure of salt 1 is shown in Fig. 2. With Si–C1–C2/C2′ angles being 113°–118°, the stabilization of this cation by the β-silicon effect is not evident. Otherwise, these angles would be expected to lie around 90°.²²

Fig. 2 Molecular structure of the cation in [Me₄C₄–SiMe₃][al–f–al] (1) with thermal ellipsoids set at 50% probability level. The [al–f–al]⁻ anion was omitted for clarity. Scheme: Si (yellow), C (grey), H (white). Selected distances (pm), bond angles (deg), and torsion angles (deg): Si–C1 192.2(2), C1–C2 151.8(2), C1–C2′ 152.6(2), C2–C3 138.9(2), C2′–C3 138.5(2), C2–C2′ 179.4(2), Si–C1–C2 117.9(1), Si–C1–C2′ 113.0(1), C2–C1–C2′ 72.2(1), C2–C3–C2′ 80.6(1), and C1–C2–C3–C2′ 25.5(1).

This cation can be seen as a silylated cyclobutadiene and is closely related to the already known homoaromatic [R₄C₄–H]⁺, [R₄C₄–Cl]⁺, [^tBu₄C₄–OH]⁺ and the neutral [R₄C₄–AlX₃] (R = H, Me, ^tBu, Ph; X = Cl, Br).^23–29 Of these, the protonated cations [R₄C₄–H]⁺ with R = H, Me, Ph were only characterized by NMR at −40 to −70 °C,²⁷ while with R = ^tBu they were shown to be isolable with a large variety of anions, like Br⁻ or [SbF₆]⁻.²⁶ Also the chlorinated and hydroxylated cations [Ph₄C₄–Cl]⁺ and [^tBu₄C₄–OH]⁺ and the neutral [Me₄C₄–AlCl₃] were shown to be stable at r.t. and could be isolated.^23,24,26,29

A comparison of selected structural parameters, calculated NPA and PABOON partial charges and π⁽*⁾(C2–C3–C2′)-orbital energies of the compounds is found in Table 2. In order to allow for a better comparison, these calculations were performed on the methyl-substituted derivatives for all compounds. The [(RSi)₃SiR₂]⁺ cations (R = ^tBu₂MeSi, ^tBu) can also be seen as silicon analogues of these compounds but will not be discussed.^10,11 When comparing the convolution angles (C1–C2–C2′–C3) of 1, [^tBu₄C₄–H]⁺, [Ph₄C₄–Cl]⁺, [^tBu₄C₄–OH]⁺ and [Me₄C₄–AlX₃], their absolute values are relatively similar and range between 37.3° and 31.5°, except for [Ph₄C₄–Cl][Nb₂OCl₉] with a dihedral angle of only 4.3°. However, the dihedral angles in 1 and [Me₄C₄–AlX₃] are positive, while in [^tBu₄C₄–H]⁺, [^tBu₄C₄–OH]⁺ and [Ph₄C₄–Cl]⁺ they are negative. This is a consequence of the (C2–)Me groups being bent, which leads to repulsion of the sterically most demanding group. The relatively small dihedral angle in [Ph₄C₄–Cl]⁺ results from resonance of the phenyl moieties with the (C2–C2′) orbital, which is an intermediate between a σ and a π orbital. This leads to an increased C2–C2′ distance compared to that in the other compounds (203 vs. ∼180 pm).^27,30

Table 2 Selected experimental (calculated) properties of different [R₄C₄–E]⁽⁺⁾ compounds (E = SiMe₃, H, Cl, OH, AlCl₃, and AlBr₃). Distances are given in pm, angles are given in ° and orbital energies are given in eV. The calculated values always refer to [Me₄C₄–E]⁽⁺⁾ for better comparability; BP86-D3(BJ)/def-TZVP

	1	[^tBu4aC4–H]^+ (ref. 26)	[Ph4C4–Cl]^+ (ref. 23)	[^tBu4C4–OH]^+ (ref. 26)	[Me4C4–AlCl3] (ref. 31)	[Me4C4–AlBr3]	Me4C4
a HOMO/LUMO+1. b HOMO−2/LUMO+1. c HOMO−1/LUMO+1. d HOMO−6/LUMO+1. e HOMO/LUMO.
Bond distances (pm) and dihedral angles (deg)
d(C1–C2)	151.8/152.6 (152.7)	152.4 (153.4)	152.9/154.4 (153.2)	152.3/153.8 (154.2)	151.0 (151.5)	(151.6)	(159.1)
d(C2–C2′)	179.4 (183.2)	180.6 (187.5)	203.3 (195.5)	183.3 (190.7)	177.4 (183.1)	(184.4)	(208.5)
d(C2–C3)	138.5/138.9 (140.2)	140.7 (140.2)	138.7/140.4 (140.6)	139.4/139.6 (140.2)	138.7 (140.2)	(140.2)	(134.7)
C1–C2–C2′–C3	31.7 (29.3)	−37.3 (−27.7)	−4.3 (−22.1)	−36.3 (−26.2)	31.5 (28.5)	(27.3)	(0.0)
NPA/PABOON partial charges for the methyl derivatives [Me 4 C 4 –EY x ] ^(+)
δ(C1)	(−0.43/−0.14)	(−0.27/−0.05)	(−0.09/0.09)	(0.26/0.15)	(−0.52/−0.14)	(−0.54/−0.13)	(0.00/0.01)
δ(C2)	(0.27/0.21)	(0.28/0.19)	(0.30/0.15)	(0.17/0.15)	(0.27/0.27)	(0.28/0.27)	(0.00/0.01)
δ(C3)	(0.00/−0.02)	(0.02/0.01)	(−0.01/0.01)	(0.02/0.03)	(−0.04/−0.05)	(−0.05/−0.05)	(0.00/0.01)
δ(C1 + 2 × C2 + C3)	(0.11/0.26)	(0.31/0.34)	(0.50/0.40)	(0.62/0.48)	(−0.02/0.35)	(−0.03/0.36)	(−0.01/0.04)
δ(Me4C4)	(0.51/0.82)	(0.75/0.90)	(1.00/1.03)	(1.16/1.01)	(0.25/0.67)	(0.25/0.67)	(0.00/0.00)
δ(E)	(0.49/0.18)	(0.25/0.10)	(0.00/−0.03)	(−0.16/−0.01)	(−0.25/−0.67)	(−0.25/−0.67)	(—)
Energies of the (anti-)bonding π(C2–C3–C2′)-orbitals of the methyl derivatives [Me 4 C 4 –EY x ] ^(+)
E π*(C2–C3–C2′)	(−5.60)^a	(−6.04)^a	(−6.14)^b	(−6.02)^c	(−1.92)^d	(−1.92)^d	(−1.70)^e
E π(C2–C3–C2′)	(−10.36)^a	(−11.75)^a	(−12.12)^b	(−11.90)^c	(−7.33)^d	(−7.04)^d	(−3.74)^e

---

When looking at the bonding π(C2–C3–C2′) orbitals of the methylated derivatives of the discussed compounds (Table 2), a correlation between their energies and the partial charge of the Me₄C₄ moiety is evident, with a higher partial charge leading to lower orbital energies. From a frontier orbital point of view, this implies that the cations [Me₄C₄–SiMe₃]⁺, [R₄C₄–H]⁺, [R₄C₄–Cl]⁺, and [^tBu₄C₄–OH]⁺ are more electron-deficient than the neutral [Me₄C₄–AlX₃]. This is also evident when simply looking at the total charge of these molecules. Interestingly, the energies of the π*(C2–C3–C2′) orbitals seem to be less affected by the partial charge of the Me₄C₄ moiety, but mostly by the total charge of the molecules. Therefore, the energy of this orbital is nearly the same for [Me₄C₄–AlCl₃] and Me₄C₄, while for the cationic species it is lower by ∼4 eV.

Evaluating the homoaromatic character of [R₄C₄–E]⁽⁺⁾

Since the structural parameters of the discussed compounds are very similar, especially d(C2–C2′) and d(C2–C3), an unambiguous comparison of the C2–C2′ interactions is not possible (except for [Ph₄C₄–Cl]⁺, which does not show this interaction). This interaction is a measure of homoaromaticity and can be determined from the difference in NMR chemical shifts between C2/C2′ and C3 (Table 3).^26,27 In allylic systems, the terminal C atoms (here C2/C2′) bear a positive charge, resulting in the deshielding of these. The interaction between C2 and C2′ leads to their shielding, combined with the transfer of the positive charge to C3 (deshielding). For homoaromatic systems a negative value for Δ(δ¹³C_(C2) − δ¹³C_(C3)) is expected, while for allylic systems this difference should be positive.²⁶

Table 3 Experimental ¹³C NMR chemical shifts of [R₄C₄–E]⁽⁺⁾ in ppm (R = H, Me, ^tBu, and Ph; E = SiMe₃, H, Cl, OH, AlCl₃, and AlBr₃)

Cation	δ(C1)	δ(C2/C2′)	δ(C3)	δ(C2) − δ(C3)
a Cyclopentenylium cation as reference for an allylic cation.
[Me4C4–SiMe3]^+	66.8	166.0	170.4	−4.4
[^tBu4C4–OH]^+ (ref. 26)	101.0	161.5	184.9	−23.4
[Me4C4–Cl]^+ (ref. 27)	76.0	191.5	174.4	+17.1
[Me4C4–AlCl3] (ref. 29)	—	162.0	164.3	−2.3
[Me4C4–H]^+ (ref. 27)	57.8	171.3	171.3	0.0
[^tBu4C4–H]^+ (ref. 26)	78.5	156.6	196.6	−40.0
[Ph4C4–H]^+ (ref. 27)	52.5	190.0	152.3	+38.6
[H4C4–H]^+ (ref. 27)	54.0	133.5	187.6	−54.1
[H6C5–H]^+^a (ref. 27)	48.7	234.7	145.7	+89.0

---

With [H₄C₄–H]⁺ and the cyclopentenylium cation [H₆C₅–H]⁺ being the prototypes for homoaromatic and allylic cations, respectively, the homoaromatic character of the discussed compounds and influence of the substituents can be evaluated. Exchanging the H substituents for Me moieties in [R₄C₄–H]⁺ leads to hyperconjugation of the C–H bond to C2. As a result, the C2–C2′ interactions are decreased and C2 is deshielded. Therefore the difference between δ¹³C_(C2) and δ¹³C_(C3) is more positive (0.0 vs. −54.1 ppm for [H₄C₄–H]⁺). The methylated compounds [Me₄C₄–SiMe₃]⁺ and [Me₄C₄–AlCl₃] show similar differences in the shielding of C2 and C3 and therefore are considered to have a similar homoaromatic character as [Me₄C₄–H]⁺. Only [Me₄C₄–Cl]⁺ shows a comparatively high deshielding of C2 due to low homoaromaticity, which is a consequence of the hyperconjugation of the σ(C–Cl) orbital to the (C2–C2′) orbital.

When looking at the C2–C2′ interactions of [^tBu₄C₄–H]⁺ and [^tBu₄C₄–OH]⁺, they would be expected to be even weaker than in [Me₄C₄–H]⁺ and [Me₄C₄–Cl]⁺, respectively, due to the stronger electron-donating properties of the ^tBu moieties. However, the NMR chemical shifts suggest a significantly increased homoaromatic character. We assign this to the bulkiness of the ^tBu moieties leading to a repulsion of the C3–^tBu and C2–^tBu groups. As a result, the C1–C2–C2′–C3 dihedral angle is higher than that for the methylated derivatives (Table 2). Phenyl substituents seem to completely prevent the C2–C2′ interactions due to resonance and charge delocalization onto the phenyl residue(s). This follows from the NMR chemical shifts of [Ph₄C₄–H]⁺ and from the structural parameters of [Ph₄C₄–Cl]⁺ (dihedral angle and d(C2–C2′)).

Taking a closer look at the dihedral angles in the discussed compounds, a correlation between these and Δ(δ¹³C_(C2) − δ¹³C_(C3)) is evident. The higher the dihedral angle, the stronger the C2–C2′ interaction in the compound. For [H₄C₄–H]⁺ this angle was calculated to be 33.5° (BP86-D3(BJ)/def-TZVP), which is in agreement with this thesis. Interestingly, the distances d(C2–C2′) and d(C2–C3) are only slightly affected by these C2–C2′ interactions (Table 2).

Investigations towards release of Me₄C₄ from 1

While information on the reactivities of most of the discussed compounds is scarce, [R₄C₄–AlX₃] was shown to be a source of cyclobutadienes R₄C₄ (CBDs) by use of coordinating solvents, like DMSO, due to abstraction of AlCl₃.^28,32–34 Besides the discussed AlX₃ adducts cyclobutene dicarboxylic acid anhydrides and [Fe(CO₃)(C₄H₄)] can also be used for the generation of CBDs.³⁵ CBDs are anti-aromatic and, therefore, unsubstituted CBD undergoes dimerization readily at T > 35 K.³⁶ Thus, small CBDs have to be generated in situ. Only when they bear large substituents, dimerization can be prevented.³⁷

By abstraction of the [Me₃Si]⁺ moiety, 1 might be used as a tetramethylcyclobutadiene (Me₄C₄) donor as well. The advantage of 1 over [Me₄C₄–AlX₃] as a CBD donor would be its increased stability, which allows for storage in a glove box for more than a year. NMR spectra of [Me₄C₄–AlX₃] show partial coalescence of the signals already at 20 °C.²⁹ In contrast, all signals of 1 are resolved, including the ⁵J_H–H coupling of 0.46 Hz. The increased stability very likely results from the higher Lewis acidity of [Me₃Si]⁺ over AlX₃ (FIA = 539 vs. 425/438 kJ mol⁻¹, X = Cl/Br). These FIAs were calculated in an environment with the polarity of CH₂Cl₂ (ε_r = 8.9) using COSMO,¹⁷ in order to account for the different charges of the Lewis acids. The effect is also evident by addition of AlX₃ to [Me₄C₄–AlX₃] in order to increase the Lewis acidity, i.e. the formation of [Me₄C₄–Al₂X₆]. It shows an increased thermal stability and reduced coalescence compared to [Me₄C₄–AlX₃].²⁹

Reaction with [NMe₄]F

Due to the high stability of the Si–F bond, we reacted 1 with [NMe₄]F in o-DFB/CH₂Cl₂ at r.t., in order to generate Me₃SiF and Me₄C₄. However, only negligible amounts of Me₃SiF formed. The main products were [NMe₄]⁺[F_1+x–Al(OR^F)_3−x]⁻ (x = 0, 1), HOR^F and 3 due to deprotonation of 1 (eqn (6a)). The formation of the anions [F_1+x–Al(OR^F)_3−x]⁻ occurs due to the high Lewis acidity of [al–f–al]⁻.¹⁹ The deprotonation of 1 suggested that a non-charged nucleophile, like 4-dimethylaminopyridine (DMAP), could be helpful to prevent deprotonation of the cation.

Reaction with DMAP

The reaction of 1 with an excess of DMAP in a mixture of o-DFB and CH₂Cl₂ at r.t. yielded mainly DMAP–Al(OR^F)₃, [F–Al(OR^F)₃]⁻ (reaction with the anion) and the adduct of [Me₄C₄–SiMe₃]⁺ with DMAP (4, eqn (6b)). We were able to obtain single crystals of both compounds at −40 °C from the reaction solution (see the ESI† for details). The crystal structure and NMR spectra of 4 showed that the cation is obtained as an enantiomeric mixture, with the DMAP and the [Me₃Si]⁺ moieties being in syn-conformation, i.e. in (S,R) and (R,S) configurations, which is attributed to the orientation of the LUMO of 1 (see Fig. S-60†). A similar adduct between Me₄C₄–AlCl₃ and PPhCl₂ was already proposed as an intermediate in the synthesis of phosphole oxides.³³ Due to the syn-conformation of the DMAP and Me₃Si moieties it seemed possible to remove both of them in the form of [DMAP–SiMe₃]⁺ under the release of Me₄C₄ by gentle warming/heating. However, heating of 4 to 100 °C did not result in the elimination of [DMAP–SiMe₃]⁺, but only led to the formation of 3, [DMAP–H]⁺[f–al]⁻ and other unidentified products.

Reaction with diethylether

Unexpectedly, one of the minor side products in the reaction of 1 with DMAP was Me₃SiF, providing evidence for the reaction of [Me₄C₄–SiMe₃]⁺ with a fluoride ion source. Since 1 is stable in o-DFB over several days, the Lewis basic [F–Al(OR^F)₃]⁻ anion ([f–al]⁻)¹⁹ has to be considered as the fluoride ion source. This is in agreement with the findings that the NMR spectra of 1 never showed the presence of [f–al]⁻, independent of the reaction stoichiometry.³⁸ Therefore, we dissolved 1 in Et₂O at r.t., which is known to induce the dissociation of [al–f–al]⁻ into Et₂O–Al(OR^F)₃ and [f–al]⁻.¹⁹ NMR spectra of this reaction mixture revealed the formation of Me₃SiF and complete decomposition of 1 (eqn (6c)), but no evidence for the expected dimerization product of Me₄C₄ could be found.³⁴ Instead, the NMR spectra suggested the formation of oligomerization products. When this reaction was performed in the presence of 2-butyne, partial formation of C₆Me₆ was observed, similar to the reaction of [Me₄C₄–AlCl₃] with 2-butyne and DMSO.³⁴ Therefore, we assume this reaction is (weak) evidence for the intermediate release of CBD from 1. However, analogous reactions of 1 with other electron-deficient or electron-rich dienophiles (MeO₂C–C≡C–CO₂Me, Me₃Si–C≡C–SiMe₃) never gave the desired Diels–Alder products,²⁹ but only the known oligomerization products and complete retention of the alkynes.

It should be noted that the reaction solution for the synthesis of 1 also contained C₆Me₆ and these oligomerization products. The reason for this is that in the first stage of the reaction of Me₃Si–F–Al(OR^F)₃ with 2-butyne the [f–al]⁻ anion is formed. Therefore, 1, [f–al]⁻ and 2-butyne are present in solution at the same time. Thus, 1 readily reacts with [f–al]⁻ upon its initial synthesis, resulting in its decomposition and accounting for the relatively low yield of 28%. Eventually, the formation of [al–f–al]⁻ from [f–al]⁻ and Me₃Si–F–Al(OR^F)₃ suppresses this decomposition reaction.

Rationalization

Why is there such a difference in the reactivity of alkynes with Me₄C₄ released from 1 and from [Me₄C₄–AlX₃]? Me₄C₄ is an electron-rich diene (high HOMO energy) and therefore should react with electron-deficient dienophiles (low LUMO energy). While the π-LUMO energy of −1.92 eV for [Me₄C₄–AlX₃] is rather high and similar to that for free Me₄C₄, it is much lower for 1 with an energy of −5.60 eV (Table 1). For this reason [Me₄C₄–AlX₃] is a poor dienophile and the released Me₄C₄ alone undergoes Diels–Alder reactions with the added alkynes. In contrast, the π-LUMO energy of even very electron-deficient alkynes, like F₃C–C≡C–CF₃ (−2.70 eV), is significantly higher than that of 1. As a result, the evolving Me₄C₄ reacts with [Me₄C₄–SiMe₃]⁺ instead of other dienophiles, leading to oligomerization. The same problem is likely to arise when using the other cationic cyclobutenyl cations as their π-LUMO energies are expected to be in the same region as those of 1.

Conclusion

By the reaction of Me₃Si–F–Al(OR^F)₃ with different alkenes and alkynes the synthesis of non-classical silylium ions was investigated. However, most of these reactions only led to oligomerizations in which such silylium ions may be intermediates; they were assessed by calculations (Table 1). Replacing Me₃Si–F–Al(OR^F)₃ with silylium ions, generated in situ from [Ph₃C]⁺[al–f–al]⁻ and Me₃SiH, also did not yield the desired non-classical silylium ions. Instead, hydrosilylation of the alkenes and alkynes was observed. Preliminary tests suggest that these hydrosilylation reactions can be performed with only catalytic amounts of [Ph₃C]⁺[al–f–al]⁻.³⁹ However, this should be investigated in a separate study by specialists. Halide abstraction reactions from bromo-vinyl/alkyl silanes by Ag⁺[al–f–al]⁻ seemed to be successful, but resulted in the formation of bromo silanes and C₂H₂/C₂H₄ due to the reaction of the silylium ions with solvated AgBr. From the reaction of Me₃Si–F–Al(OR^F)₃ with 2-butyne, a salt of the stable silylated tetramethyl cyclobutenyl cation [Me₄C₄–SiMe₃]⁺ was obtained. Attempts to release the CBD Me₄C₄ from this compound did not result in the planned Diels–Alder reactions, but only in oligomerization products. We attribute this to the comparatively low π-LUMO energy of [Me₄C₄–SiMe₃]⁺, leading to the reaction of this cation with the evolving Me₄C₄.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Albert-Ludwigs-Universität Freiburg, the ERC project UniChem and the DFG. We would like to acknowledge the MagRes facility of the University of Freiburg and Fadime Bitgül for the measurement of the NMR spectra and Daniel Kratzert for the valuable discussions of the crystallographic data.

References

1. (a) G. A. Olah and G. K. Surya Prakash, ed. Carbocation Chemistry, John Wiley & Sons, Hoboken, New Jersey, 2004; (b) H. Meerwein and K. van Emster, Ber. Dtsch. Chem. Ges. A/B, 1922, 55, 2500.
2. G. A. Olah, J. Am. Chem. Soc., 1972, 94, 808.
3. (a) P. v. R. Schleyer, D. Lenoir, P. Mison, G. Liang, G. K. S. Prakash and G. A. Olah, J. Am. Chem. Soc., 1980, 102, 683; (b) H. C. Brown, Acc. Chem. Res., 1986, 19, 34; (c) S. Winstein and D. S. Trifan, J. Am. Chem. Soc., 1949, 71, 2953; (d) H. C. Brown, The Nonclassical Ion Problem, Springer US, Boston, MA, 1977.
4. F. Scholz, D. Himmel, F. W. Heinemann, P. v. R. Schleyer, K. Meyer and I. Krossing, Science, 2013, 341, 62.
5. (a) B. Chiavarino, M. E. Crestoni, J. Lemaire, P. Maitre and S. Fornarini, J. Chem. Phys., 2013, 139, 71102; (b) O. Mó, M. Yáñez, J.-F. Gal, P. C. Maria and J.-C. Guillemin, J. Phys. Org. Chem., 2002, 15, 509; (c) B. Chiavarino, M. E. Crestoni and S. Fornarini, Chem. Commun., 2002, 1418.
6. X. Li and J. A. Stone, J. Am. Chem. Soc., 1989, 111, 5586.
7. H.-U. Siehl, S. Brixner, C. Coletti, N. Re, B. Chiavarino, M. E. Crestoni, A. de Petris and S. Fornarini, Int. J. Mass Spectrom., 2013, 334, 58.
8. M. F. Ibad, P. Langer, A. Schulz and A. Villinger, J. Am. Chem. Soc., 2011, 133, 21016.
9. (a) T. Müller, C. Bauch, M. Ostermeier, M. Bolte and N. Auner, J. Am. Chem. Soc., 2003, 125, 2158; (b) S. Duttwyler, Q.-Q. Do, A. Linden, K. K. Baldridge and J. S. Siegel, Angew. Chem., Int. Ed., 2008, 47, 1719; (c) J. B. Lambert, S. Zhang and S. M. Ciro, Organometallics, 1994, 13, 2430; (d) J. B. Lambert, S. Zhang, C. L. Stern and J. C. Huffman, Science, 1993, 260, 1917.
10. S. Inoue, M. Ichinohe, T. Yamaguchi and A. Sekiguchi, Organometallics, 2008, 27, 6056.
11. A. Sekiguchi, T. Matsuno and M. Ichinohe, J. Am. Chem. Soc., 2000, 122, 11250.
12. A. Burcat and E. Goos, Int. J. Chem. Kinet., 2018, 7, 793.
13. (a) A. Sekiguchi, Science, 2004, 305, 1755; (b) R. West, M. J. Fink and J. Michl, Science, 1981, 214, 1343; (c) I. Bejan and D. Scheschkewitz, Angew. Chem., Int. Ed., 2007, 46, 5783.
14. T. E. Mallouk, G. L. Rosenthal, G. Mueller, R. Brusasco and N. Bartlett, Inorg. Chem., 1984, 23, 3167.
15. K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, J. Fluorine Chem., 2000, 101, 151.
16. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press/Taylor and Francis, Boca Raton, 90th edn, 2010.
17. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
18. S. P. Hoffmann, T. Kato, F. S. Tham and C. A. Reed, Chem. Commun., 2006, 767.
19. A. Martens, P. Weis, M. C. Krummer, M. Kreuzer, A. Meierhöfer, S. C. Meier, J. Bohnenberger, H. Scherer, I. Riddlestone and I. Krossing, Chem. Sci., 2018, 9, 7058.
20. C. A. Reed, Acc. Chem. Res., 1998, 31, 325.
21. (a) V. G. Baonza, O. R. Montoro, M. Taravillo, M. Cáceres and J. Núñez, J. Chem. Phys., 2004, 121, 11156; (b) C. Mediavilla, J. Tortajada and V. G. Baonza, Chem. Phys. Lett., 2008, 454, 387.
22. S. G. Wierschke, J. Chandrasekhar and W. L. Jorgensen, J. Am. Chem. Soc., 1985, 107, 1496.
23. E. Hey, F. Weller and K. Dehnicke, Z. Anorg. Allg. Chem., 1983, 502, 45.
24. R. F. Bryan, J. Am. Chem. Soc., 1964, 86, 733.
25. H. H. Freedman and A. E. Young, J. Am. Chem. Soc., 1964, 86, 734.
26. G. Maier, R. Emrich, K.-D. Malsch, K.-A. Schneider, M. Nixdorf and H. Irngartinger, Chem. Ber., 1985, 118, 2798.
27. G. A. Olah, J. S. Staral, R. J. Spear and G. Liang, J. Am. Chem. Soc., 1975, 97, 5489.
28. J. B. Koster, G. J. Timmermans and H. van Bekkum, Synthesis, 1971, 1971, 139.
29. P. B. J. Driessen and H. Hogeveen, J. Am. Chem. Soc., 1978, 100, 1193.
30. M. Simonetta and S. Winstein, J. Am. Chem. Soc., 1954, 76, 18.
31. C. Krüger, P. J. Roberts, Y.-H. Tsay and J. B. Koster, J. Organomet. Chem., 1974, 78, 69.
32. (a) Š. Janková, J. Schulz, S. Hybelbauerová, I. Císařová, P. Štěpnička and M. Kotora, Eur. J. Org. Chem., 2013, 2013, 44; (b) P. B. J. Driessen and H. Hogeveen, J. Organomet. Chem., 1978, 156, 265; (c) M. J. Marsella, S. Estassi, L.-S. Wang and K. Yoon, Synlett, 2004, 192.
33. K. S. Fongers, H. Hogeveen and R. F. Kingma, Tetrahedron Lett., 1983, 24, 1423.
34. H. Hogeveen, H. Jorritsma, P. A. Wade, F. van Rantwijk, J. B. Koster, J. J. Prooi, A. Sinnema and H. van Bekkum, Tetrahedron Lett., 1974, 15, 3915.
35. T. Bally and S. Masamune, Tetrahedron, 1980, 36, 343.
36. A. Fattahi, L. Lis, Z. Tian and S. R. Kass, Angew. Chem., Int. Ed., 2006, 45, 4984.
37. (a) H. Irngartinger and H. Rodewald, Angew. Chem., Int. Ed., 1974, 13; (b) H. Kimling and A. Krebs, Angew. Chem., Int. Ed., 1972, 11, 932.
38. (a) J. Possart, A. Martens, M. Schleep, A. Ripp, H. Scherer, D. Kratzert and I. Krossing, Chem.–Eur. J., 2017, 23, 12305; (b) M. Rohde, L. O. Müller, D. Himmel, H. Scherer and I. Krossing, Chem.–Eur. J., 2014, 20, 1218.
39. (a) R. J. Wehmschulte and L. Wojtas, Inorg. Chem., 2011, 50, 11300; (b) M. Kira, T. Hino and H. Sakurai, Chem. Lett., 1992, 21, 555.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, procedures, weights, and 1D- and 2D-NMR spectra of the reactions are displayed. Details of the quantum chemical calculations are given together with crystallographic details. CCDC 1868136–1868138. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc04591g

---