Open Access Article
Open Access ArticlePicture of the wet electron: a localized transient state in liquid water†
Michele
Pizzochero
 *a,
Francesco
Ambrosio‡
*a,
Francesco
Ambrosio‡
 b and
Alfredo
Pasquarello
b and
Alfredo
Pasquarello
 b
b
aChaire de Physique Numérique de la Matière Condensée (C3MP), Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: michele.pizzochero@epfl.ch
bChaire de Simulation à l'Echelle Atomique (CSEA), Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland
First published on 19th June 2019
Abstract
A transient state of the excess electron in liquid water preceding the development of the solvation shell, the so-called wet electron, has been invoked to explain spectroscopic observations, but its binding energy and atomic structure have remained highly elusive. Here, we carry out hybrid functional molecular dynamics to unveil the ultrafast solvation mechanism leading to the hydrated electron. In the pre-hydrated regime, the electron is found to repeatedly switch between a quasi-free electron state in the conduction band and a localized state with a binding energy of 0.26 eV, which we assign to the wet electron. This transient state self-traps in a region of the liquid which extends up to ∼4.5 Å and involves a severe disruption of the hydrogen-bond network. Our picture provides an unprecedented view on the nature of the wet electron, which is instrumental to understanding the properties of this fundamental species in liquid water.
Introduction
Since its discovery more than fifty years ago,1 the hydrated electron has been the focus of seamless and intensive experimental2–7 and theoretical8–16 research effort. Besides the fundamental interest in understanding the response of liquid water to an excess charge, this species is relevant to numerous applications, including its role, e.g., as a reducing agent in synthetic chemistry or in inducing mutagenic lesions in DNA.17,18 It is now well-established that, under thermodynamic equilibrium conditions, the hydrated electron is accommodated in a quasi-spherical electrophilic cavity with a radius of ∼1.8 Å formed upon the re-arrangement of about five water molecules.8,19–21 It occupies a s-like ground state within the band gap of the solvent,17,22 from which it can be excited to p-like states through optical transitions of ∼1.7 eV.1 Notwithstanding the large number of studies on the hydrated electron, the atomistic mechanism leading to its formation and the nature of its precursors have remained poorly understood.On the experimental side, there is widespread consensus that two transient precursor states precede the formation of the hydrated electron, namely (i) the quasi-free electron and (ii) the wet electron.23–26 The latter is a short-lived state, which is thought to form upon the trapping of the excess electron (eaq) at defective water molecule sites,27 likely where broken hydrogen bonds are present possibly due to thermal fluctuations of the solvent.23,24 When the trapping is ineffective, the eaq remains within the conduction states of the aqueous solvent, giving rise to a quasi-free electron28 delocalized over distances of ∼40 Å.29 Building on spectroscopic observations, the following dynamics for the formation of the hydrated electron have been tentatively invoked.23 First, immediately after injection into liquid water, eaq effectively acts as a quasi-free electron. Next, it is trapped at a broken hydrogen-bond site leading to the formation of the solvation shell of the equilibrated eaq, with the entire process being accompanied by a continuous shrinking of the localization length.29 Though plausible, this experimentally inferred mechanism remains vague and many issues need to be clarified. For instance, a thorough knowledge of the energetics and atomic structure of the wet electron is fully missing, including the degree of perturbation to the hydrogen-bond network required to trap the excess charge. In particular, it remains to be ascertained whether a “trap-seeking” or “trap-digging” mechanism is operative,30, the latter being analogous to the self-trapping polaron. Moreover, it is an open question whether the wet electron steadily collapses into the hydrated one right after trapping23 or rather undergoes a sequence of trapping and subsequent detrapping processes.31
Earlier theoretical investigations did not succeed in distinguishing the two above mentioned precursor species in bulk water and their interplay. Molecular dynamics simulations carried out on bulk water systems identified suitable trapping sites and further estimated their concentration and lifetime distributions.30,32–35 However, the large number of molecules involved in such calculations required the use of simplified classical interactions, by which the electronic structure of the solvent is not explicitly accounted for. On the other hand, ab initio simulations are well-known to be routinely affordable only on a small number of molecules and have been used in this context to study the properties of the wet electron by attaching one extra negative charge to a small water cluster composed of very few molecules.36,37 However, the minimal model adopted casts doubt on the extent to which it can be representative of the more complex bulk liquid water system.
Here, we perform ab initio molecular dynamics simulations of a realistic model of bulk water to elucidate the nature of the excess electron in the early stages of the solvation process. For the very first time, we determine its energy level and the accompanying structural features before thermodynamic equilibrium is established. Overall, our findings shed new light on the elusive wet electron and offer an appealing theoretical picture to the interpretation of experimental observations.
Computational model
We model the excess electron in liquid water by adding an extra charge to a periodically repeated cubic cell containing 128 water molecules at the experimental density. The electronic structure is described through a hybrid functional that reproduces the experimental band gap of liquid water and partially suppresses the self-interaction error. The functional is supplemented with nonlocal van der Waals interactions, which ensure that the structural properties of liquid water and its mass density are properly reproduced. The adopted functional has been extensively benchmarked and successfully used in the case of the hydrated electron.8 Here, we perform adiabatic molecular dynamics simulations. This approach admittedly neglects electron scattering processes on the basis that the trapping of the wet electron has been measured to occur on a hundred femtosecond time scale,24 while the time of electron thermalization is estimated to be an order of magnitude faster, thus leading to an effective decoupling of the two physical processes.27 Reported energy values correspond to averages between occupied and unoccupied single-particle energy levels, to ensure optimal compliance with the generalized Koopmans' theorem.38Results
Energetics and dynamics of excess electrons
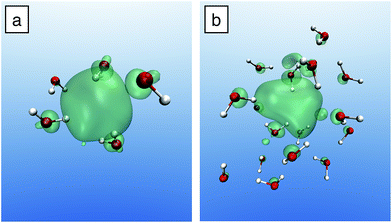
We monitor the molecular dynamics simulation of the extra electron by following the evolution of its energy level in time. The first picosecond of the solvation dynamics is shown in Fig. 1(a). Because of the abrupt transition at 275 fs, two regimes can easily be distinguished in accordance with experiment.24 First, we identify the fully hydrated regime (after ∼275 fs), in which the one-particle level remains approximately constant and is pinned deep in the band gap of liquid water. The energy level at ∼−1.6 eV in Fig. 1(a) is consistent with the experimental vertical ionization energy (VIE) at 3.2–3.6 eV,22,40 considering the position of the conduction band w.r.t. the vacuum level (V0 = −0.7–1.0 eV, ref. 8 and 41), the finite-size effect (0.7 eV, ref. 8), and subsequent residual relaxation. In Fig. 2(a), we illustrate the relative charge density and recognize the well-known configuration of the hydrated electron consisting of a spherical-like distribution coordinated on average by five water molecules.8 Next, we focus on the pre-solvated regime (before ∼275 fs), in which the energy level of the excess electron oscillates in the vicinity of the continuum of the conduction states. In Fig. 2(b), the charge density in correspondence of the first minimum of the energy level (at ∼40 fs) is given. This is a trapped state in which the charge density is localized, albeit over an extended area which includes several water molecules. In contrast, when the energy level occurs in the conduction band, the excess charge is found to be delocalized over the full simulation cell (not shown). Overall, a picture emerges in which the hydrated eaq is preceded by a pre-solvated regime with quite distinct dynamic, energetic, and structural properties.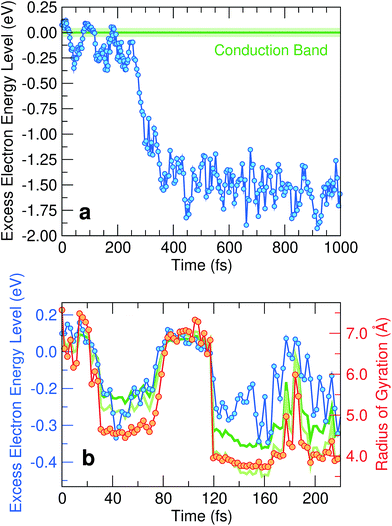 | ||
| Fig. 1 (a) Time evolution of the energy level of the excess electron w.r.t. to the average conduction band minimum. The average of the conduction band minimum (horizontal green line) with the shaded area representing the standard deviation of its distribution has been obtained from a simulation of neat water.(b) Magnification of the first 220 fs of the evolution together with the corresponding radius of gyration of the excess electron. Energy levels obtained from the particle-in-a-box and the hydrogen-like atom models proposed in ref. 39 are also shown as light and dark green lines, respectively. | ||
We analyze in more detail the two distinct precursors among which the pre-hydrated electron switches like in two-state system dynamics [cf.Fig. 1(b)]. The energy levels of these two states lie either at or slightly below the conduction band edge. To gain insight into their spatial extension, we determine their radius of gyration. As shown in Fig. 1(b), the energy level of the excess electron strongly correlates with the radius of gyration, thereby indicating that it is largely ruled by localization effects. Such a correlation has been quantified in a previous study,39 in which two simple yet effective models connecting the energy level of the excess electron E with its radius of gyration Rgyr have been proposed, i.e. the particle-in-a-box model (EPIB) and the hydrogen-like atom model (Ehydrogenic). In atomic units, such relations can be expressed as
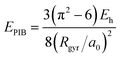 | (1) |
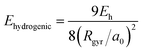 | (2) |
Through the above equations, we have estimated the energy levels of the excess electron in the early time dynamics based on the radius of gyration. The corresponding energies are given in Fig. 1(b), in which a nice agreement between the models and the explicit first-principles calculation can be observed.
For pre-hydrated states with energy levels in the continuum, we find an average radius of gyration of ∼7.5 Å. This value corresponds to half the size of our simulation cell (15.64 Å), further supporting their delocalized character. We recognize these states as being quasi-free electron precursors. Their radii of gyration have recently been estimated to be ∼40 Å,29 consistent with a fully delocalized charge density in our simulation cell. For pre-hydrated states with energy levels deeper in the band gap, we remark that their radii of gyration assume well-defined values for periods of about 50 fs, suggesting a distinctive characteristic for these transient states. Their radii of gyration are ∼4.5 Å, slightly larger than the radius of gyration of the hydrated electron (2.5 Å).8 This signals the formation of a trapped state with a localized charge distribution that we assign to the experimentally observed wet electron.23,24,31
We obtain the binding energy of the wet electron by averaging the energy level of the pre-hydrated state over the time interval in which the radius of gyration is smaller than 4.5 Å. We find that its energy level lies at 0.26 eV below the bottom of the conduction band edge. In Fig. 3, this energy level is compared with the s-like and p-like levels of the hydrated electron, which fall at 2.75 and 1.00 eV,8 respectively. On the basis of these binding energies, we exclude that the wet electron is closely related to the excited p-like state of the hydrated electron, as proposed in the literature.25,36,42 This is further supported by the fact that the cavity of the hydrated electron is not yet formed upon the creation of the wet electron. The remarkably low binding energy of the wet electron emphasizes the distinct nature of this precursor with respect to the hydrated one. In fact, in previous non-adiabatic one-electron simulations,36 it has been postulated that the wet electron could be associated with an excited localized p-like state that survives for over 1 ps well above the vacuum level. In order to address this possibility, we have carried out time-dependent density functional theory calculations for the wet electron configurations and have inspected the oscillator strength over an excitation energy window of ∼1 eV. In this range, we do not detect any strong transition to a localized p-like state and verify that the final states are delocalized.
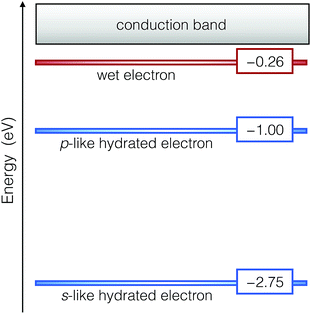 | ||
| Fig. 3 Energy levels of the wet and the hydrated electrons with respect to the conduction band of liquid water. | ||
Atomic structure of the wet electron
Following our identification of the wet electron, we analyze its structural properties. To locate the center of its charge density, we first consider the average position of the electron wave function. Then, we determine the radial distribution functions of oxygen [gO(r)] and hydrogen [gH(r)] atoms with respect to this center. These functions are given in Fig. 4, where they are compared with those of the fully hydrated case. For the wet electron, we remark that gH(r) starts developing at lower radii than gO(r), indicating that an electrostatic preference is already operative in this case. Furthermore, the cavity associated with the wet electron is significantly smaller than that obtained for the hydrated electron, as can be inferred from the principal peaks in gO(r) and gH(r), which are shifted towards smaller distances. We gain further insight into the size of the electron cavity through an analysis based on Voronoi volumes. Our investigation yields an average Voronoi volume around the wet electron of 20.50 Å3, thereby clearly indicating that its cavity is smaller than that of the fully hydrated electron (23.96 Å3, ref. 8).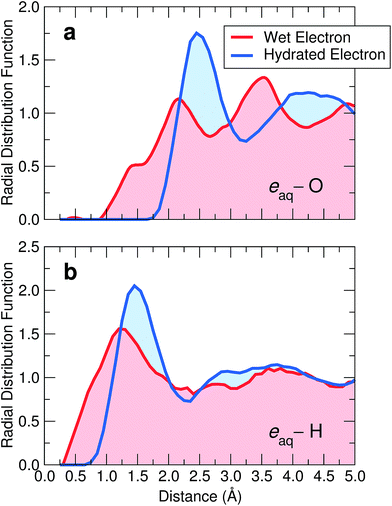 | ||
| Fig. 4 Radial distribution functions of (a) oxygen and (b) hydrogen atoms with respect to the center of the excess electron for the wet (red) and the hydrated (blue) electron. | ||
In the case of the hydrated electron, the first peak in gO(r) matches the extent of the charge density as given by the radius of gyration (2.5 Å).8 In contrast, for the wet electron, the radius of gyration (∼4.5 Å) extends well beyond the position of the first O peak (2.1 Å), indicating that the charge density is not fully accommodated within the cavity, consistent with Fig. 2(b). Overall, the distribution functions of the wet electron appear less structured. To understand the role of the disorder in shaping such cavities, we estimate the degree of distortion through the deviation of the flattening f of the involved ellipsoid from the perfect spherical symmetry expected for a s-like ground state (f = 0). We calculate the flattening by taking the major (minor) semi-axis as the longest (shortest) distance between H pairs coordinating the excess electron. On average, we find f = 0.58 for the wet electron, noticeably larger than that for the fully hydrated electron (f = 0.25).8
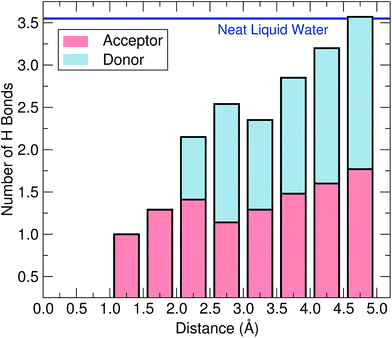
Next, we address the physical origin of the trapping of the wet electron. Based on spectroscopic evidence, it has been suggested that this species forms at a broken hydrogen bond.23 To examine this possibility, we compare the hydrogen-bond network in the vicinity of the wet electron with that of neat liquid water. As a definition of a hydrogen bond, we rely on a well-established geometrical criterion,43,44 which consists in assuming that two water molecules are hydrogen-bonded when the interatomic distance between their oxygen atoms is smaller than 3.50 Å and their corresponding O–H⋯O bond angle larger than 140°. For neat water, we find the number of H bonds per molecule to be 3.55, in close agreement with the estimate of 3.58 derived from experimental data.45 In Fig. 5, we show the number of H bonds as a function of distance from the wet electron center. At large distances, the bulk value is recovered, but the number of H bonds strongly decreases when approaching the wet electron. More specifically, at the shortest distances this number is found to be more than halved compared to that of neat liquid water and remains perturbed up to ∼4.5 Å, consistent with the radius of gyration of the wet electron. Hence, the water molecules are more loosely bonded in the region over which the charge density extends. Since the wet electron does not affect the local water density, we attribute this property to ultrafast librational motions of the water molecules, which take place on the same time scale as the formation of the wet electron.5,6,23 Further analysis of hydrogen bonds in terms of donor and acceptor types reveals that only acceptor-type hydrogen bonds occur at distances smaller than 2.0 Å from the wet electron. As can be seen in Fig. 4(b), this radius encloses the full first peak in the gH(r), which hence results from an orientation of the water molecules towards the negative charge density. Overall, the adopted criterion leads to about two H atoms oriented towards the negative charge center and up to six broken hydrogen bonds in the region of the wet electron. These results indicate that the wet electron impacts the structure of liquid water both by reorienting the water molecules in the immediate vicinity of its center and by weakening the water network over a region corresponding to the extension of its charge density. It is worth noticing in this context that such a disruption of the hydrogen-bond network is a feature that the wet and the hydrated electron have in common.20,46 This allows us to further clarify the mechanism leading to the formation of the hydrated electron. In fact, we suggest that the role of the wet electron as a precursor is to locally break the hydrogen-bond network in liquid water, in order to “prepare” a suitable site where the subsequent equilibration towards the hydrated electron can occur.
Discussion and conclusion
We here discuss our findings in light of available experimental observations. On the basis of spectroscopic measurements,23 a mechanism has been postulated, in which the initially delocalized excess electron acquires a localized characteristic upon trapping in a transient state before collapsing into the hydrated electron. Our simulations qualitatively support this mechanism but additionally reveal the underlying dynamics. Indeed, the wet electron is not found to decay steadily into its hydrated form, but rather undergoes repeated trapping and subsequent detrapping before the thermodynamic equilibrium prevails (cf.Fig. 1). The first evidence pointing to the wet electron consists of a state absorbing in the near infrared region (0.9–1.6 eV).24 Our assignment of the wet electron to a state lying at 0.26 eV below the conduction band together with the assumption of an electron affinity of 0.8–1.0 eV for liquid water8,41 led us to ascribe the observed absorption to transitions involving final states above the vacuum level. Concerning the atomic structure, we have confirmed that broken hydrogen-bond sites play a role in the conversion of the quasi-free electron to the wet electron state, as has previously been surmised.23 However, our simulations indicate that a “trap-digging” process is at the origin of the formation of the wet electron, thus ruling out its description in terms of pre-existing trapping sites, as widely assumed so far.23,24,27,30,32–34 This can be inferred from the development of the wide region around the wet electron in which the hydrogen-bond network is perturbed, which is unlikely to ensue from a thermal fluctuation of the neat liquid. In addition, we remark that a simulation of neat water of similar size and duration does not yield energy levels as deep as 0.26 eV (cf.Fig. 1), while it properly reproduces the experimental estimate of the number of hydrogen bonds per molecule. As far as the involved time scales are concerned, the one pertaining to the trapping of the quasi-electron into the wet electron state and the one associated with the formation of the hydrated electron can be distinguished. Migus et al. assigned lifetimes of 110 and 240 fs to the respective processes,24 but a consensual assessment is still lacking and reported timescales range from 50 to 500 fs for both processes.42 This order of magnitude is consistent with the evolution in our model (cf.Fig. 1).In conclusion, we carried out a comprehensive investigation of the pre-hydrated excess electron through hybrid functional molecular dynamics simulations. Before the collapse into the hydrated structure, the excess electron is found to alternate between a quasi-free state and a localized state with a binding energy of 0.26 eV. In the latter state, the hydrogen-bond network is severely disrupted over a large region of 4.5 Å, corresponding to the extension of the electron charge density. We identified this state as the so-called wet electron, providing a picture in accordance with experimental observations.
Methods
We use the spin-polarized PBEh(α) hybrid functional47 with the fraction of Fock exchange α set to 0.40, which yields a Kohn–Sham band gap of 8.8 eV for liquid water in accordance with experimental and theoretical estimates.48 There is ample evidence in the literature concerning the reliability of hybrid functionals similar to the one used in this work for the treatment of aqueous systems.49–52 The van der Waals interactions are described through the nonlocal rVV10 functional,53,54 in which the parameter b is set to 5.3 to correctly reproduce the experimental mass density of liquid water.55 We take advantage of the implementation provided in the CP2K suite of codes.56 The core–valence interactions are described through Goedecker–Teter–Hutter pseudopotentials and the valence electron wave functions are expanded in a triple-ζ polarized (TZP) basis. The charge density is expanded in a plane-wave basis set defined by a cutoff of 800 Ry. Molecular dynamics simulations were performed in the Born–Oppenheimer scheme, in which the electrons are constantly thermalized to the ground state. The equations of motion are integrated with the Verlet algorithm and a time step of 0.48 fs. The simulation is started from an equilibrated configuration of neat liquid water.55 We carry out four molecular dynamics runs in the NVT ensemble (see ESI†), in which the temperature is maintained at 350 K to ensure a frank diffusive motion via the use of a Nosé–Hoover thermostat.57,58 We also perform four additional runs in the NVE ensemble and find equivalent physical properties for the wet electron (see ESI†), ruling out any effect associated with the thermostat. We do not explicitly include quantum nuclear motions, but their effect on the band-gap renormalization is accounted for by the choice of the fraction α.8 The adopted methodology is the same as that used in ref. 8, in which an excellent description was achieved for the fully hydrated electron as far as the VIE, the s → p transition, the thermodynamic redox level, and the radius of gyration are concerned. This allows us to compare our results for the wet electron in a consistent manner with those of the hydrated one. To check finite-size effects, we additionally carry out a simulation of the wet electron in a cell containing 64 water molecules, and find that its energy level does not depend on the supercell size within less than 20 meV. The trajectory analyzed in this work is freely available on the Materials Cloud platform (DOI: 10.24435/materialscloud:2019.0033/v1).Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. P. is financially supported by the Swiss National Science Foundation (Grants 162612 and 172543). This work has been performed in the context of the National Center of Competence in Research (NCCR): Materials' Revolution: Computational Design and Discovery of Novel Materials (MARVEL) of the Swiss National Science Foundation. Our simulations have been carried out at the Swiss National Supercomputing Centre (CSCS). We thank P. Gono for helpful interactions.References
- E. J. Hart and J. W. Boag, J. Am. Chem. Soc., 1962, 84, 4090–4095 CrossRef CAS.
- H. A. Schwarz, J. Phys. Chem., 1991, 95, 6697–6701 CrossRef CAS.
- M. J. Tauber and R. A. Mathies, J. Am. Chem. Soc., 2003, 125, 1394–1402 CrossRef CAS PubMed.
- D. H. Paik, I.-R. Lee, D.-S. Yang, J. S. Baskin and A. H. Zewail, Science, 2004, 306, 672–675 CrossRef CAS PubMed.
- M. F. Emde, A. Baltuška, A. Kummrow, M. S. Pshenichnikov and D. A. Wiersma, Phys. Rev. Lett., 1998, 80, 4645–4648 CrossRef CAS.
- C. Silva, P. K. Walmhout, K. Yokoyama and P. F. Barbara, Phys. Rev. Lett., 1998, 80, 1086–1089 CrossRef CAS.
- A. E. Bragg, J. R. R. Verlet, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2004, 306, 669–671 CrossRef CAS PubMed.
- F. Ambrosio, G. Miceli and A. Pasquarello, J. Phys. Chem. Lett., 2017, 8, 2055–2059 CrossRef CAS PubMed.
- F. Uhlig, O. Marsalek and P. Jungwirth, J. Phys. Chem. Lett., 2012, 3, 3071–3075 CrossRef CAS PubMed.
- L. Turi, J. Chem. Theory Comput., 2015, 11, 1745–1755 CrossRef CAS PubMed.
- O. Marsalek, F. Uhlig, J. VandeVondele and P. Jungwirth, Acc. Chem. Res., 2012, 45, 23–32 CrossRef CAS PubMed.
- M. Boero, M. Parrinello, K. Terakura, T. Ikeshoji and C. C. Liew, Phys. Rev. Lett., 2003, 90, 226403 CrossRef PubMed.
- P. J. Rossky and J. Schnitker, J. Phys. Chem., 1988, 92, 4277–4285 CrossRef CAS.
- R. E. Larsen, W. J. Glover and B. J. Schwartz, Science, 2010, 329, 65–69 CrossRef CAS PubMed.
- L. Turi and Á. Madarász, Science, 2011, 331, 1387 CrossRef PubMed.
- R. E. Larsen, W. J. Glover and B. J. Schwartz, Science, 2011, 331, 1387 CrossRef.
- J. M. Herbert and M. P. Coons, Annu. Rev. Phys. Chem., 2017, 68, 447–472 CrossRef CAS PubMed.
- K. R. Siefermann and B. Abel, Angew. Chem., Int. Ed., 2011, 50, 5264–5272 CrossRef CAS PubMed.
- L. Turi and P. J. Rossky, Chem. Rev., 2012, 112, 5641–5674 CrossRef CAS PubMed.
- J. Wilhelm, J. VandeVondele and V. V. Rybkin, Angew. Chem., Int. Ed., 2019, 58, 3890–3893 CrossRef CAS PubMed.
- Z. C. Holden, B. Rana and J. M. Herbert, J. Chem. Phys., 2019, 150, 144115 CrossRef PubMed.
- Y. Tang, H. Shen, K. Sekiguchi, N. Kurahashi, T. Mizuno, Y.-I. Suzuki and T. Suzuki, Phys. Chem. Chem. Phys., 2010, 12, 3653–3655 RSC.
- D. Nordlund, H. Ogasawara, H. Bluhm, O. Takahashi, M. Odelius, M. Nagasono, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2007, 99, 217406 CrossRef CAS PubMed.
- A. Migus, Y. Gauduel, J. L. Martin and A. Antonetti, Phys. Rev. Lett., 1987, 58, 1559–1562 CrossRef CAS PubMed.
- F. H. Long, H. Lu and K. B. Eisenthal, Phys. Rev. Lett., 1990, 64, 1469–1472 CrossRef CAS PubMed.
- R. Laenen, T. Roth and A. Laubereau, Phys. Rev. Lett., 2000, 85, 50–53 CrossRef CAS PubMed.
- A. Mozumder, Int. J. Radiat. Appl. Instrum. C Radiat. Phys. Chem., 1988, 32, 287–291 CAS.
- P. Palianov, P. Martin, F. Quéré and S. Pommeret, J. Exp. Theor. Phys., 2014, 118, 489–493 CrossRef CAS.
- J. Savolainen, F. Uhlig, S. Ahmed, P. Hamm and P. Jungwirth, Nat. Chem., 2014, 6, 697 CrossRef CAS PubMed.
- W. M. Bartczak and K. Pernal, Res. Chem. Intermed., 2001, 27, 891–900 CrossRef CAS.
- M. Assel, R. Laenen and A. Laubereau, J. Chem. Phys., 1999, 111, 6869–6874 CrossRef CAS.
- L. Turi, A. Madarász and P. J. Rossky, J. Chem. Phys., 2006, 125, 014308 CrossRef PubMed.
- J. Schnitker, P. J. Rossky and G. A. Kenney-Wallace, J. Chem. Phys., 1986, 85, 2986–2998 CrossRef CAS.
- K. A. Motakabbir and P. J. Rossky, Chem. Phys., 1989, 129, 253–262 CrossRef CAS.
- M. Skorobogatiy, I. Park and J. Joannopoulos, Comput. Mater. Sci., 2005, 32, 96–106 CrossRef CAS.
- F. J. Webster, J. Schnitker, M. S. Friedrichs, R. A. Friesner and P. J. Rossky, Phys. Rev. Lett., 1991, 66, 3172–3175 CrossRef CAS PubMed.
- K. S. Kim, I. Park, S. Lee, K. Cho, J. Y. Lee, J. Kim and J. D. Joannopoulos, Phys. Rev. Lett., 1996, 76, 956–959 CrossRef CAS PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- L. D. Jacobson and J. M. Herbert, J. Am. Chem. Soc., 2011, 133, 19889–19899 CrossRef CAS PubMed.
- A. T. Shreve, T. A. Yen and D. M. Neumark, Chem. Phys. Lett., 2010, 493, 216–219 CrossRef CAS.
- F. Ambrosio, Z. Guo and A. Pasquarello, J. Phys. Chem. Lett., 2018, 9, 3212–3216 CrossRef CAS PubMed.
- C.-R. Wang, T. Luo and Q.-B. Lu, Phys. Chem. Chem. Phys., 2008, 10, 4463–4470 RSC.
- E. Schwegler, G. Galli and F. Gygi, Phys. Rev. Lett., 2000, 84, 2429–2432 CrossRef CAS PubMed.
- A. Luzar and D. Chandler, Phys. Rev. Lett., 1996, 76, 928–931 CrossRef CAS PubMed.
- A. K. Soper, F. Bruni and M. A. Ricci, J. Chem. Phys., 1997, 106, 247–254 CrossRef CAS.
- L. D. Jacobson and J. M. Herbert, J. Chem. Phys., 2010, 133, 154506 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- W. Chen, F. Ambrosio, G. Miceli and A. Pasquarello, Phys. Rev. Lett., 2016, 117, 186401 CrossRef PubMed.
- T. Todorova, A. P. Seitsonen, J. Hutter, I.-F. W. Kuo and C. J. Mundy, J. Phys. Chem. B, 2006, 110, 3685–3691 CrossRef CAS PubMed.
- C. Zhang, D. Donadio, F. Gygi and G. Galli, J. Chem. Theory Comput., 2011, 7, 1443–1449 CrossRef CAS PubMed.
- R. A. DiStasio, B. Santra, Z. Li, X. Wu and R. Car, J. Chem. Phys., 2014, 141, 084502 CrossRef PubMed.
- A. P. Gaiduk, J. Gustafson, F. Gygi and G. Galli, J. Phys. Chem. Lett., 2018, 9, 3068–3073 CrossRef CAS PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 CrossRef.
- F. Ambrosio, G. Miceli and A. Pasquarello, J. Phys. Chem. B, 2016, 120, 7456–7470 CrossRef CAS PubMed.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc05101a |
| ‡ Present address: Computational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), Istituto CNR di Scienze e Tecnologie Molecolari (ISTM-CNR), Via Elce di Sotto 8, 06123 Perugia, Italy, and CompuNet, Istituto Italiano di Tecnologia, Via Morego 30, 16163 Genova, Italy. |
| This journal is © The Royal Society of Chemistry 2019 |