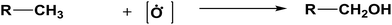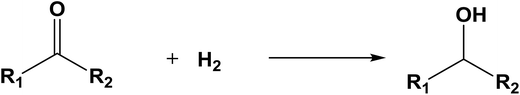Open Access Article
Open Access ArticleAccurate quantum chemical energies for 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 000 organic molecules†
000 organic molecules†
Badri
Narayanan
 ab,
Paul C.
Redfern
b,
Rajeev S.
Assary
b and
Larry A.
Curtiss
*b
ab,
Paul C.
Redfern
b,
Rajeev S.
Assary
b and
Larry A.
Curtiss
*b
aDepartment of Mechanical Engineering, University of Louisville, Louisville, Kentucky 40292, USA
bMaterials Science Division, Argonne National Laboratory, Argonne, Illinois 60439, USA. E-mail: curtiss@anl.gov
First published on 27th June 2019
Abstract
The energies of the 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules in the GDB-9 database have been calculated at the G4MP2 level of theory and then were used to calculate their enthalpies of formation. This database contains organic molecules having nine or less atoms of carbon, nitrogen, oxygen, and fluorine, as well as hydrogen atoms. The accuracy of the G4MP2 energies was investigated on a subset of 459 of the molecules having experimental enthalpies of formation with small uncertainties. On this subset the G4MP2 enthalpies of formation have an accuracy of 0.79 kcal mol−1, which is similar to its accuracy previously reported for the smaller G3/05 test set. An error analysis of the theoretical enthalpies of formation of the 459 molecules is presented in terms of the size and type of the molecules. Three different density functionals (B3LYP, ωB97X-D, M06-2X) were also assessed on 459 molecules of accurate enthalpy data for comparison with the G4MP2 results. The G4MP2 energies for the 133 K molecules provide a database that can be used to calculate accurate reaction energies as well as to assess new or existing experimental enthalpies of formation. Several examples are given of types of reactions that can be predicted using the G4MP2 database of energies. The G4MP2 energies of the GDB-9 molecules will also be useful in future investigations of applications of machine learning to quantum chemical data.
000 molecules in the GDB-9 database have been calculated at the G4MP2 level of theory and then were used to calculate their enthalpies of formation. This database contains organic molecules having nine or less atoms of carbon, nitrogen, oxygen, and fluorine, as well as hydrogen atoms. The accuracy of the G4MP2 energies was investigated on a subset of 459 of the molecules having experimental enthalpies of formation with small uncertainties. On this subset the G4MP2 enthalpies of formation have an accuracy of 0.79 kcal mol−1, which is similar to its accuracy previously reported for the smaller G3/05 test set. An error analysis of the theoretical enthalpies of formation of the 459 molecules is presented in terms of the size and type of the molecules. Three different density functionals (B3LYP, ωB97X-D, M06-2X) were also assessed on 459 molecules of accurate enthalpy data for comparison with the G4MP2 results. The G4MP2 energies for the 133 K molecules provide a database that can be used to calculate accurate reaction energies as well as to assess new or existing experimental enthalpies of formation. Several examples are given of types of reactions that can be predicted using the G4MP2 database of energies. The G4MP2 energies of the GDB-9 molecules will also be useful in future investigations of applications of machine learning to quantum chemical data.
I. Introduction
Knowledge of thermochemical data of molecules is very important in many areas of science. Thermochemical data provide the information needed to determine stabilities and reactivities of molecules present in combustion, battery electrolytes, drugs, the atmosphere, catalysis, etc. It is especially important that the thermochemical data for molecules be of chemical accuracy (<1 kcal mol−1) for such applications. Composite quantum chemical methods have been developed that can give molecular energies accurate to better than 1 kcal mol−1. This includes methods such as the Gn theory,1–4 the Complete Basis Set (CBS) methods,5–7 the correlation consistent Composite Approaches (ccCA),8–10 the multicoefficient correlation methods (MCCMs),11–13 Weizmann (Wn) methods,14–17 and the Wuhan-Minnesota scaling WMS method.18 In addition, accuracies of as small as 0.1 kcal mol−1 can be obtained for small molecules using much more expensive and elaborate methods.19–21 While density functional methods are faster, even the latest methods have not yet reached an accuracy of better than 1 kcal mol−1.22,23 With the power of today's computers and using quantum chemical methods capable of 1 kcal mol−1 accuracy it is now possible to predict energies of tens of thousands of molecules that can provide a database for calculating millions of reaction energies. Such a database of energies can also provide information to assess the accuracy of experimental data on enthalpies of formation of molecules in the literature, many of which have significant uncertainties.In this paper we report on the calculation of the energies of 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 molecules in the GDB-9 database24 using the G4MP2 method1 with the goal of providing accurate data for these molecules to use in calculating reaction energies and assessing existing enthalpies of formation. In addition, the accurate energies of these molecules can provide the data needed for development of low cost machine learning methods for predicting much larger sets of molecular energies. The GDB-9 data base contains all molecules of up to nine heavy atoms of the first row (C, N, O, F) and hydrogens. The G4MP2 method has an accuracy of better than 1 kcal mol−1 (ref. 1) based on the G3/05 test set, which has a limited number of large molecules.25 We used a small subset of the GDB-9 molecules that have very accurate experimental enthalpies of formation to ensure that the G4MP2 method maintains its accuracy on the larger molecules in the GDB-9 dataset. This subset also provides an opportunity to assess the accuracy of some popular density functional methods for thermochemical data of larger molecules, which has not previously been done extensively for larger molecules. The G4MP2 energies are used to calculate reaction energies for five different types of reactions to illustrate how the database of energies can be used to calculate a range of accurate reaction energies. In Section II we describe the database and molecular notation used as well as the quantum chemical methods. In Section III analysis of the errors in enthalpies of formation of a subset of the molecules with accurate experimental data is presented for G4MP2 theory as well as for three widely used density functional methods. In Section IV the calculation of a selection of reaction energies from the database is presented. Finally, conclusions are drawn in Section V.
296 molecules in the GDB-9 database24 using the G4MP2 method1 with the goal of providing accurate data for these molecules to use in calculating reaction energies and assessing existing enthalpies of formation. In addition, the accurate energies of these molecules can provide the data needed for development of low cost machine learning methods for predicting much larger sets of molecular energies. The GDB-9 data base contains all molecules of up to nine heavy atoms of the first row (C, N, O, F) and hydrogens. The G4MP2 method has an accuracy of better than 1 kcal mol−1 (ref. 1) based on the G3/05 test set, which has a limited number of large molecules.25 We used a small subset of the GDB-9 molecules that have very accurate experimental enthalpies of formation to ensure that the G4MP2 method maintains its accuracy on the larger molecules in the GDB-9 dataset. This subset also provides an opportunity to assess the accuracy of some popular density functional methods for thermochemical data of larger molecules, which has not previously been done extensively for larger molecules. The G4MP2 energies are used to calculate reaction energies for five different types of reactions to illustrate how the database of energies can be used to calculate a range of accurate reaction energies. In Section II we describe the database and molecular notation used as well as the quantum chemical methods. In Section III analysis of the errors in enthalpies of formation of a subset of the molecules with accurate experimental data is presented for G4MP2 theory as well as for three widely used density functional methods. In Section IV the calculation of a selection of reaction energies from the database is presented. Finally, conclusions are drawn in Section V.
II. Methods
The computations of the enthalpies of formation of the molecules in the GDB-9 database were carried out with the G4MP2 method.1 G4MP2 is a composite method based on G4 theory,2 but with reduced perturbation theory levels to lower the computational cost. More specifically, in the G4MP2 method second-order perturbation theory is used in place of the time consuming fourth-order perturbation theory components in the G4 method. As a result the G4MP2 method is approximately six to eight times faster than the G4 method.1 Other parts of the method remain the same as in G4 theory including the CCSD(T) component, geometries, and zero-point energies. It was assessed on the G3/05 test set of accurate experimental data and found to have a mean absolute deviation of 1.04 kcal mol−1 for 454 enthalpies of formation, ionization potentials, electron affinities, and proton affinities. For the 138 hydrocarbons and substituted hydrocarbons in the G3/05 test set the mean absolute deviation was 0.77 kcal mol−1. In order to better assess the likely accuracy of G4MP2 for the GDB-9 database of 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 molecules we have selected 459 molecules from the Pedley compilation26 that have very accurate (<1 kcal mol−1) gas phase enthalpies of formation. More details on this test set and how it was selected is given in the next section. All calculations were carried out with the Gaussian code.27
296 molecules we have selected 459 molecules from the Pedley compilation26 that have very accurate (<1 kcal mol−1) gas phase enthalpies of formation. More details on this test set and how it was selected is given in the next section. All calculations were carried out with the Gaussian code.27
In addition, we have carried out density functional calculations on these 459 molecules with three density functional methods. The B3LYP28 density functional results on these molecules were included in this study because they are part of the G4MP2 calculation with B3LYP being used for the geometry optimizations. Since the development of the hybrid GGA B3LYP functional, numerous other functionals with better performance have been reported.22,23 We chose two other popular functionals to assess on the 459 molecules, namely, M06-2X,29 a hybrid meta-GGA functional, and ωB97X-D,30 a GGA functional with dispersion correction. The 6-31G(2df,p) basis set used for the B3LYP functional, while the 6-311+G(3df,2p) basis (at B3LYP/6-31G(2df,p) geometries) is used for the M06-2X and ωB97X-D functionals. A smaller basis set was used for B3LYP as it gives better results than the larger basis set. It has been noted previously that improvement in the basis sets does not always lead to improvement in results as is the case with wave function based methods.25 It has been suggested that this is due to cancelation of errors from an overestimation of the basis set superposition error that compensates for the lack of a dispersion correction.31
We performed G4MP2 calculations for 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 molecules belonging to the GDB-9 database24,32 containing varying amounts of C, H, O, N, and F atoms; as aforementioned, the maximum number of non-hydrogen (heavy) atoms in any molecule in this database is 9. The molecules with 9 non-hydrogen atoms dominate the database, comprising ∼83% of the molecules (i.e., 111
296 molecules belonging to the GDB-9 database24,32 containing varying amounts of C, H, O, N, and F atoms; as aforementioned, the maximum number of non-hydrogen (heavy) atoms in any molecule in this database is 9. The molecules with 9 non-hydrogen atoms dominate the database, comprising ∼83% of the molecules (i.e., 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128) in the GDB-9 database as shown in Table 1; in comparison, there are only 3 molecules with one heavy atom, namely CH4, NH3, and H2O. This is expected, owing to the large number of elemental combinations, and isomers possible for molecules made-up of 9 heavy atoms. In terms of molecule types, those made up exclusively of H, C, O and N atoms (listed as HCON) are most prominent (∼50%), followed by HCO (∼34%). For each molecule in the GDB-9 dataset, we adopted the DFT-relaxed (using the B3LYP functional) configurations from ref. 24 and 32 to perform calculations at the G4MP2 level of theory. We found that 581 molecules out of the 133
128) in the GDB-9 database as shown in Table 1; in comparison, there are only 3 molecules with one heavy atom, namely CH4, NH3, and H2O. This is expected, owing to the large number of elemental combinations, and isomers possible for molecules made-up of 9 heavy atoms. In terms of molecule types, those made up exclusively of H, C, O and N atoms (listed as HCON) are most prominent (∼50%), followed by HCO (∼34%). For each molecule in the GDB-9 dataset, we adopted the DFT-relaxed (using the B3LYP functional) configurations from ref. 24 and 32 to perform calculations at the G4MP2 level of theory. We found that 581 molecules out of the 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 molecules in the original GDB-9 database (refs) show imaginary modes of vibration; these molecules are discarded from this study. For the remaining 133
877 molecules in the original GDB-9 database (refs) show imaginary modes of vibration; these molecules are discarded from this study. For the remaining 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 molecules, we computed zero-point energies, energies (at 0 K), enthalpies, free energies, standard enthalpies of formation, and atomization energies. The G4MP2 values, and atomic coordinates of all the molecules are stored within an Atomic Simulation Environment (ASE) database33 compatible with JSON and SQLite3 backends. The molecules and their corresponding G4MP2 data are all cross-indexed by their chemical formula, SMILES, and InChI keys. This makes it straightforward to retrieve G4MP2 for a class of compounds, isomers, or specific molecule from this database using a Python script (an example Python script to retrieve data is provided in the ESI†). Furthermore, the use of such a database enables fast/efficient search for data (on-demand) necessary for various machine-learning studies.
296 molecules, we computed zero-point energies, energies (at 0 K), enthalpies, free energies, standard enthalpies of formation, and atomization energies. The G4MP2 values, and atomic coordinates of all the molecules are stored within an Atomic Simulation Environment (ASE) database33 compatible with JSON and SQLite3 backends. The molecules and their corresponding G4MP2 data are all cross-indexed by their chemical formula, SMILES, and InChI keys. This makes it straightforward to retrieve G4MP2 for a class of compounds, isomers, or specific molecule from this database using a Python script (an example Python script to retrieve data is provided in the ESI†). Furthermore, the use of such a database enables fast/efficient search for data (on-demand) necessary for various machine-learning studies.
| Number of heavy atoms | Number of molecules | Constituent elements of molecule | Number of molecules |
|---|---|---|---|
| 1 | 3 (CH4, H2O, NH3) | HCON | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 573 573 |
| 2 | 5 | HCO | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
| 3 | 9 | HCN | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 092 |
| 4 | 31 | HC | 4849 |
| 5 | 129 | HCOFN | 1061 |
| 6 | 615 | HCFN | 734 |
| 7 | 3171 | HCOF | 244 |
| 8 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 205 205 |
HCF | 90 |
| 9 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
III. Assessment of expected accuracy of G4MP2 for the GDB-9 database
In order to assess the accuracy of the G4MP2 method for the GDB-9 database we selected all molecules from the database that had an experimental value in the Pedley compilation26 with an uncertainty of less than 1 kcal mol−1. This resulted in a total of 510 molecules. Comparing the G4MP2 and experimental values we found a number of values in disagreement by substantially more than 1 kcal mol−1. In order to ensure that we had a reasonably accurate experimental test set we examined more closely all experimental values that differed by more than 2.50 kcal mol−1 with G4MP2, of which there were 63. We then checked to see if there were any other recent experimental values that conflicted with the Pedley values. In 12 cases (see ESI†) there were other values that differed by more than 1 kcal mol−1, the quoted uncertainty of the Pedley value. In those cases we eliminated them from the test set as we could not verify their accuracy. That left 51 cases of differences greater than 2.5 kcal mol−1. In those cases we used an isodesmic scheme34 to evaluate the questionable experimental values. The isodesmic scheme is one previously developed using G2MP2 energies34 and very accurate experimental values for small molecules. This isodesmic scheme was found to give enthalpies of formation accurate to 0.5 kcal mol−1.34 We eliminated 39 molecules from the test set based on the criterion that the suspect experimental value differed by more than 2 kcal mol−1 from the G2MP2 isodesmic enthalpy of formation. These experimental enthalpies of formation will be the subject of further high level quantum chemical calculations. The remaining 12 with differences greater than 2.50 kcal mol−1 were kept in the test set as there was no basis to discard them. The resulting test set, referred to as the Pedley test set, has 459 molecules including 175 hydrocarbons and 284 substituted hydrocarbons. We note that we have selected this test set for assessing the accuracy of G4MP2 on the organic molecules as opposed to others that are available35,36 because it is based on experimental numbers from a compilation, all of which have a quoted uncertainty. About 92 of the 459 molecules are included in the G3/05 test set, which also included molecules containing S and Cl as well as some larger systems.The Pedley test set of 459 enthalpies of formation is given in Table S2 of the ESI.† Also given in the table are the G4MP2 calculated enthalpies of formation and the experimental enthalpies of formation along with the differences between the two. Table 2 gives a summary of the results in terms of mean absolute deviations (MAD) between experimental values and the G4MP2 values. The MAD between experiment and G4MP2 for the Pedley test set is 0.79 kcal mol−1, which is comparable to MAD of 0.77 kcal mol−1 of the smaller G3/05 test set of similar type molecules. The breakdown in terms of types of molecules (hydrocarbon and substituted hydrocarbons) is also similar. Fig. 1 shows the MAD as a function of the number of heavy atoms (CNOF) in the molecule. This plot shows a gradually increasing error with size of the molecule for G4MP2. This is expected and has been found previously for long chain alkanes.37 The increase in error with size is due to the increase in the number of electron pairs. In Fig. 2 we have plotted the error per electron pair as a function of number of heavy atoms. This shows that the size of the error is quite level with increasing molecule size. In terms of calculating reaction energies from G4MP2 enthalpies of formation (see Section IV), the resulting reaction energies should be quite accurate because they are based on breaking one or a couple of bonds, whereas the enthalpies of formation are based on breaking all bonds in the molecule, i.e. they are calculated from atomization energies (along with temperature corrections, elemental standard states, and zero-point energies).38
| Molecule typea | G4MP2b | B3LYPc | M06-2Xc | ωB97X-Dc |
|---|---|---|---|---|
| a Number of molecules given in parentheses. b G4MP2 MAD for the G3/05 test set25 given in parentheses. The G3/05 test set has 38 hydrocarbons, 100 substituted hydrocarbons, and 138 molecules in total, 92 of which are in common with the Pedley test set. c The B3LYP energies were calculated with the 6-31G(2df,p) basis at the B3LYP/6-31G(2df,p) geometry; the M06-2X and ωB97X-D energies were calculated with the 6-311+G(3df,2p) basis at the B3LYP/6-31G(2df,p) geometry. The zero-point energies used for the density functional results are unscaled ones from B3LYP/6-31G(2df,p). | ||||
| Hydrocarbons (175) | 0.68 (0.63) | 2.77 | 3.06 | 1.35 |
| Substituted hydrocarbons (284) | 0.86 (0.83) | 4.74 | 2.51 | 2.16 |
| Total (459) | 0.79 (0.77) | 3.99 | 2.71 | 1.85 |
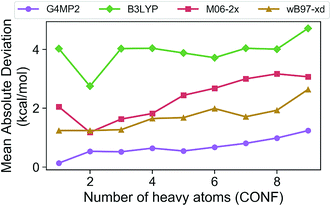 | ||
| Fig. 1 Mean absolute deviations (MAD) of G4MP2 and three DFT methods for the Pedley test set of 459 molecules as a function of number of heavy atoms. | ||
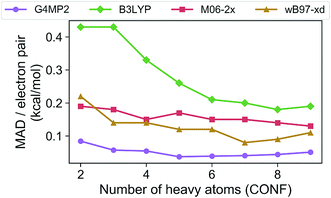 | ||
| Fig. 2 Mean absolute deviations (MAD) per electron pair of the G4MP2 and three DFT methods for the Pedley test set of 459 molecules as a function of number of heavy atoms. | ||
The Pedley test provides an opportunity to assess the accuracy of some popular density functional methods for thermochemical data of larger molecules. Previous test sets of thermochemical data used for assessing density functional have not included as extensive a set of larger molecules as the Pedley set established for this work. An error analysis on the Pedley test set was carried out for three popular DFT methods B3LYP,28 M06-2X,29 and ωB97X-D.30 The results for these three functionals are given in Table 2 with details for all 459 molecules given in ESI Tables 3–5.† The ωB97X-D functional performs the best with a mean absolute deviation of 1.85 kcal mol−1 for the 459 molecules. M06-2X has an mean absolute deviation of 2.71 kcal mol−1. B3LYP has the largest mean absolute deviation of the three at 3.99 kcal mol−1. Thus, even the best functional tested has a mean absolute deviation of more than twice as large as G4MP2. Fig. 1 shows the MAD for the three functionals as a function of the number of heavy atoms (CNOF) in the molecule. The plots show a generally increasing error with size of the molecule for the three functionals. In Fig. 2 the error per electron pair is plotted as a function of number of heavy atoms, which shows that the error remains approximately constant as the molecule size increases with the exception of B3LYP that shows a decreasing trend. The trends for M06-2X and ωB97X-D are similar to G4MP2.
IV. Analysis of the energies of the 133 K molecules in the GD9 database
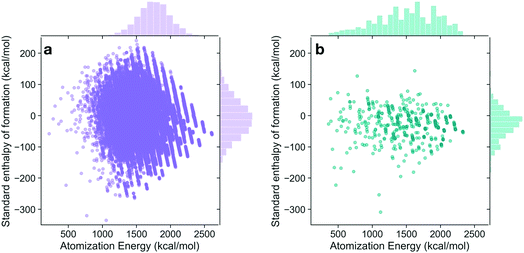
The energies of the 133 K molecules were calculated at the G4MP2 level of theory and are available from the ESI† on the Web.33Fig. 3 shows a plot of the atomization energies vs. the enthalpies of formation that illustrate the distribution of both types of energies. It is noted that for the 133 K molecules, the enthalpies of formation have a much larger range of positive values than those of the Pedley test set of 459 molecules while the atomization energies have a similar range of values. The reason for the difference in distributions for the more positive enthalpies of formation is probably because the GDB-9 set includes some hypothetical molecules that can be more unstable (i.e., positive enthalpies of formation). This type of molecule would be hard to synthesize, and thus are not present in the Pedley test set. Otherwise the Pedley test seems to be a good representation of the GDB-9 set.The trends in the G4MP2 enthalpies of formation with the types of atoms in the molecules are shown in Fig. 4 and 5. In Fig. 4 the enthalpies of formation of the 130 K organic molecules are classified into various groups of atom types. This figure indicates that addition of oxygen and fluorine to the molecules generally increases their stability, i.e. they have more negative enthalpies of formation, whereas addition of nitrogen has the opposite effect. In Fig. 5 the enthalpies of formation of CHO type molecules as a function of number of oxygen atoms is shown. It is apparent from this figure that increasing the number of oxygens in the molecules generally increases their stability.
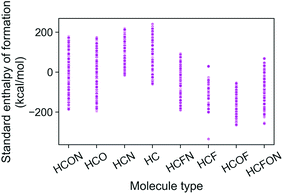 | ||
| Fig. 4 Standard enthalpy of formation from G4MP2 calculations of the 133 K organic molecules classified into various groups of atom types. | ||
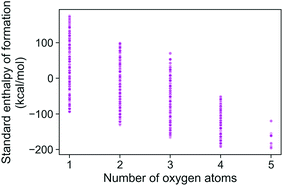 | ||
| Fig. 5 Standard enthalpy of formation of CHO type molecules as a function of different number of oxygen atoms, as obtained from G4MP2 calculations. | ||
Since the G4MP2 energy calculation also includes the B3LYP/6-31G(2df,p) method for geometry optimization, we also obtained these energies for the 133 K molecules in the GDB-9 database and they are included in the ESI† on the Web.33 The mean absolute deviation between these B3LYP energies and the G4MP2 energies is 4.54 kcal mol−1. The breakdown of the mean absolute deviations for B3LYP with G4MP2 as a function of size of the molecule and type of molecule is given in ESI Fig. 1.† The error increases slightly with size of molecule. In addition, the B3LYP results in this figure indicate that the molecules containing fluorine have much larger deviations with G4MP2 than those not containing fluorine.
The database of G4MP2 enthalpies of formation provides a source of data for the derivation of accurate energies of millions of reactions involving organic molecules up to nine heavy atoms. To illustrate this we have calculated some energies for five different types of reactions from the G4MP2 energies and tabulate them in Table 3. These include (1) alcohol oxidation, (2) alkane oxidation, (3) ether hydrolysis, (4) hydrogenolysis, and (5) carbonyl reduction. Energies for all of these types of reactions are expected to be accurate to about 1 kcal mol−1 based on the accuracy of the G4MP2 energies. In addition to the reaction energies that can be derived, the large database of enthalpies of formation also provides a basis on which to assess existing or newly measured enthalpies of formation. The method by which the enthalpies of formation can be obtained from the database of G4MP2 energies33 is described in the ESI.†
V. Conclusions
Energies for the ∼133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules in the GDB-9 database, containing organic molecules having nine or less atoms of carbon, nitrogen, oxygen, and fluorine as well as hydrogen atoms, have been calculated at the G4MP2 level of theory. The following conclusions can be drawn from this study:
000 molecules in the GDB-9 database, containing organic molecules having nine or less atoms of carbon, nitrogen, oxygen, and fluorine as well as hydrogen atoms, have been calculated at the G4MP2 level of theory. The following conclusions can be drawn from this study:
(1) The accuracy of the G4MP2 energies was investigated on a subset of 459 of the molecules having experimental enthalpies of formation with small uncertainties and was found to have an accuracy of 0.79 kcal mol−1, which indicates the G4MP2 enthalpies of formation of the GDB-9 database should have a similar accuracy.
(2) Three different density functionals (B3LYP, ωB97X-D, M06-2X) were also assessed on 459 molecules of accurate enthalpy data for comparison with the G4MP2 results and the latter two were found to be much more accurate that B3LYP, but less accurate than G4MP2.
(3) The G4MP2 energies for the 133 K molecules provide a database that can be used to calculate accurate reaction energies as well as to assess new or existing experimental enthalpies of formation.
The G4MP2 energies of the GDB-9 molecules will also be useful in future investigations of applications of machine learning to quantum chemical data by providing a large database of accurate energies for machine learning to develop new low cost methods for accurately predicting enthalpies of formation of the millions of molecules having more than nine heavy atoms, as well as reaction energies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. We acknowledge a generous grant of computer time from the ANL Laboratory Computing Resource Center (Bebop).References
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105 CrossRef PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 810–825 CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- J. W. Ochterski, G. A. Petersson and J. A. Montgomery, J. Chem. Phys., 1996, 104, 2598–2619 CrossRef CAS.
- J. W. Ochterski, G. A. Petersson and K. B. Wiberg, J. Am. Chem. Soc., 1995, 117, 11299–11308 CrossRef CAS.
- N. J. DeYonker, T. R. Cundari and A. K. Wilson, J. Chem. Phys., 2006, 124, 114104 CrossRef PubMed.
- N. J. DeYonker, B. R. Wilson, A. W. Pierpont, T. R. Cundari and A. K. Wilson, Mol. Phys., 2009, 107, 1107–1121 CrossRef CAS.
- A. Mahler and A. K. Wilson, J. Chem. Theory Comput., 2013, 9, 1402–1407 CrossRef CAS PubMed.
- P. L. Fast and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 6111–6116 CrossRef CAS.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 3898–3906 CrossRef CAS.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 43–52 RSC.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kallay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS PubMed.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2013, 9, 4769–4778 CrossRef CAS PubMed.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856 CrossRef CAS.
- Y. Zhao, L. X. Xia, X. B. Liao, Q. He, M. X. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2018, 20, 27375–27384 RSC.
- A. Tajti, P. G. Szalay, A. G. Csaszar, M. Kallay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vazquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- A. Karton, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 292–310 CAS.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2005, 123, 124107 CrossRef PubMed.
- J. B. Pedley, Thermochemical Data and Structures of Organic Compounds, CRC Press, 1994 Search PubMed.
- M. J. Frisch, et al., Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834 CrossRef CAS PubMed.
- https://datarepository.wolframcloud.com/resources/GDB9-Database .
- https://doi.org/10.18126/M23P9G .
- K. Raghavachari, B. B. Stefanov and L. A. Curtiss, J. Chem. Phys., 1997, 106, 6764–6767 CrossRef CAS.
- A. Karton, S. Daon and J. M. L. Martin, Chem. Phys. Lett., 2011, 510, 165–178 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- P. C. Redfern, P. Zapol, L. A. Curtiss and K. Raghavachari, J. Phys. Chem. A, 2000, 104, 5850–5854 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221–7230 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc02834j |
| This journal is © The Royal Society of Chemistry 2019 |