Open Access Article
Open Access ArticleCrisscrossing coordination networks: ligand doping to control the chemomechanical properties of stimuli-responsive metallogels†
Junghwan
Kim
and
Dongwhan
Lee
 *
*
Department of Chemistry, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea. E-mail: dongwhan@snu.ac.kr
First published on 25th February 2019
Abstract
Metallogels respond to external stimuli by changing their mechanical properties. To gain a fine control over this phase-shifting event, we have designed and introduced intentional structural mismatches into the otherwise tightly knit metal–organic networks. Built using biphenolate-derived multidirectional/multidentate ligands, these soft materials display markedly different rheological properties depending on the level of “ligand doping”, as well as the type of metal ion serving as a key structural support. A zinc metallogel optimized through this process responds to acids, both in the gas stream and liquid phase, by a rapid gel–sol transition and visually discernible colour change.
Introduction
Metal–organic networks are spontaneous assemblies of metal ions and multi-nucleating ligands to form higher-order architectures. Representative examples include metal–organic frameworks (MOFs)1–6 and metallogels.7–22 Here, the reversible nature of metal–ligand bonding is exploited to achieve long-range structural ordering beyond the immediate coordination sphere through self-correcting and self-reinforcing processes.Unlike crystalline MOFs, metallogels are soft amorphous materials. Through entanglement and cross-linking of extended metal–ligand networks, however, they acquire sufficient mechanical strength to entrap and bear the weight of solvent molecules inside. While metallogels could undergo sol–gel transitions just like simple organic gelators,23–27 the presence of metal centres provides an added advantage of utilizing coordination chemistry to control the mechanical properties of the bulk material. For example, if the making and breaking of metal–ligand bonds are driven by chemical stimuli, such as ligand exchange, local chemical events can be amplified to sol–gel phase transitions, and readily checked by a straightforward “tube inversion test”.8–12,14–17,23–25,27–30
Despite the conceptual appeal and operational simplicity, however, one critical drawback of metallogel-based chemical detection is its slow response kinetics. Specifically, the pristine gel should be sufficiently robust to withstand thermal and mechanical stress and retain its shape, but needs to disassemble rapidly and turn into a solution upon a chemical triggering event. While proof-of-concept systems are currently available for metallogel-based chemical sensing,17,31–36 a rational design principle is needed to strike a fine balance between mechanical stability and chemical sensitivity. In this paper, we disclose our structure design and synthetic strategies to meet this important challenge (Fig. 1).
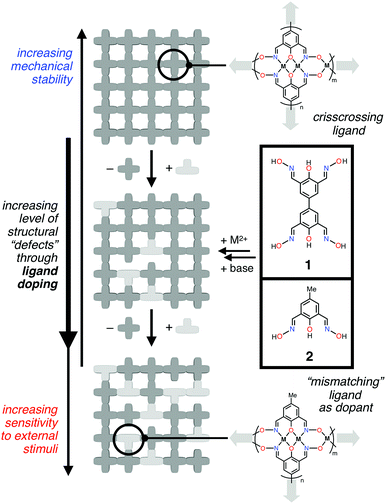 | ||
| Fig. 1 Schematic representations of idealized metal–ligand networks constructed from ligand 1 and its “half-unit” derivative 2 serving as a chain terminator to create structural defects. | ||
As outlined in Fig. 1, we have developed a new multinucleating chelate 1 as a fused form of the simpler half-unit ligand 2. Through binding of transition metal ions, 1 could furnish tightly knit grid-like 2D/3D networks that evolve into a gel-like structure. An intentional doping with the half-unit ligand 2, however, introduces structural “defects”, which systematically decrease the viscoelasticity of the metallogel. For an optimized system, the gel-to-fluid transition is (i) induced by ligand exchange with exogenously added acid, either in solution or in the gas phase, (ii) made faster by changing either the metal centre or increasing the level of ligand doping, and (iii) monitored simultaneously by indicator molecules trapped inside the gel matrix. To the best of our knowledge, this is the first example of metallogels, in which structural doping of the ligand system controls the mechanical properties and sensory response kinetics of the bulk material.37–39 Important lessons that we have learned from this rule-finding study are discussed in the following sections.
Background and design principles
Mechanical properties of soft materials are determined by how stress dissipates through a series of chemical bonds.40,41 To fine-tune such properties, interconnected networks have advantages over linear structures. While a strand of polymer readily loses mechanical tension by simple bond cleavage, a strand in a network structure could still maintain the tension through cross-linking with nearby strands. According to this phantom network theory, the mechanical properties of network structures can be altered by structural defects introduced intentionally, just like doping in electronic materials.42–47 For example, functional groups of the monomers can be modified strategically to evaluate the effects of primary defects48–50 or topological defects such as loops48,51 on the elastic properties of polymer gels and elastomers.Taking inspiration from polymer chemistry, we wished to develop metallogels having mechanical properties that are tunable by ligand design and defect doping. For this purpose, a pair of multinucleating/multidirectional ligands were needed: one participating in chain propagation, and the other functioning as a chain terminator. For this purpose, ligands 1 and 2 (Fig. 1), built upon a salicylaldoxime motif, emerged as ideal candidates.
As exemplified by the dinuclear clathrochelate complex I,52 and end-capped tetranuclear complexes II and III,53,54 shown in Fig. 2, the central [N,O,N]-donor array of 2 can support phenoxide-bridged bimetallic centres. A structurally characterized trinuclear complex IV55 demonstrates that the deprotonated oximate-O atom of the simple salicylaldoxime ligand 3 (Fig. 2) could serve also as a bridge to connect two tris(chelate) mononuclear complexes by coordinating to the third metal in the middle.
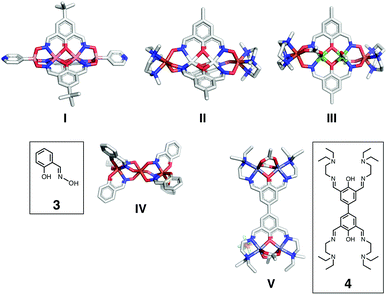 | ||
| Fig. 2 Capped-stick representations of crystallographically determined polynuclear metal complexes I (CSD code: YIYQEE),52II (CSD code: RELZAK),52III (CSD code: ZIGQIP),53IV (CSD code: VIFWIS),55 and V (CSD code: VIJQUA),56 along with the chemical structures of the ligands 3 and 4. | ||
To build cross-linked grids of these basic structural motifs, it is necessary to “fuse” two units of 2 into a single ligand platform 1 for bidirectional network growth through metallation (Fig. 1 and 3). A structurally related ligand 4 is known to support a tetranuclear complex (V, Fig. 2),56 but the chemistry of the 4,4′-biphenolate-derived ligand has remained surprisingly undeveloped since the initial report.
Using the structurally characterized metal complexes (Fig. 2) as starting points, we first constructed simple models of metal–ligand networks anticipated from 1, either with (i) M2L or (ii) M3L metal–ligand stoichiometry (Fig. 3). It should be noted that these highly idealized structures could serve only as 3D skeletal models to assess the spatial arrangements and the degree of steric constraints when multiple ligand fragments are brought into close proximity by either all six-coordinate (Fig. 3a) or four-coordinate (Fig. 3b) metal centres. In reality, the actual amorphous structure, trapped kinetically in the metallogel formation process (vide infra), would lie somewhere in between these two extremes of crystalline structural ordering.57,58 Despite such caveats, both structures modeled in Fig. 3 seemed reasonable, with no apparent interligand steric crowding or unusual coordination geometry. We thus proceeded to carry out actual synthesis to check the feasibility of the ideas proposed in Fig. 1.
Results and discussion
Ligand synthesis and metallation
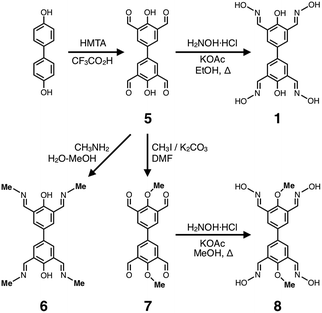
The biphenol tetraoxime ligand 1 was prepared in two steps from 4,4′-biphenol (Scheme 1) via the known tetraformyl precursor 5.56 Condensation of 5 with hydroxylamine furnished 1. Using the intermediate 5, structural analogues of 1 were also prepared, which share a common biphenyl skeleton, but do not have either the terminal oxime-O donor (6) or bridging phenolate-O donor (8) groups, as shown in Scheme 1.Metallogels of 1 were prepared in a straightforward manner by simply mixing DMF solutions of the deprotonated ligand and metal salt (Fig. 4). In a typical experiment, a Zn metallogel was prepared by adding a DMF solution of zinc(II) acetate into a rapidly stirred solution of 1 and Et3N. An immediate sol-to-gel transition was observed and confirmed by a simple tube inversion test (Fig. 4a). To improve the structural homogeneity, the mixture could be sonicated for 10 min and heated at 90 °C for several hours without structural collapse or deterioration of the gel-like properties.
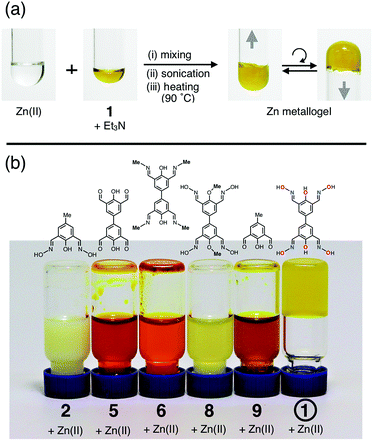 | ||
| Fig. 4 (a) Formation of a zinc metallogel of 1 (4 wt%), and (b) comparative studies with five different analogues and derivatives of 1 to identify structural parameters required for gelation. | ||
Comparative studies with five structural derivatives of 1 (Fig. 4b) established that the formation of metallogels requires the presence of both (i) oximate-[N,O] and (ii) phenoxide-O donors, in conjunction with (iii) biaryl-linked extended ligand scaffolds. No gelation occurred for the truncated half-unit ligand 2, oximate-free ligands 5 and 6, phenol-protected 8, or half-unit ligand 9 without oximate, when treated with zinc(II) under identical conditions. A free-standing gel is obtained only for 1, which satisfies the structural requirements for multi-directional network growth, as modeled in Fig. 1 and 3.
Morphology and spectroscopic analysis
To investigate the morphology and internal structure of the metallogel, samples were dried with supercritical CO2 (SCO2) to remove unreacted starting materials and entrapped solvent molecules. Using a standard setup to dry MOF samples (Fig. S1†), the zinc metallogel (ca. 10 mL) was subjected to a constant flow (0.3 mL min−1) of SCO2 (200 mL; 200 bar; T = 45 °C) to obtain yellow powdery aerogels (Fig. 5a). | ||
| Fig. 5 (a) Photographic, (b) SEM, and (c) cross-sectional TEM images of Zn aerogel of 1 prepared by SCO2 drying (see text for experimental details). | ||
As shown in Fig. 5b, the SEM image of the Zn-aerogel reveals porous internal structures, in which fibrils of cross-linked metal–ligand assemblies interconnect to create mesoscopic morphologies, leaving void spaces in between. A cross-sectional TEM image (Fig. 5c) of a thinly (ca. 80 nm) sliced sample, prepared by ultramicrotomy of aerogel particles, established that the porous structure spans across the bulk material, not being confined to the surface region. In addition, EDX analysis (Fig. S2†) confirmed an even spatial distribution of elemental C, N, O, and Zn across the entire sample. Similar observations were made for the aerogel samples of either cobalt(II) (Fig. S3†) or copper(II) (Fig. S4†) in conjunction with 1.
A strong binding of Zn(II) should be aided by deprotonation of the phenol and oxime groups of the free ligand. The IR spectrum of the free ligand 1 (Fig. S5†) has intense bands at 2700–3500 cm−1 from the O–H stretching modes of phenol and oxime groups. In stark contrast, these features essentially disappear in the IR spectrum of the zinc aerogel (Fig. S5†), indicating that (i) the majority of the O-donor groups, either phenol or oxime, become deprotonated to bind the metal, and (ii) unreacted free ligands are not incorporated into the metallogel network and thus readily removed by SCO2 drying.
Gel-to-sol phase transition responding to gas-phase chemicals
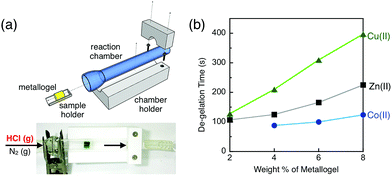
With experimental evidence obtained for the involvement of metal–ligand bonds in the gel-like properties of the bulk material (Fig. 4, 5, and S2†), we proceeded to exploit the visually discernible sol–gel transition for gas-phase chemical detection. A logical choice of target is a volatile acid, such as HCl, which can protonate the ligand to facilitate demetallation and provide chloride anions to assist such ligand substitution processes.For precise measurements of the response kinetics, a controlled gas delivery system was built to ensure a constant pressure and flow rate (Fig. 6 and S6†). In each measurement, a custom-made Teflon sample holder was loaded with a fixed amount of metallogel of known wt%, and placed inside a transparent glass vessel. The entire unit was assembled, and connected to the gas delivery system (Fig. 6a). The reaction was initiated by delivery of gaseous HCl (5%, v/v, diluted in N2) to the reaction chamber at a constant flow rate of 0.5 L min−1; the progress of the reaction was monitored by taking digital images at fixed time intervals (Fig. S7†). A small hole was made at the bottom of the Teflon sample holder to facilitate the drainage of the solutionized sample, which marked the completion of the reaction as well.
As plotted in Fig. 6b, the gel-to-sol transition takes a longer time as the wt% of the gelating material increases. This general and anticipated trend was observed consistently with the metallogels prepared with cobalt(II), copper(II), and zinc(II). At a fixed wt%, however, the response rates are remarkably different depending on the metal of choice, despite the fact that they all share the same ligand 1. Intriguingly, the experimentally observed order of robustness, copper(II) > zinc(II) > cobalt(II), correlates nicely with the Irving–Williams series of the relative stabilities of first-row transition metal complexes.59
While care should be taken in interpreting the behaviour of the amorphous gel materials using simple M–L bonding models alone, our experimental results convincingly demonstrate the practical utility of metallogels for gas-phase chemical detection, and the tunability of the response kinetics by varying the metal ion.
Reversible sol–gel transition and colour switching
If the gel-to-sol transition can be triggered by an acid (Fig. 6), it should be feasible to reverse this process by “back-titration” with a base. The majority (>95 wt%) of the gel volume is taken up by the solvent, which could serve as a fluidic reservoir for non-escaping reporter molecules that can simultaneously track this process. In Fig. 7 is demonstrated how this dual mode of response, as a combination of phase transition and colourimetric change, is implemented with the Zn metallogel.With no d–d or CT-type optical transitions to interfere with the encapsulated pH indicators, zinc(II) is an ideal metal of choice to build the gelating network for such purposes. An added bonus is the kinetic lability, as well as the stereochemical promiscuity of the d10 metal, which ensures rapid ligand exchange that is crucial for reversible phase switching under ambient conditions. In contrast, a cobalt(II)- or copper(II)-based system shows intense transitions in the visible region, which interfere with the colourimetric sensory response.
As a proof-of-concept, Zn metallogels (4 wt%) were prepared by simply adding representative pH indicators, such as bromophenol blue, bromocresol green, methyl orange, and thymol blue, to the reaction batch. As shown in Fig. 7a, the presence of these reporter molecules did not affect the formation of metallogels, which, upon treatment with CF3CO2H, underwent an immediate gel-to-sol transition with a concomitant colour change (Fig. 7b). The reversible nature of this process is established by restoration of the initial gel state as well as the indicator colour, following treatment with Et3N (Fig. 7c). By increasing the initial concentration of the sample to 12%, this reversible sol–gel switching could be repeated at least six times, although its cyclability is practically limited by the dilution effect.
Ligand doping to control the mechanical properties of the bulk material
The gel–sol transition rate is a critical parameter to improve the performance of metallogels as a chemical sensor. In the metallogel, the cross-linked fibrous backbone (<5 wt%) supports the weight of the entire matrix (>95 wt%) against gravity. By controlling the mechanical properties of the metal–ligand network, degelation kinetics could be adjusted to the desired sensitivity.While we have demonstrated that the choice of metal ions can have a profound impact on the mechanical stability of the metallogels (Fig. 6b), the ligand is another important structural component that can be engineered to fine-tune the viscoelastic properties of the bulk material. For crystalline MOFs, one type of ligand can partially be replaced with another type of ligand. Typical strategies include solid–solution mixing or post-synthetic modification to enhance sorption, catalytic, electrical, or magnetic properties of the doped crystalline materials.60–68 In the polymer network synthesis, monomers having different numbers of functional groups can be mixed in different ratios to create defects, thereby controlling the mechanical properties of the bulk material.51,69–72 Considering the close relevance of metallogels to MOFs (in terms of structural components) and organic polymer gels (in terms of physico-mechanical properties), it is surprising that ligand doping has rarely been exploited to control the viscoelastic properties of the bulk material.37–39
Apparently, this is a challenging task. Even our own results (Fig. 4) show that a seemingly minor structural modification of the gelating motif 1, either in the ligand backbone (i.e.2) or metal-binding groups (i.e.5, 6, 8, and 9), fails to produce metallogels; the reaction either remains fluidic or simply turns into precipitates. Instead of a trial-and-error approach, we decided to adopt a systematic strategy of introducing the half-unit ligand 2 as a chain-terminating agent to suppress network growth. A total of 11 samples were thus prepared (Fig. 8), in which the ratio between the ligands 1 and 2 was varied systematically while maintaining the overall “amount” of the ligand donor groups constant across the entire set.
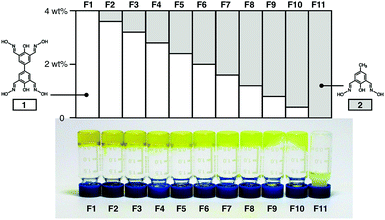 | ||
| Fig. 8 Formulation of zinc metallogels F1–F11 prepared with ligands 1 and 2 in varying wt% (top), and photographic images of the 11 samples upon a tube inversion test (bottom). | ||
As shown in Fig. 8, an increasing level of ligand doping of 2 (in gray bar) into 1 (in white bar) results in a gradual attenuation of gelating properties, as visually inspected by a simple inversion test. While F1–F6 maintain a gel-like behaviour, the mixture either has untrapped solvent escaping the gel matrix, or flows down the vertical wall beyond F7 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 = 4
2 = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, wt/wt). For a more precise, quantitative measure of the viscoelastic properties as a function of the ligand doping level, we proceeded to carry out rheological studies.
6, wt/wt). For a more precise, quantitative measure of the viscoelastic properties as a function of the ligand doping level, we proceeded to carry out rheological studies.
Using a standard setup, metallogel samples were placed between two plates, and their viscoelastic behaviour was measured in response to the oscillatory deformation in the range of ω = 10−1 to 102 rad s−1 (Fig. 9a and b). For a side-by-side comparison of the formulations F1–F7, data points at ω = 10 rad s−1 are plotted. As shown in Fig. 9c and S8,† both the storage modulus and loss modulus decrease systematically with an increasing level of ligand doping. With structural defects introduced by network-terminating ligand 2, the metal–ligand network becomes less ordered, and less effective in dissipating energy under mechanical stress. This result is consistent with the qualitative trend observed in Fig. 8.73
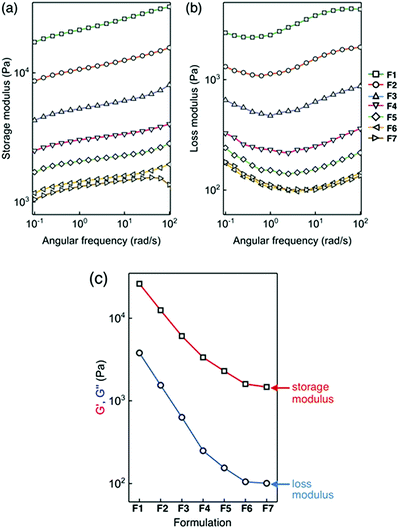 | ||
| Fig. 9 (a) Storage modulus and (b) loss modulus of zinc metallogels F1–F7. In (c) are plotted storage and loss moduli determined at ω = 10 rad s−1. | ||
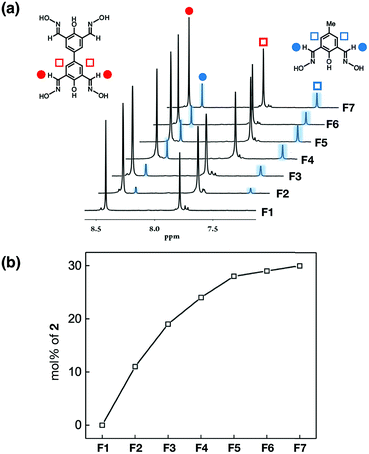
To confirm that doping with ligand 2 is indeed responsible for the attenuation of the mechanical properties of the metallogels (Fig. 8 and 9), we have converted samples F1–F7 to the corresponding aerogels by SCO2 drying. As shown in Fig. S9,† the IR spectra of powdery aerogels F1–F7 are all similar, and consistently show a lack of intense features in the 2700–3500 cm−1 energy window corresponding the phenol/oxime O–H vibrations of the free ligands. To quantify the amount of each ligand that is actually incorporated into the metal–ligand network, each aerogel sample was subjected to acid hydrolysis for complete structural disassembly. From the mixture were isolated free ligands 1 and 2, which were analysed by 1H NMR spectroscopy. As shown in Fig. 10a, the 1H NMR spectrum of each sample shows well-resolved proton resonances from the imine and phenyl ring portions of the ligands 1 and 2, which aided quantification by peak integration. The batch-to-batch reproducibility of this ligand composition analysis was established by 1H NMR (Fig. S10†) and HPLC (Fig. S11†) analysis of the representative aerogel samples, prepared with 25%, 50%, and 75% of the mismatching ligand 2 as the dopant. Each formulation was divided into three individual batches, which were subjected independently to acid digestion, and analysed by integration of ligand proton resonances (Fig. S10†) and HPLC peaks (Fig. S11†) to confirm a consistent ratio of 1 and 2 for the given formulations.
A plot of the mol% of the recovered ligand 2vs. formulations (from F1 to F7) shows a systematic increase and gradual saturation in the % incorporation of the ligand 2 into the metallogel network (Fig. 10b). The formation of a gel-like structure should require a critical network density, which is largely maintained by the ligand 1. An increasing fraction of the mismatching ligand 2 would produce fragmented strands and incomplete cross-junctions that do not reach the critical network density and are thus removed in the process of SCO2 drying. As a consequence, a non-proportional relationship exists between the feed ratio of the monomers (i.e.1vs.2) and their actual incorporation into the aerogel material obtained. This trend is what is observed experimentally in Fig. 10b.
Comparative powder X-ray diffraction studies on mixed-ligand metallogels (Fig. S12†) revealed qualitatively similar patterns in terms of the relative intensities and 2θ values. Their broad and weak diffraction features indicate the absence of long-range atomic ordering and little crystallinity, as anticipated from the kinetically trapped nature of the metal–ligand assembly. More importantly, these PXRD patterns are distinctively different from the intense and well-resolved features obtained from the metal precursor Zn(acac)2·xH2O or the free ligands 1 and 2 (Fig. S12†). No residual starting material, either an unreacted metal salt or a non-coordinated ligand, is thus left behind after metallogel assembly and SCO2 washing.
A uniform distribution of the metal and the ligands 1 and 2 across the bulk material was also established by EDX analysis of mixed-ligand metallogels (Fig. S13†). To ascertain batch-to-batch reproducibility, the bulk material was divided into three separate samples and analysed individually, in a manner similar to the ligand composition analyses by 1H NMR spectroscopy (Fig. S10†) and HPLC (Fig. S11†). Collectively, these results support the notion that an increasing amount of network-terminating “dopant” 2, which is randomly incorporated at the microscopic molecular level, yet evenly distributed at the macroscopic level, is indeed responsible for the decreased viscoelasticity of the bulk material (Fig. 9).
Mechanical strength and degelation response rate
With a close correlation established between the level of ligand doping and mechanical stability of the metallogels (Fig. 8 and 9), we proceeded to investigate its functional relevance. Specifically, we wished to test whether an attenuated mechanical stability, designed with intention, would indeed translate directly to an enhanced sensitivity toward chemical stimuli.To exploit the acid-triggered degelation (Fig. 6) and colourimetric monitoring with entrapped pH indicators (Fig. 7), a simple experimental setup was devised. As shown in Fig. 11, gravity-driven mixing and diffusion of the upper-layer acid (trifluoroacetic acid) solution into the bottom-layer metallogel was monitored by taking digital images at fixed time intervals. A marked pH difference between the two layers provides an excellent colour contrast to follow the progressive advance of the acid front into the basic gel matrix over time until a complete structural collapse is reached.
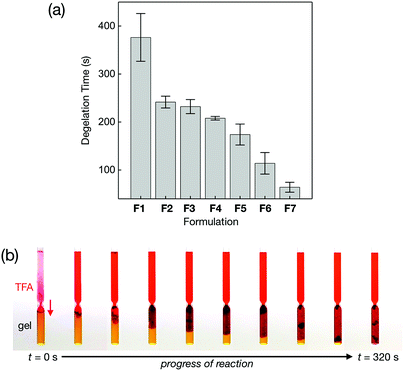 | ||
| Fig. 11 (a) Plots of the average degelation time of ligand-doped metallogel samples F1–F7, and (b) time-lapse photographic images of a representative experimental setup of F1 taken at r.t. | ||
Metallogel samples F1–F7 were prepared as in Fig. 8. For each sample, measurements were carried out six times, and the average value and standard deviation plotted. As shown in Fig. 11a, the rate of acid-triggered degelation correlates well with structural defects; the system F7 with the highest level of ligand doping responds >6 times faster than the undoped system F1. With an optimal level of doping, F7 is barely strong enough to withstand gravity and maintains gel-like properties under ambient conditions, but collapses rapidly upon acidification. Considering that >95 wt% of the gel is taken up by the solvent, the difference in the response rate is best explained by the intrinsic chemomechanical properties of the metal–ligand network itself, rather than disparate diffusion of the acid through the matrix.
For the undoped system F1, the acid-triggered degelation time remains essentially constant when the ligand–metal ratio is varied from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 1
3 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, but drops significantly (>3 times) when the metal ion is depleted down to a 1
2, but drops significantly (>3 times) when the metal ion is depleted down to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Fig. S14†). This empirical observation is consistent with the structural model postulated in Fig. 3. A decrease in the amount of the metal ion below the ideal M2L or M3L stoichiometry would result in fragmented strands or incomplete cross-junctions compromising mechanical strength. Above the ligand–metal ratio of 1
1 ratio (Fig. S14†). This empirical observation is consistent with the structural model postulated in Fig. 3. A decrease in the amount of the metal ion below the ideal M2L or M3L stoichiometry would result in fragmented strands or incomplete cross-junctions compromising mechanical strength. Above the ligand–metal ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, on the other hand, the excess amount of metal ions would remain uncoordinated or exchange with ligand-bound metal centres, without significantly affecting the stability of the existing network.
3, on the other hand, the excess amount of metal ions would remain uncoordinated or exchange with ligand-bound metal centres, without significantly affecting the stability of the existing network.
Conclusions
Metallogels were constructed by using a pair of ligands that function as chain-propagating and chain-terminating groups in the network growth. These soft materials undergo chemically driven gel–sol transitions at either the liquid–gel or the air–gel interface, the response kinetics of which can be controlled by changing either the metal centre or the level of ligand doping. Collectively, our findings highlight the importance of rational ligand design and systematic compositional tuning of the metallogels to strike the right balance between physical stability and chemical sensitivity, all realised by a single system at the material level. Efforts are currently underway to generalise and refine this concept with other types of ligands, and expand the scope of signal transduction schemes to metallogel-based sensors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Samsung Science and Technology Foundation (SRFC-MA1502-02).Notes and references
- S. Kaskel, The Chemistry of Metal–Organic Frameworks, 2 Volume Set: Synthesis, Characterization, and Applications, Wiley-VCH, Weinheim, 2016 Search PubMed.
- C. H. Hendon, A. J. Rieth, M. D. Korzyński and M. Dincă, ACS Cent. Sci., 2017, 3, 554–563 CrossRef CAS PubMed.
- H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS PubMed.
- C. K. Brozek and M. Dincă, Chem. Soc. Rev., 2014, 43, 5456–5467 RSC.
- V. Guillerm, D. Kim, J. F. Eubank, R. Luebke, X. Liu, K. Adil, M. S. Lah and M. Eddaoudi, Chem. Soc. Rev., 2014, 43, 6141–6172 RSC.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- Y. Yu, Y. Shi and B. Zhang, Acc. Chem. Res., 2018, 51, 1711–1721 CrossRef CAS PubMed.
- O. Kotova, R. Daly, C. M. G. dos Santos, M. Boese, P. E. Kruger, J. J. Boland and T. Gunnlaugsson, Angew. Chem., Int. Ed., 2012, 51, 7208–7212 CrossRef CAS PubMed.
- P. Dastidar, S. Ganguly and K. Sarkar, Chem.–Asian J., 2016, 11, 2484–2498 CrossRef CAS PubMed.
- Y.-R. Liu, L. He, J. Zhang, X. Wang and C.-Y. Su, Chem. Mater., 2009, 21, 557–563 CrossRef CAS.
- A. J. McConnell, C. S. Wood, P. P. Neelakandan and J. R. Nitschke, Chem. Rev., 2015, 115, 7729–7793 CrossRef CAS PubMed.
- M.-O. M. Piepenbrock, G. O. Lloyd, N. Clarke and J. W. Steed, Chem. Rev., 2010, 110, 1960–2004 CrossRef CAS PubMed.
- A. Mehdi, C. Reye and R. Corriu, Chem. Soc. Rev., 2011, 40, 563–574 RSC.
- A. Y. Tam and V. W. Yam, Chem. Soc. Rev., 2013, 42, 1540–1567 RSC.
- M. Martínez-Calvo, O. Kotova, M. E. Möbius, A. P. Bell, T. McCabe, J. J. Boland and T. Gunnlaugsson, J. Am. Chem. Soc., 2015, 137, 1983–1992 CrossRef PubMed.
- Y. Sun, S. Li, Z. Zhou, M. L. Saha, S. Datta, M. Zhang, X. Yan, D. Tian, H. Wang, L. Wang, X. Li, M. Liu, H. Li and P. J. Stang, J. Am. Chem. Soc., 2018, 140, 3257–3263 CrossRef CAS PubMed.
- X. Yan, T. R. Cook, J. B. Pollock, P. Wei, Y. Zhang, Y. Yu, F. Huang and P. J. Stang, J. Am. Chem. Soc., 2014, 136, 4460–4463 CrossRef CAS PubMed.
- R. R. Salunkhe, Y. V. Kaneti, J. Kim, J. H. Kim and Y. Yamauchi, Acc. Chem. Res., 2016, 49, 2796–2806 CrossRef CAS PubMed.
- X. Cao, C. Tan, M. Sindoro and H. Zhang, Chem. Soc. Rev., 2017, 46, 2660–2677 RSC.
- T. Kitao, Y. Zhang, S. Kitagawa, B. Wang and T. Uemura, Chem. Soc. Rev., 2017, 46, 3108–3133 RSC.
- Q. Yang, Q. Xu and H.-L. Jiang, Chem. Soc. Rev., 2017, 46, 4774–4808 RSC.
- A. Carné-Sánchez, G. A. Craig, P. Larpent, T. Hirose, M. Higuchi, S. Kitagawa, K. Matsuda, K. Urayama and S. Furukawa, Nat. Commun., 2018, 9, 2506–2513 CrossRef PubMed.
- J. H. van Esch and B. L. Feringa, Angew. Chem., Int. Ed., 2000, 39, 2263–2266 CrossRef CAS PubMed.
- P. Terech and R. G. Weiss, Chem. Rev., 1997, 97, 3133–3160 CrossRef CAS PubMed.
- L. E. Buerkle and S. J. Rowan, Chem. Soc. Rev., 2012, 41, 6089–6102 RSC.
- M. de Loos, B. L. Feringa and J. H. van Esch, Eur. J. Org. Chem., 2005, 3615–3631 CrossRef CAS.
- K. Hanabusa and M. Suzuki, Polym. J., 2014, 46, 776–782 CrossRef CAS.
- A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002–8018 CrossRef CAS PubMed.
- M. Häring and D. D. Díaz, Chem. Commun., 2016, 52, 13068–13081 RSC.
- J. W. Steed, Chem. Commun., 2011, 47, 1379–1383 RSC.
- P. Biswas, S. Ganguly and P. Dastidar, Chem.–Asian J., 2018, 13, 1941–1949 CrossRef CAS PubMed.
- W. Miao, L. Zhang, X. Wang, H. Cao, Q. Jin and M. Liu, Chem.–Eur. J., 2013, 19, 3029–3036 CrossRef CAS PubMed.
- P. Chen, Q. Li, S. Grindy and N. Holten-Andersen, J. Am. Chem. Soc., 2015, 137, 11590–11593 CrossRef CAS PubMed.
- S. Sarkar, S. Dutta, S. Chakrabarti, P. Bairi and T. Pal, ACS Appl. Mater. Interfaces, 2014, 6, 6308–6316 CrossRef CAS PubMed.
- Q. Lin, T. T. Lu, X. Zhu, B. Sun, Q. P. Yang, T. B. Wei and Y. M. Zhang, Chem. Commun., 2015, 51, 1635–1638 RSC.
- S. Bhattacharya, S. Sengupta, S. Bala, A. Goswami, S. Ganguly and R. Mondal, Cryst. Growth Des., 2014, 14, 2366–2374 CrossRef CAS.
- Polymer-appended multidentate ligands have previously been used to study the effects of network defect sites on the diffusive motions of entrapped fluorescent labels as spectroscopic “tracers”.38,39.
- A. Habicht, S. Czarnecki, T. Rossow and S. Seiffert, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 19–29 CrossRef CAS.
- T. Rossow, A. Habicht and S. Seiffert, Macromolecules, 2014, 47, 6473–6482 CrossRef CAS.
- A. Vintiloiu and J.-C. Leroux, J. Controlled Release, 2008, 125, 179–192 CrossRef CAS PubMed.
- G. M. Kavanagh and S. B. Ross-Murphy, Prog. Polym. Sci., 1998, 23, 533–562 CrossRef CAS.
- E. R. Duering, J. Chem. Phys., 1994, 101, 8169–8192 CrossRef CAS.
- K. Oh, J. Oh, H. Choi and Y. Bae, Macromolecules, 1998, 31, 7328–7335 CrossRef CAS.
- M. Rubinstein and S. Panyukov, Macromolecules, 1997, 30, 8036–8044 CrossRef CAS.
- M. Rubinstein and S. Panyukov, Macromolecules, 2002, 35, 6670–6686 CrossRef CAS.
- P. J. Flory, Polym. J., 1985, 17, 1–12 CrossRef CAS.
- P. J. Flory, Proc. R. Soc. A, 1976, 351, 351–380 CrossRef CAS.
- H. Zhou, E.-M. Schön, M. Wang, M. J. Glassman, J. Liu, M. Zhong, D. Díaz Díaz, B. D. Olsen and J. A. Johnson, J. Am. Chem. Soc., 2014, 136, 9464–9470 CrossRef CAS PubMed.
- A. L. Andrady, M. A. Llorente, M. A. Sharaf, R. R. Rahalkar, J. E. Mark, J. L. Sullivan, C. U. Yu and J. R. Falender, J. Appl. Polym. Sci., 1981, 26, 1829–1836 CrossRef CAS.
- K. Müllen, Nat. Rev. Mater., 2016, 1, 15013–15014 CrossRef.
- M. J. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Science, 2016, 353, 1264–1268 CrossRef CAS PubMed.
- M. Pascu, M. Marmier, C. Schouwey, R. Scopelliti, J. J. Holstein, G. Bricogne and K. Severin, Chem.–Eur. J., 2014, 20, 5592–5600 CrossRef CAS PubMed.
- C. Krebs, M. Winter, T. Weyhermüller, E. Bill, K. Wieghardt and P. Chaudhuri, Chem. Commun., 1995, 1913–1915 RSC.
- S. Khanra, T. Weyhermuller, E. Bill and P. Chaudhuri, Inorg. Chem., 2006, 45, 5911–5923 CrossRef CAS PubMed.
- M. Holynska, R. Clerac, T. Langer, R. Pottgen and S. Dehnen, Polyhedron, 2013, 52, 1425–1430 CrossRef CAS.
- E. Asato, M. Chinen, A. Yoshino, Y. Sakata and K. Sugiura, Chem. Lett., 2000, 678–679 CrossRef CAS.
- J. K. H. Hui and M. J. MacLachlan, Coord. Chem. Rev., 2010, 254, 2363–2390 CrossRef CAS.
- Q. Liu, Y. Wang, W. Li and L. Wu, Langmuir, 2007, 23, 8217–8223 CrossRef CAS PubMed.
- H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 3192–3210 RSC.
- Z. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS PubMed.
- O. Kozachuk, I. Luz, F. X. Llabrés i Xamena, H. Noei, M. Kauer, H. B. Albada, E. D. Bloch, B. Marler, Y. Wang, M. Muhler and R. A. Fischer, Angew. Chem., Int. Ed., 2014, 53, 7058–7062 CrossRef CAS PubMed.
- R. Ameloot, M. Aubrey, B. M. Wiers, A. P. Gómora-Figueroa, S. N. Patel, N. P. Balsara and J. R. Long, Chem.–Eur. J., 2013, 19, 5533–5536 CrossRef CAS PubMed.
- P. Deria, J. E. Mondloch, O. Karagiaridi, W. Bury, J. T. Hupp and O. K. Farha, Chem. Soc. Rev., 2014, 43, 5896–5912 RSC.
- G. Barin, V. Krungleviciute, O. Gutov, J. T. Hupp, T. Yildirim and O. K. Farha, Inorg. Chem., 2014, 53, 6914–6919 CrossRef CAS PubMed.
- Z. Fang, J. P. Dürholt, M. Kauer, W. Zhang, C. Lochenie, B. Jee, B. Albada, N. Metzler-Nolte, A. Pöppl, B. Weber, M. Muhler, Y. Wang, R. Schmid and R. A. Fischer, J. Am. Chem. Soc., 2014, 136, 9627–9636 CrossRef CAS PubMed.
- J. Park, Z. U. Wang, L.-B. Sun, Y.-P. Chen and H.-C. Zhou, J. Am. Chem. Soc., 2012, 134, 20110–20116 CrossRef CAS PubMed.
- S. Marx, W. Kleist and A. Baiker, J. Catal., 2011, 281, 76–87 CrossRef CAS.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 4176–4183 CrossRef CAS PubMed.
- D. Chan, Y. C. Ding, R. H. Dauskardt and E. A. Appel, ACS Appl. Mater. Interfaces, 2017, 9, 42217–42224 CrossRef CAS PubMed.
- K. Kawamoto, M. Zhong, R. Wang, B. D. Olsen and J. A. Johnson, Macromolecules, 2015, 48, 8980–8988 CrossRef CAS.
- K. Schwenke, M. Lang and J. U. Sommer, Macromolecules, 2011, 44, 9464–9472 CrossRef CAS.
- R. Wang, J. A. Johnson and B. D. Olsen, Macromolecules, 2017, 50, 2556–2564 CrossRef CAS.
- While Flory–Stockmayer theory is widely used to predict the gelation point of step-growth polymers, it is difficult to apply this model to our system. As shown in Fig. 4, ligand 2 forms insoluble precipitates upon metallation, which could not be characterized further to determine the “conversion of monomer groups” required for modeling..
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures and additional data (1H and 13C NMR spectra, FT-IR spectra, HR-MS and elemental analysis) of the newly synthesized compounds. See DOI: 10.1039/c8sc05480k |
| This journal is © The Royal Society of Chemistry 2019 |