Open Access Article
Open Access ArticleDavydov splitting and singlet fission in excitonically coupled pentacene dimers†‡
Bettina Sabine
Basel§
a,
Constantin
Hetzer§
b,
Johannes
Zirzlmeier§
a,
Dominik
Thiel
a,
Rebecca
Guldi
b,
Frank
Hampel
 b,
Axel
Kahnt
b,
Axel
Kahnt
 c,
Timothy
Clark
c,
Timothy
Clark
 *d,
Dirk Michael
Guldi
*d,
Dirk Michael
Guldi
 *a and
Rik R.
Tykwinski
*a and
Rik R.
Tykwinski
 *e
*e
aDepartment of Chemistry and Pharmacy, Interdisciplinary Center for Molecular Materials (ICMM), Friedrich-Alexander-Universität (FAU), Egerlandstrasse 3, 91058 Erlangen, Germany. E-mail: dirk.guldi@fau.de
bDepartment of Chemistry and Pharmacy, Interdisciplinary Center for Molecular Materials (ICMM), Friedrich-Alexander-Universität (FAU), Nikolaus-Fiebiger-Strasse 10, 91058 Erlangen, Germany
cLeibniz Institute of Surface Engineering (IOM), Permoserstr. 15, D-04318 Leipzig, Germany
dDepartment of Chemistry and Pharmacy, Computer-Chemistry-Center (CCC), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Nägelsbachstrasse 25, 91052 Erlangen, Germany. E-mail: tim.clark@fau.de
eDepartment of Chemistry, University of Alberta, Edmonton, Alberta, T6G 2G2, Canada. E-mail: rik.tykwinski@ualberta.ca
First published on 6th March 2019
Abstract
Singlet fission (SF) allows two charges to be generated from the absorption of a single photon and is, therefore, potentially transformative toward improving solar energy conversion. Key to the present study of SF is the design of pentacene dimers featuring a xanthene linker that strictly places two pentacene chromophores in a rigid arrangement and, in turn, enforces efficient, intramolecular π-overlap that mimics interactions typically found in condensed state (e.g., solids, films, etc.). Inter-chromophore communication ensures Davydov splitting, which plays an unprecedented role toward achieving SF in pentacene dimers. Transient absorption measurements document that intramolecular SF evolves upon excitation into the lower Davydov bands to form a correlated triplet pair at cryogenic temperature. At room temperature, the two spin-correlated triplets, one per pentacene moiety within the dimers, are electronically coupled to an excimer state. The presented results are transferable to a broad range of acene morphologies including aggregates, crystals, and films.
Introduction
Singlet fission (SF) is a spin-allowed photophysical process, in which an excited singlet state is transformed rapidly and efficiently into two triplet excited states.1–5 Although SF was first observed more than fifty years ago in crystalline systems,6–8 interest has only recently been rekindled, as SF could serve as a means to overcome the theoretical limit for solar cell performance first introduced by Shockley and Queisser.9–14 Chromophores must fulfill a basic requirement of energy conservation for SF, in which the first singlet excited-state energy must be similar to or greater than twice the energy of the lowest-lying triplet excited state; E(S1) ≈ 2E(T1) or E(S1) > 2E(T1).1–5,15,16 In addition, rates play a crucial role in determining the efficiency of SF; the chromophore-system should demonstrate fast conversion of the singlet locally excited 1(S1S0) state into two spin-coupled local triplet excited 1(T1T1) states in order to compete efficiently with parasitic deactivation pathways such as fluorescence, internal conversion, and intersystem crossing.1–5 The rate of SF depends strongly on the electronic coupling matrix elements between the chromophores and the free-energy difference between the states involved.4,5Substantial efforts have been made to develop molecular systems suitable for efficient SF, and the number of chromophores that fulfill the necessary requirements, although somewhat limited, is currently increasing to include acenes,17–22 diphenylisobenzofurans,23–25 carotenoids,26,27 rylenes,28–30 and others.31–33 With a wider selection of potential SF-chromophores available, the more difficult task of deciphering the mechanistic and morphological details associated with SF must now be addressed.
Three different SF mechanisms have been proposed so far: the direct mechanism,34,35 where the (S1S0) state decays directly to 1(T1T1); the mediated mechanism, in which the 1(T1T1) formation is facilitated by coupling to a (virtual) charge-transfer (CT) intermediate;36,37 and the state-mixing or quantum coherent mechanism, where a coherent superposition of the (S1S0),1(T1T1) and (sometimes) the CT state, is generated directly after excitation.38,39
Studies of SF in the solid state are often challenging because of timescales that are too fast to allow mechanistic aspects to be unraveled. Moreover, independent fine-tuning of mechanistic variables such as polarity, inter-chromophore distance, and the effective π-conjugation between two chromophores can be very complex in solid-state samples. To overcome the limitations of solid-state analyses, SF in specially designed dimers has been investigated in dilute solution. Under such conditions, the rate of SF is reduced, and valuable insight regarding factors that influence the mechanism and yield can be elucidated more easily.20,36,40–45 An important difference between measurements in solution and in the solid state arises from the significant electronic influence of neighboring molecules in the latter. Packing of pentacene derivatives in the solid state, for example, is often characterized by significant, direct π-overlap of neighboring chromophores.46–49
Strong intermolecular π–π interactions, then, lead to inter-chromophore coupling and Davydov splitting. More specifically, Davydov splitting arises from the overlap of the wavefunctions of two translationally inequivalent molecules in the unit cells of crystals.46,50 To be consistent with previous reports on acene dimers,51–54 we refer to Davydov splitting rather than the synonymous exciton splitting.55 Excited-state properties and dynamics that lead to Davydov splitting have been reported for e.g., polycrystalline single crystals,50 acene films,56 and nanoaggregates.57,58 Davydov splitting of the lowest singlet excited state has been predicted for pentacene crystals to lead to an electronic situation that is favorable for fast SF.59 Importantly, it has been shown for crystalline perfluoropentacene that excimer states formed from Davydov states act as intermediates that favor SF, rather than compete with it.60 For films of diketopyrrolopyrroles with marked Davydov splitting, excimer states formed on photoexcitation have been identified as a multi-excitonic 1(T1T1) state en route to triplet decorrelation.61
In the case of dimers containing two “monomeric” chromophores, overlap of the wavefunction localized on each of the two monomers leads to Davydov splitting into two dimer states.51 In dilute solutions, direct π-overlap in, for example, perylenediimide dimers leads to Davydov splitting, which results in a scenario in which excimer formation is favored and SF is disfavored.62,63 Lately, a lively debate has arisen about the nature of excimer states in tetracenes and pentacenes. In the case of concentrated TIPS-tetracene solutions, a correlated triplet pair state with excimer character was identified,64 whereas in tetracene dimers a S1-excimer state acts as intermediate in SF.19 The impact of a CT-character is also highly controversial. No CT-character was found for singlet excimer states, which mediate SF in microcrystalline pentacene films with Davydov splitting of the S1 ← S0 transition.65 In contrast, singlet excited states in pentacene single crystals, which show Davydov splitting of the S1 state, are predicted to possess CT-character and support SF.59 Different conclusions are also drawn for the role of acene-centered excimer states in SF. On the one hand, excimers states in concentrated TIPS-tetracene solutions with absorption features of singlet and triplet states are identified as intermediates in SF.64 On the other hand, excimer states found in the same system, are diagnosed to act as trap states that are detrimental to SF.66 These observations are consistent with the fact that a competition exists in tetracene dimers between excimer formation and SF.54,67
Such debates underline the necessity to test the role and nature of excimer states in acene-based SF. We opted for Davydov splitting as a suitable parameter to distinguish between different kinds of excimers and their corresponding roles. Our idea is based on the nature of Davydov splitting: it is caused by electronic interactions between, for example, neighboring acenes in their electronic ground-states. This contrasts excimer states, which emerge when two neighboring acenes interact solely in their electronically excited state.65 The focus of our investigation is to dissect the role of excimers, which emerge from photoexcitable dimer states in the form of Davydov splitting. Notably, SF in pentacene dimers that show Davydov splitting in solution has not been demonstrated to date.
In the present study, we have designed four pentacene dimers, in which a xanthene linker is used to position the two pentacene-chromophores in a rigid arrangement, which, in turn, enforces strong co-facial π–π-interactions.¶20,68 Using these pentacene dimers in dilute solution, we outline the role of inter-chromophore coupling through direct π-overlap, which leads to solid-state-like Davydov splitting. Transient absorption spectroscopy enables us to define the influence of Davydov splitting on the excited-state processes. In particular, we outline excimer state formation following excitation of Davydov split pentacene energy levels in dilute solution and at variable temperatures. In doing so, we confirm fast SF and identify the nature of excimer states in excitonically coupled pentacenes.
Results and discussion
Synthesis
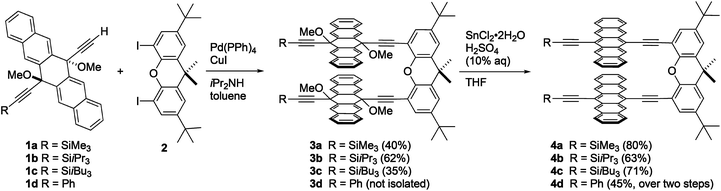
The synthesis of xanthene-linked pentacene dimers was based on the Sonogashira cross-coupling of terminal alkyne building blocks 1a–1d69 with 4,5-diiodo-2,7-di-tert-butyl-9,9-dimethylxanthene 270 to give intermediates 3a–c in 35–62% yield, respectively (Scheme 1, see ESI‡ for synthetic details). In the case of 3d, the desired product could not be isolated pure, and, therefore, the crude mixture was taken directly on to the next step without further purification. With 3a–d in hand, SnCl2-mediated reductive aromatization71 in the presence of H2SO4 furnished dimers 4a–d in good yields. Compounds 4a–d are stable toward air and moisture under normal laboratory conditions and show good solubility in common organic solvents like CHCl3, CH2Cl2, THF, and toluene (ca. 6 mg mL−1). Thermal analysis of 4a–dvia differential scanning calorimetry revealed decomposition temperatures that range from 240 °C for 4d to 296 °C for 4b.Structural analysis
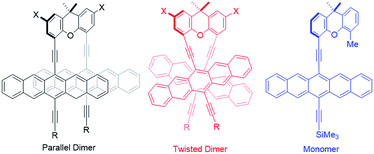
Crystallographic analyses have established that acene dimers can adopt either a “parallel” or “twisted” orientation of the two chromophores in the solid state.19 X-ray analysis of dimers 4b and 4c reveals a parallel alignment of the two pentacene moieties – Fig. S22–S25.‡ The structures of both dimers highlight the intramolecular proximity of the two pentacene-moieties with close contacts in the solid of 3.3–3.6 Å for 4b and 3.0–3.5 Å for 4c. Importantly, the increased steric bulk of the more solubilizing SiiBu3 does not appear to significantly affect the stacking distances between pentacenes in the solid state, although the relative intramolecular orientation of the two pentacenes differs slightly – Fig. S23.‡Calculations – insight into Davydov splitting
Two lowest energy conformations were found for 4a–d by classical molecular-dynamics (MD) simulations in the gas phase (Fig. 1). The two conformations identified in the MD simulations were optimized using density-functional theory (DFT) with the B3LYP65 and ωB97XD66 density functionals, the former were augmented by the D3 dispersion corrections.72–75 All DFT-calculations used the 6-31G(d) basis set. Initial calculations for 4a showed that the xanthene substitution (i.e., X = tBu in Fig. 1) does not affect the relative stabilities of the “parallel” and “twisted” conformations, so that the remaining calculations were performed on the unsubstituted derivatives 4a′–4d′ (i.e., X = H).Table 1 shows the results of the DFT calculations, which emphasize that, in the absence of intermolecular crystal-packing interactions, the twisted conformation is more stable in each dimer. The two density functionals agree quite closely on the relative stabilities of the two conformations. The different conformational preference between solution and solid-state structures is attributed to intermolecular interactions in the latter. The “parallel” conformer is found to be between 4 and 20 kcal mol−1 less stable than the “twisted” conformer – Table 1. For both 4b′ and 4c′, the conformations of the substituents may, however, not be the most stable one, so that the relative energies for these compounds must be treated with caution. Nonetheless, we can conclude from the DFT calculations that the twisted conformation should predominate in solution. As is evident from Fig. 1, the π-overlap between the pentacene moieties is larger in the parallel than in the “twisted” conformation. Please note that this does not have a large effect on the calculated spectra. A comparison of the absorption spectra of the two conformers using the semiempirical AM1 Hamiltonian76 with configuration interaction including only single excitations (CIS) and an active space of 64 occupied and 64 virtual orbitals and polarized-continuum model solvation in benzonitrile is given in Fig. S26.‡
| Compoundb | R | X | E tot | ZPE | B3LYP-D3/6-31G(d) | ωB97XD/6-31G(d) | |||
|---|---|---|---|---|---|---|---|---|---|
| E rel | E tot | ZPE | E rel | ||||||
| a E tot [a.u.] = total energies, ZPE [kcal mol−1] = zero-point vibrational energies, Erel [kcal mol−1] = relative energies (Erel = Born–Oppenheimer + ZPE). b See Fig. 1 for molecular structures. | |||||||||
| 4a | Me3Si | tBu | Twisted | −3704.57138 | 754.05 | 0.0 | |||
| 4a | Me3Si | tBu | Parallel | −3704.55976 | 753.90 | 7.1 | |||
| 4a′ | Me3Si | H | Twisted | −3390.02898 | 611.81 | 0.0 | −3388.90169 | 618.75 | 0.0 |
| 4a′ | Me3Si | H | Parallel | −3390.01728 | 611.64 | 7.2 | −3388.89133 | 618.77 | 6.5 |
| 4b′ | iPr3Si | H | Twisted | −3861.80233 | 830.31 | 0.0 | −3860.51648 | 838.88 | 0.0 |
| 4b′ | iPr3Si | H | Parallel | −3861.79525 | 829.88 | 4.0 | −3860.51101 | 838.98 | 3.5 |
| 4c′ | iBu3Si | H | Twisted | −4097.72225 | 938.09 | 0.0 | −4096.35749 | 947.32 | 0.0 |
| 4c′ | iBu3Si | H | Parallel | −4097.69073 | 937.06 | 18.8 | −4096.32419 | 946.42 | 20.0 |
| 4d′ | Ph | H | Twisted | −3034.76298 | 585.15 | 0.0 | −3033.58242 | 592.43 | 0.0 |
| 4d′ | Ph | H | Parallel | −3034.73965 | 584.30 | 13.8 | −3033.55747 | 591.74 | 15.0 |
Exciton/Davydov splitting is often discussed within the context of H-/J-coupling:77 the upper Davydov band relates here to the H-feature, while the lower is synonymous with the J-feature.78 To discuss the Davydov splitting in 4a–d in terms of H- and J-bands, however, would be at least partially incorrect as H-/J-couplings are only applicable for coplanar and parallel configurations.55,77 The twisted conformers of 4a–d that predominate in solution do not conform to the coplanar/parallel picture. Therefore, we believe that the terms upper and lower Davydov bands provide a more accurate description.
Calculations show that Davydov splitting is observed for all singlet excited states, albeit small (<0.03 eV) except for the lowest singlet excited state, which is split by 0.35 eV in the twisted conformer of 4a (Fig. 2). The corresponding splitting in the “parallel” conformation is lower (0.26 eV). In contrast, appreciable Davydov splitting is predicted to be absent in a corresponding monomer that features only one pentacene moiety. On the other hand, both the calculations and experiments suggest that, while Davydov splitting undoubtedly dominates our observations, other considerations likely complicate the spectrum. The Davydov-split bands (combinations of HOMO → LUMO and HOMO−1 → LUMO+1), the lower-energy of which is calculated to have very low intensity (calculated oscillator strength 0.031), mix with other single excitations, so that the splitting is larger than expected. More specifically, the lower band mixes with HOMO → LUMO+1 and HOMO−1 → LUMO, and the higher one with HOMO−5 → LUMO+6 and HOMO−6 → LUMO+5 (relevant orbitals are shown in Fig. S28‡). Most importantly, these orbitals are unsymmetrical combinations of π-MOs centered on the two chromophores and, in turn, rather strong mixing with the Davydov bands is possible. When turning to the triplet excited state, a much smaller splitting of 0.007 eV is found.
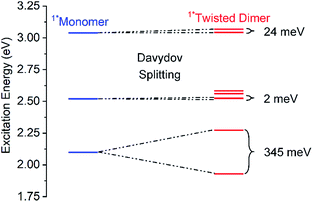 | ||
| Fig. 2 Energy-level diagram of the calculated singlet excited states of the twisted dimer conformation of 4a (red) in comparison to the monomer reference (blue). Davydov splitting is indicated by the correlation lines and the splitting energy is given in meV. For the corresponding triplet excited state levels see Fig. S27.‡ | ||
Steady state absorption and electrochemistry – observation of Davydov splitting
To confirm intramolecular Davydov splitting, we performed steady state absorption measurements with 4a–d at room temperature in toluene, THF, and benzonitrile; 6,13-bis(triisobutylsilylethynyl)pentacene (TIBS) was used as a reference. A comparison of the spectra for 4a–d and TIBS reveals a number of distinct differences. First, all vibronic fine structure in the absorption spectra of 4a–d show a red shift of about 20 nm compared to TIBS, as a result of stabilization by van der Waals interactions.77 Second, in all solvents, the extinction coefficients across the visible range are lower than the linear sum of two pentacene moieties. This effect is particularly strong for the fundamental 0–0* absorption at around 660 nm – Fig. 3. Third, additional absorption features develop in the long-wavelength region between 680 and 800 nm (Fig. 3).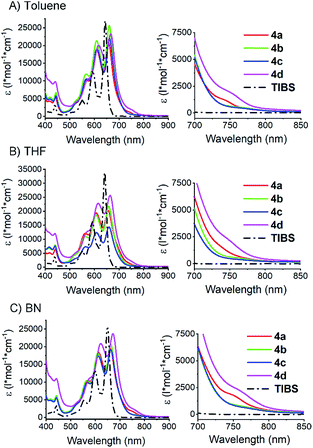 | ||
| Fig. 3 Steady state absorption spectra of dimers 4a–d and TIBS in different solvents. Measured in (A) toluene, (B) THF, and (C) benzonitrile (BN) at room temperature. On the right: expansions of the absorption features that are identified as lower energy Davydov bands (see also Fig. S29‡). | ||
To rule out that these results stem from aggregation, their concentration dependency was examined, and it was established that the Lambert–Beer relationship was upheld – Fig. 4 and S30–S34.‡ In short, the appearance of the additional absorptions is consistent with Davydov splitting. The Davydov features show solvent dependency, and they are poorly resolved in THF, slightly better resolved in toluene, and clearly visible in benzonitrile – Fig. 3 (especially for compounds 4a and 4d). Specifically, the solvent viscosity increases from THF (η(25 °C) = 0.456 mPa s) to toluene (η(25 °C) = 0.560 mPa s) and to benzonitrile (η(25 °C) = 1.267 mPa s),79 suggesting Davydov splitting is contingent on the solvent viscosity. Considering the impact that viscosity exerts on nuclear motions, our findings are rationalized in terms of cooling of intramolecular vibrations and, in turn, freezing intramolecular π-overlap between the two pentacenes. Independent confirmation for this hypothesis comes from temperature-dependent absorption measurements in 2-methyltetrahydrofuran (MeTHF) – Fig. 5. In particular, the Davydov bands, which were poorly resolved at room temperature, are seen as distinct maxima in the lower temperature regime.
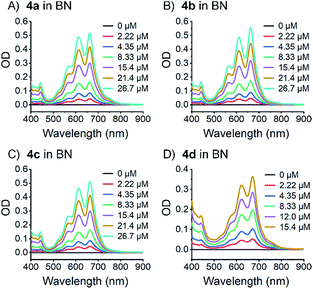 | ||
| Fig. 4 Steady state absorption spectra of dimers 4a–d (A)–(D) in benzonitrile (BN) at different concentrations and room temperature. | ||
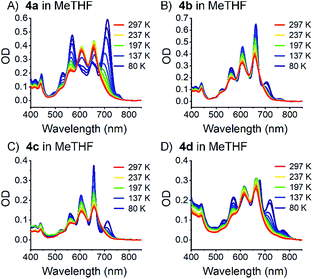 | ||
| Fig. 5 Steady state absorption spectra of dimers 4a–d (A)–(D) measured in MeTHF at variable temperatures (80 to 297 K). | ||
Davydov splitting in 4a–d is also supported by electrochemical characterization. Rather than observing a single, two-electron oxidation at around +0.45 V as seen in the case of the one-electron oxidation of TIBS, a pair of oxidations is observed: +0.22 and +0.51 V for 4a, +0.19 and +0.50 V for 4b, and +0.20 and +0.51 V for 4c – Fig. S35.‡ All values are given versus Fc/Fc+ (ferrocene/ferrocenium).|| At the same time, a single two-electron reduction is noted for 4a–c at ca. −1.6 V, which is slightly more negative than seen for TIBS at −1.44 V. As a matter of fact, the two different oxidations agree with AM1 full CI calculations. Here, we considered two occupied and two virtual orbitals in the active space as well as an SCRF solvent model for benzonitrile. The splitting is 0.2 eV between the two lowest-lying doublet states of the molecular radical cation at the ωB97XD-optimized geometry of the neutral molecule.
Transient absorption measurements at cryogenic temperatures – observing singlet fission
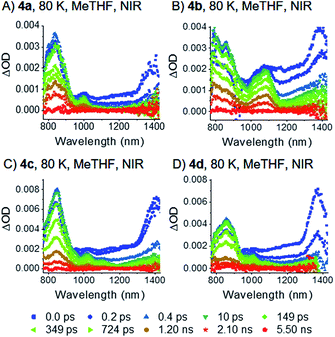
To observe the excited-state dynamics upon exciting Davydov levels, femtosecond transient absorption (fsTA) spectroscopy was performed at 80 K by irradiation at 730 nm. 730 nm excites the dimers into their low-energy Davydov bands. The datasets obtained were analyzed with multi-wavelength and global analyses (see ESI‡ for details). A global analysis with a sequential model was performed to identify the decay dynamics. Low temperature experiments were performed in MeTHF.Upon photoexcitation, the typical fingerprint absorptions of the pentacene singlet excited (S1S0) state at around 1400 nm form instantaneously for all four dimers36 – Fig. 6.** The (S1S0) state decays with lifetimes of less than 200 fs and new absorption features, which evolve at around 480 and 515 nm, are in sound agreement with the pentacene triplet excited state (Fig. 7 and S36‡). Independent evidence for our spectral assignment comes from triplet sensitization experiments with N-methylfulleropyrrolidine (N-MFP) – Fig. S40.‡80 This result, in combination with the very fast formation dynamics (<200 fs), substantiates the notion of intramolecular SF. In turn, the triplet features indicate the presence of the (T1T1) state.
 | ||
| Fig. 7 EAS of dimers 4a–d (A)–(D) in frozen argon-saturated MeTHF, VIS. The data were recorded at 80 K. Spectra were obtained by global analysis with a sequential model of the transient absorption data measured upon femtosecond pump-probe experiments with 730 nm excitation. Fig. S36‡ displays the raw data and Fig. S39‡ the single wavelength kinetics and corresponding fits. | ||
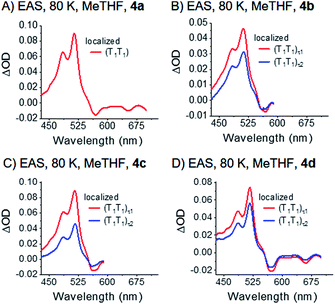
Interestingly, the decay of the (T1T1) state is biphasic for 4b, 4c, and 4d. Consequently, we used a kinetic model with two states, (T1T1)τ1 and (T1T1)τ2, for the global fit. We considered two different options, parallel (Fig. S38‡) and sequential (Fig. 7) models. In the former, (T1T1)τ1 and (T1T1)τ2 are populated simultaneously and decay in parallel. In the latter, (T1T1)τ1 is populated initially and decays to (T1T1)τ2. Importantly, the (T1T1)τ1 spectrum agrees much better with the triplet spectra generated by photosensitization with N-MFP for the sequential rather than parallel model. Much more of a concern is, however, the fact that the (T1T1)τ1 spectra are very different for each dimer when using the parallel model. As such, the sequential model is more realistic for the global analysis. In this context, the transition between the different (T1T1) states does not necessarily correspond to an electronic transition, but is likely to relate to a relaxation process. As such, the two (T1T1) states in the kinetic model may correspond to the same electronic state. Once formed, the (T1T1)τ2 state relaxes to the ground state. The underlying time constants for (T1T1)τ1 and (T1T1)τ2 are 269 ps/1.3 ns, 509 ps/1.3 ns, and 173 ps/1.0 ns for 4b, 4c, and 4d, respectively. For 4a, only a single lifetime of 1.2 ns results. Notably, the pico- to nanosecond (T1T1) lifetimes in 4a–d are in stark contrast to the microsecond lifetimes of pentacene triplet excited states formed via intersystem crossing in, for example, TIBS. We take such a dramatic difference as support for the presence of two correlated local triplet excited states per dimer, that is, a correlated triplet (T1T1) pair. Here, fast deactivation via triplet–triplet annihilation occurs, as recently documented.80 As aforementioned, 4a (R = SiMe3) gives rise to a single (T1T1) state at 80 K (mono-exponential decay), while for 4b–4d bi-exponential decays were found. As the substituent size increases from 4a to 4b–4d, it seems reasonable to postulate that the biphasic decay relates to geometric rearrangements of the substituents – this will be explained in more detail below.
Transient absorption measurements in liquid solution at cryogenic temperature – a correlated triplet pair with excimer character
Having established that singlet fission occurs in dimers 4a–d, we examine now the effect of intramolecular vibrations on the excited state dynamics. Therefore, fsTA measurements by using the same 730 nm excitation were performed at 157 K in liquid MeTHF. Overall, a decrease of all excited state lifetimes is observed on moving from frozen to liquid solutions. This temperature dependence indicates activation barriers that may be related to geometric rearrangements – vide infra.For 4c and d, the 1400 nm fingerprint absorption of the pentacene singlet excited (S1S0) state is visible within the first 200 fs after excitation – Fig. S42.‡ In contrast, the acceleration of the singlet fission process for 4a and b leads to (S1S0) state lifetimes that are below our instrumental time resolution. Due to the short lifetime, it is only possible to deconvolute the singlet excited (S1S0) state by global analysis in the NIR region of 4d – Fig. S43.‡
Notably, the correlated triplet pair states (T1T1) of 4a–c, which were at 80 K completely consistent with the sensitized triplet T1, appear much broader at 157 K – Fig. 8 and S41.‡ Considering this broadening in turn with the close proximity of the two triplet states, the two triplets of the correlated triplet-pair are, in contrast to the 80 K experiments, electronically coupled and, in turn, (partially) delocalized at 157 K. In detail, we hypothesize that such an electronic delocalization of the spin-correlated (T1T1) leads to a mixed state in the dimers. They feature a mix of delocalized excimer and localized triplet exited state character. In other words, the pure (T1T1) states at 80 K possess a slight character of delocalization at 157 K and are denoted as “partially delocalized” (T1T1)τ1 and (T1T1)τ2.
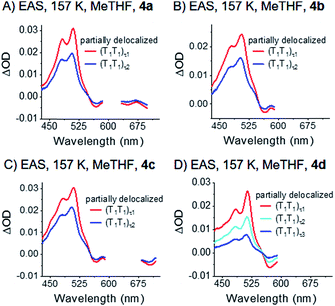 | ||
| Fig. 8 EAS of dimers 4a–d (A)–(D) measured in liquid argon-saturated MeTHF. The data were recorded at 157 K. Spectra were obtained by global analysis with a sequential model of the transient absorption data measured upon femtosecond pump-probe experiments with 730 nm excitation. Fig. S41‡ displays the raw data and Fig. S44‡ the single wavelength kinetics and corresponding fits. | ||
Overall, the decay dynamics possess lifetimes for (T1T1)τ1 and (T1T1)τ2 of 13 and 218 ps for 4a; 56 and 318 ps for 4b; 21 and 221 ps for 4c. For 4d, the decay is tri-exponential with 4, 25, and 144 ps.
The (T1T1) decay dynamics, which are monoexponential for 4a and biexponential for 4d at 80 K, are biexponential and even triexponential, respectively, at 157 K. These observations are likely related to the size of the respective trialkylsilyl-substituents: 4a features the smallest substituents and 4d the largest. Importantly, the observed temperature-dependencies exclude the possibility of different triplet pair states per molecule with different electronic natures. It is more likely that multiple conformations of the highly branched substituents exist in the excited state. Librations between these different conformations can lead to multi-exponential fits.81
Transient absorption measurements at room temperature – pentacene excimer states
As Fig. 5 indicates, the absorption features in the long-wavelength region are weak at room temperature. Excitation into the lower Davydov bands at room temperature necessitated a change of solvent from MeTHF to benzonitrile – Fig. 3. Notable is, however, that such a solvent change and an increase in temperature are accompanied by a broadening and red-shifting. Consequently, we used a 20 nm red-shifted excitation wavelength to excite exclusively into the lower Davydov band.Again, a significant decrease of all excited state lifetimes is observed by increasing the temperatures from 157 K to room temperature. Upon photoexcitation at 750 nm, typical fingerprint absorptions of the pentacene singlet excited (S1S0) state were not observed; most likely, due to a lifetime below our instrumental time resolution.
Compounds 4a–c reveal two equally intense, broad and overlapping maxima in the visible range at around 480 and 510 nm. These maxima are at the positions of the maxima of the correlated triplet pair states at 80 K. The defined shape and intensity ratio are, however, completely lost upon going from 80 K to 295 K (see Fig. 10). Compound 4d shows a further feature at 440 nm – Fig. 9 and S45–S47.‡ Additional minima in 4a–d at ca. 610–630 and 660–680 nm resemble the ground state absorption of the corresponding dimers. By virtue of the broad and featureless characteristics of the absorption bands at 480 and 510 nm, which is very uncommon for pentacene excited states, we ascribe this feature to an excimer state.
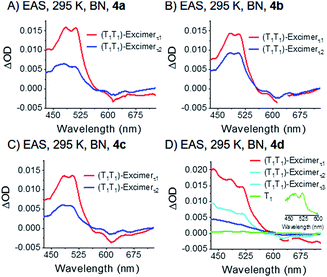 | ||
| Fig. 9 EAS of dimers 4a–d (A)–(D) measured at room temperature in argon-saturated benzonitrile (BN). The data were recorded at room temperature (295 K). Spectra were obtained by global analysis with a sequential model of the transient absorption data measured upon femtosecond pump-probe experiments with 750 nm excitation. Fig. S45‡ displays the raw data and Fig. S48‡ the single wavelength kinetics and corresponding fits. | ||
It is, thus, hypothesized that the correlated triplet pair states become more and more delocalized as the temperature increases. This implies the two triplet excited states, one localized on each pentacene and electronically decoupled at 80 K, transform with increasing temperature to an excimer state that is delocalized over both pentacenes of the dimer. To sum up these observations, we conclude that the states observed in room temperature experiments consist of two electronically interacting triplet excited states. These form a spin-correlated pair state (T1T1) over the entire temperature range. As the electronic interaction increases with temperature, the formation of a single excimer state is enabled, which is delocalized over the two pentacenes at room temperature.
Upon global analysis with a sequential model, two species, that is, (T1T1)-excimerτ1 and (T1T1)-excimerτ2, are identified for 4a–c – Fig. 9. Overall, the decay dynamics for the two excimers correlate with the size of the substituents: 5 and 50 ps for 4a; 12 and 85 ps for 4b; 29 and 99 ps for 4c. Again, the underlying substituent size-dependency corroborates our hypothesis that the multiexponential decays of the excimer states are caused by librations between different conformations of the substituents.
Compound 4d is a notable exception, and the decay is triexponential rather than biexponential with lifetimes of 2, 11, and 76 ps that correspond to (T1T1)-excimerτ1, (T1T1)-excimerτ2, and (T1T1)-excimerτ3, respectively. In addition, a small amount of a transient is identified with maxima at 480 and 520 nm which resembles the pentacene triplet excited state – Fig. 9D, inset. The lifetime exceeds several nanoseconds, although the amount formed is too low to determine the correct lifetime. We attribute this state to uncorrelated triplet (T1 + T1). The slightly different behavior of 4dversus the others of the series is rationalized by the notably increased electronic communication between the pentacenes and the pendent phenyl substituent of the alkyne.
Summary of transient absorption measurements – the nature and role of the excimer states in singlet fission
Upon photoexcitation of all four dimers 4a–d at 80 K, the signatures of a pentacene (S1S0) state are detectable and feature lifetimes close to the time resolution of our experimental setup (<200 fs). This singlet excited state transforms into a spin-correlated triplet pair state (T1T1), which mainly decays via triplet–triplet annihilation (TTA) back to the ground state (see Fig. 11). Moving to higher temperatures leads to an increase of molecular vibrational motion and to a scenario in which localization of the triplets on the individual pentacenes is lost (see Fig. 10). In other words, the two triplet excited states in (T1T1) are electronically coupled at room temperature by vibrational modes to form an excimer state. Extrapolation of the (S1S0) lifetimes to room temperature implies that they are far shorter than the time resolution of our experimental setup, and, thus, not detectable. It is, therefore, impossible to draw a meaningful conclusion about the excimeric character of (S1S0) at room temperature. Please note the work on microcrystalline pentacene films, which does show a Davydov splitting of the S1 ← S0 absorptions.65 Comparing 4a–d with a recently published J-coupled pentacene dimer provides insight into the CT-character of (S1S0). For example, a combination of excitonic and CT-coupling in (S1S0) counteracts to the strong excitonic features in the ground-state absorption spectrum.43 As 4a–d show a strong Davydov distortion in the ground-state, it is rather unlikely that (S1S0) of 4a–d mixes strongly with a CT-state. Moreover, a comparison of the (T1T1)-excimers in 4a–d with the absorption spectra of the TIPS-pentacene radical anion and radical cation did not reveal any CT-bands in the transient excimer spectra (Fig. S49 and S50‡).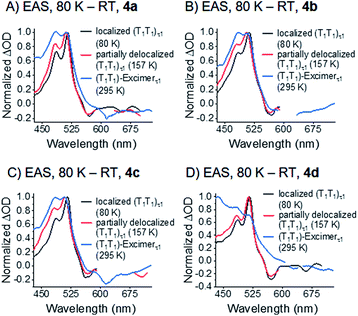 | ||
| Fig. 10 EAS of the τ1 state of the correlated triplet pair of dimers 4a–d (A)–(D) at different temperature. See Fig. 7–9 for the corresponding global fits. | ||
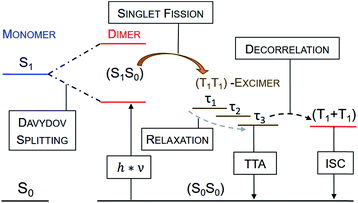 | ||
| Fig. 11 Generalized mechanistic scheme illustrating all observed transitions and transient species at room temperature. No (T1T1)-excimerτ3 was observed for dimers 4a–c. Triplet–triplet annihilation (TTA) is the main deactivation channel of the (T1T1)-excimer state for all dimers. Only dimer 4d shows a minor amount of free triplet, which is most likely generated by decorrelation and, therefore, termed as (T1 + T1). The (S1S0) state is not directly observable at room temperature due to a too short lifetime, but its population is evidenced by measurements at cryogenic temperatures (see Fig. 6). | ||
Conclusions
A xanthene spacer has been used to link two pentacene chromophores and provides four dimers in which the pentacene moieties show direct intramolecular π-overlap in solution and the solid-state. These dimers have been designed specifically to explore processes that are linked to Davydov splitting and its effect on SF. To this end, quantum chemical calculations, steady state absorption, and electrochemical measurements have been used to corroborate that π–π-interactions cause Davydov bands. The absorption characteristics of the dimers suggest that the Davydov splitting depends on the solvent viscosity, and this premise is confirmed by temperature dependent absorption measurements in MeTHF between 80 and 295 K. As such, the strength of the direct intramolecular π-overlap between the pentacene chromophores is dictated by vibrational motions. Calculations and observations both suggest that Davydov splitting is strengthened by mixing with other π–π single excitations between unsymmetrical combinations of the π-orbitals of the individual pentacene moieties.Transient absorption measurements establish the excited state dynamics of SF occurring after exciting the excitonically split states. Temperature-dependent assays in liquid and frozen solutions facilitate the observation, and subsequent identification of a correlated triplet (T1T1) pair at 80 K, which becomes more and more coupled electronically upon increasing the temperature to form an excimer state at 295 K as the product of ultra-fast SF. Notably, the role and nature of the (T1T1)-excimer states in 4a–d is not inconsistent with a recent study, in which an excimer state of likely (T1T1) character fails to promote triplet decorrelation:66 for tetracene monomers in solution, which lack fixed and/or defined orientation relative to each other, direct SF leading to decorrelated T1 states occurs at intermolecular distances larger than active in excimer formation, where triplet–triplet annihilation dominates. Note that SF is endothermic in tetracene but exothermic in pentacene. Additional differences exist: most importantly, 4a–d are rigid dimers with electronic ground-state interactions and directly accessible photoexcited dimer-states, as demonstrated by Davydov splitting. Nevertheless, the excimer states in the tetracene monomer solution and in 4a–d undergo both (mostly) triplet–triplet annihilation.
It would be very interesting to see if the tetracene excimer states can be localized by reducing the thermal energy. Such experiments are challenging, but the results would be of utmost importance for unraveling the true nature of the tetracene excimer. They would also provide further insight into the importance of photoexcitable dimer-states as a result of Davydov splitting.
Hopefully, the results presented will guide the way to such experiments and promote more facile analyses mechanisms of SF for acenes in a broad range of morphologies that might exhibit Davydov splitting such as, for example, aggregates, crystals, and films.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for support of their work in this area from the DFG Cluster of Excellence “Engineering of Advanced Materials” (grant numbers GU 517/17-1 and 182849149 – SFB 953), “Solar Technologies go Hybrid” (an initiative of the Bavarian State Ministry for Science, Research and Art), and the Emerging Fields Initiative “Singlet Fission” (supported by FAU). In Canada support from the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canadian Foundation for Innovation (CFI) is gratefully acknowledged. B. S. B. gratefully acknowledges financial support in form of a PhD scholarship from “Studienstiftung des deutschen Volkes”. We thank Dr Dan Lehnherr for the initial synthesis of compound S2. The authors acknowledge M. Thoss, P. B. Coto and R. R. Seelam for helpful discussions.Notes and references
- J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS.
- C. E. Swenberg and W. T. Stacy, Chem. Phys. Lett., 1968, 2, 327–328 CrossRef CAS.
- N. Geacintov, M. Pope and F. Vogel, Phys. Rev. Lett., 1969, 22, 593–596 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- L. Yang, M. Tabachnyk, S. L. Bayliss, M. L. Böhm, K. Broch, N. C. Greenham, R. H. Friend and B. Ehrler, Nano Lett., 2015, 15, 354–358 CrossRef CAS PubMed.
- S. R. Yost, J. Lee, M. W. B. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao, K. Johnson, M. Y. Sfeir, M. G. Bawendi, T. M. Swager, R. H. Friend, M. A. Baldo and T. Van Voorhis, Nat. Chem., 2014, 6, 492–497 CrossRef CAS PubMed.
- B. Ehrler, K. P. Musselman, M. L. Böhm, R. H. Friend and N. C. Greenham, Appl. Phys. Lett., 2012, 101, 153507 CrossRef.
- P. J. Jadhav, P. R. Brown, N. Thompson, B. Wunsch, A. Mohanty, S. R. Yost, E. Hontz, T. Van Voorhis, M. G. Bawendi, V. Bulović and M. A. Baldo, Adv. Mater., 2012, 24, 6169–6174 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114102 CrossRef PubMed.
- G. B. Piland, J. J. Burdett, R. J. Dillon and C. J. Bardeen, J. Phys. Chem. Lett., 2014, 5, 2312–2319 CrossRef CAS PubMed.
- W. L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X. Y. Zhu, Science, 2011, 334, 1541–1545 CrossRef CAS PubMed.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS PubMed.
- N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2016, 138, 617–627 CrossRef CAS PubMed.
- T. Yamakado, S. Takahashi, K. Watanabe, Y. Matsumoto, A. Osuka and S. Saito, Angew. Chem., 2018, 130, 5536–5541 CrossRef.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X. Y. Zhu, Nat. Chem., 2017, 9, 341–346 CrossRef CAS PubMed.
- H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205 CrossRef CAS PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, J. Am. Chem. Soc., 2010, 132, 16302–16303 CrossRef CAS PubMed.
- J. N. Schrauben, J. L. Ryerson, J. Michl and J. C. Johnson, J. Am. Chem. Soc., 2014, 136, 7363–7373 CrossRef CAS PubMed.
- A. Akdag, A. Wahab, P. Beran, L. Rulíšek, P. I. Dron, J. Ludvík and J. Michl, J. Org. Chem., 2015, 80, 80–89 CrossRef CAS PubMed.
- J. Yu, L.-M. Fu, L.-J. Yu, Y. Shi, P. Wang, Z.-Y. Wang-Otomo and J.-P. Zhang, J. Am. Chem. Soc., 2017, 139, 15984–15993 CrossRef CAS PubMed.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS PubMed.
- S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135, 14701–14712 CrossRef CAS PubMed.
- E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2016, 8, 1120 CrossRef CAS PubMed.
- E. A. Margulies, J. L. Logsdon, C. E. Miller, L. Ma, E. Simonoff, R. M. Young, G. C. Schatz and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 663–671 CrossRef CAS PubMed.
- P. E. Hartnett, E. A. Margulies, C. M. Mauck, S. A. Miller, Y. Wu, Y.-L. Wu, T. J. Marks and M. R. Wasielewski, J. Phys. Chem. B, 2016, 120, 1357–1366 CrossRef CAS PubMed.
- C. E. Miller, M. R. Wasielewski and G. C. Schatz, J. Phys. Chem. C, 2017, 121, 10345–10350 CrossRef CAS.
- S. Lukman, J. M. Richter, L. Yang, P. Hu, J. Wu, N. C. Greenham and A. J. Musser, J. Am. Chem. Soc., 2017, 139, 18376–18385 CrossRef CAS PubMed.
- J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597–8607 CrossRef CAS PubMed.
- E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X. Y. Zhu, M. Y. Sfeir, L. M. Campos and N. Ananth, ACS Cent. Sci., 2016, 2, 316–324 CrossRef CAS PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, S. R. Reddy, B. T. Phelan, M. D. Krzyaniak, P. B. Coto, M. K. Volland, R. M. Young, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Chem, 2018, 4, 1092–1111 CAS.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103 CrossRef PubMed.
- M. H. Farag and A. I. Krylov, J. Phys. Chem. C, 2018, 122, 25753–25763 CrossRef CAS.
- M. Chen, Y. J. Bae, C. M. Mauck, A. Mandal, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2018, 140, 9184–9192 CrossRef CAS PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, B. T. Phelan, M. D. Krzyaniak, S. R. Reddy, P. B. Coto, N. E. Horwitz, R. M. Young, F. J. White, F. Hampel, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Nat. Commun., 2017, 8, 15171 CrossRef CAS PubMed.
- E. Kumarasamy, S. N. Sanders, M. J. Y. Tayebjee, A. Asadpoordarvish, T. J. H. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low, D. W. Paley, J. C. Dean, B. Choi, G. D. Scholes, M. L. Steigerwald, N. Ananth, D. R. McCamey, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2017, 139, 12488–12494 CrossRef CAS PubMed.
- T. Sakuma, H. Sakai, Y. Araki, T. Mori, T. Wada, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. A, 2016, 120, 1867–1875 CrossRef CAS PubMed.
- S. Lukman, K. Chen, J. M. Hodgkiss, D. H. P. Turban, N. D. M. Hine, S. Dong, J. Wu, N. C. Greenham and A. J. Musser, Nat. Commun., 2016, 7, 13622 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, S. N. Sanders, E. Kumarasamy, L. M. Campos, M. Y. Sfeir and D. R. McCamey, Nat. Phys., 2017, 13, 182–188 Search PubMed.
- S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss, J. Wu, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2015, 25, 5452–5461 CrossRef CAS.
- H. Yamagata, J. Norton, E. Hontz, Y. Olivier, D. Beljonne, J. L. Brédas, R. J. Silbey and F. C. Spano, J. Chem. Phys., 2011, 134, 204703 CrossRef CAS PubMed.
- J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452–483 CrossRef CAS PubMed.
- Q. Miao, X. Chi, S. Xiao, R. Zeis, M. Lefenfeld, T. Siegrist, M. L. Steigerwald and C. Nuckolls, J. Am. Chem. Soc., 2006, 128, 1340–1345 CrossRef CAS PubMed.
- E. Busby, T. C. Berkelbach, B. Kumar, A. Chernikov, Y. Zhong, H. Hlaing, X. Y. Zhu, T. F. Heinz, M. S. Hybertsen, M. Y. Sfeir, D. R. Reichman, C. Nuckolls and O. Yaffe, J. Am. Chem. Soc., 2014, 136, 10654–10660 CrossRef CAS PubMed.
- S. Tretiak, W. M. Zhang, V. Chernyak and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13003 CrossRef CAS.
- J. D. Cook, T. J. Carey and N. H. Damrauer, J. Phys. Chem. A, 2016, 120, 4473–4481 CrossRef CAS PubMed.
- T. J. Carey, J. L. Snyder, E. G. Miller, T. Sammakia and N. H. Damrauer, J. Org. Chem., 2017, 82, 4866–4874 CrossRef CAS PubMed.
- X. Feng and A. I. Krylov, Phys. Chem. Chem. Phys., 2016, 18, 7751–7761 RSC.
- J. Seibt, P. Marquetand, V. Engel, Z. Chen, V. Dehm and F. Würthner, Chem. Phys., 2006, 328, 354–362 CrossRef CAS.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797–14805 RSC.
- S.-H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef PubMed.
- M. J. Y. Tayebjee, K. N. Schwarz, R. W. MacQueen, M. Dvořák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, J. Phys. Chem. C, 2016, 120, 157–165 CrossRef CAS.
- D. Beljonne, H. Yamagata, J. L. Brédas, F. C. Spano and Y. Olivier, Phys. Rev. Lett., 2013, 110, 226402 CrossRef CAS PubMed.
- K. Kolata, T. Breuer, G. Witte and S. Chatterjee, ACS Nano, 2014, 8, 7377–7383 CrossRef CAS PubMed.
- C. M. Mauck, P. E. Hartnett, E. A. Margulies, L. Ma, C. E. Miller, G. C. Schatz, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2016, 138, 11749–11761 CrossRef CAS PubMed.
- K. E. Brown, W. A. Salamant, L. E. Shoer, R. M. Young and M. R. Wasielewski, J. Phys. Chem. Lett., 2014, 5, 2588–2593 CrossRef CAS PubMed.
- K. M. Lefler, K. E. Brown, W. A. Salamant, S. M. Dyar, K. E. Knowles and M. R. Wasielewski, J. Phys. Chem. A, 2013, 117, 10333–10345 CrossRef CAS PubMed.
- H. L. Stern, A. J. Musser, S. Gelinas, P. Parkinson, L. M. Herz, M. J. Bruzek, J. Anthony, R. H. Friend and B. J. Walker, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7656–7661 CrossRef CAS PubMed.
- H. Marciniak, I. Pugliesi, B. Nickel and S. Lochbrunner, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235318 CrossRef.
- C. B. Dover, J. K. Gallaher, L. Frazer, P. C. Tapping, A. J. Petty Ii, M. J. Crossley, J. E. Anthony, T. W. Kee and T. W. Schmidt, Nat. Chem., 2018, 10, 305 CrossRef CAS PubMed.
- H. Liu, V. M. Nichols, L. Shen, S. Jahansouz, Y. Chen, K. M. Hanson, C. J. Bardeen and X. Li, Phys. Chem. Chem. Phys., 2015, 17, 6523–6531 RSC.
- S. R. Reddy, P. B. Coto and M. Thoss, Chem. Phys., 2018, 515, 628–634 CrossRef CAS.
- D. Lehnherr, A. H. Murray, R. McDonald and R. R. Tykwinski, Angew. Chem., Int. Ed., 2010, 49, 6190–6194 CrossRef CAS PubMed.
- Y. Morisaki and Y. Chujo, Tetrahedron Lett., 2005, 46, 2533–2537 CrossRef CAS.
- J. L. Marshall, D. Lehnherr, B. D. Lindner and R. R. Tykwinski, ChemPlusChem, 2017, 82, 967–1001 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052 CrossRef PubMed.
- F. C. Spano, Annu. Rev. Phys. Chem., 2006, 57, 217–243 CrossRef CAS PubMed.
- CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press, Taylor & Francis, 2018 Search PubMed.
- J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 CrossRef CAS PubMed.
- F. R. Beierlein, O. G. Othersen, H. Lanig, S. Schneider and T. Clark, J. Am. Chem. Soc., 2006, 128, 5142–5152 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to Professor Fritz Wasgestian on the occasion of his 85th birthday. |
| ‡ Electronic supplementary information (ESI) available: Supplemental Information includes synthetic protocols, details about the analysis of photophysical data, 50 figures and X-ray crystallographic data for 1a (cif), 1d (cif), 4b (cif), and 4c (cif). CCDC 1839936, 1839935, 1839934 and 1839933. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc00384c |
| § These authors contributed equally. |
| ¶ Xanthene linked tetracenes have been reported.19,67 |
| || Compound 4d is unstable under voltage and its electrochemistry was, therefore, not further evaluated. |
| ** The fingerprint at 450 nm is absent; probably due to the wavelength dependent character (chirp) of the instrument response function (IRF); it is with our setup stronger for measurements in the visible (430–760 nm) than in the NIR (800–1500 nm). This renders an extraction of very short-lived species (<200 fs) far more challenging for the visible than for the NIR. |
| This journal is © The Royal Society of Chemistry 2019 |