DOI:
10.1039/C9SC00770A
(Edge Article)
Chem. Sci., 2019,
10, 5807-5814
Continuous nonenzymatic cross-replication of DNA strands with in situ activated DNA oligonucleotides†
Received
14th February 2019
, Accepted 28th April 2019
First published on 30th April 2019
Abstract
Continuous enzyme-free replication of oligonucleotides is central for open-ended evolution experiments that mimic the origin of life. Here, we studied a reaction system, whereby two 24mer DNA templates cross-catalyzed each other's synthesis from four 12mer DNA fragments, two of which were in situ activated with the condensing agent 1-ethyl-3-(3-dimethylamino-propyl)carbodiimide (EDC). We circumvented the problem of product inhibition by melting the stable product duplexes for their reuse as templates in the following ligation step. The system reproduced itself through ligation/melting cycles and survived exponential dilution. We quantified EDC-induced side reactions in a detailed kinetic model. The model allowed us to analyze the effects of various reaction rates on the system's kinetics and confirmed maximal replication under the chosen conditions. The presented system enables us to study nonenzymatic open-ended evolution experiments starting from diverse sequence pools.
Introduction
How functional sequences arose from random oligonucleotide pools produced by polymerization of nucleobases on the early Earth1–4 is an intriguing and open question. Efficient replication of oligonucleotides seems to be essential for this process5 but had to occur in the absence of complex proteins.6 To prove that replication of RNA is possible by RNA itself, much of the origin of life research has been focused on evolving a ribozyme with polymerase activity. However, even the best designs of polymerase ribozymes7,8 cannot yet copy full lengths of their own sequences, inhibiting further open-ended evolution studies. These ribozymes are more than 100 nucleotides in length, and it is unclear which pathways could have originally led to such long specific sequences on the early Earth.9
Replication-by-ligation of short oligonucleotides could provide a solution to the problems of sequence replication and strand elongation towards the first ribozymes.10–13 Von Kiedrowski studied replication-by-ligation of 3mer oligonucleotide fragments on 6mer templates using 1-ethyl-3-(3-dimethylamino-propyl)carbodiimide (EDC) as a condensing agent under isothermal conditions.14,15 This isothermal replication was limited to short strands.
Templated ligation of longer strands at a constant temperature would lead to the formation of stable product duplexes inhibiting further strand replication.16 This stable product formation is known as a problem of product inhibition. Additionally, the studies of von Kiedrowski used a more efficient replication with a phosphoramidate bond forming at the ligation site instead of the naturally occurring phosphodiester bond.17 DNA systems with a phosphoramidate bond are not biologically motivated and would be incompatible with the deep sequencing analysis required to study sequence space evolution from random strands.
Here, we studied replication-by-ligation of 12mer oligonucleotide fragments on 24mer templates using EDC. EDC is used in the origin of life field as a model molecule to study polymerization, replication, and ligation under abiotic conditions.18–21 The chosen ligation chemistry allowed us to form natural phosphodiester bonds at the ligation site. To overcome product inhibition, we used temperature cycling22 as a possible nonequilibrium setting for the origin of life. Such a setting could have existed on the early Earth in temperature gradients across water filled porous volcanic rocks.23,24
The nonenzymatic chemistry under high temperature conditions makes side reactions a significant possibility. However, side reactions are likely inevitable in any complex environment due to the prebiotic clutter.25 We showed that our system reproduced over several ligation/melting cycles and survived the exponential dilution conditions despite the side reactions. Thus, temperature cycling as a means to overcome product inhibition in the absence of enzymes seems to be a realistic possibility.
Results and discussion
Experimental system
We implemented our system (“Input DNA” in Fig. 1a) with two 24mer DNA templates ab and BA and complementary fragments A (12mer), ∼B (15mer, with 12 bases binding to ab), b (12mer), and ∼a (21mer, with 12 bases binding to BA). The template sequences consisted of adenine and thymine nucleobases and did not form hairpins. The strands ∼a (tagged a) and ∼B (tagged B) contained polycytidine tags at the 5′-ends for individual detection via electrophoresis (Fig. S1b†). Phosphate groups at the 3′-ends of ∼a and ∼B allowed for the ligation reaction.
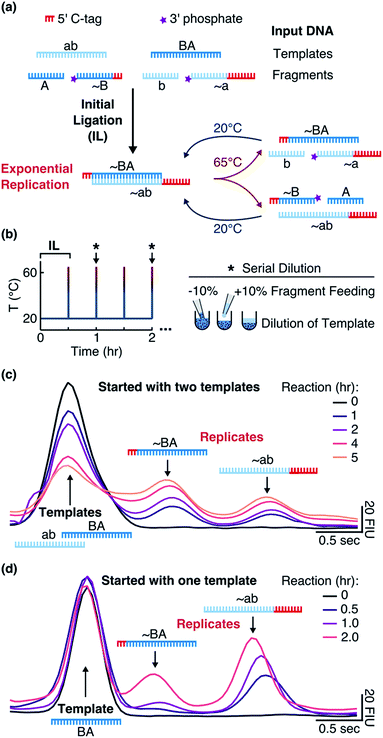 |
| | Fig. 1 Replication system and detection. (a) When the templates were mixed with the fragments and EDC at 20 °C, an initial ligation (IL) occurred that formed the replicates ∼BA and ∼ab. By implementing temperature cycling, the replicates were then exponentially amplified. (b) The reaction was cycled between 20 °C for 0.5 hours and 65 °C for 1 second with the heating and cooling rates of 8 and 6 °C s−1, respectively. Every hour (black star and arrow), 10% of the reaction volume was replaced with 10% of the fragment mix in the reaction buffer. (c) Tagged replicates separated from the templates on a microfluidic gel electrophoresis chip. Reactions were started with 1 μM of each template and 10 μM of each fragment in the reaction buffer and the aliquots were taken after 0, 1, 2, 4, and 5 hours. (d) The same as in (c) but reactions were started with 1 μM of only template BA and aliquots were taken after 0, 0.5, 1, and 2 hours. Additional details are explained in ESI 1.† | |
Addition of EDC started a nonenzymatic ligation of the fragments on the corresponding templates (“Initial Ligation” in Fig. 1a), producing the tagged replicates ∼BA (27mer with a 3nt tag) and ∼ab (33mer with a 9nt tag) with a phosphodiester bond at the ligation site. Once the replicates formed, they were cross-catalytically replicated with the help of temperature cycling (“Exponential Replication” in Fig. 1a).
Surviving replicator
To monitor the reaction, we ran aliquots from different time points on a Bioanalyzer instrument (Fig. 1c) and quantified product formation by fitting Gaussian functions as described in ESI 1.† We observed that the concentration of each motif (BA + ∼BA or ab + ∼ab) consistently increased (Fig. 2a). Due to the hourly dilution scheme, the concentration of the initial templates at the same time decreased exponentially. In total, each motif amplified (2.2 ± 0.5)-fold within 6 hours (Table S1†), while only 59% of the original templates were still present after 6 hours. Therefore, despite diluting the templates, the information-containing motifs ab and BA survived in the system.
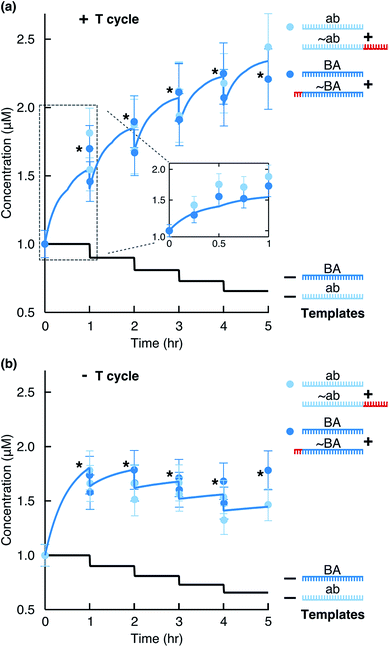 |
| | Fig. 2 Replication by ligation. The stars mark data points just before a dilution step. The solid blue line shows the full kinetics simulation of the system. The solid black line indicates the calculated concentration of each template considering the dilution steps. (a) Concentration of replicates from Fig. 1c quantified for the total ab and BA motifs (light and dark blue circles). For hours 1, 2, 3, and 4, concentrations before and after the dilution steps were quantified. The inset shows time points taken within the first hour and the simulation result for the first hour. (b) The reaction performed in the absence of temperature cycling but with dilution/feeding steps. | |
Without the 3′-phosphates (Fig. S2a†) or in the absence of templates (Fig. S2b†), the reaction did not produce clear product peaks. The survival of the replicating strands depended critically on temperature cycling. In its absence, the system could not overcome product inhibition and the replicating strands slowly diluted under the feeding/dilution conditions of the reaction (Fig. 2b).
To make sure that the reaction products acted as templates as reaction progressed, we also started the reaction with one template BA. In this case, ∼BA could form only after ∼ab formed. Indeed, we observed the formation of ∼ab that then triggered the formation of ∼BA (Fig. 1d).
These results indicate that 24nt-long DNA strands with defined sequences can replicate by ligation in a templated fashion under simple in situ activation conditions. Similar conditions could also support oligonucleotide polymerization18–20 as a possible source of short strands on the early Earth.
EDC-driven side reactions
When carbodiimides, such as EDC, are used for condensation of carboxylic acids with weak nucleophiles, like carboxylic acids or pyrophosphates,19 an unwanted side reaction arises as a consequence of the relatively low nucleophilicity. In the side reaction, the O-acylisourea intermediate rearranges into the stable non-reactive N-acylurea.20
To search for signs of side reactions in our system, we took a closer look at the fragments incubated with EDC over time. We observed that the fragments bearing 3′-phosphate groups decreased in concentration and a shoulder formed next to the peak assigned to fragment ∼a (Fig. 3a). Shoulder formation only occurred in the presence of the 3′-phosphate group (Fig. S3b†), suggesting that it originated from a side reaction between EDC and the 3′-phosphate group (Fig. S3c†). Since the EDC-modified fragments are less negatively charged and 155 Da heavier than unmodified fragments, they were expected to run slower in a gel electrophoresis experiment, confirmed by the position of the shoulder on the right of the peak. Additionally, we identified in the HPLC-MS analysis the masses for an ‘∼a + EDC’ side product (corresponding to the structure in Fig. S3c†) and for a circularization product of ∼a (Fig. S4, ESI 2, Table S2†).
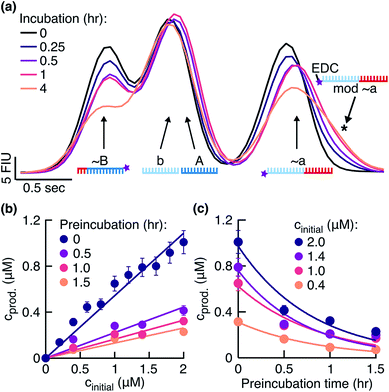 |
| | Fig. 3 Effect of fragment side reaction on the ligation rate. (a) Fragments were incubated in the reaction buffer under the temperature cycling conditions. Peaks were identified using the ladder peak (Fig. S3a†). The signal from the phosphorylated fragments decreased and a shoulder formed on the right of the ∼a peak (black star). (b) Product concentrations 0.5 hours after the start of the reaction plotted against initial template concentrations. Reactions were started with fragments preincubated in the reaction buffer for 0, 0.5, 1, and 1.5 hours before the addition of templates. Linear fits gave ligation rates klig of 1.08 ± 0.04, 0.44 ± 0.04, 0.32 ± 0.02, and 0.26 ± 0.02 h−1, respectively. The respective replication yields were (61 ± 10)%, (28 ± 10)%, (19 ± 4)%, and (15 ± 3)% in 0.5 hours. (c) Data from (b) replotted to demonstrate the exponential decrease in product concentrations during the preincubation in EDC. The exponential fits yielded the rate constants of 1.14 ± 0.12, 1.14 ± 0.24, 1.38 ± 0.36, and 1.26 ± 0.24 h−1 for the initial template concentrations of 2.0, 1.4, 1.0, and 0.4 μM, respectively. | |
The fragment ∼B decreased in concentration over time as well (Fig. 3a). This result suggested that EDC also modified ∼B at its 3′-phosphate group. The expected shoulder in this case was overlaid by the dominant peak combined from the individual peaks of fragments b and A. Our system successfully replicated despite the observed side reaction (Fig. 2a).
In the next step, we investigated and compared the influence of the ligation and side reaction rates in the system. To measure the ligation rate under the reaction conditions, we followed the reactions with varied initial template concentrations for 0.5 hours and quantified the product concentrations (Fig. 3b, dark purple filled circles). The product concentration showed linear dependence on the initial template concentration, suggesting underlying exponential behavior of the reaction. The ligation rate obtained from the linear fit was 1.08 ± 0.04 h−1. The experiment resulted in a replication yield of (61 ± 10) % in 0.5 hours, where the replication yield is defined as the replicate concentration at time t divided by the template concentration at time t = 0.
To quantify the effect of the side reaction on the ligation rate, we next incubated the fragments in EDC for 0.5, 1.0, or 1.5 hours in the absence of templates under the temperature cycling conditions of the reaction. After the so-called preincubation time without templates, we added the template strands to start the ligation reaction. The ligation rate decreased to 0.44 ± 0.04, 0.32 ± 0.02, and 0.26 ± 0.02 h−1 after 0.5, 1.0, and 1.5 hours of preincubation, respectively (Fig. 3b). Respective replication yields were (28 ± 10)%, (19 ± 4)%, and (15 ± 3)% in 0.5 hours. For a preincubation time of 1.5 hours, the replication rate and yield decreased 4-fold compared to no preincubation.
To approximate the side reaction rate, we studied the product concentration decrease over the fragment preincubation time (Fig. 3c). The exponential fits with assumed zero asymptote averaged to an effective first order rate constant of 1.23 ± 0.11 h−1 with the error given as the standard deviation. Despite the same order of magnitude between the ligation and side reaction rates, the designed system survived the exponential dilution and successfully replicated for several ligation/melting cycles.
Kinetic model of the replication reaction
The design and further optimization of replication systems requires a deeper understanding of the underlying kinetic behavior. We modeled the reaction with a set of rate equations (eqn (1)–(23)). Eqn (1)–(4) describe the reversible formation of the intermolecular complexes between templates and their complementary fragments with association and dissociation rate constants k12nton and k12nt,Toff, where T refers to the temperature dependence of the dissociation rate. Following the formation of the complex, an irreversible ligation reaction occurs with a ligation rate klig (eqn (5) and (6)). We did not differentiate between the ligation kinetics for templates and replicates that contained tags since the tags had little effect on the ligation reaction (Fig. 4a). The resulting complex reversibly dissociates with dissociation and association rate constants k24nt,Toff and k24nton (eqn (7)). Complementary fragments also reversibly bind to each other with association and dissociation rate constants k12nton and k12nt,Toff (eqn (8) and (9)).| | 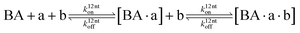 | (1) |
| | 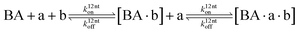 | (2) |
| | 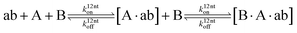 | (3) |
| | 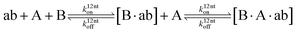 | (4) |
| |  | (5) |
| |  | (6) |
| | 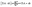 | (7) |
| | 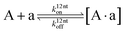 | (8) |
| | 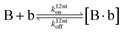 | (9) |
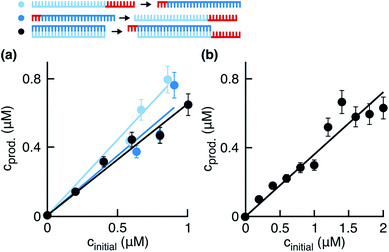 |
| | Fig. 4 Ligation rate for the simulation. (a) Product concentrations 0.5 hours after the start of the reaction. Templates were replaced with ∼ab or ∼BA (light and dark blue points) for the initial ligation, or the initial ligation was started with templates as before (black points). The ligation rates from the linear fits were 1.78 ± 0.08, 1.40 ± 0.14, 1.32 ± 0.06 h−1, respectively. Respective replication yields were (87 ± 11)%, (67 ± 15)%, and (55 ± 6)% in 0.5 hours. (b) Product concentrations quantified 10 min after the start of the reaction. The linear fit produced a ligation rate of 2.16 ± 0.12 h−1, with a replication yield of (39 ± 7) % in 10 minutes. | |
We observed in the previous experiments that the replication rate slowed down during the first 30 minutes of the reaction (Fig. 2a, inset). We assumed that the product inhibition and side reactions had already affected the reaction, and the ligation rate quantified from these data was being underestimated. To obtain the value of klig independent of the product inhibition and side reaction effects, we measured product concentrations 10 min after the start of the reaction for different initial template concentrations (Fig. 4b). The linear fit gave a ligation rate of 2.16 ± 0.12 h−1, about two-fold higher than when measuring product formation after 30 minutes.
We modeled the association rate as length-independent and obtained the value for k12nton and k24nton from the literature26,27 (ESI 3†). The rates k12nt,20°Coff, k12nt,65°Coff, k24nt,20°Coff, and k24nt,65°Coff were estimated from the analysis of melting curves, as described in detail in ESI 3.† We did not explicitly model the hydrolysis of EDC because a more than 2500-fold excess of EDC over DNA is expected to be present at the end of the reaction28–30 (ESI 3†). To model feeding and dilution, we introduced rates kfeed and kdil defined by the experimental feeding and dilution protocol.
We next added side reaction pathways to the system of equations. Based on the experimental observation (Fig. 3a, S4†), we allowed the fragments ‘B’ and ‘a’ to turn into side products with a side reaction rate ks.r. independent of the fragments being in a free or a bound state (eqn (10)–(17)). The resulting fragments B* and a* still bind to complementary fragments, templates, and replicates (eqn (18)–(23)).
| |  | (10) |
| | 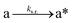 | (11) |
| | 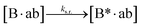 | (12) |
| | 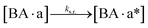 | (13) |
| | 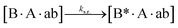 | (14) |
| | 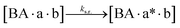 | (15) |
| | 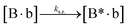 | (16) |
| | 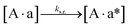 | (17) |
| | 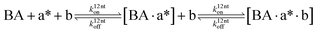 | (18) |
| | 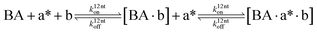 | (19) |
| | 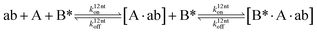 | (20) |
| | 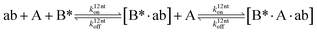 | (21) |
| | 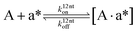 | (22) |
| | 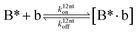 | (23) |
However, B* and a* cannot support ligation (
eqn (18)–(21)), sequestering templates and replicates from the reaction.
To simulate the reaction curves, we solved 23 ODEs based on eqn (1)–(23) in MATLAB (Table S4†). We then performed a least squared curve fit of the ODE solution to our data with ks.r. as a fit parameter and the above approximated side reaction rate (Fig. 3c) as an initial value. For the upper and lower bounds of k12nt,20°Coff and k24nt,20°Coff value estimates (ESI 3†), the fit produced the ks.r. values of 2.69 h−1 and 2.63 h−1, respectively. This was higher, but still in good agreement with the experimental data. The discrepancy between the fitted and originally approximated ks.r. values likely originated from the temperature dependence of the measured side reaction rate or from the effects of the EDC hydrolysis product, its urea, on the DNA duplex stability. Both effects were not explicitly modeled. The theoretical fit reproduced well the experimental behavior of the system (Fig. 2a, solid blue line).
When the data were fit in the absence of temperature cycling (Fig. 2b), the fitted side reaction rate was 10 times lower. This lower rate confirmed the expectation that the side reaction is strong at elevated temperatures even though the temperature spikes lasted seconds in the experiment.
The model is central to optimizing reaction conditions that support sustained replication. It shows that the replication system is very sensitive to the modulation of the ligation and side reaction rates. An increase in the side reaction rate and decrease in the ligation rate led to a system with a negative fitness (Fig. 5a, red and purple lines). However, an increase in the ligation rate or decrease in the side reaction rate by a factor of 1.5 significantly enhanced the replication (Fig. 5a, orange solid and dashed lines). The model also predicted that a decrease in the side reaction rate by a factor of 2 would result in a much stronger enhancement of replication compared to the effect from the increase in the ligation rate by the same factor (Fig. 5b). Since the side reaction rate showed such a strong inhibiting effect, the focus should be placed on finding ways to reduce it. This can be achieved by, for example, finding a condensing agent with less side product formation, e.g. diamidophosphate,31 a mechanism for a turnover of by-products, or a more gentle environment for strand separation.
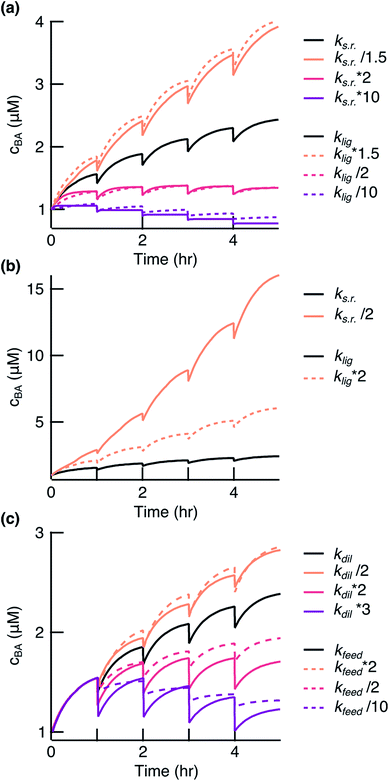 |
| | Fig. 5 Simulation of the ligation reaction. Black lines show the fit results to the experimental data. (a) The survival of the replicates depended on balancing ks.r. and klig. (b) Decreasing ks.r. gave a stronger effect than enhancing klig. (c) The survival of the replicates also depended on balancing feeding and dilution. | |
Finding a balance between dilution and feeding is of equal importance. A higher dilution rate or less fragment feeding resulted in a negative fitness of the system (Fig. 5c, red and purple lines). It could be of interest to decrease the dilution rate or increase the feeding to drive stronger amplification (Fig. 5c, orange lines). However, a too low dilution rate would lift the environmental pressure that we desire for fast evolution experiments. There is also a limit to how strong the feeding could be before feeding concentration of fragments becomes insoluble. We have also presented in the ESI† how other parameters affect the replication reaction (Fig. S6†). Taken together, the model will serve as a powerful tool to guide towards a faster and less wasteful replicator.
Conclusions
The presented DNA cross-replicator is a first but essential step towards open-ended evolution experiments from random oligonucleotides. In our system, 24mer strands replicated within a realistic timeframe and with linkage-chemistry enabling analysis by sequencing. Melting allowed the reuse of strands in the replication reaction leading to the survival of the system against the exponential dilution despite the side reactions. The presented reaction works on a defined set of DNA strands. However, it is expected that any two strands brought together by a template in the presence of EDC and 3′-phosphate groups would ligate. The efficiency of templated ligation between random strands would likely depend on the geometry and, thus, the sequence composition of the ligation site.32 The resulting longer molecules can then serve as templates in other reactions. The presented reaction opens a window to study how specific sequences were selected from random pools of short oligonucleotides likely present on the prebiotic Earth.
Experimental
Materials
100 mM MOPS at pH 6.5, adjusted with NaOH, was used as the control buffer. 400 mM EDC freshly dissolved in the control buffer was used as the reaction buffer. MOPS was purchased from Sigma Life Science (M1254-100G) and EDC-HCl was purchased from Carl Roth GmbH (Art.-Nr. 2156.2). Only nuclease-free water from Ambion (AM9932) was used in all experiments.
DNA oligonucleotides
All DNA oligonucleotides were purchased from biomers.net GmbH with HPLC purification. The sequences were as follows. Template BA: 5′-TTT ATT ATT TTA TAT TAT TTA TTT-3′, template ab: 5′-AAA TAA ATA ATA TAA AAT AAT AAA-3′, replicate ∼BA: 5′-CCC TTT ATT ATT TTA TAT TAT TTA TTT-3′, replicate ∼ab: 5′-CCC CCC CCC AAA TAA ATA ATA TAA AAT AAT AAA-3′, fragment ∼B: 5′-CCC TTT ATT ATT TTA-3′ (with or without a 3′-phosphate group for reaction or control experiments), fragment b: 5′-TAA AAT AAT AAA-3′, fragment A: 5′-TAT TAT TTA TTT-3′, fragment ∼a: 5′-AAA TAA ATA ATA-3' (with or without a 3′-phosphate group for reaction or control experiments), normalization strand (Fig. S1a†): 5′-TAG TTA TGT CGA TAC GAG ACA ACA CCA TAT GCA TTT AAG TCG CTT GAA ATT GCT ATA AGC AGA GCA CTC GTA TCG ACA TAA CTA-3′.
General reaction procedure
The DNA was mixed on ice at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with 2× reaction buffer in a maximum recovery PCR tube (Axygen, a brand of Corning Life Sciences). Promptly, the tube was placed in a qTower3G cycler (Analytik Jena AG) at 20 °C to start temperature cycling (with 8 °C s−1 heating rate, 6 °C s−1 cooling rate). For serial dilution, the cycler was paused 2 seconds before the end of the corresponding 20 °C step and the tube was placed on ice. 10% of the reaction volume was precipitated for analysis and the volume was replaced with 5% volume of the fragment mix in water (each fragment at 20× its initial concentration) and with another 5% volume of the 2× reaction buffer. The tube was promptly placed back in the cycler, and the cycler program was continued. At the end of the reaction run time, the full sample volume was precipitated.
1 ratio with 2× reaction buffer in a maximum recovery PCR tube (Axygen, a brand of Corning Life Sciences). Promptly, the tube was placed in a qTower3G cycler (Analytik Jena AG) at 20 °C to start temperature cycling (with 8 °C s−1 heating rate, 6 °C s−1 cooling rate). For serial dilution, the cycler was paused 2 seconds before the end of the corresponding 20 °C step and the tube was placed on ice. 10% of the reaction volume was precipitated for analysis and the volume was replaced with 5% volume of the fragment mix in water (each fragment at 20× its initial concentration) and with another 5% volume of the 2× reaction buffer. The tube was promptly placed back in the cycler, and the cycler program was continued. At the end of the reaction run time, the full sample volume was precipitated.
We performed the standard ethanol precipitation33 with addition of 2 μl (for a sample volume of 30 μl) of glycogen (10 mg ml−1), which is known to enhance the precipitation of short oligonucleotides. We allowed the DNA to precipitate overnight at 4 °C before centrifugation, cleaning the pellet with 70% ethanol, and air drying it. The precipitation efficiency of more than 85% was quantified independently with standards.
Reaction analysis method
The precipitated samples were re-dissolved in x/50 × v volume of water, where x is the initial concentration of one of the templates and v is the volume of the sample used for precipitation. The samples were loaded onto a Bioanalyzer chip (Agilent Small RNA Kit) and the Bioanalyzer assay was performed according to the company's protocol. Quantification was performed as explained in detail in ESI 1.† Quantification with the Agilent Bioanalyzer instrument established in this paper for ssDNA allowed us to quantify many samples in a parallel fashion using a minimal amount of material per analysis (1 μl of 50 nM concentrated DNA strand per sample), roughly 100 times less than with HPLC.
All the concentration data from the Bioanalyzer instrument are presented with a 10% error bar, which was the pipetting error. We observed that after the data normalization and concentration calibration, the 10% pipetting error remained as the major error source (ESI 1).†
Melting curves
Melting curves were measured using a C1000™ Thermal Cycler with a CFX96™ detection system (Bio-Rad Laboratories) at a rate of 0.083 °C s−1 in either the control buffer or the reaction buffer. Eva Green dye (Biotium Inc.) was used at a 1× concentration for detection. Templates and replicates were measured at 1 μM concentration each, while all fragments were measured at 10 μM concentration each.
Quantification of the dissociation rates
Each melting curve was baseline corrected and normalized to depict the fraction of bound strands on the y axis. The association constant, Ka, was quantified from the Arrhenius plot following the description in the literature,34 using an in-house written LabVIEW routine (LabVIEW 2010, National Instruments). The dissociation rate, koff, was then quantified from Ka = kon/koff, where the association rate, kon (0.4 μM−1 s−1), was taken from the literature.26,27
Simulation and data fitting
The ODEs were solved in MATLAB using the solver ode15s. The experimental data were fitted with the lsqcurvefit tool with ks.r. as a fit parameter. The MATLAB code that allows running the simulation, fitting the data, and plotting the results is attached to this paper.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support came from the German Research Foundation (DFG) through Transregional Collaborative Research Center (SFB/Transregio) 235 Projects 07 and 16, the Simons Foundation (Grant Number 327125), and the Quantitative Biosciences Munich (QBM) Graduate School. We thank Georg Urtel and Eiman Osman for critical discussions related to this work, Stefanie Leiner for her expertise in chemistry, Matthias Morasch, Christina Dirscherl, Patrick Kudella, and Lorenz Keil for valuable comments on the manuscript.
References
- W. Huang and J. P. Ferris, J. Am. Chem. Soc., 2006, 128, 8914–8919 CrossRef CAS PubMed.
- M. Morasch, C. B. Mast, J. K. Langer, P. Schilcher and D. Braun, ChemBioChem, 2014, 15, 879–883 CrossRef CAS PubMed.
- L. Da Silva, M. C. Maurel and D. Deamer, J. Mol. Evol., 2015, 80, 86–97 CrossRef CAS PubMed.
- P. A. Monnard, A. Kanavarioti and D. W. Deamer, J. Am. Chem. Soc., 2003, 125, 13734–13740 CrossRef CAS PubMed.
- M. Eigen and P. Schuster, Naturwissenschaften, 1977, 64, 541–565 CrossRef CAS.
- W. Gilbert, Nature, 1986, 319, 618 CrossRef.
- A. Wochner, J. Attwater, A. Coulson and P. Holliger, Science, 2011, 332, 209–212 CrossRef CAS PubMed.
- D. P. Horning and G. F. Joyce, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9786–9791 CrossRef CAS PubMed.
- M. Sosson and C. Richert, Beilstein J. Org. Chem., 2018, 14, 603–617 CrossRef CAS PubMed.
- L. K. L. Cheng and P. J. Unrau, Cold Spring Harbor Perspect. Biol., 2010, 2, a002204 CAS.
- J. Attwater, A. Raguram, A. S. Morgunov, E. Gianni and P. Holliger, eLife, 2018, 7, e35255 CrossRef PubMed.
- H. Mutschler, A. Wochner and P. Holliger, Nat. Chem., 2015, 7, 502–508 CrossRef CAS PubMed.
- T. A. Lincoln and G. F. Joyce, Science, 2009, 323, 1229–1232 CrossRef CAS PubMed.
- G. von Kiedrowski, Angew. Chem., Int. Ed. Engl., 1986, 25, 932–935 CrossRef.
- D. Sievers and G. Von Kiedrowski, Chem.–Eur. J., 1998, 4, 629–641 CrossRef CAS.
- J. W. Szostak, J. Syst. Chem., 2012, 3, 2 CrossRef CAS.
- G. von Kiedrowski, B. Wlotzka, J. Helbing, M. Matzen and S. Jordan, Angew. Chem., Int. Ed. Engl., 1991, 30, 423–426 CrossRef.
- M. Jauker, H. Griesser and C. Richert, Angew. Chem., Int. Ed., 2015, 54, 14564–14569 CrossRef CAS PubMed.
- B. T. Burcar, M. Jawed, H. Shah and L. B. McGown, Origins Life Evol. Biospheres, 2015, 45, 31–40 CrossRef CAS PubMed.
- J. P. Ferris, G. Ertem and V. Agarwal, Origins Life Evol. Biospheres, 1989, 19, 165–178 CrossRef CAS.
- M. Todisco, T. P. Fraccia, G. P. Smith, A. Corno, L. Bethge, S. Klussmann, E. M. Paraboschi, R. Asselta, D. Colombo, G. Zanchetta, N. A. Clark and T. Bellini, ACS Nano, 2018, 12, 9750–9762 CrossRef CAS PubMed.
- T. N. Grossmann, A. Strohbach and O. Seitz, ChemBioChem, 2008, 9, 2185–2192 CrossRef CAS PubMed.
- C. B. Mast, S. Schink, U. Gerland and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8030–8035 CrossRef CAS PubMed.
- M. Kreysing, L. Keil, S. Lanzmich and D. Braun, Nat. Chem., 2015, 7, 203–208 CrossRef CAS PubMed.
- R. Krishnamurthy, Acc. Chem. Res., 2017, 50, 455–459 CrossRef CAS PubMed.
- T. E. Ouldridge, P. Šulc, F. Romano, J. P. K. Doye and A. A. Louis, Nucleic Acids Res., 2013, 41, 8886–8895 CrossRef CAS PubMed.
- D. Y. Zhang and E. Winfree, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS PubMed.
- A. Williams and I. T. Ibrahim, Chem. Rev., 1981, 81, 589–636 CrossRef CAS.
- N. Wrobel, M. Schinkinger and V. M. Mirsky, Anal. Biochem., 2002, 305, 135–138 CrossRef CAS PubMed.
- M. Tena-Solsona, B. Rieß, R. K. Grötsch, F. C. Löhrer, C. Wanzke, B. Käsdorf, A. R. Bausch, P. Müller-Buschbaum, O. Lieleg and J. Boekhoven, Nat. Commun., 2017, 8, 15895 CrossRef CAS PubMed.
- C. Gibard, S. Bhowmik, M. Karki, E. K. Kim and R. Krishnamurthy, Nat. Chem., 2018, 10, 212–217 CrossRef CAS PubMed.
- K. Kawamura and F. Okamoto, Nucleic Acids Symp. Ser., 2000, 44, 217–218 CrossRef.
-
J. Sambrook, E. F. Fritsch and T. Maniatis, Molecular cloning: a laboratory manual, Cold Spring Harbor Laboratory, 1989 Search PubMed.
- J.-L. Mergny and L. Lacroix, Oligonucleotides, 2003, 13, 515–537 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Figures, details of data quantification, HPLC-MS analysis, and the kinetic model and simulation. See DOI: 10.1039/c9sc00770a |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Annalena
Salditt
a,
Annalena
Salditt
 a,
Julian
Stamp
a,
Julian
Stamp
 a,
Philipp
Schwintek
a,
Philipp
Schwintek
 a,
Job
Boekhoven
a,
Job
Boekhoven
 b and
Dieter
Braun
b and
Dieter
Braun
 *a
*a



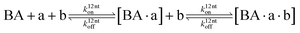
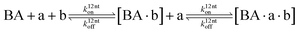
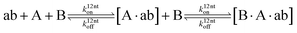
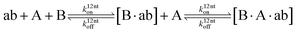


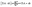



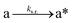
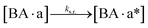
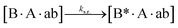
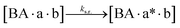
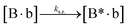
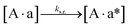
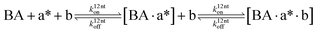
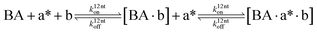
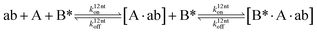
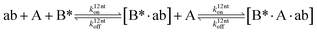


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with 2× reaction buffer in a maximum recovery PCR tube (Axygen, a brand of Corning Life Sciences). Promptly, the tube was placed in a qTower3G cycler (Analytik Jena AG) at 20 °C to start temperature cycling (with 8 °C s−1 heating rate, 6 °C s−1 cooling rate). For serial dilution, the cycler was paused 2 seconds before the end of the corresponding 20 °C step and the tube was placed on ice. 10% of the reaction volume was precipitated for analysis and the volume was replaced with 5% volume of the fragment mix in water (each fragment at 20× its initial concentration) and with another 5% volume of the 2× reaction buffer. The tube was promptly placed back in the cycler, and the cycler program was continued. At the end of the reaction run time, the full sample volume was precipitated.
1 ratio with 2× reaction buffer in a maximum recovery PCR tube (Axygen, a brand of Corning Life Sciences). Promptly, the tube was placed in a qTower3G cycler (Analytik Jena AG) at 20 °C to start temperature cycling (with 8 °C s−1 heating rate, 6 °C s−1 cooling rate). For serial dilution, the cycler was paused 2 seconds before the end of the corresponding 20 °C step and the tube was placed on ice. 10% of the reaction volume was precipitated for analysis and the volume was replaced with 5% volume of the fragment mix in water (each fragment at 20× its initial concentration) and with another 5% volume of the 2× reaction buffer. The tube was promptly placed back in the cycler, and the cycler program was continued. At the end of the reaction run time, the full sample volume was precipitated.


