Open Access Article
Open Access ArticleSteric and electronic control of an ultrafast isomerization†
Tyler M.
Porter
 ,
Andrew L.
Ostericher
and
Clifford P.
Kubiak
,
Andrew L.
Ostericher
and
Clifford P.
Kubiak
 *
*
Department of Chemistry and Biochemistry, University of California San Diego, 9500 Gilman Drive, La Jolla, California, USA. E-mail: ckubiak@ucsd.edu
First published on 11th July 2019
Abstract
Synthetic control of the influence of steric and electronic factors on the ultrafast (picosecond) isomerization of penta-coordinate ruthenium dithietene complexes (Ru((CF3)2C2S2)(CO)(L)2, where L = a monodentate phosphine ligand) is reported. Seven new ruthenium dithietene complexes were prepared and characterized by single crystal X-ray diffraction. The complexes are all square pyramidal and differ only in the axial vs. equatorial coordination of the carbonyl ligand. Fourier Transform Infrared (FTIR) spectroscopy was used to study the ν(CO) bandshapes of the complexes in solution, and these reveal rapid exchange between two or three isomers of each complex. Isomerization is proposed to follow a Berry psuedorotation-like mechanism where a metastable, trigonal bipyramidal (TBP) intermediate is observed spectroscopically. Electronic tuning of the phosphine ligands L = PPh3, P((p-Me)Ph)3, ((p-Cl)Ph)3, at constant cone angle is found to have little effect on the kinetics or thermodynamic stabilities of the axial, equatorial and TBP isomers of the differently substituted complexes. Steric tuning of the phosphine ligands over a range of phosphine cone angles (135 < θ < 165°) has a profound impact on the isomerization process, and in the limit of greatest steric bulk, the axial isomer is not observable. Temperature dependence of the FTIR spectra was used to obtain the relative thermodynamic stabilities of the different isomers of each of the seven ruthenium dithietene complexes. This study details how ligand steric effects can be used to direct the solution state dynamics on the picosecond time scale of discrete isomers energetically separated by <2.2 kcal mol−1. This work provides the most detailed description to date of ultrafast isomerization in the ground states of transition metal complexes.
Introduction
We have recently reported on the exchange dynamics of an ultrafast (picosecond) isomerization in a pentacoordinate ruthenium complex, Ru((CF3)2C2S2)(CO)(P(Ph)3)2.1 The fluctional nature of this complex was first reported by Miller and Balch in 1971 (Fig. 1).2 Early reports highlighted the isolation of two different crystalline forms (violet (1a) and orange (1c)) with solid state square pyramidal structures that differed only in the axial vs. equatorial coordination of the CO ligand.2–5 While interconversion of the two forms was observable in solution,2 the details were not revealed until the recently published study.1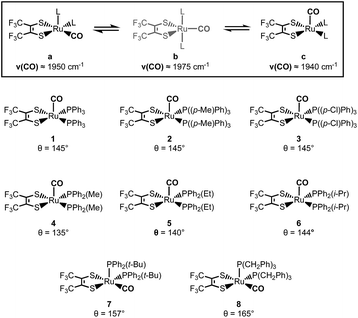 | ||
| Fig. 1 Isomerization process for 1 (top).1 The eight structurally characterized ruthenium complexes and their respective phosphine cone angles (bottom). | ||
Through the use of 2D IR spectroscopy, the equatorial (1a) and axial (1c) isomers of complex 1 were observed to exchange in picoseconds (kex ≈ 10−12) through an observable, trigonal bipyramidal (TBP) intermediate (1b).1 Additional spectroscopic and DFT analyses suggested that the mechanism of isomerization followed a Berry pseudorotation-like (BPR) pathway (1a ↔ 1b ↔ 1c). To further probe the steric and electronic effects, that govern this low barrier isomerization, we investigated seven new ruthenium dithietene complexes and report herein on their synthesis, characterization, and exchange dynamics as a function of the steric and electronic character of the phosphine ligands.
Here, the steric and electronic effects of the monodentate phosphine ligands are readily accounted for by consideration of the phosphine cone angles and their relative σ-donor strengths.6 Complexes 1–3 address the influence of phosphine electronic effects, as para-substitution on the phenyl rings perturbs the σ-donor strength while the cone angle remains fixed. In complexes 4–8 however, the σ-donor strength of the phosphine ligand remains relatively constant, while the cone angle can be varied across a 30° span (135° < θ < 165°).
Results and discussion
Complexes 2–8 were synthesized following a modified literature procedure, in brief: under an inert atmosphere, ruthenium dodecacarbonyl was suspended in dry, degassed heptanes and refluxed for one hour in the presence of 1,2-hexafluorodithioketone ((CF3)2C2S2). After one hour, and the formation of an orange precipitate, six equivalents of the respective phosphine ligand was subsequently added to the flask under a stream of dry nitrogen. The resulting reaction mixture was then refluxed for an additional twelve hours and complexes 2–8 were isolated as the second red (or green for 7) band by column chromatography using an eluant of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 DCM
3 DCM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexanes. Single crystals suitable for X-ray diffraction were then grown from dichloromethane (DCM)
hexanes. Single crystals suitable for X-ray diffraction were then grown from dichloromethane (DCM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pentane mixtures (acetonitrile for 6) at −30 °C (2–6: orange crystals, 7 and 8: violet crystals).
pentane mixtures (acetonitrile for 6) at −30 °C (2–6: orange crystals, 7 and 8: violet crystals).
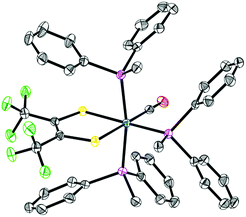
Single crystal X-ray diffraction studies revealed that all complexes were square-pyramidal and differed only in the orientation of the carbonyl ligand about the metal center. The orange crystals (2–6) were found to have the CO ligand in the apical site while the violet crystals (7 and 8) were found to have the CO ligand in the equatorial plane (Fig. 2). While each complex is predicted to have additional stable isomers,1–5 their crystallization is remarkably condition dependent and any additional isomers have yet to be crystallized. It is rather surprising however, that 7 and 8 crystallize as the COequatorial isomer as previous studies indicated it is the thermodynamically less favorable isomer.1,2 Nevertheless, this does reveal initial effects of phosphine substitution, and suggests that increased ligand sterics favor the sterically less encumbered COequatorial isomer.3 Minor variations in the bonding parameters are observed (Tables 1 and S9†), suggesting a similar electronic structure for all complexes. Comparison of the C–C and C–S bond distances of the 1,2-dithioketone ligand allow determination of the dithioketone (and metal) oxidation state.7–9 For complexes 1–8, average C–C and C–S bond distances of 1.354 Å and 1.733 Å, respectively, are in excellent agreement with a doubly reduced dithietene ligand (C–C: 1.337 Å and C–S: 1.761 Å),7,9 suggesting a Ru(II), 16 e− complex. This assignment is additionally supported through preparation of the hexa-coordinate, trisphosphine complex, Ru((CF3)2C2S2)(CO)(P(Ph)2(Me))3 (9, Fig. 3).
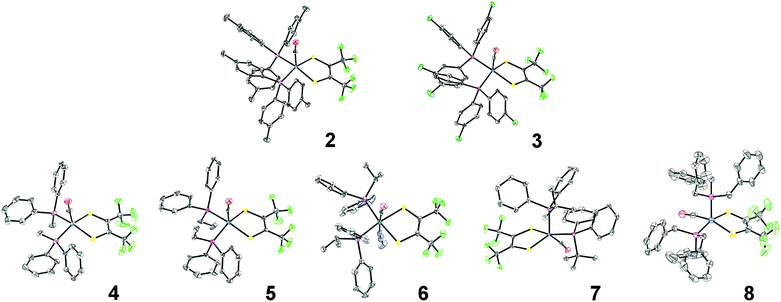 | ||
| Fig. 2 ORTEP structures of complexes 2–8. Thermal ellipsoids are shown at 50% probability. Hydrogen atoms and co-crystallized solvent molecules have been omitted for clarity and a single position is shown where rotational disorder of the CF3 groups exists. Notes on refinement and crystallographic data is included in the ESI.† | ||
| Bond (Å) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| COap | COeq | COap | COap | COap | COap | COap | COeq | COeq | (P(Ph)2Me)3 | ||
| a Values were adapted from previously published structures.3–5 b Crystals were ground from acetonitrile solutions and the structure was found to contain a coordinating acetonitrile molecule. | |||||||||||
| C(2)–C(3) | 1.350 | 1.359 | 1.357 | 1.359 | 1.354 | 1.356 | 1.343 | 1.347 | 1.350 | 1.350 | 1.353 |
| C(2)–S(1) | 1.735 | 1.718 | 1.728 | 1.727 | 1.735 | 1.733 | 1.762 | 1.732 | 1.741 | 1.765 | 1.735 |
| C(3)–S(2) | 1.726 | 1.717 | 1.741 | 1.737 | 1.740 | 1.737 | 1.756 | 1.737 | 1.727 | 1.752 | 1.735 |
Based upon simple principles of electron counting, complex 9 is expected to have a doubly reduced dithiolate ligand, giving the 18 e−, Ru(II) complex. This is in excellent agreement with observed C–C and C–S bond distances of 1.350 Å and 1.765/1.752 Å respectively, supporting a Ru(II) assignment for 9, and 1–8 as well. It is important to note that the tris-phosphine adduct has only been isolated for complex 4, where the relatively small cone angle (θ = 135°) is believed to allow the coordination of an additional phosphine ligand. While complex 9 does not appear to undergo dynamic exchange on the picosecond timescale (as judged by the narrow ν(CO) band shape, Fig. S1†), significantly broadened, partially coalesced NMR signals do suggest dynamics on the NMR timescale (kex < 104 s−1, Fig. S29–S30†). Clearly, additional studies are required, however this remains outside of the scope of the current investigation and here 9 aids only in providing a structural benchmark for Ru(II)/dithiolate(2-) oxidation states.
Upon dissolution of 2–8 into dichloromethane (DCM) a unique, significantly broadened ν(CO) band is observed for each complex, behavior indicative of exchange dynamics occurring on the vibrational timescale (Fig. 4, S2 and S3).1,10–19 Owing to the similar line shape observed for complexes 1–3 (Fig. S2†) phosphine electronic effects appear to have little impact on the isomerization reaction. However, variation of the phosphine cone angles is observed to have substantial impact (Fig. 4). At small ligand cone angles (θ < 145°, 4 and 5) two significantly broadened, partially coalesced ν(CO) bands are observed (Fig. 4) in the vicinity of 1936 and 1970 cm−1. In comparison to complex 1, the observed ν(CO) bands are in excellent agreement with the COequatorial (1a: ν(CO) ≈ 1960 cm−1) and COaxial (1c: ν(CO) ≈ 1940 cm−1) isomers, while the partially coalesced spectra suggests relatively slow exchange dynamics (in comparison to the highly coalesced ν(CO) bands for 1–3 and 6–8). Interestingly, two-component spectral deconvolutions are less than sufficient to reproduce the observed FTIR line shape (Fig. S4†) and instead, at-least three Voigt functions are required to fit the ν(CO) bands in the vicinity of 1975 cm−1, 1965 cm−1, and 1932 cm−1. These findings are again in excellent agreement with the reported frequencies for complex 1 (ν(CO) ≈ 1a: 1950 cm−1, 1b: 1980 cm−1, 1c: 1960 cm−1),1 and additionally suggests the presence of the COTBP intermediate.
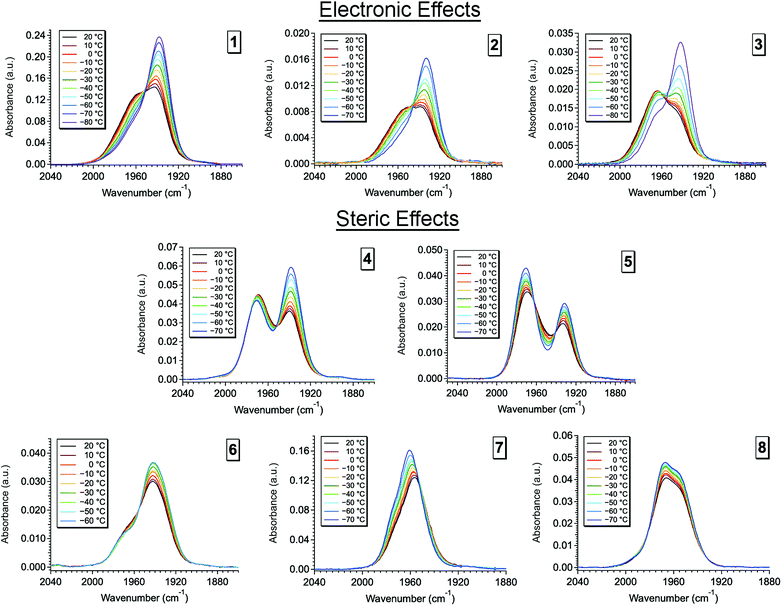 | ||
| Fig. 4 Variable temperature Fourier transform infrared (VT-FTIR) spectra of complexes 2 and 4–8 in DCM across a temperature range of 20 °C to −70 °C. | ||
As the ligand cone angle is increased (θ ≈ 145°, 2, 3, and 6), the ν(CO) band in solution is observed to coalesce into a broad absorbance (FWHM ≈ 50 cm−1) centered near 1958 cm−1, where the nearly identical ν(CO) line shapes (in comparison to 1) suggest very similar solution state dynamics and energetics. Thus, similarly sized phosphine ligands display similar isomerization dynamics, even when their electronic differences are significant. These observations are confirmed through spectral deconvolution, where again, three Voigt functions in the vicinity of 1978 cm−1, 1960 cm−1, and 1940 cm−1 are required to fit the experimental line shape (Fig. S5†). These findings in addition to the nearly identical variable temperature response (Fig. S2†) support very similar solution state dynamics for complexes 1–3 and 6.
At large cone angles (θ > 145°, 7 and 8), a near complete coalescence of the ν(CO) band is observed, and unlike complexes 1–6, only two-component deconvolutions were required (Fig. S6†). While this behavior would initially indicate faster exchange rates in comparison to complexes 1–6, a more likely explanation is inhibition of one of the isomerization pathways. Here, the deconvoluted center line frequencies (ν(CO) ≈ 1960 cm−1 and 1975 cm−1) are in excellent agreement with observation of the COequatorial and COTBP isomers, with a notable lack of intensity in the vicinity of 1940 cm−1. This suggests an absence of the COaxial isomer, which is well supported by crystallographic and density functional theory (DFT) studies (vide infra), where the COaxial isomer is believed to be too sterically encumbered with high cone angle phosphine ligands.
The thermodynamics of the isomerization reaction were investigated through the use of variable temperature Fourier transform infrared (VT-FTIR) spectroscopy. The VT-FTIR spectra of complexes 2–8 (Fig. 4, S2 and S3†) were recorded using a SPECAC flow-through optical cryostat (Model: GS21525-C) and a Bruker Equinox 55 FTIR spectrometer. The samples were enclosed in a CaF2 crystal windowed FTIR flow cell, contained in a vacuum jacketed housing, that was cooled using a liquid nitrogen/ethanol slurry to within 1 °C of the desired temperature using a built-in temperature controller. FTIR spectra for each complex were collected across a 90 °C span from 20 °C to −70 °C. After solvent subtraction, the VT-FTIR line shapes for each complex were fit using constrained Voigt functionals in accord with the aforementioned spectral deconvolutions (Fig. S10–S13†). The Voigt functionals were constrained by ±5 cm−1 about the isomers center line frequencies, with FWHM constraints of 1–20 cm−1, and peak heights of 0.001–0.05 a.u. Using the determined spectral areas the population ratios of the isomers for complexes 4–8 were then determined (Tables S11–S17†), allowing application of a Van 't Hoff analysis (Fig. S14† and Table 2).
| Complex | Pathway | (kcal mol−1) | ΔHi (kcal mol−1) | ΔSi (e.u.) |
|---|---|---|---|---|
| 4 | COeq to COTBP | 0.9 (0.2) | 1.4 (0.3) | 1.9 (0.6) |
| COTBP to COax | −0.8 (0.2) | −2.2 (0.2) | 4.7 (0.9) | |
| COeq to COax | 0.094 (0.007) | −0.76 (0.08) | −2.9 (0.4) | |
| 5 | COeq to COTBP | 1.6 (0.2) | 1.96 (0.09) | 1.1 (0.4) |
| COTBP to COax | −1.4 (0.2) | −2.1 (0.1) | −2.2 (0.5) | |
| COeq to COax | 0.26 (0.01) | −0.08 (0.04) | −1.2 (0.2) | |
| 7 | COeq to COTBP | 1.29 (0.04) | 0.95 (0.03) | −1.2 (0.1) |
| 8 | COeq to COTBP | −0.40 (0.01) | 0.62 (0.03) | 3.4 (0.1) |
In accord with previous studies,1 the trigonal bipyramidal isomer was found to be the highest in energy (ΔHi), lying on average 1.2 kcal mol−1 and 2.1 kcal mol−1 higher in energy than the COequatorial and COaxial isomers, respectively. Overall, isomerization from the COequatorial to COTBP was found to be an endergonic process while isomerization from COTBP to COaxial was exergonic (Table 2). While isomerization between the COequatorial and COTBP isomers was observed for complexes 7 and 8; interestingly, the isomerization from COequatorial to COTBP in 8 was found to be exergonic, suggesting an entropically driven isomerization.
While ligand sterics likely play a major role in the thermal isomerization process, the changes in entropy across the entire series would suggest that solvation dynamics may also contribute to the overall reaction. While solvent studies are currently underway, this concept is not surprising as the reordering of solvent about each isomer would be expected to play a key role. This is especially true for an isomerization reaction occurring on the same dynamic timescale as solvent reorientation.20–24 It is important to note however, that the thermochemical values are highly dependent on the peak locations of the spectral deconvolutions, and therefore should be only taken as estimates. Higher ordered 2D IR spectroscopy will be required to better resolve the role of steric effects in setting the relative stabilities of the different isomers, and the dynamics of exchange between them.
Despite the limitations of linear spectroscopy, additional support for these observations is obtained through the use of density functional theory (DFT). Due to computational time constraints however, DFT calculations were only performed on complexes 5 and 7 using the ORCA computational software package (version 3.0.3).25–29 At the BP86 level of theory, all hydrogen, carbon, and fluorine atoms were treated with Ahlrichs' def2-SVP basis set while all sulfur, phosphorus, oxygen, and ruthenium atoms were treated with the def2-TZVP basis set.30–38 Relativistic effects were applied through the zero-order regular approximation (ZORA), dispersion corrections were applied with a Becke–Johnson damping scheme (D3BJ), and solvation was accounted for using the conductor-like screening model (COSMO) in DCM.39–41 Initial geometries were adapted from the reported crystal structures and geometry optimizations were confirmed to be minima by frequency calculations performed at the same level of theory.
In agreement with previous studies, all three isomers for 5 were found to be minima while only the COequatorial and COTBP isomers were favorable for 7 (Fig. S7†). The COaxial isomer for complex 7 consistently converged to a structure matching the COequatorial isomer (Fig. S8†). These findings support that the COaxial isomer is too sterically encumbered at large cone angles and are in agreement with experimental observations. Upon comparison of the bonding parameters from crystallography to DFT, only minor variations are observed, suggesting DFT well represents the electronic structure complexes 5 and 7 (Tables S9 and S10†). This is further confirmed by comparison of the DFT predicted FTIR with experiment (Fig. S9†). Here the DFT calculated ν(CO) bands are in excellent agreement with experiment suggesting the DFT calculated structures match those observed experimentally. This is well supported by previous studies,1 and offers further support for the presence of the described isomers in these systems.
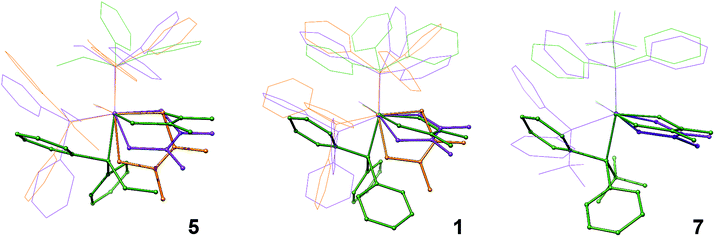
While previous studies have proposed the isomerization shown in Fig. 1, where isomerization is mediated by the trigonal bipyramidal intermediate, the direct isomerization between COaxial and COequatorial could not be ruled out.1 Owing to the scope of the current investigation, this question is partly answered through superposition of the DFT structures. When the Ru, CO, and P atoms of each isomer are superimposed, one isomerization pathway is revealed. Starting from the COaxial isomer shown in orange, structural rearrangement between the COaxial (orange) and COequatorial (violet) occurs by a slight, 45° twist of the dithietene ligand.
From there, isomerization between the COequatorial (violet) and COTBP (green) isomers occurs by a second dithietene twist (<35°), which opens a coordination site on the ruthenium atom that was formerly occupied by the dithietene sulfur atom. This newly opened coordination site allows the phosphine ligand to “slide” into place forming the COTBP isomer (green). This suggests that the COTBP isomer cannot be accessed directly from the COaxial isomer without a complete dithietene twist. While the thermochemical data initially suggests that the COTBP is acting as an intermediate, this is only one slice along a multi-dimensional reaction pathway, and all three isomers may in fact be interconverting directly. The magnitude required for the second dithietene twist (COequatorial to COTBP) decreases as phosphine cone angle is increased. This is most clearly seen in complex 7 (Fig. 5, right), where very little movement of the dithietene ligand is needed. Consistent with previous findings,1 several low-frequency normal modes (ν < 1000 cm−1) have been identified for complexes 5 and 7 with nuclear displacements in alignment with these proposed rearrangement pathways.
Conclusions
While higher ordered spectroscopy will be required to fully understand the isomerization dynamics in these systems, it is clear that relatively large transition metal complexes can have remarkably low barriers to structural rearrangements. These findings clearly show the impact of ligand steric effects and their large influence over equatorial–axial ligand exchange and raise new questions about the role of solvent dynamics. This work provides the most detailed description to date of ultrafast isomerization in the ground states of transition metal complexes.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors acknowledge the W. M. Keck Center for Integrated Biology for use of their computing cluster, Dr Curtis Moore and Dr Milan Gembicky for assistance with X-ray crystallographic studies, and Dr Anthony Mrse of the UCSD NMR facility. T. M. P. and C. P. K. acknowledge support from NSF: CHE1461632 and CHE1759460.Notes and references
- T. M. Porter, J. Wang, Y. Li, B. Xiang, C. Salsman, J. S. Miller, W. Xiong and C. P. Kubiak, Chem. Sci., 2019, 10(1), 113–117 RSC.
- A. L. Balch and J. Miller, Inorg. Chem., 1971, 10(7), 1410–1415 CrossRef CAS.
- I. Bernal, A. Clearfield, E. F. Epstein, J. S. Ricci, A. Balch and J. S. Miller, Chem. Commun., 1973, 2, 39–40 RSC.
- I. Bernal, A. Clearfield and J. S. Ricci, J. Cryst. Mol. Struct., 1974, 4(1), 43–54 CrossRef CAS.
- A. Clearfield, E. F. Epstein and I. Bernal, J. Coord. Chem., 1977, 6(4), 227–240 CrossRef CAS.
- C. A. Tolman, Chem. Rev., 1977, 77(3), 313–348 CrossRef CAS.
- B. S. Lim, D. V. Fomitchev and R. H. Holm, Inorg. Chem., 2001, 40(17), 4257–4262 CrossRef CAS.
- Y. Yan, C. Keating, P. Chandrasekaran, U. Jayarathne, J. T. Mague, S. DeBeer, K. M. Lancaster, S. Sproules, I. V. Rubtsov and J. P. Donahue, Inorg. Chem., 2013, 52(11), 6743–6751 CrossRef CAS.
- R. Eisenberg and H. B. Gray, Inorg. Chem., 2011, 50(20), 9741–9751 CrossRef CAS.
- B. Cohen and S. Weiss, J. Chem. Phys., 1980, 72(12), 6804 CrossRef CAS.
- F.-W. Grevels, J. Jacke, W. E. Klotzbücher, C. Krüger, K. Seevogel and Y.-H. Tsay, Angew. Chem., Int. Ed., 1987, 26(9), 885–887 CrossRef.
- F.-W. Grevels, K. Kerpen, W. E. Klotzbücher, R. E. D. McClung, G. Russell, M. Viotte and K. Schaffner, J. Am. Chem. Soc., 1998, 120(40), 10423–10433 CrossRef CAS.
- I. A. Nilsen, D. G. Osborne, A. M. White, J. M. Anna and K. J. Kubarych, J. Chem. Phys., 2014, 141(13), 134313 CrossRef.
- A. N. Giordano and B. J. Lear, J. Phys. Chem. A, 2015, 119(15), 3545–3555 CrossRef CAS.
- P. A. Eckert and K. J. Kubarych, J. Phys. Chem. A, 2017, 121(3), 608–615 CrossRef CAS.
- J. J. Turner and M. Bühl, Infrared Dynamics of Iron Carbonyl Diene Complexes, J. Phys. Chem. A, 2018, 122(14), 3497–3505 CrossRef CAS.
- T. Ito, T. Hamaguchi, H. Nagino, T. Yamaguchi, J. Washington and C. P. Kubiak, Science, 1997, 277(5326), 660–663 CrossRef CAS.
- C. H. Londergan and C. P. Kubiak, Chem.–Eur. J., 2003, 9(24), 5962–5969 CrossRef CAS.
- T. M. Porter, G. P. Heim and C. P. Kubiak, J. Am. Chem. Soc., 2018, 140(40), 12756–12759 CrossRef CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. S. Maroncelli, J. Phys. Chem., 1995, 99(48), 17311–17337 CrossRef CAS.
- M. L. Horng, K. Dahl, G. Jones and M. Maroncelli, Chem. Phys. Lett., 1999, 315(5), 363–370 CrossRef CAS.
- J. Zheng, K. Kwak, J. Asbury, X. Chen, I. R. Piletic and M. D. Fayer, Science, 2005, 309(5739), 1338 CrossRef CAS.
- B. J. Lear, S. D. Glover, J. C. Salsman, C. H. Londergan and C. P. Kubiak, J. Am. Chem. Soc., 2007, 129(42), 12772–12779 CrossRef CAS PubMed.
- C. P. Kubiak, Inorg. Chem., 2013, 52(10), 5663–5676 CrossRef CAS PubMed.
- F. Neese, J. Comput. Chem., 2003, 24(14), 1740–1747 CrossRef CAS.
- S. Kossmann and F. Neese, Chem. Phys. Lett., 2009, 481(4–6), 240–243 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356(1–3), 98–109 CrossRef CAS.
- R. Izsák and F. Neese, An overlap fitted chain of spheres exchange method, J. Chem., 2011, 135(14), 144105 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS.
- S. Huzinaga, J. Andzelm, E. Radzio-Andzelm, Y. Sakai, H. Tatewaki and M. Klobukiwski,Gaussian Basis Sets for Molecular Calculations, Elsevier Science, 1983, vol. 16, p. 434 Search PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. E. Preuß, Theor. Chem. Acc., 1990, 77(2), 123–141 Search PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97(4), 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100(8), 5829–5835 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- D. A. Pantazis and F. Neese, All-electron scalar relativistic basis sets for the 6p elements, Theor. Chem. Acc., 2012, 131(11), 1292 Search PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7(3), 677–684 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5(9), 2229–2238 CrossRef CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4(6), 908–919 CrossRef CAS PubMed.
- S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110(6), 2235–2245 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: A collection of additional NMR, FTIR, DFT, and crystallographic data. See DOI: 10.1039/c9sc02359c |
| This journal is © The Royal Society of Chemistry 2019 |