 Open Access Article
Open Access ArticleSynergistic adsorptions of Na2CO3 and Na2SiO3 on calcium minerals revealed by spectroscopic and ab initio molecular dynamics studies†
Yann
Foucaud
 *a,
Michaël
Badawi
*a,
Michaël
Badawi
 *b,
Lev O.
Filippov
ac,
Odile
Barres
a,
Inna V.
Filippova
ac and
Sébastien
Lebègue
*b
*b,
Lev O.
Filippov
ac,
Odile
Barres
a,
Inna V.
Filippova
ac and
Sébastien
Lebègue
*b
aUniversité de Lorraine, CNRS, GeoRessources Laboratory, F-54000 Nancy, France. E-mail: yann.foucaud@univ-lorraine.fr; michael.badawi@univ-lorraine.fr; sebastien.lebegue@univ-lorraine.fr
bLaboratoire de Physique et Chimie Théoriques, Université de Lorraine, UMR 7019 – CNRS, BP239, Boulevard des Aiguillettes, 54 506 Vandoeuvre-lès-Nancy Cedex, France
cNational University of Science and Technology MISIS, 119049 Moscow, Russia
First published on 7th October 2019
Abstract
The synergistic effects between sodium silicate (Na2SiO3) and sodium carbonate (Na2CO3) adsorbed on mineral surfaces are not yet understood, making it impossible to finely tune their respective amounts in various industrial processes. In order to unravel this phenomenon, diffuse reflectance infrared Fourier transform and X-ray photoelectron spectroscopies were combined with ab initio molecular dynamics to investigate the adsorption of Na2SiO3 onto bare and carbonated fluorite (CaF2), an archetypal calcium mineral. Both experimental and theoretical results proved that Na2CO3 adsorbs onto CaF2 with a high affinity and forms a layer of Na2CO3 on the surface. Besides, at low Na2SiO3 concentration, silica mainly physisorbs in a monomeric protonated form, Si(OH)4, while at larger concentration, significant amounts of polymerised and deprotonated forms are identified. Prior surface carbonation induces an acid–base reaction on the surface, which results in the formation of the basic forms of the monomers and the dimers, i.e. SiO(OH)3− and Si2O3(OH)42−, even at low coverage. Their adsorption is highly favoured compared to the acid forms, which explains the synergistic effects observed when Na2SiO3 is used after Na2CO3. The formation of the basic form on the bare surface is observed only by increasing the surface coverage to 100%. Hence, when Na2CO3 is used during a separation process, lower Na2SiO3 concentrations are needed to obtain the same effect as with lone Na2SiO3 in the separation process.
1. Introduction
With an estimated annual worldwide market value of 8.9 billion USD in 2017,1 alkali silicate reagents are among the most used inorganic reagents worldwide. These environmentally friendly reagents have been intensively studied over past decades2–6 since they commonly serve as a basis for the production of a large range of silica-containing materials.7–9 Besides, their interesting properties lead to a wide range of industrial applications as additives, including detergents, foundries, adhesives, surface coatings, and water treatment.9,10 Alkali silicate glasses, especially sodium silicate (Na2SiO3), are also widely used in the froth flotation process, a method based on the adsorption of amphiphilic reagents (collectors) onto mineral surfaces to extract metals from ores. Nowadays, more than 2 billion tons of non-ferrous ores are processed annually by flotation, which has become an unavoidable route to extract metals from rocks, including high-tech and critical metals. Na2SiO3 is one of the most common reagents used in the froth flotation process where it plays two key roles, because of its aforementioned properties. First, it increases the efficiency of the flotation process since it prevents slime coating/aggregating by decreasing particle–particle interactions. Second, due to its high affinity for gangue minerals, mostly silicates, it adsorbs onto their surfaces and prevents the adsorption of the collector, keeping the surfaces hydrophilic, i.e. depressed. Therefore, Na2SiO3 is commonly used in the flotation separation of rare earth minerals,11 zinc minerals,12 iron minerals,13 scheelite (CaWO4),14–17 fluorite (CaF2),18,19 apatite [Ca5(PO4)3(OH,F)],20,21 and many other minerals.For decades, researchers worldwide have investigated the behaviour of Na2SiO3 in aqueous solutions. It is assumed that it dissociates into silica tetrahedra (SiO4) which can be in SiO44−, SiO3(OH)3−, SiO2(OH)22−, SiO(OH)3−, and Si(OH)4 forms depending on the solution pH and the total silica concentration.22–24 Moreover, some authors demonstrated that silica tetrahedra can polymerise, also depending on the pH, the total silica concentration, and the SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na2O ratio, a high ratio inducing a high polymerisation degree.23,25–28 In dilute solutions (∼1 × 10−3 mol L−1) and for low to moderate SiO2
Na2O ratio, a high ratio inducing a high polymerisation degree.23,25–28 In dilute solutions (∼1 × 10−3 mol L−1) and for low to moderate SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na2O ratio, usually used in flotation, the main species of Na2SiO3 are Si(OH)4 for pH < 9.4, SiO(OH)3− for 9.4 < pH < 12.6, and SiO2(OH)22− for pH > 12.6.29 Also, it is assumed that the polymerisation reaction depends strongly on the SiO(OH)3− and SiO2(OH)22− concentrations in solution.30 To limit operating costs, most flotation processes worldwide are performed at pH 7–11, which means that the silica monomers are dominant, in both Si(OH)4 and SiO(OH)3− forms.
Na2O ratio, usually used in flotation, the main species of Na2SiO3 are Si(OH)4 for pH < 9.4, SiO(OH)3− for 9.4 < pH < 12.6, and SiO2(OH)22− for pH > 12.6.29 Also, it is assumed that the polymerisation reaction depends strongly on the SiO(OH)3− and SiO2(OH)22− concentrations in solution.30 To limit operating costs, most flotation processes worldwide are performed at pH 7–11, which means that the silica monomers are dominant, in both Si(OH)4 and SiO(OH)3− forms.
Besides, some authors have highlighted strong positive synergistic effects when Na2SiO3 is used in flotation pulps where the pH is controlled beforehand by sodium carbonate (Na2CO3).14,15,28,31 In other words, the prior addition of Na2CO3 induces a higher efficiency of Na2SiO3 in terms of gangue mineral depression, which allows a better flotation selectivity and, hence, higher metal grades in the flotation concentrates. At the moment, although the adsorption of Na2SiO3 species has been considerably investigated,29,32–35 very few studies have been conducted on the Na2CO3/Na2SiO3 system in flotation17,28,31,36 and the synergistic effects exhibited by this reagent combination are still poorly understood. Some authors have successfully investigated surface reactivity and synergistic adsorptions/reactions by Fourier transform infrared spectroscopy (FTIR),37–40 by X-ray photoelectron spectroscopy (XPS),41–43 and by ab initio molecular dynamics (AIMD)37,44–46 with couplings between the above-mentioned techniques. In the present study, we use a combination of diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS), XPS, and AIMD simulations to gain an understanding of the molecular mechanisms involved in the Na2SiO3 adsorption onto bare surfaces and onto surfaces prior treated with Na2CO3. Fluorite (CaF2), a simple cubic calcium-bearing mineral, was chosen for this study since it is considered as an archetype of minerals that can be depressed by Na2SiO3.
2. Materials and methods
2.1. Materials
The spectroscopic studies were conducted with pure CaF2 mineral acquired from Mexico. Chemical analyses were carried out using inductively coupled plasma-atomic emission spectrometry (ICP-AES) for major elements and ion-sensitive electrode (ISE) for fluorine (Table 1). Fluorite was of satisfactory purity although 1.26% Si was present, indicating contamination by quartz. The pure mineral was crushed in an agate mortar and dry sieved to obtain a −40+20 μm size fraction. All the reagents used (Na2SiO3, Na2CO3, and NaOH) were supplied by Aldrich and were of technical quality.| Ca (%) | P (%) | Si (%) | Mg (%) | Al (%) | Fe (%) | Na (%) | K (%) | Ti (%) | Mn (%) | F (%) | LOI (%) | Total (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50.06 | <LOD | 1.26 | <LOD | 0.03 | <LOD | <LOD | <LOD | <LOD | <LOD | 44.59 | 2.36 | 98.30 |
2.2. Spectroscopic studies
Each test was conducted with 0.5 g of −40+20 μm fraction of pure CaF2. For the control sample, i.e. without the addition of any reagent, CaF2 was treated in 5 mL of deionised water (R = 18.2 MΩ cm) at pH 10 during 15 min. For the other tests, each reagent (Na2CO3 and Na2SiO3) was prepared in aqueous solution with deionised water at pH 10, prior to the conditioning stage. When the reagents were used alone, the mineral was treated in 5 mL of the reagent solution during 15 min. After the conditioning stage, the sample was filtered using ashless filter paper and rinsed three times with deionised water. When the reagents were used in combination, they were added sequentially: the mineral was first conditioned in 5 mL of Na2CO3 solution during 15 min and the conditioning solution was eliminated. Then, the sample was washed three times with deionised water and conditioned with 5 mL of Na2SiO3 solution during 15 min. The same solid/liquid separation and washing procedure was applied at the end of the conditioning stage. The pH was adjusted to 10 for solution preparation and during the conditioning stage by adding 0.1 M NaOH or HCl solution. Since Na+ and Cl− are assumed to not adsorb on mineral surfaces, they are eventually located in the electrical double layer from which they are likely to be eliminated during the washing procedure. In the reference sample (pure CaF2), neither Na+ nor Cl− ions were detected by XPS analyses, which substantiates the previous assumption.FTIR analyses were conducted with the diffuse reflectance method to maximise the surface signal. The spectra were recorded using a Bruker IFS 55 spectrometer equipped with a large-band mercury-cadmium-telluride (MCT) liquid-nitrogen-cooled detector and associated with a diffuse reflectance attachment (Harrick Corporation). The FTIR spectra were acquired in the mid-infrared range between 4000 cm−1 and 600 cm−1 with a spectral resolution of 2 cm−1. Dry mineral samples were analysed without dilution in potassium bromide (KBr), used as a reference.
The XPS spectra were acquired using an X-ray photoelectron spectrometer, a Kratos Axis Ultra DLD, equipped with a monochromatic Al Kα X-ray source (1486.7 eV) operated at 120 W (8 mA and 15 kV). The wide-scan spectra were recorded with a resolution of 1.0 eV and a pass energy of 160 eV while the high-resolution spectra were acquired with a resolution of 0.1 eV and a pass energy of 20 eV. For carbon and oxygen, the resolution was decreased to 0.05 eV. The hybrid mode was employed, using a magnetic-electrostatic lens and a charge neutraliser since the samples were not conducting. After the acquisition, the adventitious carbon was used as a reference with the C–C bond binding energy set at 284.6 eV. Vision 2.2.10 software, supplied by Kratos Analytical (Manchester, UK), was employed to process the data.
2.3. AIMD simulations
For AIMD simulations, a primitive cubic cell of CaF2 was generated and fully relaxed to obtain lattice parameters a = b = c = 5.46 Å. Then, a (111) surface was created from the relaxed bulk since the (111) cleavage plane represents the most exposed surface for CaF2.47–49 A supercell containing 72 atoms (24 Ca and 48 F) was obtained, which is constituted of 2 layers of calcium atoms and 4 layers of fluorine atoms including one plane of 12 seven-coordinated calcium atoms on the (111) surface. To avoid any unwanted interaction due to the periodicity of the cell, a vacuum of 10 Å was set between the uppermost atom, including the added molecules, and the upper limit of the cell following the z axis. For all the calculations, 3 layers of bottom atoms in the cell (1 layer of calcium atoms and 2 layers of fluorine atoms) were frozen to their bulk positions.The structure and total energy of the systems were determined by density functional theory calculations,50,51 using the Vienna ab initio simulation program (VASP).52 The semilocal Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional proposed by Perdew and co-workers53 was employed, in the generalized gradient approximation (GGA). The projector-augmented wave (PAW) method54,55 was used to describe the electron–ion interactions with a plane wave cutoff of 300 eV and the Kohn–Sham equations51 were solved self-consistently56 until the energy difference between the cycles became lower than 10−5 eV. A Methfessel and Paxton smearing57 of σ = 0.1 eV was employed to help the total energy convergence. Due to the large size of the cell, all the calculations were performed using the Γ-point only. Structural relaxations were realised until all the forces were smaller than 0.05 eV A−1. The D2 correction of Grimme58 was used to include van der Waals forces. A Nosé–Hoover thermostat was used and the temperature was set to 300 K. The time step was 1 fs and, to reach a total simulation time of 100 ps, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps were realized.
000 steps were realized.
The internal adsorption energies of species on the (111) fluorite surface were calculated based on the average energy of each system computed for the last 90 ps of the simulation, to exclude a 10 ps thermalisation period. The total internal adsorption energy was calculated as the difference between the energy of the surface with the adsorbed molecule(s) and the sum of the energies of the non-adsorbed surface and the isolated molecule(s). The energies of those systems systematically correspond to optimised geometries since they were calculated in AIMD simulations, either when the molecule is isolated or when it is adsorbed. The dispersion contribution to the total adsorption energy was calculated in a similar way by considering the dispersion contribution only.
3. Results
3.1. Adsorption of each of Na2CO3 and Na2SiO3 alone on CaF2
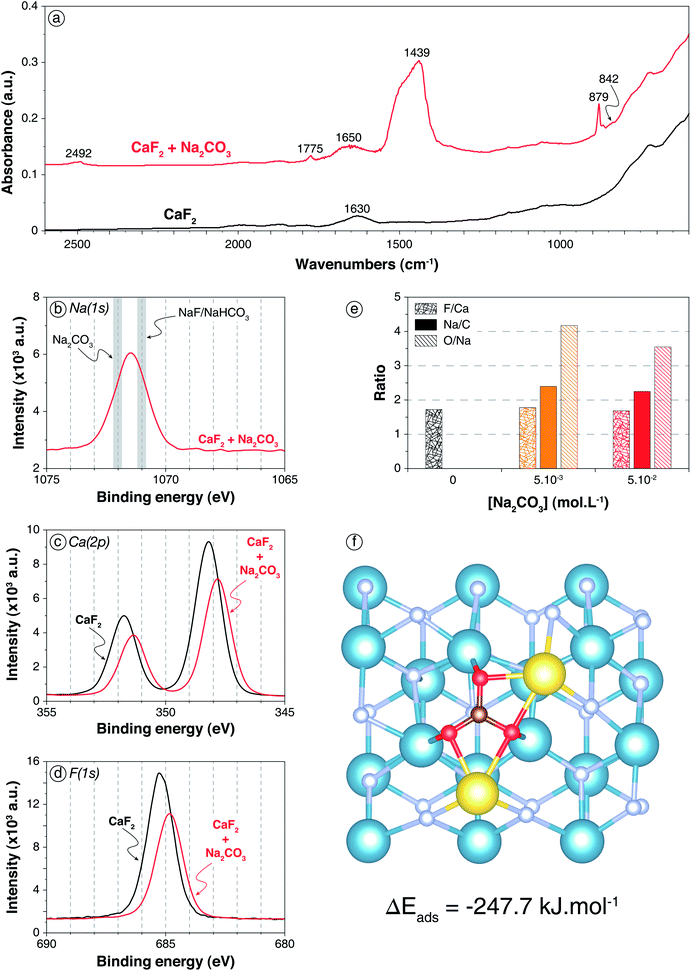 | ||
| Fig. 1 Carbonation of CaF2 surface by Na2CO3 addition. (a) Infrared spectra of CaF2 conditioned in deionised water (black) and in a 5 × 10−2 mol L−1 Na2CO3 solution (red). (b) XPS Na(1s) spectrum of the sample conditioned in a 5 × 10−2 mol L−1 Na2CO3 solution, with the common binding energies of Na–O and Na–F bonds (from Moulder62). (c) XPS Ca(2p) spectra of the sample conditioned in water and of the sample conditioned in a 5 × 10−2 mol L−1 Na2CO3 solution. (d) XPS F(1s) spectra of the sample conditioned in water and of the sample conditioned in a 5 × 10−2 mol L−1 Na2CO3 solution. (e) F/Ca, Na/C, and O/Na ratios of CaF2 conditioned in deionised water (black), in a 5 × 10−3 mol L−1 Na2CO3 solution (orange), and in a 5 × 10−2 mol L−1 Na2CO3 solution (red). The ratios were calculated with the corresponding component (C–O from CO3) for O and C. (f) Snapshot of a top view of the (111) CaF2 surface with a Na2CO3 molecule adsorbed onto the surface after 35 ps of AIMD simulation. The blue, grey, red, maroon, and yellow spheres represent the calcium, fluorine, oxygen, carbon, and sodium atoms, respectively. | ||
To confirm the previous conclusions and to gain an understanding of the molecular mechanisms involved in the CaF2 surface carbonation, XPS analyses were performed on CaF2 conditioned in deionised water, in a 5 × 10−2 mol L−1 Na2CO3 solution, and in a 5 × 10−3 mol L−1 Na2CO3 solution, at pH 10. First, for CaF2 conditioned in deionised water, calcium, fluorine, and oxygen were identified (Table S1 in ESI†) along with contaminant elements such as C, corresponding to adventitious carbon, and Si (3.0 at%), the presence of which had been previously highlighted by chemical analyses (Table 1). The O(1s) spectrum exhibited two components with binding energies of 532.1 eV (11.1 at%) and 533.2 eV (3.4 at%) that were attributed to adsorbed carbonate and water molecules, respectively (Fig. S1 in ESI†), which was in accordance with the DRIFT spectrum of pure CaF2 (Fig. 1a). Besides, the F/Ca atomic ratio of 1.73 indicated that the surface was depleted in terms of fluorine atoms since the theoretical F/Ca ratio should be 2 (Table S2 in ESI†). This could be attributed to the fact that the (111) surface, which is the main cleavage plane for fluorite,45–47 exhibits seven-coordinated calcium atoms while they are eight-coordinated in the fluorite crystal.49,63,64 This under-coordination means that the first atomic layer is constituted of only 7 fluorine atoms along with 2 calcium atoms, which results in a surface F/Ca ratio of 1.75, in agreement with the ratio measured here. Overall, no hydroxyl groups as well as no sodium atoms were identified on pure CaF2, indicating that the fluorite surface was not hydroxylated at pH 10.
The two different Na2CO3 concentrations led to similar trends for XPS that were, consistently, more pronounced for 5 × 10−2 mol L−1. The following discussion will thus focus on results for the highest concentration. First, sodium atoms were identified (4.5 at%) with a Na(1s) binding energy of around 1071.5 eV (Fig. 1b): this corresponded to an intermediate value between Na–O bonds of Na2CO3 species62 and Na–F bonds of NaF or Na–O bonds of NaHCO3, the binding energy of which is known to be lower. However, DRIFTS results demonstrated the absence of NaHCO3 (Fig. 1a), which means that the binding energy of 1071.5 eV corresponds to an intermediate value between Na–O bonds of Na2CO3 and Na–F bonds. Besides, the Ca(2p3/2) and Ca(2p1/2) binding energies were shifted from 348.2 eV and 351.8 eV for pure CaF2 to 347.8 eV and 351.3 eV, respectively, for CaF2 + Na2CO3 (Fig. 1c). This shift was attributed to the presence of Ca–O bonds that have lower binding energies than Ca–F bonds.62 Moreover, the F(1s) binding energy was shifted from 685.2 eV for pure CaF2 to 684.8 eV for CaF2 + Na2CO3 (Fig. 1d), demonstrating the existence of the aforementioned F–Na bonds, along with F–Ca bonds.62 The O(1s) spectrum presented two components with binding energies of 531.7 eV (15.9 at%) and 533.6 eV (0.8 at%) for 5 × 10−2 mol L−1 Na2CO3 (Table S1 and Fig. S1 in ESI†). The first one was attributed to C–O bond of Na2CO3,62 while the second one could be ascribed to C–O bond of NaHCO3, which was present in very small amounts as the DRIFTS results demonstrated (Fig. 1a). However, the second component, with a binding energy of 533.6 eV, exhibited in the O(1s) spectrum for 5 × 10−2 mol L−1 Na2CO3 was absent for 5 × 10−3 mol L−1 Na2CO3. This demonstrated that the CO32− ions were more likely to adsorb onto CaF2 since, at low Na2CO3 concentration, no HCO3− species were identified on the surface. Besides, the F/Ca ratio was not significantly affected by the addition of Na2CO3 (Fig. 1e) regardless of the concentration. The Na/CO3 ratio was 2.40 at low Na2CO3 concentration and 2.25 at high Na2CO3 concentration, indicating that the layer formed on the surface was Na2CO3 with an excess of Na+, probably adsorbed along with HO− ions, which however decreased when Na2CO3 concentration was increased. Overall, Na2CO3 adsorbed onto CaF2 mostly in Na2CO3 form (Fig. 1e), establishing Ca–O and Na–F bonds with the surface atoms (Fig. 1b–d). Small amounts of NaHCO3 were exhibited at high Na2CO3 concentration, which was in accordance with the DRIFTS results (Fig. 1a).
AIMD simulations confirmed that, when a Na2CO3 molecule was set onto the CaF2 (111) surface, it adsorbed with each oxygen atom establishing an O–Ca bond with a different calcium atom (Fig. 1f). Their average lengths for the whole simulation were 2.36, 2.36, and 2.43 Å with a standard deviation of around 0.10 Å. Each sodium atom established two Na–F bonds with surface fluorine atoms with dNa–F1 = 2.41 Å and dNa–F2 = 2.45 Å (Fig. 1f). Also, each sodium atom was bonded to two oxygen atoms of the CO32− ion with dNa–O1 = dNa–O2 = 2.35 Å on average. The Na2CO3 molecule adsorbed with ΔEads = −247.7 kJ mol−1 including ΔEdisp = −91.3 kJ mol−1, which indicated a highly favoured adsorption as well as high induced dipole-induced dipole forces. This theoretical result was in agreement with both DRIFTS and XPS results that allowed identification of carbonate and Ca–O/Na–F bonds on the surface, respectively.
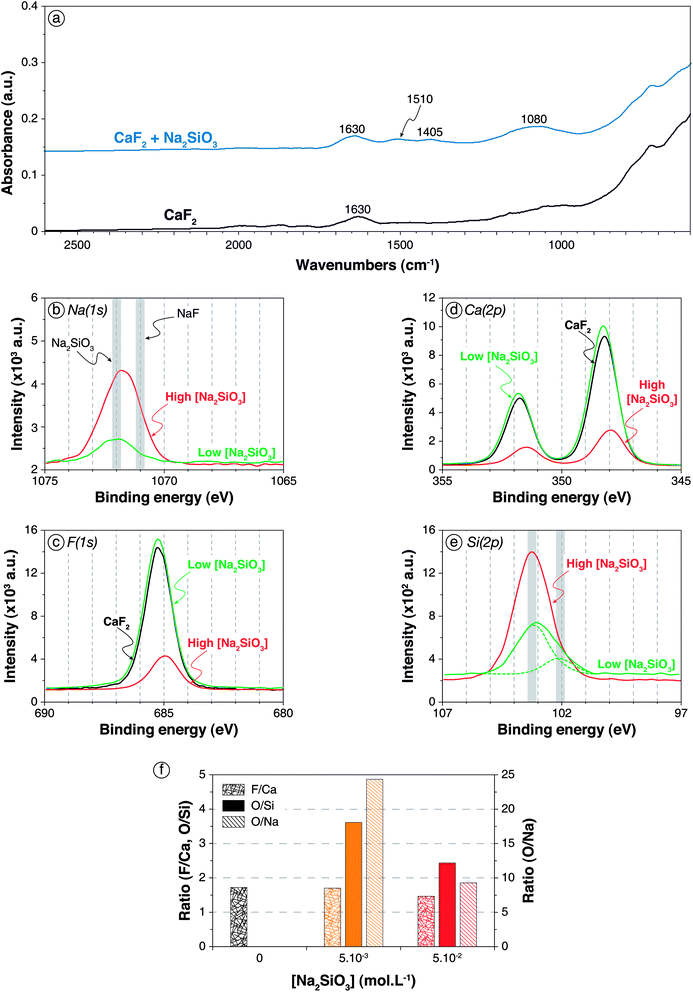 | ||
| Fig. 2 Adsorption of Na2SiO3 onto CaF2 surface. (a) Infrared spectra of CaF2 conditioned in deionised water (black) and in a 5 × 10−2 mol L−1 Na2SiO3 solution (blue). (b) XPS Na(1s) spectra of CaF2 conditioned in a 5 × 10−3 mol L−1 (green) and a 5 × 10−2 mol L−1 (red) Na2SiO3 solution, with the common binding energies of Na–O and Na–F bonds (from Moulder62). (c) XPS F(1s) spectra of CaF2 conditioned in deionised water (black) and in 5 × 10−3 mol L−1 (green) and 5 × 10−2 mol L−1 (red) Na2SiO3 solutions. (d) XPS Ca(2p) spectra of CaF2 conditioned in deionised water (black) and in 5 × 10−3 mol L−1 (green) and 5 × 10−2 mol L−1 (red) Na2SiO3 solutions. (e) XPS Si(2p) spectra of CaF2 conditioned in a 5 × 10−3 mol L−1 (green) and a 5 × 10−2 mol L−1 (red) Na2SiO3 solution, with the common binding energies of SiO2 and Si–O–X bonds.56–58 (f) F/Ca, O/Si, and O/Na ratios of CaF2 conditioned in deionised water (black), in a 5 × 10−3 mol L−1 Na2SiO3 solution (orange), and in a 5 × 10−2 mol L−1 Na2SiO3 solution (red). The ratios were calculated with the corresponding component for O and Si. | ||
For low Na2SiO3 concentration (5 × 10−3 mol L−1), small amounts of sodium atoms (0.84 at%) along with silica atoms (5.7 at% compared to 3.0 at% for pure CaF2) were identified by XPS (Table S1 in ESI†), indicating the adsorption of Na2SiO3 onto CaF2. The Na(1s) binding energy was 1071.9 eV, which mostly corresponded to Na–O bonds (Fig. 2b). Hence, it could be considered that the adsorbed Na atoms were mainly bonded to silica tetrahedra in anionic form. Moreover, the F(1s) as well as the Ca(2p) binding energies were not affected by the adsorption of Na2SiO3 at low concentration (Fig. 2c and d), indicating a physisorption of silica tetrahedra onto the CaF2 surface. The Si(2p) spectrum exhibited two main components (Fig. 2e) at 102.1 eV (1.2 at%) and 103.2 eV (4.5 at%), which could be attributed to Si–O bonds and Si–O–Si bonds, respectively.67–69 The low-energy component (102.1 eV) could be ascribed to a Si–O bond in which the oxygen atom is either partly charged (Si–O−) or stabilised by a sodium atom (Si–O–Na) or a calcium atom (Si–O–Ca), as Na and Ca exhibit lower electronegativity than Si,70 inducing lower Si(2p) binding energy. Furthermore, the high-energy component (103.2 eV) could also be related to Si–O–H bonds since H and Si display similar electronegativity.70 Overall, the Si(2p) spectrum was difficult to interpret considering the influence of chemical environment on binding energies, since the chemical environment of the oxygen atom (Si–O−, Si–O–H, Si–O–Na, Si–O–Ca, and Si–O–Si) affects significantly the Si(2p) binding energies. The F/Ca ratio was not affected by the Na2SiO3 adsorption at low concentration, indicating no chemical modification of the surface (Fig. 2f). Moreover, the O/Si ratio was 3.61 and the O/Na ratio was 24.35 (Fig. 2f), which corresponded to an overall formula of Si6.75O24.35NaH20.70, very close to Si(OH)4. Hence, at low Na2SiO3 concentrations, the silica was mostly in monomeric protonated form, i.e. Si(OH)4.
At high Na2SiO3 concentration, sodium (4.2 at%) and silica (16.1 at%) were also identified on the surface (Table S1 in ESI†). No significant changes in Na(1s) and F(1s) binding energies were observed compared to low Na2SiO3 concentration (Fig. 2b and c). However, the Ca(2p3/2) and Ca(2p1/2) binding energies were shifted from 348.2 eV and 351.8 eV for pure CaF2 to 348.0 eV and 351.5 eV, respectively (Fig. 2d). Though of low significance, it could correspond to the formation of Ca–O bonds. The Si(2p) spectrum exhibited only a component at 103.2 eV (Fig. 2e) that was ascribed to polymerised silica tetrahedra that induced a binding energy close to that of quartz.62 Besides, the F/Ca ratio significantly decreased from 1.73 for pure CaF2 to 1.47 for CaF2 conditioned with high Na2SiO3 concentration (Fig. 2f). Since no calcium atoms were present in deionised water, this decrease was attributed to a surface depletion in terms of fluorine atoms. Considering the appearance of Ca–O bonds discussed previously, it could be considered that silica tetrahedra substituted fluorine atoms on the surface. The O/Si ratio was 2.45 (Fig. 2f), which indicated the adsorption of silica was in polymerised forms onto CaF2. Also, the O/Na ratio was 9.30 which still indicated that protonated forms were dominant on the surface (Fig. 2f). The overall formula was Si3.80O9.30NaH2.4, which corresponded to moderately polymerised silica in protonated and anionic forms.
To investigate the adsorption of Na2SiO3 as well as the increase of Na2SiO3 concentration, four different phenomena were studied by AIMD simulations: (1) the adsorption of monomeric protonated forms of silica, i.e. Si(OH)4; (2) the adsorption of anionic forms of silica, i.e. SiO(OH)3−; (3) the increase of the surface coverage with protonated monomers; and (4) the adsorption of polymerised forms of silica, i.e. Si2O(OH)6.
(1) The lone molecule of Si(OH)4 adsorbed in its molecular form with ΔEads = −100.7 kJ mol−1 including ΔEdisp = −46.4 kJ mol−1 (Fig. 3a and b), which confirmed the physisorption suggested by XPS results at low Na2SiO3 concentrations (Fig. 3c). Three oxygen atoms were bonded to three surface calcium atoms (Fig. 3b) with average Ca–O bond lengths of 2.65 Å, 2.78 Å, and 2.65 Å. The hydrogen atoms of the three –OH groups established H-bonds with surface fluorine atoms (Fig. 3b), the average lengths of which were all 1.66 Å.
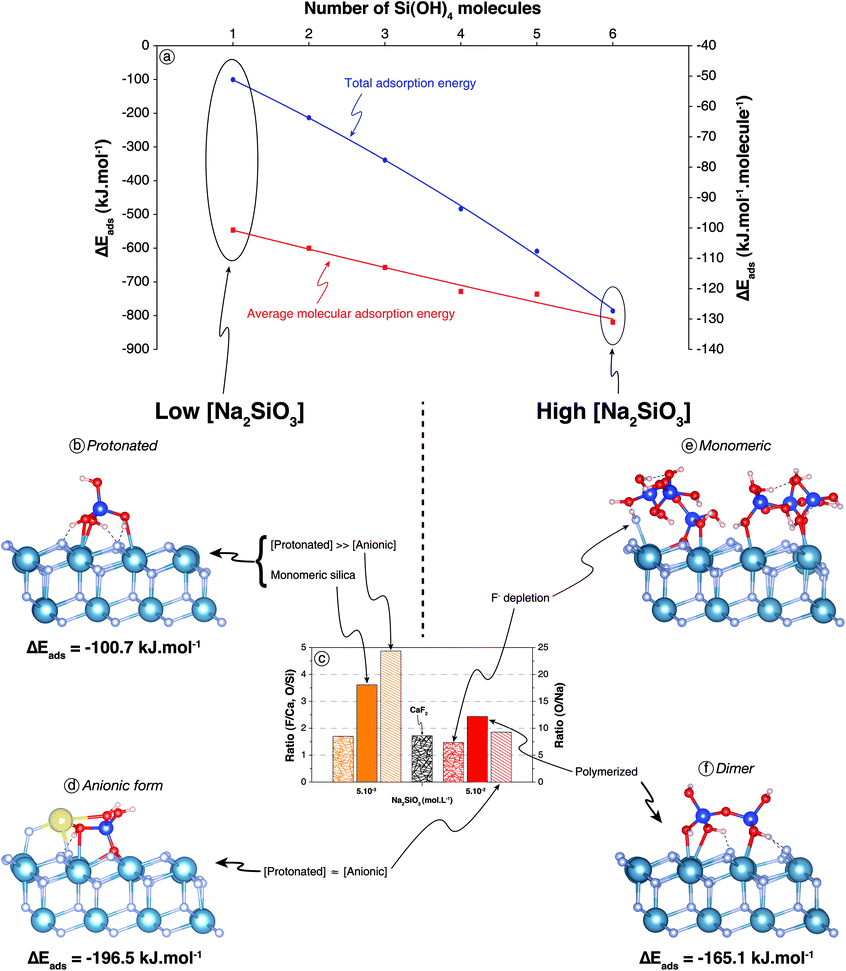 | ||
| Fig. 3 (a) Total and molecular adsorption energies as a function of surface coverage for Si(OH)4 molecules onto bare CaF2 surface. (b) Snapshot of a side view of the (111) CaF2 surface with a Si(OH)4 molecule adsorbed after 50 ps of AIMD simulation. (c) F/Ca, O/Si, and O/Na ratios of CaF2 conditioned in different conditions; refer to Fig. 2f for legends. (d) Snapshot of a side view of the (111) CaF2 surface with a NaSiO(OH)3 molecule adsorbed after 50 ps of AIMD simulation. (e) Snapshot of a side view of the (111) CaF2 surface with six Si(OH)4 molecules (100% coverage) adsorbed after 50 ps of AIMD simulation. (f) Snapshot of a side view of the (111) CaF2 surface with a Si2O(OH)6 molecule adsorbed after 50 ps of AIMD simulation. The light blue, grey, red, dark blue, and yellow spheres represent calcium, fluorine, oxygen, silicon, and sodium atoms, respectively. Dashed lines represent hydrogen bonds. | ||
(2) For the adsorption of SiO(OH)3− form, a sodium atom was added on the surface near the SiO(OH)3− molecule to keep the cell electrically neutral. During the simulation, the non-protonated oxygen atom ejected a fluorine atom from the surface and established three O–Ca bonds with three different surface calcium atoms, substituting a F− in the upper fluorine atom layer (Fig. 3d). The ejected fluorine atom re-adsorbed onto a surface calcium atom and the sodium atom. Overall, the following reaction occurred:
| Surf–F + NaSiO(OH)3 = Surf–SiO(OH)3 + NaF | (1) |
The average distance between the non-protonated oxygen and the three surrounding calcium atoms was 2.54 Å. One protonated oxygen atom established an O–Ca and an O–Na bond with dO–Ca = 2.72 Å and dO–Na = 2.27 Å. The adsorption energy was ΔEads = −196.5 kJ mol−1 including ΔEdisp = −56.9 kJ mol−1: the anionic form of silica tetrahedron, i.e. SiO(OH)3−, adsorbed with significantly higher energy in absolute value compared to the Si(OH)4 form.
(3) To assess the influence of total silica concentration in solution, the surface coverage was successively increased to reach six Si(OH)4 molecules, i.e. 100% coverage (Fig. 3a and e). From two to five molecules, the adsorption configuration was roughly the same as that with one Si(OH)4 molecule, establishing however two Ca–O bonds instead of three. The molecules interacted with each other when they co-adsorbed, inducing a slight increase of adsorption energies in absolute values, from −100.7 kJ per mol per molecule for one molecule to −121.8 kJ per mol per molecule for five molecules (Fig. 3a). When added, the sixth molecule of Si(OH)4 formed spontaneously SiO(OH)3− and substituted a surface fluorine atom (Fig. 3e), which recombined with the proton to form HF on the surface:
| Surf–F + 6 Si(OH)4 = Surf–SiO(OH)3 + HF + 5 Si(OH)4 | (2) |
This reaction, which induced an increase in absolute value of the adsorption energy to −131.1 kJ per mol per molecule, was in agreement with XPS results that demonstrated a depletion in fluorine atoms and the existence of Ca–O bonds when the Na2SiO3 concentration was high (Fig. 3c).
(4) Si2O(OH)6 adsorbed in its molecular form establishing four Ca–O bonds between four terminal (non-bonding) oxygen atoms and four different surface calcium atoms with dO–Ca = 2.53 Å for three bonds and dO–Ca = 3.65 Å for the fourth bond (Fig. 3f). Moreover, as for the Si(OH)4 monomer, hydrogen atoms of the –OH groups established hydrogen bonds with surface fluorine atoms (Fig. 3b and f). Energetically speaking, the dimer adsorbed with ΔEads = −165.1 kJ mol−1 including ΔEdisp = −70.4 kJ mol−1, which represented a significantly lower adsorption energy in absolute value compared to two monomers, regardless of their acid–base form.
3.2. Adsorption of Na2SiO3 on carbonated CaF2 surface
The DRIFT spectrum of CaF2 treated with 5 × 10−2 mol L−1 of Na2CO3 and 5 × 10−2 mol L−1 of Na2SiO3 sequentially is significantly different from the spectra of CaF2 conditioned with each reagent alone (Fig. 4a). First, the bands located at 2492 cm−1 and at 1775 cm−1, previously attributed to Na2CO3/CaCO3, were no longer present when the two reagents were used together. Moreover, compared to CaF2 conditioned with Na2CO3 only, the band at 879 cm−1, ascribed to Na2CO3/CaCO3, was significantly weaker while the band located at 842 cm−1, attributed to NaHCO3, exhibited a higher intensity (Fig. 4a). This indicated a higher amount of adsorbed NaHCO3 when CaF2 was conditioned with Na2CO3 + Na2SiO3. Also, CaF2 conditioned only with Na2CO3 displayed one band at 1439 cm−1 and another at 1650 cm−1 while two peaks were present in each aforementioned zone for CaF2 conditioned with Na2CO3 + Na2SiO3: two bands located at 1732 and 1667 cm−1 and two other bands at 1470 and 1383 cm−1 were exhibited (Fig. 4a), corresponding to both carbonate and hydrogencarbonate species. Furthermore, the band corresponding to Si–O asymmetric stretching vibration was narrower and shifted to 1057 cm−1 with a shoulder at 1023 cm−1 when CaF2 was conditioned with Na2CO3 + Na2SiO3 (Fig. 4a). According to the literature, this could be attributed either to a higher amount of SiO(OH)3− form rather than Si(OH)4 form for silica tetrahedra or to a lower amount of polymerised silica on the surface.23,65,66 Considering the higher amounts of NaHCO3, it could be considered that one or both of the following reactions occurred on the surface:| Si(OH)4 + CO32− = SiO(OH)3− + HCO3− | (3) |
| Si2O(OH)6 + CO32− + H2O = SiO(OH)3− + Si(OH)4 + HCO3− | (4) |
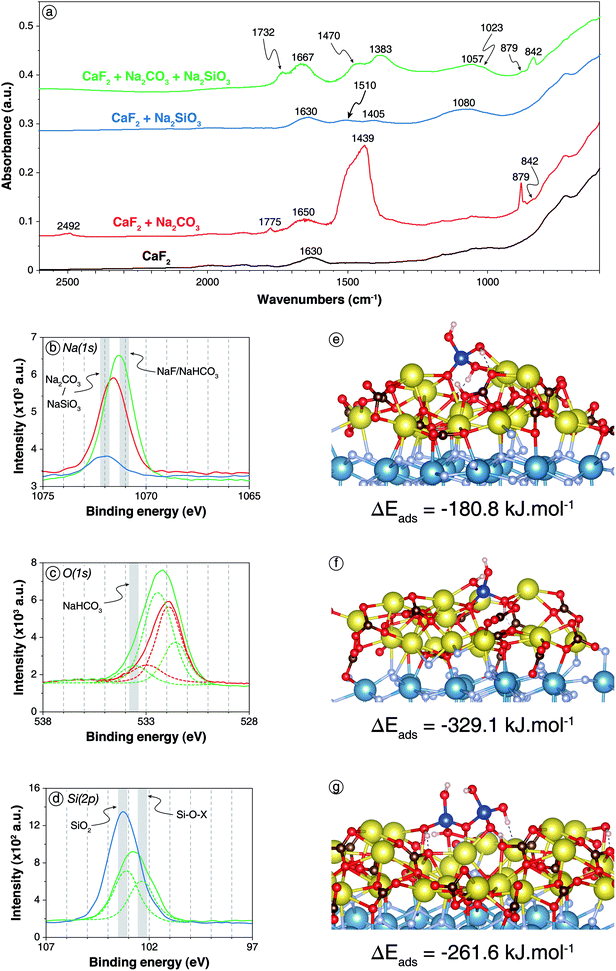 | ||
| Fig. 4 Adsorption of Na2SiO3 onto carbonated CaF2 surface. (a) Infrared spectra of CaF2 conditioned in deionised water (black), in a 5 × 10−2 mol L−1 Na2CO3 solution (red), in a 5 × 10−2 mol L−1 Na2SiO3 solution (blue), and in a 5 × 10−2 mol L−1 Na2CO3 solution prior to in a 5 × 10−2 mol L−1 Na2SiO3 solution (green). (b) XPS Na(1s) spectra of the three last aforementioned samples (same colour scheme). (c) XPS O(1s) spectra of CaF2 conditioned in a 5 × 10−2 mol L−1 Na2CO3 solution (red) and in a 5 × 10−2 mol L−1 Na2CO3 solution prior to in a 5 × 10−2 mol L−1 Na2SiO3 solution (green). d. XPS Si(2p) spectra of CaF2 conditioned in a 5 × 10−3 mol L−1 Na2SiO3 solution (blue) and in a 5 × 10−3 mol L−1 Na2CO3 solution prior to in a 5 × 10−3 mol L−1 Na2SiO3 solution (green). (e) Snapshot of a side view of the carbonated (111) CaF2 surface with a Si(OH)4 molecule adsorbed onto the surface exhibiting a proton exchange. (f) Snapshot of a side view of the carbonated (111) CaF2 surface with a NaSiO(OH)3 molecule adsorbed onto the surface. (g) Snapshot of a side view of the carbonated (111) CaF2 surface with a Si2O(OH)6 molecule adsorbed on the surface exhibiting a proton exchange. For colour scheme of spheres, refer to Fig. 1 and 2. Dashed lines represent hydrogen bonds. | ||
XPS analyses were also conducted on CaF2 conditioned with low reagent concentrations, i.e. 5 × 10−3 mol L−1 for each, or with high reagent concentrations, i.e. 5 × 10−2 mol L−1. For low reagent concentrations, sodium atoms were identified (5.0 at%) with Na(1s) binding energies of 1071.3 eV, which was significantly lower than the 1071.6 eV or 1071.9 eV displayed for CaF2 + Na2CO3 and CaF2 + Na2SiO3, respectively (Fig. 4b). This shift could be attributed to the formation of NaHCO3 on the surface since this latter exhibits lower Na(1s) binding energy than Na2CO3.62 Moreover, the peak at 533.6 eV exhibited in the O(1s) spectrum for CaF2 + Na2CO3 + Na2SiO3, which was absent for CaF2 + Na2CO3 and CaF2 + Na2SiO3, corresponded to NaHCO3.71 The O/Si ratio was 4.03, which was slightly higher than the 3.61 exhibited for Na2SiO3 alone at the same concentration, indicating a possible depolymerisation of silica species on the surface induced by the carbonate layer.
When the reagent concentrations were increased to 5 × 10−2 mol L−1, the surface chemical responses were very similar to those observed at low reagent concentrations. Interestingly, the Si(2p) spectrum displayed two components, at 103.1 eV (5.6 at%) and 102.3 eV (4.6 at%), while only one component at 103.2 eV was identified for CaF2 + Na2SiO3 at the same concentration (Fig. 4d). Although the interpretation of Si(2p) spectra was difficult, the component at 103.1 eV was previously ascribed to Si–O–Si, i.e. polymerised silica, while the component at 102.3 eV was ascribed to Si–O–Na, i.e. non-polymerise and deprotonated silica.
To confirm these results, AIMD simulations were conducted on a carbonated surface. A complete layer of Na2CO3 was set on the (111) CaF2 surface: a natrite supercell was created and fully relaxed at 0 K before generating the (110) surface, which presented crystallographic properties very close to those of the (111) fluorite surface. The natrite slab was then set on the (111) fluorite slab so that the CO32− anions and the Na+ cations corresponded spatially to Ca2+ cations and F− anions, respectively. This carbonated surface was then used for the adsorption of Na2SiO3 at 300 K. As for bare CaF2 surface, the adsorption of three different species was investigated: (1) the protonated monomer, i.e. Si(OH)4; (2) the basic form of the monomer, i.e. NaSiO(OH)3; and (3) the protonated form of the dimer, i.e. Si2O(OH)6.
The Si(OH)4 molecule placed onto the carbonated (111) CaF2 surface adsorbed establishing five Na–O bonds with two Na–O bonds formed by two different oxygen atoms and one Na–O bond by the last oxygen atom (Fig. 4e) with average bond lengths of between 2.36 and 2.88 Å. Each hydrogen atom established a hydrogen bond with an oxygen atom of the Na2CO3 layer. Besides, sometimes during the simulation, a proton was transferred from the Si(OH)4 molecule to a CO32− anion of the Na2CO3 surface layer (Fig. 4e). After a few picoseconds, it was transferred back to the Si(OH)4, indicating that the two configurations coexisted on the surface with similar energy. This reaction on the surface was in good agreement with the formation of NaHCO3 previously demonstrated by DRIFTS and XPS (Fig. 4a–d). Overall, Si(OH)4 adsorbed onto the carbonated surface with ΔEads = −180.8 kJ mol−1 including ΔEdisp = −45.0 kJ mol−1 compared to ΔEads = −100.8 kJ mol−1 including ΔEdisp = −46.4 kJ mol−1 onto the bare surface.
The NaSiO(OH)3 molecule placed onto the carbonated (111) CaF2 surface adsorbed with the deprotonated oxygen atom establishing four Na–O bonds with average bond lengths of between 2.34 and 2.70 Å (Fig. 4f). Moreover, each protonated oxygen atom established one Na–O bond with the Na2CO3 layer with similar bond lengths. The hydrogen atoms formed hydrogen bonds with surface oxygen atoms while the sodium atom also adsorbed onto the Na2CO3 layer. Overall, the NaSiO(OH)3 molecule adsorbed with ΔEads = −329.1 kJ mol−1 including ΔEdisp = −73.7 kJ mol−1, which was significantly higher than for the bare surface.
The Si2O(OH)6 molecule set on the carbonated surface adsorbed with three non-bonding and the bonding oxygen atoms each establishing two Na–O bonds with average bond lengths of between 2.30 and 2.80 Å (Fig. 4g). Also, one proton was transferred durably from Si2O(OH)6 to a CO32− anion of the surface, forming the Si2O2(OH)5− species (Fig. 4g). Episodically during the simulation, a second proton was transferred between the adsorbed molecule and the surface, forming the Si2O3(OH)42− molecule. Overall, the dimer adsorbed with ΔEads = −261.6 kJ mol−1 including ΔEdisp = −87.9 kJ mol−1, which represented significantly higher adsorption energies in absolute values compared to the bare surface.
XPS and DRIFTS results demonstrated that the prior treatment with Na2CO3 could induce a depolymerisation of silica on the surface. Hence, a Si2O(OH)6 molecule was set onto bare and carbonated surfaces along with an H2O molecule, which is mandatory to enable the depolymerisation reaction. However, this reaction was not observed spontaneously.
Overall, based on the previous results, the following conclusions could be drawn, at pH 10:
(1) Conditioning with Na2CO3 induced the formation of a carbonate layer at CaF2 surface.
(2) Na2SiO3 adsorbed on CaF2 surface in both Si(OH)4 and SiO(OH)3− forms, with significant amount of polymerised forms of silica at the studied concentrations.
(3) The CO32− ions contained in the surface carbonate layer accepted a proton from silica: NaHCO3 was formed while deprotonated and/or depolymerised silica forms became dominant on the surface. The deprotonated forms of silica adsorbed better than the protonated forms, which could explain the synergistic effects observed between the two reagents.
3.3. Discussion
Considering the experimental and theoretical results, we demonstrated that the Na2CO3 layer formed on the surface induced a proton exchange between the silica molecules and the carbonated surface, even at low coverage (1 molecule, i.e. 16.7% coverage). This proton exchange occurred for the acid forms of the monomer [Si(OH)4] and dimer [Si2O(OH)6], and, hence, probably for all the n-mers. This resulted in the formation of the basic, i.e. anionic, forms of these molecules, which adsorbed with significantly higher adsorption energies compared to their acid forms (Table 2). This proton exchange was observed for the bare surface only for high surface coverage (6 molecules, i.e. 100% coverage). These results explained the positive synergistic effects on the gangue minerals depression observed when the reagents are used in combination: the prior surface carbonation allows the formation of the anionic species of silica molecules by a surface acid–base reaction. It induces chemisorption of these molecules onto the surface for low coverage while a high coverage is needed to observe the same phenomenon on the bare surface. Increasing the solution pH would also lead to observation of the same phenomenon by increasing the amount of anionic silica species in solution. However, it would also result in hydroxylation of the surface cations, which would prevent the collector adsorption on all surfaces, including on the target mineral(s) surface.| Molecule | Number | Surface | ΔEads (kJ per mol per molecule) | ΔEdisp (kJ per mol per molecule) | Comments |
|---|---|---|---|---|---|
| Si(OH)4 | 1 | Bare | −100.7 | −46.4 | — |
| Si(OH)4 | 6 | Bare | −131.1 | −49.4 | Formation of HF by surface substitution of F− by SiO(OH)3− |
| NaSiO(OH)3 | 1 | Bare | −196.5 | −56.9 | Formation of NaF by surface substitution of F− by SiO(OH)3− |
| Si2O(OH)6 | 1 | Bare | −165.1 | −70.4 | — |
| Si(OH)4 | 1 | Carbonated | −180.8 | −45.0 | Partial formation of SiO(OH)3− by proton exchange with the surface |
| NaSiO(OH)3 | 1 | Carbonated | −329.1 | −73.7 | — |
| Si2O(OH)6 | 1 | Carbonated | −261.6 | −87.9 | Formation of Si2O(OH)5− and partial formation of Si2O(OH)42− by proton exchanges with the surface |
4. Conclusion
In this article, we used a combination of surface spectroscopic methods (DRIFTS and XPS) and AIMD simulations to gain an understanding in the adsorption mechanisms of Na2SiO3 on fluorite, which represents an archetype of salt-type minerals. In particular, the synergistic effects observed when Na2SiO3 is used in combination with Na2CO3 in the froth flotation process were investigated. Both experimental and theoretical results demonstrated that Na2CO3 adsorbs onto fluorite and forms a carbonate layer on the surface. Also, they proved that Si(OH)4, the most stable form of Na2SiO3 in dilute aqueous solutions at pH < 9.4, physisorbs with ΔEads = −100.7 kJ mol−1 while SiO(OH)3−, stable for pH > 9.4, chemisorbs onto the surface by substituting a fluorine atom, with ΔEads = −196.5 kJ mol−1. The dimer Si2O(OH)6, representing polymerised forms stable for higher silica concentrations, physisorbs with ΔEads = −165.1 kJ mol−1, which is significantly lower than that for two monomers. The surface carbonation, induced by the prior addition of Na2CO3, leads to an acid–base reaction on the surface that results in the formation of the deprotonated forms of silica, regardless of the polymerisation degree, i.e. SiO(OH)3−, Si2O2(OH)5−, and Si2O3(OH)42−. Also, experimental studies demonstrated that the surface carbonation leads to a silica depolymerisation on the surface. The anionic forms adsorbed with higher adsorption energies in absolute values compared to acid forms, as well as the monomers compared to the dimers. The formation of anionic forms on the bare surface needs either high silica coverage or high solution pH to be observed. Hence, at a moderate pH, a lower amount of Na2SiO3 is needed when the surface is carbonated to produce the same effect, explaining the strong synergistic effects highlighted when Na2SiO3 is used in combination with Na2CO3. Also, the deprotonation in solution by a pH increase would lead to hydroxylation of all the surfaces and then a global depression of all the minerals including the target mineral. This work allowed a gain in the understanding of the depressing effect of the combination of Na2SiO3 and Na2CO3 and could lead to a reduction of the Na2SiO3 amounts used worldwide in the flotation industry by using Na2CO3 instead of NaOH to control the pH.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was granted access to the HPC resources of TGCC and CINES under the allocations 2018-A0050910306 and 2019-A0060910433 made by GENCI. The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 821265 for the FineFuture project. We also acknowledge the support of Labex Ressoures 21, supported by the French National Research Agency through the national programme “Investissements d’Avenir” with reference ANR-10-LABX-21-LABEX RESSOURCES 21. Aurélien Renard, from the Laboratoire de Chimie Physique et Microbiologie pour les Matériaux et l’Environnement (UMR UL-CNRS 7564), is also acknowledged for the XPS analyses.References
- Markets and Markets, 2018.
- A. Pedone, G. Malavasi, A. N. Cormack, U. Segre and M. C. Menziani, Chem. Mater., 2007, 19, 3144–3154 CrossRef CAS.
- T. Nakamura and M. Ogawa, Langmuir, 2012, 28, 7505–7511 CrossRef CAS PubMed.
- P.-H. Chien, Y. Jee, C. Huang, R. Dervişoğlu, I. Hung, Z. Gan, K. Huang and Y.-Y. Hu, Chem. Sci., 2016, 7, 3667–3675 RSC.
- K. M. Alotaibi, L. Shiels, L. Lacaze, T. A. Peshkur, P. Anderson, L. Machala, K. Critchley, S. V. Patwardhan and L. T. Gibson, Chem. Sci., 2017, 8, 567–576 RSC.
- K. Baral, A. Li and W.-Y. Ching, J. Phys. Chem. A, 2017, 121, 7697–7708 CrossRef CAS PubMed.
- G. Lagaly, W. Tufar, A. Minihan and A. Lovell, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2000 Search PubMed.
- V. Kahlenberg, CHIMIA International Journal for Chemistry, 2010, 64, 716–722 CrossRef CAS.
- J. E. Shelby, Introduction to glass science and technology, Royal Society of Chemistry, Cambridge, 2nd edn, 2005 Search PubMed.
- J. Swenson and S. Adams, Phys. Rev. Lett., 2003, 90, 155507 CrossRef PubMed.
- L. O. Filippov, Q. Dehaine and I. V. Filippova, Miner. Eng., 2016, 95, 96–106 CrossRef CAS.
- M. Ejtemaei, M. Irannajad and M. Gharabaghi, Int. J. Miner. Process., 2012, 114–117, 40–47 CrossRef CAS.
- D. S. Rao, T. V. VijayaKumar, S. S. Rao, S. Prabhakar and G. B. Raju, Int. J. Miner., Metall. Mater., 2011, 18, 515–522 CrossRef CAS.
- L. O. Filippov, Y. Foucaud, I. V. Filippova and M. Badawi, Miner. Eng., 2018, 123, 85–94 CrossRef CAS.
- N. Kupka and M. Rudolph, Int. J. Min. Sci. Technol., 2018, 28, 373–384 CrossRef CAS.
- X. Yang, Miner. Eng., 2018, 125, 111–119 CrossRef CAS.
- Y. Foucaud, I. V. Filippova and L. O. Filippov, Powder Technol., 2019, 352, 501–512 CrossRef CAS.
- S. Song, A. Lopez-Valdivieso, C. Martinez-Martinez and R. Torres-Armenta, Miner. Eng., 2006, 19, 912–917 CrossRef CAS.
- W. Zhou, J. Moreno, R. Torres, H. Valle and S. Song, Miner. Eng., 2013, 45, 142–145 CrossRef CAS.
- H. Sis and S. Chander, Miner. Eng., 2003, 16, 577–585 CrossRef CAS.
- G. W. Qi, C. Klauber and L. J. Warren, Int. J. Miner. Process., 1993, 39, 251–273 CrossRef CAS.
- I. Halasz, M. Agarwal, R. Li and N. Miller, Catal. Lett., 2007, 117, 34–42 CrossRef CAS.
- J. L. Bass and G. L. Turner, J. Phys. Chem. B, 1997, 101, 10638–10644 CrossRef CAS.
- K. I. Marinakis and H. L. Shergold, Int. J. Miner. Process., 1985, 14, 177–193 CrossRef CAS.
- C. W. Lentz, Inorg. Chem., 1964, 3, 574–579 CrossRef CAS.
- D. Dimas, I. Giannopoulou and D. Panias, J. Mater. Sci., 2009, 44, 3719–3730 CrossRef CAS.
- J. Nordström, E. Nilsson, P. Jarvol, M. Nayeri, A. Palmqvist, J. Bergenholtz and A. Matic, J. Colloid Interface Sci., 2011, 356, 37–45 CrossRef PubMed.
- K. I. Marinakis, 1980.
- Y. Han, W. Liu and J. Chen, Appl. Surf. Sci., 2016, 370, 403–409 CrossRef CAS.
- P. S. Roller and G. Ervin, J. Am. Chem. Soc., 1940, 62, 461–471 CrossRef CAS.
- 4, 488, 959, 1984, 17.
- E. Potapova, M. Grahn, A. Holmgren and J. Hedlund, J. Colloid Interface Sci., 2010, 345, 96–102 CrossRef CAS PubMed.
- N. V. Tran, A. K. Tieu, H. Zhu, H. T. T. Ta, T. D. Ta and H. M. Le, J. Phys. Chem. C, 2018, 122, 20827–20840 CrossRef CAS.
- D. Azizi and F. Larachi, Colloids Surf., A, 2018, 537, 126–138 CrossRef CAS.
- B. S. Shin and K. S. Choi, Mining, Metallurgy & Exploration, 1985, 2, 223–226 Search PubMed.
- N. Kupka and M. Rudolph, Miner. Eng., 2018, 129, 120–128 CrossRef CAS.
- T. Ogawa, T. Aonuma, T. Tamaki, H. Ohashi, H. Ushiyama, K. Yamashita and T. Yamaguchi, Chem. Sci., 2014, 5, 4878–4887 RSC.
- X. Li, Z.-J. Zhao, L. Zeng, J. Zhao, H. Tian, S. Chen, K. Li, S. Sang and J. Gong, Chem. Sci., 2018, 9, 3426–3437 RSC.
- X. Liu, Y. Tang, M. Shen, W. Li, S. Chu, B. Shan and R. Chen, Chem. Sci., 2018, 9, 2469–2473 RSC.
- P. Zhou, X. Hou, Y. Chao, W. Yang, W. Zhang, Z. Mu, J. Lai, F. Lv, K. Yang, Y. Liu, J. Li, J. Ma, J. Luo and S. Guo, Chem. Sci., 2019, 10, 5898–5905 RSC.
- I. Píš, E. Magnano, S. Nappini and F. Bondino, Chem. Sci., 2019, 10, 1857–1865 RSC.
- G. Lovat, E. A. Doud, D. Lu, G. Kladnik, M. S. Inkpen, M. L. Steigerwald, D. Cvetko, M. S. Hybertsen, A. Morgante, X. Roy and L. Venkataraman, Chem. Sci., 2019, 10, 930–935 RSC.
- C. Shen, I. Cebula, C. Brown, J. Zhao, M. Zharnikov and M. Buck, Chem. Sci., 2012, 3, 1858 RSC.
- H. H. Kristoffersen, T. Vegge and H. A. Hansen, Chem. Sci., 2018, 9, 6912–6921 RSC.
- Y. Foucaud, S. Lebègue, L. O. Filippov, I. V. Filippova and M. Badawi, J. Phys. Chem. B, 2018, 122, 12403–12410 CrossRef CAS PubMed.
- Y. Foucaud, M. Badawi, L. Filippov, I. Filippova and S. Lebègue, Miner. Eng., 2019, 143, 106020 CrossRef CAS.
- T. C. Parks and W. W. Barker, J. Solid State Chem., 1977, 20, 397–407 CrossRef CAS.
- P. W. Tasker, Le Journal de Physique Colloques, 1980, 41, C6–C488 CrossRef.
- N. H. de Leeuw, J. A. Purton, S. C. Parker, G. W. Watson and G. Kresse, Surf. Sci., 2000, 452, 9–19 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. A. Miller and C. H. Wilkins, Anal. Chem., 1952, 24, 1253–1294 CrossRef CAS.
- M. Roche, Caractérisation de l'état de surface des fluorines et application à la flottation des minerais de fluorine du district du Tarn (Montroc - Le Burc), PhD thesis, Université de Nancy I, 1973 Search PubMed.
- K. I. Marinakis and H. L. Shergold, Int. J. Miner. Process., 1985, 14, 161–176 CrossRef CAS.
- J. F. Moulder, Handbook of X-ray photoelectron spectroscopy: a reference book of standard spectra for identification and interpretation of XPS data, Perkin-Elmer Corporation, Eden Prairie, Minn, Update, 1992 Search PubMed.
- Y. Foucaud, M. Badawi, L. O. Filippov, I. V. Filippova and S. Lebègue, J. Phys. Chem. B, 2018, 122, 6829–6836 CrossRef CAS PubMed.
- Y. Foucaud, M. Badawi and L. Filippov, Miner. Eng., 2019, 135, 156–159 CrossRef CAS.
- H. Jansson, D. Bernin and K. Ramser, AIP Adv., 2015, 5, 067167 CrossRef.
- R. Gaggiano, I. De Graeve, J. M. C. Mol, K. Verbeken, L. A. I. Kestens and H. Terryn, Surf. Interface Anal., 2013, 45, 1098–1104 CrossRef CAS.
- E. Merlen, J. Lynch, M. Bisiaux and F. Raatz, Surf. Interface Anal., 1990, 16, 364–368 CrossRef CAS.
- T. L. Barr, J. Phys. Chem., 1978, 82, 1801–1810 CrossRef CAS.
- S. Carniato, J.-J. Gallet, F. Rochet, G. Dufour, F. Bournel, S. Rangan, A. Verdini and L. Floreano, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085321 CrossRef.
- L. Pauling, The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry, Cornell Univ. Press, Ithaca, New York, 3rd edn, 17 print, 2000 Search PubMed.
- A. Shchukarev and D. Korolkov, Cent. Eur. J. Chem., 2004, 2, 347–362 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc03366a |
| This journal is © The Royal Society of Chemistry 2019 |
