Revealing the role of the Rh valence state, La doping level and Ru cocatalyst in determining the H₂ evolution efficiency in doped SrTiO₃ photocatalysts

Abstract

SrTiO₃ (STO) has favorable opto-electronic properties for overall water splitting. Nevertheless, realizing a higher efficiency is impeded by its band gap which can only harvest UV light. In order to extend the spectral response towards visible light, STO is (co)doped with lanthanum (La) and rhodium (Rh). However, notwithstanding the amount of visible light absorbed, the H₂ evolution rates are remarkably governed by the valence state of Rh, La doping level and ruthenium (Ru) cocatalyst loading. Hence, it is essential to unravel the underlying effect of doping on the photophysical processes to gain insight into material design. To this end, charge carrier dynamics was probed over a wide time (sub-picosecond to microsecond) and spectral (visible to IR) region using transient absorption spectroscopy. Depending on the dopant composition, an interplay between the electron trapping and the kinetics of the electron transfer to the Ru cocatalyst was rationalized. For Rh⁴⁺:STO, free electrons probed at 3435 nm decayed virtually completely by 20 ps resulting in a kinetic competition between the electron trapping and the electron transfer to Ru cocatalyst. In the case of Rh³⁺:STO, free electrons decayed by a factor of three by 100 ps, thus demonstrating the effect of Rh valence state on the electron lifetime. The time constant and quantum yield of electron transfer from Rh³⁺:STO to the Ru cocatalyst were found to be 1.6 ps and 14.7%, respectively. In addition to a longer electron lifetime, enhanced electron transfer to the Ru cocatalyst makes Rh³⁺:STO one of the promising photocatalysts for H₂ generation. Engineering the energetic position of the dopant within the band gap to avoid undesirable carrier trapping is crucial to enhance the efficiency of photocatalytic reactions.

---

Introduction

Photocatalytic water splitting is one of the promising and inexpensive ways to convert sunlight (solar energy) into chemical energy, e.g., H₂.^1–6 The primary process in photocatalytic water splitting is the absorption of light by the semiconductor (photocatalyst) leading to the formation of charge carriers. The next step is the migration of charge carriers towards the surface of the photocatalyst where they participate in reduction/oxidation reactions with water. Several parameters govern the efficiency of photocatalytic water splitting. In essence, efficient charge transport to the surface of a photocatalyst is very critical to improve the efficiency. Another important factor is the ability of a photocatalyst to harness a wide part of the solar spectrum. To this end, current research is devoted (but not limited) to developing novel materials that possess a higher light harvesting efficiency in conjunction with improved charge transport properties.

Among the various types of materials investigated for the photocatalytic water splitting application, SrTiO₃ (STO) has recently attracted significant interest.^7–11 STO is an n-type semiconductor with a perovskite-type cubic structure of ABO₃. The conduction band (CB) and valence band (VB) of STO are characterized by the titanium 3d (Ti 3d) and oxygen 2p (O 2p) states, respectively. STO has appropriate CB and VB positions to allow both reduction and oxidation reactions with water to yield H₂ and O₂, respectively. However, STO only absorbs ultraviolet (UV) light owing to its optical band gap of 3.2 eV. In order to extend the spectral response towards visible light, in-gap states have to be induced through doping with metal cations. Moreover, its susceptibility towards the substitution of dopants at both Sr and Ti sites of the STO crystal lattice makes it a unique material for bandgap engineering.¹² Previous reports^13–16 have efficiently demonstrated the extension of optical absorption beyond 500 nm by (co)doping with various metals such as antimony (Sb), rhodium (Rh), chromium (Cr) and iridium (Ir). Niishiro et al. and Furuhashi et al. reported on enhancing the visible light absorption by using Rh doping. Doping STO with only Rh resulted in the Rh⁴⁺ valence state while codoping with Sb partly transformed the valence state of Rh from Rh⁴⁺ to Rh³⁺ consequently enhancing the H₂ evolution rate.^14,17 Konta et al.¹³ and Kawasaki et al.¹⁵ reported that doping STO with Ir could extend the absorption up to 580 nm. However, changing the valence state of Ir from Ir⁴⁺ to Ir³⁺ resulted in the virtual absence of photoelectrochemical activity.¹⁵ In a similar line, Ishii et al. reported the effect of Cr and Ta doping on the hydrogen evolution efficiency.¹⁶ The H₂ evolution rate increased by a factor of six when Ta was codoped with Cr, which converted the Cr valence state from Cr⁶⁺ to Cr³⁺. As described in these examples, it is amenable that an increase in the visible light absorption by doping does not always improve the photocatalytic activity. Instead, the valence state of the metal dopant seems to play a key role in determining the efficiency of the photocatalytic reaction. Hence, there is a pressing need to obtain a mechanistic understanding of the precise role of the metal dopant's valence state in photocatalytic reactions. Such studies offer unique insights into designing novel doped STO materials with superior performance by allowing efficient conversion of visible light.

Another aspect that critically affects photocatalytic performance is the amount of dopant introduced into the host lattice. Ishii et al.¹⁶ investigated the effect of the Cr doping level on the H₂ evolution efficiency. The amount of H₂ released was found to decrease when the Cr doping level exceeds 6 mol%. For a given dopant, the photocatalytic performance decreases when the dopant amount is above or below the optimum level. Nonetheless, a comprehensive understanding of why only a particular doping level enhances the photocatalytic activity remains elusive.

Doping a semiconductor with transition metal cations holding d electrons extends the absorption towards longer wavelengths by forming in-gap states. Consequently, these impurity states formed by doping are likely to act as recombination and trapping centers for charge carriers. Note that the photocatalytic reaction occurs only at the interface between the photocatalyst and water/electrolyte. This condition requires efficient migration of charge carriers from bulk to the surface by avoiding undesirable recombination and trapping. To enhance the efficiency of photocatalytic reactions, cocatalyst particles are generally loaded on the surface of the photocatalyst.¹⁸ Charge transfer from the photocatalyst to the cocatalyst is another key process in determining the efficiency of the photocatalytic reaction.^18,19 Thus, elucidating the factors affecting the efficiency of the charge transfer process is crucial for designing novel photocatalytic materials.

Inspired by the unique opto-electronic properties of STO, significant effort is devoted to finding a new combination of metal dopants to further enhance the efficiency of photocatalytic reactions. In this regard, the effect of La and Rh (co)doping on the photocatalytic activity is being investigated by our group.²⁰ Table S1† summarizes the H₂ evolution rate depending on the valence state of Rh and on the La doping level. The valence state of Rh was determined using X-ray photoelectron spectroscopy (XPS). STO doped with only Rh predominantly forms Rh⁴⁺ valence states and is denoted as Rh⁴⁺:STO. Using a 4 mol% La codoping level, the Rh⁴⁺ valence states were transformed to Rh³⁺ (owing to charge compensation), which is referred to as Rh³⁺:STO (4 mol% La). On further increasing the La codoping level to 10 mol%, the Rh⁴⁺ valence states were further converted to Rh³⁺ and is indicated as Rh³⁺:STO (10 mol% La). The H₂ evolution rate for Rh⁴⁺:STO is less by a factor of more than three compared to Rh³⁺:STO (4 mol% La). Furthermore, for Rh³⁺:STO, increasing the La doping level from 4 to 10 mol% while maintaining a constant Rh doping level (4 mol%) resulted in a significantly lower (<1 μmol per hour) H₂ evolution rate (Table S1†).²⁰ In addition to the effect of La/Rh doping, loading of Ru cocatalyst particles significantly influenced the efficiency of the H₂ evolution rate. Without the loading of the Ru cocatalyst on La/Rh doped STO, the H₂ evolution was virtually absent²⁰ (Fig. S1†), signifying the indispensable role of the Ru cocatalyst in realizing an efficient H₂ evolution.

Rh³⁺:STO (4 mol% La) is a very promising H₂ evolution photocatalyst in the Z-scheme configuration which demonstrated a solar-to-hydrogen (STH) energy conversion efficiency of 1% (ref. 8) when prepared using the particle transfer method. To the best of our knowledge, this is the highest water splitting efficiency of a particle-based Z-scheme to date. Techno-economic analysis by Pinaud et al.²¹ showed that the particle transfer method is one of the simplest and cost-effective approaches to produce H₂ as compared to photoelectrodes or PV-electrolysers. In order to further enhance the STH value, it is essential to develop an understanding of the key factors responsible for realizing a higher efficiency with Rh³⁺:STO (4 mol% La).

In the work presented here, we examine the following three specific questions: (i) how does the valence state of Rh influence the H₂ evolution rate? (ii) what causes the lack of photocatalytic activity in 10 mol% La doped Rh³⁺:STO? and (iii) what factors determine the kinetics/efficiency of the electron transfer to the Ru cocatalyst. To this end, time-resolved diffuse reflectance (TDR) spectroscopy is employed as a tool. Note that TDR is essentially similar to transient absorption spectroscopy (TAS) except that in the former the TA signal is monitored in the diffuse reflection mode because of the opaque nature of the photocatalyst powder samples. This technique was efficiently used in the past to examine carrier dynamics in various types of photocatalysts.^19,22–26 Carrier dynamics was probed from a sub-picosecond to a microsecond over a broad energy range (from visible to IR) to comprehensively understand and distinguish the unique electron decay pathways. This type of detailed study aided in unraveling the effect of dopant amount and composition on the interplay between electron trapping and electron transfer to the Ru cocatalyst. Results from this systematic investigation are correlated with the H₂ evolution rates to gain insight into improving the STH value of La/Rh doped STO, which is a key requirement for the practical implementation of the photocatalytic water splitting technology.

Results and discussion

Effect of La/Rh doping on the opto-electronic properties and the band energy diagram of STO

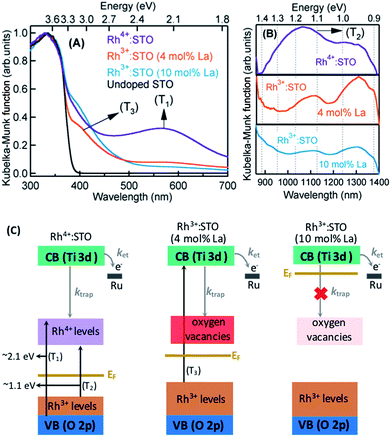
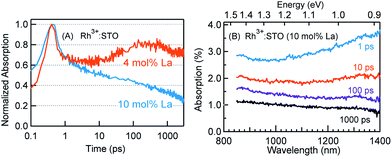
The crystal structure of STO is favorable to the substitution of different types of dopants. A precise determination of the dopant substitution site within the STO crystal lattice is rather complex. Nevertheless, the most probable sites for substitution can be understood by correlating the ionic radii of the dopant ions with those of the elements constituting the STO crystal lattice. The ionic radii of La³⁺, Sr²⁺ and Ti⁴⁺ are 103.2, 118, and 60.5 pm, respectively. Based on these values, substitution of La³⁺ with bigger sized Sr²⁺ is likely while its substitution with smaller sized Ti⁴⁺ sites is not feasible. In the case of the Rh dopant, preferential substitution of Rh ions in the Ti⁴⁺ sites of the STO crystal lattice is well documented.^17,20,27,28 When STO is doped with only Rh, the valence state of Rh was found to be predominantly Rh⁴⁺. The XPS measurements clearly corroborated this observation (Fig. S2†). Note that the Rh⁴⁺ ion is in the d⁵ configuration (Rh 4d t⁵_2g e⁰_g) with an unpaired electron.^14,28,29 In order to understand the influence of Rh doping, ground-state optical absorption spectra for La/Rh doped STO are recorded (Fig. 1A and B). Spectral features noticed in Fig. 1A and B are correlated with the literature data^28,30 to draw the energy band diagram depicted in Fig. 1C.

Fig. 1 Ground-state optical absorption spectra measured in the diffuse reflection mode in the (A) visible and (B) NIR region for La/Rh doped STO. (C) The proposed band energy diagram indicating the likely Fermi level position (E_F), major optical transitions and photophysical processes such as the rate of electron trapping to defect states, k_trap, and the rate of electron transfer to the Ru cocatalyst, k_et, depending on the dopant composition and doping level as indicated. Note that the position of the Ru metal is not drawn by considering the changes in the Fermi level of La/Rh doped STO.

For Rh⁴⁺:STO, the presence of a broad absorption peak centered around ≈590 nm is due to transition (T₁ in Fig. 1C) from the VB maxima to the in-gap Rh⁴⁺ unoccupied levels. A broad absorption band between 1000 and 1100 nm is also observed which is assigned to the d–d transitions between the Rh³⁺ and Rh⁴⁺ species (T₂ in Fig. 1C). Note that optical transition from the Rh⁴⁺ unoccupied levels to the CB is unlikely as these levels are unoccupied. Note also that, even in the case of Rh⁴⁺:STO, the presence of small amounts of Rh³⁺ occupied levels just above the VB is possible leading to absorption between 385 and 500 nm. Earlier reports from both experiments and theoretical calculations^27–29 consistently demonstrated a p-type behavior with the Fermi level position located between the Rh⁴⁺ unoccupied and Rh³⁺ occupied levels for Rh⁴⁺:STO as indicated in Fig. 1C.

In the case of Rh³⁺:STO (4 mol% La) (doped with 4 mol% Rh and 4 mol% La), a change in the valence state of Rh from Rh⁴⁺ to Rh³⁺ is confirmed using XPS, while no change in the valence state of Ti or Sr is detected (Fig. S2†). A previous study using Sb as a codopant along with Rh yielded a similar type of Rh valence state transition from Rh⁴⁺ to Rh³⁺.^13,14 The Rh valence state change is due to the charge compensation effect upon La codoping. Note that for synthesizing both Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO, similar reaction conditions such as calcination temperature and atmosphere are employed to rule out such effects on the Rh valence state change. Note that despite La/Rh doping, the bulk crystal structure/phase is well retained as confirmed using XRD (Fig. S3†). Compared to Rh⁴⁺:STO, a significant reduction in the broad absorption peaks around 590 and 1000 nm is observed for Rh³⁺:STO (4 mol% La). The absorption from 385 to 500 nm is due to the transition from the Rh³⁺ occupied (donor) levels present above the VB to the CB (T₃ in Fig. 1C). The Mott–Schottky (M–S) plot is obtained to estimate the flat band potential for Rh³⁺:STO (4 mol% La) through which the Fermi level position can be estimated. A negative slope in the M–S plot (Fig. S4†) indicated a p-type behavior for Rh³⁺:STO (4 mol% La). Due to La codoping, which is an n-type dopant, a further shift in the Fermi level towards the CB is expected for Rh³⁺:STO (4 mol% La) when compared to Rh⁴⁺:STO.

We now discuss the different types of defect (trap) states and their electronic nature in Rh³⁺:STO (4 mol% La). Due to the substitution of Rh³⁺ in Ti⁴⁺ sites of the STO crystal lattice, the formation of oxygen vacancies is inevitable to compensate for the charge and to maintain electronic neutrality.^31–37 However, determining the precise energy position of oxygen vacancy states within the bandgap of Rh³⁺:STO (4 mol% La) is rather difficult because it is mutually correlated and complex. We propose that oxygen vacancy states are present rather deep within the bandgap as indicated in Fig. 1C. In addition, it is essential to stress that charge trapping by other types of defects such as reduced Ti⁴⁺ states^35,36 and Sr vacancies³⁸ cannot be completely ruled out. Nevertheless, we consider that oxygen vacancy states are one of the major and regularly attributed defects in STO.³⁹ A detailed study of the electronic nature of the defect states in Rh³⁺:STO (4 mol% La) is indeed essential, which is, however, beyond the scope of the current study.

For Rh³⁺:STO (10 mol% La), an increase in the La doping level from 4 to 10 mol% converted virtually all Rh⁴⁺ to Rh³⁺. The features in the ground-state optical absorption spectra remain virtually the same as for Rh³⁺:STO (4 mol% La). The absorption from 385 to 500 nm is due to the transition from the Rh³⁺ occupied levels present above the VB to the CB. A positive slope in the M–S plot for Rh³⁺:STO (10 mol% La) suggested an n-type behavior, which is in contrast to the p-type Rh³⁺:STO (4 mol% La) (Fig. S4†). Due to the n-type behavior of Rh³⁺:STO (10 mol% La) and the accompanying shift in the Fermi level closer to the CB, filling of electron trapping defect states (oxygen vacancies) present below the Fermi level is expected. Hence, the concentration of oxygen vacancies is proposed to be smaller for Rh³⁺:STO (10 mol% La) compared to Rh³⁺:STO (4 mol% La). This notion is in good agreement with an earlier work which clearly demonstrated a decrease in the concentration of oxygen vacancies and a concomitant increase in the n-type conduction upon substituting Sr²⁺ sites of the STO crystal lattice with La³⁺.³⁷

The bandgap of undoped STO is 3.2 eV owing to onset in the optical absorption around 385 nm. Under visible light (≥400 nm) excitation, efficient generation of CB electrons is not expected if the optical transition is to occur solely from the VB to the CB as the pump energy is smaller than the band gap of STO. Hence, in order to elicit an efficient visible light (≥400 nm) induced photocatalytic activity, optical transition from the Rh³⁺ donor levels present above the VB to the CB is essential.

In the subsequent discussion, the effect of Rh valence state is presented first followed by elucidation of the effect of La doping level on the charge dynamics. The effect of electron trapping on the efficiency and kinetics of electron transfer to the Ru cocatalyst is examined. Lastly, we outline the reason for the virtually absent photocatalytic activity for Rh³⁺:STO (10 mol%).

Probing free electron dynamics at 3435 nm

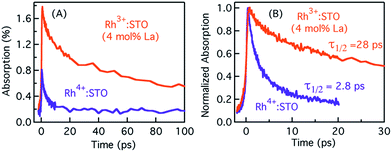
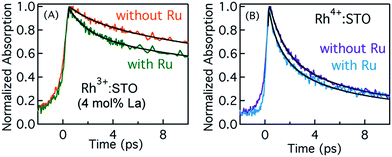
Typically, the dynamics of photogenerated free electrons in semiconductors is probed in the infrared (IR) region.^40–43 The IR probe light typically monitors the intra-band transition close to the CB levels. Before discussing the electron dynamics probed at 3435 nm, it is essential to exclude possible vibrational modes coupled to this probe energy. To this end, a typical FT-IR measurement under the steady-state condition was conducted. The absence of any detectable signal around 3435 nm (2911 cm⁻¹) ruled out any potential (overlapping) contribution from the vibrational modes influencing electron dynamics (Fig. S5†). Furthermore, a control experiment with a scavenger was carried out to determine the nature of carriers probed at 3435 nm. A faster decay of the TA signal in the presence of the AgNO₃ electron scavenger (Fig. S6†) further corroborated that free electrons are probed at 3435 nm. Fig. 2 shows the femtosecond electron dynamics for Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO obtained using a 400 nm pump. The photogenerated free electrons decay virtually completely by 20 ps for Rh⁴⁺:STO. However, for Rh³⁺:STO (4 mol% La), the free electron lifetime exceeds 100 ps. A similar trend was also noticed at the 266 nm pump (Fig. S7†). To further understand the decay pathway of free electrons, the effect of pump fluence was investigated. For both Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO, the electron dynamics was not significantly affected despite increasing the pump fluence by a factor of four (Fig. S8†). This observation indicates that the major decay pathway for free electrons is via trapping but not by the second-order type direct recombination with holes. The half lifetime (τ_1/2), i.e., the time at which the initial concentration of electrons reduces to half of its initial value, is found to be 2.8 ps and 28 ps for Rh⁴⁺:STO and Rh³⁺:STO (4 mol% La), respectively. The rate constant of electron trapping (1/τ_1/2) for Rh⁴⁺:STO and Rh³⁺:STO (4 mol% La) is estimated to be ≈0.36 ps⁻¹ and ≈0.036 ps⁻¹, respectively. A prompt quenching of mobile electrons within 20 ps for Rh⁴⁺:STO is due to the efficient electron trapping to the in-gap Rh⁴⁺ unoccupied levels. In the case of Rh³⁺:STO (4 mol% La), the electron lifetime is significantly longer (>100 ps) compared to that of Rh⁴⁺:STO suggesting that a majority of the electrons reach the shallow trap levels where they are still mobile upon thermal release of carriers to the CB. In addition to the shallow trapping process, deep trapping of electrons to oxygen vacancies is also expected to proceed for Rh³⁺:STO (4 mol% La), which results in the formation of immobile electrons which will be discussed in the next part.

Fig. 2 Femtosecond TDR profiles probed at 3435 nm showing (A) the signal magnitude and (B) the corresponding normalized transients for Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO. A 400 nm pump with a fluence of 0.5 μJ per pulse is employed for this measurement.

Probing trapped electron dynamics at 920 nm

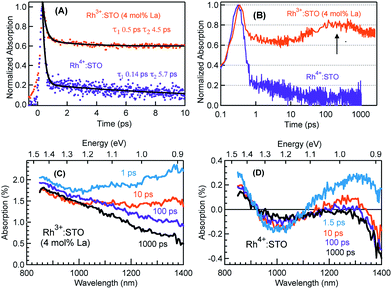
Fig. 3 presents the femtosecond transients for Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO monitored at 920 nm using the 400 nm pump. Based on the conclusions drawn from previous reports on doped STO, deep trapped electrons are majorly probed at 920 nm.^40,41 The decay dynamics for Rh³⁺:STO (4 mol% La) is very distinct from that of Rh⁴⁺:STO. To start with, the decay dynamics of Rh³⁺:STO (4 mol% La) is discussed.

Fig. 3 Femtosecond TDR profiles probed at 920 nm using the 400 nm pump with a fluence of 0.6 μJ per pulse for Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO showing the decay in (A) the linear scale till 10 ps where solid dark lines are a result of the double exponential function fit and (B) normalized transients in the semi-log plot where the arrow indicates a signal increase around 100 ps. Transient absorption (TA) spectra monitored from 850 nm to 1400 nm at different delay times for (C) Rh³⁺:STO (4 mol% La) and (D) Rh⁴⁺:STO conducted using the 400 nm pump.

To elucidate the ultrafast decay component within 1 ps (Fig. 3A), the decay dynamics of Rh³⁺:STO (4 mol% La) is compared with that of undoped STO. A similarity in the decay of both these samples within 1 ps is noticed. The similarity suggests that this ultrafast decay component likely originates from the optical transition from the VB to trap levels just below the CB where free carrier generation did not occur (Fig. S9†). Following the initial fast decay component, the TA signal remains unchanged till 10 ps after which it starts to increase and reaches a maximum (the arrow in Fig. 3B) around 100 ps. In addition, the TA signal does not show appreciable decay till 3000 ps. A similar observation was also made at different pump fluences (Fig. S10†), which further suggests the nature of carriers probed at 920 nm as deeply trapped electrons. To further discern the origin of this unique signal increase in Rh³⁺:STO (4 mol% La), TA spectra are recorded as depicted in Fig. 3C. The TA signal magnitude at 100 ps is higher than that at 10 ps, which is consistent with the signal increase in Rh³⁺:STO (4 mol% La) shown in Fig. 3B. Moreover, in the TA spectra, the absence of appreciable decay in the region between 850 and 1100 nm hints at the narrow energy distribution of the oxygen vacancy levels. The plausible mechanism for noticing the signal increase around 100 ps is proposed to be due to the trapping of CB free electrons to deep traps. Yamada et al. previously proposed the possibility of such a type of transition to occur in STO based heterostructures.⁴⁴ Note that the free electrons probed at 3435 nm (Fig. 2) decay over a factor of three by 100 ps, where deep trapping to oxygen vacancies forms one of the decay pathways. In order to determine whether the CB free electrons are the ones which are getting deep trapped, an experiment in the presence of Ru cocatalyst is conducted. Note that electron transfer from Rh³⁺:STO (4 mol% La) to the Ru cocatalyst is possible only if the electron is mobile. As expected, the signal increase around 100 ps is not observed due to the transfer (which otherwise get deep trapped) of free electrons to the Ru cocatalyst (Fig. S11†). This can be further proved by comparing the dynamics obtained using a 500 nm pump (Fig. S12†). Note that optical transition from Rh³⁺ levels to CB must occur to generate electrons in the CB under visible light excitation. When the energy of the pump light is decreased from 400 to 500 nm, the effective number of free electrons generated in the CB is reduced. As an inadequate number of electrons in the CB are generated, their decay via deep trapping would be less evident. Hence, a reduction in the trend of signal increase is anticipated under the 500 nm pump compared to that under the 400 nm, which is indeed observed. Furthermore, the decay behavior probed at 920 nm is distinct from that of the transients probed at 680, 1200, and 1400 nm wavelengths (Fig. S13†). This observation allows disregarding overlapping time-dependent contribution to the decay probed at 920 nm. In short, the rise in the TA signal is likely due to the occurrence of steady deep trapping of CB free electrons to oxygen vacancies.

Next, the dynamics of electron trapping in Rh⁴⁺:STO is discussed (Fig. 3A and B). In stark contrast to what was observed for Rh³⁺:STO (4 mol% La), the TA signal magnitude promptly decreased by ≈80% with a time constant of 0.14 ps. The virtually absent pump fluence dependence in this process suggests that the electron decay is primarily via trapping (Fig. S14†). Note that considering the time resolution of the measurement system (140 femtoseconds) employed for this experiment, a significant part of electrons gets trapped to the unoccupied Rh⁴⁺ levels within the time resolution. Hence, the time constant of 0.14 ps to describe electron trapping is regarded as an upper limit. This type of prompt quenching indicates the role of the in-gap Rh⁴⁺ unoccupied levels as efficient electron trapping centers. Unlike in Rh³⁺:STO (4 mol% La), a rise in the TA signal when probed at 920 nm is not observed for Rh⁴⁺:STO. This observation may be explained by considering a significantly prompt and efficient electron trapping to the Rh⁴⁺ levels when compared to oxygen vacancies. However, we emphasize that further studies are needed to unambiguously determine this process.

In order to understand the energetic position of these Rh⁴⁺ levels within the bandgap, TA spectra are recorded from 850 nm to 1400 nm (Fig. 3D). The TA spectra have a minor positive and negative feature attributed to free carrier absorption and absorption bleaching, respectively. The first bleaching around 1010 nm is correlated to the d–d transition (T₂ in Fig. 1C) and is explained as follows. Due to the prompt and efficient electron trapping within 0.14 ps, the Rh⁴⁺ levels within the band gap of Rh⁴⁺:STO are filled rather instantaneously. As the in-gap Rh⁴⁺ levels start to be filled, the feasibility of a d–d transition reduces resulting in a bleaching signal (Fig. S15†). Considering a good agreement in the positions of both the ground-state absorption peak (Fig. 1B) and bleaching at around 1000 nm, the position of the Rh⁴⁺ levels within the band gap is determined to be ≈1.15 eV above the Rh³⁺ occupied levels. The TA signal recorded at 1010 nm (Fig. S16†) showed a slow recovery (>1000 ps), suggesting that the release of the trapped electrons from the Rh⁴⁺ levels by recombination with holes and/or de-trapping is rather an inefficient process. In addition to the bleaching signal at 1010 nm, a second bleaching signal is noticed around 1375 nm (≈0.90 eV). However, the dynamics probed at 1375 nm is different than that at 1010 nm (Fig. S17†). Note that the Rh⁴⁺ defect levels are not to be perceived as one single band. Rather, these levels are distributed with a maximum centered at ≈1.15 eV above the Rh³⁺ occupied levels. Due to the trapping, electrons first occupy the closer Rh⁴⁺ levels (≈1.15 eV above the VB) followed by the less dense Rh⁴⁺ levels around 0.90 eV. It is proposed that the delay in witnessing the second bleaching is essentially the time required for electrons to subsequently relax into the Rh⁴⁺ levels around 0.9 eV. Apart from this proposed model, another possible mechanism may explain the second bleaching and needs to be explored further.

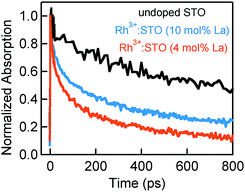
Fig. 4 presents the microsecond decay dynamics of the shallow trapped electrons for undoped STO, Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO. In these experiments, a 355 nm pump which promotes the VB to CB transition is utilized to allow comparison with undoped STO. Previous reports demonstrated with shallow trapped electrons being probed in the NIR region between 1500 nm and 1800 nm.^40,41 Charge dynamics in a microsecond time scale is governed by the collective contribution from various photophysical processes that occur from a sub-picosecond to hundreds of nanoseconds. The TA signal for La/Rh doped STO is significantly smaller and decays faster compared to that of the undoped STO. In contrast to Rh³⁺:STO (4 mol% La), no detectable TA signal is found for Rh⁴⁺:STO due to the efficient and prompt electron trapping to the in-gap Rh⁴⁺ levels. The trapped electrons in the Rh⁴⁺ levels cannot participate in the photocatalytic reaction due to the absence of the driving energy for the reduction reaction.

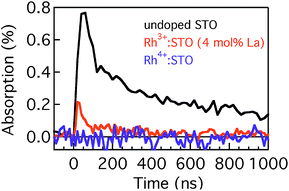Fig. 4 Microsecond TDR profiles for undoped STO, Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO probed between 1500 nm and 1800 nm and using the 355 nm pump.

In short, a longer electron lifetime is noticed for Rh³⁺:STO (4 mol% La) compared to Rh⁴⁺:STO, which is expected to enhance the H₂ evolution rate. For Rh⁴⁺:STO, the presence of in-gap Rh⁴⁺ unoccupied levels which function as the electron trapping center is demonstrated. Undesirable electron trapping to the Rh⁴⁺ levels significantly decreases the magnitude of free electrons available for the photocatalytic reaction.

Effect of the La doping level on the electron dynamics in Rh³⁺:STO

In this section, the effect of increasing the La doping level from 4 to 10 mol% in Rh³⁺:STO on the charge dynamics is presented. Fig. 5 shows the effect of La doping level on the electron dynamics probed at 3435 nm. Note that for this measurement, a 266 nm pump which enables bandgap transition is utilized to allow comparison of electron dynamics with undoped STO. Comparison of the decay with undoped STO demonstrates a shorter electron lifetime of La doped Rh³⁺:STO. Furthermore, comparing the dynamics for different La doping levels indicates a longer lifetime for Rh³⁺:STO (10 mol% La) compared to Rh³⁺:STO (4 mol% La). A similar observation was also made for the 400 nm pump (Fig. S18†). As shown in Fig. 1C, due to the n-type nature of Rh³⁺:STO (10 mol% La) and the associated shift in the Fermi level towards CB, the concentration of deep trapping centers (oxygen vacancies) is expected to be smaller compared to Rh³⁺:STO (4 mol% La). This effect concurrently reduces the number of electrons that decay via deep trapping for Rh³⁺:STO (10 mol% La). Hence, the free electron lifetime is expected to be longer upon increasing the La doping level.

Fig. 5 Femtosecond TDR time profiles comparing the electron decay dynamics for undoped STO, Rh³⁺:STO (10 mol% La) and Rh³⁺:STO (4 mol% La). These transients are probed at 3435 nm using a 266 nm pump with a fluence of 1 μJ per pulse.

If the efficiency of deep trapping decreased upon increasing the La doping level, elucidating the dynamics of deeply trapped electrons would offer further insights. To this end, the decay behavior of deeply trapped electrons (920 nm probe) is investigated (Fig. 6A). Unlike for Rh³⁺:STO (4 mol% La), a rise in the signal around 100 ps is not observed for Rh³⁺:STO (10 mol% La). A similar observation is made at a different pump fluence (Fig. S19†). The TA spectra (Fig. 6B) are recorded for Rh³⁺:STO (10 mol% La) from 850 to 1400 nm to further confirm this process. The TA signal decays faster throughout the probed region without showing the unique signal increase around 100 ps. This is in contrast to Rh³⁺:STO (4 mol% La), for which the TA signal between 850 nm and 1100 nm barely showed any appreciable decay till 1000 ps (Fig. 3C). This comparison indicates that the efficiency of electron deep trapping in Rh³⁺:STO (10 mol% La) is less than that in Rh³⁺:STO (4 mol% La). To further understand this process, hole decay dynamics is compared between Rh³⁺:STO (4 mol% La) and Rh³⁺:STO (10 mol% La). From previous reports,⁴¹ probing in the visible region (around 550 nm) is commonly associated with the hole dynamics in STO (Fig. S20†). Ideally, a prolonged hole lifetime is expected with an increase in the efficiency of electron trapping, which reduces the number of electrons available for recombination with holes. Considering this logic, a longer hole lifetime is anticipated for Rh³⁺:STO (4 mol% La) compared to Rh³⁺:STO (10 mol% La), owing to the efficient electron deep trapping in the former. Indeed, the hole decay dynamics for Rh³⁺:STO (4 mol% La) is consistently found to be slower compared to Rh³⁺:STO (10 mol% La) at different pump fluences (Fig. S21†).

Fig. 6 (A) Normalized femtosecond TDR profiles probed at 920 nm for Rh³⁺:STO (4 mol% La) and Rh³⁺:STO (10 mol% La) recorded using the 400 nm pump with a fluence of 0.6 μJ per pulse. (B) TA spectra for Rh³⁺:STO (10 mol% La) recorded from 850 nm to 1400 nm at different delay times using the 400 nm pump.

In short, an increase in the n-type character is noticed for Rh³⁺:STO (10 mol% La) compared to Rh³⁺:STO (4 mol% La). In addition, a reduction in the efficiency of electron deep trapping is observed with an increase in the La doping level from 4 to 10 mol%.

Effect of Rh valence state on the efficiency and kinetics of electron transfer to the Ru cocatalyst

In order to elucidate the importance of Ru as an electron accepting cocatalyst, the amount of H₂ released for Rh³⁺:STO (4 mol% La) with and without the Ru cocatalyst is compared (Fig. S1†). The H₂ evolution was found to be virtually absent when the Ru cocatalyst particles were not loaded on Rh³⁺:STO (4 mol% La). This observation indicates the indispensable role of Ru cocatalyst in realizing the photocatalytic H₂ evolution. Thus, elucidating the factors affecting the key process of electron transfer to the Ru cocatalyst is crucial.

Fig. 7A compares the decay of free electrons probed at 3435 nm for Rh³⁺:STO (4 mol% La) with and without the Ru cocatalyst. A faster decay in the presence of Ru cocatalyst indicates the occurrence of electron transfer. A similar observation was made when the pump energy was changed from 400 to 266 nm (Fig. S23†). If electrons are transferred to the Ru, the lifetime of holes is expected to be longer for Rh³⁺:STO (4 mol% La) upon the Ru cocatalyst loading as there will be fewer electrons available for recombination with holes. Indeed, a longer hole lifetime (Fig. S24†) for Rh³⁺:STO (4 mol% La) with the Ru cocatalyst further corroborates the occurrence of electron transfer. Theoretical modeling of these transients was carried out to determine the time constant and the quantum yield/efficiency of the electron transfer process. The procedure employed for this purpose is detailed in Appendix 1 (ESI†). From the theoretical analysis, the time constant (1/k_et) and the quantum yield of electron transfer from Rh³⁺:STO (4 mol% La) to the Ru was estimated to be 1.6 ps and 14.7%, respectively.

Fig. 7 Femtosecond TDR transients corresponding to free electrons probed at 3435 nm for (A) Rh³⁺:STO (4 mol% La) and (B) Rh⁴⁺:STO loaded with and without the Ru cocatalyst. A 400 nm pump with a fluence of 0.4 μJ per pulse is employed to conduct these measurements. Solid lines are fits according to the theoretical model to estimate the time constant and quantum yield of electron transfer.

Fig. 7B presents the dynamics of free electrons (400 nm pump and 3435 nm probe) in Rh⁴⁺:STO with and without the Ru cocatalyst loading. The electron dynamics in Rh⁴⁺:STO is marginally yet non-negligibly affected by the Ru cocatalyst loading. A similar observation was made when the pump energy is changed to 266 nm (Fig. S22†). Note that the difference in the decay (Fig. 7B) of Rh⁴⁺:STO with and without Ru is faintly discernible only till 3 ps, while it is virtually similar after 4 ps. From this observation, it is amenable that electron transfer to the Ru is kinetically hindered by the prompt and efficient electron trapping to the Rh⁴⁺ in-gap defect levels. This notion is in stark contrast in the case of Rh³⁺:STO (4 mol% La), where a clear difference in the decay is observed till 10 ps. From the theoretical analysis, the time constant for electron transfer (1/k_et) from Rh⁴⁺:STO to Ru was found to be around 0.29 ps. However, the fitted line in Rh⁴⁺:STO (with Ru) from the theoretical modeling inadequately represents the experimental results in early 0.5 ps and after 4 ps. Hence, a precise determination of the quantum yield of electron transfer in Rh⁴⁺:STO could not be made. Unlike in Rh³⁺:STO (4 mol% La), the yield of electron transfer to the Ru in Rh⁴⁺:STO is directly affected by the efficient electron trapping to the in-gap Rh⁴⁺ levels. It is suspected that the quantum yield of electron transfer would be lower in Rh⁴⁺:STO compared to Rh³⁺:STO (4 mol% La). Nonetheless, by comparing the kinetics of electron transfer, it is clear that the valence state of Rh does play a key role in electron transfer to the Ru cocatalyst.

Effect of increasing the La codoping level to 10 mol% in Rh³⁺:STO on the H₂ evolution

In this last section, the origin of the absence of H₂ evolution for Rh³⁺:STO (10 mol% La) is presented (Table S1†). As discussed earlier, loading of the Ru cocatalyst is critical to achieve the H₂ evolution. These Ru cocatalyst particles are loaded onto doped STO using the photodeposition process during which RuCl₃ (Ru³⁺) is reduced to Ru metal. Despite following a similar photodeposition procedure, the Ru particles were efficiently deposited only for Rh³⁺:STO (4 mol% La) while being barely found on the surface of Rh³⁺:STO (10 mol% La) (SEM images in Fig. S25†). One of the factors that hindered the photodeposition in Rh³⁺:STO (10 mol% La) is the presence of the La₂O₃ impurity phase on the surface, unlike Rh³⁺:STO (4 mol% La). In addition, the pH of the reactant solution containing a sample to be photodeposited with RuCl₃ is found to change from 4.4 to 6.2 for Rh³⁺:STO (4 mol% La) and Rh³⁺:STO (10 mol% La), respectively. Increase in the pH for Rh³⁺:STO (10 mol% La) indicates that the basic nature of the reactant solution is enhanced, which is likely due to the presence of the segregated La₂O₃ on the surface.²⁰ A similarity in the decay behavior of both electrons and holes (Fig. S26 and S27†) after photodeposition of Ru particles further supports the inefficient loading of Ru cocatalyst particles. Thus, the absence of H₂ evolution in Rh³⁺:STO (10 mol% La) is essentially due to the absence of the Ru cocatalyst particles on the surface of Rh³⁺:STO (10 mol% La). Furthermore, etching of the surface by acid treatment to remove the oxide impurity did not result in the enhancement of H₂ evolution rate (data not shown). Despite photodeposition being a widely used technique, the actual mechanism of photodepositing the cocatalyst particles remains elusive⁴⁵ and needs a thorough investigation.

In short, the presence of the Ru cocatalyst is vital for the photocatalytic generation of H₂. The amount of H₂ evolved is correlated to the efficiency of electron transfer from La/Rh doped STO to the Ru cocatalyst particles. However, electron transfer is kinetically hindered by the undesirable trapping process in both Rh³⁺:STO (4 mol% La) and Rh⁴⁺:STO.

Based on the results discussed, we draw a perspective in the context of photocatalytic water splitting using this promising La/Rh doped STO material. By comparing the electron lifetimes for doped STO and undoped STO (Fig. 4 and 5), it is clear that doping shortens the carrier lifetime, which in principle is not preferred to realize a higher photocatalytic activity. On the other hand, this negative effect of doping is compensated by inducing a visible light absorption. Furthermore, electron lifetime is critically dependent on the Rh valence state and the resulting energetic position of the dopant within the band gap. Rh⁴⁺ is in the d⁵ configuration with an unpaired electron, leading to the formation of in-gap Rh⁴⁺ unoccupied levels that efficiently quench the photogenerated electrons. On the other hand, Rh³⁺ is in the d⁶ configuration without an unpaired electron. In addition, the Rh³⁺ levels lie close to the VB and hybridize with the O 2p states of the VB facilitating a visible light response. Thus, a key future challenge is to realize minimum carrier loss by trapping to the in-gap defect states while simultaneously harvesting a large part of the solar spectrum. To this end, controlling the energetic position of the dopant within the bandgap is critical.

In the case of Rh³⁺:STO (4 mol% La), the quantum yield of electron transfer to the Ru cocatalyst was found to be 14.7%. It is desirable to further enhance this value, for which circumventing the electron deep trapping to oxygen vacancies forms one of the approaches. Such a strategy is likely to improve the efficiency of the photocatalytic reaction in Rh³⁺:STO (4 mol% La).

Though the work presented here is not performed under the conditions reminiscent to the photocatalytic reaction (with an applied bias and water interface), understanding how electron dynamics in the bulk is affected by the doping composition and electronic properties of the photocatalyst is essential. At the same time, we emphasize that efficiency of the photocatalytic reaction is determined not only by the electron dynamics but also by the interaction between photocatalyst and water/electrolyte, pH, effective band bending at the surface, etc., which are, however, not investigated in this work. Nevertheless, considering that the photocatalytic reaction occurs only at the surface, bulk electron lifetime and its decay largely determine the efficiency of charge transport towards the surface of the photocatalyst and eventually the number of photogenerated electrons available for the reaction at the surface.

Previously, metals such as Sb and Cr were widely used as dopants in STO and the corresponding activities are reported. However, it seems La doping is critical and it works differently from Sb or Cr doping. Note that in the case of Cr and Sb, dopants are doped into the Ti site, while for La the dopants are doped into the Sr site. In addition, La codoping can be superior because the orbitals of La are not directly involved in the VB or the CB and hence less likely to form impurity levels within the band gap. Furthermore, the valence state of La in the form of La³⁺ is very stable compared with Cr (Cr³⁺ and Cr⁶⁺) and Sb (Sb³⁺ and Sb⁵⁺), so that the charge compensation effect will not be canceled by co-dopants themselves. These features particularly favor La over Cr or Sb to realize a higher photocatalytic activity.

Conclusions

Charge carrier dynamics over a wide time range was investigated in the visible light absorbing La/Rh doped SrTiO₃ photocatalysts. The probe wavelength from the visible to the IR region was varied to selectively monitor the dynamics of holes and electrons. This approach allowed us to comprehensively elucidate various decay pathways for electrons. Photophysical parameters such as electron lifetime, time constants for electron trapping to defect states and electron transfer to the Ru cocatalyst were determined depending on the dopant composition and doping level.

The valence state of Rh in doped STO was found to critically affect both the electron lifetime and the kinetics of electron transfer to the Ru cocatalyst. For Rh⁴⁺:STO, ≈80% of the photogenerated electrons get deep trapped to the in-gap Rh⁴⁺ unoccupied levels in ≤0.14 ps. These in-gap Rh⁴⁺ levels essentially acted as an electron sink. Such an efficient and prompt quenching of electrons resulted in a kinetic competition between the electron trapping and the electron transfer to the Ru cocatalyst. From the theoretical modeling, the time constant for electron transfer from Rh⁴⁺:STO to Ru was estimated to be 0.29 ps.

The free electrons in Rh³⁺:STO (4 mol% La) decayed significantly more slowly compared to those in Rh⁴⁺:STO. Deep trapping of electrons to defect states such as oxygen vacancies was discerned for Rh³⁺:STO (4 mol% La). Despite the coexisting electron deep trapping, electron transfer to the Ru cocatalyst was found to occur with a time constant of 1.6 ps with an efficiency/quantum yield of 14.7%.

For Rh³⁺:STO, increasing the La doping level from 4 to 10 mol% prolonged the lifetime of free electrons while reducing the efficiency of electron deep trapping. However, inefficient photodeposition of the Ru cocatalyst particles onto the surface of Rh³⁺:STO (10 mol% La) resulted in the absence of electron transfer to Ru and hence virtually absent photocatalytic activity.

Insights from correlating carrier dynamics with H₂ evolution efficiency aid in the rational design of photocatalysts and to unveil the fundamental loss processes reducing the efficiency of photocatalytic reactions.

Experimental methods

La and Rh doped SrTiO₃ was prepared by a two-step solid-state reaction (SSR). In the first step, SrTiO₃ was synthesized by a conventional SSR. Commercially available SrCO₃ (Kanto Chemicals, 99.9%) and rutile-type TiO₂ (rutile, Kanto Chemicals, 99.0%) powders were mixed in a mortar. The mixture was placed in an alumina crucible, heated up to 1373 K at 10 K min⁻¹ and kept at the target temperature for 10 h. The sample was allowed to cool naturally to room temperature. Subsequently, the resulting SrTiO₃ was mixed in ethanol with La₂O₃ (Kanto Chemicals, 99.99%), which had been freshly calcined in air at 1273 K for 12 h, and Rh₂O₃ (Kanto Chemicals, 99.9%). The ethanol was added to mix the oxide particles well. Finally, the mixture was heated at 1373 K for 6 h. The heating and cooling procedures were carried out in the same way as in the first step. The Rh³⁺:STO (4 mol% La) sample was synthesized by using 4 mol% Rh₂O₃ and 4 mol% La₂O₃, while doping only with 4 mol% Rh₂O₃ resulted in Rh⁴⁺:STO. The sample to investigate the effect of La doping level i.e. Rh³⁺:STO (10 mol% La) was synthesized by using 4 mol% Rh and 10 mol% La₂O₃. Formation of the lanthanum oxide (La₂O₃) impurity phase was noticed upon increasing the La doping level to 10 mol% in Rh³⁺:STO. In SSR, diffusion of unreacted impurities towards the surface is common.⁴⁶ Additional material characterization was previously carried out by Wang et al.^20,47 A nanoparticulate Ru (0.2 wt%) cocatalyst was loaded on the obtained photocatalyst by photodeposition from an aqueous methanol solution (150 mL, 10 vol%) containing RuCl₃·3H₂O. The photodeposition reaction was conducted in a Pyrex top-irradiation reaction vessel connected to a glass closed gas circulation system. Argon was introduced into the circulation system as a carrier gas. The total background pressure of argon and water vapor was approximately 5 kPa. The temperature of the reactant solution was maintained at 288 K by using cooling water. Photodeposition was performed under a 300 W xenon lamp (Lamp House, R300-3J; equipped with a cut-off filter of λ > 420 nm)^8,20,48 The Ru cocatalyst-loaded photocatalyst was collected by filtration and washed with water.

The H₂ evolution reactions in La/Rh doped STO were examined in the same closed gas circulation system. The photocatalyst (0.3 g) was dispersed in a 10 vol% aqueous methanol solution (150 mL) within a Pyrex top-irradiation type vessel. After removing air from the reaction system, the solution was illuminated by a 300 W Xe lamp fitted with a cutoff filter (λ > 420 nm). The amount of evolved H₂ was measured by gas chromatography (Shimadzu GC-8A with a TCD detector and an MS-5A column, using argon as the carrier gas).

UV–vis–NIR diffuse reflectance spectroscopy experiments were conducted using a spectrophotometer (JASCO V-670) equipped with an integrating sphere, employing a commercial material (Spectralon®) as a reference.

The XPS measurements were carried out using a monochromatic Mg Kα source (hν = 1253.6 eV) excited at 8 kV and 10 mA. The analysis chamber pressure was ∼10⁻⁶ Pa. The binding energies were corrected using the C 1s peak (285.0 eV) as a reference.

The XRD patterns of the samples were recorded with a Rigaku RINT-Ultima III diffractometer using a Cu-Kα source operated at 40 kV and 40 mA. The SEM images were recorded using the Hitachi SU8020 system.

The Mott–Schottky measurements to understand the Fermi level shift depending on the La doping level were carried out under darkness at a frequency of 1 kHz with an AC amplitude of 10 mV in a 0.1 M aqueous Na₂SO₄ solution at pH ≈ 6.8. Before conducting these measurements, oxidation–reduction cycles were performed repeatedly to stabilize the surface of the electrodes.

In the femtosecond transient diffuse reflectance (fs-TDR) measurements, a femtosecond Ti:sapphire laser with a regenerative amplifier (Spectra-Physics, Solstice; wavelength of 800 nm, pulse width of 100 fs, pulse energy of 3.5 mJ per pulse, and repetition rate of 1 kHz) was used as the light source. The output from the laser was split into four paths for the excitation of two optical parametric amplifiers (OPAs; Spectra-Physics, TOPAS Prime) and a time-plate-type harmonic generator (Spectra-Physics, TP-F) to generate 400 nm and 266 nm light and for the generation of white-light continuum by focusing the fundamental light (800 nm) into a sapphire plate. In the present study, the harmonic generator is used for the 400 and 266 nm pump pulse and one of the OPAs was employed to generate a 500 nm light. For the probe pulse, a white-light continuum covering from 500 nm to 1600 nm and a 3435 nm light generated from the other OPA with a difference-frequency generation crystal were used. The time resolution of the system was about 150 fs. The powder samples were taken in 1 mm quartz cuvettes. The diameter of the pump beam on the sample was about 0.5 mm as observed with a charge-coupled device (CCD) camera. An amplified Si photodetector and an InGaAs photodetector were used to probe in the visible and NIR parts, respectively. A liquid nitrogen cooled mercury–cadmium–telluride (HgCdTe) photodetector was used for the IR probe (3435 nm) experiments. The diffusely reflected light from the sample was passed through a grating monochromator (Princeton Instruments, Acton SP2150) for data acquisition. The transient absorption intensity of the TDR measurements is presented as percentage absorption, where absorption (%) = 100(1 − R/R₀), using R and R₀ as the intensities of the diffusely reflected light with and without excitation, respectively. A more detailed description of the fs-TDR setup is available elsewhere.^49,50

Microsecond TDR measurements were carried out using the third harmonic (355 nm, 10 Hz, ∼150 ps) of a Nd³⁺:YAG laser (Ekspla, SL311). The powder samples were taken in 1 mm quartz cuvettes. The pump beam diameter on the sample surface was about 6 mm. A steady-state xenon lamp (Unisoku, USP-OBB-75XE) was used as the probe light source. The time resolution of the setup was roughly 25 ns. The diffusely reflected light from the sample in the NIR region between 1500 nm and 1800 nm was introduced into an InGaAs photodetector (Thorlabs, DET20C/M, 800–1800 nm) after passing through a 1500 nm long-pass filter. The signal from the detector was then introduced into a digital oscilloscope (LeCroy, 6200A).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by “Research Project for Future Development: Artificial Photosynthetic Chemical Process (ARPChem)” (METI/NEDO, Japan: 2012–2022). Dr Yusuke Okabayashi is acknowledged for help with the LabVIEW program for data acquisition in the microsecond TDR experiment. T. H. acknowledges support from Grants-in-Aid for Scientific Research (A) (No. 16H02417) and for Young Scientists (A) (No. 15H05494) from the Japan Society for the Promotion of Science (JSPS).

References

1. D. M. Fabian, S. Hu, N. Singh, F. A. Houle, T. Hisatomi, K. Domen, F. E. Osterlohf and S. Ardo, Energy Environ. Sci., 2015, 8, 2825–2850.
2. T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535.
3. F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320.
4. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. X. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
5. X. B. Chen, S. H. Shen, L. J. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570.
6. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
7. S. Okunaka, H. Tokudome and R. Abe, Catal. Sci. Technol., 2016, 6, 254–260.
8. Q. Wang, T. Hisatomi, Q. X. Jia, H. Tokudome, M. Zhong, C. Z. Wang, Z. H. Pan, T. Takata, M. Nakabayashi, N. Shibata, Y. B. Li, I. D. Sharp, A. Kudo, T. Yamada and K. Domen, Nat. Mater., 2016, 15, 611–615.
9. L. C. Mu, Y. Zhao, A. L. Li, S. Y. Wang, Z. L. Wang, J. X. Yang, Y. Wang, T. F. Liu, R. T. Chen, J. Zhu, F. T. Fan, R. G. Li and C. Li, Energy Environ. Sci., 2016, 9, 2463–2469.
10. J. Wang, J. Zhao and F. E. Osterloh, Energy Environ. Sci., 2015, 8, 2970–2976.
11. T. Arai, S. Sato, T. Kajino and T. Morikawa, Energy Environ. Sci., 2013, 6, 1274–1282.
12. D. F. Wang, J. H. Ye, T. Kako and T. Kimura, J. Phys. Chem. B, 2006, 110, 15824–15830.
13. R. Konta, T. Ishii, H. Kato and A. Kudo, J. Phys. Chem. B, 2004, 108, 8992–8995.
14. R. Niishiro, S. Tanaka and A. Kudo, Appl. Catal., B, 2014, 150, 187–196.
15. S. Kawasaki, R. Takahashi, K. Akagi, J. Yoshinobu, F. Komori, K. Horiba, H. Kumigashira, K. Iwashina, A. Kudo and M. Lippmaa, J. Phys. Chem. C, 2014, 118, 20222–20228.
16. T. Ishii, H. Kato and A. Kudo, J. Photochem. Photobiol., A, 2004, 163, 181–186.
17. K. Furuhashi, Q. X. Jia, A. Kudo and H. Onishi, J. Phys. Chem. C, 2013, 117, 19101–19106.
18. J. H. Yang, D. G. Wang, H. X. Han and C. Li, Acc. Chem. Res., 2013, 46, 1900–1909.
19. R. B. Singh, H. Matsuzaki, Y. Suzuki, K. Seki, T. Minegishi, T. Hisatomi, K. Domen and A. Furube, J. Am. Chem. Soc., 2014, 136, 17324–17331.
20. Q. Wang, T. Hisatomi, S. S. K. Ma, Y. B. Li and K. Domen, Chem. Mater., 2014, 26, 4144–4150.
21. B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. B. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. L. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002.
22. A. Furube, T. Asahi, H. Masuhara, H. Yamashita and M. Anpo, J. Phys. Chem. B, 1999, 103, 3120–3127.
23. S. R. Pendlebury, X. L. Wang, F. Le Formal, M. Cornuz, A. Kafizas, S. D. Tilley, M. Gratzel and J. R. Durrant, J. Am. Chem. Soc., 2014, 136, 9854–9857.
24. J. Ravensbergen, F. F. Abdi, J. H. van Santen, R. N. Frese, B. Dam, R. van de Krol and J. T. M. Kennis, J. Phys. Chem. C, 2014, 118, 27793–27800.
25. M. Barroso, A. J. Cowan, S. R. Pendlebury, M. Gratzel, D. R. Klug and J. R. Durrant, J. Am. Chem. Soc., 2011, 133, 14868–14871.
26. M. Forster, R. J. Potter, Y. C. Ling, Y. Yang, D. R. Klug, Y. Li and A. J. Cowan, Chem. Sci., 2015, 6, 4009–4016.
27. K. Iwashina and A. Kudo, J. Am. Chem. Soc., 2011, 133, 13272–13275.
28. S. Kawasaki, K. Akagi, K. Nakatsuji, S. Yamamoto, I. Matsuda, Y. Harada, J. Yoshinobu, F. Komori, R. Takahashi, M. Lippmaa, C. Sakai, H. Niwa, M. Oshima, K. Iwashina and A. Kudo, J. Phys. Chem. C, 2012, 116, 24445–24448.
29. B. Modak and S. K. Ghosh, J. Phys. Chem. C, 2015, 119, 23503–23514.
30. Q. Y. Wu, J. J. Cen, K. R. Goodman, M. G. White, G. Ramakrishnan and A. Orlov, ChemSusChem, 2016, 9, 1889–1897.
31. T. Takata and K. Domen, J. Phys. Chem. C, 2009, 113, 19386–19388.
32. C. Lee, J. Destry and J. L. Brebner, Phys. Rev. B: Solid State, 1975, 11, 2299–2310.
33. D. Ricci, G. Bano, G. Pacchioni and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 224105.
34. M. Miyauchi, M. Takashio and H. Tobimatsu, Langmuir, 2004, 20, 232–236.
35. G. Q. Zhang, W. S. Jiang, S. X. Hua, H. F. Zhao, L. G. Zhang and Z. C. Sun, Nanoscale, 2016, 8, 16963–16968.
36. X. F. Hao, Z. M. Wang, M. Schmid, U. Diebold and C. Franchini, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 6.
37. T. Inoue, N. Seki, J. Kamimae, K. Eguchi and H. Arai, Solid State Ionics, 1991, 48, 283–288.
38. T. Mizoguchi, Y. Sato, J. P. Buban, K. Matsunaga, T. Yamamoto and Y. Ikuhara, Appl. Phys. Lett., 2005, 87, 241920.
39. H. Tan, Z. Zhao, W. Zhu, E. N. Coker, B. Li, M. Zheng, W. Yu, H. Fan and Z. Sun, ACS Appl. Mater. Interfaces, 2014, 6, 19184–19190.
40. A. Yamakata, H. Yeilin, M. Kawaguchi, T. Hisatomi, J. Kubota, Y. Sakata and K. Domen, J. Photochem. Photobiol., A, 2015, 313, 168–175.
41. A. Yamakata, J. J. M. Vequizo and M. Kawaguchi, J. Phys. Chem. C, 2015, 119, 1880–1885.
42. Y. Suzuki, D. H. K. Murthy, H. Matsuzaki, A. Furube, Q. Wang, T. Hisatomi, K. Domen and K. Seki, J. Phys. Chem. C, 2017, 121, 19044–19052.
43. A. Yamakata, T. Ishibashi and H. Onishi, Chem. Phys. Lett., 2001, 333, 271–277.
44. Y. Yamada, H. K. Sato, Y. Hikita, H. Y. Hwang and Y. Kanemitsu, Phys. Rev. Lett., 2013, 111, 047403.
45. K. Wenderich and G. Mul, Chem. Rev., 2016, 116, 14587–14619.
46. J. B. Smith and T. Norby, Solid State Ionics, 2006, 177, 639–646.
47. Q. Wang, Y. B. Li, T. Hisatomi, M. Nakabayashi, N. Shibata, J. Kubota and K. Domen, J. Catal., 2015, 328, 308–315.
48. Y. Sasaki, A. Iwase, H. Kato and A. Kudo, J. Catal., 2008, 259, 133–137.
49. A. Furube, Z. S. Wang, K. Sunahara, K. Hara, R. Katoh and M. Tachiya, J. Am. Chem. Soc., 2010, 132, 6614–6615.
50. T. Asahi, A. Furube, H. Fukumura, M. Ichikawa and H. Masuhara, Rev. Sci. Instrum., 1998, 69, 361–371.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8se00487k

‡ Current affiliation: Centre for Energy & Environmental Science, Shinshu University, 4-17-1 Wakasato, Nagano-shi, Nagano 380-8553, Japan.

---