Mechanism of C–P bond formation via Pd-catalyzed decarbonylative phosphorylation of amides: insight into the chemistry of the second coordination sphere†
Wen-Yan
Tong
a,
Thu D.
Ly
b,
Tao-Tao
Zhao
a,
Yan-Bo
Wu
 *a and
Xiaotai
Wang
*a and
Xiaotai
Wang
 *bc
*bc
aThe Key Laboratory of Energy Conversion and Storage of Shanxi Province, Institute of Molecular Science, Shanxi University, Taiyuan, 030006, Shanxi, People's Republic of China. E-mail: wyb@sxu.edu.cn
bDepartment of Chemistry, University of Colorado Denver, Campus Box 194, P. O. Box 173364, Denver, Colorado 80217-3364, USA. E-mail: Xiaotai.Wang@ucdenver.edu
cHoffmann Institute of Advanced Materials, Shenzhen Polytechnic, 7098 Liuxian Boulevard, Nanshan District, Shenzhen 518055, P. R. China
First published on 25th November 2019
Abstract
We report on the basis of DFT computations a plausible and detailed reaction mechanism for the first Pd-catalyzed decarbonylative phosphorylation of amides forming C–P bonds, which reveals, among other things, crucial events in the second coordination sphere, including ion pair and hydrogen bonding interactions as well as proton transfer.
Organophosphorus compounds, which contain a direct C–P bond, have found a wide range of applications in medicinal chemistry, agrochemicals, and materials sciences.1 This has motivated research on the methodology for generating C–P bonds. Classical approaches to C–P bonds include the Michaelis–Arbuzov reaction and those using organolithium or Grignard reagents, but these reactions suffer from air sensitivity, toxicity, or poor chemoselectivity.2 The Hirao reaction3 ushered in transition metal-catalyzed cross-coupling methods for C–P bond formation, and the C-coupling partners include aryl halides,4 sulfonates,5 diazonium salts,6 boronic acids,7 silanes,8 pivalates,9 and sulfides.10
Organic amides are stable and readily available compounds. The amide (O)C–N bond is strong due to the nN to πC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O* resonance, and as such, its oxidative addition to a transition metal center is generally extremely difficult. Szostak and co-workers first discovered that N-glutarimide amides exhibit unusually high reactivity in Pd-catalyzed acyl and decarbonylative cross-coupling reactions proceeding via metal insertion into the amide (O)C–N bond.11 The high reactivity is attributed to a decrease of the π conjugation resulting from the geometric twisting of the N-glutarimide amides (Fig. S1, ESI†). Following from the discovery of this unique mode of amide bond activation, Szostak and co-workers have recently accomplished the first transition metal-catalyzed decarbonylative phosphorylation of amides using Pd or Ni catalysts, as shown by the representative reactions in Scheme 1.12 These reactions form C–P bonds in the products (aryl phosphonates) and show high yields, chemoselectivity, and functional group tolerance, thereby having potential synthetic application. The experimentalists proposed a mechanistic outline involving (O)C–N bond oxidative addition to M(0), decarbonylation, and reductive elimination.
O* resonance, and as such, its oxidative addition to a transition metal center is generally extremely difficult. Szostak and co-workers first discovered that N-glutarimide amides exhibit unusually high reactivity in Pd-catalyzed acyl and decarbonylative cross-coupling reactions proceeding via metal insertion into the amide (O)C–N bond.11 The high reactivity is attributed to a decrease of the π conjugation resulting from the geometric twisting of the N-glutarimide amides (Fig. S1, ESI†). Following from the discovery of this unique mode of amide bond activation, Szostak and co-workers have recently accomplished the first transition metal-catalyzed decarbonylative phosphorylation of amides using Pd or Ni catalysts, as shown by the representative reactions in Scheme 1.12 These reactions form C–P bonds in the products (aryl phosphonates) and show high yields, chemoselectivity, and functional group tolerance, thereby having potential synthetic application. The experimentalists proposed a mechanistic outline involving (O)C–N bond oxidative addition to M(0), decarbonylation, and reductive elimination.
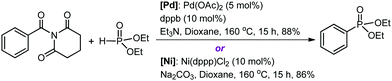 | ||
| Scheme 1 Pd- and Ni-catalyzed decarbonylative phosphorylation reactions. Note: dppb = 1,4-bis(diphenylphosphino)butane and dppp = 1,3-bis(diphenylphosphino)propane. | ||
We have chosen to study the Pd-catalyzed reaction (Scheme 1) by DFT computation because it is molecularly better-defined with all the species in homogeneous solution.‡ We aim at establishing a plausible and detailed mechanism that can elucidate intriguing questions, such as how the dialkylphosphite substrate undergoes formal proton transfer to the glutarimide moiety and why the reaction favors phosphoryl-aryl over phosphoryl-acyl coupling. When we were in the process of carrying out this work, the Yu and Fu group reported a DFT study on the mechanism of the Ni-catalyzed reaction (Scheme 1), which consists of four main steps: oxidative addition (the rate-determining step), phosphorylation, decarbonylation, and reductive elimination.13 There are significant differences between their proposed Ni-catalyzed reaction mechanism and the Pd-catalyzed reaction mechanism that we have computed and presented below. The two reactions operate with different metal catalysts under different conditions, so they can have quite different mechanistic details.
In the presence of 1,4-bis(diphenylphosphino)butane (dppb) and Et3N (Scheme 1), the pre-catalyst Pd(OAc)2 would be initially reduced to active Pd(0) complexes, and this chemistry is known from previous studies.14 Since one equiv. of dppb is consumed as a reductant, the palladium-containing products would be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Pd
1 Pd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
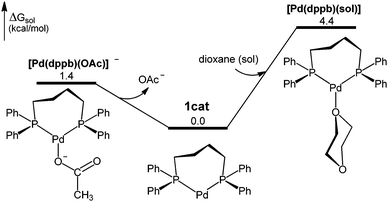
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dppb complexes, for which we have optimized three structures: [Pd(dppb)] (1cat), [Pd(dppb)(OAc)]−, and [Pd(dppb)(sol)] (Fig. 1).151cat is the most stable of the three species and therefore considered as the catalyst resting state (Fig. S2, ESI†).
dppb complexes, for which we have optimized three structures: [Pd(dppb)] (1cat), [Pd(dppb)(OAc)]−, and [Pd(dppb)(sol)] (Fig. 1).151cat is the most stable of the three species and therefore considered as the catalyst resting state (Fig. S2, ESI†).
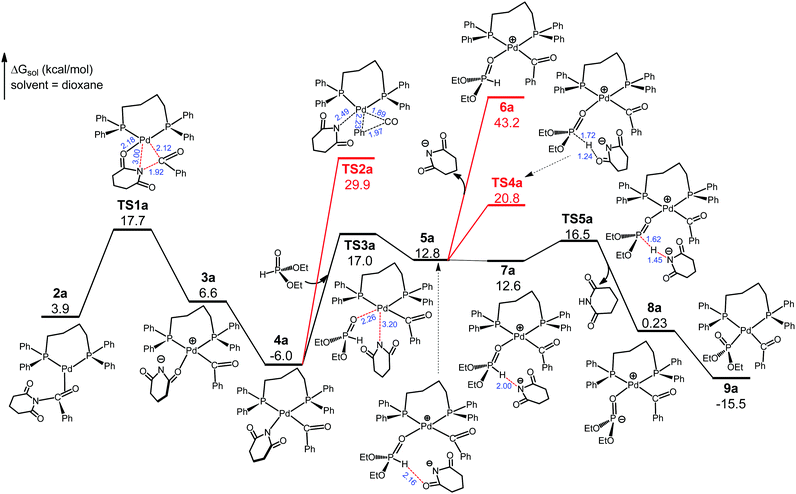
Referring to previous computational studies on transition metal-catalyzed (O)C–N bond activation of N-glutarimide amides,16 we envisioned that 1cat would take up the substrate N-benzoylglutarimide via palladium coordination to the benzoyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. Thus, we located four isomeric complexes (2a–2d, Fig. S3, ESI†) by considering the unsymmetrical structures of 1cat and N-benzoylglutarimide, and explored the reaction pathways through each of them. The favorable pathway, which proceeds through 2a, is presented and discussed in the main text, and the analogous, less favorable pathways through 2b–2d are given in Fig. S4–S6 (ESI†). As shown in Fig. 2, 2a undertakes oxidative addition viaTS1a to insert the metal atom into the amide (O)C–N bond. The Pd–O(glutarimide) ligation at 2.18 Å in TS1a helps stabilize this transition state, which is 17.7 kcal mol−1 with respect to 1cat. TS1a proceeds to the square planar Pd(II) complex 3a, which rearranges to give the more stable 4a with a Pd(II)–N(glutarimide) dative bond. The rearrangement has a sizable driving force (ΔG = −12.6 kcal mol−1) because the N atom with a negative charge is a better donor for Pd(II). Decarbonylation from 4a can be ruled out because it would meet the exceedingly high barrier TS2a that is 35.9 kcal mol−1 relative to 4a. Thus, we consider 4a to take up the substrate diethylphosphite.
O group. Thus, we located four isomeric complexes (2a–2d, Fig. S3, ESI†) by considering the unsymmetrical structures of 1cat and N-benzoylglutarimide, and explored the reaction pathways through each of them. The favorable pathway, which proceeds through 2a, is presented and discussed in the main text, and the analogous, less favorable pathways through 2b–2d are given in Fig. S4–S6 (ESI†). As shown in Fig. 2, 2a undertakes oxidative addition viaTS1a to insert the metal atom into the amide (O)C–N bond. The Pd–O(glutarimide) ligation at 2.18 Å in TS1a helps stabilize this transition state, which is 17.7 kcal mol−1 with respect to 1cat. TS1a proceeds to the square planar Pd(II) complex 3a, which rearranges to give the more stable 4a with a Pd(II)–N(glutarimide) dative bond. The rearrangement has a sizable driving force (ΔG = −12.6 kcal mol−1) because the N atom with a negative charge is a better donor for Pd(II). Decarbonylation from 4a can be ruled out because it would meet the exceedingly high barrier TS2a that is 35.9 kcal mol−1 relative to 4a. Thus, we consider 4a to take up the substrate diethylphosphite.
 | ||
| Fig. 2 Free energy profile of the pathway from oxidative addition to ligand exchange and proton transfer. Selected bond distances are given in Å (the same below). | ||
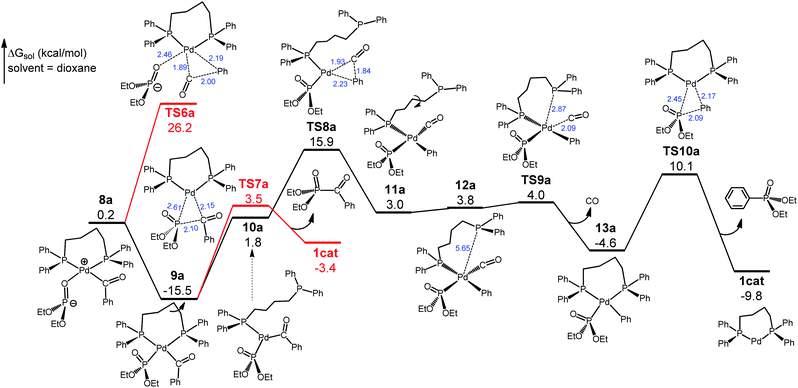
We have traced the interchange transition state TS3a where 4a substitutes diethylphosphite for glutarimide to form 5a. A salient feature of 5a is that the glutarimide anion remains in the second coordination sphere through ion pair and hydrogen bonding interactions with the first sphere, forming an O⋯H(phosphite) hydrogen bond at 2.16 Å. This is crucial for the subsequent steps because separation of the glutarimide anion from the first sphere—the 5a → 6a process—would incur a huge energy cost and hence shut down the reaction. The phosphite-to-glutarimide proton transfer from 5a would meet the higher barrier TS4a. Thus, 5a proceeds to 7a with a N⋯H(phosphite) hydrogen bond, opening up a lower-energy pathway for proton transfer viaTS5a, which gives 8a with the detachment of charge-neutral glutarimide from the second sphere. Complex 8a isomerizes to the more stable 9a with Pd–P ligation because the P atom with a negative charge is a better donor for Pd(II). The reaction pathway thus far is through 1cat → 2a → TS1a → 3a → 4a → TS3a → 5a → 7a → TS5a → 8a → 9a, and the two reacting partners converge on the same metal center of 9a. We next consider the ensuing decarbonylation and reductive elimination/coupling processes.
As shown in Fig. 3, no direct decarbonylation pathway from 9a could be found probably due to the increased steric hindrance around the Pd(II) center arising from the Pd–P coordination. Hypothetically, 9a can revert to 8a to launch decarbonylation via the five-coordinate TS6a, but this barrier would be 41.7 kcal mol−1 with respect to 9a and hence can be ruled out. Phosphoryl-acyl reductive elimination/coupling from 9aviaTS7a would be kinetically viable, giving diethyl benzoylphosphonate and regenerating 1cat, but this step would be highly unfavorable thermodynamically (ΔG = 12.1 kcal mol−1). Thus, we continue searching for a pathway leading to the experimentally observed phosphoryl-aryl coupling product. In 9a the diphosphine ligand dppb has four CH2 units, thereby forming a seven-membered flexible chelate ring, the opening of which through the loss of one of the P coordinations would have a smaller energy cost compared with disrupting five-membered chelate rings. Thus, we have located the open-ring intermediate 10avia the C–C bond rotation, and 10a introduces the four-coordinate decarbonylation transition state TS8a that is 31.4 kcal mol−1 with respect to 9a. This barrier, although somewhat high, can be overcome at the experimental temperature (160 °C). It is worth noting that TS8a is lower than TS6a by 10.3 kcal mol−1. TS8a proceeds to 11a, which further isomerizes to the rotamer 12a to undertake intramolecular substitution viaTS9a. This interchange step is facile and leads to 13a with the extrusion of the by-product CO(g). Complex 13a then undertakes phosphoryl-aryl reductive elimination/coupling viaTS10a to deliver diethyl phenylphosphonate and regenerate 1cat. For the complete reaction pathway (Fig. 2 and 3), the largest energy span is from 9a to TS8a, 31.4 kcal mol−1, which is attainable at the experimental temperature (160 °C). Thus, decarbonylation viaTS8a is the rate-determining step. On another important note, the continuous evolution of the gaseous CO by-product in the decarbonylation phase keeps shifting the equilibrium position forward, thereby driving the reaction from 9a to the final products. The formation of diethyl phenylphosphonate (the phosphoryl-aryl coupling product) has a larger overall driving force (ΔG = −9.8 kcal mol−1) than the formation of diethyl benzoylphosphonate (the phosphoryl-acyl coupling product) (ΔG = −3.4 kcal mol−1), although the latter is kinetically easier (Fig. 3). Given that the reaction occurs under the conditions of thermodynamic control (160 °C and 16 h), the computed energetics can explain the chemoselectivity that favors phosphoryl-aryl over phosphoryl-acyl coupling.
In summary, we have utilized DFT calculations to elucidate the detailed mechanism of the first Pd-catalyzed decarbonylative phosphorylation of amides. The work has provided valuable insights into this new C–P bond forming reaction. The dialkylphosphite substrate undertakes proton transfer to the glutarimide anion in the second coordination sphere. The flexible diphosphine ligand can shift between bidentate and monodentate coordination as necessary to enable decarbonylation from Pd(II). The chemoselectivity of C–P cross-coupling originates from a thermodynamic control of product formation. Taken together, the findings of this study will have implications for better understanding transition metal-catalyzed amide bond cross-coupling and C–P bond forming reactions. Finally, we wish to emphasize the important differences between our Pd-catalyzed reaction mechanism and the Ni-catalyzed reaction mechanism described in ref. 13:
(1) In the Pd system, the additive Et3N does not enter the main reaction, and its role is to help initiate the pre-catalyst Pd(OAc)2 as established by earlier studies.14 The dialkylphosphite substrate undertakes coordination to Pd(II), followed by proton transfer to the glutarimide anion in the second coordination sphere, and this process (the 4a–9a course in Fig. 2) is molecularly well-defined, kinetically feasible, and thermodynamically favorable. In the Ni system, the additive Na2CO3 has been entered as a discrete NaCO3− ion in the reaction pathway to calculate the deprotonation of the Ni(II)-coordinated dialkylphosphite (see Fig. 1 in ref. 13).
(2) Decarbonylation viaTS8a has been found to be the rate-determining step in the Pd-catalyzed reaction, whereas oxidative addition has been described as the rate-determining step in the Ni-catalyzed reaction.
(3) The computed energetics can explain the chemoselectivity of the Pd-catalyzed reaction that favors phosphoryl-aryl over phosphoryl-acyl coupling. There is no discussion on chemoselectivity in the work on the Ni-catalyzed reaction.
The authors acknowledge support for this work from the NSFC (Grant No. 21720102006, 21273140 and 21471092), the One Hundred-Talent Program of Shanxi Province, the OIT Program, Shanxi “1331 Project” Engineering Research Center (PT201807), the Shanxi 1331KIRT, the High-Performance Computing Center of Shanxi University, and the University of Colorado Denver.
Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) L. D. Quin, A Guide to Organophosphorus Chemistry, Wiley Interscience, New York, 2000 Search PubMed; (b) J.-P. Majoral, New Aspects in Phosphorus Chemistry, Springer, Berlin, 2010, vol. 1–5 Search PubMed; (c) P. J. Murphy, Organophosphorus Reagents, Oxford University Press, Oxford, UK, 2004 Search PubMed; (d) C. Queffélec, M. Petit, P. Janvier, D. A. Knight and B. Bujoli, Chem. Rev., 2012, 112, 3777–3807 CrossRef; (e) G. Németh, Z. Greff, A. Sipos, Z. Varga, R. Székely, M. Sebestyén, Z. Jászay, S. Béni, Z. Nemes, J.-L. Pirat, J.-N. Volle, D. Virieux, Á. Gyuris, K. Kelemenics, É. Áy, J. Minarovits, S. Szathamary, G. Kéri and L. Őrfi, J. Med. Chem., 2014, 57, 3939–3965 CrossRef PubMed.
- A. K. Bhattacharya and G. Thyarajan, Chem. Rev., 1981, 81, 415–430 CrossRef CAS.
- (a) T. Hirao, T. Masunaga, Y. Ohshiro and T. Agawa, Synthesis, 1981, 56–57 CrossRef CAS; (b) T. Hirao, T. Masunaga, N. Yamada, Y. Ohshiro and T. Agawa, Bull. Chem. Soc. Jpn., 1982, 55, 909–913 CrossRef CAS.
- (a) J. L. Montchamp and Y. R. Dumond, J. Am. Chem. Soc., 2001, 123, 510–511 CrossRef CAS; (b) M. Kalek, A. Ziadi and J. Stawinski, Org. Lett., 2008, 10, 4637–4640 CrossRef CAS; (c) A. J. Bloomfield and S. B. Herzon, Org. Lett., 2012, 14, 4370–4373 CrossRef CAS; (d) E. L. Deal, C. Petit and J. L. Montchamp, Org. Lett., 2011, 13, 3270–3273 CrossRef CAS; (e) O. Berger, C. Petit, E. Deal and J. L. Montchamp, Adv. Synth. Catal., 2013, 355, 1361–1373 CrossRef CAS; (f) M. Kalek and J. Stawinski, Organometallics, 2008, 27, 5876–5888 CrossRef CAS; (g) E. Jablonkai and G. Keglevich, Tetrahedron Lett., 2013, 54, 4185–4188 CrossRef CAS; (h) Y. Wu, L. Liu, K. Yan, P. Xu, Y. Gao and Y. Zhao, J. Org. Chem., 2014, 79, 8118–8127 CrossRef CAS; (i) R. Yu, X. Chen, S. F. Martin and Z. Wang, Org. Lett., 2017, 19, 1808–1811 CrossRef CAS.
- (a) K. S. Petrakis and T. L. Nagabhushan, J. Am. Chem. Soc., 1987, 109, 2831–2833 CrossRef CAS; (b) D. A. Holt and J. M. Erb, Tetrahedron Lett., 1989, 30, 5393–5396 CrossRef CAS; (c) W. C. Fu, C. M. So and F. Y. Kwong, Org. Lett., 2015, 17, 5906–5909 CrossRef CAS.
- R. Berrino, S. Cacchi, G. Fabrizi, A. Goggiamani and P. Stabile, Org. Biomol. Chem., 2010, 8, 4518–4520 RSC.
- M. Andaloussi, J. Lindh, J. Sövmarker, P. J. R. Sjöberg and M. Larhed, Chem. – Eur. J., 2009, 15, 13069–13074 CrossRef CAS.
- H. Luo, H. Liu, X. Chen, K. Wang, X. Luo and K. Wang, Chem. Commun., 2017, 53, 956–958 RSC.
- J. Yang, T. Chen and L. B. Han, J. Am. Chem. Soc., 2015, 137, 1782–1785 CrossRef CAS.
- J. Yang, J. Xiao, T. Chen, S. F. Yin and L. B. Han, Chem. Commun., 2016, 52, 12233–12236 RSC.
- (a) G. Meng and M. Szostak, Org. Lett., 2015, 17, 4364–4367 CrossRef CAS; (b) G. Meng and M. Szostak, Angew. Chem., Int. Ed., 2015, 54, 14518–14522 CrossRef CAS.
- C. Liu and M. Szostak, Angew. Chem., Int. Ed., 2017, 56, 12718–12722 CrossRef CAS.
- Y. Xu, B. Wang, J. Jiang, H. Yu and Y. Fu, J. Org. Chem., 2019, 84, 9474–9479 CrossRef CAS PubMed.
- (a) F. Ozawa, A. Kubo and T. Hayashi, Chem. Lett., 1992, 2177–2180 CrossRef CAS; (b) C. Amatore, A. Jutand and A. Thuilliez, Organometallics, 2001, 20, 3241–3249 CrossRef CAS.
- No Pd0(dppb) complexes containing an additional Et3N ligand could be optimized.
- C.-L. Ji and X. Hong, J. Am. Chem. Soc., 2017, 139, 15522–15529 CrossRef CAS.
- (a) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- (a) D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS; (b) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional computational results and Cartesian coordinates and energies of the optimized structures. See DOI: 10.1039/c9cc07923h |
| ‡ Geometries were optimized and characterized by frequency calculations to be minima or transition states at the B3LYP17/BS1 level in the gas phase, where BS1 represents the mixed basis set with SDD18 for palladium and 6-31G(d) for other elements. Single-point energies were obtained by M0619/BS2//B3LYP/BS1 calculations with solvation effects modeled by SMD20 in 1,4-dioxane (the experimentally used solvent); BS2 denoting the mixed basis set with SDD for palladium and 6-311++G(d,p) for other elements. The energies were converted to zero-point energy-corrected Gibbs free energies at 298.15 K and 1 atm, using the B3LYP/BS1 frequencies. All calculations were performed with Gaussian 09.21 |
| This journal is © The Royal Society of Chemistry 2020 |