A C20-based 3D carbon allotrope with high thermal conductivity†
Yupeng
Shen
 ,
Fancy Qian
Wang
,
Jie
Liu
,
Fancy Qian
Wang
,
Jie
Liu
 and
Qian
Wang
and
Qian
Wang
 *
*
Center for Applied Physics and Technology, Department of Materials Science and Engineering, HEDPS, BKL-MEMD, College of Engineering, Peking University, Beijing 100871, China. E-mail: qianwang2@pku.edu.cn
First published on 4th June 2019
Abstract
Stimulated by the high thermal conductivity of diamond together with the light mass and rich resources of carbon, a great deal of effort has been devoted to the study of the thermal conductivity of carbon-based materials. In this work, we systematically study the thermal transport properties of a three dimensional (3D) C20 fullerene-assembled carbon allotrope, HSP3-C34, in which all carbon atoms are in sp3 hybridization. The stability of HSP3-C34 is confirmed and its thermal conductivity is obtained by using first principles calculations combined with solving the linearized phonon Boltzmann transport equation. At room temperature, the thermal conductivity of HSP3-C34 is 731 W m−1 K−1, which is larger than those of many 3D carbon allotropes, such as BCO-C16 (452 W m−1 K−1), 3D graphene (150 W m−1 K−1) and T-carbon (33 W m−1 K−1). A detailed analysis of its phonons reveals that three acoustic branches are the main heat carriers at room temperature, and the optical branches gradually become important with increasing temperature. A further study on the harmonic and anharmonic properties of HSP3-C34 uncovers that the main reasons for the high thermal conductivity are the weak anharmonicity and large group velocity resulting from the strong sp3 bonding. This study provides new insights on searching for carbon allotropes with high thermal conductivity.
1. Introduction
Fullerenes, first discovered in 1985 as carbon cage molecules with high symmetry,1 have attracted tremendous attention because of their special geometries, intriguing properties and various applications in photophysics,2 superconductivity,3 photovoltaic cells,4–6 electronic devices,7etc. In these practical applications, fullerenes are usually assembled into 3D functional materials rather than in the form of molecules.8 Therefore, it is particularly important to design and synthesize new materials by using fullerenes as structural units. As the smallest fullerene in the fullerene family, C20 is of special interest because of its unique geometric configuration, consisting of only twelve pentagons that break the “isolated pentagon rule” in fullerene science.9–12 Since the successful synthesis of C20 fullerene,13 many efforts have been devoted to studying C20 fullerene-based 2D and 3D crystalline structures.14–17 Some C20-based materials have been experimentally synthesized. For instance, Wang et al.18 reported the synthesis of a crystallized solid form of C20 by using an Ar+ ion irradiation method. Iqbal et al.19 obtained a solid phase of dodecahedral C20via ultraviolet laser ablation on polycrystalline diamond close to a nickel substrate. As phonon spectra strongly depend on the complexity of the assembly because of the interactions between the fullerene molecules, the resulting phonons with complicated dispersions would significantly affect the thermal conductivity. Therefore, rational design of C20-based structures may lead to satisfactory thermal conductivity.Usually, if fullerene molecules are simply stacked together without forming bonds, the resulting structures will possess ultralow thermal conductivity, which has been confirmed by previous results (0.1–0.7 W m−1 K−1).20–22 The ultralow thermal conductivity is due to the weak interactions between the molecules.21 But, when bonding takes place in the assembling of fullerenes, a remarkable thermal conductivity can be achieved.16 On the other hand, the hybridization of carbon atoms shows great flexibility (sp, sp2 and sp3). A 3D crystal made of all sp3-hybridized carbon atoms could have low anharmonicity,23 leading to a high thermal conductivity. Diamond is such an example.24 Besides, when all the carbon atoms are in sp3 hybridization, the structure could be highly electrically resistant so that it can be used as a thermal material in electronic devices without concern about short circuits. However, only a few C20-based 3D structures with full sp3 hybridization have been reported.25
Herein, we focus on C20 cages as building blocks for bulk thermal materials, and a 3D carbon allotrope is generated, which is the same as the clathrate H configuration proposed by Karttunen et al.25 This structure possesses a hexagonal unit cell with all 34 carbon atoms in sp3 hybridization, thus it is named HSP3-C34. By using state-of-the-art first-principles calculations and the Boltzmann transport approach, we confirm the superior stability, wide band gap (4.48 eV) and high lattice thermal conductivity (731 W m−1 K−1) at room temperature, resulting from the unique geometry of HSP3-C34.
2. Computational methods
The structure of HSP3-C34 is fully relaxed and its electronic structure is calculated using the density functional theory (DFT) and the projector augmented wave (PAW)26 method as implemented in the Vienna ab initio simulation package (VASP).27 The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA)28 is applied to treat the electronic exchange–correlation interaction. In the geometry relaxation process, the convergence thresholds are set to 10−8 eV and 10−6 eV Å−1 for total energy and force component, respectively. The energy cutoff of plane waves is set to 520 eV, and a 9 × 9 × 10 Monkhorst–Pack k-mesh is used to sample the first Brillouin zone. The phonon dispersion of the structure is calculated by using the PHONOPY package,29 and the thermal stability is studied using ab initio molecular dynamics (AIMD) simulations with temperature controlled by the Nosé thermostat.30 To acquire the band gap with high accuracy, the electronic band structure is recalculated using the Heyd–Scuseria–Ernzerhof (HSE06)31,32 functional for the exchange–correlation interaction.By solving the phonon Boltzmann transport equation (BTE) in the ShengBTE package,33 we can obtain the intrinsic thermal conductivity of a structure. The calculation of thermal conductivity within the ShengBTE package requires harmonic second order interatomic force constants (IFCs) and anharmonic third order force IFCs as input files. To obtain the thermal conductivity of HSP3-C34, firstly we construct a 2 × 2 × 2 supercell containing 272 atoms for the calculations of second order and third order IFCs. These calculations are performed within the VASP. After that, we set the cutoff radius, scalebroad parameter and k-point meshes to the 7th nearest neighbors, 0.1 and 13 × 13 × 13, respectively, to ensure the accuracy of thermal conductivity calculation. For comparison, the thermal conductivity of diamond is also calculated. The second order and third order IFCs of diamond are acquired using a 3 × 3 × 3 supercell. The cutoff radius, scalebroad parameter and k-point meshes are set to the 7th nearest neighbors, 0.1 and 30 × 30 × 30, respectively. Our resulting thermal conductivity of diamond is 2055 W m−1 K−1 at room temperature, which is consistent with the results of previous studies.34–37
3. Results and discussion
3.1 Geometric structure and electronic properties
Using C20 as the building unit, we construct a 3D carbon allotrope (HSP3-C34) that has a hexagonal unit cell, containing 34 carbon atoms all in sp3 hybridization. The constructing process of HSP3-C34 is shown in Fig. 1. Starting from C20 (Fig. 1a): we first construct a C20-based six-membered ring through face-sharing between C20 units (Fig. 1b), and then we extend the six-membered ring to the entire plane (Fig. 1c); thus, we can get a C20-based 2D layer. After that, we expand the structure into a 3D material by forming bonds between the layers (Fig. 1d). The side view of the optimized HSP3-C34 structure is plotted in Fig. 1e and the top view is the same as that of the 2D layer (Fig. 1c). This allotrope crystallizes in the space group P6/mmm (191) with equilibrium lattice constants a = b = 6.88 Å, and c = 5.59 Å. Through the assembly of C20 cages, we note that HSP3-C34 not only possesses the five-membered carbon rings from C20, but it also has four-membered and six-membered rings. The atomic Wyckoff positions of the optimized HSP3-C34 are given in the ESI.† We note this structure is the same as the clathrate H structure proposed by Karttunen et al.25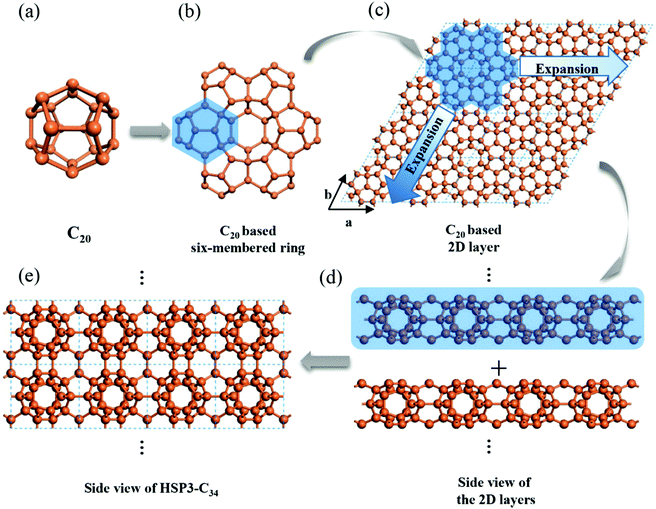 | ||
| Fig. 1 Geometric configurations of (a) C20 fullerene, (b) C20-based six-membered ring and (c) C20 based 2D layer. Side views of (d) stacking process of the 2D layers and (e) optimized HSP3-C34. | ||
In C20 fullerene, all the carbon atoms are in sp2 hybridization. For most 3D structures assembled by C20 fullerene, such as simple-cubic-like (SCL) phase,38 3D polymers15 and Fcc-C22 crystal,17 they contain carbon atoms in both sp2 and sp3 hybridizations. However, in HSP3-C34, all carbon atoms are in sp3 hybridization, which could lead to low anharmonicity. The underlying reason is that when all the carbon atoms are in sp3 hybridization, the tetrahedral coordination geometry results in a compact packing configuration with strong bonding. The anharmonicity is thus reduced23 and the phonon relaxation time is increased.39 These features could lead to higher thermal conductivity. Thus, HSP3-C34 would exhibit better performance in thermal transportation than other C20-based 3D structures.
First of all, we verify the stability of HSP3-C34. To test the energetic stability of HSP3-C34, we calculate the total energy of HSP3-C34. For comparison, the calculations of some other 3D carbon allotropes such as diamond, T6,40 bct-C441 and H1842 are also carried out. The results are given in Table 1, which shows that even though the energy of HSP3-C34 is slightly higher than that of diamond, it is energetically more favorable than many other 3D carbon allotropes.
| Structure | Space group | E tot |
|---|---|---|
| HSP3-C34 | P6/mmm | −8.96 |
| Diamond |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
−9.09 |
| T6 | P42/mmc | −8.64 |
| bct-C4 | I4/mmm | −8.89 |
| H18 | P6/mmm | −8.75 |
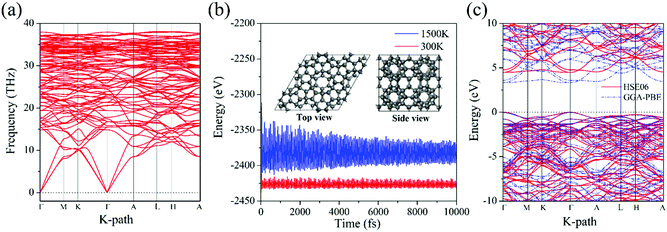
We next calculate the phonon dispersion to examine the dynamic stability. The calculated results are plotted in Fig. 2a. The phonon spectra show no imaginary modes in the whole Brillouin zone, confirming that HSP3-C34 is dynamically stable. We then perform ab initio molecular dynamics (AIMD) simulations to study the thermal stability. A 2 × 2 × 2 supercell is constructed to simulate the bulk material for minimizing the constraint of the periodic boundary conditions, and to explore the possibility of structure reconstruction. As shown in Fig. 2b, the total potential energies fluctuate around constant values at 300 K and even 1500 K, respectively, and the geometric structure remains nearly intact after being heated for 10 picoseconds (ps). These results suggest that HSP3-C34 is thermally stable at room temperature, and can withstand high temperature (1500 K), providing a broad working temperature range because of its high thermal stability. To verify the mechanical stability, we further calculate the linear elastic constants of HSP3-C34. The results are listed in Table 2. In general, for a stable hexagonal lattice, there are only five independent elastic constants, namely C11, C12, C13, C33 and C44, which must obey the Born–Huang criteria: C11 > C12, C44 > 0 and (C11 + C12) C33 > 2C132.43 We find that the calculated elastic constants of HSP3-C34 satisfy the above criteria; hence, HSP3-C34 is mechanically stable.
| C11 | C12 | C13 | C33 | C44 |
|---|---|---|---|---|
| 885.7 | 89.1 | 110.3 | 855.9 | 376.6 |
We then study the electronic band structure of HSP3-C34. The results are plotted in Fig. 2c. We find that both the valence band maximum (VBM) and the conduction band minimum (CBM) are located on the Γ point, indicating that HSP3-C34 is a direct band gap semiconductor. The band gap calculated at the GGA-PBE level is 3.36 eV, while it is 4.48 eV at the HSE06 level, indicating that HSP3-C34 can be highly electrically resistant. In the electronics industry, thermal materials often need to possess good electrical insulation properties, otherwise they could lead to the short circuit of electronic components. Therefore, the large band gap enables HSP3-C34 to have better applications in the field of thermal conductive materials. In addition, different from the metallic graphite and indirect-bandgap diamond, HSP3-C34 is semiconducting with a gap of 4.48 eV, corresponding to the wavelength of 277 nm, showing the potential to be used in deep ultraviolet (UV) light emitting diodes (LEDs) and laser diodes (LDs).
To explore the bonding nature of carbon atoms in HSP3-C34, we calculate the electron localization function (ELF), as it is a useful physical quantity that characterizes the chemical bond properties of a material. The values of ELF are renormalized between 0.00 and 1.00, which correspond to very low charge density and fully localized electrons, respectively, while the value of 0.50 represents that the electrons are fully delocalized. For comparison, the ELF of diamond is also calculated. The calculated ELF results for the (010), (110) and (001) planes of HSP3-C34, and for the (110) plane of diamond are plotted in Fig. 3. One can see that the electrons are all localized on the C–C bonds in the four-, five- and six-membered rings of HSP3-C34, as shown in Fig. 3a, b and c, respectively, implying the strong σ bonding states between the carbon atoms in HSP3-C34, which is similar to the situation of the electrons in the zigzag chains of the (110) plane in diamond, as shown in Fig. 3d. In addition, all the carbon atoms in HSP3-C34 are in sp3 hybridization, leading to the compact packing of atoms and the formation of carbon rings with high symmetry. Thus, the strong interatomic bonding and tetrahedral arrangement lead to the high thermal conductivity of HSP3-C34.
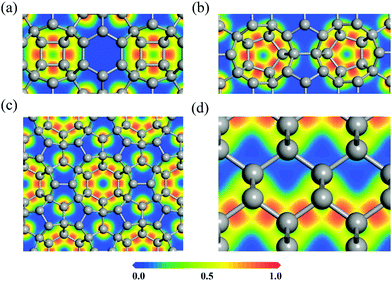 | ||
| Fig. 3 (a–c) Electron localization functions (ELFs) of the (010), (110) and (001) plane of HSP3-C34, respectively. (d) ELF of the (110) plane of diamond. | ||
3.2 Lattice thermal conductivity
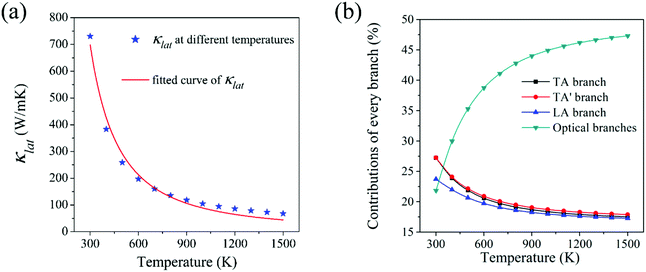
Lattice thermal conductivity (κlat) is the most critical indicator for measuring the ability of heat conduction. Materials with high thermal conductivity have broad application in the field of heat dissipation. The intrinsic lattice thermal conductivity of HSP3-C34 in the temperature ranging from 300 K to 1500 K is calculated by solving the linearized phonon Boltzmann transport equation (BTE).44,45 As shown in Fig. 4a, the thermal conductivity of HSP3-C34 is 731 W m−1 K−1 at room temperature (300 K). Compared with many other 3D carbon allotropes, such as BCO-C16 (452 W m−1 K−1),46 3D graphene (150 W m−1 K−1)47 and T-carbon (33 W m−1 K−1),46 HSP3-C34 exhibits better heat transport properties. We fit the relationship of thermal conductivity with temperature and find that the thermal conductivity is proportional to 1/T1.395, confirming that three-phonon scattering plays a leading role in the thermal transportation of HSP3-C34. We next analyze the contribution of different phonon modes to the thermal conductivity. As shown in the Fig. 4b, when the temperature is 300 K, the contributions of the three acoustic branches (TA, TA′ and LA) to the thermal conductivity are 27%, 27% and 24%, respectively, while the other optical phonon branches only account for 22%, suggesting that the acoustic branches are the main heat carriers at room temperature. As the temperature rises gradually, the contribution of the optical branches to the thermal conductivity increases, and when the temperature reaches 1500 K, the contribution rate of the optical branches reaches as high as 47%. This is because with the increase of temperature, more and more high-frequency optical branches are excited and participate in the heat conduction process.Then, we study the intrinsic physical mechanism of HSP3-C34 to find out the reason for the high thermal conductivity. As diamond is one of the best thermal conductors and all the carbon atoms in diamond are also sp3 hybridized, we chose diamond as a comparison for calculation. There are two major factors affecting thermal conductivity of materials: anharmonicity and harmonicity.
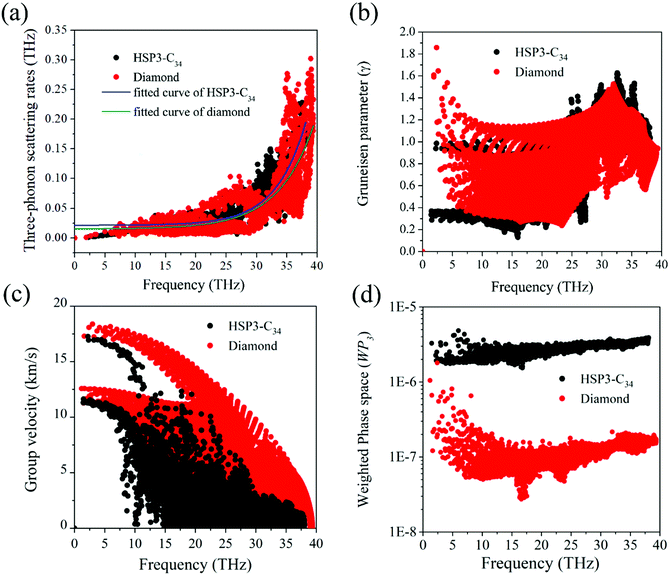
For the anharmonic properties, we calculate the three-phonon scattering rates and Grüneisen parameter of HSP3-C34 and diamond, which are shown in Fig. 5a and b. The three-phonon scattering rates characterize the intensity of phonon scattering in the heat transport process. When other factors are the same, the larger the scattering rates, the lower the thermal conductivity. From Fig. 5a, we can conclude that the three-phonon scattering rates of HSP3-C34 and diamond share a similar changing trend and basically the same magnitude. We further plot the regression curves of the scattering rates of the two structures in Fig. 5a, indicating that they have similar three-phonon scattering rates. These results mean that the small three-phonon scattering rate of HSP3-C34 is one of the reasons for the high thermal conductivity. Besides, we evaluate the anharmonicity of HSP3-C34 and diamond quantitatively by calculating the Grüneisen parameter (γ) with 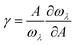 , where the parameter A is the volume of the unit cell and the parameter ωλ is the angular frequency. Structures with soft lattices or structures with atoms not well-packed in the lattices are likely to possess strong anharmonicity, in other words, a large Grüneisen parameter.23 The results in Fig. 5b show that both HSP3-C34 and diamond have small Grüneisen parameters with a similar distribution, indicating weak anharmonicity between the carbon atoms in the two structures. This is because the carbon atoms in both HSP3-C34 and diamond are in a strict tetrahedral arrangement (sp3 hybridization) and the bonds are strong covalent bonds, thus leading to similar weak anharmonicity in the two structures. Hence, weak anharmonicity of HSP3-C34 contributes to the high thermal conductivity.
, where the parameter A is the volume of the unit cell and the parameter ωλ is the angular frequency. Structures with soft lattices or structures with atoms not well-packed in the lattices are likely to possess strong anharmonicity, in other words, a large Grüneisen parameter.23 The results in Fig. 5b show that both HSP3-C34 and diamond have small Grüneisen parameters with a similar distribution, indicating weak anharmonicity between the carbon atoms in the two structures. This is because the carbon atoms in both HSP3-C34 and diamond are in a strict tetrahedral arrangement (sp3 hybridization) and the bonds are strong covalent bonds, thus leading to similar weak anharmonicity in the two structures. Hence, weak anharmonicity of HSP3-C34 contributes to the high thermal conductivity.
For better understanding the results, we next turn our attention to the harmonic properties: phonon group velocity Vg and three phonon phase space P3. We first investigate the phonon group velocity of the two structures. The results are plotted in Fig. 5c. When the frequency is approaching zero (the long-wavelength limit), the group velocities of both diamond and HSP3-C34 acquire two peak values, because the two acoustic phonon branches TA and TA′ are degenerate near the long-wavelength limit. For HSP3-C34, the peak values are about 17.0 km s−1 and 11.4 km s−1, which resemble the results of diamond, 17.5 km s−1 and 12.5 km s−1. Even though in the high frequency region, the group velocity of HSP3-C34 is lower than that of diamond, the value is still rather large. Besides, according to Fig. 4b, the main contribution to thermal conductivity of HSP3-C34 at 300 K is from three low-frequency acoustic phonon branches, so the group velocity in the low frequency region dominates the thermal conductivity at room temperature. Hence, we can conclude that the large group velocity of HSP3-C34 is also one of the reasons for the high thermal conductivity.
Then, we calculate the three phonon phase space P3. The three-phonon phase space is an important parameter to quantify the number of phonon scattering channels in the heat transport process. When the energy and momentum conservation are satisfied, the scattering events could happen and the phonon scattering channels are available.48 If a structure possesses a relatively larger three-phonon phase space, it means that there are more scattering channels in the material, thus leading to greater resistance that the heat will encounter during conduction. So, in general, the three-phonon phase space is negatively correlated with the thermal conductivity of the material. The calculated results are plotted in Fig. 5d, from which we can find that in the whole frequency region, the three-phonon phase space of HSP3-C34 is always significantly higher than that of diamond, which results from the larger number of atoms per unit cell in HSP3-C34. So, one can see that due to the larger three-phonon phase space, the thermal conductivity of HSP3-C34 is reduced as compared to that of diamond.
4. Conclusions
Based on state-of-the-art theoretical calculations, we confirm that the C20-based 3D carbon allotrope, HSP3-C34, is dynamically and thermally stable. The band gap of HSP3-C34 is 4.48 eV, indicating that it can be highly electrically resistant. By solving the linearized phonon Boltzmann transport equation, we find that HSP3-C34 possesses a high thermal conductivity of 731 W m−1 K−1 at room temperature, showing potential as a thermal material for applications in heat dissipation devices. A further study on its intrinsic mechanism demonstrates that the weak anharmonicity and large group velocity contribute to the high thermal conductivity. These results show that the 3D carbon allotropes formed from assembling fullerenes with all carbon atoms in sp3 hybridization can exhibit intriguing thermal properties.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
This work is partially supported by grants from the National Key Research and Development Program of the Ministry of Science and Technology of China (Grants No. 2016YFE0127300 and No. 2017YFA0205003) and the National Natural Science Foundation of China (NSFC-21773004), and is supported by the High Performance Computing Platform of Peking University, China.References
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS
.
- M. Regehly, E. A. Ermilov, M. Helmreich, A. Hirsch, N. Jux and B. Röder, J. Phys. Chem. B, 2007, 111, 998–1006 CrossRef CAS PubMed
.
- K. Umemoto, S. Saito and A. Oshiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 16186 CrossRef CAS
.
- R. D. Kennedy, A. L. Ayzner, D. D. Wanger, C. T. Day, M. Halim, S. I. Khan, S. H. Tolbert, B. J. Schwartz and Y. Rubin, J. Am. Chem. Soc., 2008, 130, 17290–17292 CrossRef CAS PubMed
.
- S. K. Hau, Y.-J. Cheng, H.-L. Yip, Y. Zhang, H. Ma and A. K.-Y. Jen, ACS Appl. Mater. Interfaces, 2010, 2, 1892–1902 CrossRef CAS
.
- Y.-J. Cheng, F.-Y. Cao, W.-C. Lin, C.-H. Chen and C.-H. Hsieh, Chem. Mater., 2011, 23, 1512–1518 CrossRef CAS
.
- N. Martín, L. Sánchez, B. Illescas and I. Pérez, Chem. Rev., 1998, 98, 2527–2548 CrossRef PubMed
.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed
.
- H. Kroto, Nature, 1987, 329, 529 CrossRef CAS
.
- T. Schmalz, W. A. Seitz, D. J. Klein and G. Hite, J. Am. Chem. Soc., 1988, 110, 1113–1127 CrossRef CAS
.
- N. A. Poklonski, S. V. Ratkevich and S. A. Vyrko, J. Phys. Chem. A, 2015, 119, 9133–9139 CrossRef CAS PubMed
.
- N. A. Poklonski, S. A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevich, N. N. Hieu and A. A. Kocherzhenko, Mater. Res. Express, 2019, 6, 042002 CrossRef
.
- H. Prinzbach, A. Weiler, P. Landenberger, F. Wahl, J. Wörth, L. T. Scott, M. Gelmont, D. Olevano and B. v. Issendorff, Nature, 2000, 407, 60 CrossRef CAS PubMed
.
- N. Konstantinidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 104434 CrossRef
.
- S. Okada, Y. Miyamoto and M. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245405 CrossRef
.
- Y. Shen, F. Q. Wang, J. Liu, Y. Guo, X. Li, G. Qin, M. Hu and Q. Wang, Nanoscale, 2018, 10, 6099–6104 RSC
.
- I. Spagnolatti, M. Bernasconi and G. Benedek, EPL, 2002, 59, 572 CrossRef CAS
.
- Z. Wang, X. Ke, Z. Zhu, F. Zhu, M. Ruan, H. Chen, R. Huang and L. Zheng, Phys. Lett. A, 2001, 280, 351–356 CrossRef CAS
.
- Z. Iqbal, Y. Zhang, H. Grebel, S. Vijayalakshmi, A. Lahamer, G. Benedek, M. Bernasconi, J. Cariboni, I. Spagnolatti and R. Sharma, Eur. Phys. J. B, 2003, 31, 509–515 CrossRef CAS
.
- A. Giri and P. E. Hopkins, J. Phys. Chem. Lett., 2017, 8, 2153–2157 CrossRef CAS PubMed
.
- J. Y. Kim and J. C. Grossman, Nano Lett., 2016, 16, 4203–4209 CrossRef CAS PubMed
.
- R. Yu, N. Tea, M. Salamon, D. Lorents and R. Malhotra, Phys. Rev. Lett., 1992, 68, 2050 CrossRef CAS PubMed
.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS
.
- A. Ward, D. Broido, D. A. Stewart and G. Deinzer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125203 CrossRef
.
- A. J. Karttunen, T. F. Fassler, M. Linnolahti and T. A. Pakkanen, lnorg. Chem., 2010, 50, 1733–1742 CrossRef PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef
.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef
.
- Y. Li, L. Xu, H. Liu and Y. Li, Chem. Soc. Rev., 2014, 43, 2572–2586 RSC
.
- A. Inyushkin, A. Taldenkov, V. Ralchenko, A. Bolshakov, A. Koliadin and A. Katrusha, Phys. Rev. B, 2018, 97, 144305 CrossRef CAS
.
- L. Wei, P. Kuo, R. Thomas, T. Anthony and W. Banholzer, Phys. Rev. Lett., 1993, 70, 3764 CrossRef CAS PubMed
.
- A. Sukhadolau, E. Ivakin, V. Ralchenko, A. Khomich, A. Vlasov and A. Popovich, Diamond Relat. Mater., 2005, 14, 589–593 CrossRef CAS
.
- K. Plamann and D. Fournier, Phys. Status Solidi A, 1996, 154, 351–369 CrossRef CAS
.
- Y. Miyamoto and M. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 161401 CrossRef
.
- Z. Liu, X. Wu, V. Varshney, J. Lee, G. Qin, M. Hu, A. K. Roy and T. Luo, Nano Energy, 2018, 45, 1–9 CrossRef CAS
.
- S. Zhang, Q. Wang, X. Chen and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18809–18813 CrossRef CAS
.
- K. Umemoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504 CrossRef PubMed
.
- C.-X. Zhao, C.-Y. Niu, Z.-J. Qin, X. Y. Ren, J.-T. Wang, J.-H. Cho and Y. Jia, Sci. Rep., 2016, 6, 21879 CrossRef CAS PubMed
.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef
.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS
.
-
J. M. Ziman, Electrons and phonons: the theory of transport phenomena in solids, Oxford University Press, 1960 Search PubMed
.
- S.-Y. Yue, G. Qin, X. Zhang, X. Sheng, G. Su and M. Hu, Phys. Rev. B, 2017, 95, 085207 CrossRef
.
- Y. Han, J.-Y. Yang and M. Hu, Nanoscale, 2018, 10, 5229–5238 RSC
.
- L. Lindsay and D. Broido, J. Phys.: Condens. Matter, 2008, 20, 165209 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02202c |
| This journal is © the Owner Societies 2020 |