Structural and reorientational dynamics of tetrahydroborate (BH4−) and tetrahydrofuran (THF) in a Mg(BH4)2·3THF adduct: neutron-scattering characterization†
Mirjana
Dimitrievska
 *ab,
Marina
Chong
*ab,
Marina
Chong
 c,
Mark E.
Bowden
c,
Mark E.
Bowden
 c,
Hui
Wu
b,
Wei
Zhou
b,
Iffat
Nayyar
c,
Bojana
Ginovska
c,
Thomas
Gennett
a,
Tom
Autrey
c,
Craig M.
Jensen
d and
Terrence J.
Udovic
c,
Hui
Wu
b,
Wei
Zhou
b,
Iffat
Nayyar
c,
Bojana
Ginovska
c,
Thomas
Gennett
a,
Tom
Autrey
c,
Craig M.
Jensen
d and
Terrence J.
Udovic
 b
b
aNational Renewable Energy Laboratory (NREL), 5013 Denver W Pkwy, Golden, CO 80401, USA. E-mail: mirjana.dimitrievska@nrel.gov; mirjana.dimitrievska@nist.gov
bNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD 20899-6102, USA
cPacific Northwest National Laboratory (PNNL), Richland, WA 99352, USA
dUniversity of Hawaii Manoa, Department of Chemistry, Honolulu, HI 96822-2275, USA
First published on 20th November 2019
Abstract
Metal borohydrides are considered promising materials for hydrogen storage applications due to their high volumetric and gravimetric hydrogen density. Recently, different Lewis bases have been complexed with Mg(BH4)2 in efforts to improve hydrogenation/dehydrogenation properties. Notably, Mg(BH4)2·xTHF adducts involving tetrahydrofuran (THF; C4H8O) have proven to be especially interesting. This work focuses on exploring the physicochemical properties of the THF-rich Mg(BH4)2·3THF adduct using neutron-scattering methods and molecular DFT calculations. Structural analysis, based on neutron diffraction measurements of Mg(11BH4)2·3TDF (D – deuterium), has confirmed a lowering of the symmetry upon cooling, from monoclinic C2/c to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) via a triclinic distortion. Vibrational properties are strongly influenced by the THF environment, showing a splitting in spectral features as a result of changes in the bond lengths, force constants, and lowering of the overall symmetry. Interestingly, the orientational mobilities of the BH4− anions obtained from quasielastic neutron scattering (QENS) are not particularly sensitive to the presence of THF and compare well with the mobilities of BH4− anions in unsolvated Mg(BH4)2. The QENS data point to uniaxial 180° jump reorientations of the BH4− anions around a preferred C2 anion symmetry axis. The THF rings are also found to be orientationally mobile, undergoing 180° reorientational jumps around their C2 molecular symmetry axis with jump frequencies about an order of magnitude lower than those for the BH4− anions. In contrast, no dynamical behavior of the THF rings is observed with QENS for a more THF-deficient 2Mg(BH4)2·THF adduct. This lack of comparable THF mobility may reflect a stronger Mg2+–THF bonding interaction for lower THF/Mg(BH4)2 stoichiometric ratios, which is consistent with DFT calculations showing a decrease in the binding energy with each additional THF ring in the adduct. Based on the combined experimental and computational results, we propose that combining THF and Mg(BH4)2 is beneficial to (i) preventing weakly bound THF from coming free from the Mg2+ cation and reducing the concentration of any unwanted impurity in the hydrogen and (ii) disrupting the stability of the crystalline phase, leading to a lower melting point and enhanced kinetics for any potential hydrogen storage applications.
via a triclinic distortion. Vibrational properties are strongly influenced by the THF environment, showing a splitting in spectral features as a result of changes in the bond lengths, force constants, and lowering of the overall symmetry. Interestingly, the orientational mobilities of the BH4− anions obtained from quasielastic neutron scattering (QENS) are not particularly sensitive to the presence of THF and compare well with the mobilities of BH4− anions in unsolvated Mg(BH4)2. The QENS data point to uniaxial 180° jump reorientations of the BH4− anions around a preferred C2 anion symmetry axis. The THF rings are also found to be orientationally mobile, undergoing 180° reorientational jumps around their C2 molecular symmetry axis with jump frequencies about an order of magnitude lower than those for the BH4− anions. In contrast, no dynamical behavior of the THF rings is observed with QENS for a more THF-deficient 2Mg(BH4)2·THF adduct. This lack of comparable THF mobility may reflect a stronger Mg2+–THF bonding interaction for lower THF/Mg(BH4)2 stoichiometric ratios, which is consistent with DFT calculations showing a decrease in the binding energy with each additional THF ring in the adduct. Based on the combined experimental and computational results, we propose that combining THF and Mg(BH4)2 is beneficial to (i) preventing weakly bound THF from coming free from the Mg2+ cation and reducing the concentration of any unwanted impurity in the hydrogen and (ii) disrupting the stability of the crystalline phase, leading to a lower melting point and enhanced kinetics for any potential hydrogen storage applications.
Introduction
Using hydrogen as an energy carrier provides an opportunity to achieve zero-emission propulsion, which will help to reduce the consumption of fossil fuels and limit the extent of anthropogenic contributions to climate change.1 Storing hydrogen in chemical bonds, i.e., hydrogen storage materials, is one approach to storing and transporting hydrogen that provides greater volumetric and gravimetric hydrogen densities compared to compressed hydrogen gas. Hydrogen storage materials must fulfill a wide range of requirements to be industrially applicable. Among these, a high hydrogen content, fast kinetics of hydrogen desorption and absorption at low operating temperature and pressure, and a high purity of the released hydrogen are the most important. Promising alternatives for hydrogen storage include carbon nanostructures,2,3 liquid organic hydrogen carriers,4 metal organic frameworks5 and complex borohydrides.6Metal borohydrides [M(BH4)n] are considered as attractive materials for hydrogen storage applications due to their high volumetric and gravimetric hydrogen densities. M(BH4)n are largely ionic compounds composed of tetrahedral hydrogen-rich molecular BH4− anions counterbalanced by metal cations, Mn+. Among the alkali- and alkaline-earth-based borohydrides, magnesium borohydride [Mg(BH4)2] displays very interesting properties both from fundamental and application points of view. Mg(BH4)2 has a more favorable thermodynamic stability in comparison to, e.g., LiBH4, while still maintaining attractive hydrogen storage capacities of 14.9 mass%.7,8 However, the reaction kinetics of Mg(BH4)2, which is still not fully understood, along with its decomposition pathways occurring in a multi-step process only at 600 K,9,10 and its limited reversibility,11 make Mg(BH4)2 still unsuitable for practical applications.
Recently, different additives have been used in order to enhance the kinetics of hydrogen release from Mg(BH4)2.12–15 These studies have found that the onset temperature of hydrogen release could be reduced upon addition of metal fluorides13–15 or by mechanically milling Mg(BH4)2 with TiO2.15 Additionally, accelerated thermal dehydrogenation of Mg(BH4)2 was observed in mixtures with LiBH4.16–18
Several studies have also suggested that adducts of Mg(BH4)2 complexed with solvent molecules might lead to beneficial enhancements in hydrogen kinetics.19–23 Among these, adducts with tetrahydrofuran (THF = C4H8O) have proven to be especially interesting, as it was found that THF binds to the Mg2+ and appears to modify its chemistry, increasing both selectivity and kinetics for H2 release (and reversible uptake).23 However, the specific role of THF in the hydrogenation and dehydrogenation process is still ambiguous, and as such, in-depth foundational studies of the THF interactions with BH4− and Mg2+ may provide further insight.
Investigating physicochemical properties of Mg(BH4)2·xTHF adducts constitutes a challenge from an experimental point of view, as selectivity to different components, e.g., BH4− and THF, is required. Neutron scattering techniques are invaluable in this case, as they offer selectivity to a given component through isotopic (H/D) labeling. In the case of incoherent neutron scattering techniques (neutron vibrational spectroscopy (NVS) and quasielastic neutron scattering (QENS)) related to hydrogen self-motions, deuteration can significantly reduce the scattered intensity, thereby masking the deuterated component to neutrons. Additionally, QENS also provides space/time resolution at a molecular level through the momentum transfer dependence of the magnitudes measured. On the other hand, structural information, which is crucial for the understanding of vibrational and dynamical results, can be provided from neutron powder diffraction (NPD) measurements.
This work focuses on exploring the structural, vibrational, and dynamical properties of the THF-rich Mg(BH4)2·3THF adduct through neutron-scattering methods and molecular DFT calculations. Some additional limited experimental and theoretical comparisons with Mg(BH4)2 and the relatively THF-poorer 2Mg(BH4)2·THF adduct provide further insights concerning the dependences of BH4− and THF dynamics on adduct stoichiometry. In some experiments, selective masking of the THF molecules within the Mg(BH4)2·xTHF adducts via their deuteration allowed us to isolate and characterize more effectively the individual behaviors of the BH4− anions and THF molecules.
Experimental details
Materials
To facilitate neutron scattering measurements, all samples were prepared using 11B-enriched Mg(11BH4)2 from Katchem24 as a starting material; this leads to a significant reduction of the neutron absorption otherwise due to the 10B isotope in natural boron. Moreover, for some neutron scattering measurements, where appropriate, synthesized adducts with fully deuterated THF (i.e., TDF) were used.Sample preparation and storage were conducted either in a nitrogen glovebox or on a Schlenk line. The solvents were dried over molecular sieves and verified by NMR for purity before use.
Two Mg(BH4)2·xTHF adduct stoichiometries were prepared with THF/Mg(BH4)2 stoichiometric ratios x = 3 and 0.5, as previously described in ref. 23. Briefly, diethyl ether was added to a round-bottom flask containing 400 mg of α-phase Mg(BH4)2 until the borohydride was dissolved. In a subsequent step, a stoichiometric quantity, 0.5 or 3 equivalents of THF or TDF per Mg(BH4)2, was added by a micropipette to the ether solution at room temperature and stirred for 30 min. The excess ether was then removed in vacuo at room temperature for 12 hours to yield the THF adducts of Mg(BH4)2. This vacuum treatment did not remove THF, since prolonged exposure of Mg(BH4)2·3THF under vacuum did not change its stoichiometry or crystallinity.
Room-temperature XRD data for Mg(BH4)2·3THF confirmed the formation of the known monoclinic structure. The indexing of comparable XRD data for the more THF-deficient 2Mg(BH4)2·THF (i.e., x = 0.5) also suggested primarily a single phase with monoclinic symmetry but of as-of-yet unknown structure and exact stoichiometry.
Methods
All neutron scattering measurements were performed at the National Institute of Standards and Technology Center for Neutron Research using 0.5 g of each powdered sample mounted in a thin-walled annular geometry (5 cm height × 1.2 cm annulus diameter) inside a He-filled, indium o-ring-sealed, cylindrical Al sample cell.Neutron powder diffraction (NPD) measurements were performed between 5 K and 300 K using the BT-1 High-Resolution Neutron Powder Diffractometer25 with the Cu(311) monochromator at λ = 1.5397(2) Å and an in-pile collimation of 60 min of arc. Neutron vibrational spectroscopy (NVS) measurements were performed at 4 K using the Filter-Analyzer Neutron Spectrometer (FANS)26 with both the Cu(220) and pyrolytic graphite PG(002) monochromators and pre- and post-collimations of 20′ of arc, yielding a full-width-at-half-maximum (fwhm) energy resolution of about 3% of the neutron energy transfer. QENS measurements were performed up to 315 K using two complementary instruments: the Disc Chopper Spectrometer (DCS)27 between 4 K and 315 K using an incident neutron wavelength (λ) of 4.5 Å, 10 Å and 12 Å with respective fwhm resolutions of 67 μeV, 17 μeV and 10.9 μeV and respective maximum attainable elastic scattering vector (Q) values of around 2.62 Å−1, 1.18 Å−1 and 0.98 Å−1; and the High Flux Backscattering Spectrometer (HFBS)28 between 4 K and 315 K [plus up to 350 K during an elastic-scattering fixed-window scan (FWS)] using an incident neutron wavelength of 6.27 Å (2.08 meV) with a fwhm resolution of 0.8 μeV and a maximum attainable Q value of 1.75 Å−1. Instrumental resolution functions were determined from QENS spectra at lower temperatures free of quasielastic scattering, i.e., at 4 K. QENS data were analyzed using the DAVE software package.29
Solid-state density-functional theory (DFT) calculations were performed using the Quantum-Espresso package.30 A cutoff energy of 544 eV and a 2 × 2 × 1 k-point mesh (generated using the Monkhorst–Pack scheme) were used and found to be enough for the total energy to converge within 0.01 meV per atom. Crystal structures were first fully optimized, based on the experimental structures, and are presented in the ESI.† For comparison with the NVS measurements, simulated phonon densities of states (PDOSs) were generated from the DFT-optimized structures using the supercell method (2 × 2 × 1 cell size) with finite displacements (0.02 Å) and were appropriately weighted to take into account the total neutron scattering cross sections of the different elements. Gas phase DFT calculations were done using the B3LYP functional31–34 and the Gaussian 6-31+G* basis set35,36 to calculate the binding energies of the 1st, 2nd and 3rd THF molecules to Mg(BH4)2. The optimized geometries were verified by the absence of imaginary frequencies from the frequency analysis in the harmonic oscillator/rigid-rotor approximation. The frequencies were also used to calculate the enthalpic and entropic contributions to the free energy for binding. All calculations were done using the NWChem software.37
Structural depictions were made using the VESTA (Visualization for Electronic and Structural Analysis) software.38 For all figures, standard uncertainties are commensurate with the observed scatter in the data, if not explicitly designated by vertical error bars.
Results and discussion
Structural behavior and vibrational dynamics of Mg(BH4)2·3THF
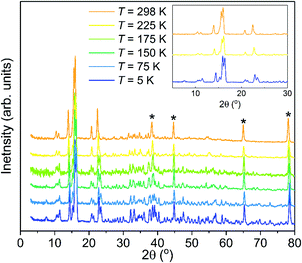
Neutron powder diffraction measurements of the partially deuterated sample, Mg(BH4)2·3TDF, upon heating from 5 K to 298 K indicate a phase transition in the temperature range between 175 and 225 K, as shown in Fig. 1. Prior low-temperature (100 K) and room-temperature (298 K) XRD measurements of Mg(BH4)2·3THF suggested two crystalline forms of this material with triclinic (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )39 and monoclinic (space group C2/c)40 structures, respectively. To confirm these structures, Rietveld refinements of the NPD patterns (at 298 K and 225 K) above and (at 5 K) below this phase transition were performed. The analysis corroborated a lowering of the symmetry upon decreasing the temperature, from monoclinic C2/c to P
)39 and monoclinic (space group C2/c)40 structures, respectively. To confirm these structures, Rietveld refinements of the NPD patterns (at 298 K and 225 K) above and (at 5 K) below this phase transition were performed. The analysis corroborated a lowering of the symmetry upon decreasing the temperature, from monoclinic C2/c to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) via a triclinic distortion from respective α, β, and γ values of 90°, 144.992(4)°, and 90° at 298 K to 102.596(3)°, 103.984(4)°, and 92.239(3)° at 5 K. Fig. S1 in the ESI† presents the model refinements of the NPD data at 298 K, 225 K, and 5 K. Table S1 and supplemental CIF files, also in the ESI,† summarize the structural analysis details. It should be noted that the lattice parameters from ref. 40 were associated with a different unit cell convention than that used in this paper. Converting these parameters to the present convention yield values of a = 12.120 Å, b = 12.646 Å, c = 20.216 Å, and β = 144.96°, which are in good agreement with our values. We note that the slightly smaller lattice constants associated with the present results are consistent with the incorporation of TDF, instead of THF, in our NPD samples. Molecular vibrational amplitudes associated with deuterated molecules are somewhat smaller than their hydrogenated analogues, leading to slightly less space required to accommodate the former molecules compared to that for the latter.
via a triclinic distortion from respective α, β, and γ values of 90°, 144.992(4)°, and 90° at 298 K to 102.596(3)°, 103.984(4)°, and 92.239(3)° at 5 K. Fig. S1 in the ESI† presents the model refinements of the NPD data at 298 K, 225 K, and 5 K. Table S1 and supplemental CIF files, also in the ESI,† summarize the structural analysis details. It should be noted that the lattice parameters from ref. 40 were associated with a different unit cell convention than that used in this paper. Converting these parameters to the present convention yield values of a = 12.120 Å, b = 12.646 Å, c = 20.216 Å, and β = 144.96°, which are in good agreement with our values. We note that the slightly smaller lattice constants associated with the present results are consistent with the incorporation of TDF, instead of THF, in our NPD samples. Molecular vibrational amplitudes associated with deuterated molecules are somewhat smaller than their hydrogenated analogues, leading to slightly less space required to accommodate the former molecules compared to that for the latter.
Fig. 2 shows the molecular and crystal structures of the low- and room-temperature Mg(BH4)2·3TDF phases. It is apparent that the packing of molecules in both crystalline forms takes place in a layered lattice, with interchangeable layers of BH4− anions and TDF rings. The three TDF molecules and two BH4− anions are located around the central Mg2+ cation in a trigonal bipyramidal motif. The BH4− anions are bonded to the Mg2+ cation via double hydrogen bridges. The coordination polyhedron of Mg2+ can be described by a distorted pentagonal-bipyramidal geometry, where the axial vertices are occupied by the O atoms of the two apical TDF rings, while the four bridging H atoms from the BH4− anions and the O atom from the third TDF ring lie mostly in the equatorial plane. The detachment of the apical TDF rings from the BH4− anions is observed from the O–Mg–O angles of 172.1° and 163.6° in the respective P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and C2/c structures, as well as from the slightly longer Mg–O distances to the apical TDF molecules. However, the arrangement of the Mg, O, and two B atoms in the equatorial plane is perfectly coplanar, with low deviations from the ideal angle of 120° in a trigonal bipyramidal coordination geometry. Higher values of the B–Mg–B angle in comparison to both B–Mg–O angles are observed due to a more repulsive force between the negatively charged BH4− anions than between the coordinated TDF ring and BH4− anion. No significant distortion of the TDF rings or BH4− anions has been observed in either crystalline form, with bond lengths and bond angles not being different from the expected values.41 However, the interatomic Mg and B separations of 2.49 Å in P
and C2/c structures, as well as from the slightly longer Mg–O distances to the apical TDF molecules. However, the arrangement of the Mg, O, and two B atoms in the equatorial plane is perfectly coplanar, with low deviations from the ideal angle of 120° in a trigonal bipyramidal coordination geometry. Higher values of the B–Mg–B angle in comparison to both B–Mg–O angles are observed due to a more repulsive force between the negatively charged BH4− anions than between the coordinated TDF ring and BH4− anion. No significant distortion of the TDF rings or BH4− anions has been observed in either crystalline form, with bond lengths and bond angles not being different from the expected values.41 However, the interatomic Mg and B separations of 2.49 Å in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and 2.46 Å in C2/c are slightly greater than 2.41 Å reported for pristine α-Mg(BH4)2.41
and 2.46 Å in C2/c are slightly greater than 2.41 Å reported for pristine α-Mg(BH4)2.41
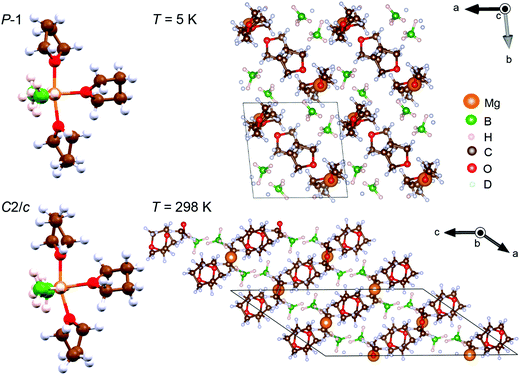 | ||
Fig. 2 Molecular and crystal structures of the low-temperature (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry) and room-temperature (C2/c symmetry) Mg(BH4)2·3TDF phases. symmetry) and room-temperature (C2/c symmetry) Mg(BH4)2·3TDF phases. | ||
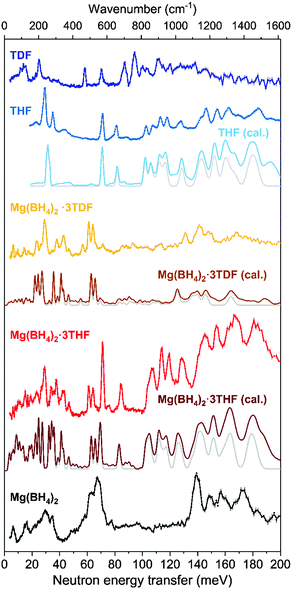
The neutron vibrational spectra for Mg(BH4)2·3THF and Mg(BH4)2·3TDF at 4 K based on FANS measurements are shown in Fig. 3 and compared with the simulated phonon density of states (PDOS) from the DFT-optimized triclinic structure, indicating overall good agreement between experiment and theory. Further information about the character, symmetry, and energies of the different phonon modes contributing to the simulated PDOSs can be found in the ESI.†
Upon comparison of the Mg(BH4)2·3THF NVS spectrum with that of pristine α-Mg(BH4)2, obvious peak splitting in the lower frequency region (<80 meV) is observed. This is mostly due to the coordination of THF rings, which affects the bonding between the Mg atoms and BH4− anions. Based on the structural data, the presence of THF rings causes extension of the interatomic distance between the Mg and B atoms and reduction in the B–Mg–B angle in comparison to the pristine α-Mg(BH4)2.
Direct comparison between NVS spectra of Mg(BH4)2·3THF and Mg(BH4)2·3TDF, as well as the mode identification obtained from the DFT PDOS calculations, can help distinguish the modes dominated by the vibrational displacements of the BH4− anions and those of the THF molecules. This is due to the fact that, while the TDF spectrum by itself is measurable, as can be seen in Fig. 3, its overall contribution to the Mg(BH4)2·3TDF spectrum is very small, thus accentuating the BH4− contributions. Additionally, it should be mentioned that the noticeable shift in peak positions between the crystalline THF and TDF compounds is due to the mass difference between H and D atoms, where heavier D atoms cause peak-shifting to lower energy transfer.
By analyzing the spectra in this way, it can be seen that most peaks observed in the low-energy region from 20 to 65 meV (1 meV ≈ 8.066 cm−1) for Mg(BH4)2·3THF in Fig. 3 correspond to the BH4− librational (torsional) modes.42 Moving to higher energy-transfer values, two sharp features are observed at around 70 and 84 meV, and are attributed to vibrations related to THF ring deformations and CH2 wagging.43 Furthermore, a number of sharp peaks are noticeable in the 100–190 meV spectral region of Mg(BH4)2·3THF, of which eight peaks centered at around 107, 114, 120, 128, 144, 154, 167 and 182 meV are particularly intense. According to group-theory calculations,44,45 BH4− anions have a high tetrahedral (Td) symmetry for which the irreducible representation in the Mulliken notation can be written as Γ = A1 ⊕ E ⊕ 2F2, while THF rings have two-fold rotational (C2) symmetry with the irreducible representation given as Γ = 17A ⊕ 16B. Here, the A and B modes are non-degenerate, while the E modes are doubly degenerate, and the F modes are triply degenerate. Having in mind this notation and comparing the results with the DFT simulations and the experimental spectra of pristine α-Mg(BH4)2, THF, and TDF, the very intense peaks observed in the 100–190 meV region could be resolved as follows: the peaks observed at 144 and 154 meV mostly correspond to the asymmetric bending vibrations of BH4− (F2 symmetry mode), while the peaks at 167 and 183 meV are attributed to the symmetric bending vibrations of BH4− (E symmetry mode). The lower energy peaks at 107, 114, 120, 128, 144 meV are related to the A and B modes of THF, corresponding mostly to stretching vibrations.
Reorientational dynamics of Mg(BH4)2·3THF
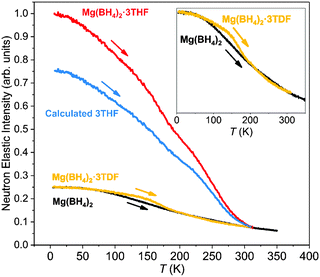
The neutron-elastic-scattering fixed-window scan (FWS) presents a plot of the temperature dependence of the neutron scattering intensity at zero energy transfer. As such, a direct comparison of the FWSs measured from the different compounds provided some insights into the reorientational dynamics of the THF and BH4− groups in these materials. Fig. 4 shows the FWS for Mg(BH4)2·3THF and Mg(BH4)2·3TDF measured on HFBS at Q = 0.87 Å−1 between 4 K and 315 K [limited by the decomposition temperature of Mg(BH4)2·3THF]. The FWS for pristine α-Mg(BH4)2 was measured as a reference in a similar temperature region, from 4 K to 350 K. Again, due to the much lower incoherent neutron scattering cross section of D in comparison to H, the contribution of TDF molecules to the FWS could be neglected (to first order), allowing for all FWSs to be scaled according to their number of H atoms. The FWS of Mg(BH4)2·3THF, with a total of 32 H atoms, was normalized to 1 at the lowest temperature, while FWS plots of Mg(BH4)2·3TDF and α-Mg(BH4)2, with a total of 8 H atoms each, were scaled to 1/4 of the value of Mg(BH4)2·3THF at the lowest measured temperature of 4 K. Assuming that the FWS for Mg(BH4)2·3TDF reflects only the dynamical contributions of the BH4− anions allows the estimation of the dynamical contributions solely from the three THF molecules in Mg(BH4)2·3THF (labeled in Fig. 4 as “Calculated 3THF”) by subtracting the FWS of Mg(BH4)2·3TDF from that of Mg(BH4)2·3THF.Upon heating from 4 K, a fall-off in intensity with increasing temperature occurs for all scans depicted in Fig. 4, reflecting the composite Debye–Waller-type hydrogen vibrational displacements associated with the THF and BH4− groups. Above certain threshold temperatures (at around 230 K for THF and 160 K for BH4− in the adducts) the fall-offs accelerate, signaling that THF and BH4− reorientational jumps are coming into the HFBS resolution window with frequencies beginning to exceed 107–108 s−1. As temperatures further increase, the fall-off in intensity begins to slow again, signaling that the reorientational jump frequencies are now approaching the order of 1010 s−1 and moving out of the HFBS dynamic range window. For Mg(BH4)2·3THF, this seems to occur above around 300 K for THF and 190 K for BH4−.
Comparison of the FWSs from Mg(BH4)2·3TDF and pristine α-Mg(BH4)2, presented in the inset in Fig. 4, shows differences in the slopes of the two curves in the lower-temperature region, up to 200 K, leading to the conclusion that the BH4− anions in Mg(BH4)2·3TDF have lower reorientational mobilities compared to the BH4− anions in Mg(BH4)2 at the same temperature in this region. However, above 200 K, BH4− anions in both compounds behave the same, based on the overlap of the FWS plots. The drastic change of the reorientational mobilities of the BH4− anions in the 200 K temperature region coincides with the triclinic to monoclinic structural phase transition for Mg(BH4)2·3TDF, as explained previously by the NPD experiments. Additionally, the noticeable change in slope above about 175 K for the FWS component intensity for THF in Mg(BH4)2·3THF likely marks a change in the Debye–Waller factor for THF due to this same phase transition.
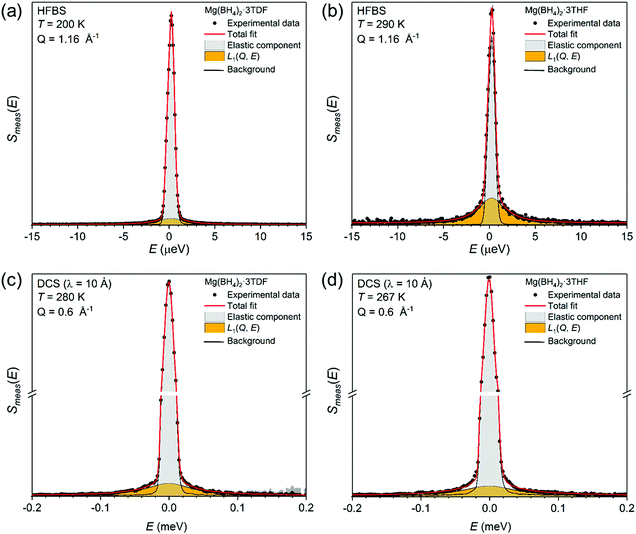
Complementary QENS measurements on the DCS and HFBS instruments were undertaken to gain further insights concerning the reorientational behavior of both THF and BH4− groups. Fig. 5 presents two exemplary QENS spectra for Mg(BH4)2·3TDF measured at (a) 280 K and (c) 200 K, and two spectra for Mg(BH4)2·3THF measured at (b) 267 K and (d) 290 K, on two instruments at different resolutions [(a) and (b) on HFBS with 0.8 μeV resolution; and (c) and (d) on DCS with 16.9 μeV resolution]. All QENS spectra were adequately fit with a delta function and a single Lorentzian component, both convoluted with the resolution function, above a flat background. For all temperatures, the width of the Lorentzian function, Γ, associated with each component group was found to be Q-independent over the measured Q-range (Fig. S2 in the ESI†), consistent with simple localized hydrogen jump motions46 for both THF and BH4− groups, as opposed to long-range diffusive motions.
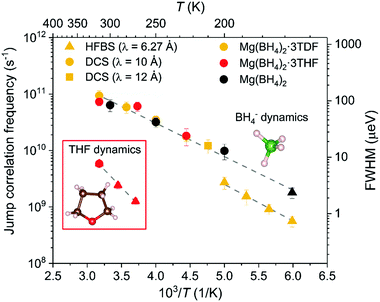
Fig. 6 conveys the Arrhenius-like dependencies between 160 K and 320 K of the fundamental jump correlation frequency τ1−1 = Γ/(2ℏ) vs. T−1 for Mg(BH4)2·3TDF, Mg(BH4)2·3THF, and pristine α-Mg(BH4)2.
Similarities in the BH4− reorientational jumps for Mg(BH4)2·3TDF, Mg(BH4)2·3THF and unsolvated Mg(BH4)2 lead to the conclusion that the mobilities of the BH4− anions are not noticeably affected by the presence of THF rings in the higher-temperature region from 200 K to 320 K, displaying jump correlation frequencies of the order of 1010 to 1011 s−1, in agreement with those previously reported in Mg(BH4)2.47 Further lowering the temperature, from 200 K to 160 K, leads to a sudden 75% drop in the BH4− jump frequencies, compared to the trending values above 200 K. This decrease is explained by the phase transition of Mg(BH4)2·3TDF from the monoclinic to the triclinic structure with a smaller unit cell size, presumably leading to enhanced steric effects and thus smaller jump frequencies. This is further portrayed by the calculated activation energies for reorientations, Ea, (derived from the slope (−Ea/kB) of the linear fit to ln(τi1−1) vs. T−1), where a higher barrier is observed in the triclinic structure, i.e., Ea = 137(3) meV for T ≤ 200 K, compared to the monoclinic structure with Ea = 113(3) meV for T > 200 K.
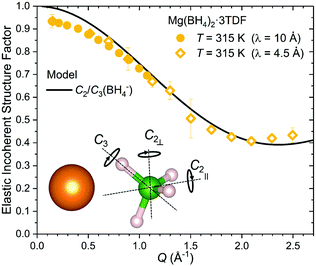
The nature of the reorientational mechanism of the BH4− anions in Mg(BH4)2·3TDF and Mg(BH4)2·3THF was determined by the calculated Elastic Incoherent Structure Factor (EISF) over the large Q-range accessible with DCS and using 4.5 Å incident wavelength neutrons. Fig. 7 shows the experimentally derived EISF data at 315 K due solely to the BH4− anions in Mg(BH4)2·3TDF. Based on the invariant Lorentzian widths with Q, two possible localized hydrogen motions are expected in this system, rotations around any one of the three two-fold (C2) or four three-fold (C3) molecular symmetry axes of the BH4− units. For BH4− rotations around a C2-axis, the tetrahedral anions have two equal equilibrium orientations, while for BH4− rotations around a C3-axis, the tetrahedral anions have three equal equilibrium orientations, while one hydrogen atom remains immobile. In both cases, the final expression for the EISF is identical and given by:46
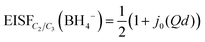 | (1) |
Another type of dynamics could be identified from Fig. 6, observed from the HFBS measurements of Mg(BH4)2·3THF. Order-of-magnitude-slower jump correlation frequencies, in the range of 109 s−1 to 1010 s−1, when compared to BH4− anions at the same temperature, could be attributed to the localized hydrogen motion associated with the THF rings. This is further confirmed by investigating possible reorientational mechanisms of the THF molecules in Mg(BH4)2·3THF and comparing with the experimentally obtained EISF.
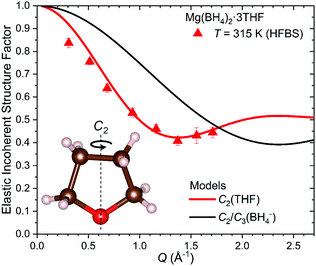
Due to the C2 symmetry of the THF ring and the Q-independent Lorentzian widths obtained from the QENS fitting of Mg(BH4)2·3THF measured on the HFBS instrument, the only possible localized motion of H atoms involves two-fold jumps around the anchored C2-axis, which passes through the O atom and the middle of the opposite C–C bond within the THF ring [C2(THF) model]. Such THF reorientations involve much larger moments of inertia than for BH4− reorientations, since the former also require the jump displacements of the C atoms. In this case, the EISF is given as:
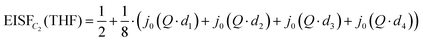 | (2) |
Considering that the BH4− anions have an active dynamical behavior in the measured temperature range, the EISF associated with the BH4− anions should also be included in the calculation of the total EISF for Mg(BH4)2·3THF. The total EISF is calculated by including the weighting factors based on the number of H atoms in front of the EISF of each chemical group. Considering that there are a total of 32 H atoms, with 24 present in the three THF rings, and 8 present in the two BH4− anions, the total EISF is given as:
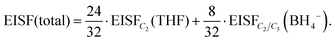 | (3) |
In the HFBS data measured, the elastic peak contribution is actually the sum of the elastic peak intensities due to both THF and BH4− reorientations, whereas the fitted quasielastic contribution is due only to the slower THF reorientations. The much faster BH4− reorientations yield quasielastic scattering that is an order of magnitude too broad to be observed by HFBS and resides as broad background scattering buried under the flat baseline. In order to extract the EISF solely due to the THF molecules, it is necessary to determine the amount of THF elastic scattering intensity by calculating and subtracting the BH4− elastic scattering intensity from the total elastic scattering measured. This can be done with the aid of eqn (3) and the fact that the EISF behavior for the BH4− anions is known. The mathematical details are outlined in the ESI.† The resulting experimental EISF for THF reorientations in Mg(BH4)2·3THF at 315 K is shown in Fig. 8 and is in good agreement with the theoretically predicted EISF from eqn (2) for two-fold THF jumps. The very different Q-dependent behavior of the comparative EISF plot for BH4− reorientations in Fig. 8 provides further corroboration that we are indeed observing two-fold THF reorientations in the HFBS data.
Effect of THF concentration on Mg(BH4)2·xTHF properties
The structural results show that THF is bound to the Mg2+ cation and there is little direct interaction between THF and the BH4− anion at the investigated temperatures. With three THF molecules bound to each Mg2+ cation, it is tempting to predict that the interactions between the Mg2+ cation and the BH4− anion will be weaker in THF-containing compounds. It is therefore surprising that no measurable change was observed in the rotational dynamics of the BH4− anion between the unsolvated α-Mg(BH4)2 and the solvated Mg(BH4)2·3THF adduct.One possible explanation for this is the asymmetry in the Mg2+–BH4− alignment that arises in the THF adducts. In unsolvated α-Mg(BH4)2, the BH4− anions sit approximately equidistant between two Mg2+ cations, with distances of around 2.41 Å and are oriented such that one of their C2 anion symmetry axes is effectively aligned with the Mg–B–Mg bond direction. In Mg(BH4)2·3THF, the Mg–B distance is slightly larger, 2.46–2.49 Å, but each BH4− anion only interacts with one Mg2+ cation. The next-nearest Mg2+ is more than 6 Å away. One would expect that this decreased Mg2+–BH4− interaction, arising from the competing Mg+–THF coordination and evidenced by a larger Mg–B distance would lead to an enhanced BH4− orientational mobility compared to that in Mg(BH4)2. Yet, in the Mg(BH4)2·3THF crystal structure, the Mg–B bond direction is not as well aligned with the corresponding BH4−C2 symmetry axis (see Fig. 7) as in the unsolvated compound. Because of this misalignment, one can expect more steric interference with the adjacent Mg2+ cation while performing the BH4− two-fold reorientation. The counterpositioning of these two opposing effects on BH4− mobility may indeed result in similar BH4− reorientational dynamics for Mg(BH4)2 and Mg(BH4)2·3THF as observed. This is also corroborated by the fact that the BH4− librational energy around this easy C2-axis in Mg(BH4)2·3THF is located between 25 meV and 28 meV by the DFT PDOS calculations and NVS experiments, which is very similar to the calculated and observed BH4− librational energy around the Mg–B–Mg axes in unsolvated Mg(BH4)2 phases.42 Hence, it is not unreasonable to expect the corresponding rotational potential wells and dynamics to also be similar.
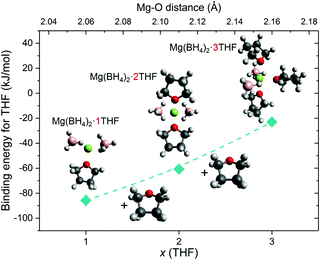
In addition to the observed BH4− mobility, one can speculate that a relatively weak Mg2+–THF interaction in Mg(BH4)2·3THF is one key factor for enabling the THF rings to be orientationally mobile, undergoing 180° reorientational jumps around their C2 molecular symmetry axis. In order to explore this proposition further, molecular DFT calculations and additional QENS and NVS experiments were conducted for samples with a lower amount of THF present in the adduct. DFT calculations for Mg(BH4)2·THF, Mg(BH4)2·2THF and Mg(BH4)2·3THF isolated clusters showed a slight lengthening of the Mg–O distance with each additional THF molecule that coordinates to the Mg2+ cation. The calculated Mg–O distance for the Mg(BH4)2·THF adduct is 2.06 Å, whereas addition of a second THF results in a symmetric structure with two Mg–O distances of 2.11 Å. Adding the third THF molecule results in further distancing of the THF molecules from Mg2+ and bond distances of 2.15–2.17 Å. Fig. 9 presents the zero-point corrected electronic energies calculated based on the gas-phase reference models for all compounds, which correspond more closely to low-temperature conditions. The calculated energies show that the first THF molecule binds most strongly with −85.7 kJ mol−1, the second one binds with −60.7 kJ mol−1, and the third one binds with −23.0 kJ mol−1 (Table S2 in the ESI†). Absolute energies and geometries of the structures are provided in Tables S3 and S4 in the ESI.† We expect that the simplicity of the molecular model and its treatment in the gas phase introduce entropic inaccuracies, and as such, result in positive binding free energies. However, because the DFT treatment is consistent for each addition reaction, we can reliably estimate the relative weakening in the binding energy for each subsequent THF molecule. This observation suggests that the reorientational dynamics of the THF rings may be more hindered in a material with a lower amount of solvent present. Indeed, comparative QENS measurements on the samples with the substoichiometric compositional ratio 2Mg(BH4)2·THF and 2Mg(BH4)2·TDF have shown no observable reorientational dynamics of the THF rings within the resolution window of the spectrometer (Fig. S4 in the ESI†), which is in line with a stronger binding energy of the THF rings to the Mg2+ cations. Additionally, no noticeable changes in the H dynamics of the BH4− anions are observed in this case either (Fig. S5 in the ESI†), leading to the conclusion that the THF solvent does not seem to appreciably affect the BH4− dynamical behavior in Mg(BH4)2·xTHF adducts. (Comparative NVS spectra of these substoichiometric compounds are provided in Fig. S6 in the ESI.†)
The presence of a much stronger interaction between the THF and the Mg2+ cation for lower THF/Mg(BH4)2 stoichiometric ratios implies that using a more THF-deficient Mg(BH4)2·xTHF adduct will reduce the amount of THF that might be released from the adduct during the concomitant thermal release of hydrogen. Indeed, thermal desorption measurements showed that such adducts with lower THF/Mg(BH4)2 ratios required higher temperatures to liberate THF. Hence, with respect to potential hydrogen-storage applications, the beneficial properties of the THF solvent can be retained over a greater temperature range while reducing the concentration of any unwanted impurity in the released hydrogen.
Conclusions
Various neutron scattering experiments, including NPD, NVS, FWS, and QENS, as well as molecular DFT calculations, were employed to gain deeper insights into the structural, vibrational, and dynamical properties of Mg(BH4)2·3THF. Structural analysis has confirmed a lowering of the symmetry upon cooling, from monoclinic C2/c to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) via a triclinic distortion, with the phase transition occurring around 200 K. Vibrational properties are strongly influenced by the THF environment. In particular, splitting in spectral features is observed and explained by the lowering of the overall symmetry. Interestingly, for the monoclinic structure, the orientational mobilities of the BH4− anions obtained from QENS are not particularly sensitive to the presence of THF and compare well with the mobilities of BH4− anions in unsolvated Mg(BH4)2. In contrast, a decrease in the BH4− jump frequencies is observed in the triclinic low-temperature structure and correlated with the enhanced steric effects presumably due to the smaller unit cell volume. Uniaxial jump reorientations of the BH4− anions around a two-fold (C2, 180° jumps) axis are observed over the whole temperature range. The THF rings are also shown to be dynamically active, with orientational mobilities about an order of magnitude slower than for the BH4− anions, and with a reorientational mechanism also corresponding to uniaxial two-fold 180° jumps around the THF C2 symmetry axis. In contrast, no noticeable reorientations of the THF rings are observed in the case of a more THF-deficient 2Mg(BH4)2·THF adduct. This may be, at least in part, a consequence of a relatively stronger Mg2+–THF bonding interaction, as the Mg2+ cation likely coordinates with only one THF molecule in this adduct. This is unlike THF-rich Mg(BH4)2·3THF, where each Mg2+ cation coordinates with three THF molecules. Indeed, DFT calculations show a decrease in the binding energy with each additional THF coordinated to the Mg2+ cation.
via a triclinic distortion, with the phase transition occurring around 200 K. Vibrational properties are strongly influenced by the THF environment. In particular, splitting in spectral features is observed and explained by the lowering of the overall symmetry. Interestingly, for the monoclinic structure, the orientational mobilities of the BH4− anions obtained from QENS are not particularly sensitive to the presence of THF and compare well with the mobilities of BH4− anions in unsolvated Mg(BH4)2. In contrast, a decrease in the BH4− jump frequencies is observed in the triclinic low-temperature structure and correlated with the enhanced steric effects presumably due to the smaller unit cell volume. Uniaxial jump reorientations of the BH4− anions around a two-fold (C2, 180° jumps) axis are observed over the whole temperature range. The THF rings are also shown to be dynamically active, with orientational mobilities about an order of magnitude slower than for the BH4− anions, and with a reorientational mechanism also corresponding to uniaxial two-fold 180° jumps around the THF C2 symmetry axis. In contrast, no noticeable reorientations of the THF rings are observed in the case of a more THF-deficient 2Mg(BH4)2·THF adduct. This may be, at least in part, a consequence of a relatively stronger Mg2+–THF bonding interaction, as the Mg2+ cation likely coordinates with only one THF molecule in this adduct. This is unlike THF-rich Mg(BH4)2·3THF, where each Mg2+ cation coordinates with three THF molecules. Indeed, DFT calculations show a decrease in the binding energy with each additional THF coordinated to the Mg2+ cation.
Although the physicochemical behavior of this THF-solvated Mg(BH4)2 adduct determined from this combined experimental and computational study is of general fundamental interest, the observed and calculated interplay between Mg2+ cations, BH4− anions, and THF adduct molecules also has likely technological relevance toward understanding better the role of THF for improving the hydrogen desorption/absorption cycling properties of Mg(BH4)2. The dynamical results for different THF/Mg(BH4)2 stoichiometric ratios suggest little direct interaction, in general, between the THF molecules and the BH4− anions, whereas the THF–Mg2+ interaction is strongly ratio-dependent, with stronger interactions occurring for the lower THF/Mg(BH4)2 ratios. Hence, we would propose that using lower THF/Mg(BH4)2 ratios is beneficial to (i) preventing weakly bound THF from coming free from the Mg2+ cation and (ii) disrupting the stability of the crystalline phase leading to a lower melting point and enhanced kinetics.
Authors’ contributions
M. D., T. A. and T. J. U. conceived and planned the experiments. M. D. and T. J. U. carried out the experiments. W. Z., I. N. and B. G. planned and carried out the DFT calculations. M. C. contributed to sample preparation. M. D., M. B., H. W., T. A., B. G., T. G., C. J. and T. J. U. contributed to the interpretation of the results. M. D. took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript.Legal disclamer
The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
M. D. gratefully acknowledges support from the US DOE Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under Contract No. DE-AC36-08GO28308. The authors gratefully acknowledge support from the Hydrogen Materials – Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network under the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office. Pacific Northwest National Laboratory is a multi-program national laboratory operated by Battelle for the U.S. Department of Energy under Contract DE-AC05-76RL01830.References
- C. Liu, F. Li, L.-P. Ma and H.-M. Cheng, Adv. Mater., 2010, 22, E28–62 CrossRef CAS PubMed.
- N. P. Stadie, J. J. Vajo, R. W. Cumberland, A. A. Wilson, C. C. Ahn and B. Fultz, Langmuir, 2012, 28, 10057–10063 CrossRef CAS PubMed.
- A. F. Gross, J. J. Vajo, S. L. Van Atta and G. L. Olson, J. Phys. Chem. C, 2008, 112, 5651–5657 CrossRef CAS.
- D. Teichmann, W. Arlt, P. Wasserscheid and R. Freymann, Energy Environ. Sci., 2011, 4, 2767–2773 RSC.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O’Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS PubMed.
- S. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- K. Chłopek, C. Frommen, A. Léon, O. Zabara and M. Fichtner, J. Mater. Chem., 2007, 17, 3496–3503 RSC.
- Y. Nakamori, K. Miwa, A. Ninomiya, H. Li, N. Ohba, S. Towata, A. Züttel and S. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045126 CrossRef.
- N. Hanada, K. Chłopek, C. Frommen, W. Lohstroh and M. Fichtner, J. Mater. Chem., 2008, 18, 2611–2614 RSC.
- G. L. Soloveichik, Y. Gao, J. Rijssenbeek, M. Andrus, S. Kniajanski, R. C. Bowman, S.-J. Hwang and J.-C. Zhao, Int. J. Hydrogen Energy, 2009, 34, 916–928 CrossRef CAS.
- G. Severa, E. Rönnebro and C. M. Jensen, Chem. Commun., 2010, 46, 421–423 RSC.
- H.-W. Li, K. Kikuchi, Y. Nakamori, K. Miwa, S. Towata and S. Orimo, Scr. Mater., 2007, 57, 679–682 CrossRef CAS.
- E. G. Bardají, N. Hanada, O. Zabara and M. Fichtner, Int. J. Hydrogen Energy, 2011, 36, 12313–12318 CrossRef.
- R. J. Newhouse, V. Stavila, S.-J. Hwang, L. E. Klebanoff and J. Z. Zhang, J. Phys. Chem. C, 2010, 114, 5224–5232 CrossRef CAS.
- I. Saldan, C. Frommen, I. Llamas-Jansa, G. N. Kalantzopoulos, S. Hino, B. Arstad, R. H. Heyn, O. Zavorotynska, S. Deledda, M. H. Sørby, H. Fjellvåg and B. C. Hauback, Int. J. Hydrog, Energy, 2015, 40, 12286–12293 CAS.
- H. Hagemann, V. D’Anna, J.-P. Rapin, R. Černý, Y. Filinchuk, K. C. Kim, D. S. Sholl and S. F. Parker, J. Alloys Compd., 2011, 509(Suppl. 2), S688–S690 CrossRef CAS.
- E. G. Bardají, Z. Zhao-Karger, N. Boucharat, A. Nale, M. J. van Setten, W. Lohstroh, E. Röhm, M. Catti and M. Fichtner, J. Phys. Chem. C, 2011, 115, 6095–6101 CrossRef.
- A. Nale, M. Catti, E. G. Bardají and M. Fichtner, Int. J. Hydrogen Energy, 2011, 36, 13676–13682 CrossRef CAS.
- J. Chen, Y. S. Chua, H. Wu, Z. Xiong, T. He, W. Zhou, X. Ju, M. Yang, G. Wu and P. Chen, Int. J. Hydrogen Energy, 2015, 40, 412–419 CrossRef CAS.
- Y. Yang, Y. Liu, Y. Zhang, Y. Li, M. Gao and H. Pan, J. Alloys Compd., 2014, 585, 674–680 CrossRef CAS.
- S. Zhao, B. Xu, N. Sun, Z. Sun, Y. Zeng and L. Meng, Int. J. Hydrogen Energy, 2015, 40, 8721–8731 CrossRef CAS.
- G. Soloveichik, J.-H. Her, P. W. Stephens, Y. Gao, J. Rijssenbeek, M. Andrus and J.-C. Zhao, Inorg. Chem., 2008, 47, 4290–4298 CrossRef CAS PubMed.
- M. Chong, T. Autrey, C. Jensen, M. Chong, T. Autrey and C. M. Jensen, Inorganics, 2017, 5, 89 CrossRef.
- The Mention of All Commercial Suppliers in This Paper Is for Clarity. This Does Not Imply the Recommendation or Endorsement of These Suppliers by NIST.
- J. K. Stalick; E. Prince; A. Santoro; I. G. Schroder and J. J. Rush, Materials Science Applications of the New National Institute of Standards and Technology Powder Diffractometer, in Neutron Scattering in Materials Science II, ed. D. A. Neumann, T. P. Russell, B. J. Wuensch, Materials Research Society, Pittsburgh, 1995, vol. 376, pp. 101–106 Search PubMed.
- T. J. Udovic, C. M. Brown, J. B. Leão, P. C. Brand, R. D. Jiggetts, R. Zeitoun, T. A. Pierce, I. Peral, J. R. D. Copley, Q. Huang, D. A. Neumann and R. J. Fields, The Design of a Bismuth-Based Auxiliary Filter for the Removal of Spurious Background Scattering Associated with Filter-Analyzer Neutron Spectrometers, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 588, 406–413 CrossRef CAS.
- J. R. D. Copley and J. C. Cook, The Disk Chopper Spectrometer at NIST: A New Instrument for Quasielastic Neutron Scattering Studies, Chem. Phys., 2003, 292, 477–485 CrossRef CAS.
- A. Meyer, R. M. Dimeo, P. M. Gehring and D. A. Neumann, The High Flux Backscattering Spectrometer at the NIST Center for Neutron Research, Rev. Sci. Instrum., 2003, 74, 2759–2777 CrossRef CAS.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. Visseaux, M. Terrier, A. Mortreux and P. Roussel, Eur. J. Inorg. Chem., 2010, 2867–2876 CrossRef CAS.
- E. B. Lobkovskii, L. V. Titov, S. B. Psikha, M. Y. Antipin and Y. T. Struchkov, J. Struct. Chem., 1983, 23, 644–646 CrossRef.
- Y. Filinchuk, R. Černý and H. Hagemann, Chem. Mater., 2009, 21, 925–933 CrossRef CAS.
- M. Dimitrievska, J. L. White, W. Zhou, V. Stavila, L. E. Klebanoff and T. J. Udovic, Phys. Chem. Chem. Phys., 2016, 18, 25546–25552 RSC.
- B. Cadioli, E. Gallinella, C. Coulombeau, H. Jobic and G. Berthier, J. Phys. Chem., 1993, 97, 7844–7856 CrossRef CAS.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. – Cryst. Mater., 2009, 221, 15–27 Search PubMed.
- M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef PubMed.
- M. Bee, Quasielastic Neutron Scattering, Principles and Applications in Solid State Chemistry, Biology and Materials Science, CRC Press, Bristol, England, Philadelphia, 1988 Search PubMed.
- D. Blanchard, J. B. Maronsson, M. D. Riktor, J. Kheres, D. Sveinbjörnsson, E. Gil Bardají, A. Léon, F. Juranyi, J. Wuttke, K. Lefmann, B. C. Hauback, M. Fichtner and T. Vegge, J. Phys. Chem. C, 2012, 116, 2013–2023 CrossRef CAS.
- A. V. Skripov, A. V. Soloninin, O. A. Babanova, H. Hagemann and Y. Filinchuk, J. Phys. Chem. C, 2010, 114, 12370–12374 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1963436 and 1963437. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cp03311d |
| This journal is © the Owner Societies 2020 |