The shift in urea orientation at protein surfaces at low pH is compatible with a direct mechanism of protein denaturation†
Ivan Pires
de Oliveira
 ab and
Leandro
Martínez
ab and
Leandro
Martínez
 *a
*a
aInstitute of Chemistry and Center for Computing in Engineering & Science, University of Campinas, Campinas, SP 13083-970, Brazil. E-mail: leandro@iqm.unicamp.br
bDepartment of Pharmacology, Institute of Biomedical Sciences, University of São Paulo, São Paulo, Brazil
First published on 2nd December 2019
Abstract
Surface-specific spectroscopic data has shown that urea undergoes a shift in orientation at protein surfaces in acidic media. Since urea denatures proteins at a wide range of pHs, the variable chemical nature of protein–urea interactions has been used to support an indirect mechanism of urea-induced denaturation. Here, we use molecular dynamics simulations, minimum-distance distribution functions (MDDFs), and hydrogen-bond analysis, to characterize the interactions of urea with proteins at neutral and low pH, as defined by the protonation state of acidic residues. We obtain the expected preferential solvation by urea and dehydration, consistently with urea-induced denaturation, while the MDDFs allow for a solvent-shell perspective of protein–urea interactions. The distribution functions are decomposed into atomic contributions to show that there is indeed a shift in the orientation of urea molecules in the vicinity of acidic side-chains, as shown by the experimental spectroscopic data. However, this effect is local, and the interactions of urea with the other side chains and with the protein backbone are essentially unaffected at low pH. Therefore, hydrophobic solvation and urea–backbone hydrogen bonds can play a role in a direct mechanism of urea-induced protein denaturation without contradicting the observed variations in the chemical nature of protein–urea interactions as a function of the acidity of the solution.
Introduction
The balance of protein–protein and protein–solvent interactions determines the most stable protein conformations according to the equilibrium of the folding reaction.1,2 Thus, the stability of the protein folded states is directly related to the solvation structures.3 The folding equilibrium depends on the composition of the solution in which the protein is embedded. For instance, the presence of cosolvent stabilizers (polyols, trimethylamine N-oxide, TMAO) or denaturing agents (urea, guanidinium chloride), affect the free energy of protein folding.4–6One of the most widely studied protein denaturing agents is urea.7 The denaturing effect of urea is currently understood in terms of the direct substitutions of protein–protein bonds with protein–urea interactions, both at residue side-chains and at the backbone.8–10 Still, many complementary explanations for the denaturant effect of urea involving indirect effects on protein hydration have been provided.11 Urea promotes the dehydration of most (but not all) proteins,12 favoring structures with greater surface area, which are characteristic of denatured states.13,14 Further studies suggested that the interactions of urea with the protein backbone are fundamental for the denaturing effect,8,15–18 while others have suggested that the solvation of non-polar side chains by urea is the key driving force for stabilizing the denatured states.14,19,20
The most accepted view of urea action involves direct interactions with the protein.21 However, the experimental characterization of these interactions using surface-specific spectroscopic methods has been used to support an indirect mechanism of protein denaturation.16,22,23 In one important study, Cremer and co-workers24,25 used vibrational-sum spectroscopy to probe the orientation of urea molecules at the surface of proteins. They found that the orientation of the urea molecules is dependent on the absolute charge of the surface, thus on the pH of the solution. At high pH (∼9), spectroscopic data suggest that urea molecules are oriented with NH groups pointing towards the surface, and at low pH (∼3) the urea carbonyl faces the protein instead. This change in orientation should perturb the hydrogen bonding between the protein, urea, and the vicinal water structure.24 Since urea denatures proteins both at high and low pH, and since the structural nature of urea–protein interactions appeared to be highly dependent on the pH, they suggest that the mechanism of protein denaturation by urea should be indirect. In other words, it is difficult to envision a direct-interaction mechanism explaining the denaturing role of urea in a wide range of pHs if the molecular interactions are structurally different at each protein protonation state.24 Bakker and co-workers23 extended these results to show that the orientation of urea at the protein surface follows the orientation of the water molecules, while the orientation of the amide groups of the protein backbone remains unaffected. They also suggest that urea is mostly surrounded by water, also supporting an indirect mechanism for the denaturing effect. Therefore, these experiments challenge the current consensual view of the urea-induced denaturation mechanism.
Molecular dynamics (MD) simulations allow the detailed study of protein–solvent interactions by means of distribution functions. Kirkwood–Buff (KB) integrals26–28 connect the distribution functions with experimental solvation data, more precisely with preferential interaction parameters.8,28–34 Due to the structural complexity of the proteins, radial distribution function (RDFs or g(r)) are not adequate to obtain a detailed picture of protein solvation at a molecular level. Thus, we have been exploring the use of distribution functions computed from the minimum-distance between solute and solvent atoms, the MDDFs (or gmd(r)).29,35 The MDDFs are similar to radial distribution functions, but the molecular counting is performed for each smallest distance between any atoms of the solute and solvent molecules (see Methods). This definition is most adequate for non-spherical molecules and retains the same thermodynamic interpretation of the RDFs,29 while allowing an intuitive characterization of the solvation shell of the solute. Martínez and Shimizu29 have recently shown that these distribution functions can be used, with appropriate normalization, to compute KB integrals, even if the solute and solvent are structurally complex. In particular, it was shown that osmolytes which are in overall excluded from the protein can nevertheless display specific interactions and density augmentation at the protein surface, without contradicting the experimental preferential interaction parameters.29 The density augmentation of urea at the protein solvation shell has been also confirmed in these studies,29,35 and showed a correlation with hydrogen-bonding interactions with the protein backbone and hydrophobic side-chains.22,35,36 Moreover, the decomposition of the MDDFs into residue-type contributions revealed that urea interacts strongly with charged residues of the protein, particularly with aspartate and glutamate acidic side-chains.
In this work, we explore the structure and thermodynamics of urea–protein interactions as a function of the protonation state of acidic residues using MD simulations and minimum-distance distribution functions. We confirm that there is a shift in the orientation of urea molecules with the protonation of the acidic side chains, as observed experimentally.23,24 Nevertheless, this reorientation is local and interactions of urea with the protein backbone and other side-chains are not affected. Therefore, a general mechanism of protein denaturation by urea through direct urea–protein interactions is possible and consistent with the vibrational-sum spectroscopic experimental data.
Methods
General formalism
Let us consider a ternary solution containing the protein (species p), water (species w) and a cosolvent (species c). The protein is considered to be at infinite dilution, and the molar concentrations of water and the cosolvent are ρw and ρc, respectively. Here, the cosolvent is urea. The distribution of the cosolvent around the protein can be described by the distance-dependence of the ensemble average number density nc(r) of cosolvent molecules relative to the density of a random distribution, nc*(r), | (1) |
The KB integral associated with the cosolvent can be defined, in general, by
 | (2) |
 . For a minimum-distance count, the equality ρc = nc*(r) only holds for large r, and S(r) is dependent on the shape of the solute.29 The practical calculation of the Gpc consists of the counting of solvent molecules within a sufficiently large distance R, above which protein–solvent interactions can be disconsidered for practical purposes. Thus, eqn (2) reduces to
. For a minimum-distance count, the equality ρc = nc*(r) only holds for large r, and S(r) is dependent on the shape of the solute.29 The practical calculation of the Gpc consists of the counting of solvent molecules within a sufficiently large distance R, above which protein–solvent interactions can be disconsidered for practical purposes. Thus, eqn (2) reduces to | (3) |
We define the “protein domain” as the volume around the solute where protein–solvent interactions cannot be neglected (thus, where r < R). The KB integrals as defined in eqn (2) and (3) can be interpreted as the excess volume occupied by the cosolvent in the protein domain, relative to a random distribution.45–47 A positive KB integral indicates an accumulation of solvent molecules in the protein domain. In contrast, if the KB integral is negative, the solvent is effectively excluded. One or other result is dependent on the thermodynamics of solute–solvent and solvent–solvent interactions.
The differences between KB integrals indicate which solvent component is preferentially found in the protein domain. The preferential solvation parameter for the cosolvent can be obtained with, for example,28,33,46,48
| Γpc(R) ≈ ρc[Gpc(R) − Gpw(R)] | (4) |
| Γpw(R) ≈ ρw[Gpw(R) − Gpc(R)]. | (5) |
Rigorously, the denaturing or stabilizing effect of a cosolvent depends on the relative stability of its interactions with the protein in the native versus denatured states. However, it is generally possible to interpret the role of the cosolvent on the stability of the protein from the analysis of its interactions with the native state only, because denaturing agents are found interact favorably with hydrophobic residues and with the protein backbone, and these interactions are only magnified in the denatured states. Alternatively, stabilizers of the protein structure tend to be excluded from the protein surface, implying a large relative affinity to water, an effect that is also magnified when the hydrophobic core of the protein is exposed. Thus, in most cases, cosolvents that accumulate on the vicinity of the protein do it even further when the surface of the protein increases by denaturation, and cosolvents that are excluded from the protein surface are even further excluded following denaturation. The determination of the preferential binding coefficient in the native state is, then, sufficient for the understanding of the general stabilizing or destabilizing effects of the cosolvent on the protein structure. This is in general important, because the native states are well characterized, while denatured states are poorly defined in many cases and, in particular, very hard to probe by molecular modeling or simulations.
Molecular dynamics simulations
Molecular Dynamics (MD) simulations were performed for the enzyme Burkholderia cepacia lipase (BCL), PDB ID: 1YS154 with the complexed ligand, hexylphosphonic acid (R)-2-methyl-3-phenylpropyl ester, removed from the initial crystallographic structure. This enzyme has three domains: U1 (residues 118–166), U2 (residues 215–261) and C (1–117; 167–214; 262–320) shown in Fig. 1.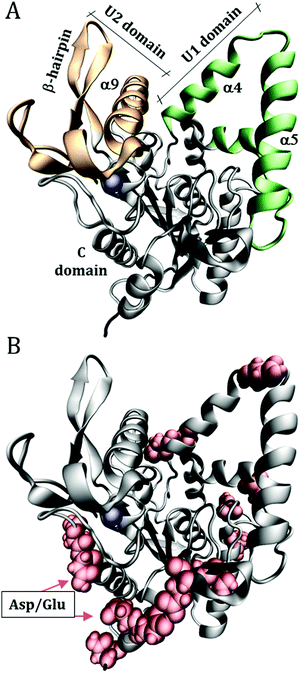 | ||
| Fig. 1 Structure of Burkholderia cepacia lipase (PDB ID: 1YS1), showing (A) the U1 and U2 domains that define the catalytic groove. (B) Surface acidic aspartic and glutamic residues, which were protonated to emulate the solution at low pH. The blue sphere is a calcium ion. | ||
The initial configurations were built using Packmol,55,56 containing the protein, water, urea, and Na+ and Cl− ions to neutralize the net protein charge. 10 systems were constructed as detailed in Table 1. Only the superficial aspartic (Asp) and glutamic (Glu) acid residues were protonated, specifically: Asp2; Asp21; Glu28; Glu35; Asp36; Asp56; Glu63; Asp102; Glu118; Asp121; Asp130; Asp159; Asp288; Glu302; Asp303, as shown in Fig. 1B. The pKas of Asp and Glu residues were estimated with the PropKa tool of VMD to be ∼4 and ∼5 for superficial Asp and Glu residues, respectively.57,58 Therefore, at pH ∼ 3 most of the side chains are expected to be protonated. As we will show, the effect of the protonation of the side chain is a local one, thus the possible incorrect definition of the most probable protonation state of some side-chain does not affect the conclusions of this work, and the use of rigorous constant pH simulations59,60 is not necessary here.
| System | Acid residue protonation | Notation | Average cubic box side length (Å) | Number of molecules/concentration (mol L−1) | |
|---|---|---|---|---|---|
| Water | Urea | ||||
| Abbreviations: P: protein, W: water, U: urea; d: deprotonated acid residues, p: protonated acidic residues. | |||||
| 1 | Deprotonated | PW_d | 86.95 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800/56.12 800/56.12 |
0 |
| 2 | PWU1_d | 88.30 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800/53.63 800/53.63 |
400/0.97 | |
| 3 | PWU3_d | 87.54 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130/48.27 130/48.27 |
1200/3.07 | |
| 4 | PWU6_d | 86.27 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130/39.46 130/39.46 |
2400/6.52 | |
| 5 | PWU12_d | 84.52 | 8800/26.10 | 4000/11.80 | |
| 6 | Protonated | PW_p | 87.03 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800/56.10 800/56.10 |
0 |
| 7 | PWU1_p | 88.34 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800/53.62 800/53.62 |
400/0.97 | |
| 8 | PWU3_p | 87.55 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130/48.31 130/48.31 |
1200/3.04 | |
| 9 | PWU6_p | 86.27 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130/39.49 130/39.49 |
2400/6.50 | |
| 10 | PWU12_p | 84.57 | 8800/26.11 | 4000/11.79 | |
Simulations were performed using NAMD 2.1261,62 and figures and visualizations were performed using VMD.57 The systems were equilibrated as follows: (a) the solvent was relaxed by performing 1000 steps of Conjugate-Gradient (CG) minimization followed by 200 ps of MD simulations, with all the protein atoms fixed; (b) keeping only the Cα atoms of the protein fixed, 500 CG minimization steps were performed, followed by another 200 ps of MD simulations; (c) all the protein atoms were released, and 2.2 ns of MD simulations were performed. The final coordinates and velocities of these last simulations were used to start production runs of 20 ns. All equilibration and production simulations were performed in the NPT ensemble at 1 atm and 298.15 K. The pressure was controlled using a Langevin barostat63 with 200 fs period, 100 fs decay and a piston temperature of 298.15 K. Constant temperature was set using a Langevin bath64 with a 10 ps−1 damping coefficient. The CHARMM36 force field was used for the protein,65 and the TIP3P model was used for water.61 The bonded and Lennard-Jones parameters for urea of the CHARMM36 force-field were used, in association with the charges of a Kirkwood–Buff force-field (KBFF) for urea.30 This combination was used because the original KBFF force-field for urea was defined with a geometrical rule for combining atomic radii, which is not compatible with the CHARMM force-field for proteins. We have previously demonstrated that this combination reproduces quantitatively urea preferential interaction parameters in protein solvation.29 A 12 Å cutoff was used for short-range interactions, and long-range electrostatic interactions were computed with the Particle-Mesh Ewald Summation method.66 10 independent simulations adopting the above protocols were performed for each system, for a total of 2000 ns of simulation (10 systems × 10 replicas × 20 ns).
By performing 10 short (20 ns) instead of long simulations for each system, we guarantee that the BCL structure retains its native conformation, and obtain sufficient sampling of the structure of the solvent. Therefore, we studied the solvation structure of the native state of the protein, without concurrent non-equilibrium denaturation effects in the time-scale of the simulations. As discussed in the previous section, the understanding of the solvation structures of the native state is usually sufficient for the interpretation of the denaturing or stabilizing effects of cosolvents. Thus, the native conformation of BCL was mostly preserved in the time scale of these simulations (Fig. S12, ESI†). The analyzes were implemented for this work within the MDAnalysis tools and are available at http://m3g.iqm.unicamp.br/mdanalysis, including root mean square deviations (RMSD), hydrogen bond count (Hbonds), minimum-distance distribution functions, gmd(r), and Kirkwood–Buff integrals.29,67
The minimum-distance distribution functions were computed with a discretized version of eqn (1) in which the density was computed from the average number of minimum-distances at each 0.1 Å bin. The KB integrals and preferential interaction parameters were computed according to eqn (3) and (4), and the preferential hydration parameter according to eqn (5). We used R = 10 Å, a distance above which MDDFs were converged for practical purposes.29 In Fig. S16 (ESI†) we show that the preferential interaction parameters do not vary significantly for R varying from 7 Å to 14 Å such that R = 10 Å is a safe choice for the minimum-distance radius of the protein domain. The bulk densities of water and of the urea, reported in Table 1, were computed from the simulations at distances r > 10 Å. In all figures the standard errors are obtained from the fluctuations of each property observed in the 10 simulations performed. Because of the fast convergence of solvation structures, the fluctuations are sometimes too small to be perceived. Survival times of hydrogen bonds were obtained by computing a intermittent time-correlation function, consisting on the probability that a hydrogen bond is found at time t given that it was found at an initial reference time zero.68 Mono-exponential fits were used to compute characteristic survival times.
Results and discussion
Lipases are arguably the most important group of proteins used as biocatalysis in industry, motivating the understanding of their stability in non-conventional solvents.69 The Burkholderia cepacia lipase (BCL) structure, studied here, is mostly α-helical, as shown in Fig. 1. Domains U1 and U2 form a groove whose aperture is modulated by the polarity of the medium, such that enzyme activation occurs at aqueous–organic interfaces.70 Domain C residues are exposed to the solvent at the opposite position from the active site and are mostly polar. The acidic superficial residues that might be protonated at low pH are found predominantly in this region.Previously,35 we have shown that the interactions of urea with the BCL occurs with all types of residues’ side-chains and with the backbone, supporting the presence of direct urea-BCL interactions. Now, MD simulations were performed for the BCL enzyme in water and urea, and emulating neutral or acidic pH conditions, using a force-field which reproduces quantitatively protein–urea preferential interaction parameters (see Methods).29,30 The solvation structures were obtained from averages of 10 short (20 ns) simulations such that no denaturation takes place in the time-scale of the simulations. Minimum-distance distribution functions were used to probe the effect of the protonation state of acid residues on the orientation of water and urea at the protein surface and on specific protein–solvent interactions. We carried out the protonation of aspartic and glutamic acid side chains of the surface of the protein, to emulate a pH ∼ 3,71 for which a shift in urea orientation on the protein surface was reported by Cremer and co-workers.24 The figures in this article use the following notation for the systems simulated: P: protein, W: water, U: urea; 1, 3, 6, and 12 are the urea concentrations used, and “p” and “d” indicate the protonated and deprotonated states of acidic side-chains. A detailed account of the systems studied is shown in Table 1, in the Methods section.
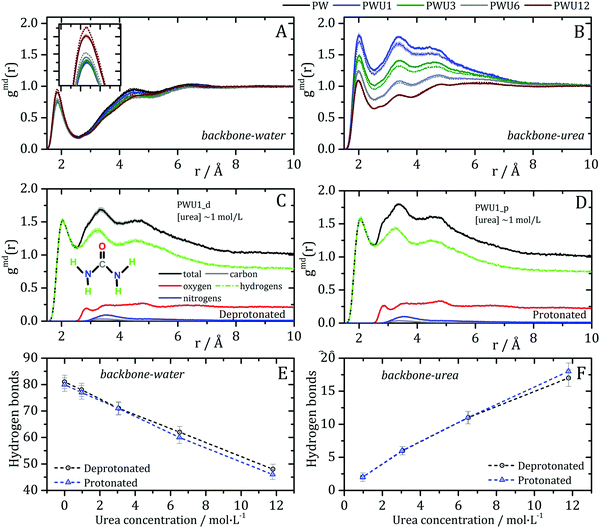
The MDDFs computed for water and urea relative to the protein in different protonation states are shown in Fig. 2. Water density is increased relative to the bulk at hydrogen bonding distances (∼1.8 Å), as expected. A second peak at ∼2.7 Å is characteristic of the second hydration shell. The protonation of the acidic residues at the surface of the protein decreases slightly the hydrogen-bonding peak and leads to a small stabilization of the second peak as shown in Fig. 2A and B. However, these effects are small. The addition of cosolvent indicates that the urea stabilizes protein–water hydrogen bonds, but excludes water molecules from the second solvation shell and from other non-specific interactions. This is consistent with experimental evidence that urea can be found frequently surrounded by water molecules perturbing water structure in the vicinity of the protein surface,23 and with the substitution of water by urea at the vicinity of aliphatic groups.19 Nevertheless, urea–protein distribution functions, shown in Fig. 2C, reveal that urea also interacts directly with the protein surface through hydrogen-bonds. The density augmentation of urea at the protein surface is characterized by a broad band that indicates direct hydrogen-bonding but also water-mediated and less specific interactions. Indeed, as shown previously, urea displays interactions leading to an increased density at the vicinity of charged, polar, and hydrophobic residues.19,35 With the increase in urea concentration, its relative density at the protein surface progressively decreases, suggesting that the most favorable protein–urea interactions are saturated. The protonation of superficial acidic residues has only a minor effect on urea–protein distribution functions (blue curves in Fig. 2C).
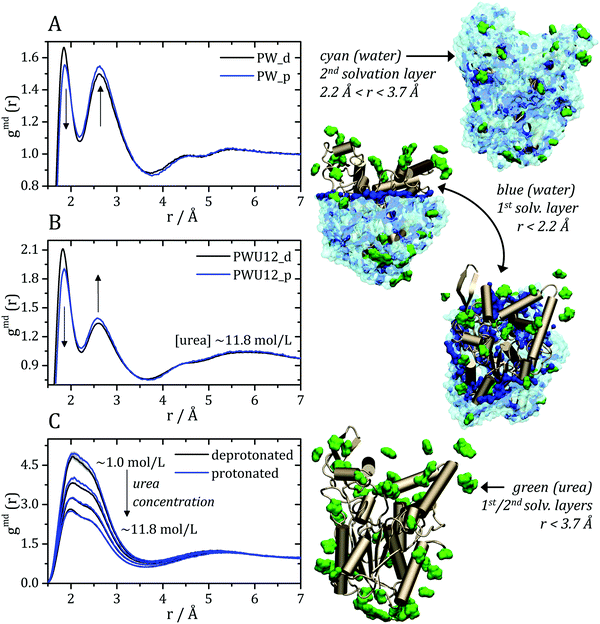 | ||
| Fig. 2 Minimum-distance distribution functions (gmd) for water and urea relative to the protein. In each plot, data associated with the deprotonated (black) and protonated (blue) states of acidic residues are shown. (A) Water–protein MDDFs (gmd(r)) in water and (B) in a ∼11.8 mol L−1 aqueous solution of urea (PWU12 system); (C) urea–protein gmd(r) in urea solutions at all concentrations. Standard errors are shown by shadows, and are too small to be perceived in some cases. In (A and B) arrows indicate the direction of change of the gmd(r) peaks with the protonation of Asp and Glu residues. In (C), the arrow indicates the change in the gmd(r) according the increment of urea concentrations. The snapshots of the simulations, on the right, illustrate water and urea interactions with the protein surface, as can be deduced from the distribution functions. Distribution functions for water in solutions of urea of different concentrations are shown in Fig. S1 (ESI†), and are similar to the ones shown in panel (B). | ||
Kirkwood–Buff integrals computed from the MDDFs of water and urea are shown in Fig. 3. KB integrals correspond to the difference between the volume effectively occupied by the solvent in the solution, relative to the volume it would occupy in the absence of the solute, but with bulk solvent density. The integrals are negative if the solvent is excluded relative to the homogenous solution, and positive if the solvent density increases by the presence of the solute.8,72 The distance-dependence of KB integrals derived from the MDDFs can be easily interpreted: the integrals decrease sharply until the first solute–solvent minimum-distances are found. This sharp decrease is associated with the van der Waals volume of the protein. The solvent accumulation at the surface of the protein compensates partially this excluded volume, and the integrals increase slightly. Generally, the first and second solvation shells are mostly determinant for the final KBI values, as previously observed.29,42 The profiles of the integrals as a function of the distance between the solute and the solvent can be easily associated with the corresponding MDDFs.29 As shown in Fig. 3A, water is excluded from the protein domain, essentially because of the protein steric volume. The density augmentation at hydrogen-bonding distances observed in the MDDFs (Fig. 2A and B) is far from being enough to compensate for the excluded protein volume. On the other side, the accumulation of urea at the vicinity of the protein is able to completely compensate the excluded protein volume at low urea concentrations (∼1 mol L−1). At greater urea concentrations the KBIs are negative for similar reasons as those of water KBIs. The fact that KBIs are generally less negative for urea than for water is consistent with the picture of the protein being dehydrated.
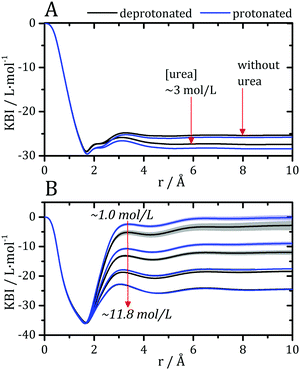 | ||
| Fig. 3 Kirkwood–Buff integrals for water and urea relative to the protein, computed from minimum-distance counts using eqn (3). (A) Protein–water KBI without urea and in ∼3 mol L−1 aqueous urea solutions. (B) Protein–urea KBIs at different concentrations of the denaturant. KB integrals for water at other urea concentrations are shown in Fig. S2 (ESI†) and are similar. The protonation of acidic residues decreases slightly the KBIs for urea. | ||
Preferential interaction parameters (Γpc and Γpw) can be computed from the KBIs using eqn (4) and (5), and obtained experimentally. The preferential interaction parameters for water and urea relative to BCL were computed from the KB integrals of Fig. 3 and are shown in Fig. 4. The preferential hydration parameter, Γpw, is negative at all concentrations probed, as shown in Fig. 4A. Therefore, the density of water at the protein vicinity is smaller than that expected for an ideal solution, and the protein is effectively dehydrated in the presence of urea. The urea preferential interaction parameters, Γpc, are positive, as shown in Fig. 4B, and confirm that urea is concentrated at the protein vicinity relative to its concentration in the bulk solution. This is the expected result for most proteins in aqueous solutions of urea.12 The preferential accumulation of urea increases with increasing urea concentration until ∼7 mol L−1, but was observed to decrease (while still positive) at the highest concentration (Fig. 4B). This can be the result of the saturation of the urea interaction sites at the protein surface or force-field limitation for high urea concentrations. Nevertheless, we will see that the effects of residue protonation on the urea structure are consistent at all concentrations.
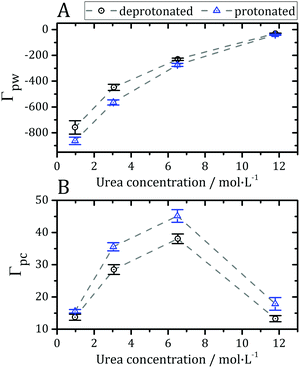 | ||
| Fig. 4 (A) Preferential hydration parameter (Γpw from eqn (5)) and (B) preferential interaction parameter for urea (Γpc from eqn (4)) at different concentrations of denaturant. Negative Γpw and positive Γpc parameters indicate that the protein is preferentially solvated by urea, thus being dehydrated by the presence of the osmolyte, as expected in most cases for protein–urea interactions.12,73,77 | ||
The preferential interactions with urea suggest that the denaturant favors structures with greater surface area, justifying the denaturing effect.73 The protonation of acidic side-chains decreases Γpw and increases Γpc, as shown in Fig. 4A and B, such that it promotes the strengthening of protein–urea interactions relative to protein–water interactions. This is consistent with some experimental evidence that urea has an increased denaturing effect at low pH.74–76 Therefore, the protein becomes preferentially dehydrated, and thus preferentially solvated by urea, in these solutions, at every pH.
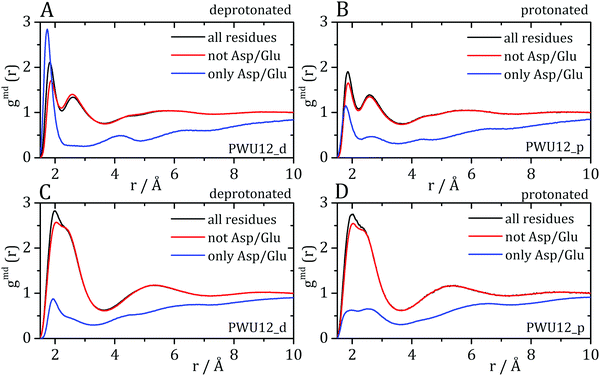
Cremer and co-workers24,25 and by Bakker and co-workers,23 observed an inversion of water and urea orientations at protein surfaces at low pH. The MDDFs of water and urea considering, as the solute, only the side chains of acidic residues are shown in Fig. 5. Fig. 5A and B show that protonation of the side-chains decrease the stability of their hydrogen-bonds with water molecules, such that the MDDF peak at ∼1.8 Å decreases significantly. The number of hydrogen bonds of these residues with water also decreases (Fig. S3A, ESI†). Fig. 5C and D show that the effect of a low pH on protein–urea interactions is more complex: the hydrogen bonding peak, which is quite sharp for the deprotonated side-chains, decreases from the ∼1 mol L−1 to higher urea concentrations. The number of protein–urea hydrogen bonds is only marginally affected by the protonation of the acidic side-chains (Fig. S3–S6, ESI†). Most clear, however, is the significant increase in the peak at ∼2.7 Å. As these are distribution functions computed from the minimum-distance between solute and solvent atoms, the peak at ∼2.7 Å is suggestive of the intermediation of the protein–urea interaction by a water molecule.
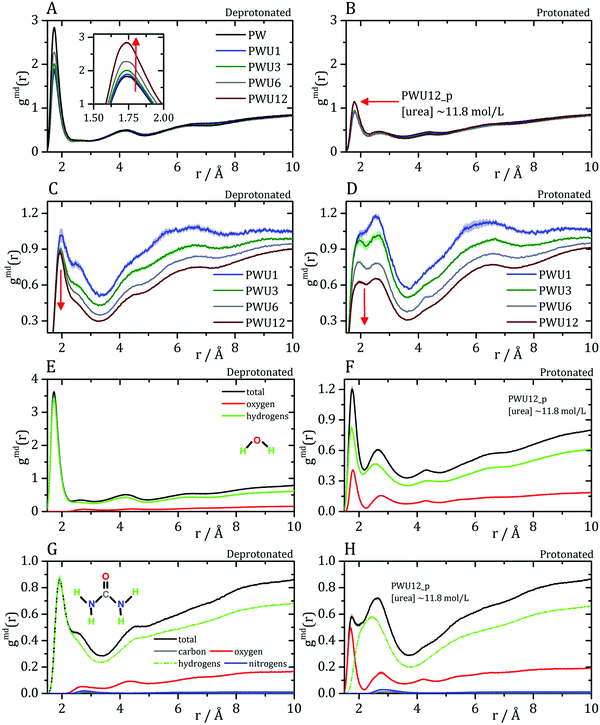 | ||
| Fig. 5 Water–protein minimum distance distribution functions (gmd(r)) considering only acidic residue for (A) deprotonated Asp/Glu and (B) protonated Asp/Glu. Urea–protein gmd(r) with (C) deprotonated Asp/Glu and (D) protonated Asp/Glu. Red arrows indicate the change in the profile with an increase in urea concentration. These distribution functions can be decomposed into atomic contributions providing information on the orientation of the solvent molecules,29 (E and F) atomic contributions to the water MDDFs. (G and H) Atomic contributions to the urea MDDFs. In both cases, an inversion of the orientation of the solvent molecules is observed, as indicated by the formation of hydrogen bonds through the urea or water oxygen atoms. Solvent atomic contributions to the MDDFs for the other concentrations of urea are available in Fig. S7 and S8 (ESI†). | ||
MDDFs can be decomposed into atomic contributions, providing a detailed view of solute–solvent interactions.29 In this case, we decompose the MDDFs for water and urea relative to the acidic chains states to understand the effect of protonation. Fig. 5E and F illustrate the contributions of each water atom type to the total water-distribution around acidic residues in deprotonated and protonated states, respectively. For instance, Fig. 5E shows that the hydrogen-bonds between deprotonated acidic residues and water occur only through the water hydrogen atoms, as expected. Upon protonation, these residues become hydrogen-bond donors, and as shown in Fig. 5F the water oxygen atoms start to contribute to the hydrogen-bonding peak. These results are expected and indicate that there is an inversion of orientation of part of the water molecules at the protein surface associated with the protonation of acidic residues.
The decomposition of the MDDFs of urea relative to acidic residues into atomic contributions is more interesting than that of water. While the residues are deprotonated, urea can only form hydrogen-bonds through its hydrogen atoms, as expected and shown in Fig. 5G. With the protonation of the side-chains, however, hydrogen-bonding can occur with urea acting both as hydrogen-donor or acceptor. As shown in Fig. 5H, the hydrogen-bonding peak appears to be dominated by urea oxygen atoms. Specifically, the oxygen atom of urea contributes to 85% of the peak at ∼1.7 Å, and 36% of the MDDF at 1.9 Å. In this range of distances only interactions through hydrogen bonds can be found, and the MDDFs show that the stronger ones (shorter distances) are formed through the urea oxygen atom in the protonated state of the acidic residues. Thus, urea passes from being a hydrogen-bond donor to both a donor and acceptor, with the stronger hydrogen bonds occurring through its oxygen atom. The direct counting of the number of urea atoms, of each type, at each distance from the protonable residues confirms the orientational shift suggested by the MDDFs, as shown in Fig. 6.
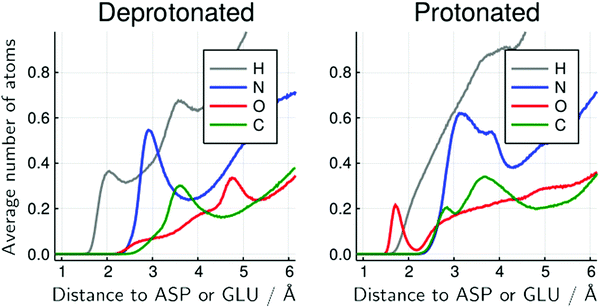 | ||
| Fig. 6 Average number of urea atoms of each type distant from the side-chain of protonable acidic residues for the 6 mol L−1 urea solution. The inversion of the configuration of urea molecules is visible by the presence of urea oxygen atoms (red) close to the acidic residues, in the protonated form but not in the deprotonated form. There is also a significant reduction in the number of urea hydrogen atoms in the immediate vicinity of these residues. Similar figures for other urea concentrations and for water atoms are available at the ESI† (Fig. S20–S26). | ||
The change in structure and stability of hydrogen bonds can be confirmed by the direct analysis of the hydrogen bonds of urea with acidic residues, shown in Fig. 7. Here, as defined in VMD,57 a contact was considered a hydrogen bond if two electronegative atoms X and Y are within 3.0 Å and if the angle between the X–H and H–Y vectors is less than 20°. With this definition all possible interactions that are usually considered hydrogen bonds are summed up (thus, while intuitive, the hydrogen bond analysis loses resolution relative to the MDDFs shown in Fig. 5).
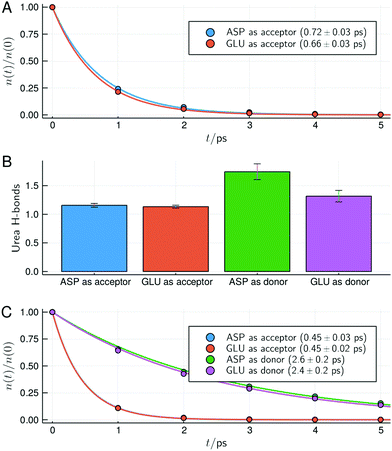 | ||
| Fig. 7 Survival times and types of hydrogen bonds between urea and the side-chain of acidic residues for the protein in 6 mol L−1 solution of urea. (A) Survival times of hydrogen bonds for the deprotonated acidic residues. (B) Number of hydrogen bonds with the protonated acidic residues act as hydrogen acceptors or donors of hydrogen (the deprotonated form of the residues can only act as hydrogen acceptors). (C) Survival times of the hydrogen bonds with the side chains of acidic residues in the protonated form. In (A and C) characteristic times and standard deviations computed from the fits of the data of the simulation replicas are shown. Similar figures for the other urea concentrations are available as ESI† (Fig. S13–S15). | ||
While deprotonated, Asp and Glu residues can only act as hydrogen bond acceptors. Fig. 7A shows that urea hydrogen bonds with these residues display a survival characteristic time of ∼0.7 ps. When Asp and Glu residues become protonated at the surface of the protein, they can act both as donor or acceptors, as shown in Fig. 7B. In the protonated form, Asp and Glu hydrogen bonds are found to be slightly more likely to occur with these residues acting as donors, even if urea has 4 polar hydrogen atoms and a single oxygen atom. The survival times of the hydrogen bonds of urea with Asp and Glu residues in the protonated form are shown in Fig. 7C. Upon protonation, the survival times of the hydrogen bonds in which Asp and Glu act as acceptors slightly decrease (from ∼0.7 to 0.45 ps), thus becoming less stable. Interestingly, the survival times hydrogen bonds in which Asp and Glu residues act as donors are much greater (∼2.5 ps). This is consistent with their shorter interaction distances observed in the MDDFs, and explain how urea can finally form more hydrogen bonds with the protonated acidic residues using its oxygen atom than using its four hydrogen atoms. Also, the increased stability of these hydrogen bonds, associated with the destabilization of water–protein interactions explain why the protein is further dehydrated when protonated, as shown by preferential interaction parameters (Fig. 4).
Therefore, the interactions of urea with the side-chains of acidic residues are significantly affected by protonation, with urea assuming the role of a hydrogen bond acceptor. These atomic contributions of the protein–urea MDDFs are consistent with the reorientation of the urea molecules at the protein surface observed experimentally.24 This shift was interpreted as an indication that urea should denature proteins by indirect mechanisms because the molecular interactions are different in each orientation despite urea acting as a denaturant at every pH. Here we will show that the interactions of urea with the protein backbone and other residues are not affected by the protonation of acidic residues, and thus are consistent with the most accepted denaturing effect by direct interactions.
In Fig. 8 and 9 we show the MDDFs and hydrogen bond analysis computed considering, as the solute, subsets of the protein structure not including the superficial acidic residues. In Fig. 8 we show the MDDFs computed considering as the solute all residues except acidic ones (red lines). By comparing these distribution functions in the protonated and deprotonated states of the protein, it is evident that protonation does not affect the solvation of other residues (detailed decompositions of the distribution function in different protein subsets are shown in Fig. S9 and S10, ESI†). The perturbation in the protein–solvent interactions is local and restricted to acidic side-chains. Fig. 9 shows that hydrogen bonds between urea and all other (not superficial-acidic) residues are also invariant, confirming the locality of the protonation effects. Hydrogen bonds formed by urea with the protein through its oxygen atom (BCL as donor) are more stable than those formed through its hydrogen atoms (BCL as acceptor) as judged by their survival times.
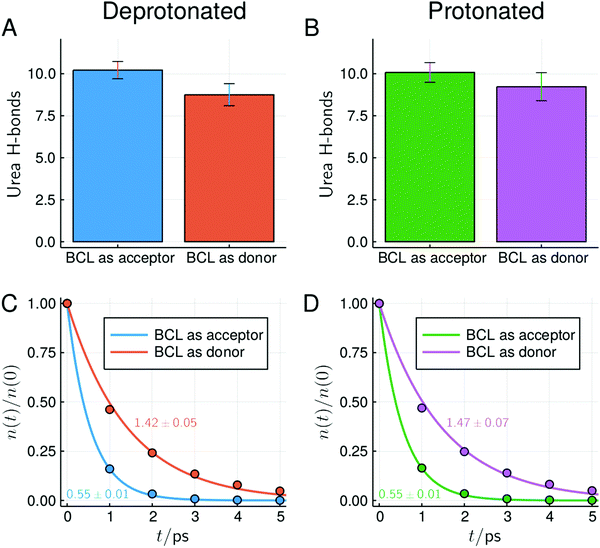 | ||
| Fig. 9 Number and survival times of hydrogen bonds between BCL and urea at ∼6 mol L−1, considering only residues not forming direct contacts with superficial acidic residues in the crystallographic structure (similar plots and overall statistics of hydrogen bonds for other concentrations can be found in Fig. S17–S19 and Table S1, ESI†). Characteristic survival times (in ps) obtained from the single-exponential fit and standard deviations within simulations are shown. | ||
Given that the hydrogen bonds with the protein backbone are generally considered important for solvent-induced protein denaturation, we highlight in Fig. 10 the MDDFs for water and urea relative to the protein backbone atoms only, their atomic compositions, and the number of backbone–solvent hydrogen bonds. The MDDFs of Fig. 10A and B show that both water and urea form hydrogen bonds with the backbone of BCL, and that there is a second solvation peak for urea at ∼3.3 Å. This second peak suggests that there are urea molecules that interact with the protein backbone intermediated by a water molecule, or might be indirect accumulation of urea in the neighbourhood of the backbone by its interactions with the side-chains. The important observation here is that, however, the protonation of acidic side-chains leads only to minor perturbations of these distribution functions. That is, the effect of protonation of the side-chains is not propagated decisively to water–backbone and urea–backbone interactions. There is no inversion in urea orientation in the vicinities of the protein backbone (Fig. 10C and D). Urea–backbone hydrogen bonds occur with urea acting exclusively as a hydrogen donor, and no shift in the atomic contributions to the MDDF can be observed at greater distances. Similarly, the number water–backbone and urea–backbone hydrogen bonds is essentially unaffected by the protonation of the acidic side chains (Fig. 10E and F).
 | ||
| Fig. 10 Solvent–backbone interactions: minimum-distance distribution functions for (A) water and (B) urea with protein backbone atoms. Deprotonated and protonated systems are represented by dashed and solid lines, respectively. The protonation of the acidic side-chains affects only marginally the distribution functions, thus the general properties of backbone solvation are not altered. (C and D) show that the atomic contributions to urea–backbone MDDFs are not altered either, such that there is no inversion in urea configuration in this case. The number of hydrogen-bonds of the BCL backbone with (E) water and (F) urea molecules is also insensitive to the protonation of the acidic side-chains. Fig. S11 (ESI†) shows the MDDFs computed for the amine and carbonyl groups of the backbone and confirm that hydrogen bonding with urea occurs predominantly with the carbonyl groups. | ||
Conclusion
At low pH, the side-chains of acidic residues at the surface of proteins are expected to be protonated affecting the interactions of the protein with the solvent molecules. MD simulations with specialized force-fields and minimum-distance distribution functions allow a precise characterization of these interactions. Protonation of acidic side-chains increases slightly the strength of protein–urea interactions relative to protein–water interactions, such that the preferential dehydration effect is increased and the denaturing effect of urea might be maximized in acidic media. This occurs because the water–protein hydrogen bonds are destabilized by protonation, while protein–urea hydrogen bonds in which urea acts as a hydrogen bond acceptor are more stable than those in which it acts as a hydrogen bond donor. The protonated acid side-chains interact with the solvent molecules, particularly with urea, through the inversion of the configuration of the hydrogen bonds. Urea acts an hydrogen bond donor for the negatively charged side-chains, but also (and preferentially) as a hydrogen bond acceptor for the protonated side-chains. Therefore, there is reorientation of the urea and water molecules induced by the change in pH, consistently with the experimental spectroscopy data.23,24 Nevertheless, this shift in the nature of the protein–urea interactions is localized on the acidic side chains. The distribution functions of urea and water relative to the protein for all other residues are essentially unaffected. In particular, the interactions of urea with the protein backbone and with non-polar residues are preserved in strength and chemical nature, and support the most accepted mechanisms of urea-induced denaturation by direct interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the financial support of CAPES for a graduate fellowship (I. P. O.), FAPESP grants 2010/16947-9, 2013/08293-7, and 2018/24293-0, and I. P. O. postdoctoral fellowship (process number 2017/02201-4).References
- Q. Zou, B. J. Bennion, V. Daggett and K. P. Murphy, The molecular mechanism of stabilization of proteins by TMAO and its ability to counteract the effects of urea, J. Am. Chem. Soc., 2002, 124, 1192–1202 CrossRef CAS PubMed.
- J. Rösgen, B. M. Pettitt and D. W. Bolen, Protein folding, stability, and solvation structure in osmolyte solutions, Biophys. J., 2005, 89, 2988–2997 CrossRef PubMed.
- D. Eisenberg and A. D. McLachlan, Solvation energy in protein folding and binding, Nature, 1986, 319, 199–203 CrossRef CAS PubMed.
- G. I. Makhatadze, Thermodynamics of Protein Interactions with Urea and Guanidinium Hydrochloride, J. Phys. Chem. B, 1999, 103, 4781–4785 CrossRef CAS.
- C. N. Pace, Methods in Enzymology, 1986, vol. 131, pp. 266–280 Search PubMed.
- J. Heyda, M. Kožíšek, L. Bednárova, G. Thompson, J. Konvalinka, J. Vondrášek and P. Jungwirth, Urea and guanidinium induced denaturation of a Trp-cage miniprotein, J. Phys. Chem. B, 2011, 115, 8910–8924 CrossRef CAS PubMed.
- P. J. Rossky, Protein denaturation by urea: slash and bond, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16825–16826 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Cosolvent effects on protein stability, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- P. Ganguly, P. Boserman, N. F. A. van der Vegt and J.-E. Shea, Trimethylamine N-oxide Counteracts Urea Denaturation by Inhibiting Protein–Urea Preferential Interaction, J. Am. Chem. Soc., 2018, 140, 483–492 CrossRef CAS PubMed.
- B. Moeser and D. Horinek, Unified description of urea denaturation: backbone and side chains contribute equally in the transfer model, J. Phys. Chem. B, 2014, 118, 107–114 CrossRef CAS PubMed.
- B. J. Bennion and V. Daggett, The molecular basis for the chemical denaturation of proteins by urea, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5142–5147 CrossRef CAS PubMed.
- S. N. Timasheff, Protein–solvent preferential interactions, protein hydration, and the modulation of biochemical reactions by solvent components, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 9721–9726 CrossRef CAS PubMed.
- A. Kumar, P. Attri and P. Venkatesu, Effect of polyols on the native structure of α-chymotrypsin: a comparable study, Thermochim. Acta, 2012, 536, 55–62 CrossRef CAS.
- M. Candotti, S. Esteban-Martín, X. Salvatella and M. Orozco, Toward an atomistic description of the urea-denatured state of proteins, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5933–5938 CrossRef CAS PubMed.
- J.-R. Huang, F. Gabel, M. R. Jensen, S. Grzesiek and M. Blackledge, Sequence-specific mapping of the interaction between urea and unfolded ubiquitin from ensemble analysis of NMR and small angle scattering data, J. Am. Chem. Soc., 2012, 134, 4429–4436 CrossRef CAS PubMed.
- M. C. Stumpe and H. Grubmüller, Interaction of urea with amino acids: implications for urea-induced protein denaturation, J. Am. Chem. Soc., 2007, 129, 16126–16131 CrossRef CAS PubMed.
- A. Das and C. Mukhopadhyay, Urea-mediated protein denaturation: a consensus view, J. Phys. Chem. B, 2009, 113, 12816–12824 CrossRef CAS PubMed.
- W. K. Lim, J. Rösgen and S. Walter Englander, Urea, but not guanidinium, destabilizes proteins by forming hydrogen bonds to the peptide group, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 2595–2600 CrossRef CAS PubMed.
- L. Hua, R. Zhou, D. Thirumalai and B. J. Berne, Urea denaturation by stronger dispersion interactions with proteins than water implies a 2-stage unfolding, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16928–16933 CrossRef CAS PubMed.
- M. C. Stumpe and H. Grubmüller, Polar or Apolar—The Role of Polarity for Urea-Induced Protein Denaturation, PLoS Comput. Biol., 2008, 4, e1000221 CrossRef PubMed.
- D. Horinek and R. R. Netz, Can simulations quantitatively predict peptide transfer free energies to urea solutions? Thermodynamic concepts and force field limitations, J. Phys. Chem. A, 2011, 115, 6125–6136 CrossRef CAS PubMed.
- L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, Investigating the hydrogen-bonding model of urea denaturation, J. Am. Chem. Soc., 2009, 131, 9304–9310 CrossRef CAS PubMed.
- S. Strazdaite, K. Meister and H. J. Bakker, Orientation of polar molecules near charged protein interfaces, Phys. Chem. Chem. Phys., 2016, 18, 7414–7418 RSC.
- X. Chen, L. B. Sagle and P. S. Cremer, Urea orientation at protein surfaces, J. Am. Chem. Soc., 2007, 129, 15104–15105 CrossRef CAS PubMed.
- Y. Zhang and P. S. Cremer, Chemistry of Hofmeister anions and osmolytes, Annu. Rev. Phys. Chem., 2010, 61, 63–83 CrossRef CAS PubMed.
- J. G. Kirkwood and F. P. Buff, The Statistical Mechanical Theory of Solutions. I, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- K. E. Newman, Kirkwood–Buff solution theory: derivation and applications, Chem. Soc. Rev., 1994, 23, 31–40 RSC.
- V. Pierce, M. Kang, M. Aburi, S. Weerasinghe and P. E. Smith, Recent applications of Kirkwood-Buff theory to biological systems, Cell Biochem. Biophys., 2008, 50, 1–22 CrossRef CAS PubMed.
- L. Martínez and S. Shimizu, Molecular Interpretation of Preferential Interactions in Protein Solvation: A Solvent-Shell Perspective by Means of Minimum-Distance Distribution Functions, J. Chem. Theory Comput., 2017, 13, 6358–6372 CrossRef PubMed.
- S. Weerasinghe and P. E. Smith, A Kirkwood−Buff Derived Force Field for Mixtures of Urea and Water, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS.
- S. Shimizu and C. L. Boon, The Kirkwood–Buff theory and the effect of cosolvents on biochemical reactions, J. Chem. Phys., 2004, 121, 9147–9155 CrossRef CAS PubMed.
- P. E. Smith, Cosolvent Interactions with Biomolecules: Relating Computer Simulation Data to Experimental Thermodynamic Data, J. Phys. Chem. B, 2004, 108, 18716–18724 CrossRef CAS.
- I. L. Shulgin and E. Ruckenstein, A protein molecule in an aqueous mixed solvent: fluctuation theory outlook, J. Chem. Phys., 2005, 123, 054909 CrossRef PubMed.
- D. R. Canchi, P. Jayasimha, D. C. Rau, G. I. Makhatadze and A. E. Garcia, Molecular mechanism for the preferential exclusion of TMAO from protein surfaces, J. Phys. Chem. B, 2012, 116, 12095–12104 CrossRef CAS PubMed.
- I. P. Oliveira and L. Martínez, Molecular basis for competitive solvation of the Burkholderia cepacia lipase by sorbitol and urea, Phys. Chem. Chem. Phys., 2016, 18, 21797–21808 RSC.
- D. R. Canchi and A. E. García, Backbone and side-chain contributions in protein denaturation by urea, Biophys. J., 2011, 100, 1526–1533 CrossRef CAS PubMed.
- P. K. Mehrotra and D. L. Beveridge, Structural analysis of molecular solutions based on quasi-component distribution functions. Application to [H2CO]aq at 25 °C, J. Am. Chem. Soc., 1980, 102, 4287–4294 CrossRef CAS.
- K. Coutinho, R. Rivelino, H. C. Georg and S. Canuto, in Solvation Effects on Molecules and Biomolecules, ed. S. Canuto, Springer, 2008, pp. 159–189 Search PubMed.
- V. Zeindlhofer, D. Khlan, K. Bica and C. Schröder, Computational analysis of the solvation of coffee ingredients in aqueous ionic liquid mixtures, RSC Adv., 2017, 7, 3495–3504 RSC.
- M. Mezei, Modified Proximity Criteria for the Analysis of the Solvation of a Polyfunctional Solute, Mol. Simul., 1988, 1, 327–332 CrossRef.
- S.-C. Ou and B. M. Pettitt, Solute–Solvent Energetics Based on Proximal Distribution Functions, J. Phys. Chem. B, 2016, 120, 8230–8237 CrossRef CAS PubMed.
- B. M. Baynes and B. L. Trout, Proteins in Mixed Solvents: A Molecular-Level Perspective, J. Phys. Chem. B, 2003, 107, 14058–14067 CrossRef CAS.
- W. Song, R. Biswas and M. Maroncelli, Intermolecular Interactions and Local Density Augmentation in Supercritical Solvation: A Survey of Simulation and Experimental Results, J. Phys. Chem. A, 2000, 104, 6924–6939 CrossRef CAS.
- A. C. Furlan, F. W. FÁvero, J. Rodriguez, D. Laria and M. S. Skaf, in Solvation Effects on Molecules and Biomolecules, ed. S. Canuto, 2008, pp. 433–453 Search PubMed.
- E. A. Oprzeska-Zingrebe and J. Smiatek, Aqueous ionic liquids in comparison with standard co-solutes: Differences and common principles in their interaction with protein and DNA structures, Biophys. Rev., 2018, 10, 809–824 CrossRef CAS PubMed.
- D. Harries and J. Rösgen, A practical guide on how osmolytes modulate macromolecular properties, Methods Cell Biol., 2008, 84, 679–735 CAS.
- M. A. Schroer, J. Michalowsky, B. Fischer, J. Smiatek and G. Grübel, Stabilizing effect of TMAO on globular PNIPAM states: preferential attraction induces preferential hydration, Phys. Chem. Chem. Phys., 2016, 18, 31459–31470 RSC.
- I. L. Shulgin and E. Ruckenstein, A Protein Molecule in a Mixed Solvent: The Preferential Binding Parameter via the Kirkwood-Buff Theory, Biophys. J., 2006, 90, 704–707 CrossRef CAS PubMed.
- S. N. Timasheff, The control of protein stability and association by weak interactions with water: how do solvents affect these processes?, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 67–97 CrossRef CAS PubMed.
- P. E. Smith, Chemical potential derivatives and preferential interaction parameters in biological systems from Kirkwood-Buff theory, Biophys. J., 2006, 91, 849–856 CrossRef CAS PubMed.
- S. Shimizu and D. J. Smith, Preferential hydration and the exclusion of cosolvents from protein surfaces, J. Chem. Phys., 2004, 121, 1148–1154 CrossRef CAS PubMed.
- D. R. Canchi, P. Jayasimha, D. C. Rao, G. I. Makhatadze and A. E. Garcia, Molecular Mechanism for the Preferential Exclusion of Osmolytes from Protein Surfaces, Biophys. J., 2013, 104, 189a CrossRef.
- S. Shimizu, Estimating hydration changes upon biomolecular reactions from osmotic stress, high pressure, and preferential hydration experiments, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1195–1199 CrossRef CAS PubMed.
- A. Mezzetti, J. D. Schrag, C. S. Cheong and R. J. Kazlauskas, Mirror-image packing in enantiomer discrimination molecular basis for the enantioselectivity of B. cepacia lipase toward 2-methyl-3-phenyl-1-propanol, Chem. Biol., 2005, 12, 427–437 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J. M. Martínez and L. Martínez, Packing optimization for automated generation of complex system's initial configurations for molecular dynamics and docking, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- G. B. Goh, B. S. Hulbert, H. Zhou and C. L. Brooks 3rd, Constant pH molecular dynamics of proteins in explicit solvent with proton tautomerism, Proteins, 2014, 82, 1319–1331 CrossRef CAS PubMed.
- J. Shen, Z. Yue, H. Zgurskaya and W. Chen, Constant pH Molecular Dynamics Reveals How Proton Release Drives the Conformational Transition of a Transmembrane Efflux Pump, J. Chem. Theory Comput., 2017, 13, 6405–6414 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- A. Brünger, C. L. Brooks and M. Karplus, Stochastic boundary conditions for molecular dynamics simulations of ST2 water, Chem. Phys. Lett., 1984, 105, 495–500 CrossRef.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, CHARMM: a program for macromolecular energy, minimization, and dynamics calculations, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- L. Martínez, MDAnalysis, 2017 Search PubMed.
- A. Luzar and D. Chandler, Hydrogen-bond kinetics in liquid water, Nature, 1996, 379, 55–57 CrossRef CAS.
- F. Hasan, A. A. Shah and A. Hameed, Industrial applications of microbial lipases, Enzyme Microb. Technol., 2006, 39, 235–251 CrossRef CAS.
- I. P. de Oliveira, G. E. Jara and L. Martínez, Molecular mechanism of activation of Burkholderia cepacia lipase at aqueous-organic interfaces, Phys. Chem. Chem. Phys., 2017, 19, 31499–31507 RSC.
- R. I. Zalewski, Acid Derivatives, 1992, vol. 2, pp. 305–369 Search PubMed.
- S. Shimizu and N. Matubayasi, Preferential solvation: dividing surface vs excess numbers, J. Phys. Chem. B, 2014, 118, 3922–3930 CrossRef CAS PubMed.
- S. N. Timasheff and G. Xie, Preferential interactions of urea with lysozyme and their linkage to protein denaturation, Biophys. Chem., 2003, 105, 421–448 CrossRef CAS PubMed.
- R. A. Deshpande, M. I. Khan and V. Shankar, Equilibrium unfolding of RNase Rs from Rhizopus stolonifer: pH dependence of chemical and thermal denaturation, Biochim. Biophys. Acta, 2003, 1648, 184–194 CrossRef CAS.
- C. N. Pace, C. Nick Pace, D. V. Laurents and R. E. Erickson, Urea denaturation of barnase: pH dependence and characterization of the unfolded state, Biochemistry, 1992, 31, 2728–2734 CrossRef CAS PubMed.
- C. N. Pace, C. Nick Pace, D. V. Laurents and J. A. Thomson, pH dependence of the urea and guanidine hydrochloride denaturation of ribonuclease A and ribonuclease T1, Biochemistry, 1990, 29, 2564–2572 CrossRef CAS PubMed.
- A. N. Rajeshwara, K. N. Gopalakrishna and V. Prakash, Preferential interaction of denaturants with rice bran lipase, Int. J. Biol. Macromol., 1996, 19, 1–7 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1: protein–water MDDFs for water not shown in Fig. 2. Fig. S2: KBIs for water not shown in Fig. 3. Fig. S3–S6: hydrogen-bonding analyzes. Fig. S7 and S8: MDDFs computed for acidic residues, for concentrations not shown in Fig. 5. Fig. S9 and S10: decomposition of the MDDFs into the contributions of each protein subset of atoms. Fig. S11: MDDFs for backbone chemical groups. Fig. S12: RMSD of the BCL in all simulations. Fig. S13–S15: survival times and number of hydrogen bonds of urea with acidic residues. Fig. S16: choice of the radius of the protein domain. Fig. S17–S19: number and survival times of hydrogen bonds with all residues except those in contact with protonable residues. Fig. S20–S26: number of urea and water atoms of each type distant from protonable residues. Table S1: summary of Fig. S17–S19 and Fig. 9. See DOI: 10.1039/c9cp05196a |
| This journal is © the Owner Societies 2020 |