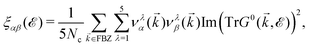Enhanced anisotropic electrical conductivity of perturbed monolayer β12-borophene
Doan Quoc
Khoa
ab,
Nguyen N.
Hieu
 *c and
Bui Dinh
Hoi
*d
*c and
Bui Dinh
Hoi
*d
aDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam
bFaculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: doanquockhoa@tdtu.edu.vn
cInstitute of Research and Development, Duy Tan University, Da Nang, Vietnam. E-mail: hieunn@duytan.edu.vn
dDepartment of Physics, University of Education, Hue University, 34 Le Loi, Hue City, Vietnam. E-mail: buidinhhoi@hueuni.edu.vn
First published on 18th November 2019
Abstract
β12-Borophene is a perfect planar nanolattice comprising of massless Dirac fermions and massless/massive triplet fermions considering the inversion symmetry lattice model. In this paper, a detailed study of the electric field and the effects of low concentrations of impurities on the electronic phase and the electrical conductivity of β12-borophene is presented. As a direct manner to judge the electronic features of pristine and perturbed monolayer β12-borophene, the five-band tight-binding Hamiltonian model, the T-matrix theory, the linear response theory, and the Green's function approach are investigated. Our investigation reveals that the massless Dirac and triplet fermions become massive when an electric field is applied. Also, we found out that the electric current and eventually the electrical conductivity are not the same along different directions and an enhancement of around 18.53% (15.38%) for the x-direction (in-plane) component is observed at a certain thermal energy. Furthermore, the metal-to-semiconductor electronic phase transition in the presence of different impurity atoms results in a 197.16% (198.23%) enhancement in x- (in-plane-) component of electrical conductivity. The results provide a basis of designing novel electronic devices based on β12-borophene.
1 Introduction
Two-dimensional (2D) materials with monoatomic thickness are at the forefront of materials science. 2D structures, as the most active systems, have been found to show novel, unique and exotic behaviors in the last decade. The considerable interest of this dimensionality begun with 2D honeycomb lattices including two atoms per unit cell such as graphene,1 silicene,2–4 germanene,5,6 and stanene.7 The rich features of these lattices originate from their Dirac cones.1,3,8,9 Beyond these materials, phosphorene,10–12 arsenene13 and antimonene14 have been also experimentally synthesized and recently, the group-III (group 13) monolayer materials have attracted the field of condensed matter physics.15 The left nearest-neighbor of carbon in the periodic table is boron, which can be arranged in a single-layer, i.e. borophene, as one of the monolayers of group III.16–22 Borophene is different than other 2D materials due to its electron mobility, band gaps and anisotropic properties, which lead to the coexistence of both massless Dirac fermions and massless/massive triplet fermions.23,24 Such features are absent in other 2D materials.Experimentally, synthesis of borophenes on Ag(111) of several types introduces it as one of the most promising candidates in the current material science.25 Borophene has an unstable honeycomb lattice because the boron atom (with three valence electrons) possesses one less electron than the carbon atom, however, it has been shown that one is able to stabilize it by adding more boron atoms in the honeycomb lattice, in order to balance out the in-plane bonds.16,17 Thus, many borophenes have been proposed,17–20 but β12-borophene grown on Ag(111) is the most stable monolayer-boron structure, which interacts weakly with the silver surface.21,22,26,27 β12-Borophene is particularly metallic.17–19,28,29 It has been shown that the most stable allotrope of borophene in terms of thermodynamical, mechanical and dynamical features is β12-borophene because the other allotropes interact strongly with the respective substrates and, at least mechanically, are not stable.30 The Dirac fermions in β12-borophene are well observed by angle-resolved photoemission spectroscopy, first-principles calculations and the tight-binding Hamiltonian model.16–20,23,25
During growth, in reality, many external factors act as perturbations on the principle system such as electric field, impurity, magnetic field, chemical doping, etc.31,32 As is well-known, in most electronic device applications, systems are required to integrate with the gate voltage, which injects charge carriers into the system. On the other hand, samples can be also easily altered via external chemical impurities. Indeed, the systems under study carry a different amount of charges compared to their pure state because applied gate voltage or impurities will change the occupation of bonding and anti-bonding orbitals. Overall, the initial ground state of the system will be altered significantly. These facts motivate researchers to investigate the effect of physical and chemical external perturbations on the electronic properties of 2D systems. Although this is well-explored for other 2D materials,33–37 the response of β12-borophene to impurities and electric field (stemming from the gate voltage) has been not well explored to date. Another important topic not yet thoroughly addressed theoretically in the literature about β12-borophene is the linear response of pristine and impurity-induced charge current to the electric field, i.e. electrical conductivity tensor, which is an orientation-dependent quantity in general. To date, most studies in this regard have been based on first-principles calculations and experimental observations. While many questions on β12-borophene remain challenging, it is also interesting and important to theoretically find the possible responses of electric current to the external field.
The broad aims of this work are to use the tight-binding model, linear response theory, the Green's function approach, and T-matrix scattering theory to theoretically address/report the following: (i) to provide a detailed discussion on the electronic phase transition of β12-borophene in the presence of an electric field and dilute charged impurities, (ii) to describe the anisotropic electrical conductivity quantity when β12-borophene is subjected to an electric field and the impurity doping. Performing this comprehensive study, first of all, we confirm the electronic nature of charge carriers in β12-borophene reported in ref. 23 and 25. Then, we examine in detail the perturbed electronic features as well as the respective conductivities. The outcomes have important consequences for designing real electronic devices based on β12-borophene.
The paper is organized as follows. In Section 2, we use the tight-binding Hamiltonian model for pz orbitals with the inversion symmetry feature as well as the Green's function technique to address the electronic band structure and electronic density of states (DOS) of β12-borophene. In Section 3, we calculate the anisotropic electrical conductivity of β12-borophene with the help of linear response theory. Section 4 deals with the electric field effects on the electronic phase and the electrical conductivity tensor results. In Section 5, dilute charged impurities are doped to the system randomly using the T-matrix scattering factor and the Born approximation. Also, the conditions for the electronic phase transition and correspondingly the electrical conductivity changes are discussed. We summarize the important results in Section 6.
2 Theoretical framework
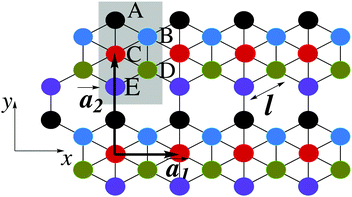
This section intends to review the structure of β12-borophene as well as the electronic configuration of boron atoms and their hybridization based on the tight-binding (TB) Hamiltonian model. The gray rectangle, the unit cell of β12-borophene consists of five atoms labeled as A, B, C, D and E, as illustrated in Fig. 1. One less electron in boron atoms (relative to carbon) does not allow the creation of in-plane σ bonds and atom C plays the role of nearly perfect electron donor in filling the honeycomb σ bonds38 of the borophene lattice. In the β12-borophene lattice, four bonds form for atoms A and E, five bonds form for atoms B and D and six bonds form atoms for C. This lattice can be generated using the lattice basis vectors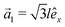 and
and 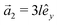 superimposed on Fig. 1, where l ≃ 1.69 Å is the boron–boron distance.39 The vectors êi are unit vectors pointing in the i = {x, y} direction.
superimposed on Fig. 1, where l ≃ 1.69 Å is the boron–boron distance.39 The vectors êi are unit vectors pointing in the i = {x, y} direction.
The TB approximation along with the related terminology and definitions to describe the properties of tightly bound electrons in β12-borophene, only in terms of the pz orbitals in the real space reads:
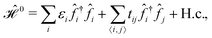 | (1) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) i (
i (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) †i) can be each of the {â,
†i) can be each of the {â, ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) , ĉ,
, ĉ, ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) or ê} atoms in the unit cell referring to the on-site annihilation (creation) operator for electrons at the i-th site of the lattice. The coefficient tij (tab = tde = −2.04 eV, tac = tce = −1.79 eV, tae = −2.12 eV, tbc = tcd = −1.84 eV, and tbd = −1.91 eV) is the hopping parameter between nearest neighbor atomic sites i and j (shown by the symbol 〈…〉) as well as εi (εa = εe = 0.196 eV, εb = εd = −0.058 and εc = −0.845 eV) implies the on-site energy.23,25 These hopping energies show that the transfer energies are symmetric along the x axis. Note that the set of on-site and hopping energies depend strongly on the interaction between the substrate atoms and the boron atoms of the principle system. However, we focus on the most relevant one in experiment, the so-called inversion symmetric model. The Hamiltonian in the real space can be transferred to the momentum space using the Fourier transformation. After fairly simple calculations, thus, the Hamiltonian can be expressed in a matrix form as:
or ê} atoms in the unit cell referring to the on-site annihilation (creation) operator for electrons at the i-th site of the lattice. The coefficient tij (tab = tde = −2.04 eV, tac = tce = −1.79 eV, tae = −2.12 eV, tbc = tcd = −1.84 eV, and tbd = −1.91 eV) is the hopping parameter between nearest neighbor atomic sites i and j (shown by the symbol 〈…〉) as well as εi (εa = εe = 0.196 eV, εb = εd = −0.058 and εc = −0.845 eV) implies the on-site energy.23,25 These hopping energies show that the transfer energies are symmetric along the x axis. Note that the set of on-site and hopping energies depend strongly on the interaction between the substrate atoms and the boron atoms of the principle system. However, we focus on the most relevant one in experiment, the so-called inversion symmetric model. The Hamiltonian in the real space can be transferred to the momentum space using the Fourier transformation. After fairly simple calculations, thus, the Hamiltonian can be expressed in a matrix form as: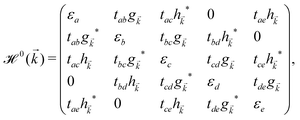 | (2) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and h
and h![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) are given by:
are given by: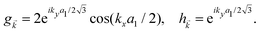 | (3) |
It is expected that the first Brillouin zone (FBZ) be also a rectangle with the lattice parameters −π/a1 ≤ kx ≤ π/a1 and −π/a2 ≤ ky ≤ π/a2 along the x and y direction, respectively. However, in order to see the symmetric behavior of bands in the momentum space, we can conveniently use a shifted FBZ, 0 ≤ kx ≤ 2π/a1 and −π/a2 ≤ ky ≤ π/a2 in the numerical calculations.23 With the aid of this Hamiltonian model, we will address the electronic features of β12-borophene in the next section. By diagonalizing the Hamiltonian (2), the electronic dispersion energies of charge carriers can be easily obtained. Hence, the non-trivial solutions require that:
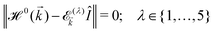 | (4) |
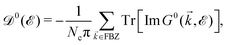 | (5) |
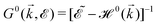 , where
, where 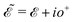 and o+ = 5 meV is the broadening factor. Therefore, one deduces (the expression for each element is too lengthy and has not been presented here):
and o+ = 5 meV is the broadening factor. Therefore, one deduces (the expression for each element is too lengthy and has not been presented here): | (6) |
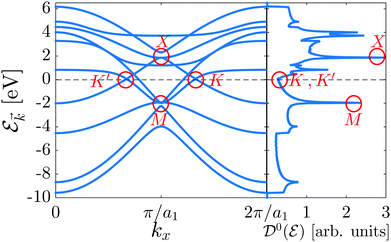
As shown in the electronic band structure of Fig. 2, left panel, the inversion symmetric model contains four high-symmetry points {K, K′, X, M} in the FBZ of β12-borophene for which two massless Dirac fermions are located at K = (2π/3a1, 0), K′ = (2π/3a1, 0) points and two massless and massive triplet fermions occur at M = (π/a1, π/a2) and X = (π/a1, 0) point, respectively. These features introduce the metallic phase of β12-borophene. As is well-known, in the band structure, flat bands corresponding to extremum points introduce the degenerate states in the electronic DOS diagram, resulting in the emergence of van Hove singularities (the highest peaks in DOS). Therefore, in the DOS diagram, right panel of Fig. 2, the van Hove singularity in the conduction band comes from the X point (massive triplet fermion), while in the valence band, the M point (massless triplet fermion) leads to the van Hove singularity. On the other hand, two massless Dirac fermions, as well as the C atomic electronic wave functions, contribute to the metallic phase of the system and DOS curve in the vicinity of the Fermi level (![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) F = 0 eV), as expected. Let us turn to the main aim of the paper, i.e. investigating the anisotropic electrical conductivity.
F = 0 eV), as expected. Let us turn to the main aim of the paper, i.e. investigating the anisotropic electrical conductivity.
3 Anisotropic electrical conductivity
In this section, we intend to briefly review the fundamental physics of electrical conductivity, which, in general, is anisotropic due to the differential form of the Ohm's law Jα = σαβEβ. For the applied electrostatic potential along the β direction, there is an electric density response along the α direction within the linear response theory for which {α, β} ∈ {x, y}.40,41 Since the electric current may respond to the applied electric field in different directions, the electrical conductivity can generally be represented as a tensor: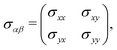 | (7) |
Electrical conductivity relates charge flow to electrostatic potential, both of which need to be specified by direction as well as magnitude – they are vector quantities. Therefore electrical conductivity must be defined in relation to a direction in a crystal, and the magnitude of the electrical conductivity may be different in different directions. Crystalline materials are generally anisotropic, so the magnitude of many physical properties depends on direction in the crystal. The occurrence of anisotropy depends on the symmetry of the crystal structure. Since the β12-borophene monolayer is a crystal with lower symmetry, it is anisotropic for many properties, including thermal and electrical conductivity.
The electrical behavior of matter is expressed by this tensor and can be calculated via the Kubo–Greenwood formula.42–46 In this approach, a general formula to calculate electronic transport coefficients can be obtained from the current–current time–correlation functions using Kubo's quantum-statistical linear response theory,47,48 which will allow the correlation functions to be factorized into products of single-particle Green's functions and their time derivatives. The correlation functions of the electric current operators are defined as:40
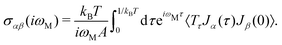 | (8) |
For the purpose of this paper, i.e. the static direct-current density, we focus on the relevant ω → 0 limit. By these means and evaluating the time-auto-correlation function in the Heisenberg picture in the limit of dimension d = 2, one deduces:
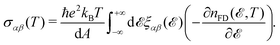 | (9) |
and nFD = 1/[1 + exp(
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) /kBT)] is the Fermi–Dirac distribution function. Also,
/kBT)] is the Fermi–Dirac distribution function. Also, 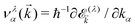 is the group velocity of massless and massive fermions. Here, we have used a widely used conventional system of units ħ = kB = e = 1 and thus the calculated conductivities would be in arbitrary units and show the qualitative behavior of the system.
is the group velocity of massless and massive fermions. Here, we have used a widely used conventional system of units ħ = kB = e = 1 and thus the calculated conductivities would be in arbitrary units and show the qualitative behavior of the system.
To have an idea how the electrical conductivity will allow electricity or thermal energy to travel through β12-borophene, we have plotted the pristine responses along different directions, namely xx, yy and xy in Fig. 3 for an interval of thermal energy 0.1 eV ≤ kBT ≤ 4.9 eV. As is well-known, metals allow heat (thermal energy) to travel through them quite quickly, making them the most conductive among all classes of materials. In conventional metals, the delocalized electrons are free to move within the lattice and an increase in the temperature increases the phonons, which restricts the movement of the delocalized electrons. This, in turn, leads to a decrease in electrical conductivity. However, as mentioned before, although the electrons of boron atoms in the β12-borophene structure are highly delocalized due to the C atoms and the inversion symmetry between atoms, they are bonded to each other with covalent bonds in which the electrons are held in fixed positions. On the other hand, our model is for only pz orbitals, perpendicular to the sheet, so that the heat will generate new channels of motion for electrons concerning those of the isolated single layer. Thereby, it is expected that the conductivity should increase with the heat or thermal energy, as shown in Fig. 3. This is one of the advantageous of pristine β12-borophene for some special purposes.
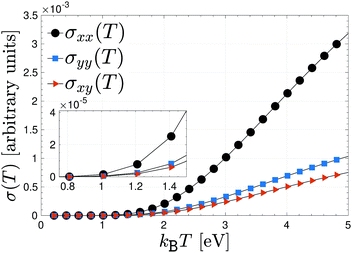 | ||
| Fig. 3 Anisotropic electrical conductivity of pristine β12-borophene as a function of thermal energy kBT. | ||
In the low-thermal energy region, the conductivities are isotropic and almost zero up to 1 eV and a strong anisotropic conductivity, which is increasing linearly with different slopes, appears as soon as the thermal energy is increased further. In fact, in the low-thermal energy limit, there is no priority for the charge carriers in terms of the direction because the thermal energy is not high enough to start the excitation and transition, for this reason, the magnitude of the electrical conductivity may not be different in different directions. Such behavior is the same for all components of eqn (7), however, the highest contribution of electric current stems from the charge current correlation between two different times along the x direction, whereas the lowest one originates from the in-plane component. This implies that the in-plane charge current in β12-borophene sheet does not travel well through it. Note that the xx electric correlation originates mainly from the {K, K′, X} point and the yy case arises mostly from the M point of the FBZ. This helps us to isolate the contribution of FBZ points to the total electrical conductivity of the desired system easily, which has not been done yet to date.
After formulating the electrical conductivity tensor, we will study the effects of the perturbations on the charge current in the next sections. To this end, we consider two perturbation factors, namely a perpendicular electric field and dilute charged impurities, which are present mostly in experimental studies.
4 Electric field effects
As the first perturbation, we consider the electric field. Electric field tunes the electronic features of β12-borophene. We noticed that the β12-borophene is a metal, however, applying the electric field may change the electronic phase. We will consider the case of an electron entering a uniform electric field between two parallel gate plates. The potential difference between the plates is V and the gate plates are aligned along the x-direction and the charge carriers in β12-borophene enter the field at right angles to the field lines. As is well known, there is a force on the electron and depending on the electric field direction, charged particles move if projected into an electric field. Then, the electron orbits accelerate and so lose energy by radiation and therefore slow down and their orbit decreases. For this reason, there are changes in the formed electronic states when the electric field is present and accordingly the electric current and electrical conductivity will be altered as well.Consider two gates with electrostatic potentials V/2 and −V/2 at the top and bottom of the monolayer β12-borophene. Since the pristine dynamics of charge carriers is based on an inversion symmetric model, the effect of gate voltage V on C atoms can be neglected. The electric field effects can be described by a simple TB Hamiltonian model in the real space as:
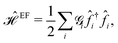 | (10) |
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) i =
i = ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) {A,B,C,D,E} = {V, V, 0, −V, −V}, respectively, is the site-dependent gate potential. Thus, the new electric field-induced Hamiltonian
{A,B,C,D,E} = {V, V, 0, −V, −V}, respectively, is the site-dependent gate potential. Thus, the new electric field-induced Hamiltonian 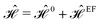 in reciprocal-space is given by
in reciprocal-space is given by | (11) |
 | (12) |
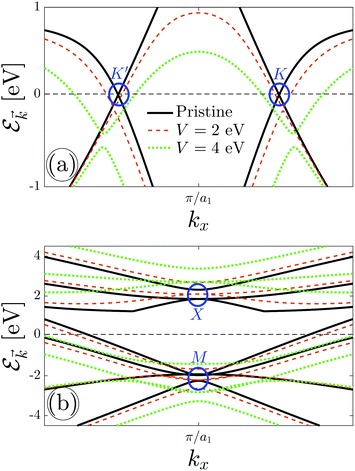
The results for electronic band structure in the presence of an electric field are shown in Fig. 4. For the sake of convenience, we plot Dirac fermions at {K, K′} points and triplet ones at {X, M} points separately in Fig. 4(a) and (b), respectively. At first glance, it is observed that the energy gap of the massless Dirac points increases with increasing the electric field, see Fig. 4(a). The possible energy for charge carriers in the case of pristine β12-borophene is from −10 eV to +6 eV, however, applying the perpendicular electric field widens it due to the band gap opening. This, in turn, manifests itself in the position and height of van Hove singularities in DOS, which are not shown here. On the other hand, Fig. 4(b) tells us the massive triplet fermions at the X point do not feel any transition and their energy position is shifted up only, while in the valence band, the massless triplet fermions at the M point convert to the massive ones. This effective mass transition affects the total charge current of the system as well as the conductivities. Considerably, this change in dispersion provides deviations in the behavior of the temperature-dependent electrical conductivities. One could state that considering the perpendicular electric field on the C atoms may change these treatments. The C atoms may indeed come into play role in charge screening effects, which prevents such transitions, however, the inversion symmetry between other atoms concerning the C atom confirms that the results will not be changed significantly.
We know that the formulated perpendicular electric field stems from the gate voltage, which across a high conductivity (x direction) will produce a large amount of current, as well as across a low conductivity (in-plane) will produce a smaller amount of electric current. The voltage is the push that causes the current to flow. So, it is expected to have an increasing trend for σxx as well as a decreasing trend for σxy with V at strong enough potentials.
Fig. 5 depicts the voltage participation in the electrical conductivities of the desired system for the given thermal energy kBT = 3 eV. Noticeably, all components do not exhibit the same behavior concerning the voltage and σxx is enhanced more compared to other ones. To compare the values of conductivities in the absence and presence of the perpendicular electric field, we use the percentage difference value between the initial value of σ at V = 0 eV and its minimum as well as its maximum value. In contrast to the pristine sheet, the calculations show that the conductivity along the x direction is enhanced around 18.53% at V = 4 eV, while it is reduced around 3.73% at V = 2 eV. On the other hand, the yy component is not enhanced and a reduction around 7.32% is observed at V = 3 eV. As for the in-plane conductivity, an enhancement around 15.38% is evident at V = 1.4 eV while at strong electric fields, σxy is decreased significantly around 104.76% compared to the pristine case.
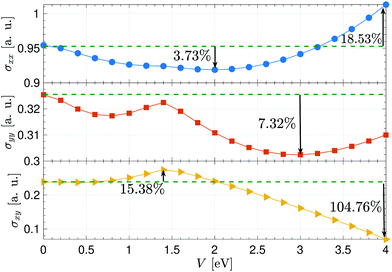 | ||
| Fig. 5 Anisotropic electrical conductivity of electric field-induced β12-borophene as a function of electrostatic potential V at the thermal energy kBT = 3 eV. | ||
Another remarkable point in every curve is the contribution of each point of FBZ to the conductivities. The findings here illustrate that the {K, K′, X} points play vital roles in the enhanced conductivity of the system compared to M points, which would be useful in real applications. Conductivities portrayed in Fig. 5 are for intermediate thermal energies, however, similar behavior could be shown for more or less supplied thermal energies. Further, it is worthwhile mentioning that overlapping non-hybridized pz electrons are modulated by the gate voltage and emergence of the band gap in the energy dispersion of the system allows it to be switched off. The consequence of raising the possibility of charge movements using a perpendicular electric field would logically be an enhancement for β12-borophene as a reliable material for future electronic devices.
It can be seen that the electrical conductivity is susceptible to external physical perturbation. Let us consider another perturbation to complete the present study and to make it closer to experimental expectations.
5 Dilute charged impurity scattering effects
Now in this section, to inspect the impurity doping effects, we need to be equipped with sufficient tools to compare the electrical conductivity of the pristine and impurity-containing β12-borophene. In doing so, the Born approximation and the T-matrix theory are used, wherein the impurity concentration ni and impurity scattering (IS) potential νi are the new variables to be considered. Consider a monolayer β12-borophene subjected to many charged impurity atoms with low-density concentrations. The average over their random local configuration is taken into account, meaning that the location of the impurity is not of consequence any more in the present paper. The short-range potential induced by the impurities is introduced as a Dirac delta function potential with the constant parameter νi in the reciprocal space, given by:| U = νiÎ, | (13) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ), describing the electronic correlation between guest electrons, depends only on the energy, given by:40,41
), describing the electronic correlation between guest electrons, depends only on the energy, given by:40,41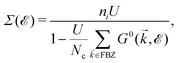 | (14) |
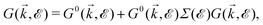 | (15) |
When the concentration of impurities is relatively dilute, electron-impurity scattering may introduce discrete energy levels. However, as the impurity density increases, additional bands may form. These levels broaden into impurity bands when the concentration of impurities increases. In realistic systems, the DOSs near the minima or maxima of bands strongly depend on the electron-impurity scattering. From the physical point of view, midband and midgap states appear in the DOS of the system when impurities are present. In the case of our pristine system, which is metallic, midband states take place. As for the origin of midband and midgap states, the DOS relation tells us that the impurity-induced DOS is related to the poles of interacting Green's functions containing the poles of self-energy. Thus, the new poles associated with impurities come into play role in impurity-induced DOS at energy ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) IS satisfying the equation:
IS satisfying the equation:
det[1 − UḠ0(![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) IS)] = 0. IS)] = 0. | (16) |
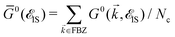 . The solution of this equation leads to the midband and midgap states. Using the perturbed Green's functions, we investigate the electrical conductivity of the monolayer β12-borophene lattice for two scenarios: (i) the same impurity atoms characterized by different ni and the same νi and (ii) different impurity atoms characterized by different νi and the same ni. Note that the Born approximation may fail to describe the system at higher scattering potentials and impurity concentrations, from this point, our model remains valid only for low limits of impurities. Let us analyze each scenario in detail.
. The solution of this equation leads to the midband and midgap states. Using the perturbed Green's functions, we investigate the electrical conductivity of the monolayer β12-borophene lattice for two scenarios: (i) the same impurity atoms characterized by different ni and the same νi and (ii) different impurity atoms characterized by different νi and the same ni. Note that the Born approximation may fail to describe the system at higher scattering potentials and impurity concentrations, from this point, our model remains valid only for low limits of impurities. Let us analyze each scenario in detail.
Immediately, eqn (5) will make the electronic DOS of the system available. For the present paper, bearing in mind that the electronic phase transition occurs around the Fermi level ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 0 eV, we calculate
= 0 eV, we calculate ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0) to see whether the presence of foreign impurity atoms alters the electronic phase of the system or not. It is noted that different values of impurity concentrations refer to the same impurity types, while different values of impurity scattering potential refer to the various impurity types. The difference between the on-site energies of boron atoms and doping atoms directly affects the value of
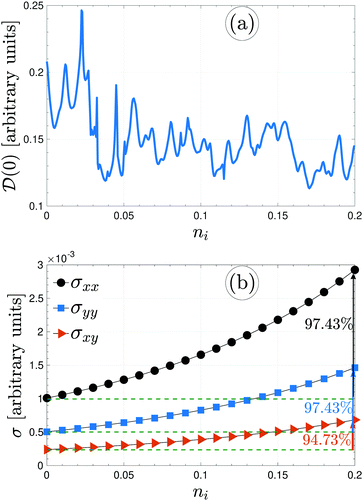
(0) to see whether the presence of foreign impurity atoms alters the electronic phase of the system or not. It is noted that different values of impurity concentrations refer to the same impurity types, while different values of impurity scattering potential refer to the various impurity types. The difference between the on-site energies of boron atoms and doping atoms directly affects the value of ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0). Fig. 6(a) illustrates that ni will inherently increase and the value of DOS decreases at
(0). Fig. 6(a) illustrates that ni will inherently increase and the value of DOS decreases at ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 0 eV and fluctuates depending on the ni. This can be understood from this fact that the qualitative shape of the DOS depends on impurities because the total number of available states corresponds to the area under the curve of the DOS, which is proportional to the electron density of the system. Changing the number of available states at the Fermi level then leads to different values of
= 0 eV and fluctuates depending on the ni. This can be understood from this fact that the qualitative shape of the DOS depends on impurities because the total number of available states corresponds to the area under the curve of the DOS, which is proportional to the electron density of the system. Changing the number of available states at the Fermi level then leads to different values of ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0). Alongside,
(0). Alongside, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0) does not become zero for the dilute regime of impurities, meaning that the system is still metallic. Having obtained these analytical results, it is now time to calculate the electrical conductivity tensor of β12-borophene when the same impurity atoms are doped, and then compare them with that of the pristine case.
(0) does not become zero for the dilute regime of impurities, meaning that the system is still metallic. Having obtained these analytical results, it is now time to calculate the electrical conductivity tensor of β12-borophene when the same impurity atoms are doped, and then compare them with that of the pristine case.
Inspecting Fig. 6(b), the direction-dependent electrical conductivity of the pristine and the same impurity-doped β12-borophene could be compared at a given thermal energy kBT = 3 eV. For the case of the same impurities with the scattering potential νi = 100 meV, the impurity concentration ni is changed up to 0.2. This figure shows that all components of the conductivity increase by doping the same impurity atoms. The potential created by impurities behaves as a barrier or well for host electrons (against the motion of the electrons) depending on the sign of νi. The scattering amplitude of the pure system's electrons is increased with impurity level. However, the strength of νi = 0.1 eV is not high enough to act as a barrier or well and it is expected that the conductivities be increased with ni, as confirmed in Fig. 6(b). On the other hand, from Fig. 6(a), we noticed that the electronic phase of the system is not changed and the ni system is metallic. So the σ must be increased with ni. It is observed that random doping by the same impurities leads a 97.43% and 94.73% enhancement for the xx/yy and xy component of electrical conductivity of β12-borophene, respectively.
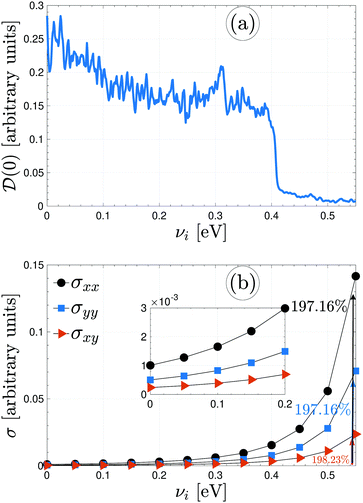
Plotted in panels (a) and (b) of Fig. 7 are the perturbed electronic DOS at the Fermi level and the perturbed electrical conductivity components of β12-borophene via different impurity atoms, respectively. Fig. 7(a) shows that ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0) decreases with increasing the scattering potential of impurities from 0 to 0.55 eV (higher energies are not allowed because of the Born approximation) and approaches zero for sure, resulting in an electronic phase transition from metal to p-doped semiconductor (because νi > 0). As easily conceivable from this decreasing trend of
(0) decreases with increasing the scattering potential of impurities from 0 to 0.55 eV (higher energies are not allowed because of the Born approximation) and approaches zero for sure, resulting in an electronic phase transition from metal to p-doped semiconductor (because νi > 0). As easily conceivable from this decreasing trend of ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (0), adding stronger νi provides more distracting paths for moving electrons. On the other hand, the changing in the DOS could also be a result of significant variations in the low energy band structure. Eventually, less σ is expected for νi > 0.5 eV. However, up to the dilute limit, all components are increasing with νi. While a 197.16% enhancement is found for xx/yy components, a 198.23% enhancement is observed for the in-plane one.
(0), adding stronger νi provides more distracting paths for moving electrons. On the other hand, the changing in the DOS could also be a result of significant variations in the low energy band structure. Eventually, less σ is expected for νi > 0.5 eV. However, up to the dilute limit, all components are increasing with νi. While a 197.16% enhancement is found for xx/yy components, a 198.23% enhancement is observed for the in-plane one.
Comparing Fig. 6 and 7 reveals that the contribution of different impurity atoms to the electrical conductivity of β12-borophene is more than for the same impurity atoms, which could be a consequence of relatively higher limitation on the path of propagating electrons in the presence of the same impurities. Further, we are at a point to conclude that the enhancement of conductivity of the system when doping impurities (either the same or different ones) randomly is more significant than the electric field.
6 Summary
In summary, we have investigated the effect of electric field and dilute charged impurities on the electronic properties of the β12-borophene monolayer using the tight-binding model combined with the T-matrix scattering theory, the linear response theory, and the Green's function approach. In particular, the novel electronic phase and the anisotropic electrical conductivity arising from the changed bonding and anti-bonding mechanisms are explored. Based on a metal to p-doped semiconductor phase transition occurring via the electric field, at a given temperature, we found an enhanced x- and in-plane-component of the electrical conductivity around 18.53% and 15.38%, respectively. However, we achieved a better enhancement of about 197.16% and 198.23%, respectively, for these conductivities when different dilute charged impurities are doped randomly to the β12-borophene surface. Our results have important implications for designing new logic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant No. 103.01-2017.361.References
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef CAS.
- C.-C. Liu, H. Jiang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195430 CrossRef.
- M. Ezawa, Phys. Rev. Lett., 2012, 109, 055502 CrossRef PubMed.
- L. Tao, E. Cinquanta, D. Chiappe, C. Grazianetti, M. Fanciulli, M. Dubey, A. Molle and D. Akinwande, Nat. Nanotechnol., 2015, 10, 227 CrossRef CAS PubMed.
- L. Li, S.-z. Lu, J. Pan, Z. Qin, Y.-q. Wang, Y. Wang, G.-y. Cao, S. Du and H.-J. Gao, Adv. Mater., 2014, 26, 4820 CrossRef CAS PubMed.
- M. Derivaz, D. Dentel, R. Stephan, M.-C. Hanf, A. Mehdaoui, P. Sonnet and C. Pirri, Nano Lett., 2015, 15, 2510 CrossRef CAS PubMed.
- F. Zhu, W. Chen, Y. Xu, C. Gao, D. Guan, C. Liu, D. Qian, S.-C. Zhang and J. Jia, Nat. Mater., 2015, 14, 1020 CrossRef CAS PubMed.
- B. Feng, H. Li, C.-C. Liu, T.-N. Shao, P. Cheng, Y. Yao, S. Meng, L. Chen and K. Wu, ACS Nano, 2013, 7, 9049 CrossRef CAS PubMed.
- Y. Xu, B. Yan, H.-J. Zhang, J. Wang, G. Xu, P. Tang, W. Duan and S.-C. Zhang, Phys. Rev. Lett., 2013, 111, 136804 CrossRef PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033 CrossRef CAS PubMed.
- F. Xia, H. Wang and Y. Jia, Nat. Commun., 2014, 5, 4458 CrossRef CAS PubMed.
- C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423 CrossRef.
- S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112 CrossRef CAS PubMed.
- C. Kamal, A. Chakrabarti and M. Ezawa, New J. Phys., 2015, 17, 083014 CrossRef.
- M. H. Evans, J. D. Joannopoulos and S. T. Pantelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045434 CrossRef.
- H. Tang and S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115412 CrossRef; H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443 CrossRef CAS PubMed.
- E. S. Penev, S. Bhowmick, A. Sadrzadeh and B. I. Yakobson, Nano Lett., 2012, 12, 2441 CrossRef CAS PubMed.
- H. Liu, J. Gao and J. Zhao, Sci. Rep., 2013, 3, 3238 CrossRef PubMed.
- Y. Liu, E. S. Penev and B. I. Yakobson, Angew. Chem., Int. Ed., 2013, 52, 3156 CrossRef CAS PubMed.
- Z. Zhang, Y. Yang, G. Guo and B. I. Yakobson, Angew. Chem., Int. Ed., 2015, 54, 13022 CrossRef CAS PubMed.
- M. Ezawa, Phys. Rev. B, 2017, 96, 035425 CrossRef.
- P. T. T. Le, T. C. Phong and M. Yarmohammadi, Phys. Chem. Chem. Phys., 2019, 21, 21790 RSC.
- B. Feng, O. Sugino, R.-Y. Liu, J. Zhang, R. Yukawa, M. Kawamura, T. Iimori, H. Kim, Y. Hasegawa and H. Li, et al. , Phys. Rev. Lett., 2017, 118, 096401 CrossRef PubMed.
- B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563 CrossRef CAS PubMed.
- B. Feng, J. Zhang, R.-Y. Liu, T. Iimori, C. Lian, H. Li, L. Chen, K. Wu, S. Meng, F. Komori and I. Matsuda, Phys. Rev. B, 2016, 94, 041408(R) CrossRef.
- H. Tang and S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134113 CrossRef.
- C. Özdoğan, S. Mukhopadhyay, W. Hayami, Z. B. Güenç, R. Pandey and I. Boustani, J. Phys. Chem. C, 2010, 114, 4362 CrossRef.
- B. Peng, H. Zhang, H. Shao, Z. Ning, Y. Xu, G. Ni, H. Lu, D. W. Zhang and H. Zhu, Mater. Res. Lett., 2017, 5(6), 399 CrossRef CAS.
- H. D. Bui, L. T. T. Phuong and M. Yarmohammadi, EPL (Europhys. Lett.), 2018, 124(2), 27001 CrossRef.
- M. Yarmohammadi, Phys. Rev. B, 2018, 98(15), 155424 CrossRef CAS.
- H. D. Bui and M. Yarmohammadi, J. Magn. Magn. Mater., 2018, 465, 646 CrossRef CAS.
- B. D. Hoi and M. Yarmohammadi, Phys. Lett. A, 2018, 382, 3298 CrossRef CAS.
- P. T. T. Le and M. Yarmohammadi, Chem. Phys., 2019, 519, 1 CrossRef CAS.
- P. T. T. Le, M. Davoudiniya and M. Yarmohammadi, Phys. Chem. Chem. Phys., 2019, 21, 238 RSC.
- B. D. Hoi and M. Yarmohammadi, Europhys. Lett., 2018, 122(1), 17005 CrossRef.
- C. C. Lee, B. Feng, M. D’angelo, R. Yukawa, R.-Y. Liu, T. Kondo, H. Kumigashira, I. Matsuda and T. Ozaki, Phys. Rev. B, 2018, 97(7), 075430 CrossRef CAS.
- X. Zhang, J. Hu, Y. Cheng, H. Y. Yang, Y. Yao and S. A. Yang, Nanoscale, 2016, 8(33), 15340 RSC.
- G. D. Mahan, Many Particle Physics, Plenum Press, New York, 1993 Search PubMed.
- G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, New York, 2nd edn, 2014 Search PubMed.
- B. Velicky, Phys. Rev., 1969, 184, 614 CrossRef CAS.
- S. F. Edwards, Philos. Mag., 1958, 3(33), 1020 CrossRef CAS.
- S. F. Edwards, Philos. Mag., 1959, 4(46), 1171 CrossRef CAS.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570 CrossRef.
- D. A. Greenwood, Proc. Phys. Soc., 1958, 71, 585 CrossRef CAS.
- V. Christoph and G. Ropke, Phys. Status Solidi B, 1985, 131, 11 CrossRef CAS.
- D. Zubarev, D. Zubarev, V. Morozov and G. Ropke, Statistical Mechanics of Nonequilibrium Processes, Volume 1 (See 3527400834): Basic Concepts, Kinetic Theory, Statistical Mechanics of Nonequilibrium Processes, Wiley, 1996 Search PubMed.
| This journal is © the Owner Societies 2020 |

![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)