Theoretically predicted surface morphology of FCC cobalt nanoparticles induced by Ru promoter†
Lili
Liu
 ab,
Mengting
Yu
ab,
Qiang
Wang
ab,
Mengting
Yu
ab,
Qiang
Wang
 *a,
Bo
Hou
*a,
Bo
Hou
 a,
Litao
Jia
ac,
Congbiao
Chen
a and
Debao
Li
*ac
a,
Litao
Jia
ac,
Congbiao
Chen
a and
Debao
Li
*ac
aState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, No.27 South Taoyuan Road, Taiyuan, Shanxi 030001, People's Republic of China. E-mail: wqiang@sxicc.ac.cn; dbli@sxicc.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, People's Republic of China
cDalian National Laboratory for Clean Energy, Dalian, 116023, China
First published on 14th November 2019
Abstract
The experimental shape control of metallic Co nanoparticles (NPs) remains a great challenge in terms of their direct characterization for the further rational design and optimization of efficient nanocatalysts nowadays, especially when a low promoter content is involved. Thus, spin-polarized density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulations have been carried out to investigate the adsorption configurations and growth trend of Run clusters on Co surfaces to systemically explore the surface morphology of Co NPs induced by Ru promotion in Co-based Fischer–Tropsch synthesis (FTS). The predicted Run aggregation adsorption patterns on Co(100) and Co(110) surfaces combined with the recent results for Co(111) and Co(311) surfaces show the thermodynamic growth tendency that Run aggregates are favorable for planar layered growth on Co surfaces under realistic FTS reaction conditions, which is consistent with the experimental EELS spectral results. The addition of Ru promoter has an important role in tuning the stability of the exposed facets of face-centered-cubic (FCC) Co NPs, accompanied by the change from truncated octahedron to rhombic dodecahedron morphology. At high Ru content, the increased high index Co(311) and Co(110) surfaces, including more active step and kink sites, are desirable for the enhanced activity of FCC Co NPs.
1. Introduction
With the increasing demand for and limited availability of petroleum resources, alternative and sustainable routes starting with synthesis gas (CO + H2) derived from coal, natural gas, or biomass to produce chemicals and fuels are more desirable.1,2 The typical process based on synthesis gas is Fischer–Tropsch synthesis (FTS),3–5 a heterogeneous catalytic technique for the production of clean transportation fuels and various hydrocarbons by different catalysts.6–9 Co-based catalysts are promising for long-chain hydrocarbons and distinguished from other FTS catalysts by higher intrinsic activity, higher selectivity towards paraffin, higher resistance toward deactivation and lower activity for the competing water gas shift reaction.10–13 Cobalt catalysts for industrial applications usually contain not only catalytically active cobalt and supports, but also small amounts of promoters to improve the activity, selectivity, and stability of the catalysts.14–17Modification of catalysts with promoters, especially noble metals, shows great promise to attain optimum catalytic performance through changing the structure, size and dispersion or modifying the electronic characters of the active phase.18–20 Extensive studies, including detailed characterization, have suggested that enhanced Co reducibility and higher selectivity for heavier (C5+) hydrocarbons could be achieved by adding ruthenium promoter to cobalt catalysts.21–23 Balakrishnan et al. found that Ru promoted Co catalysts exhibit higher catalytic stability because the Ru inhibits the C–C coupling reaction and prevents the deposition and growth of C species on the catalyst surface.24 The addition of Ru can also shift the temperature required to reduce cobalt oxide to the metallic state to a significantly lower temperature, resulting in a higher Co site density during FTS catalysis.25,26 In contrast to the decreased TOF by the introduction of Pd and Pt, the turnover frequency (TOF) based on a Ru modified Co surface evaluated by H2 uptake is increased to some extent, owing to the increased bridge-type adsorption of CO facilitating the dissociation of CO into carbon and oxygen.27
Several groups of researchers have been devoted to investigating the location and distribution of the Ru promoter in reduced cobalt catalysts, aiming to unveil the significant functioning mechanisms of the involvement of Ru promotion and the interaction of Co and Ru in FTS reaction. The experimental results obtained with Ru, Re, Pt, and Ir promoters as reduction promoters revealed that the majority of the promoter introduced by co-impregnation with cobalt remains monometallic particles located in the microscopic structure of the cobalt catalysts.23,28–30 Iglesia et al. disclosed the formation of intermetallic particles rather than CoRu alloy during the precursor solution reduction process.31,32 They believed that Ru promoter added in a separate second step of the oxidation–reduction procedures would lead to separate Co and Ru phases and a large fraction of the Ru remaining exposed near the outer crystallite surfaces after calcination. This was demonstrated subsequently by Ru K-edge EXAFS radial distribution functions with Ru as the reduction promoter by Kungurova et al.33 A recent report has concluded that the Ru aggregates precipitated as individual atoms or as small clusters on the surface of the Co NPs after a two-step reduction process of Co precursors.34
Although the promotion role and the location of Ru in Co-based catalysts has been recognized, such surface structures of Ru promoters on metallic Co and the morphology of Co NPs decorated by Ru promoter still represent a great challenge for direct characterization, even if Ru was identified in patches on Co particles by EELS spectrum imaging by Shannon et al.35 Since it is experimentally difficult to study the properties of individual NPs at the atomic level, theoretical approaches are highly suitable to provide information about the structure and morphology of NPs.36,37 Many excellent theoretical studies have been successfully conducted concerning the equilibrium morphology of metal NPs in reaction conditions, such as: metallic Fe and iron carbide promoted by K2O,38,39 Cu NPs supported by ZnO,36 Pt NPs etched by HCl,40 Ru NPs under a hydrogen atmosphere,41 and Pd, Pt, and Rh NPs under NO and CO gas environments.42 However, there is no systematic investigation offering atomic information regarding the structures of Ru promoters on Co NPs. The stabilized effect of the Ru promoter on the morphology of Co NPs was also generally neglected in previous experimental studies.43 Therefore, it is necessary to apply a theoretical model to predict the morphology evolution of Co NPs induced by Ru promoter.
In this work, we investigated the structures and adsorption pattern of Run clusters on Co(100) and Co(110) surfaces based on spin-polarized density functional theory calculations and ab initio molecular dynamics simulations, and combined with those recently reported results on Co(111) and Co(311) surfaces,44 with the aim of further systematically determining the morphology evolution of face-centered-cubic (FCC) Co NPs stabilized by Ru promoter. The elucidation of the facet-dependent equilibrium morphology of Ru-promoted metallic Co NPs is expected to provide useful guidance for advanced experimental characterization, which is important for understanding the effect of Ru promoter in Co-based FTS.
2. Computational details
2.1 Models
FCC crystalline cobalt was chosen as the model in view of its excellent stability and FTS activity with a diameter <20 nm. The determined equilibrium lattice constant of FCC Co is 3.53 Å, which is consistent with the experimental result45 (3.55 Å) and theoretical value (3.52 Å,46 3.54 Å47). The Co surface was modeled by periodic slabs consisting of four layers in the (100) surface and six layers in the (110) surface, with p(4 × 4) and p(3 × 4) supercells in lateral directions, respectively. The optimized structures of Co(100) and Co(110) surfaces as well as the possible adsorption sites are shown in Fig. S1.† During the computational process, the Ru atoms and upper two atomic layers were relaxed without any symmetry or direction restrictions to optimize the surface structure, while the remaining atoms were frozen to simulate the bulk structure for the description of Run adsorption on Co surfaces. The Brillouin zone integration was achieved by summation over specially selected k-points using the Monkhorst-Pack scheme,48 where (9 × 9 × 9) and (3 × 3 × 1) k-point meshes were chosen for bulk and Co surfaces, respectively. The vacuum region of 15 Å was applied to prevent interactions between the periodically repeating slabs.2.2 Methods
All the static calculations were carried out by spin-polarized density functional theory (DFT) implemented in the Vienna Ab Initio Simulation Package (VASP).49,50 The exchange correlation energy of the electrons was treated within the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerh (PBE) of exchange–correlation functional.51 The interactions between ion cores and valence electrons were described by the projector augmented wave (PAW) method.52,53 The solution of the Kohn–Sham equations was expanded in a plane-wave basis set with a cutoff energy of 400 eV. Final convergence criteria for the energy and Hellmann–Feynman forces were 10−5 eV and 0.03 eV Å−1, respectively. Bader charge analysis54,55 was carried out to obtain the effective charge of different atoms in the Run adsorption system. The location and energy of transition states (TSs) of the Ru atom diffusion were determined with the climbing image nudged elastic band (CI-NEB) method,56 and the vibrational frequencies were analyzed to confirm the transition state with only one imaginary frequency. In addition, ab initio molecular dynamics (AIMD) simulations were performed to probe the growth trend of the Ru nanoclusters on the Co surfaces within the NVT canonical ensemble. A detailed description of the AIMD simulations is available in the literature.443. Results and discussion
3.1 Morphology and surface stability of pure FCC Co NPs
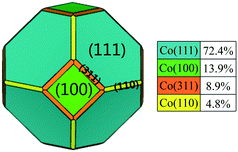
The pure FCC Co unit cell adopts a space point group of Oh with high symmetry. The equilibrium shape and relative surface distribution of FCC Co were obtained by Wulff construction based on the bulk symmetries and calculated surface energies. As shown in Fig. 1, FCC Co exhibits a regular truncated octahedron shape and contains four different facets. It is covered predominantly with eight close-packed (111) facets, accounting for about 72.4% of the total surface area. The remaining three exposed facts, (100), (311) and (110), cover relatively smaller fractions of surface area, namely, 13.9%, 8.9%, and 4.8%, respectively. The stability order of the exposed facets follows the ascending order: Co(110) < Co(311) < Co(100) < Co(111) with surface energies of 0.161, 0.158, 0.157 and 0.132 eV Å−2, respectively, where Co(111) is the most stable surface and Co(311) is the least stable surface. It is worth noting that the metal-promoters interaction under operating conditions might affect the corresponding morphology, stability and reactivity of exposed crystallographic facets. Therefore, it is necessary to explore the effect of Ru promoter on the structure and morphology of Co NPs in real FTS conditions.3.2 Structure and adsorption pattern of Run clusters on FCC Co
The investigation of the Run adsorption on Co(100) and Co(110) surfaces combined with previous studies on the Co(111) and Co(311) surfaces44 is expected to build a comprehensive understanding of the morphology of Ru-promoted Co NPs. For Run adsorption on Co surfaces, both two-dimensional monolayer structures and three-dimensional structures with partial Ru atoms deposited on Co surfaces were examined. Possible initial structures for Run cluster adsorption on Co surfaces at different coverages were constructed and optimized to find the most preferred Run adsorption pattern, as presented in Fig. S2 and S3.† The most stable adsorption configurations of Run (n = 1–8) clusters on Co(100) and Co(110) surfaces are shown in Fig. 2 and 3, and the energetic results along with the structural information are listed in Tables 1 and 2.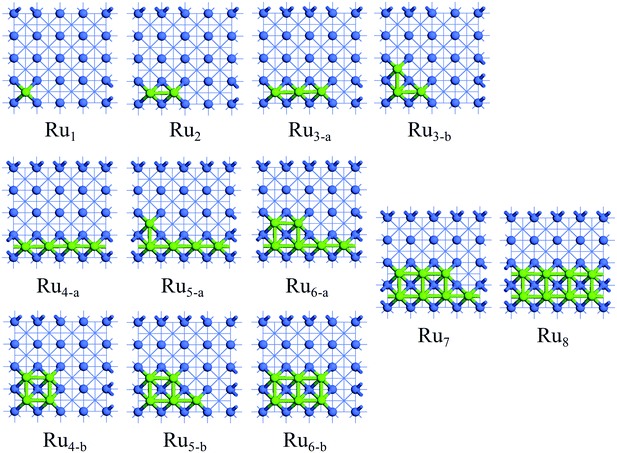 | ||
| Fig. 2 The stable adsorption configurations of Run (n = 1–8) on Co(100) surface. The Co and Ru atoms are shown as blue and light green spheres, respectively. | ||
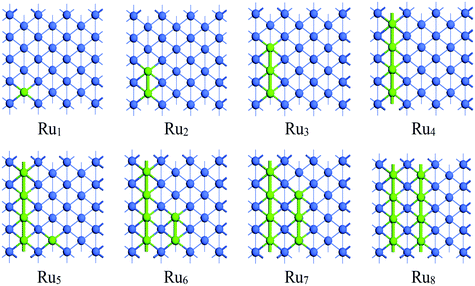 | ||
| Fig. 3 The stable adsorption configurations of Run (n = 1–8) on Co(110) surface. The Co and Ru atoms are shown as blue and light green spheres, respectively. | ||
| Run | E(Run/ads) | E(Ruads/av) | ΔE(Ruads) | E agg | E growth | E int(Ruads) | E int(Ru–Co) | E int/av(Ru–Co) | d Ru–Ru | q |
|---|---|---|---|---|---|---|---|---|---|---|
| Ru1 | −5.26 | −5.26 | −5.26 | −6.45 | −6.45 | −0.18 | ||||
| Line-based adsorption pattern | ||||||||||
| Ru2-a/b | −10.76 | −5.38 | −5.51 | −0.12 | −0.25 | −0.25 | −7.29 | −3.65 | 2.57 | −0.19 |
| Ru3-a | −16.51 | −5.50 | −5.74 | −0.25 | −0.49 | −0.74 | −12.17 | −4.06 | 2.53 | −0.21 |
| Ru4-a | −22.76 | −5.69 | −6.25 | −0.43 | −0.99 | −1.73 | −14.10 | −3.53 | 2.51 | −0.18 |
| Ru5-a | −28.46 | −5.69 | −5.70 | −0.44 | −0.45 | −2.18 | −16.26 | −3.25 | 2.51 | −0.16 |
| Ru6-a | −34.96 | −5.83 | −6.50 | −0.57 | −1.24 | −3.42 | −16.92 | −2.82 | 2.46 | −0.14 |
| Square-based adsorption pattern | ||||||||||
| Ru3-b | −16.40 | −5.47 | −5.63 | −0.21 | −0.38 | −0.63 | −10.94 | −3.65 | 2.52 | −0.15 |
| Ru4-b | −22.92 | −5.73 | −6.52 | −0.47 | −1.26 | −1.89 | −11.56 | −2.89 | 2.41 | −0.10 |
| Ru5-b | −28.64 | −5.73 | −5.72 | −0.47 | −0.47 | −2.36 | −15.04 | −3.01 | 2.46 | −0.11 |
| Ru6-b | −34.91 | −5.82 | −6.27 | −0.56 | −1.00 | −3.36 | −16.76 | −2.79 | 2.47 | −0.11 |
| Ru7-a/b | −41.27 | −5.90 | −6.36 | −0.64 | −1.11 | −4.47 | −19.10 | −2.73 | 2.48 | −0.13 |
| Ru8-a/b | −48.16 | −6.02 | −6.89 | −0.76 | −1.63 | −6.11 | −19.64 | −2.46 | 2.47 | −0.12 |
| 3D structures | ||||||||||
| Ru5-c | −28.16 | −5.63 | −0.38 | −1.88 | −12.02 | −2.40 | 2.49 | −0.07 | ||
| Ru6-c | −33.98 | −5.66 | −0.41 | −2.44 | −15.20 | −2.53 | 2.50 | −0.07 | ||
| Ru7-c | −40.40 | −5.77 | −0.52 | −3.61 | −17.48 | −2.50 | 2.50 | −0.09 | ||
| Ru8-c | −46.79 | −6.68 | −0.59 | −4.74 | −19.17 | −2.40 | 2.51 | −0.10 | ||
| Run | E(Run/ads) | E(Ruads/av) | ΔE(Ruads) | E agg | E growth | E int(Ruads) | E int(Ru–Co) | E int/av(Ru–Co) | d Ru–Ru | q |
|---|---|---|---|---|---|---|---|---|---|---|
| Ru2 | −11.45 | −5.72 | −6.03 | −0.31 | −0.62 | −6.39 | −8.46 | −4.23 | 2.52 | −0.17 |
| Ru3 | −17.56 | −5.85 | −6.11 | −0.44 | −0.69 | −9.97 | −12.98 | −4.33 | 2.50 | −0.18 |
| Ru4 | −24.47 | −6.12 | −6.91 | −0.70 | −1.50 | −14.36 | −15.71 | −3.93 | 2.50 | −0.20 |
| Ru5 | −29.89 | −5.98 | −5.42 | −0.56 | −0.01 | −17.26 | −20.40 | −4.08 | 2.49 | −0.17 |
| Ru6 | −35.98 | −6.00 | −6.09 | −0.58 | −0.68 | −20.82 | −22.43 | −3.74 | 2.49 | −0.15 |
| Ru7 | −42.11 | −6.02 | −6.13 | −0.60 | −0.71 | −24.42 | −26.28 | −3.68 | 2.50 | −0.14 |
| Ru8 | −48.90 | −6.11 | −6.79 | −0.70 | −1.37 | −28.68 | −28.33 | −3.54 | 2.50 | −0.16 |
The adsorption pattern of Run on Co(110) surface is quite different from that on Co(100) surface owing to its corrugated surface structure. A single Ru atom favors adsorbing at the five-fold (5F) site at the corrugated bottom on Co(110) surface. Further addition of Ru atoms to the 5F site prior to other sites was confirmed. For the adsorption of Run (n = 1–4), the newly added Ru atoms of the most stable adsorption configuration are adsorbed with direct Ru–Ru interactions along the corrugated direction, gradually forming a linear chain on Co(110) surface. On further addition of Ru atoms, due to the limitation of surface size, the most stable aggregated Run clusters (n = 5–8) become another parallel independent chain with all of the Ru atoms adsorbed at the 5F sites. The most stable adsorption configuration Ru8 is the double-chained structure, which can be regarded as the combination of two Ru4 structures. Therefore, it can be inferred that the initial adsorption of the Ru atoms on Co(110) surface is in the line-band-layer pattern and a monolayer Ru covered surface can be expected at high coverage.
The two-dimensional dispersed configurations were also investigated for the Run adsorption on Co(100) and Co(110) surfaces, higher in energy than that of the aggregated configurations, indicating the strong aggregation ability of Ru atoms. In addition, the three-dimensional clusters are found to be energetically less stable than the most stable two-dimensional isomers, owing to their higher surface energies caused by the more edge and vertex atoms. To verify this conclusion, the possible structures and energies of the large Ru11 clusters were calculated. The most stable Ru11 adsorption configurations on Co(100) and Co(110) surfaces are presented in Fig. S4 and S5† and are found to be in line with the above obtained adsorption mechanism.
Generally, the Co–Ru interaction affected by the distinct Co surface structures is reflected in the hybrid d orbitals between the Co and Ru, as shown in Fig. S6.† The projected d orbitals of the Co(100) and Co(110) surfaces shifted towards a lower energy after Run adsorption, leading to the electronic loss of Co surfaces. In addition, there is a stronger d-orbital mixing near the Fermi level between the adsorbed Ru11 cluster on Co(110) surface than on Co(100) surface, implying the stronger binding strength between the Co(110) surface and the Ru11 cluster, coinciding with the trend of adsorption energies. The results of the electronic properties analysis suggest that compared with the flat Co(111) and Co(100) surfaces, the corrugated Co(311) and Co(110) surfaces have stronger Ru/Co interaction, accompanied by more electron transfer, which conforms to the trend of adsorption energy.
It can be obtained from the data of Tables S1 and S2† that Co(110) surface has the strongest affinity and aggregation potential of Run at low coverage, while the affinity of the Co(100) surface becomes stronger and the aggregation potential of Co(111) surface becomes higher as the Run size increases. Based on the results of the calculated interaction energies, it is found that the Ru–Ru interaction increases while the average Ru–Ru bond gradually decreases as the Run cluster becomes larger, indicating that the increased stability is accompanied by the increased Run cluster size. Although the interaction energy between each Ru adatom and both Co surfaces decreases, the total interaction energy between the Run cluster and both Co surfaces increases with increasing adsorbed Ru atoms. Therefore, the bonding of Run clusters and Co surfaces is enhanced. In addition, the value of growth energies of the Run clusters adsorbed on Co surfaces decreases with the increase in size of the Run cluster. Growth of Run clusters on Co surfaces is thermodynamically favorable and exothermic. With the Run cluster size increasing, the growth characteristics of the Run clusters on Co surfaces appear to be significantly different. It is worth noting that there is a local minimum in the decreasing stepwise adsorption energies and growth energies when the Run clusters size increases to Ru4 among all adsorption configurations on the Co surfaces, indicating that Ru4 is the critical size of growth of Run clusters.
Consequently, it is believed that the two-dimensional aggregation structures are favored on Co surfaces and this thermodynamic preference can be expected to give monolayer growth. The obtained aggregation properties of Run clusters agree well with the previous experiment results,35 where the Ru promoter is present in islands on Co particles at a thickness of one monolayer or at most two monolayers.
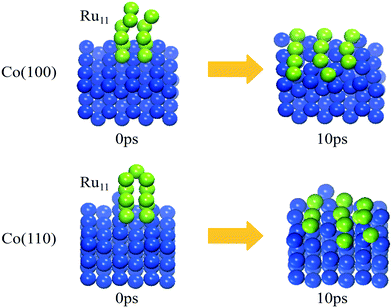
The trajectories of the Ru11 structure evolution on Co(100) and Co(110) surfaces from AIMD simulations are displayed in Video S1 and S2.† Not surprisingly, the supported Ru11 cluster undergoes restructuring rapidly and reaches the final equilibrium structures (shown in Fig. 4) after 10 ps: a square-based row structure of Ru11 on the Co(100) surface and a parallel independent chain structure of Ru11 on the Co(110) surface, similar to the energetically most favorable Ru11 configurations from DFT calculation. These results indicate that the Ru atoms in the upper layers are inclined to migrate to the Co surfaces with more Co–Ru bonds, similar to that of Co(111) and Co(311) surfaces. Thus, this phenomenon can serve as direct evidence for Ru clusters preferring two dimensional aggregation structures on FCC Co surfaces under realistic cobalt-based FTS reaction conditions, consistent with the experimental results35 by EELS spectrum imaging that Ru was associated with cobalt particles in patches at a thickness of one monolayer or at most two monolayers.
3.3 Morphology of FCC Co NPs induced by Ru promoter
Based on the preferential Ru adsorption pattern, the growth energies with respect to the size of Run clusters on FCC Co surfaces were investigated. As shown in Fig. S8,† the Ru4 cluster has the highest growth energy during the growth of Ru clusters to form periodic structures, indicating that a Ru4 cluster is most likely to exist on the Co surfaces. Surface energy determines the crystallite morphology of FCC Co and is considered to be an important index for evaluating the relative stability of active surfaces. The most stable structural unit of Ru4 with the greatest probability is subsequently used to calculate the surface energy of each surface with different Ru content.According to the definition of surface energy, the lower the surface energy is, the more stable the surface structure is. The surface energies of Co surfaces modified by Ru at different Ru/Co atomic ratios are listed in Table 3. It is found that the surface energies can be tuned by Ru content. As the surface Ru/Co atomic ratio increases, all surface energies decrease, meaning that the stability of all facets upon Ru adsorption can be enhanced significantly. From the variation curves in Fig. S9,† the surface energies decrease slightly with the surface Ru/Co ratio from 1/168 to 1/48, while they decrease sharply when the surface Ru/Co ratio is lower than 1/24. In addition, the relative stability of each surface can be altered by different Ru coverage. When the Ru/Co ratio increases to 1/12, the Co(110) surface is even more stable than the Co(111) surface. The results reflected that Ru promoter plays an important role in tuning the stability of these Co surfaces.
| Surface | γ 0Co(hkl) | γ adsCo(hkl) with Ru/Co ratio | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1/168 | 1/120 | 1/96 | 1/48 | 1/24 | 1/12 | |
| Co(111) | 0.132 | 0.126 | 0.124 | 0.122 | 0.111 | 0.090 | 0.048 |
| Co(100) | 0.158 | 0.153 | 0.150 | 0.148 | 0.139 | 0.120 | 0.082 |
| Co(311) | 0.161 | 0.154 | 0.151 | 0.149 | 0.137 | 0.112 | 0.063 |
| Co(110) | 0.157 | 0.150 | 0.146 | 0.144 | 0.129 | 0.100 | 0.042 |
The addition of Ru plays an important role in the modification of surface stability, and the change of stability of the exposed facets would further affect the morphology of FCC Co NPs. The Wulff shape of FCC Co NPs with different Ru content was constructed by minimizing the total surface energy, and the contribution of crystal facets to the total surface area was also determined to quantify the morphological changes. To clearly visualize the morphology evolution of FCC Co NPs induced by Ru promoter, all the constructed Wulff shapes are summarized and organized in Video S3.† As shown in Fig. 5, the crystallite morphology changed slightly with Ru/Co ratio from 1/168 to 1/24, showing an octahedron-like shape similar to the structure of pure FCC Co NPs. With Ru/Co up to 1/12, the corresponding morphology of the FCC Co NPs is a rhombic dodecahedron composed of Co(111) and Co(110) facets, apparently distinct from that with low Ru content.
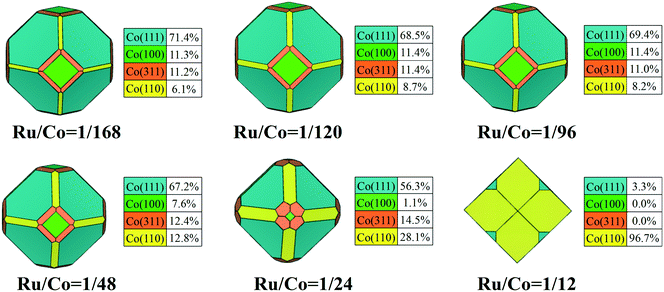 | ||
| Fig. 5 The equilibrium shapes of FCC Co modified using different Ru content values, and the fraction of each facet. | ||
With the increase of Ru/Co ratio, Co(311) and Co(110) facets are predicted to expose more area at the cost of the proportion of the Co(111) and Co(100) facets decreasing. Until the Ru/Co ratio is 1/24, Co(111) remains the predominately exposed surface of FCC Co, accounting for 56.3% of the total surface area because of its high stability. As the Ru/Co ratio continues to increase, the overall contribution from flat facets decreases in the equilibrium morphology, while the corrugated facets show a considerable surface area. This reveals that the morphology of the FCC Co nanoparticles is predominately dictated by the (111) and (110) facets once the Ru/Co ratio reaches 1/12. Obviously, Ru adsorption leads to dramatic changes in the surface morphology and the exposed facets of the Co nanocrystals, and high Ru content can help to facilitate the exposure of the high Miller index surfaces.
The existence of Ru promoter leads to the change in surface morphology and the relative ratios of exposed facets, which may affect the intrinsic activity and selectivity of the Co catalyst. It is reported that the Co(111) surface has a very low reactivity towards direct CO dissociation, with an activation energy barrier of 2.48 eV.63 However, the C2 hydrocarbon formation could be facilitated and the CH4 formation could be suppressed by the stepped-Co(111) surface, owing to the step sites involved.64 For the Co(100) surface, the calculated barrier (1.52 eV) for the H-assisted route is comparable to the direct route and also much higher than what is typically expected from FTS experiments.65–67 In addition, the CO dissociation at step and kink sites is predicted to have the highest relative rate of all adsorption site types exposed on FCC Co NPs, these active sites generally exposed in the high index Co(311) and Co(110) surfaces are mainly responsible for the activity of the Co catalyst.68 What is clear from our results is that the overall contribution from corrugated Co(311) and/or Co(110) surfaces increases in the equilibrium morphology with increasing Ru content, concurrently occurring with increment of step B5 sites as well as kink 5F sites. These step and kink sites are more facile for CO dissociation on FCC Co NPs,47 owing to the lower activation energy, as also concluded for Ru NPs.69 The more active sites with higher intrinsic activity participating in the reaction could effectively enhance the catalytic activity of the Co catalyst. The results revealed that the high index facets stabilized by the increased Ru content would exhibit high activity for CO activation, which is valuable for developing more efficient and stable Co catalysts with higher reactivity for FTS reactions.
4. Conclusions
Combining density functional theory and ab initio molecular dynamic simulations, the adsorption configurations and growth trends of Run clusters on FCC Co surfaces in Fischer–Tropsch catalysis were investigated in order to clarify the facet-dependent equilibrium morphology of metallic Co NPs stabilized by Ru promoter. It is found that the difference in the adsorption patterns of Run clusters on Co surfaces arises from their distinct surface structures as well as Co–Ru interactions. The aggregation properties leading to the planar growth of Run clusters from the DFT calculations were demonstrated by the AIMD results, indicating that it is possible to predict accurately the growth process of Ru promoter on FCC Co catalysts. In addition, the Ru promoter shows different stabilization abilities on the exposed facets of the FCC Co NPs and has great influence on the crystallographic morphology. Increased Ru content can facilitate the formation of high index active facets at large percentages; for example, Co(311) and Co(110) surfaces are predicted to expose more area, instead of Co(111) and Co(100) surfaces, meaning that more active sites with higher intrinsic activity participate in the reaction. As far as we know, this work is the first attempt to explore the surface morphology of FCC Co induced by Ru in a systematic way, which will help to design desired FTS catalysts rationally with high performance.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the National Natural Science Foundation of China (Grant No. 21736007, 21872162, 21703273), the “Transformational Technologies for Clean Energy and Demonstration”, the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA 21020202) and the ShanXi Provincial Research Foundation for Basic Research (No. 201701D221242). The authors are grateful to Lvliang's cloud computing center for computational resources by the Tianhe-2.References
- F. Jiao, J. Li, X. Pan, J. Xiao, H. Li, H. Ma, M. Wei, Y. Pan, Z. Zhou and M. Li, Science, 2016, 351, 1065–1068 CrossRef CAS PubMed.
- J. Li, Y. He, L. Tan, P. Zhang, X. Peng, A. Oruganti, G. Yang, H. Abe, Y. Wang and N. Tsubaki, Nat. Catal., 2018, 1, 787–793 CrossRef CAS.
- A. J. Markvoort, R. A. van Santen, P. A. Hilbers and E. J. Hensen, Angew. Chem., Int. Ed., 2012, 51, 9015–9019 CrossRef CAS PubMed.
- X. Peng, K. Cheng, J. Kang, B. Gu, X. Yu, Q. Zhang and Y. Wang, Angew. Chem., Int. Ed., 2015, 54, 4553–4556 CrossRef CAS PubMed.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2002, 124, 11568–11569 CrossRef CAS PubMed.
- Q. Zhang, J. Kang and Y. Wang, ChemCatChem, 2010, 2, 1030–1058 CrossRef CAS.
- R. Zhang, G. Wen, H. Adidharma, A. G. Russell, B. Wang, M. Radosz and M. Fan, ACS Catal., 2017, 7, 8285–8295 CrossRef CAS.
- H. M. T. Galvis, J. H. Bitter, C. B. Khare, M. Ruitenbeek, A. I. Dugulan and K. P. de Jong, Science, 2012, 335, 835–838 CrossRef PubMed.
- I. K. van Ravenhorst, C. Vogt, H. Oosterbeek, K. W. Bossers, J. G. Moya-Cancino, A. P. van Bavel, A. M. J. van der Eerden, D. Vine, F. M. F. de Groot, F. Meirer and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2018, 57, 11957–11962 CrossRef CAS PubMed.
- I. A. Filot, R. A. van Santen and E. J. Hensen, Angew. Chem., Int. Ed., 2014, 53, 12746–12750 CrossRef CAS PubMed.
- G. Wen, Q. Wang, R. Zhang, D. Li and B. Wang, Phys. Chem. Chem. Phys., 2016, 18, 27272–27283 RSC.
- C. Qin, B. Hou, J. Wang, Q. Wang, G. Wang, M. Yu, C. Chen, L. Jia and D. Li, ACS Catal., 2018, 8, 9447–9455 CrossRef CAS.
- H. Liu, R. Zhang, L. Ling, Q. Wang, B. Wang and D. Li, Catal. Sci. Technol., 2017, 7, 3758–3776 RSC.
- P. Senecal, S. D. M. Jacques, M. Di Michiel, S. A. J. Kimber, A. Vamvakeros, Y. Odarchenko, I. Lezcano-Gonzalez, J. Paterson, E. Ferguson and A. M. Beale, ACS Catal., 2017, 7, 2284–2293 CrossRef CAS.
- G. Prieto, M. I. S. De Mello, P. Concepción, R. Murciano, S. B. C. Pergher and A. N. Martínez, ACS Catal., 2015, 5, 3323–3335 CrossRef CAS.
- Y. Liu, B. de Tymowski, F. Vigneron, I. Florea, O. Ersen, C. Meny, P. Nguyen, C. Pham, F. Luck and C. Pham-Huu, ACS Catal., 2013, 3, 393–404 CrossRef CAS.
- G. R. Johnson and A. T. Bell, ACS Catal., 2016, 6, 100–114 CrossRef CAS.
- S. Kattel, W. Yu, X. Yang, B. Yan, Y. Huang, W. Wan, P. Liu and J. G. Chen, Angew. Chem., Int. Ed., 2016, 55, 7968–7973 CrossRef CAS PubMed.
- H. Wang, W. Zhou, J. X. Liu, R. Si, G. Sun, M. Q. Zhong, H. Y. Su, H. B. Zhao, J. A. Rodriguez, S. J. Pennycook, J. C. Idrobo, W. X. Li, Y. Kou and D. Ma, J. Am. Chem. Soc., 2013, 135, 4149–4158 CrossRef CAS PubMed.
- K. M. Cook, H. D. Perez, C. H. Bartholomew and W. C. Hecker, Appl. Catal., A, 2014, 482, 275–286 CrossRef CAS.
- O. Kungurova, N. Shtertser, G. Chermashentseva, I. Simentsova and A. Khassin, Catalysis in Industry, 2017, 9, 23–30 CrossRef.
- T. N. Phaahlamohlaka, D. O. Kumi, M. W. Dlamini, R. Forbes, L. L. Jewell, D. G. Billing and N. J. Coville, ACS Catal., 2017, 7, 1568–1578 CrossRef CAS.
- C. J. Weststrate, A. M. Saib and J. W. Niemantsverdriet, Catal. Today, 2013, 215, 2–7 CrossRef CAS.
- N. Balakrishnan, B. Joseph and V. R. Bhethanabotla, Appl. Catal., A, 2013, 462–463, 107–115 CrossRef CAS.
- R. Phienluphon, L. Shi, J. Sun, W. Niu, P. Lu, P. Zhu, T. Vitidsant, Y. Yoneyama, Q. Chen and N. Tsubaki, Catal. Sci. Technol., 2014, 4, 3099–3107 RSC.
- M. J. Parnian, A. Taheri Najafabadi, Y. Mortazavi, A. A. Khodadadi and I. Nazzari, Appl. Surf. Sci., 2014, 313, 183–195 CrossRef CAS.
- N. Tsubaki, S. Sun and K. Fujimoto, J. Catal., 2001, 199, 236–246 CrossRef CAS.
- C. Pirola, M. Scavini, F. Galli, S. Vitali, A. Comazzi, F. Manenti and P. Ghigna, Fuel, 2014, 132, 62–70 CrossRef CAS.
- T. Jermwongratanachai, G. Jacobs, W. Ma, W. D. Shafer, M. K. Gnanamani, P. Gao, B. Kitiyanan, B. H. Davis, J. L. S. Klettlinger, C. H. Yen, D. C. Cronauer, A. J. Kropf and C. L. Marshall, Appl. Catal., A, 2013, 464–465, 165–180 CrossRef CAS.
- W. Ma, G. Jacobs, R. A. Keogh, D. B. Bukur and B. H. Davis, Appl. Catal., A, 2012, 437–438, 1–9 CrossRef CAS.
- E. Iglesia, S. L. Soled, R. A. Fiato and G. H. Via, J. Catal., 1993, 143, 345–368 CrossRef CAS.
- E. Iglesia, S. L. Soled, R. A. Fiato and G. H. Via, Dispersion, support, and bimetallic effects in Fischer-Tropsch synthesis on cobalt catalysts/Studies in Surface Science and Catalysis, 1994, vol. 81, pp. 433–442 Search PubMed.
- O. A. Kungurova, A. A. Khassin, S. V. Cherepanova, A. A. Saraev, V. V. Kaichev, N. V. Shtertser, G. K. Chermashentseva, E. Y. Gerasimov, E. A. Paukshtis, O. V. Vodyankina, T. P. Minyukova and G. Abou-Jaoude, Appl. Catal., A, 2017, 539, 48–58 CrossRef CAS.
- J. Hong, E. Marceau, A. Y. Khodakov, L. Gaberová, A. Griboval-Constant, J.-S. Girardon, C. L. Fontaine and V. Briois, ACS Catal., 2015, 5, 1273–1282 CrossRef CAS.
- M. Shannon, C. Lok and J. Casci, J. Catal., 2007, 249, 41–51 CrossRef CAS.
- M. Duan, J. Yu, J. Meng, B. Zhu, Y. Wang and Y. Gao, Angew. Chem., Int. Ed., 2018, 57, 6464–6469 CrossRef CAS PubMed.
- W. Piskorz, J. Gryboś, F. Zasada, P. Zapała, S. Cristol, J.-F. Paul and Z. Sojka, J. Phys. Chem. C, 2012, 116, 19307–19320 CrossRef CAS.
- C.-F. Huo, B.-S. Wu, P. Gao, Y. Yang, Y.-W. Li and H. Jiao, Angew. Chem., Int. Ed., 2011, 50, 7403–7406 CrossRef CAS PubMed.
- S. Zhao, X.-W. Liu, C.-F. Huo, X.-D. Wen, W. Guo, D. Cao, Y. Yang, Y.-W. Li, J. Wang and H. Jiao, Catal. Today, 2016, 261, 93–100 CrossRef CAS.
- Q. Li, M. Rellan-Pineiro, N. Almora-Barrios, M. Garcia-Rates, I. N. Remediakis and N. Lopez, Nanoscale, 2017, 9, 13089–13094 RSC.
- L. Liu, M. Yu, B. Hou, Q. Wang, B. Zhu, L. Jia and D. Li, Nanoscale, 2019, 11, 8037–8046 RSC.
- J. Meng, B. E. Zhu and Y. Gao, J. Phys. Chem. C, 2018, 122, 6144–6150 CrossRef CAS.
- T. N. Phaahlamohlaka, M. W. Dlamini, M. W. Mogodi, D. O. Kumi, L. L. Jewell, D. G. Billing and N. J. Coville, Appl. Catal., A, 2018, 552, 129–137 CrossRef CAS.
- L. Liu, M. Yu, Q. Wang, B. Hou, Y. Liu, Y. Wu, Y. Yang and D. Li, Catal. Sci. Technol., 2018, 8, 2728–2739 RSC.
- N. Ashcroft and N. Mermin, Solid State Physics, Thomson Learning/Inc., Florence, 1976, p. 404 Search PubMed.
- J. Swart, E. Van Steen, I. Ciobîcă and R. Van Santen, Phys. Chem. Chem. Phys., 2009, 11, 803–807 RSC.
- M. A. Petersen, J.-A. van den Berg, I. M. Ciobica and P. van Helden, ACS Catal., 2017, 7, 1984–1992 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- R. Bader, International Series of Monographs on Chemistry, 1990, vol. 22, pp. 9–15 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- P. Li, J. Liu, N. Nag and P. Crozier, Appl. Catal., A, 2006, 307, 212–221 CrossRef CAS.
- G. R. Johnson and A. T. Bell, J. Catal., 2016, 338, 250–264 CrossRef CAS.
- M. Wang, S. Guo, Z. Li, Z. Ma, J. Wang, B. Hou, L. Jia and D. Li, Fuel, 2019, 241, 669–675 CrossRef CAS.
- Y. Yang, L. Jia, B. Hou, D. Li, J. Wang and Y. Sun, J. Phys. Chem. C, 2014, 118, 268–277 CrossRef CAS.
- Y. Yang, L. Jia, B. Hou, D. Li, J. Wang and Y. Sun, Catal. Sci. Technol., 2014, 4, 717–728 RSC.
- S. Li, H. Li, J. Liu, X. Xue, Y. Tian, H. He and Y. Jia, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045410 CrossRef.
- J.-X. Liu, H.-Y. Su, D.-P. Sun, B.-Y. Zhang and W.-X. Li, J. Am. Chem. Soc., 2013, 135, 16284–16287 CrossRef CAS PubMed.
- C. Chen, Q. Wang, G. Wang, B. Hou, L. Jia and D. Li, J. Phys. Chem. C, 2016, 120, 9132–9147 CrossRef CAS.
- P. van Helden, I. M. Ciobîcă and R. L. Coetzer, Catal. Today, 2016, 261, 48–59 CrossRef CAS.
- Z.-J. Wang, Z. Yan, C.-J. Liu and D. W. Goodman, ChemCatChem, 2011, 3, 551–559 CrossRef CAS.
- C. G. Cooper, T.-H. Nguyen, Y.-J. Lee, K. M. Hardiman, T. Safinski, F. P. Lucien and A. A. Adesina, Catal. Today, 2008, 131, 255–261 CrossRef CAS.
- W. Chen, T. Lin, Y. Dai, Y. An, F. Yu, L. Zhong, S. Li and Y. Sun, Catal. Today, 2018, 311, 8–22 CrossRef CAS.
- H. Li, G. Fu and X. Xu, Phys. Chem. Chem. Phys., 2012, 14, 16686–16694 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy01892a |
| This journal is © The Royal Society of Chemistry 2020 |