Exceptionally low charge trapping enables highly efficient organic bulk heterojunction solar cells

Abstract

In this study, we investigate the underlying origin of the high performance of PM6:Y6 organic solar cells. Employing transient optoelectronic and photoemission spectroscopies, we find that this blend exhibits greatly suppressed charge trapping into electronic intra-bandgap tail states compared to other polymer/non-fullerene acceptor solar cells, attributed to lower energetic disorder. The presence of tail states is a key source of energetic loss in most organic solar cells, as charge carriers relax into these states, reducing the quasi-Fermi level splitting and therefore device V_OC. DFT and Raman analyses indicate this suppression of tail state energetics disorder could be associated with a higher degree of conformational rigidity and uniformity for the Y6 acceptor. We attribute the origin of such conformational rigidity and uniformity of Y6 to the presence of the two alkyl side chains on the outer core that restricts end-group rotation by acting as a conformation locker. The resultant enhanced carrier dynamics and suppressed charge carrier trapping are proposed to be a key factor behind the high performance of this blend. Low energetic disorder is suggested to be a key factor enabling reasonably efficient charge generation in this low energy offset system. In the absence of either energetic disorder or a significant electronic energy offset, it is argued that charge separation in this system is primarily entropy driven. Nevertheless, photocurrent generation is still limited by slow hole transfer from Y6 to PM6, suggesting pathways for further efficiency improvement.

---

Broader context

Despite recent dramatic breakthroughs in the efficiency of organic solar cells (now over 18%), the underlying mechanisms to produce such high device performance remain controversial. Herein we investigate the origin of high performance of PM6:Y6 system through transient photophysical and optoelectronic analyses, coupled with energetic and DFT analyses. Transient optoelectronic and photoemission spectroscopies indicate this blend exhibits a greatly suppressed density of electronic tail states compared to other polymer: non-fullerene acceptor solar cells, corresponding to a reduction in energetic disorder. The presence of tail states is a key source of energetic loss in most organic solar cells, as charge carriers trap into these states, reducing effective charge carrier mobility and increasing the reaction order of effective bimolecular recombination. DFT and Raman analyses indicate this absence of tail states could be associated with a higher degree of conformational rigidity and uniformity of the Y6 acceptor due to the presence of the two alkyl side chains on the outer core that restricts end-group rotation by acting as a conformation locker. The resultant enhanced carrier dynamics and suppressed charge carrier trapping are proposed to be key factors behind the high performance of this blend. In contrast, ultrafast transient absorption studies indicate that the performance of this blend is limited by kinetic competition between hole transfer versus Y6 exciton decay. This suggests a substantial opportunity for further device efficiency enhancement through molecular design to suppress this non-radiative exciton decay or accelerate hole transfer, which would provide pathways towards organic solar cells with efficiencies approaching 20%.

Over the last two years, dramatic advances have been reported in the efficiency of organic solar cells (OSCs), with state-of-the-art efficiencies exceeding 18%,¹ motivating increased research and commercial interest in these devices. Indeed, such high efficiencies are now approaching predicted limits to the efficiency of such devices.² These remarkable efficiency advances have been driven in particular by the development of new non-fullerene acceptors (NFAs). However, the underlying origins of these advances remain controversial.^2–10 In this study, we focus on one particularly promising, high efficiency blend, that of the NFA Y6 (also known as BTP-4F) blended with the donor polymer PM6 (also known as PBDB-T-2F), which has yielded efficiencies of over 16% for single-junction binary blends,^11–13 and 17% in ternary blends.¹⁴ We compare the exciton and charge carrier dynamics and the material energetics in this blend to those observed in analogous, but less efficient blends, and discuss how these factors impact upon device efficiency. Our results indicate that the high performance of this blend appears to result primarily from the absence of intra-bandgap tail states (i.e.: lower energetic disorder), with the suppression of energetic losses associated with charge carrier trapping into such states being a key enabler for enhanced device performance.

The PM6:Y6 combination system has already attracted significant attention. It exhibits a remarkably higher photocurrent while maintaining a high fill factor (FF) and a low energy loss E_loss ∼ 0.55 eV (determined from the difference in energy between the optical bandgap and V_OC).¹⁵ These high performance characteristics have been attributed in part to its long wavelength absorption onset (∼900 nm) and complementary donor and acceptor absorption, large absorption extinction coefficients, and moderate HOMO and LUMO energy offsets.^5,16–19 More in depth studies by Karki et al. and Perfigon-Toro et al. have identified several additional factors which may be critical to this blend's high performance, including efficient charge generation with barrierless CT state dissociation, and a nanomorphology favourable for charge separation.^15,20,21 The achievement of both high EQEs over 80% (up to 900 nm) and a low voltage loss in this blend has been highlighted as particularly remarkable.

Solution-processed organic semiconductors are soft, and typically disordered, materials. It has been also widely observed that such materials are normally characterised by non-ideal band edges, with a significant density of states (DOS) extending into the bandgap.^22,23 Such non-ideal energetics have been suggested to be a key limit on materials and device performance,^23–29 and are indicative of energetic inhomogeneities, often associated with the presence of tail states (i.e.: shallow trap states) extending into the bandgap. The effect of tail states on the device characteristics depends on the trap depth and density, and have been reported to limit the performance of many organic semiconductor devices, with for example charge trapping into such states retarding charge transport and increase the overall recombination losses within organic solar cells.^30,31 The correlation between energetic disorder and the mobility of organic transistor performance has also been reported previously.^32,33 Low trap state densities have been suggested to be a key factor behind the remarkable efficiencies reported for solution-processed perovskite solar cells.^34,35 For organic solar cells, lower trap state densities have been correlated with higher device performance associated with faster charge transport due to reduced charge trapping (i.e.: reduced hopping sites) thus higher effective charge carrier mobility. In addition, a lower optical Urbach tail, indicative of near ideal optical absorbance onsets, has also been reported to be correlated with high performance for both perovskite and organic solar cells.^36–38 However, a quantitative understanding of the impact of energetic inhomogeneity and shallow trap state charge trapping on the limits of organic solar cell performance remains a topic of significant ongoing discussion.

We firstly optimized OSCs with the PM6:Y6 bulk heterojunction photoactive layer, yielding a power conversion efficiency of 15.5% with high photocurrent of 25.3 mA cm⁻², open-circuit voltage (V_OC) of 0.86 V, and fill factor (FF) of 71%, which is comparable to those of previously reported studies based on PM6:Y6 (Fig. 1a). One of the notable features of this blend is its outstanding capability for high photocurrent generation, despite a relatively thin thickness of the photoactive layer (d = 85 nm). This can be attributed to the high extinction coefficient of both absorbers, PM6 and Y6, with complementary absorption bands in the visible and near-infrared regions, providing a broad spectral response in external quantum efficiency (EQE) ranging from 450 to 830 nm at nearly 80% (Fig. 1b and Fig. S1, ESI†). Besides the optical properties of the materials, energy offsets are also an important factor in determining the performance of OSCs. Fig. 1c shows the energy levels of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for PM6 and Y6 films, as derived from cyclic voltammetry (CV) measurements (Fig. S2, ESI†). The ΔE_HOMO and ΔE_LUMO offsets between PM6 and Y6 are calculated to be 0.26 and 0.49 eV. Taking account of the exciton binding energy (estimated as 0.2–0.3 eV for Y6 from the difference between its optical and electric bandgaps), this suggests a near zero driving energy for hole transfer in this blend. As such, it is likely that Y6 exciton separation in this blend is primarily entropy driven, as we discuss further below.^39,40 The small energy offset is consistent with the low energy loss (E_loss ∼ 0.55 eV) for this blend, one of the smallest reported for high EQE organic solar cells.

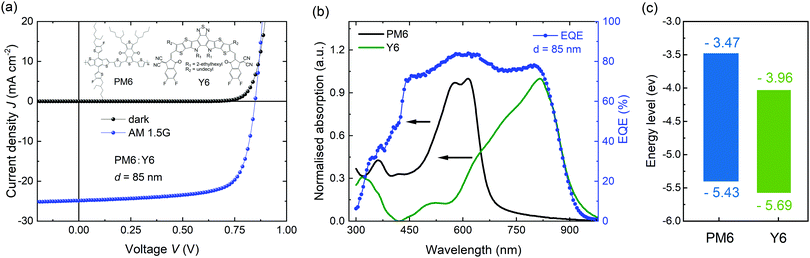Fig. 1 (a) J–V characteristics of PM6:Y6 OSCs. Inset displays the molecular structures of PM6 and Y6. (b) UV-Vis absorption of PM6 and Y6 neat films and EQE spectra of the devices. (c) Indicative energy level diagram of PM6 and Y6 determined from cyclic voltammetry data (see also in ESI†). It should be noted absolute energy levels are dependent upon measurement methodology.

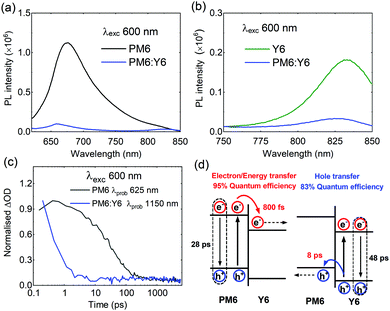
We now turn into an analysis of the factors underlying the remarkable performance of PM6:Y6 blend. Free charge generation has been recently observed in this blend using a combination of temperature-dependent time-delayed collection field (TDCF), EQE, and V_OC measurements,¹⁵ however, ultrafast kinetic studies have not been reported to date. To study the exciton behaviour, we carried out steady-state photoluminescence (PL) and ultrafast transient absorption spectroscopy measurements. The PL quenching efficiency of PM6 excitons is over 95% in the blend film, indicative of efficient electron (or energy) transfer from PM6 to Y6 at the PM6:Y6 interface, as shown in Fig. 2a. On the other hand, Y6 exciton quenching efficiency in the blend is 81% (Fig. 2b), indicative of efficient, but sub-optimal, hole transfer from Y6 excitons to PM6. Turning now to transient absorption spectroscopy (Fig. 2c and Fig. S3–S5, ESI†), we found rather short exciton lifetimes of both neat PM6 (28 ps) and Y6 (48 ps) films, significantly shorter than those reported for analogous studies of other efficient donor polymers and PCBM (e.g. P3HT of 300 ps, PffBT4T-2OD of 400 ps, PTQ10 of 800 ps, PCBM of 500 ps) but typical of those reported for low bandgap non-fullerene acceptors (e.g. ITIC of 20 ps, IDTBR of 50 ps).^10,41–43 We note the Y6 exciton decay dynamics were observed to be biphasic at some probe wavelengths, see ESI,† for details and discussion on this point. The short exciton lifetimes of PM6 and Y6 are indicative of ultrafast, non-radiative exciton decay. Intensity dependent analyses of exciton–exciton annihilation yield exciton diffusion lengths for PM6 and Y6 of 2 nm and 4.8 nm, respectively, in Fig. S3, S4 and Table S1 (ESI†),^44–46 primarily due to their short exciton lifetimes. Efficient charge generation with such short exciton lifetimes/diffusion lengths requires even faster electron/hole transfers and thus a relatively intermixed blend morphology, without large (>3 nm) 3D donor or acceptor domains. This suggests that large (∼20 nm) domains reported previously in PM6:Y6 blends are most likely not molecularly pure.⁴⁷ In PM6:Y6 blend, selective excitation of PM6 resulted in ultrafast PM6 exciton decay with a time constant of 0.8 ps (Fig. S3, ESI†), 30 times faster than PM6 exciton decay in neat films and indicative of a high (∼95%) yield of electron and/or energy transfer to Y6, consistent with the PL quenching data reported above. On the other hand, hole transfer from Y6 to PM6 is observed to be relatively slow (8 ps) (see Fig. S5, ESI†), indicating that of a Y6 exciton separation efficiency of ∼83%, again reasonably consistent with our PL quenching data. These relatively slow hole transfer kinetics, and thus sub-unity efficiency are most likely due to low energy offset driving this transfer. They may also be associated with the presence of small molecular Y6 aggregates limiting the efficiency of exciton diffusion. The presence of such molecular Y6 aggregates is consistent with reports of a (010) coherence length in PM6:Y6 blends of 2.4 nm.⁴⁷ In summary, these photophysical data indicate that Y6 exciton decay to ground state is likely to be a key factor limiting photocurrent generation and EQE in these devices. It is striking that such high overall device performance is achieved for PM6:Y6 blend solar cells despite these internal quantum efficiency limitations imposed the kinetic competition between hole transfer and Y6 exciton decay.

Fig. 2 (a) Steady-state PL spectra of films excited on 600 nm for electron transfer from PM6 and (b) hole transfer from Y6. (c) Transient absorption decay dynamics for neat PM6 and PM6:Y6 blend films. (d) A schematic showing exciton decay and charge/energy transfer processes.

We turn now to the quantification of the degree of energetic disorder and charge trapping at PM6:Y6 band edges, and its impact upon charge transport and recombination, and device V_OC. The presence of sub-bandgap tail states was investigated via charge extraction measurements at open circuit as a function of light intensity. Such studies typically yield exponential dependencies of charge carrier density n upon device V_OC (where n is normally associated with trapped charge in tail states if the device is operated far below the band edge). Equating the measured V_OC to the quasi-Fermi level splitting ΔE_f (valid in the absence of significant surface recombination, and neglecting charge gradients with the devices, as reported previously^48–52), such behaviour can be quantified by n ∝ exp(ΔE_f/2E_ch), where the characteristic energy E_ch is 25 meV suggesting ideal well-defined band edges kT of both Y6 conduction band and PM6 valence band at room temperature (see also ESI,† Note 1). Measured values of E_ch greater than 25 meV have been widely interpreted as indicative of the presence of charge accumulation in exponential tails of shallow trap states. As can be seen from Fig. 3a, a wide range of organic blend systems using NFAs show values for E_ch greater than 60 meV (unnormalised CE results are plotted in Fig. S7, ESI†); similar data have been reported before for blends with fullerene acceptors.²³ Such large values for E_ch are indicative of significant densities of shallow traps states extending into the bandgap of the material for almost all organic blends reported to date for OSC's, with estimates of the densities of these trap states typically of the order of 10¹⁸–10¹⁹ cm⁻³.⁵³ Remarkably, the PM6:Y6 system shows a much sharper increase of charge carrier density as a function of quasi-Fermi level splitting, yielding characteristic energy of 27 meV (i.e.: near-ideal behaviour). Supporting the validity of this analysis, analogous data for a crystalline silicon solar cell shows as expected ideal behaviour with E_ch = 25 meV (Fig. S7, ESI†). Very similar, nearly ideal behaviour was observed for structurally analogous blend PM6:BTP-4Cl (E_ch = 28 meV) (also plotted in Fig. 3a, where BTP-4Cl is the chlorinated analogue of Y6). The E_ch value reported here for PM6:Y6 is the smallest reported for any organic blend system using this technique.²³

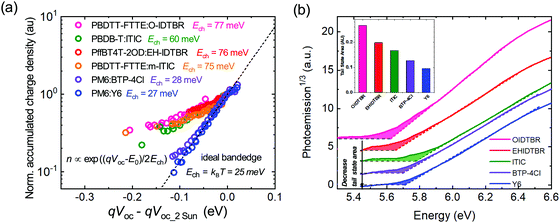Fig. 3 (a) Measurements of the accumulated charge density versus quasi-Fermi level splitting qV_OC determined from charge extraction measurements at open circuit as a function of irradiation intensity for a range of polymer:NFA blends (see ESI,† Fig. S6 for materials details). The accumulated charge density is normalised to the charge carrier density at 2 Sun open-circuit condition, and the measured V_OC's also plotted relative to these 2 Sun values (b) The photoemission spectra for selected NFA films, illustrating the extrapolated band edges (dashed lines) and the additional sub-gap tail states (the shaded areas). The insert plots the integrated areas of these tail states.

To further confirm the presence of the sub-bandgap tail states and to determine their densities, ambient photoemission spectroscopy (APS) was used as a contactless energetic probe of neat and blend films. (Fig. 3b). The onset of photoelectron emission ejected from the materials upon photoexcitation has been used to determine HOMO or the VB edge of semiconductors.^23,54 The extrapolated HOMO value of Y6 was 5.70 eV consistent with 5.69 eV measured by CV. However, the photoemission threshold energy was below the extrapolated HOMO value, indicating the presence of the sub-bandgap tail (trap/defect) states of the materials. Thus, a relative comparison of tail states in different NFAs could be made by comparing the integrated area below their photoemission threshold (shaded area in Fig. 3b). It is apparent that Y6 (and BTP-4Cl) shows the smallest integrated area, suggesting the lowest sub-bandgap tail states compared with other NFAs, confirming less energetic inhomogeneity, in good agreement with charge extraction results. It is also apparent that these trap states extend ∼100 meV below the band edges, consistent with the characteristic energies E_ch determined in Fig. 3a. Similarly, a low APS tail state density was also observed for neat PM6 (Fig. S8, ESI†).

In addition to the low sub-bandgap tail states widths found in Y6 and PM6, APS measurements further indicated a ∼100 meV shift of HOMO energy level of PM6 in the blend (Fig. S8, ESI†), i.e. its HOMO gets deeper when blended with Y6. Cyclic voltammetry data also indicated a wider electronic bandgap in the blend compared to neat films (Fig. S2, ESI†). Such energetic shifts are analogous to those reported previously for polymer:PCBM and polymer:NFA blends,^10,55 and previously assigned to larger electronic bandgaps for more mixed, amorphous molecular morphologies. Such energetics shifts have been suggested to create energetic offsets between mixed and pure domains in donor/acceptor blends which can help stabilise charge separation, and are likely to be an additional factor behind the efficiency of PM6:Y6 devices.⁵⁶

To further understand the superior performance of PM6:Y6, the effective mobilities of this blend was compared to a range of other higher performance NFAs based bulk heterojunction solar cells. These mobilities were measured by charge extraction at short circuit, with the resultant data shown in Fig. 4a. It is apparent that the PM6:Y6 device presents the highest effective charge carrier mobility of the five systems studied (all the listed devices have photoactive layer thickness range between 75–90 nm). We note that the presence of tail states or shallow trap states will result in lower effective mobilities, as charge transport requires thermal activation out of these trap states. The higher effective mobility for PM6:Y6 is therefore consistent with its lower thermal activation barrier to the mobility edge, although we note that other factors, such as the reported formation of 2D domains in this blend,⁵⁷ may also be important. In any case, the high effective mobility of PM6:Y6 blends will enable faster charge extraction from the bulk (Fig. S9, ESI†) at short circuit, favouring efficient device performance.

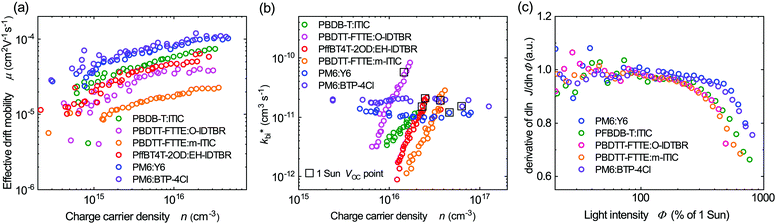Fig. 4 (a) A comparison of effective drift mobility as a function of charge carrier density for the same polymer:NFA devices studied in Fig. 3a. Mobilities determined from charge extraction measurements at short circuit. (b) Effective bimolecular recombination coefficients as a function of charge carrier density determined from transient photovoltage and charge extraction measurements at open circuit. (c) The differential of photocurrent density with respect to light intensity plotted versus light intensities. A differential of unity corresponds to linear behaviour, with sub-unity values being indicative of increased bimolecular recombination losses during charge extraction.

Besides high effective mobility, the non-geminate recombination kinetics of PM6:Y6 blend were investigated by transient photovoltage studies. Fig. 4b shows effective bimolecular recombination coefficients (k_bi*) determined from transient photovoltage and charge extraction at open-circuit for the same range of NFA based OSCs. Reconstructions of device V_OCversus light intensity from these data were in excellent agreement with experimentally measured V_OC, confirming the validity of these analyses (Fig. S10, ESI†). The PM6:Y6 also shows the least field-dependent photocurrent collection among the systems studied (Fig. S11, ESI†). Consistent with previously reported TDCF measurements,¹⁵ PM6:Y6 (as well as PM6:BTP-4Cl) shows a charge density independent k_bi*, indicative of ideal 2nd order bimolecular recombination. This contrasts to the other organic NFA blends studied which show a strong dependence of the effective bimolecular rate coefficient k_bi* on charge carrier density, which is associated with reaction order δ for recombination greater than 2. This non-ideal behaviour is assigned to the impact of charge trapping into intra-bandgap tail states (Fig. 3a) on bimolecular recombination, leading to a reaction order (δ = E_ch/kT + 1) higher than 2 when E_ch is greater than kT (see ESI,† Note 2 for further discussion).⁵⁸ This provides further support for the suppression of intra-bandgap tail states distribution in the PM6:Y6 devices. The effective bimolecular recombination coefficient (k_bi*) measured for PM6:Y6 of 1 × 10⁻¹¹ cm³ s⁻¹, is of similar magnitude to the bimolecular coefficients determined for the other blends under one Sun irradiation (the dashed circles in Fig. 4b). We thus conclude that the low voltage loss reported for this device (i.e. optical gap vs. V_OC) can not be attributed to a slow bimolecular recombination coefficient enhancing V_OC. Applying the Langevin recombination model (k_Langevin = qμ*/ε₀ε_r) to these effective mobilities and recombination data,^59,60 we obtain a Langevin reduction factor (k_br/k_Langevin) of 0.2 (see also ESI,† Note 2). This modest reduction factor is indicative of a relatively well intermixed blend morphology, as required by the short exciton lifetimes discussed above (for comparison the phase segregated blend system P3HT:PCBM exhibits a reduction factor determined by similar analyses of 10⁻³).^61,62 This near Langevin recombination agrees with analyses of the thickness dependence of PM6:Y6 device performance, where the optimal photoactive layer thickness for high device FF has been reported to be only 85 nm.¹² We note the maintenance of high PCE reported previously for thicker PM6:Y6 blends¹² primarily results from increased photocurrent with thicker photoactive layers, which is consistent with our recent study indicating narrow tail state distribution can enable more efficient photocurrent collection for thicker devices.²³ The efficiency of charge extraction versus bimolecular recombination was also analysed by the linearity of short-circuit photocurrent as a function of light intensities analysis. As can be seen from Fig. 4c (plotted in the derivative form), the PM6:Y6 device shows efficient, photocurrent collection up to 5 Sun illumination intensity without linearity loss. In contrast, the other NFA blends studied exhibited significant linearity losses at high light intensities, attributed to enhanced bimolecular recombination losses during charge extraction.⁶³ The greater linearity losses observed for the other NFA blends can be attributed to their non-ideal recombination behaviour (reaction order >2) resulting in their recombination losses increasing more rapidly as the charge density in the film is increased at higher light intensities. The efficient photocurrent collection of the PM6:Y6 devices at high light levels can be attributed to its high effective mobility and ideal behaviour of bimolecular recombination, with both factors consistent with significantly reduced energetic disorder of shallow trap states in this blend.

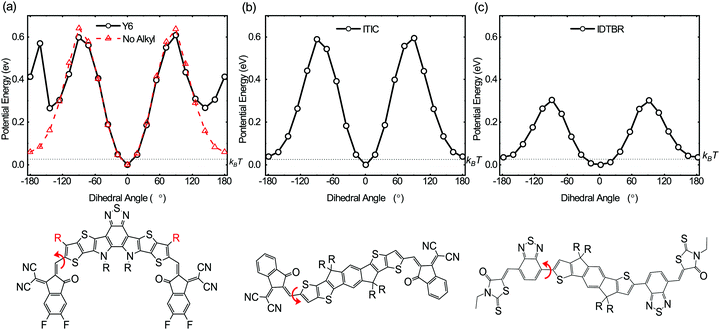
The above photophysical and transient optoelectronic analyses suggest the key unique factor behind the high performance of PM6:Y6 solar cells is the absence of charge trapping in sub-gap tail states in this blends, indicative of near ideal electronic band edges. This conclusion is in agreement with a very recent report of near ideal optical absorbance properties in analogous, and also high performance, PM6:Y11 blends.³⁸ Near ideal optical and electronic band edges are also likely to be a key factor behind the reasonably efficient charge generation observed for this blend despite the small energy level offset driving exciton separation.⁶⁴ We turn now to the consideration of the molecular origin of the low sub-gap tail states leading to low energetic inhomogeneity of the PM6:Y6 band edges. One possible reason for such low tail states comes from the conformational uniformity and rigidity of the Y6 molecule which can reduce its energetic disorder. Fig. 5 shows dihedral energy scans, calculated using DFT, of three high performing NFAs including Y6. Here we observe a clear global potential energy minimum structure in Y6 suggesting that one particular conformer (the planar structure at 0°) is thermodynamically preferred. This is different from the other two linear NFAs (ITIC and IDTBR) in which more than one low-lying potential energy structure is found suggesting co-existing different conformers. In solution, compared to Y6, ITIC and IDTBR can rotate more freely and adopt different conformations leading to a potentially larger conformational disorder; this disorder can be transferred to the solid state upon film formation, giving rise to higher conformational and thus energetic disorder. The energetic barrier to rotation to find the potential energy minima is well above k_BT suggesting that once the solid state packing is formed in films, thermodynamic relaxation to the lowest energy conformation would be difficult without additional treatment such as thermal annealing.

Fig. 5 Potential energy scans as a function of dihedral angle (red arrow) of (a) Y6, (b) ITIC and (c) IDTBR NFAs, calculated using DFT at the B3LYP level of theory with a basis set of 6-31G(d,p). One global potential energy minimum is observed for Y6 molecule (0°) compared to ITIC and IDTBR (0° and 180°), suggesting its conformational uniformity and rigidity, potentially leading to the low energetic disorder. R groups are simplified to methyl groups for simulations. The red curve in (a) refers to the dihedral scan when the red highlighted R group is replaced with a hydrogen.

It is very important to notice that both Y6 and ITIC have stabilising non-covalent interactions between the carbonyl oxygen in the end groups and the thiophene sulfur in the core, indicating that this cannot be the only factor in determining the reduced conformational disorder exhibited by Y6. We perform an additional potential energy dihedral scan for Y6, this time without any alkyl side chain on the outer core thiophene unit. We find that the potential energy landscape is now very similar to ITIC with two low-lying thermodynamic minima (at 0° and 180°), see Fig. 5a, red line. We therefore consider that the origin of Y6's conformational rigidity, and therefore low energetic disorder, is the presence of this alkyl side chain on the outer core that restricts end-group rotation by acting as a conformation locker. This provides an important insight, and a possible avenue for improving the efficiency and stability of NFAs as demonstrated here for Y6. Our simulations show that even a methyl group is sufficient to restrict such rotation, and that the addition of longer alkyl chains may not be necessary. We have previously shown how conformational changes can lead to a different energetic landscape in blends and molecular photostability in NFAs.⁶⁵ Here we implemented similar in situ accelerated photo-irradiation studies in N₂ to test the effect of conformational rigidity of the NFAs on photostability (see Fig. S12, ESI†). After irradiation, both O-IDTBR and ITIC show considerable changes in their molecular vibrational spectra, indicating significant conformational changes leading to photo instability (ESI,† Note 3). However, strikingly there are no major changes in the vibrational spectra of Y6, with no changes in relative peak intensities or positions, indicating its superior chemical and conformational stability. This stability is indicative of the relative conformational rigidity of Y6. We attribute this conformational rigidity, which in turn leads to conformational uniformity, to the molecular origin of the sharper tail edge and lower charge carrier trapping observed here for the Y6 acceptors, and may also be associated with the observation of a low optical Urbach energy for the related acceptor Y11.³⁸

We end our discussion with the consideration of the role of entropy in stabilising charge separation in PM6:Y6 blends. Several studies,^66–68 have highlighted the entropy increase resulting from converting one exciton into two charge carriers in OSCs, caused an increasing number of accessible hopping sites of the same electronic energy for two charges as they separate from each other. The free energy decrease resulting from this increasing entropy has been estimated as 0.1–0.2 eV, dependent upon the magnitude of the spatial separation, the blend nanomorphology and the degree of localisation of excitons, charges and CT states.^39,40,67,68 This entropic free energy increase is large enough to have a substantial role in stabilising charge separation in OSCs, and is also likely to be a key contributor to E_loss. Many studies have highlighted the role of electronic energy offsets and energetic disorder, as well as nanomorphology, in driving and stabilising charge separation in OSCs. However in low energetic disorder, low electronic energy offset systems, such as PM6:Y6, it appears likely that, alongside other possible considerations such as electrostatic interfacial fields,¹⁵ a dominant energetic factor stabilising charge separation is the entropy increase associated with dispersing localised charge carriers throughout the photoactive layer. The free energy loss associated with this entropy increase is likely to impose an underlying limit to the efficiency of organic solar cells.

Conclusions

In this work, we have investigated the underlying mechanisms by which PM6:Y6 blend can achieve high both a quantum efficiency photocurrent generation and a low energy loss between its optical bandgap and device open circuit voltage. In particular, we find that this material combination exhibits a remarkably narrow distribution of electronic trap states compared to other organic blend systems studied, corresponding to a low level of energetic disorder. This correlates with near ideal bimolecular recombination and high effective charge carrier mobilities. The presence of tail states is a key source of energetic loss in most organic solar cells, as charge carriers trap into these states, reducing the quasi-Fermi level splitting and therefore device V_OC. We propose this absence of tail states in the PM6:Y6 blend could be associated with a higher degree of conformational rigidity and uniformity for the Y6 acceptor. It appears the absence of this energetic loss, coupled with complementary light absorption, and reasonably efficient charge separation with a low energetic driving force, are the primary reasons for the high efficiency of these devices. It is likely the low level of energetic disorder is also key in enabling reasonably efficient charge generation in this less low energy offset system. The low energy offset for this blend suggests charge generation is primarily entropy rather than enthalpy driven.

The overall efficiency of this system is limited by sub-optimum EQE's and fill factor. The data herein suggest that the sub-optimum EQE's are limited, at least in part, by kinetic competition between hole transfer and Y6 exciton decay. This suggests an opportunity for further device efficiency enhancement through molecular design to suppress non-radiative exciton decay, particularly for the Y6 acceptor. The conformational rigidity and uniformity play an important role in this respect by reducing the energetic disorder and trap states induced by conformational variations. A resultant increase in acceptor exciton lifetime could increase the quantum efficiency of acceptor exciton separation. It would also enable the use of a less molecularly mixed blend structure, expected to suppress bimolecular recombination and thus enhance device V_OC. In addition, a modest increase in ΔE_HOMO (or reduction in Y6 exciton binding energy) could increase the efficiency of charge generation, although this would most likely result in an increase in E_loss.⁴⁴ Indeed the higher efficiency reported very recently for PM6:Y11 devices may result from a longer acceptor exciton lifetime.³⁸ Such advances could provide pathways to printable organic solar cells with efficiencies approaching 20%.

Experimental

Measurements and fabrication of OSCs are described in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the UKRI Global Challenge Research Fund project SUNRISE (EP/P032591/1), the Global Research Laboratory Program of the National Research Foundation (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2017K1A1A2013153) the UK EPSRC for the Plastic Electronics Centre for Doctoral Training (EP/L016702/1) funding, National Natural Science Foundation of China (21835006). J. L. acknowledge the funding supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2018R1A6A3A03013010). Y.-C. C. acknowledges the President's PhD Scholarship funding by Imperial College London. J. L. acknowledges the CSEM Brasil for a CASE studentship. Thanks also to the Imperial College High-Performance Computing Service and to Yifan Dong for discussion on transient absorption kinetics.

References

1. Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275.
2. S. M. Menke, N. A. Ran, G. C. Bazan and R. H. Friend, Joule, 2018, 2, 25–35.
3. D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709.
4. E. Collado-Fregoso, S. N. Pugliese, M. Wojcik, J. Benduhn, E. Bar-Or, L. Perdigón Toro, U. Hörmann, D. Spoltore, K. Vandewal, J. M. Hodgkiss and D. Neher, J. Am. Chem. Soc., 2019, 141, 2329–2341.
5. D. Baran, T. Kirchartz, S. Wheeler, S. Dimitrov, M. Abdelsamie, J. Gorman, R. S. Ashraf, S. Holliday, A. Wadsworth, N. Gasparini, P. Kaienburg, H. Yan, A. Amassian, C. J. Brabec, J. R. Durrant and I. McCulloch, Energy Environ. Sci., 2016, 9, 3783–3793.
6. F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J. S. Dennis, M. Heeney and J. Nelson, J. Am. Chem. Soc., 2019, 141, 6362–6374.
7. J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. McGarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053.
8. J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128.
9. Z. Zhou, S. Xu, J. Song, Y. Jin, Q. Yue, Y. Qian, F. Liu, F. Zhang and X. Zhu, Nat. Energy, 2018, 3, 952–959.
10. H. Cha, G. Fish, J. Luke, A. Alraddadi, H. H. Lee, W. Zhang, Y. Dong, S. Limbu, A. Wadsworth, I. P. Maria, L. Francàs, H. L. Sou, T. Du, J. Kim, M. A. McLachlan, I. McCulloch and J. R. Durrant, Adv. Energy Mater., 2019, 9, 1901254.
11. X. Xu, K. Feng, Z. Bi, W. Ma, G. Zhang and Q. Peng, Adv. Mater., 2019, 31, 1901872.
12. Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515.
13. B. Fan, D. Zhang, M. Li, W. Zhong, Z. Zeng, L. Ying, F. Huang and Y. Cao, Sci. China: Chem., 2019, 62, 746–752.
14. L. Zhan, S. Li, T.-K. Lau, Y. Cui, X. Lu, M. Shi, C.-Z. Li, H. Li, J. Hou and H. Chen, Energy Environ. Sci., 2020, 13, 635–645.
15. L. Perdigón-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763.
16. D. Liu, T. Wang, X. Ke, N. Zheng, Z. Chang, Z. Xie and Y. Liu, Mater. Chem. Front., 2019, 3, 2157–2163.
17. W. Gao, T. Liu, R. Ming, Z. Luo, K. Wu, L. Zhang, J. Xin, D. Xie, G. Zhang, W. Ma, H. Yan and C. Yang, Adv. Funct. Mater., 2018, 28, 1803128.
18. Q. He, M. Shahid, J. Wu, X. Jiao, F. D. Eisner, T. Hodsden, Z. Fei, T. D. Anthopoulos, C. R. McNeill, J. R. Durrant and M. Heeney, Adv. Funct. Mater., 2019, 29, 1904956.
19. H. Yao, Y. Cui, R. Yu, B. Gao, H. Zhang and J. Hou, Angew. Chem., Int. Ed., 2017, 56, 3045–3049.
20. A. Karki, J. Vollbrecht, A. L. Dixon, N. Schopp, M. Schrock, G. N. M. Reddy and T. Nguyen, Adv. Mater., 2019, 31, 1903868.
21. L. Zhu, M. Zhang, G. Zhou, T. Hao, J. Xu, J. Wang, C. Qiu, N. Prine, J. Ali, W. Feng, X. Gu, Z. Ma, Z. Tang, H. Zhu, L. Ying, Y. Zhang and F. Liu, Adv. Energy Mater., 2020, 1904234.
22. A. Melianas, F. Etzold, T. J. Savenije, F. Laquai, O. Inganäs and M. Kemerink, Nat. Commun., 2015, 6, 8778.
23. J. Wu, J. Luke, H. K. H. Lee, P. Shakya Tuladhar, H. Cha, S.-Y. Jang, W. C. Tsoi, M. Heeney, H. Kang, K. Lee, T. Kirchartz, J.-S. Kim and J. R. Durrant, Nat. Commun., 2019, 10, 5159.
24. J. M. Frost, M. A. Faist and J. Nelson, Adv. Mater., 2010, 22, 4881–4884.
25. J. C. Blakesley and D. Neher, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075210.
26. S. A. Hawks, G. Li, Y. Yang and R. A. Street, J. Appl. Phys., 2014, 116, 074503.
27. J. Lorrmann, M. Ruf, D. Vocke, V. Dyakonov and C. Deibel, J. Appl. Phys., 2014, 115, 183702.
28. R. A. Street, A. Krakaris and S. R. Cowan, Adv. Funct. Mater., 2012, 22, 4608–4619.
29. T. Kirchartz, B. E. Pieters, J. Kirkpatrick, U. Rau and J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115209.
30. H. Cha, J. Wu, A. Wadsworth, J. Nagitta, S. Limbu, S. Pont, Z. Li, J. Searle, M. F. Wyatt, D. Baran, J.-S. Kim, I. McCulloch and J. R. Durrant, Adv. Mater., 2017, 29, 1701156.
31. H. K. H. Lee, A. M. Telford, J. A. Röhr, M. F. Wyatt, B. Rice, J. Wu, A. de Castro Maciel, S. M. Tuladhar, E. Speller, J. McGettrick, J. R. Searle, S. Pont, T. Watson, T. Kirchartz, J. R. Durrant, W. C. Tsoi, J. Nelson and Z. Li, Energy Environ. Sci., 2018, 11, 417–428.
32. M. Nikolka, M. Hurhangee, A. Sadhanala, H. Chen, I. McCulloch and H. Sirringhaus, Adv. Electron. Mater., 2018, 4, 1700410.
33. D. Venkateshvaran, M. Nikolka, A. Sadhanala, V. Lemaur, M. Zelazny, M. Kepa, M. Hurhangee, A. J. Kronemeijer, V. Pecunia, I. Nasrallah, I. Romanov, K. Broch, I. McCulloch, D. Emin, Y. Olivier, J. Cornil, D. Beljonne and H. Sirringhaus, Nature, 2014, 515, 384–388.
34. A. Baumann, S. Väth, P. Rieder, M. C. Heiber, K. Tvingstedt and V. Dyakonov, J. Phys. Chem. Lett., 2015, 6, 2350–2354.
35. Y. Hu, E. M. Hutter, P. Rieder, I. Grill, J. Hanisch, M. F. Aygüler, A. G. Hufnagel, M. Handloser, T. Bein, A. Hartschuh, K. Tvingstedt, V. Dyakonov, A. Baumann, T. J. Savenije, M. L. Petrus and P. Docampo, Adv. Energy Mater., 2018, 8, 1703057.
36. S. Singh, C. Li, F. Panzer, K. L. Narasimhan, A. Graeser, T. P. Gujar, A. Köhler, M. Thelakkat, S. Huettner and D. Kabra, J. Phys. Chem. Lett., 2016, 7, 3014–3021.
37. A. Sadhanala, F. Deschler, T. H. Thomas, S. E. Dutton, K. C. Goedel, F. C. Hanusch, M. L. Lai, U. Steiner, T. Bein, P. Docampo, D. Cahen and R. H. Friend, J. Phys. Chem. Lett., 2014, 5, 2501–2505.
38. S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, Nat. Photonics, 2020, 14, 300–305.
39. E. Collado-Fregoso, S. N. Hood, S. Shoaee, B. C. Schroeder, I. McCulloch, I. Kassal, D. Neher and J. R. Durrant, J. Phys. Chem. Lett., 2017, 8, 4061–4068.
40. B. A. Gregg, J. Phys. Chem. Lett., 2011, 2, 3013–3015.
41. S. Dimitrov, B. Schroeder, C. Nielsen, H. Bronstein, Z. Fei, I. McCulloch, M. Heeney and J. Durrant, Polymers, 2016, 8, 14.
42. X. Liu, Y. Yan, A. Honarfar, Y. Yao, K. Zheng and Z. Liang, Adv. Sci., 2019, 6, 1802103.
43. S. D. Dimitrov, Z. Huang, F. Deledalle, C. B. Nielsen, B. C. Schroeder, R. S. Ashraf, S. Shoaee, I. McCulloch and J. R. Durrant, Energy Environ. Sci., 2014, 7, 1037.
44. H. Cha, S. Wheeler, S. Holliday, S. D. Dimitrov, A. Wadsworth, H. H. Lee, D. Baran, I. McCulloch and J. R. Durrant, Adv. Funct. Mater., 2018, 28, 1704389.
45. A. J. Lewis, A. Ruseckas, O. P. M. Gaudin, G. R. Webster, P. L. Burn and I. D. W. Samuel, Org. Electron., 2006, 7, 452–456.
46. O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888.
47. K. Jiang, Q. Wei, J. Y. L. Lai, Z. Peng, H. K. Kim, J. Yuan, L. Ye, H. Ade, Y. Zou and H. Yan, Joule, 2019, 3, 3020–3033.
48. A. Maurano, R. Hamilton, C. G. Shuttle, A. M. Ballantyne, J. Nelson, B. O’Regan, W. Zhang, I. McCulloch, H. Azimi, M. Morana, C. J. Brabec and J. R. Durrant, Adv. Mater., 2010, 22, 4987–4992.
49. C. G. Shuttle, A. Maurano, R. Hamilton, B. O’Regan, J. C. de Mello and J. R. Durrant, Appl. Phys. Lett., 2008, 93, 183501.
50. F. Deledalle, P. Shakya Tuladhar, J. Nelson, J. R. Durrant and T. Kirchartz, J. Phys. Chem. C, 2014, 118, 8837–8842.
51. S. Wheeler, F. Deledalle, N. Tokmoldin, T. Kirchartz, J. Nelson and J. R. Durrant, Phys. Rev. Appl., 2015, 4, 024020.
52. C. G. Shuttle, B. O’Regan, A. M. Ballantyne, J. Nelson, D. D. C. Bradley and J. R. Durrant, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113201.
53. R. A. Street, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075208.
54. M. Daboczi, I. Hamilton, S. Xu, J. Luke, S. Limbu, J. Lee, M. A. McLachlan, K. Lee, J. R. Durrant, I. D. Baikie and J.-S. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 46808–46817.
55. D. Baran, R. S. Ashraf, D. A. Hanifi, M. Abdelsamie, N. Gasparini, J. A. Röhr, S. Holliday, A. Wadsworth, S. Lockett, M. Neophytou, C. J. M. Emmott, J. Nelson, C. J. Brabec, A. Amassian, A. Salleo, T. Kirchartz, J. R. Durrant and I. McCulloch, Nat. Mater., 2017, 16, 363–369.
56. R. J. Kline and M. D. McGehee, J. Macromol. Sci., Polym. Rev., 2006, 46, 27–45.
57. H. Hu, K. Jiang, P. C. Y. Chow, L. Ye, G. Zhang, Z. Li, J. H. Carpenter, H. Ade and H. Yan, Adv. Energy Mater., 2018, 8, 1701674.
58. T. Kirchartz and J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165201.
59. C. Deibel and V. Dyakonov, Rep. Prog. Phys., 2010, 73, 096401.
60. C. Deibel, A. Wagenpfahl and V. Dyakonov, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075203.
61. M. C. Heiber, C. Baumbach, V. Dyakonov and C. Deibel, Phys. Rev. Lett., 2015, 114, 136602.
62. C. G. Shuttle, R. Hamilton, J. Nelson, B. C. O’Regan and J. R. Durrant, Adv. Funct. Mater., 2010, 20, 698–702.
63. M. Stolterfoht, A. Armin, B. Philippa, R. D. White, P. L. Burn, P. Meredith, G. Juška and A. Pivrikas, Sci. Rep., 2015, 5, 9949.
64. S. M. Menke, A. Cheminal, P. Conaghan, N. A. Ran, N. C. Greehnam, G. C. Bazan, T.-Q. Nguyen, A. Rao and R. H. Friend, Nat. Commun., 2018, 9, 277.
65. J. Luke, E. M. Speller, A. Wadsworth, M. F. Wyatt, S. Dimitrov, H. K. H. Lee, Z. Li, W. C. Tsoi, I. McCulloch, D. Bagnis, J. R. Durrant and J. Kim, Adv. Energy Mater., 2019, 9, 1803755.
66. F. Gao, W. Tress, J. Wang and O. Inganäs, Phys. Rev. Lett., 2015, 114, 128701.
67. S. N. Hood and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 4495–4500.
68. T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee01338b

‡ J. Wu and J. Lee contributed equally to this work.

---