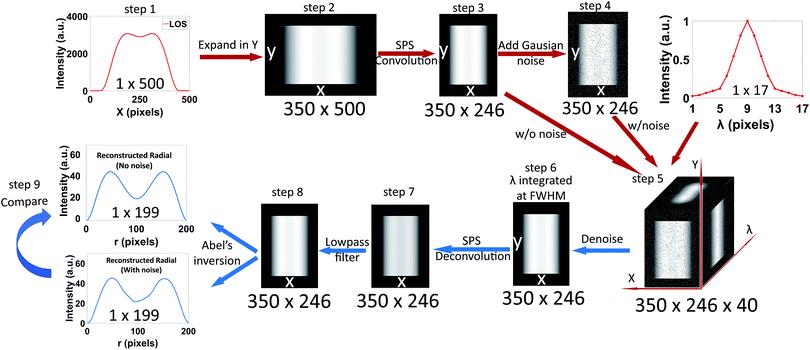
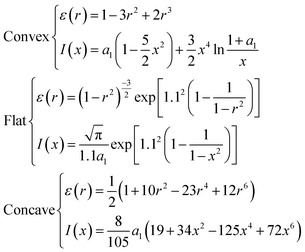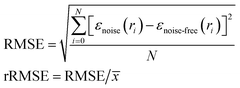Development of Abel's inversion method to extract radially resolved optical emission maps from spectral data cubes collected via push-broom hyperspectral imaging with sub-pixel shifting sampling†
Songyue
Shi
,
Kevin
Finch
,
Yue
She
and
Gerardo
Gamez
 *
*
Texas Tech University, Department of Chemistry and Biochemistry, Lubbock, TX 79409-41061, USA. E-mail: Gerardo.gamez@ttu.edu
First published on 15th November 2019
Abstract
Optical emission spectroscopy (OES) imaging is often used for diagnostics for better understanding of the underlying mechanisms of plasmas. Typical spectral images, however, contain intensity maps that are integrated along the line-of-sight. A widespread method to extract the radial information is Abel's inversion, but most approaches result in accumulation of error toward the plasma axial position, which is often the region of most interest. Here, a Fourier-transform based Abel's inversion algorithm, which spreads the error evenly across the radial profile, is optimized for OES images collected on a push-broom hyperspectral imaging system (PbHSI). Furthermore, a sub-pixel shifting (SPS) sampling protocol is employed on the PbHSI in the direction of the radial reconstruction to allow improved fidelity from the increased number of data points. The accuracy and fidelity of the protocol are characterized and optimized with a software-based 3-dimensional hyperspectral model datacube. A systematic study of the effects of varying levels of representative added noise, different noise filters, number of data points and cosine expansions used in the inversion, as well as the spatial intensity distribution shapes of the radial profile are presented. A 3D median noise filter with 3-pixel radius, a minimum of 50 points and 8 cosine expansions is needed to keep the relative root mean squared error (rRMSE) <8%. The optimized protocol is implemented for the first time on OES images of a micro-capillary dielectric barrier discharge (μDBD) source obtained via SPS PbHSI system and the extracted radial emission of different plasma species (He, N2, N2+) are shown.
Introduction
Plasma-based techniques are routinely applied in a variety of fields, including chemical analysis. The wide applications motivate increasing interests for diagnostics of plasma properties, including the identification of active plasma species, measuring electron temperature, electron density, and gas temperature, etc.1–6 While many plasma diagnostic techniques have been developed in the recent decade to measure the plasma properties mentioned above, their underlying mechanisms are still far from being fully understood in detail, especially the plasma–surface interactions. Among the diagnostic techniques, OES receives particular interests because it allows a relatively simple and cost-effective manner for directly measuring the distribution of atomic and molecular excited species, without disturbing the plasma across a wide wavelength range.1,7,8 However, the detection systems used in OES integrate all the emission information along the line-of-sight (LOS) of the light collection direction, which inherently lacks radial resolution.9Many techniques have been developed to extract the radial information from OES measurements.9–12 Abel's inversion transform is one of such techniques that reconstruct the radially resolved information out of the LOS emissions when it can be assumed that the plasma is cylindrically symmetric. The LOS profile h(x) and radial profile f(r) can be converted to each other mathematically according to the following equations:9
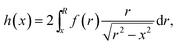 | (1) |
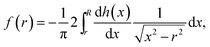 | (2) |
Push-broom, or line scanning systems are often used for spectral imaging. They have advantages of high-light throughput, simultaneous coverage of a wide wavelength range, and a fast acquisition rate.20–24 Previously we proposed a SPS protocol to achieve geometric super-resolution, or higher resolution compared to the geometric pixel size, in the spatial scanning dimension.25 This approach is particularly useful when higher resolution is needed in one dimension without having to rely on magnification techniques that restrict the field-of-view, thus requiring several images to obtain a full picture, lower light throughput, or may require expensive compound lenses to minimize inherent aberrations. One such case is the acquisition of LOS spectral images with the goal of performing Abel's inversion to reconstruct the radially resolved information because the reconstruction takes place only in the dimension where the cylindrical symmetry is assumed. In addition, it has been previously shown that an increase in the number of data points along the LOS intensity profile can lead to much better fidelity when performing the Abel's inversion radial profile reconstruction.14,18
Here, a method that allows extracting radially resolved information with a Fourier-transform based Abel's inversion algorithm from LOS spectral images obtained via SPS PbHSI is presented. A systematic study on the effect of the experimental conditions on the accuracy and fidelity of the reconstructed radial profiles is also shown. The optimized conditions are used to implement the protocol for obtaining radially resolved optical emission maps from a μDBD.
Experimental methods
Abel's inversion protocol evaluation and optimization
In this study, a non-iterative, derivative-free, Fourier-transform based Abel's inversion algorithm16,17 was implemented for the reconstruction of radially resolved images from LOS images acquired via SPS PbHSI. A software-based 3-dimensional model spectral data cubes were constructed in MATLAB (R2018a, The Math Works, Inc., USA) to evaluate the performance of Abel's inversion algorithm with respect to the fidelity of the reconstructed radially resolved information. The schematic flow chart of the model design and the Abel's inversion protocol is shown in Fig. 1. The model spectral data cubes were designed to be representative of measured spectral data cubes, as discussed in detail below, including spatial and spectral profile shapes, noise addition and filtering, as well as SPS convolution and deconvolution.Model spectral data cube
Where 0 ≤ r ≤ 1, 0 ≤ x ≤ 1, and a1 = 1 − x2,. If the radius is N pixels, the total number of pixels in the line profile will be 2N − 1. In the present study, the N is set to 50 and 200, covering the pixel range of the actual plasma emission width.
(1) The width of the spectral data cube is 500 μm, so a 1D 1 × 500-pixel array is generated with a model intensity of 560 counts at every pixel to simulate the average background intensity in the experimental data. Next, the LOS profile is generated where the total number of data points is 2N − 1 pixels, for example, 399 data points for N = 200, and the highest intensity pixel value is set to 3000. The background array is added to the LOS profile so that their center pixels are aligned with each other.
(2) A 2D matrix is generated by repeating the 1 × 500 array LOS profile 250 times in the y-dimension to make a 250 × 500 matrix. The matrix size is increased in the y-dimension by adding 50 rows, at the top and bottom, with background intensity values (560) to produce a 350 × 500 matrix.
(3) The SPS convolution algorithm is applied to the new matrix along the x-dimension, which consists of summing a 10-pixel window (equivalent to the entrance slit width) and saving the result into a new matrix. The 10-pixel window is then shifted by 2 pixel columns (representing the SPS scan step width) and so forth, so the new resulting matrix will be 350 × 246 pixels (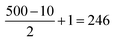 , note that here 1 pixel = 2 μm because of the shift). The 246-pixel array contains oversampled information as opposed to the regular acquisition where the scan step width is equivalent to the slit width (10 μm) resulting in only 50 pixels (500/10 = 50, 1 pixel = 10 μm).
, note that here 1 pixel = 2 μm because of the shift). The 246-pixel array contains oversampled information as opposed to the regular acquisition where the scan step width is equivalent to the slit width (10 μm) resulting in only 50 pixels (500/10 = 50, 1 pixel = 10 μm).
(4) White Gaussian noise was added homogeneously (referred to as “homogenous distribution”) throughout the matrix generated in step 3 to study its generalized effect on the Abel's inversion reconstruction fidelity. Subsequently, white Gaussian noise with a spatial distribution more representative of the spectral images measured from a μDBD plasma was added. The results in a previous μDBD plasma study25 show that the noise distribution is not uniform across the whole image area, instead, the RSD is higher at the edges of the plasma emission region. Thus, the model noise is designed to create a new matrix with higher RSD at the signal edges and 3% RSD throughout the rest of the matrix (referred to as “edge-focused distribution”) to better represent the experimental OES images.
(5) A representative peak shape in the wavelength dimension is also implemented into the model data cube from both step 3 (without noise) and step 4 (with noise). The representative spectral peak shape profile is again obtained from the measured spectral data cubes here. For example, the N2+ emission at 391 nm has a full width half maximum (FWHM) of 5 ICCD pixels and a full width of 17 ICCD pixels. Thus, the model spectral datacube matrix is expanded in the wavelength dimension with a 40-pixel array containing the spectral peak profile and added symmetrically to each side with background valued pixels. The resulting model matrix created is a 350 × 246 × 40 array.
(6) First, background subtraction is applied to the model datacube. Then, a 3D noise filter is implemented, and its properties optimized, as discussed in the next section. The model array is then cropped to a 5 pixels window centered at the peak intensity and integrated into the wavelength dimension, which yields a 350 × 246 × 1 matrix representative of a monochromatic image.
(7) The SPS deconvolution algorithm discussed in previous work25 is applied to the monochromatic matrix, then a lowpass filter with a cutoff frequency of 0.15 is used to eliminate the periodic error coming from the deconvolution.
(8) The Fourier-transform based Abel's inversion algorithm was proposed by G. Pretzier10,17 and was compiled to MATLAB function codes by C. Killer.16 The algorithm expands the undetermined radial profile into a series of cosine expansions by Fourier transform, then the unknown LOS profile is calculated via the Abel's inversion. The equations of the LOS profile are then least squares fitted to the measured LOS data and the amplitude of each expansion is calculated correspondingly. Therefore, significant input variables of the algorithm include the signal pixel radius and the number of cosine expansions. There are some requirements for the algorithm to function correctly: it is designed to work between the axial position and the edge of the LOS intensity profile signal. Thus, (a) only the signal part is kept while the background region is discarded, and (b) a profile axis auto-detection function was added to the protocol to split the profile into two parts from the axis and Abel's inversion algorithm was applied to each half independently. The axis auto-detection function calculated the FWHM of the profile first, then determined the middle-point of the FWHM row as the axial position. Finally, the two reconstructed half-profiles (1 × 100 array) were put together into a whole profile (1 × 199 array, 1 pixel = 2 μm). Here, both half-profiles shared the same middle point by averaging the axial point of each one, leading to a 1 × 199 array instead of 1 × 200 array.
(9) The comparison between the reconstructed radial profile with and without noise was used to evaluate the reconstruction fidelity of the protocol, as explained below. First, a proof-of-principle test was performed to compare the original model radial profile to one reconstructed from the corresponding noiseless LOS profile with the Abel's inversion algorithm protocol (Fig. S2†). Second, the relative root-mean-square error (rRMSE) between radial profiles reconstructed from corresponding noiseless vs. noisy LOS profiles was used to evaluate the deconvolution and reconstruction protocol fidelity robustness in the presence of noise. The rRMSE is defined as follows:
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the mean value of the noise-free radial profile. The protocol is applied to both 50 and 200 radius pixels with each shape of the model profiles.
is the mean value of the noise-free radial profile. The protocol is applied to both 50 and 200 radius pixels with each shape of the model profiles.
Reconstruction error analysis and algorithm optimization
The measured LOS hyperspectral imaging data cubes contain noise coming from multiple sources, including the fluctuation of the plasma, the stray light, and detector, which affect the reconstruction of the radially resolved image. In this study, three different types of 3-dimensional noise filters, with varying voxel radii, including 3D-mean filter, 3D-Gaussian blur, and 3D-median filter were implemented. Then, the original optical emission spatial radial profile was compared to Abel's inversion reconstructed profile in terms of the root-mean-square-error (RMSE), to assess fidelity, and the FWHM, to assess resolution losses, in order to optimize the de-noising protocol with increasing levels of added noise. In addition, the effect of the number of data points along the reconstruction dimension and the number of cosine functions used in the reconstruction algorithm was optimized in the same manner.The optimized data analysis protocol, including SPS deconvolution and Abel's inversion, was implemented to the measured LOS optical emission hyperspectral data cubes from the μDBD obtained with the PbHSI system as described below. The radially resolved emission of different plasma species was obtained and compared with the LOS images.
Atmospheric pressure dielectric barrier discharge
The μDBD source was adapted from previous work.25 The plasma source was composed of two aluminum foil ring electrodes co-axially wrapped around a 5 cm long fused silica capillary (150 μm i.d. and 360 μm o.d., Polymicro Technologies, USA). The capillary polymer coating was removed thermally. The powered electrode was placed 5 mm away from the capillary tip. The inter-electrode distance was 6 mm and a ring PTFE insulator was placed between the two electrodes. The capillary was placed perpendicular to the sample stage, which was mounted on an independent X–Y–Z platform (MTS50-Z8, Thorlabs Ltd., UK), 1 mm away from the capillary tip. In this study, an insulated copper block was used as the sample. The Helium plasma gas (99.999% purity, Ultra High Purity 5.0 Grade Helium, Airgas, USA) flow rate was set to 0.4 L min−1. The AC applied voltage (PVM500, Information Unlimited, USA) was set to 8 kV and the frequency to 30 kHz.Push broom hyperspectral imaging system (PbHSI)
The spectral and spatial optical emission information of plasma species were obtained via a PbHSI system described in previous work by Kroschk et al.24 and Shi et al.25 Briefly, the collimating and focusing optics are triplet lenses (100 mm nominal focal length, CaF2/fused silica/CaF2, Bernhard-Halle GmBH, Germany). A plane mirror is placed between the lenses to turn the light route 90 degrees. Both the mirror and the focusing lens are fixed on a motorized stage (1.6 μm bidirectional repeatability, 50 mm travel range, MTS50-Z8, Thorlabs Ltd., UK). This geometry allows the scanning of the image in x-dimension across the entrance slit of the spectrograph (IsoPlane SCT 320, Princeton Instruments, USA), which has a minimum width of 10 μm and a height of 13 mm.The 300 groves per mm grating (9.77 nm mm−1 linear dispersion and f/4.6 aperture ratio, 129 nm window) was used for plasma species identification with spectral windows of 280–409 nm, 582–711 nm, and 677–806 nm. For the 677–806 nm window, a high-pass filter with the cut-off wavelength of 500 nm was placed before the entrance slit, in order to minimize interference from the 2nd order dispersion of the shorter wavelengths.
An ICCD camera (iStar 334T, Thorlabs Ltd., UK), with a pixel size of 13 × 13 μm and 1024 × 1024 pixels, was used for data acquisition with an exposure time of 0.1 s. A homemade LabVIEW program described by Kroschk24 was applied for the automated acquisition, while the analysis and the display of the hyperspectral data cubes were accomplished by the SPS and Abel's inversion algorithms using ImageJ28 and MATLAB 2018a.
Sub-pixel shifting
The SPS deconvolution from the oversampled spectral data cubes was performed using MATLAB 2018a, as described previously.25 The expression of sub-pixel shifting (SPS) is described by Pernechele and Yang et al.29,30 Compared with typical imaging approaches, SPS allows the acquisition of higher-resolution images from the deconvolution of a series of low-resolution images obtained with a higher sampling frequency. In the present study, the optimized SPS conditions were set as: entrance slit width is 10 μm, scan step width is 2 μm, deconvolution factor is 10/2 = 5, and the cutoff frequency of the lowpass noise filter is 0.15.Results and discussion
Optimization of raw spectral data cube de-noising protocol
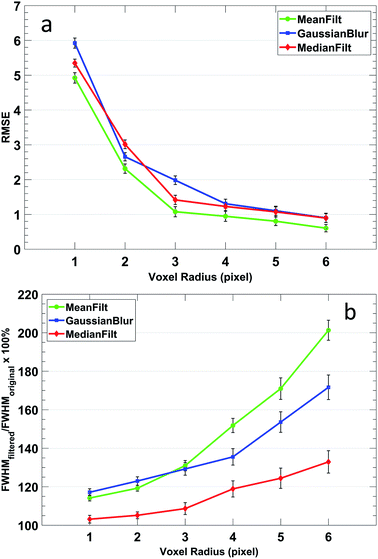
The de-noising (see step 6, Experimental methods section) of the raw 3D spectral data cube was optimized by adding 10% white Gaussian noise distributed homogeneously and comparing the performance of three different 3D noise filters. For this purpose, a one-dimension spatial profile in x, at the peak of the wavelength profile, was extracted from the model data cube after the noise filtering process and compared to the original noiseless data in terms of overall (RMSE) and resolution (FWHM) for comparison. Fig. 2 shows the results for a concave-shape radial profile when 3D mean filter, 3D Gaussian blur, and 3D median filters are implemented with varying voxel radii. The radius of the Gaussian filter is twice the standard deviation (sigma, σ) of the Gaussian function. Therefore, the sigma of the Gaussian blur filter was chosen as 0.5, 1, 1.5, 2, 2.5, 3, representing the radius from 1 to 6 pixels. It is evident that the RMSE of all the filtered profiles decreases, indicating an improvement of the noise filtering as the voxel size increases. Nonetheless, when the radius is larger than 3 pixels, the improvement of noise filtering is significantly smaller. The performance of the median and Gaussian blur filters are very similar, while the mean filter shows slightly lower RMSE. Fig. 2b shows the ratio of the filtered profile FWHM to the original noiseless profile FWHM. In general, the FWHM ratio increases as the voxel radius increases, which shows blurring or peak broadening. Among all the three filters, the 3D median filter shows the smallest broadening effect, which will be beneficial to maintain the image resolution in both the spatial and spectral dimensions. When the radius is 3 pixels, the FWHM ratio of the median filter is less than 107%, and it increases to 120% with a 4-pixel radius. Thus, the 3D median filter with a voxel radius of 3 was chosen as the optimum.Optimization of Abel's inversion algorithm parameters
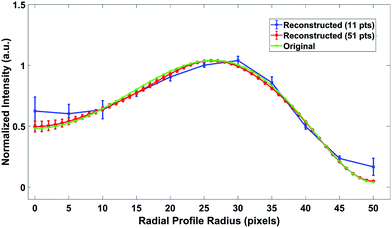
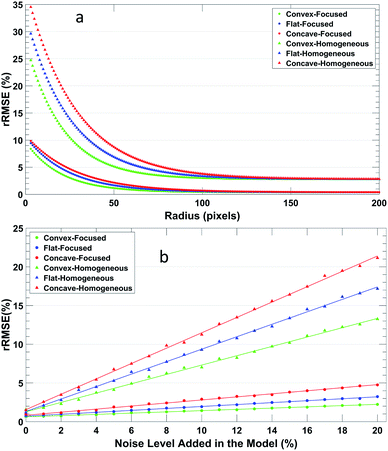
Comparison of a model concave radial profile with one reconstructed using the Abel's inversion algorithm protocol from the corresponding noiseless LOS profile (Fig. S2†) shows a perfect reconstruction of the shape, thus demonstrating that the algorithm protocol developed here is accurate. On the other hand, noise in the LOS profile can greatly affect the radial profile reconstruction fidelity and several parameters need to be optimized to minimize the effect. The Fourier-based Abel's inversion algorithm is a numerical transform approach. The undetermined radial profile is expanded into a series of cosine expansions, whose amplitudes are least-squares-fitted to the measured LOS data. Therefore, the reconstruction accuracy of the method relies on the number of data points used in the fitting. Fig. 3 shows the comparison of the reconstruction accuracy between a small (11 points) and a larger number of data points (51 points). It is evident that the reconstruction is less accurate with fewer data points, especially at the axial and edge radial positions of the signal.The effects the number of data points have on the performance of Abel's inversion algorithm was systematically evaluated by calculating the rRMSE between the reconstructed profile and the original model profile. The test range of the model data is set from a radius of 3, which is the allowed minimum input of the algorithm, to 200, corresponding to the 400 μm diameter of the OES acquisition, which is sufficient to represent the whole μDBD plasma jet area in the x-dimension. Fig. 4a shows the rRMSE of the three types of radial profile shapes as a function of the number of data points for Abel's inversion. Here, the noise level added into the model data cube with edge-focused distribution is 10% at the signal edges and 3% for the rest of the matrix, while the noise level is 10% for the whole area with the homogenous distribution. The number of cosine expansions used in Abel's inversion is 8 (optimization of that parameter is discussed in the following section). Overall, the rRMSE is much higher with less data points and decreases significantly when more data points are used for the reconstruction, which indicates a better reconstruction performance. It is clear that the edge-focused distributions show an overall lower rRMSE than the homogenous distribution for comparable conditions, thus it is important to model the particular noise characteristics representative of the plasma of interest. It is also evident that the convex-shaped profile has the lowest rRMSE, when the number of data points used is the same, while the concave-shaped profile has the highest. Furthermore, it is clear that when the number of data points is larger than 130, the rRMSE gains are not very significant. When the number of data points increases from 130 to 200, the rRMSE decreases only from ∼3.06% to ∼2.84% with homogenous distribution and only from 0.50% to 0.41% with edge-focus distribution. Therefore, it is reasonable to choose the radius size of 200 pixels as an upper limit for this study. Other studies of the effects of the number of data points on the accuracy of Abel's inversion,14 albeit with a different deconvolution algorithm (Nestor–Olsen), also show that reducing the number of data points in the fitting decreases the reconstruction accuracy, especially when the number of data points is less than 100.
The performance of Abel's inversion algorithm with different error levels added to the model datacube is shown in Fig. 4b. Here, the profile signal radius is set to 50 and the number of cosine expansions is 8. The edge-focused distribution added noise ranges from 0 to 20% at the signal edges but is fixed at 3% everywhere else, which is representative of the error in the measured spectral data cubes (<15% at the edge, 1–3% everywhere else). It is evident that the edge-focused added noise distribution leads to significantly higher reconstruction fidelity using Abel's inversion algorithm, which shows the importance of using conditions in the model which are representative of the measured data. For example, when 3% Gaussian noise is added homogeneously to the LOS concave shape profile then the reconstructed radial profile shows an RMSE of 7.7, or 3.9% rRMSE, which when compared to other studies under similar conditions, this rRMSE is significantly lower. An rRMSE of 23% was reported for direct discretization9 and ∼20% rRMSE for Legendre polynomials approximations,11 but this last study used a fitting of 128 points. One can also express the reconstruction error as relative residual percent (rRES = Σ(Inoise − Inoise-free)/ΣInoise-free × 100%) which for our study would be 5.8% rRES under the conditions cited above. For similar conditions a rRES of 30% was reported using the convolution method,10 and rRES of 9% for the Nestro–Olsen method.14 Although the cited values above are not under the exact same conditions (different denoising methods and not exactly the same profile shape), one can still get an idea of the possible advantages. Nevertheless, a study by R. Alvarez9 does compare different Abel's inversion reconstruction algorithms under the same conditions to show that the RMSE of the Fourier-based method is 3.94, Nestor–Olsen method is 12.10, and for direct discretization 20.62. In addition, Gornushkin et al. compared a discrete vs. a Fourier–Hankel Abel's inversion reconstruction algorithm, and also found the Fourier–Hankel algorithm performs better in the presence of noise.18 Furthermore, they saw a significant improvement in the Fourier–Hankel algorithm reconstructed residual error when the number of data points on the LOS diameter was increased from 8 to 40.18 It is worth noting that the rRMSE in our study is smaller (1.3%) when edge-focused noise distribution is used to better simulate the spectral images of the μDBD used for proof-of-principle here. In addition, one must keep in mind that the rRMSE and rRES represent the global fitting accuracy along the whole radius so it cannot show if the error is localized. However, the Fourier transform-based algorithm shows less error at the axis due to its nature of dispersing the error along the radius instead of accumulating the reconstruction error toward the axial position (c.f. ESI Fig. S3†). For example, for the 100 points/3% homogeneous noise case in this study the relative residual at the axial position is 1.8%, while a different study with comparable conditions shows a relative residual >20% at the axial position using the Nestro–Olsen method.14 On the other hand, it should be considered that in the case where the number of data points is very limited, the Fourier transform based method has been shown to yield less accurate radial reconstruction compared to other algorithms, for example, A. Sainz et. al.15 reported that the Nestor–Olsen method shows higher accuracy with 5 or 10 data points. It is worth mentioning that the accuracy of the discrete Fourier transform is limited by the Nyquist criteria and a minimum number of sampled data is necessary to achieve a given accuracy.31
Effects of number of cosine expansions in the inversion
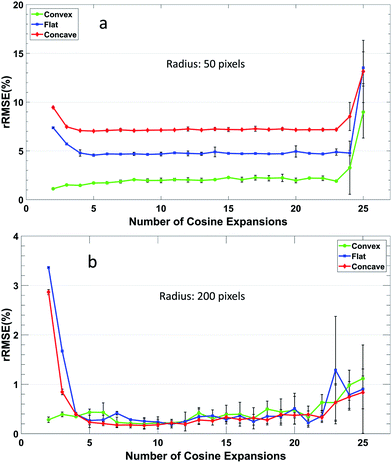
The effect of the number of cosine expansions used for Abel's inversion protocol was also studied (Fig. 5). Here, the pixel radius of the signal was set to 50 and 200 pixels, which are representative of the pixel radius range observed in the measured spectral data cubes. The edge-focused noise distribution was set to 15% at the emission signal edges and 3% everywhere else. The flat and concave shaped profiles show a much higher RMSE with a small number of cosine expansions, which subsequently decreases until 5 expansions are used. On the other hand, the convex shape is well fitted even with a low number of cosine expansions, which is expected due to the shape of a cosine function. Nevertheless, increasing the number of expansions is not always beneficial to the reconstruction, especially when the number of expansions is larger than 20 where there is a rapid increase observed in the RMSE. This is probably due to a better fitting of the added noise which will result in a deviation from the original noiseless radial profile standard. It is evident that the overall RMSE is higher for a 50 data point radius compared to a 200 data point radius. The optimized number of cosine expansions was set to 8, in order to be on the conservative side of the results and to take into account the fact that the data processing time increases approximately proportionally to the square of the number of cosine expansions (t ∝ n2).It is worth noting that Shabanov and Gornushkin proposed an absorption based method, dubbed absorption tomography, analogous to sub-pixel shifting.32 In their approach, collimated light is directed toward a laser induced plasma and a movable aperture is placed before a lens that focuses the light onto the spectrometer slit, thus the oversampling is performed in Fourier space. The method was intended for collection of LOS data where radial information would be recovered via Abel's inversion. As such, their approach aims to allow the use of higher numerical apertures to increase light throughput, while avoiding errors arising from geometric effects at the object plane due to low f-number optics,33,34 and they express their results in signal-to-noise ratio improvements of the LOS data. They did not implement Abel's inversion protocols to their results, thus preventing a comparison with the results here.
Reconstructed radially resolved plasma OES images via SPS-PbHSI
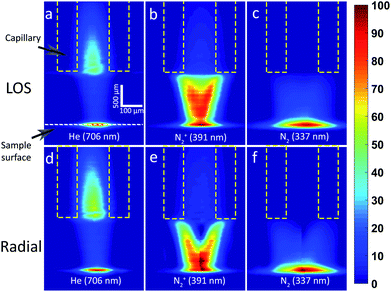
As a proof of principle, the optimized plasma OES data cube noise filter and Abel's inversion algorithm protocols were applied to spectral data cubes measured from a μDBD via SPS PbHSI. As discussed in the previous section, the RMSE calculated from the model data cube can be used to predict the reconstruction error. Taking into account that the maximum noise observed in the measured spectral data cubes is less than 15% RSD and the data of Fig. 4b, it can be expected that the RMSE from the radial reconstruction using the measured LOS data of the μDBD is <11 for concave profiles, <8 for flat profiles, and <6 for convex profiles. Fig. 6 shows the comparison between the LOS images collected (top) and the reconstructed radially resolved images (bottom) at three different wavelengths: 706.5 nm (He I, 3s 3S1–2p 3P0,1,2), 391 nm (N2+, 0–0 first negative system B 2∑u+−X2∑g+), and 337 nm (N2, 0–2 second positive system from C 3Πu–B 3Πg). Notice that the scale bar in Fig. 6 represents a longer distance in the y-dimension compared to the x-dimension (500 μm vs. 100 μm) due to the higher resolution obtained in x as a result of the SPS protocol settings.25 The dashed lines in Fig. 6 represent the position of the capillary (yellow) and the sample surface (red).It is clear that the region of higher intensity in reconstructed radially resolved He emission (Fig. 6d) seems broader in the x-dimension than the corresponding LOS emission (Fig. 6a), both inside and outside the capillary regions. This comes from the intensity distribution shape of the LOS spatial profile. The He LOS emission intensity distribution is somewhere between the flat and convex shapes. As shown in Fig. S1b,† the radial reconstruction of such a profile shape results in a spreading of the peak intensity across a wider area. The redistribution of the intensity over a wider area can also be observed in the N2 (Fig. 6b/e) and N2+ (Fig. 6c/f) emission maps where the LOS has a similar shape, closer to the sample surface. On the other hand, the LOS emission distribution of the nitrogen species in the upper half of the plasma jet is more similar to a concave shape profile (shown in Fig. S1c†), in which the intensity at the axial position is lower than the surrounding volume. As a result, the reconstructed radially resolved images, especially the N2+, yields a more pronounced hollow-cone shape. To the best of the author's knowledge, this is the first time to report the Fourier-transform based Abel's inversion algorithm optimized for the PbHSI with SPS sampling.
The peak positions of the axial intensity profiles can be used to propose how the energy is transferred from the He species in the plasma gas, which peaks earlier in the plasma effluent, to the species present in the ambient air such as first resulting in excited N2+ and finally excited N2 species due to recombination mechanisms.35–37 Nevertheless, the axial intensity peak positions of the species of interest can be different in LOS profiles compared to radially resolved maps. Here, this can be clearly observed for the N2+ case. This puts into context the significance of having access to radially resolved OES maps for plasma diagnostic purposes. Current work in our laboratory involves a systematic study on the effects of different plasma operating conditions (gas flow rate, applied voltage, etc.) and different sample surfaces on the radially resolved optical emission spectral images. The radially resolved emission maps will help to better understand the energy transfer pathways and plasma/sample interactions.
Conclusions
An optimized Fourier-transform based Abel's inversion algorithm was successfully developed for extracting radially resolved optical emission maps from spectral images collected by SPS PbHSI. Before Abel's inversion deconvolution, it is necessary to filter the noise and smooth the data profile for a better reconstruction efficiency. A 3D median filter with a 3-pixel radius proved to be optimum. Also, the systematic modeling study of the reconstruction parameters for different radial profile shapes and at varying noise levels shows that a minimum of 50 points and 8 cosine expansions is needed to keep the rRMSE <8%. The performance compares favorably against other Abel's inversion reconstruction algorithms with the added advantage of evenly distributing the error along the profile, instead of accumulating it onto the axial position. It is worth mentioning that there was no effort in this study to correct for the low f-number of the collection optics and the associated errors due to geometrical effects. Nevertheless, future studies will include a quantitative analysis confirmation of the contribution of the geometric error and it will be minimized with use of much lower numerical aperture optics or reconstruction algorithms tailored to large numerical apertures, as in.33With the implementation of the optimized Abel's inversion algorithm, the radially resolved emission of different plasma species (He, N2, N2+) in a μDBD source were successfully obtained for the first time via SPS PbHSI. The SPS protocol provides access to a higher number of data points along the dimension of the Abel's inversion deconvolution, which leads to a higher reconstruction fidelity. Moreover, the radially resolved emission maps of ambient gas species (N2, N2+) clearly show a hollow-cone shape, with axial profile peak intensities at different positions compared to the line-of-sight images. This distinctly demonstrates the importance of obtaining accurate radially resolved information for plasma diagnostics and can provide insight into mechanistic energy transfer pathways that are inaccessible via the LOS images.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Science Foundation under CHE – 1610849.References
- K. Sasaki, R. Engeln and E. V. Barnat, J. Phys. D: Appl. Phys., 2018, 51, 040202 CrossRef
.
- N. Britun, T. Minea, S. Konstantinidis and R. Snyders, J. Phys. D: Appl. Phys., 2014, 47, 224001 CrossRef
.
- L. C. Trevizan, D. Santos, R. E. Samad, N. D. Vieira, L. C. Nunes, I. A. Rufini and F. J. Krug, Spectrochim. Acta, Part B, 2009, 64, 369–377 CrossRef
.
- M. A. Gondal and T. Hussain, Talanta, 2007, 71, 73–80 CrossRef CAS PubMed
.
- K. J. McLaughlin, S. W. Butler, T. F. Edgar and I. Trachtenberg, J. Electrochem. Soc., 1991, 138, 789–799 CrossRef CAS
.
- A. J. H. Donné, Fusion Sci. Technol., 2017, 53, 379–386 CrossRef
.
- M. Šimek, J. Phys. D: Appl. Phys., 2014, 47, 463001 CrossRef
.
- A. Y. H. H. Ley and R. K. Raja Ibrahim, J. Sci. Technol., 2014, 6, 49–66 Search PubMed
.
- R. Alvarez, A. Rodero and M. C. Quintero, Spectrochim. Acta, Part B, 2002, 57, 1665–1680 CrossRef
.
- G. Pretzler, H. Jäger, T. Neger, H. Philipp and J. Woisetschläger, Z. Naturforsch., A: Phys. Sci., 1992, 47, 955–970 Search PubMed
.
- S. Ma, H. Gao, L. Wu and G. Zhang, J. Quant. Spectrosc. Radiat. Transfer, 2008, 109, 1745–1757 CrossRef CAS
.
- N. N. Sesi, D. S. Hanselman, P. Galley, J. Horner, M. Huang and G. M. Hieftje, Spectrochim. Acta, Part B, 1997, 52, 83–102 CrossRef
.
- E. De Micheli, Applied Mathematics and Computation, 2017, 301, 12–24 CrossRef
.
- G. C. Y. Chan and G. M. Hieftje, Spectrochim. Acta, Part B, 2006, 61, 31–41 CrossRef
.
- A. Sainz, A. Diaz, D. Casas, M. Pineda, F. Cubillo and M. D. Calzada, Appl. Spectrosc., 2006, 60, 229–236 CrossRef CAS
.
- C. Killer, M. Himpel and A. Melzer, Rev. Sci. Instrum., 2014, 85, 103711 CrossRef PubMed
.
- G. Pretzler and Z. Naturfors, Z. Naturforsch., A: Phys. Sci., 1991, 46, 639–641 Search PubMed
.
- I. B. Gornushkin, S. V. Shabanov and U. Panne, J. Anal. At. Spectrom., 2011, 26, 1457–1465 RSC
.
- J. Dong and R. J. Kearney, J. Quant. Spectrosc. Radiat. Transfer, 1991, 46, 141–149 CrossRef CAS
.
- F. Masia, A. Glen, P. Stephens, P. Borri and W. Langbein, Anal. Chem., 2013, 85, 10820–10828 CrossRef CAS PubMed
.
- G. Gamez, D. Frey and J. Michler, J. Anal. At. Spectrom., 2012, 27, 50–55 RSC
.
- G. Gamez, G. Mohanty and J. Michler, J. Anal. At. Spectrom., 2014, 29, 315–323 RSC
.
- G. Gamez, G. Mohanty and J. Michler, J. Anal. At. Spectrom., 2013, 28, 1016–1023 RSC
.
- M. Kroschk, J. Usala, T. Addesso and G. Gamez, J. Anal. At. Spectrom., 2016, 31, 163–170 RSC
.
- S. Shi, X. Gong, Y. Mu, K. Finch and G. Gamez, J. Anal. At. Spectrom., 2018, 33, 1745–1752 RSC
.
- M. W. Blades and G. Horlick, Appl. Spectrosc., 1980, 34, 696–699 CrossRef CAS
.
- C. J. Cremers and R. C. Birkebak, Appl. Opt., 1966, 5, 1057–1064 CrossRef CAS PubMed
.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed
.
- C. Pernechele, L. Poletto, P. Nicolosi and G. Naletto, Opt. Eng., 1996, 35, 1503–1510 CrossRef CAS
.
- H. D. Yang, K. X. Chen, Q. S. He and G. F. Jin, Spectrosc. Spectral Anal., 2009, 29, 3169–3172 CAS
.
-
S. A. T. W. H. Press, W. T. Vetterling, and B. P. Flannery, in Numerical Recipes in Fortran. The Art of Scientific Computing, Cambridge University Press, Cambridge, U.K., 1992, ch. 12, p. 494 Search PubMed
.
- S. V. Shabanov and I. B. Gornushkin, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 518–523 CrossRef CAS
.
- S. V. Shabanov and I. B. Gornushkin, Spectrochim. Acta, Part B, 2011, 66, 413–420 CrossRef CAS
.
- K. T. Walsh, J. Fielding and M. B. Long, Opt. Lett., 2000, 25, 457–459 CrossRef CAS PubMed
.
- G. C. Chan, J. T. Shelley, J. S. Wiley, C. Engelhard, A. U. Jackson, R. G. Cooks and G. M. Hieftje, Anal. Chem., 2011, 83, 3675–3686 CrossRef CAS PubMed
.
- G. C. Y. Chan, J. T. Shelley, A. U. Jackson, J. S. Wiley, C. Engelhard, R. G. Cooks and G. M. Hieftje, J. Anal. At. Spectrom., 2011, 26, 1434–1444 RSC
.
- R. B. Cody, J. A. Laramée and H. D. Durst, Anal. Chem., 2005, 77, 2297–2302 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00239a |
| This journal is © The Royal Society of Chemistry 2020 |