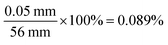Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stretchable and calibratable graphene sensors for accurate strain measurement†
Aidong
Qiu
,
Mathias
Aakyiir
 ,
Ruoyu
Wang
,
Zhaokun
Yang
,
Ayaz
Umer
,
Ivan
Lee
,
Hung-Yao
Hsu
and
Jun
Ma
,
Ruoyu
Wang
,
Zhaokun
Yang
,
Ayaz
Umer
,
Ivan
Lee
,
Hung-Yao
Hsu
and
Jun
Ma
 *
*
School of Engineering and Futures Industries Institute, University of South Australia, Mawson Lakes, SA 5095, Australia. E-mail: Jun.Ma@unisa.edu.au
First published on 20th April 2020
Abstract
Stretchable nanomaterial-based strain sensors are essential to soft electronics and robotics and wearable devices. A sensitivity graph for those reported highly stretchable sensors is often divided into a few nearly linear zones resulting in several gauge factors, which poses a challenge for calibration. We herein report that (i) a gauge factor does not have to be one constant number because calibration merely relies on the relationship between the input and the output data and (ii) calibration accuracy relates to linear regression analysis between testing data and a fitted graph, i.e. calibration accuracy corresponding to coefficient of determination (R2). It is the first time that a stretchable strain sensor is reported as a gauge, where the resolution is an essential element of a gauge. A stretchable elastomer/graphene strain sensor developed in this study is calibrated as a proper gauge to provide strain readings with high resolution up to 0.089% and accuracy of over 99.7%, where resolution refers to the minimum dimension of accurate measurement. The idea of calibration in this study could advance many published wearable sensors to gauges. Sensing parameters are also provided with practical meanings for calibration.
1. Introduction
Stretchable strain sensors have attracted increasing attention in both academia and industry due to the strong demand of strain detection on curved surfaces and soft objects. They are commonly used for the development of soft robotics and wearable devices.1–6 To reach high stretchability, fibres7 and elastomers – Ecoflex rubber,8,9 polydimethylsiloxane10–16 and nature rubber17 – have been composed with various electrically conductive fillers, including but not limited to metal nanowires,1,18,19 Pt-coated polymer nanofibers,20 carbon nanotubes,21–24 graphene,15,25,26 PEDOT:PSS,27 carbon conductive grease28 and carbonized silk.29 The efforts have been focused on pursuing high linearity,26,30 stretchability,17,21 sensitivity7,24,31,32 and cyclic stability,26,33–35 less hysteresis for resistivesensors33,36 as well as other environmental properties.31,37 Many sensors are designed as wearable devices to merely sense changes,38–40 where the numerical readings of the strain are not needed. These stretchable strain sensors are not classified as the gauges that must provide numerical strain measurement.It remains a significant challenge for stretchable nanomaterial-based strain sensors to be used as proper gauges.41 A gauge must provide accurate and precise output readings corresponding to input data with a one-on-one relationship. Calibration is needed to upgrade these stretchable strain sensors to gauges, and this requires a monotonic input–output graph to be expressed in a certain algebraic function. A monotonic graph means that the electrical output simply either increases or decreases with increasing strain in one direction. When an algebraic function is obtained from the linear regression analysis, it should be examined to find whether it can be interpreted by an electrical circuit. A linear regression analysis is usually based on the tested input–output data. The statistic expression for linear regression is
Linear regression includes both polynomial regression and simple linear regression. ‘Linear’ refers to linear coefficients of a polynomial function, such as f(x) = ax3 + bx2 + cx + d, where coefficients a, b, c and d are constants, and they are in a linear relationship. When the polynomial is degree 1, the linear function f(x) = cx + d is for simple linear regression. Expressed as graphs, a curve relates to a polynomial function and a straight line refers to a linear function, which means that R2 can be used for both curves and straight lines.
For those stretchable nanomaterial-based strain sensors reported to date, their sensitivity graphs were reported as either a nearly straight line or a curved line split into several nearly straight portions; each portion was reported to have a constant gauge factor.7,24,29 A gauge factor is the ratio of relative change of electrical output to the applied strain, which is reflected as the slope of a sensitivity graph. A sensitivity graph for resistive strain sensors is the plot of relative resistance change (calculated from output data) vs. strain (calculated from input data). One constant gauge factor represents either a straight line for the sensitivity graph or a linear relationship between the inputs and the outputs. The reason to pursue multiple constant gauge factors in the literature is not clear, and it could be for the purpose of calibration. However, multiple gauge factors in an unrelated manner pose a challenge to calibration.
From our perspectives, the relationship between input and output data does not have to be a straight-line plot for calibration. A calibration unit is an electrical circuit which interprets the math function between the inputs and the outputs. Linear functions and many polynormal functions are interpretable through electrical circuits, although linear functions feature simple electrical circuits. Other prerequisites for calibrating stretchable strain sensors include (i) reliable cyclic stability and (ii) good monotonicity between the inputs and the outputs within a reasonable strain range.42–44 Calibration under high R2 and resolution improves accuracy and precision for measurement.
Herein, we prepare a stretchable and calibratable strain sensor by sandwiching a patterned graphene film between two elastomer sheets. The input–output graph of our elastomer/graphene strain sensor follows a polynomial function which can be interpreted by an electrical circuit to enable calibration. The electrical circuit is arranged by using the Field Programmable Gate Array (FPGA) technology. Stable sensing behaviour is achieved by the fabrication processes of the sensor. In specific, viscoelastic macromolecules during vulcanization infiltrate into the graphene film, and this enhances the interface interaction between the elastomer and the film. The interaction facilitates effective strain transfer from the elastomer to the film, which confines the movement of graphene sheets within a stable region. The gauge factor of our sensor is described by a math function, by taking the first derivative of the polynomial regression function of a sensitivity graph. Numerical gauge factors are obtained by substituting the strain values into the gauge factor function. Our strain sensors can be calibrated to provide accurate and precise strain measurements. The sensors have gauge factors in a range from 34.14 to 41.10, strain resolution of 0.089% and calibration accuracy of 99.74%, which indicates potential as a strain gauge for various applications.
2. Results and discussion
2.1 Fabrication of elastomer/graphene strain sensors
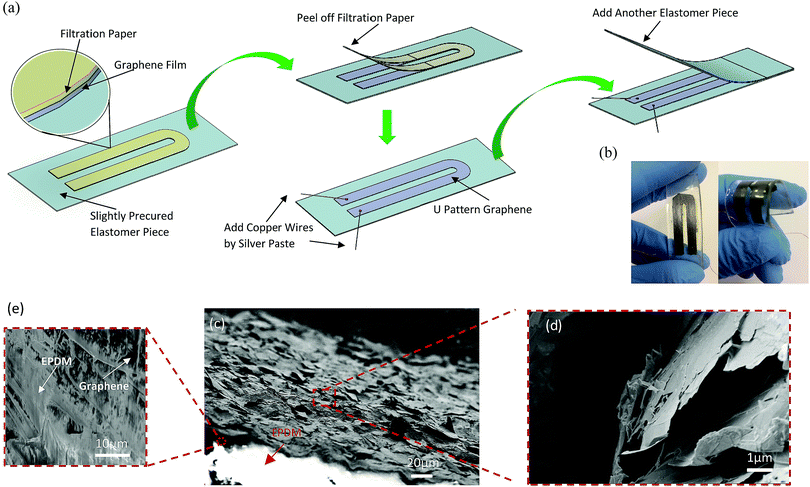
Fig. 1a illustrates a typical fabrication process of stretchable elastomer/graphene strain sensors by using graphene sheets and two types of common elastomers, i.e. ethylene-propylene-diene monomer (EPDM) and polydimethylsiloxane (PDMS). Uncured EPDM is solid, and it was cured under relatively high temperature and pressure. Excellent weathering resistance of EPDM makes an ideal substrate/matrix for sensors to be used outdoor.45 PDMS is fluid with high viscosity before curing and it was cured at atmospheric pressure and temperature. As elaborated in Experimental, graphene sheets were fabricated into a U-patterned film to perform sensing functions for our stretchable strain sensors. In brief, a graphene film was pressed onto a piece of slightly precured elastomer, followed by adding electrodes to the film. It was subsequently sealed by the following means. For an EPDM/graphene sensor, another piece of slightly precured EPDM was added onto the top of the film, followed by curing at 150 °C under 10 MPa for 25 minutes. For a PDMS/graphene sensor, a mixture of PDMS and curing agent was coated on the top, followed by curing of 24 hours at room temperature. Fig. 1b reveals a PDMS/graphene strain sensor in straight and bending conditions.In these resistive-type strain sensors, elastomers work as the substrates which not only accommodate graphene sheets (or called graphene platelets) but provide elastic deformation. Our research team has conducted extensive research on these graphene sheets since 2012.46 We utilized X-rays diffraction and Raman spectroscopy to analyse the sheets. Each sheet is few-layer graphene having thickness of 2–4 nm.47–49 These sheets stack themselves in a dried form, but their XRD pattern at 2θ of 26.18° is far less intense than that of graphite;50 this means that the stacked platelets are readily dispersible in solvent, which agrees with our lab practice. Hence, these stacked graphene sheets are different to flake graphite. The platelets have an Id/Ig ratio of ∼0.06, corresponding to electrical conductivity of 1450 S cm−1.51Fig. 1c and d contains SEM micrographs of the side view of the graphene film of around 20 μm in thickness. During the curing process, viscoelastic macromolecules infiltrated into the film (Fig. 1e), and this should increase the interface interaction between the elastomer and the film, to facilitate strain transfer from the elastomer to the film.
2.2 Performance and calibration of elastomer/graphene strain sensors
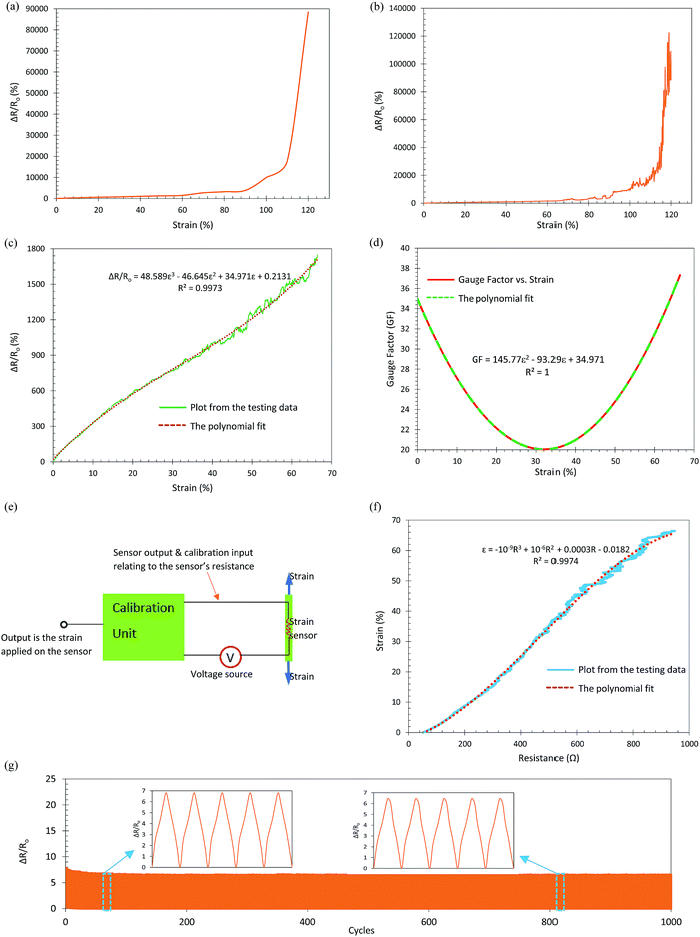
To assess these sensors, an Instron Tensile Tester was synchronized with a programmed ARDUINO-UNO system to simultaneously record extension and electrical resistance. In Fig. 2(1), the sensitivity graph reveals relative resistance change vs. applied strain. Strain ε is expressed as ΔL/L0, where ΔL is the extension and L0 is the original length.Strain resolution must be considered for a sensor to be used as a gauge, where resolution refers to the minimum dimension of an accurate measurement. In this work, the strain resolution is a consistently recorded extension interval divided by the original length of the sensor. Strain resolution is also relevant to the monotonicity of a sensitivity graph. For a typical EPDM/graphene strain sensor, the sensitivity graph is monotonic at a strain resolution of 10.00% (Fig. 2a), and less monotonic (sawtooth shape) at a higher resolution of 0.89% (Fig. 2b). A monotonic sensitivity graph means a one-on-one relationship between strain and resistance change. Resolution must be provided for calibration and high resolution is always desired.
Fig. 2c reveals the sensitivity graph of a typical EPDM/graphene sensor at a strain resolution of 0.089%. Monotonicity is obvious at strain below 12%; and the increasing non-monotonic behaviour at high strain compromises the accuracy of calibration. A strain range of 0–68% was selected as it suits human motions for the development of soft robotics.14 The resolution was set by an Instron Tensile Tester with an extension interval rate of 0.05 mm per 0.1 second (relating to 30 mm min−1 as per strain rate) for the sensor's original length of 56 mm. Thus, the strain resolution was obtained by
By conducting linear regression analysis for the testing data, a fitted function with R2 = 0.9973 for the sensitivity graph in Fig. 2c is found to be a third order polynomial function (eqn (1)), which can be used to obtain a gauge factor. Linear regaression analysis can be conducted through software Origin or Excel.
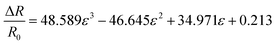 | (1) |
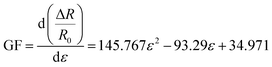 | (2) |
Calibration directly relies on the relationship between the input and output data, where a monotonic relationship (sensitivity graph) is needed. Fig. 2e schematically explains how calibration was designed and executed for a resistive strain sensor. The original input is the strain occurred on the sensor, and the sensor converts the strain into electrical resistance. The resistance inputs into a calibration unit which is a specific electrical circuit designed by the FPGA technology. In the unit, the resistance is interpreted as a relative strain which is the measured strain reading. The electrical circuit is arranged according to a polynomial regression function (eqn (3)) from the input–output testing data (Fig. 2f).
| ε = −10−9R3 + 10−6R2 + 0.0003R − 0.0182 | (3) |
To validify whether this calibration method is suitable to other stretchable strain sensors, a PDMS/graphene strain sensor was prepared and tested. The graphs in Fig. S1a–d in the ESI† were plotted from the testing data at either 30 or 60 mm min−1, where the speeds pose no effect on the sensing graphs. The calibration method clearly works in the PDMS/graphene strain sensor, because (i) we observed a monotonic input–output relationship with high R2 of 99.82% and (ii) polynomial regression functions are interpretable by the Field Programmable Gate Array (FPGA) technology. The gauge factor for the PDMS/graphene sensor is in the range of 9–20, which is lower than that of EPDM/graphene sensor. In the following section, we demonstrated how sensitive the sensor can be despite the relatively low gauge factor of the PDMS/graphene, which means that both sensors work well in potentially many applications.
Fig. 2g shows the loading–unloading graph of 1000 cycles for a typical EPDM/graphene sensor at strain 0–25%. The overall sensing performance appears to be stable. In specific, some minor changes are seen during the initial 50 cycles, which may originate from the permanent dislocation of graphene sheets inside the sensor. In the two insets for the amplified five loading–unloading cycles, slight difference in relative resistance change is observed. The evolutionary discrepancy through 1000 cycles is common for stretchable nanomaterial-based strain sensors, and it may pose a minor effect on the reliability of the sensor to work as a gauge for long-term applications. It is worth to point out that this minor effect becomes serious when tested at 68% strain, as indicated in Fig. S1e (ESI†) for the PDMS/graphene sensor. Perfect cyclic stability is a significant challenge for these sensors to work as reliable gauges. The imperfection of cyclic stability and the strain-dependant sensing behaviour may be the characteristic of resistive strain sensors based on nanomaterials. The relationship between the relative resistance change and the strain could be written as:25,39
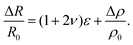 | (4) |
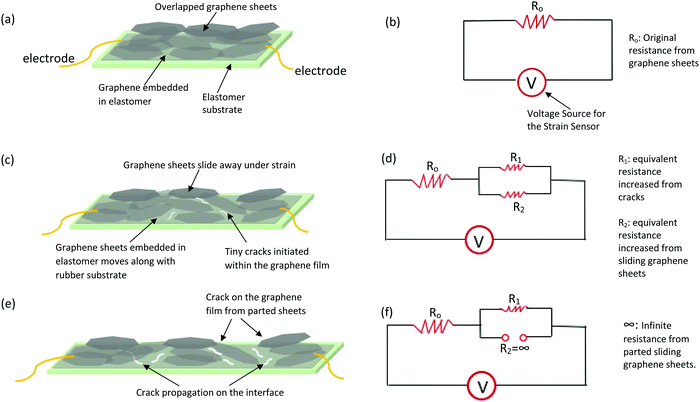
The sensing mechanism for the elastomer/graphene strain sensors is a mixture of the sliding of graphene sheets, the tunnelling effect and the propagation of cracking in the graphene film as well as the evolutionary changes at the interface between the film and the substrate. The sliding of graphene sheets decreases the overlapped area and correspondingly increases the contact resistance of the sheets.15,25,52,53 Tunnelling means that electrons can cross through nonconductive barriers, which can happen between the closely spaced nanomaterials including graphene sheets.1,54,55 Tunnelling may happen on graphene film due to (i) microcracks on the film, (ii) gaps filled with air or (iii) the elastomer molecules between the sheets. The cut-off distance of tunnelling between two parallel graphene sheets insulated by polymers was 2–3 nm.56,57 When the spacing distance between graphene sheets is over 3 nm, cracking starts to cause electrical disconnection.1
Fig. 3a reveals one piece of graphene film which was fabricated onto an elastomer substrate. During the fabrication, some graphene sheets were infiltrated into elastomer macromolecules, which would facilitate strain transfer from the elastomer to the graphene film (see Fig. 1e with relevant discussion). Fig. 3b contains an equivalent electrical circuit for an undeformed sensor, where R0 is the initial resistance.
Upon straining below 2%, graphene sheets embedded in the substrates would move along with the elastomer substrates, and this may accompany with the creation of a small number of tiny microcracks at the interface between the graphene film and the substrate; those unembedded graphene sheets at the interface would collaboratively deform, causing relative sliding between the sheets inside the film (Fig. 3c). The sliding of graphene sheets and the tunnelling effect would be the dominant sensing mechanisms at this stage. For better understanding, the resistance change is divided into two parts respectively allocated to the sliding graphene sheets and the elastic change at the interface. Fig. 3d reveals a corresponding equivalent electrical circuit, and the equivalent electrical resistance R can be expressed as:
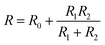 | (5) |
Upon further stretching up to ∼32% strain, cracks propagate at the elastomer/graphene interface whilst the graphene sheets slide away further. Crack propagation, sliding of the sheets and tunnelling may exist simultaneously at this stage, all of which are considered in eqn (5). When strained over 32%, the sliding graphene sheets start losing connections with each other (Fig. 3e). The sensing becomes more and more dependent on the propagating cracks between the sliding sheets as well as those cracks at the interface. Eventually, the electrical resistance from the sliding graphene sheets turned to be infinite or dysfunctional, and the sensing performance only relies on graphene sheets at the interface; the corresponding equivalent electrical circuit is shown in Fig. 3f.
When crack propagation becomes the major sensing mechanism, the sensor turns to have higher gauge factors, because the cracks at this stage increase the sensor resistance dramatically. Nevertheless, the propagation of these cracks is random for each loading–unloading cycle, which not only affects monotonicity for each cycle but results in unideal reproducibility between cycles. Although the size and number of cracks may grow with strain at this stage, the sensor was found to recover to its initial geometry upon release of strain, corresponding to the original resistance.
Stretchability is the maximum strain having desired reproducibility under cyclic loading. The stretchability was found to be 120% for an EPDM/graphene strain sensor, and 68% for a PDMS/graphene one. However, by considering high-resolution applications, we suggest stretchability of 68% for the EPDM/graphene sensor and 43% for the PDMS/graphene one. Table 1 shows that our elastomer/graphene sensors have relatively high sensitivity and stretchability; the ability of being calibratable is the most important feature, which would provide a tip for nonlinear sensing materials to conduct linear regression for calibration.
| Materials | Sensitivity (gauge factor) | Stretchability (%) | Coefficient of determination (R2) | Calibratable | Ref. |
|---|---|---|---|---|---|
| PDMS/graphene nanocellulose | 7.1 | 100 | Nonlinear | Unmentioned | 15 |
| PDMS/graphene foam | 223 | 3 | Linear | Unmentioned | 16 |
| Nature rubber/graphene | Up to 35 | 75 | Linear within 4% strain | Unmentioned | 17 |
| PDMS/graphene woven fabric | 24 | Up to 70 | Excellent | Unmentioned | 26 |
| PDMS/graphene | 106 | 10 | Nonlinear | Unmentioned | 58 |
| PDMS/graphene | 9–20 | 43 | 0.9982 | Yes | This work |
| EPDM/graphene | 20–37 | 68 | 0.9974 | Yes | This work |
Our stretchable elastomer/graphene strain sensors can provide strain measurement accurately and precisely, acting as proper gauges. Once stretchable strain sensors can tell accurate and precise strain magnitudes repeatably, they are qualified for the development of auto control systems, such as soft robotics by mimicking human motions.
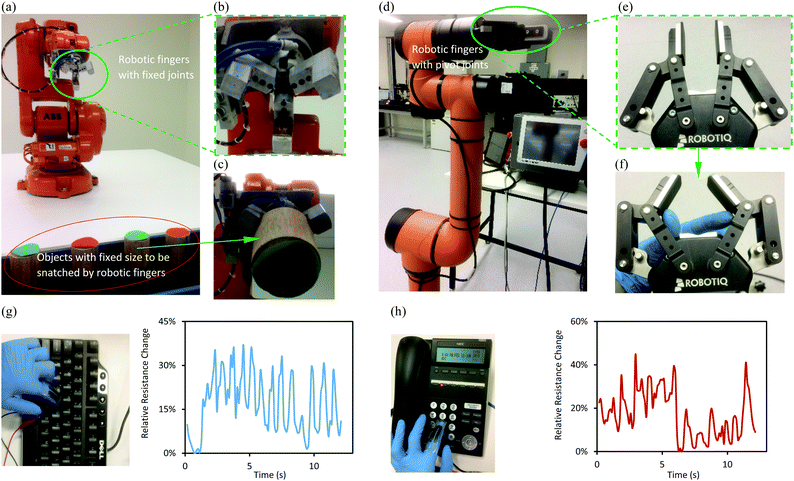
Conventional robot hands are rigid with inflexible fingers, and the objects to be picked up need to be designed in the fixed dimensions (Fig. 4a–c). A newly developed robot hand has pivoted joints grabbing objects in various sizes (Fig. 4d–f), but its rigid nature confines working capacity. Soft robotic hands are anticipated to conduct more delicate work, such as typing keyboards, dialling telephones like human beings, igniting a bomb to protect living creatures in a safe place, and picking up objects of any size from the ground, especially heavy, dirty or toxic ones. The fulfilment of soft robotic hands relies on the development of soft strain sensors, towards which wearing soft sensors on human hands is a reasonable start.
Fig. 4g–h contains photographs and electrical response graphs for our stretchable PDMS/graphene strain sensors attached onto human fingers for operation of keyboard and telephone. The output electrical responses do not start exactly from time zero, which relates to the sensor's hysteresis. Hysteresis is the time difference between the resistance change and the applied strain, and it inevitably exists on stretchable elastomer/graphene strain sensors. Hysteresis originates from the viscoelastic behaviour of elastomers and the interaction between the elastomer and the graphene. Hysteresis was measured as 0.16 seconds for the PDMS/graphene stretchable strain sensor and 0.18 seconds for the EPDM/graphene sensor.
3. Conclusion
In this study, a stretchable and calibratable graphene strain sensor was developed by a cost-effective method, where graphene was sandwiched between two elastomer sheets to have a certain degree of both restriction and freedom of movement. Depending on the strain level, the dominant sensing mechanisms switched between the sliding of graphene sheets, the tunnelling effect and the propagation of cracks on the graphene film as well as the evolutionary changes at the interface between the film and the elastomer sheets.The gauge factor of a stretchable elastomer/graphene strain sensor does not have to be a constant number(s), because calibration merely relies on the relationship between the input and output data, rather than gauge factors. Derived from a sensitivity graph, a gauge factor can be either a number or a certain algebraic function within a specified strain range.
Our stretchable elastomer/graphene strain sensors were calibratable and they provided strain readings with 0.089% resolution and over 99.70% accuracy. The calibration method is suitable to other stretchable strain sensors on the condition that (i) they have monotonic sensitivity graphs, known strain resolution, high value of R2 and cyclic stability and (ii) polynomial regression functions for their strain–resistance relationships can be processed by electrical circuits. During calibration, the data recording rate was utilized to calculate strain resolution; the relationship between strain and resistance was applied to design an electrical circuit by the FPGA technology for calibration. Calibration accuracy was related to R2.
4. Experimental details
4.1 Material
A graphite intercalation compound (GIC, Asbury 1721) was kindly provided by Asbury Carbons, Asbury, NJ, USA. Elastomer polydimethylsiloxane (PDMS, KE-106) and its curing agent CAT-RG were provided by Shin-ETSU Slicone, Taiwan. Elastomer ethylene-propylene-diene monomer (EPDM 4045, ethylene content 53–59%) and its curing agents were supplied by Jilin Petrochemicals Ltd, China.4.2 Preparation of stretchable elastomer/graphene strain sensors
A piece of filtration paper was cut into a U-shape pattern and stacked onto another piece of filtration paper. This was carefully transferred onto a filtration system. The graphene suspension was filtrated under vacuum through the stacked filtration paper. Then the U-shape filtration paper was carefully removed by a pair of pointy tweezers to obtain a patterned graphene film for the following sensor fabrication.
An EPDM piece was pressed with the patterned graphene film which was obtained from Section 4.2.1. This was followed by peeling off the filtration paper from the film. After electrodes were glued onto the graphene film by silver paste, another EPDM piece was added onto the top, followed by a full curing process of 25 minutes at 150 °C under 10 MPa.
4.3 Characterization
The structures and morphologies of our stretchable strain sensors were characterized by a scanning electron microscope, Carl Zeiss Microscopy Merlin. The tensile test was done by Instron 5567 which was synchronized with a programmed ARDUINO-UNO board to record electrical resistance simultaneously. Hysteresis and application test on human fingers for the strain sensors were performed by using a digital Source Meter (Keithley 2602B).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for financial support by the Australian Research Council (Grant LP160100717). J. M. thanks Asbury for providing graphite intercalation compounds.References
- M. Amjadi, A. Pichitpajongkit, S. Lee, S. Ryu and I. Park, ACS Nano, 2014, 8, 5154–5163 CrossRef CAS PubMed.
- N. Lu, C. Lu, S. Yang and J. Rogers, Adv. Funct. Mater., 2012, 22, 4044–4050 CrossRef CAS.
- J. Lee, S. Kim, J. Lee, D. Yang, B. C. Park, S. Ryu and I. Park, Nanoscale, 2014, 6, 11932–11939 RSC.
- X. Xiao, L. Yuan, J. Zhong, T. Ding, Y. Liu, Z. Cai, Y. Rong, H. Han, J. Zhou and Z. L. Wang, Adv. Mater., 2011, 23, 5440–5444 CrossRef CAS PubMed.
- M. A. McEvoy and N. Correll, Science, 2015, 347, 1261689 CrossRef CAS PubMed.
- C. Majidi, Soft Robot., 2014, 1, 5–11 CrossRef.
- J. Lee, S. Shin, S. Lee, J. Song, S. Kang, H. Han, S. Kim, S. Kim, J. Seo and D. Kim, ACS Nano, 2018, 12, 4259–4268 CrossRef CAS PubMed.
- S. Ryu, P. Lee, J. B. Chou, R. Xu, R. Zhao, A. J. Hart and S.-G. Kim, ACS Nano, 2015, 9, 5929–5936 CrossRef CAS PubMed.
- M. Amjadi, Y. J. Yoon and I. Park, Nanotechnology, 2015, 26, 375501 CrossRef PubMed.
- D. E. Hanson, M. Hawley, R. Houlton, K. Chitanvis, P. Rae, E. B. Orler and D. A. Wrobleski, Polymer, 2005, 46, 10989–10995 CrossRef CAS.
- J. P. Heggers, N. Kossovsky, R. W. Parsons, M. C. Robson, R. P. Pelley and T. J. Raine, Ann. Plast. Surg., 1983, 11, 38–45 CrossRef CAS PubMed.
- A. Mata, A. J. Fleischman and S. Roy, Biomed. Microdevices, 2005, 7, 281–293 CrossRef CAS PubMed.
- Q. Qin and Y. Zhu, ACS Nano, 2011, 5, 7404–7410 CrossRef CAS PubMed.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi, D. N. Futaba and K. Hata, Nat. Nanotechnol., 2011, 6, 296 CrossRef CAS PubMed.
- C. Yan, J. Wang, W. Kang, M. Cui, X. Wang, C. Y. Foo, K. J. Chee and P. S. Lee, Adv. Mater., 2014, 26, 2022–2027 CrossRef CAS PubMed.
- Q. Zheng, X. Liu, H. Xu, M.-S. Cheung, Y.-W. Choi, H.-C. Huang, H.-Y. Lei, X. Shen, Z. Wang, Y. Wu, S. Y. Kim and J.-K. Kim, Nanoscale Horiz., 2018, 3, 35–44 RSC.
- C. S. Boland, U. Khan, C. Backes, A. O’Neill, J. McCauley, S. Duane, R. Shanker, Y. Liu, I. Jurewicz and A. B. Dalton, ACS Nano, 2014, 8, 8819–8830 CrossRef CAS PubMed.
- F. Xu and Y. Zhu, Adv. Mater., 2012, 24, 5117–5122 CrossRef CAS PubMed.
- S. Gong, W. Schwalb, Y. Wang, Y. Chen, Y. Tang, J. Si, B. Shirinzadeh and W. Cheng, Nat. Commun., 2014, 5, 3132 CrossRef PubMed.
- C. Pang, G.-Y. Lee, T.-i. Kim, S. M. Kim, H. N. Kim, S.-H. Ahn and K.-Y. Suh, Nat. Mater., 2012, 11, 795 CrossRef CAS PubMed.
- X. Wang, J. Li, H. Song, H. Huang and J. Gou, ACS Appl. Mater. Interfaces, 2018, 10, 7371–7380 CrossRef CAS PubMed.
- S. Yu, X. Wang, H. Xiang, L. Zhu, M. Tebyetekerwa and M. Zhu, Carbon, 2018, 140, 1–9 CrossRef CAS.
- Y. Zheng, Y. Li, K. Dai, Y. Wang, G. Zheng, C. Liu and C. Shen, Compos. Sci. Technol., 2018, 156, 276–286 CrossRef CAS.
- J. Zhou, X. Xu, Y. Xin and G. Lubineau, Adv. Funct. Mater., 2018, 28, 1705591 CrossRef.
- G. Shi, Z. Zhao, J. H. Pai, I. Lee, L. Zhang, C. Stevenson, K. Ishara, R. Zhang, H. Zhu and J. Ma, Adv. Funct. Mater., 2016, 26, 7614–7625 CrossRef CAS.
- X. Liu, C. Tang, X. Du, S. Xiong, S. Xi, Y. Liu, X. Shen, Q. Zheng, Z. Wang, Y. Wu, A. Horner and J.-K. Kim, Mater. Horiz., 2017, 4, 477–486 RSC.
- E. Roh, B.-U. Hwang, D. Kim, B.-Y. Kim and N.-E. Lee, ACS Nano, 2015, 9, 6252–6261 CrossRef CAS PubMed.
- J. T. Muth, D. M. Vogt, R. L. Truby, Y. Mengüç, D. B. Kolesky, R. J. Wood and J. A. Lewis, Adv. Mater., 2014, 26, 6307–6312 CrossRef CAS PubMed.
- C. Wang, X. Li, E. Gao, M. Jian, K. Xia, Q. Wang, Z. Xu, T. Ren and Y. Zhang, Adv. Mater., 2016, 28, 6640–6648 CrossRef CAS PubMed.
- L. Cai, L. Song, P. Luan, Q. Zhang, N. Zhang, Q. Gao, D. Zhao, X. Zhang, M. Tu and F. Yang, Sci. Rep., 2013, 3, 3048 CrossRef PubMed.
- L. Wang, H. Wang, X.-W. Huang, X. Song, M. Hu, L. Tang, H. Xue and J. Gao, J. Mater. Chem. A, 2018, 6, 24523–24533 RSC.
- J.-H. Pu, X. Zhao, X.-J. Zha, L. Bai, K. Ke, R.-Y. Bao, Z.-Y. Liu, M.-B. Yang and W. Yang, J. Mater. Chem. A, 2019, 7, 15913–15923 RSC.
- S. Chen, Y. Song, D. Ding, Z. Ling and F. Xu, Adv. Funct. Mater., 2018, 1802547 CrossRef.
- Z. Yang, D.-Y. Wang, Y. Pang, Y.-X. Li, Q. Wang, T.-Y. Zhang, J.-B. Wang, X. Liu, Y.-Y. Yang and J.-M. Jian, ACS Appl. Mater. Interfaces, 2018, 10, 3948–3954 CrossRef CAS PubMed.
- M. Wajahat, S. Lee, J. H. Kim, W. S. Chang, J. Pyo, S. H. Cho and S. K. Seol, ACS Appl. Mater. Interfaces, 2018, 10, 19999–20005 CrossRef CAS PubMed.
- J. Lee, M. Lim, J. Yoon, M. S. Kim, B. Choi, D. M. Kim, D. H. Kim, I. Park and S.-J. Choi, ACS Appl. Mater. Interfaces, 2017, 9, 26279–26285 CrossRef CAS PubMed.
- P. Ahuja, S. Akiyama, S. K. Ujjain, R. Kukobat, F. Vallejos-Burgos, R. Futamura, T. Hayashi, M. Kimura, D. Tomanek and K. Kaneko, J. Mater. Chem. A, 2019, 7, 19996–20005 RSC.
- M. Ha, S. Lim and H. Ko, J. Mater. Chem. B, 2018, 6, 4043–4064 RSC.
- M. Amjadi, K. U. Kyung, I. Park and M. Sitti, Adv. Funct. Mater., 2016, 26, 1678–1698 CrossRef CAS.
- T. Q. Trung and N. E. Lee, Adv. Mater., 2017, 29, 1603167 CrossRef PubMed.
- A. Qiu, P. Li, Z. Yang, Y. Yao, I. Lee and J. Ma, Adv. Funct. Mater., 2019, 1806306 CrossRef.
- S. Gee, V. Akylas and W. Van Den Bogert, Proceedings of the IEEE International Conference on Microelectronic Test Structures, Long Beach, CA, USA, 1988, pp. 185–191 Search PubMed.
- A. L. Window, Strain gauge technology, Springer, 1992 Search PubMed.
- R. C. Jaeger, J. C. Suhling and R. Ramani, IEEE Trans. Compon., Packag., Manuf. Technol., Part B, 1994, 17, 97–107 CrossRef CAS.
- J. Ma, Y. Feng, J. Xu, M. Xiong, Y. Zhu and L. Zhang, Polymer, 2002, 43, 937–945 CrossRef CAS.
- I. Zaman, H. C. Kuan, Q. Meng, A. Michelmore, N. Kawashima, T. Pitt, L. Zhang, S. Gouda, L. Luong and J. Ma, Adv. Funct. Mater., 2012, 22, 2735–2743 CrossRef CAS.
- I. Zaman, H.-C. Kuan, J. Dai, N. Kawashima, A. Michelmore, A. Sovi, S. Dong, L. Luong and J. Ma, Nanoscale, 2012, 4, 4578–4586 RSC.
- G. Shi, S. Araby, C. T. Gibson, Q. Meng, S. Zhu and J. Ma, Adv. Funct. Mater., 2018, 28, 1706705 CrossRef.
- J. Ma, Q. Meng, I. Zaman, S. Zhu, A. Michelmore, N. Kawashima, C. H. Wang and H.-C. Kuan, Compos. Sci. Technol., 2014, 91, 82–90 CrossRef CAS.
- J. Ma, Q. Meng, A. Michelmore, N. Kawashima, Z. Izzuddin, C. Bengtsson and H.-C. Kuan, J. Mater. Chem. A, 2013, 1, 4255–4264 RSC.
- Q. Meng, J. Jin, R. Wang, H.-C. Kuan, J. Ma, N. Kawashima, A. Michelmore, S. Zhu and C. H. Wang, Nanotechnology, 2014, 25, 125707 CrossRef PubMed.
- M. Hempel, D. Nezich, J. Kong and M. Hofmann, Nano Lett., 2012, 12, 5714–5718 CrossRef CAS PubMed.
- J. J. Park, W. J. Hyun, S. C. Mun, Y. T. Park and O. O. Park, ACS Appl. Mater. Interfaces, 2015, 7, 6317–6324 CrossRef CAS PubMed.
- C. Lee, L. Jug and E. Meng, Appl. Phys. Lett., 2013, 102, 183511 CrossRef.
- C. Li, E. T. Thostenson and T.-W. Chou, Appl. Phys. Lett., 2007, 91, 223114 CrossRef.
- J. Hicks, A. Behnam and A. Ural, Appl. Phys. Lett., 2009, 95, 213103 CrossRef.
- A. Oskouyi, U. Sundararaj and P. Mertiny, Materials, 2014, 7, 2501–2521 CrossRef CAS PubMed.
- X. Li, R. Zhang, W. Yu, K. Wang, J. Wei, D. Wu, A. Cao, Z. Li, Y. Cheng and Q. Zheng, Sci. Rep., 2012, 2, 870 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00032a |
| This journal is © The Royal Society of Chemistry 2020 |