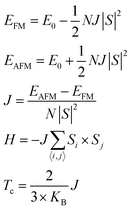Tunable electronic and magnetic properties of monolayer and bilayer Janus Cr₂Cl₃I₃: a first-principles study

Abstract

Recently, novel two-dimensional (2D) magnetic materials have drawn enormous research attention due to their interesting tunable electronic and magnetic properties. However, 2D Janus materials with intrinsic magnetism are rare. We investigate the geometric and electronic properties of monolayer (ML) and bilayer (BL) intrinsic magnetic Janus Cr₂Cl₃I₃ using first-principles calculations. We find that ML Janus Cr₂Cl₃I₃ is a magnetic semiconductor with the band gaps for the spin-α and spin-β channels being 2.11 and 3.83 eV, respectively. The magnetic ground state of ML Cr₂Cl₃I₃ can be effectively modulated by biaxial strain from the ferromagnetic (FM) state to the antiferromagnetic (AFM) state. Meanwhile, ML Cr₂Cl₃I₃ experiences an electronic phase transition from a half semiconductor (HSC) to a bipolar magnetic semiconducor (BMS) and finally a spin-unpolarized semiconductor with increasing strain. More interestingly, as the biaxial strain increases, the Curie temperature for the FM ground state increases from 36.3 K to 49.2 K. As for bilayer (BL) Cr₂Cl₃I₃, the stacking order could effectively affect the magnetic and electronic properties. The most stable stacking order is AB-II type, followed by AA-II, AB-ClI, AA-ClI, AB-ClCl and AA-ClCl stacking orders. They are all spin-polarized BMS. The magnetic and electronic properties of BL Cr₂Cl₃I₃ change with different stacking orders, possibly due to the quantum confinement effect and interlayer interactions. The stability of ML Cr₂Cl₃I₃ is confirmed by the phonon spectrum and molecular dynamics simulations. The tunable electronic properties together with intrinsic ferromagnetism enrich the diversity of Janus 2D Cr₂Cl₃I₃, which has potential applications in spintronic devices.

---

1. Introduction

Two-dimensional (2D) systems have attracted much attention in condensed matter physics. For example, the successive discoveries of integer^1,2 and fractional³ quantum Hall effects and superconductivity have introduced new physics. Since the discovery of graphene,^4,5 the family of 2D materials has grown explosively,^6–10 including many famous members such as transition metal dichalcogenides,¹¹ hexagon boron nitride,¹² carbon boron nitride,^6,8 stanene,⁹etc. It is well known that strong fluctuations prohibit long-range magnetic order at finite temperature in a 2D system, as depicted by the Mermin–Wagner theorem.¹³ Therefore, 2D magnetic materials for spintronics have not appeared until recent years.

Recently, magnetism in 2D van der Waals (vdW) materials^14–20 has attracted much attention. As a possible modulating parameter, magnetism sets up a new routine of developing 2D devices for electronic and spintronic applications.^21–24 Magnetic fields^14,25 and electric fields^23,26–28 are found to be able to tune the magnetism and tunneling resistance in few-layer CrI₃^{23,25–27,29–33} and Cr₂Ge₂Te₆.^14,34 The high magnetic transition temperatures,^14,24,35 various spin configurations,^{23,26,27,30,32,36} different electronic properties,^19,37 and higher magnetic anisotropy energy^38–40 of semiconducting magnetic materials are the center of the attention in the development of 2D magnetic devices. Janus monolayers are newly developed 2D materials with intriguing physical properties. For example, Janus transition metal dichalcogenides (TMDs)⁴¹ and GaInX₂ (X = S, Se, Te)⁴² present intrinsic dipole and piezoelectric effects. Janus MoSSe has tunable carrier mobility and obvious Rashba-type spin splitting¹¹ caused by spin–orbit coupling.⁴³ And Janus TiSO⁴⁴ and MoSSe have suitable band gaps¹¹ and optical redox potentials for photocatalysis.^11,44,45 The successful synthesis and novel properties of 2D Janus materials could allow them to work as sensors,⁴⁴ field-effect transistors, and ultra-sensitive detectors.⁴⁶

On the other hand, the successful experimental realization of 2D magnets^{21–23,27,28,30,35,47} may provide an exciting new platform for the application of low-dimensional spintronics. CrI₃ composed of three atomic layers like a sandwich provides the possibility of forming a Janus structure with intrinsic magnetism. Therefore, it is necessary to study the magnetic order and electronic structure of Janus Cr₂Cl₃I₃ with mirror symmetry broken, which could introduce new physical phenomena.^41,43,46 A deep understanding of the intrinsic physical mechanism of Janus chromium trihalides and practical methods to control their spin states are highly required.^48,49 Moreover, strain^33,50 and stacking order^{19,33,48–52} are widely used methods to modulate the tunneling magneto-resistances,^29,53 magneto-optical effects,⁵⁴ light scattering³¹ and topological properties of materials.^15,55,56

In this article, using first-principles methods with vdW interaction corrections,^57–59 we investigate the geometric, magnetic, and electronic properties and stability of ML Janus Cr₂Cl₃I₃ using hybrid functional-HSE06.^60,61 ML Janus Cr₂Cl₃I₃ breaks the out-of-plane mirror symmetry, which would introduce some new properties.^42,43,46 Moreover, the electronic properties of Cr₂Cl₃I₃ could be tuned from HSC to BMS^8,62–64 or SC, with the magnetic order transforming from FM to Néel AFM states, depending on the strength of the biaxial strain. Remarkably, the corresponding critical temperatures (T_C and T_N) of Cr₂Cl₃I₃ can be effectively tailored via changing the exchange interaction induced by the biaxial strains. In addition, the magnetic orders and electronic properties of BL Cr₂Cl₃I₃ are found to be closely related to the stacking orders. These tunable electronic and magnetic properties of 2D FM Janus Cr₂Cl₃I₃ demonstrate its great application potential in low-dimensional spintronic devices.

2. Computational details

The calculations on Cr₂Cl₃I₃ are performed by using the plane-wave basis Vienna ab initio Simulation Package (VASP) code,^65,66 based on density functional theory under the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.⁶⁷ As the PBE functional often underestimates the band gap of semiconductors,^33,63 the Heyd–Scuseria–Ernzerhof (HSE06)^60,61 screened hybrid functional is adopted to calculate the magnetic and electronic properties. The DFT-D2 method developed by Grimme⁵⁸ is adopted to describe the weak vdW interactions. Since the obtained interlayer distance for BL graphene (3.25 Å) and the binding energy per carbon atom (−25 meV) are consistent with early investigations,^57,59 we mainly use DFT-D2 to calculate the binding energy, which could provide a good description of long-range vdW interactions of 2D materials. The vacuum space in the z-direction is set as large as 16 Å to avoid the interactions between periodic images. The kinetic energy cutoff for plane waves is set to 400 eV. The geometries are fully relaxed until the total energy is converged to 10⁻⁶ eV, and the force acting on every atom is less than 10 meV Å⁻¹. Monkhorst–Pack⁶⁸k-grids of 6 × 6 × 1, 9 × 9 × 1, and 11 × 11 × 1 are adopted in Brillouin zone integration for the geometry optimization, energy and density of states (DOS) calculations, respectively. 90 uniform k-points along the high-symmetry special k-paths are used to obtain the band structure. The magnetic Janus Cr₂Cl₃I₃ breaks the out-of-plane mirror symmetry, and it introduces an intrinsic dipole moment and electric polarization.⁴² Therefore, the spin-polarization approach with dipole correction is considered in the following calculations.

In order to investigate the magnetic properties, the Curie and Néel temperatures are evaluated with the mean field approximation:

where ΔE is defined as the energy difference between FM and AFM states. E_FM and E_AFM represent the energies of the FM and AFM states, respectively. J and H are the exchange parameter and Hamilton, respectively, and S_i represents the spin operator. Each Cr atom contributes 3.00 μ_B magnetism. K_B represents the Boltzmann constant, and T_c shows the critical temperature including T_N (Néel temperature) and T_C (Curie temperature). This method is widely used to calculate the critical temperatures (T_N and T_C) of magnetic materials.³⁶

In order to confirm the stability of ML Cr₂Cl₃I₃, the phonon spectrum and density of states are calculated using the finite displacement method as implemented in the Phonopy software.⁶⁹ We use a 4 × 4 × 1 supercell for Cr₂Cl₃I₃, CrI₃ and CrCl₃. The geometries are fully relaxed until the total energy is converged to 10⁻⁸ eV and the Hellmann–Feynman force acting on every atom is less than 1 meV Å⁻¹ in the phonon spectra calculations. Ab initio molecular dynamics (AIMD) simulations are also performed in the DFT framework. 18 000 uniform k-points along high-symmetry lines are used to obtain the phonon spectra. The constant mole–volume–temperature (NVT) ensemble with the Nosé–Hoover thermostat⁷⁰ is adopted at temperatures of 300 K, 500 K, and 700 K in the AIMD simulations. The time step and total time are set to 1 fs and 10 ps, respectively.

3. Results and discussion

3.1. Geometry of ML Janus Cr₂Cl₃I₃

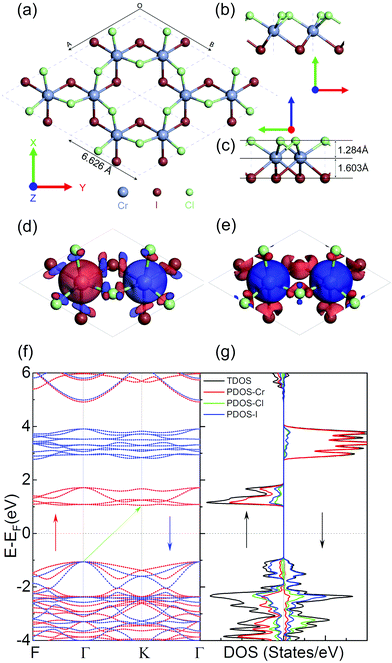
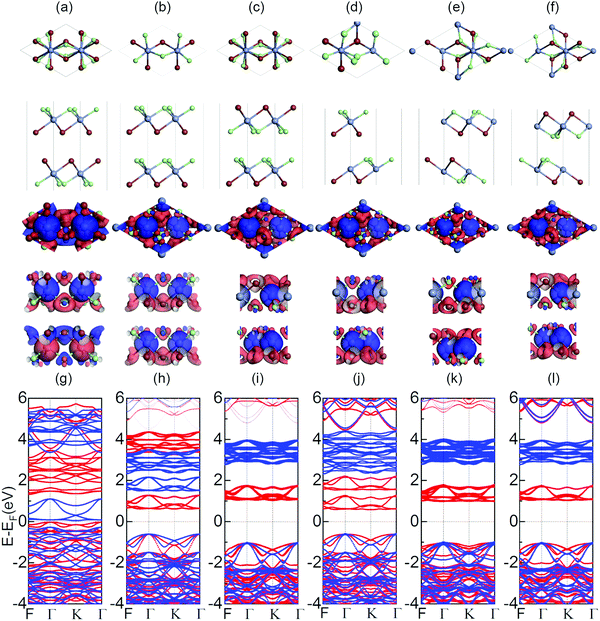
We first optimize the geometry of ML Janus Cr₂Cl₃I₃ as shown in Fig. 1a–c. Two methods (global optimization and calculation of energy vs. lattice) are used to calculate the lattice of Cr₂Cl₃I₃, and the optimized equilibrium lattice parameter is a = b = 6.626 Å (the two methods give the same result), which is smaller than CrI₃ (7.008 Å)^36,40,71 but larger than CrCl₃ (6.056 Å).⁴⁰ The vertical distance between Cr and I and Cr and Cl is 1.603 and 1.284 Å, respectively, as shown in Fig. 1c. These values are larger than CrI₃ (1.562 Å),⁴⁰ but smaller than CrCl₃ (1.335 Å).⁴⁰ The corresponding Cr–Cl and Cr–I bond length is 2.403 and 2.717 Å, respectively. These values are larger than CrCl₃ (2.358 Å),⁴⁰ but smaller than CrI₃ (2.736 Å).⁴⁰ From the optimized geometry, we can find that ML Janus Cr₂Cl₃I₃ presents the C_3v point group, different from the point group D_3d of CrI₃ and CrCl₃. As Janus Cr₂Cl₃I₃ breaks the out-of-plane structure symmetry, on the two sides are positioned I and Cl atoms, respectively, which induces an electric polarization.¹¹

Fig. 1 (a) Top and (b and c) side views of the optimized geometry of ML Janus Cr₂Cl₃I₃. The steel gray, brown, and green balls represent Cr, Cl, and I atoms, respectively. The spin density of (d) antiferromagnetic, and (e) ferromagnetic order of Cr₂Cl₃I₃; the isovalue is 0.02 e Å⁻³. (f) Band structure of ML Cr₂Cl₃I₃. Red and blue lines represent the bands of spin-α and spin-β electrons, respectively. (g) DOS of Cr₂Cl₃I₃. Black, red, green, and blue lines represent the total DOS and the projected partial DOS from Cr, Cl, and I atoms, respectively. The size of the dots in the band indicates the weight of contributions. The Γ, F, and K k-points are (0, 0, 0), (0, 1/2, 0), and (−1/3, 2/3, 0), respectively. The Fermi-level is set as 0 eV.

For ML Cr₂Cl₃I₃, Néel AFM and FM configurations are considered, as shown in Fig. 1d and e, respectively. The magnetic moment is mainly contributed by the Cr atoms, while the contribution from Cl and I atoms could be neglected. According to Hund's rule, each electron occupying the t_2g triplet state of the Cr atom has 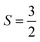, which introduces a magnetic moment of 3.0 μ_B. For the Néel AFM state, one Cr atom has a magnetic moment of 3.00 μ_B, and the other has a magnetic moment of −3.00 μ_B, which is similar to CrI₃. The total magnetic moment is 0.00 μ_B, and the spin density is shown in Fig. 1d. Another magnetic configuration is the FM state, where each Cr atom has a magnetic moment of 3.00 μ_B. Therefore, there is a total magnetic moment of 6.00 μ_B in the unit cell, as shown in Fig. 1e. The energy difference between FM and AFM order is defined as ΔE = E_AFM − E_FM. For ML Cr₂Cl₃I₃, ΔE is 31 meV, which implies that Cr₂Cl₃I₃ is in the FM ground state. The corresponding T_c is 36.3 K, which is bigger than CrCl₃ (29.7 K⁴⁰), and smaller than CrI₃ (46.4 K,⁴⁰ 45 K²⁵).

In the above section, the geometric and magnetic properties are investigated. The electronic properties are also calculated, as shown in Fig. 1f and g. ML Cr₂Cl₃I₃ is a spin-polarized semiconductor in the FM ground state. The valence band maximum (VBM) is located at the Γ point, while the conduction band minimum (CBM) is located at the K point. They are both contributed by spin-α electrons. Therefore, ML Cr₂Cl₃I₃ is a HSC, with an indirect band gap of 2.111 eV. This value is bigger than 1.941 eV of CrI₃, but smaller than 3.863 eV of CrCl₃, as shown in Fig. S2 (ESI†). There is an obvious spin-polarization in Cr₂Cl₃I₃. The band gap of the spin-α channel is 2.111 eV, while the gap of the spin-β channel is 3.874 eV. The VBM of the spin-α channel is located at the Γ point, while the CBM is located at the K point. The VBM of the spin-β channel is located at the Γ point, while the CBM is located at the F point. The overall VBM is mainly contributed by I atoms, and partially contributed by Cl and Cr atoms. By further analysis of the PDOS, the VBM mainly consists of p_x, p_y and p_z orbitals of I atoms. p_z orbitals of Cl atoms, and d_yz and d_xz orbitals of Cr atoms also make a contribution to the VBM, as shown in Fig. S3 (ESI†). This is consistent with the charge density of the VBM shown in Fig. 2a and c. The CBM is mainly contributed by d_xz, d_yz, d_xy, and d_x²−y² orbitals of Cr atoms, with a little contribution from p_z, p_y and p_x orbitals of I, and p_y orbitals of Cl atoms, which is consistent with the analysis of the charge density of the CBM shown in Fig. S4 (ESI†).

Fig. 2 (a–d) Wave functions of ML Cr₂Cl₃I₃ with HSE06 at the VBM (top (a) and side (c) views) and CBM (top (b) and side (d) views) positions. Red and blue colors represent the sign of the wave functions, and the isovalue is 0.006 e Å⁻³. The xy-averaged electrostatic potential of ML (e) Cr₂Cl₃I₃, (f) CrI₃ and (g) CrCl₃ calculated by HSE06. The black and blue dashed horizontal lines represent the vacuum energy level and Fermi level, respectively. The coffee, blue and green dashed vertical lines represent the position of the I, Cr and Cl atoms, respectively.

As the Cr atom has d electrons, spin–orbit coupling (SOC) is also taken into consideration. The corresponding band structures are shown in Fig. S5 provided in the ESI.† The indirect band gap of ML Cr₂Cl₃I₃ is reduced to 1.792 eV compared with the original value without SOC of 2.111 eV, because of the orbital splitting at the VBM and CBM with SOC. There is obvious spin–orbit splitting consisting of p_y, p_x, and d_yz orbitals at the K point, and the corresponding spin–orbit splitting is 0.119 eV. The VBM changes from the original K point to the midpoint along Γ–F symmetry lines, because of the SOC effect. The new VBM consists of p_z, d_yz, and d_xz orbitals. Moreover, there is spin–orbit splitting at the gamma point, which consists of d_z², d_yz, and d_xz orbitals located at 1.471 eV (splitting of 0.119 eV) and 2.910 eV (splitting of 0.047 eV) above the Fermi-level. For the K point, there is spin–orbit splitting located at 1.082 eV (0.056 eV splitting) and 2.931 eV (0.066 eV splitting), which consists of d_z², d_yz, and d_xz orbitals. More details can be found in Fig. S5 (ESI†).

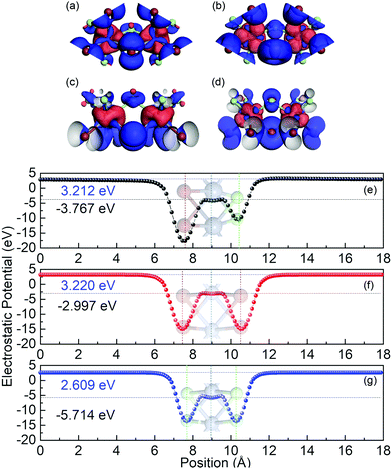
In order to evaluate the work function of Cr₂Cl₃I₃, the xy-averaged electrostatic potential is also calculated, as shown in Fig. 2(e). The Fermi-level is −3.767 eV, and the vacuum energy level is 3.212 eV. The work function (W) is defined as: Φ = E_vacuum − E_F. E_vacuum is defined as the vacuum energy level, and E_F represents the Fermi-level. The obtained Φ is 6.979 eV, compared to CrCl₃ (8.323 eV) and CrI₃ (6.217 eV). There are two valleys in the xy-averaged electrostatic potential with different depths, which is different from CrCl₃ and CrI₃ monolayers where two identical valleys appear. This is caused by the Janus structure of Cr₂Cl₃I₃. One side is I atoms, while the other side is Cl atoms. The first deeper valley is located at 7.600 Å, which corresponds to the location of the I atoms. The other valley is located at the position 9.005 Å, which corresponds to the position of the Cr atoms. Additionally, there are two small peaks located at 8.583 Å and 9.568 Å, respectively, which is consistent with the geometry of ML Cr₂Cl₃I₃. The third shallower valley is located at 10.412 Å, which corresponds to the location of the Cl atoms. Compared with CrCl₃ (Fig. 3g) and CrI₃ (Fig. 3f), the averaged electrostatic potential (including two smaller local peaks and valleys) shows an unsymmetrical property, as the Janus structure breaks the plane symmetry.

Fig. 3 (a) ΔE and (b) the energy gap of ML Cr₂Cl₃I₃ vary with the biaxial strain, ranging from −11% to 11%. The band structure of ML Cr₂Cl₃I₃ under biaxial strains of (c) −10%, (d) −8%, (e) −7.9%, (f) −4%, (g) −2%, (h) 4%, (i) 6% and (j) 10%. The insets of figure (a) present the spin densities of Cr₂Cl₃I₃ under biaxial strains of −10%, −8%, −7.9%, −4%, 6% and 10%, respectively. Here, the isovalue is 0.02 e Å⁻³. The grey and blue areas represent the AFM and FM ground states of ML Cr₂Cl₃I₃, respectively. The red circles with a cross, the blue circles with a line, and the black circles with a diagonal cross represent the gap, and the gap of spin-α and spin-β electrons, respectively.

3.2. Effect of biaxial strain

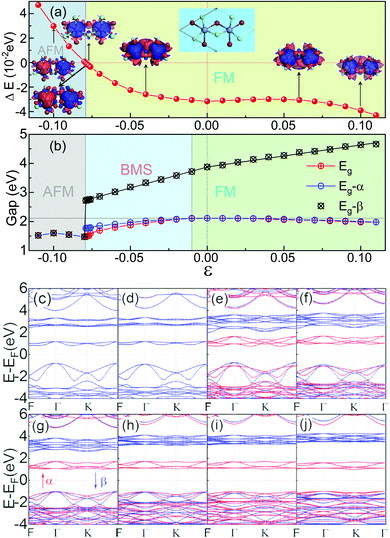
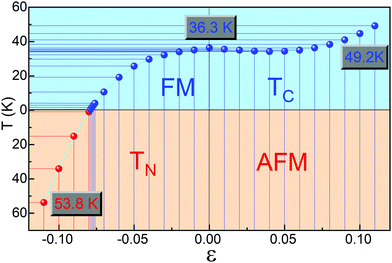
Low-dimensional materials are usually synthesized and investigated on all kinds of substrates. Usually, there is a lattice mismatch between the supported 2D material and the underlying substrate, which introduces strain into the 2D material. The strain will further tune the properties of the 2D material by changing the bonding properties.⁷² Therefore, it is highly desirable to investigate the effects of strain on the properties of 2D materials.⁷² To address this issue, we first study the effect of biaxial strains (ε) on the magnetic and electronic properties of ML Cr₂Cl₃I₃, as shown in Fig. 3. ε = (a − a₀)/a₀ is applied on ML Cr₂Cl₃I₃, where a and a₀ are the lattice constants with and without strain, respectively. The biaxial compressive strain could transform the ground state of ML Cr₂Cl₃I₃ from the FM to the AFM state. As the biaxial compressive strain increases it enforces the super-exchange interaction. Therefore, the AFM order is enhanced. ML Cr₂Cl₃I₃ could also be transferred from a HSC to a BMS, and even to a spin-unpolarized SC, as the compressive ε monotonically increases. The band gap first increases and then decreases, because of the change of the bond strength.⁶⁰ For ε = −1%, ML Cr₂Cl₃I₃ is still a direct semiconductor with a gap of 2.112 eV, but the energy level of the CBM (the midpoint along Γ–K symmetry lines, E_Q for short) is 0.01 eV lower than the K point (E_K). The VBM of the spin-β channel is 0.040 eV higher than that of the spin-α channel, while the VBMs of the spin-α and spin-β channels have the same value, in the absence of the applied strain. As a result, the ML Cr₂Cl₃I₃ has converted from a HSC to a BMS whose CBM and VBM are contributed by different spin channels. For ε = −3% and −2%, the corresponding band gaps are 2.016 and 2.071 eV, with the energy difference between E_K and E_Q being increased from 0.033 eV to 0.063 eV, respectively. The corresponding energy level splitting is also increased to 0.096 and 0.073 eV at the Γ point, as shown in Fig. 3(g). For ε = −4% and −5%, the band gaps are 1.948 and 1.887 eV, respectively, as shown in Fig. 3(f). The splitting energies are further increased from 0.127 to 0.173 eV. When ε is increased to −6%, the corresponding band gap is further decreased to 1.795 eV, and the energy difference between E_K and E_Q is increased to 0.150 eV. The corresponding splitting energy is 0.209 eV. For ε = −7%, −7.6%, −7.7%, −7.8%, and −7.9%, the corresponding gap is 1.691, 1.591, 1.514, 1.493 and 1.489 eV, respectively. The corresponding spin splitting energy is 0.253, 0.284, 0.289, 0.300 and 0.366 at the Γ point, respectively. For the biaxial compressive strains in the range of −1% to −7.9%, the corresponding spin splitting energy monotonously increases as the strain increases. When the compressive strain is increased to −8.0% (as shown in Fig. 3(d)), ΔE of ML Cr₂Cl₃I₃ increases from −0.032 eV (0) to −0.030 eV (−2%), −0.026 eV (−4%), −0.009 eV (−7%), −0.004 eV (−7.6%), −0.003 eV (−7.7%), −0.001 eV (−7.8%), −0.0004 eV (−7.9%) and 0.0008 eV (−8.0%), as shown in Fig. 3(a). The corresponding energy difference between the spin-β and α electrons is 1.762, 1.614, 1.502, 1.392, 1.315, 1.220, 1.109, 1.014, 0.975, 0.971, 0.967, 0.955, and 0 eV (−11% < ε < −8%). The corresponding T_C is 40.8, 39.4, 38.2, 36.2, 33.4, 28.9, 21.6, 11.9, 4.5, 3.2, 1.9, 0.5 K and 1.1 K (T_N), respectively. This means that the FM state is tuned into the AFM ground state as the biaxial compressive strain increases to −8%. Compared with CrI₃ (−5.7%)⁴⁰ and CrCl₃ (−2.5%,⁴⁰ −2.6%⁷¹), this value is larger. It originates from the adopted the hybrid functional-HSE06, instead of PBE or PBE+U.⁷¹ As the compressive strain continues to increase, the corresponding gap is increased to 1.550 eV (−9%), 1.601 eV (−10%) and 1.520 eV (−11%). The corresponding ΔE is 0.013, 0.030 and 0.047 eV, respectively, and the systems are tuned into the spin-unpolarized state. The corresponding T_N is 17.11, 38.4, and 60.6 K, respectively. As the strain increases, the VBM composed of p_x, p_y and p_z orbitals of I atoms is still located at the Γ point, while the CBM composed of d_xz, d_yz, d_xy, and d_x²−y² orbitals of Cr atoms is transferred from the original K point to the midpoint along Γ–K symmetry lines.

Under tensile strain, ΔE first decreases (1%, 4%), and then increases (5%, 11%) as the strain increases, as shown in Fig. 3(a). For ε = 1–4%, the corresponding gap is 2.109, 2.103, 2.100, and 2.079 eV, respectively. At ε = 5%, 6%, 7%, 8%, 9%, 10%, and 11%, the gap is 2.062, 2.048, 2.043, 2.019, 2.000, 1.977 and 1.975 eV, respectively. The gap of spin-α electrons monotonously decreases, while the gap of spin-β electrons monotonously increases. The gap follows a linear relationship: E_g-β = 3.883 + 14.582ε (−8% < ε < 0), E_g-β = 3.895 + 7.408ε (0 < ε < 11%), when ε is in the range of (−11%, 11%). The relationship between E_g-α and ε follows a quadratic function: E_g-α = 2.110 + 0.366ε − 50.319ε² (−8% < ε < 0). As the strain increases, the VBM composed of p_x, p_y and p_z orbitals of the I atoms is still located at the Γ point, while the CBM composed of d_xz, d_yz, d_xy, and d_x² orbitals of Cr atoms is transferred from the original K point to the midpoint along the Γ–K symmetry line. The corresponding results are shown in Fig. 3(c)–(g).

ΔE first decreases and then increases as the tensile biaxial strain increases. The corresponding ΔE is −0.031, −0.031, −0.030 and −0.029 eV, respectively, when ε = 1–4%. For ε = 5–11%, the corresponding ΔE is −0.030, −0.031, −0.032, −0.033, −0.036, −0.039, and −0.043 eV, respectively. The critical temperature is closely related to ΔE. As the biaxial strain increases, T_C first decreases (0% < ε < 3%) and then increases as the biaxial strain exceeds 3%. For ε = 1–3%, the corresponding T_C is 35.5, 35.0, and 34.5 K, respectively. As the biaxial strain further increases, the corresponding T_C is 34.2, 34.4, 35.0, 36.3, 38.3, 41.0, and 44.7 K. For a larger ε of 16%, the corresponding T_C can go up to 82.6 K. This is caused by the enhancement of the direct exchange interaction between Cr atoms with increasing biaxial tensile strain. The corresponding FM order is also enhanced, so T_C tends to increase (Fig. 4).

Fig. 4 The critical temperature of ML Cr₂Cl₃I₃ as a function of biaxial strain. Different colors show different magnetic ground states. The blue and red areas represent the FM and AFM ground state, respectively. The insets present the corresponding critical temperatures. The red and blue dots represent the corresponding Néel and Curie temperature, respectively.

3.3. Effect of the stacking orders

BL Cr₂Cl₃I₃ is the smallest Cr₂Cl₃I₃ multilayer system stacked by vdW interactions. It is interesting to know: (i) what are the magnetic and electronic properties of BL Cr₂Cl₃I₃ and (ii) are the magnetic and electronic properties of BL Cr₂Cl₃I₃ also closely related to the stacking configurations.

Moreover, CrX₃ (X = I, Br, Cl) is usually synthesized with multilayers stacked together by vdW interactions.^{6,9,14,22–28,30,31,35,53,73,74} So the stacking-induced modifications of the properties need to be systemically discussed. Taking BL MoSSe as a reference,¹¹ six different stacking patterns (AA-II, AA-ClI, AA-ClCl, AB-ClI, AB-II and AB-ClCl) of BL Cr₂Cl₃I₃ are considered, and the optimized geometries are shown in Fig. 5a–f, respectively. The interlayer vertical distance of the plane of the I (Cl) and Cl (I) atoms d is defined to describe the interaction between the Cr₂Cl₃I₃ layers. The corresponding distance and binding energies calculated by the DFT-D2,⁵⁸ DFT-D3,^30–32 and DFT-TS³³ methods are shown in Table 1. We can find that the AB-ClCl configuration has the smallest d = 3.01 Å calculated by DFT-D2, which is smaller than AA-II (3.145 Å) and AA-ClI (3.123 Å), AA-ClCl (3.743 Å), AB-ClI (3.807 Å), and AB-II (3.806 Å). E_b is defined as E_b = E_BL − E_ML × 2, where E_BL is the total energy of the relaxed bilayer Cr₂Cl₃I₃. The corresponding E_b for the AB-II configuration is −0.990 eV, while the corresponding values of AA-II, AA-ClI, AA-ClCl, AB-ClI, and AB-ClCl are −0.938, −0.755, −0.629, −0.810, and −0.676 eV, respectively. Therefore, the AB-II configuration is the most stable one, which is different from CrI₃³² and CrCl₃.⁷⁵ This may be caused by the symmetry breaking of Janus Cr₂Cl₃I₃. Other optimized vdW functionals (such as DFT-D3^30–32) and self-consistent screening of the Tkatchenko–Scheffler method (TS³³) are also adopted to investigate BL Cr₂Cl₃I₃, and they show the same trend. The E_b calculated by DFT-D3 for the AB-II configuration with distance 3.603 Å is −0.549 eV, while the corresponding E_b of AA-II, AA-ClI, AA-ClCl, AB-ClI and AB-ClCl is −0.487, −0.439, −0.340, −0.465 and −0.415 eV, respectively. A similar trend also appears in the DFT-TS results. The AB-II configuration is still the most stable one among the six geometries. All the results are collected in Table 1. Therefore, the discussion is established based on the DFT-D2 results in the following part. The magnetic and electronic properties are usually related to the stacking orders of 2D materials. We also investigate the magnetic order of BL Cr₂Cl₃I₃, and the corresponding spin densities are shown in the middle set of Fig. 5. The stable magnetic orders are related to the stacking orders. AA-ClI, AA-ClCl, AB-ClI, AB-II and AB-ClCl show a FM ground state, which is defined as one Cr₂Cl₃I₃ layer ferromagnetically coupled with another. The total magnetic moment is 12.00 μ_B, and each layer of Cr₂Cl₃I₃ contributes 6.00 μ_B. The magnetic moment mainly localizes at the Cr atoms, as shown in the spin densities of BL Cr₂Cl₃I₃ in Fig. 5. The corresponding ΔE is positive. AA-II shows AFM ground order, which implies one layer antiferromagnetically couples with another. The corresponding ΔE is −0.003 eV, and the total magnetic moment is 0 μ_B, as one layer contributes 6.00 μ_B and another layer contributes −6.00 μ_B. No matter what the magnetic order is, all BL Janus Cr₂Cl₃I₃ are BMSs. There are three important parameters: Δ1, Δ2 and Δ3, to characterize BMSs, as shown in Fig. S6 (ESI†), which are defined in the early work.^8,62,63 For AB-II, the corresponding Δ1, Δ2 and Δ3 are 2.111, 0.038 and 1.795 eV, respectively. AA-II is a BMS with an AFM ground state. Most BMSs have a FM ground state,⁷⁶ while an AFM BMS is quite rare. The corresponding Δ1, Δ2 and Δ3 are 0.075, 0.254 and 1.229 eV, respectively. Δ1 is quite small, so it's easy to tune the BMS into a half-metal. It should be noted here that Δ3 is big enough to ensure the stability of the half-metallicity. For all the stacking orders, the gaps of the spin-α and spin-β channels are larger than the global band gap (Table 2).

Fig. 5 (a–f) The optimized geometries of BL Cr₂Cl₃I₃ with different stacking orders with top and side views. The stacking orders of (a) AA-II, (b) AA-ClI, (c) AA-ClCl, (d) AB-ClI, (e) AB-II, and (f) AB-ClCl are shown in top and side views. (g–l) The spin densities with the FM ground state of the corresponding structures are shown in (g) AA-II, (h) AA-ClI, (i) AA-ClCl, (j) AB-ClI, (k) AB-II, and (l) AB-ClCl. The bottom set is the corresponding band structures. The isovalue is 0.02 e Å⁻³. The red and blue lines represent the contribution of spin-α and spin-β electrons, respectively.

Table 1 The distance between two Janus Cr₂Cl₃I₃ layers and the corresponding binding energy of BL Cr₂Cl₃I₃ with different stacking orders calculated by the DFT-D2, DFT-D3, and TS methods

System	DFT-D2		DFT-D3		TS
	d 0 (Å)	E b (eV)	d 0 (Å)	E b (eV)	d 0 (Å)	E b (eV)
AA-II	3.145	−0.938	3.111	−0.487	3.681	−0.503
AA-ClI	3.123	−0.755	3.073	−0.439	3.395	−0.456
AA-ClCl	3.743	−0.629	3.807	−0.340	3.362	−0.354
AB-ClI	3.807	−0.810	3.708	−0.465	3.32	−0.491
AB-II	3.806	−0.990	3.603	−0.549	3.698	−0.520
AB-ClCl	3.010	−0.676	2.977	−0.415	3.079	−0.397

---

Table 2 The distance between two Janus Cr₂Cl₃I₃ layers, and the corresponding binding energy, band gap, and band gap of spin-α and spin-β electrons of BL Janus Cr₂Cl₃I₃ with different stackings

System	Magnetic	ΔE (meV)	Gap (eV)	Gap-α (eV)	Gap-β (eV)
AA-II	AFM	−3.0	0.075	1.350	0.325
AA-ClI	FM	2.0	1.221	1.233	2.107
AA-ClCl	FM	1.0	2.071	2.080	3.813
AB-ClI	FM	70.0	1.180	1.190	2.910
AB-II	FM	8.0	1.991	2.013	3.786
AB-ClCl	FM	2.0	2.049	2.065	3.792

---

3.4. Stability of Janus Cr₂Cl₃I₃

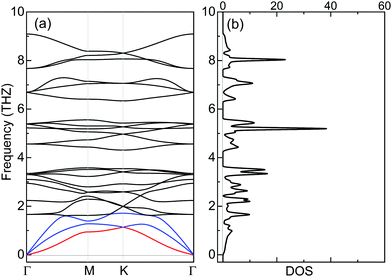
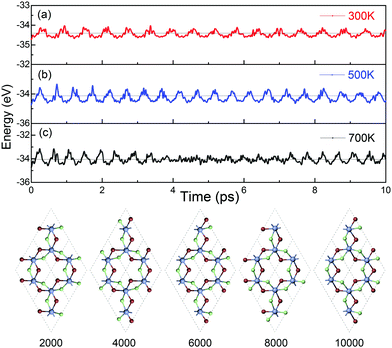
The dynamical stability of ML Cr₂Cl₃I₃ is confirmed via computing the phonon dispersion curves and phonon density of states, which show no imaginary phonon modes (Fig. 6a). The highest vibration frequency is 9.09 THz, which is higher than ML CrI₃ (7.32 THz), but smaller than CrCl₃ (10.95 THz), as shown in Fig. S7 (ESI†), reflecting the mechanical robustness of the covalent bonds. Meanwhile, certain phonon modes of Cr₂Cl₃I₃ are absent because of the breaking of mirror symmetry, which reduces the lattice from point group D_3d to C_3v, compared with CrI₃ and CrCl₃, as shown in Fig. S7 (ESI†).

Fig. 6 (a) Phonon spectrum, and (b) phonon density of states (PHDOS) of ML Cr₂Cl₃I₃.

The thermal stability of Cr₂Cl₃I₃ is also examined via ab initio molecular dynamics (AIMD) simulations. The simulated temperatures are 300, 500 and 700 K. The fluctuations of the total energy of Cr₂Cl₃I₃ at 300, 500 and 700 K are shown in Fig. 7(a)–(c), respectively. During the simulation progress, the sandwich-like structure of ML Janus Cr₂Cl₃I₃ remains intact at room temperature, and the total energy oscillates around −34.41 eV. The maximum energy fluctuation is 0.38 eV. The energy oscillates around −34.13 eV and the energy fluctuation is 0.65 eV at 500 K. The snapshots of ML Cr₂Cl₃I₃ are also presented, showing intact structures. In a word, the structures are well kept without obvious distortions in the simulated time (10 ps) at 300 K, 500 K and 700 K, as shown in Fig. 7. We note that the use of a periodic boundary condition in AIMD simulations with a relatively small system size can artificially increase the stability of the structures. A larger supercell (2 × 2 × 1 cell) is also adopted, and it shows similar results to the unit cell.

Fig. 7 Ab initio MD simulations of the evolution of the energy of ML Cr₂Cl₃I₃ under temperatures of (a) 300 K, (b) 500 K, and (c) 700 K. The total time is 10 ps. The bottom is the top views of simulation snapshots at 2, 4, 6, 8 and 10 ps of ab initio MD simulations at 300 K.

3.5. Synthetization of Janus Cr₂Cl₃I₃

2D Janus TMDs, such as MoSSe is synthesized by selenizing the MoS₂ monolayer⁷⁷ or substituted MoSe₂ monolayer with sulfurization.⁷⁸ Janus Cr₂Cl₃I₃ monolayers should be also synthesized by replacing the top-layer I atoms with Cl atoms through chlorinating the CrI₃ monolayer in chemical vapor deposition.

4. Conclusions

In conclusion, we examine the geometric, magnetic, and electronic properties of Janus Cr₂Cl₃I₃ with first-principles calculations. ML Cr₂Cl₃I₃ is a HSC with a direct band gap of 2.111 eV, showing an obvious electron spin-polarization. The electronic properties of ML Cr₂Cl₃I₃ could be effectively modulated by biaxial strains, from the HSC into a BMS, and even to a spin-unpolarized SC. As the compressive biaxial strain increases, ML Cr₂Cl₃I₃ is tuned from the FM to the AFM ground state (ε ≥ 7.9%). The corresponding T_C is 36.3 K. As the biaxial compressive and tensile strains are increased to 10%, the corresponding critical temperatures are 53.8 (T_N) and 49.2 K (T_C), respectively. Moreover, the magnetic configuration and electronic properties could also be effectively modulated by the stacking orders. For BL Cr₂Cl₃I₃, the most stable AB-II configuration presents a FM ground state. BL Cr₂Cl₃I₃ in all considered stacking orders is a BMS. Last, the phonon spectrum and AIMD confirm the dynamical and thermal stability of Cr₂Cl₃I₃. The modulated magnetic and electronic properties imply that Janus Cr₂Cl₃I₃ should be a promising candidate material for 2D spintronic devices.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank Doctor Yang Li, Prof. Xingxing Li, and Chen Si for helpful discussion. This work was partially supported by the financial support from the Natural Science Foundation of China (Grant No. 11904203), the Fundamental Research Funds of Shandong University (Grant No. 2019GN065), the President foundation of China Academy of Engineering Physics (YZJJLX2016004), China Postdoctoral Science Foundation (No. 2019M650619) and the National Key Research and Development Program of China (Grant No. 2016YFB0201203). The Shanghai Supercomputer Center, National Supercomputing Centers of Guangzhou, and Supercomputer Centers of Tsinghua and Shandong University should be acknowledged.

References

1. V. Gusynin and S. Sharapov, Phys. Rev. Lett., 2005, 95, 146801.
2. T. Mukherjee, S. Chowdhury, D. Jana and L. C. L. Y. Voon, J. Phys.: Condens. Matter, 2019, 31, 335802.
3. S. C. Zhang, T. H. Hansson and S. Kivelson, Phys. Rev. Lett., 1989, 62, 82.
4. A. K. Geim, Science, 2009, 324, 1530–1534.
5. A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
6. L. Ci, L. Song, C. Jin, D. Jariwala, D. Wu, Y. Li, A. Srivastava, Z. F. Wang, K. Storr, L. Balicas, F. Liu and P. M. Ajayan, Nat. Mater., 2010, 9, 430–435.
7. Z. Guan, J. Wang, J. Huang, X. Wu, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 22491–22498.
8. Z. Guan, W. Wang, J. Huang, X. Wu, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 28616–28624.
9. M. Liao, Y. Zang, Z. Guan, H. Li, Y. Gong, K. Zhu, X.-P. Hu, D. Zhang, Y. Xu, Y.-Y. Wang, K. He, X.-C. Ma, S.-C. Zhang and Q.-K. Xue, Nat. Phys., 2018, 14, 344–348.
10. N. Luo, W. Duan, B. I. Yakobson and X. Zou, Adv. Funct. Mater., 2020, 2000533–2000541,  DOI:10.1002/adfm.202000533.
11. Z. Guan, S. Ni and S. Hu, J. Phys. Chem. C, 2018, 122, 6209–6216.
12. D. Golberg, Y. Bando, Y. Huang, T. Terao, M. Mitome, C. Tang and C. Zhi, ACS Nano, 2010, 4, 2979–2993.
13. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136.
14. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265.
15. Y. Hou, J. Kim and R. Wu, Sci. Adv., 2019, 5, eaaw1874.
16. M. Ge, Y. Su, H. Wang, G. Yang and J. Zhang, RSC Adv., 2019, 9, 14766–14771.
17. Z. Zhang, X. Ni, H. Huang, L. Hu and F. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 115441.
18. H. Zhang, W. Qin, M. Chen, P. Cui, Z. Zhang and X. Xu, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 116003.
19. P. Jiang, C. Wang, D. Chen, Z. Zhong, Z. Yuan, Z.-Y. Lu and W. Ji, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 144401–144409.
20. S. Chen, C. Huang, H. Sun, J. Ding, P. Jena and E. Kan, J. Phys. Chem. C, 2019, 123, 17987–17993.
21. Z. Sun, Y. Yi, T. Song, G. Clark, B. Huang, Y. Shan, S. Wu, D. Huang, C. Gao, Z. Chen, M. McGuire, T. Cao, D. Xiao, W.-T. Liu, W. Yao, X. Xu and S. Wu, Nature, 2019, 572, 497–501,  DOI:10.1038/s41586-019-1445-3.
22. D. Ghazaryan, M. T. Greenaway, Z. Wang, V. H. Guarochico-Moreira, I. J. Vera-Marun, J. Yin, Y. Liao, S. V. Morozov, O. Kristanovski, A. I. Lichtenstein, M. I. Katsnelson, F. Withers, A. Mishchenko, L. Eaves, A. K. Geim, K. S. Novoselov and A. Misra, Nat. Electron., 2018, 1, 344–349.
23. S. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406–411.
24. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, P. Manh-Huong and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–294.
25. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–285.
26. S. Jiang, L. Li, Z. Wang, J. Shan and K. F. Mak, Nat. Electron., 2019, 2, 159–163.
27. K. S. Burch, Nat. Nanotechnol., 2018, 13, 532.
28. B. Huang, G. Clark, D. R. Klein, D. MacNeill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao, P. Jarillo-Herrero and X. Xu, Nat. Nanotechnol., 2018, 13, 544–549.
29. Z. Wang, I. Gutierrez-Lezama, N. Ubrig, M. Kroner, M. Gibertini, T. Taniguchi, K. Watanabe, A. Imamoglu, E. Giannini and A. F. Morpurgo, Nat. Commun., 2018, 9, 2516–2523.
30. J.-H. Yang and H. Xiang, Nat. Mater., 2019, 12, 1273–1274,  DOI:10.1038/s41563-019-0524-z.
31. B. Huang, J. Cenker, X. Zhang, E. L. Ray, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Xiao and X. Xu, Nat. Nanotechnol., 2020, 3, 212–216,  DOI:10.1038/s41565-019-0598-4.
32. N. Sivadas, S. Okamoto, X. Xu, C. J. Fennie and D. Xiao, Nano Lett., 2018, 18, 7658–7664.
33. Z. Guan, S. Ni and S. Hu, RSC Adv., 2017, 7, 45393–45399.
34. J. He, G. Ding, C. Zhong, S. Li, D. Li and G. Zhang, J. Mater. Chem. C, 2019, 7, 5084–5093.
35. M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419.
36. F. Zheng, J. Zhao, Z. Liu, M. Li, M. Zhou, S. Zhang and P. Zhang, Nanoscale, 2018, 10, 14298–14303.
37. D. Soriano, C. Cardoso and J. Fernández-Rossier, Solid State Commun., 2019, 299, 113662.
38. I. Lee, F. G. Utermohlen, D. Weber, K. Hwang, C. Zhang, J. van Tol, J. E. Goldberger, N. Trivedi and P. C. Hammel, Phys. Rev. Lett., 2020, 124, 017201.
39. J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002.
40. L. Webster and J.-A. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 144411.
41. L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248.
42. Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102.
43. Y. C. Cheng, Z. Y. Zhu, M. Tahir and U. Schwingenschlögl, EPL, 2013, 102, 57001.
44. W. Chen, X. Hou, X. Shi and H. Pan, ACS Appl. Mater. Interfaces, 2018, 10, 35289–35295.
45. K. Ren, S. Wang, Y. Luo, J.-P. Chou, J. Yu, W. Tang and M. Sun, J. Phys. D: Appl. Phys., 2020, 53, 185504.
46. R. Li, Y. Cheng and W. Huang, Small, 2018, 14, 1802091.
47. Y. Liu, Y. Huang and X. Duan, Nature, 2019, 567, 323–333.
48. M. Idrees, H. U. Din, R. Ali, G. Rehman, T. Hussain, C. V. Nguyen, I. Ahmad and B. Amin, Phys. Chem. Chem. Phys., 2019, 21, 18612–18621.
49. W. Guo, X. Ge, S. Sun, Y. Xie and X. Ye, Phys. Chem. Chem. Phys., 2020, 22, 4946–4956.
50. Z. Guan, C.-S. Lian, S. Hu, S. Ni, J. Li and W. Duan, J. Phys. Chem. C, 2017, 121, 3654–3660.
51. Z. Guan and S. Ni, Appl. Phys. A: Mater. Sci. Process., 2017, 123, 678.
52. Z. Lin, C. Si, S. Duan, C. Wang and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 155408.
53. T. Song, X. Cai, M. W.-Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214–1218.
54. M. Wu, Z. Li, T. Cao and S. G. Louie, Nat. Commun., 2019, 10, 10325–10327.
55. S. Baidya, J. Yu and C. H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 155148.
56. L. Chen, J.-H. Chung, B. Gao, T. Chen, M. B. Stone, A. I. Kolesnikov, Q. Huang and P. Dai, Phys. Rev. X, 2018, 8, 041028.
57. Y. Baskin and L. Meyer, Phys. Rev., 1955, 100, 544.
58. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
59. R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406.
60. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
61. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
62. Z. Guan, S. Ni and S. Hu, ACS Omega, 2019, 4, 10293–10301.
63. Z. Guan, C. Si, S. Hu and W. Duan, Phys. Chem. Chem. Phys., 2016, 18, 12350–12356.
64. Z. Guan, S. Ni and S. Hu, ACS Omega, 2020, 5, 5900–5910.
65. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
66. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
67. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
68. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
69. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
70. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
71. Z. Wu, J. Yu and S. Yuan, Phys. Chem. Chem. Phys., 2019, 21, 7750–7755.
72. C. Si, Z. Sun and F. Liu, Nanoscale, 2016, 8, 3207–3217.
73. C. Bao and S. Zhou, Nat. Mater., 2020, 19, 263–264,  DOI:10.1038/s41563-020-0614-y.
74. L. Thiel, Z. Wang, M. A. Tschudin, D. Rohner, I. Gutierrez-Lezama, N. Ubrig, M. Gibertini, E. Giannini, A. F. Morpurgo and P. Maletinsky, Science, 2019, 364, 973–976.
75. H. Wang, V. Eyert and U. Schwingenschloegl, J. Phys.: Condens. Matter, 2011, 23, 116003.
76. X. Li, X. Wu, Z. Li, J. Yang and J. G. Hou, Nanoscale, 2012, 4, 5680–5685.
77. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749.
78. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198.

---

Footnote

† Electronic supplementary information (ESI) available: Information on materials, energy with lattice parameters, partial orbital projected band structure, band structure of CrCl₃ and CrI₃, PDOS, band structure with SOC, band structure under certain strains of the ML Janus Cr₂Cl₃I₃ calculated by the HSE06 functional, phonon spectrum and density of states (calculated by PBE) of CrCl₃ and CrI₃. See DOI: 10.1039/d0ma00085j

---