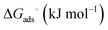Open Access Article
Open Access ArticleMelamine adsorption on carbon materials: impact of carbon texture and surface chemistry†
Lucas
Hynes
a,
Gonzalo
Montiel
bc,
Allison
Jones
a,
Donna
Riel
a,
Muna
Abdulaziz
a,
Federico
Viva
 d,
Dario
Bonetta
a,
Andrew
Vreugdenhil
d,
Dario
Bonetta
a,
Andrew
Vreugdenhil
 e and
Liliana
Trevani
e and
Liliana
Trevani
 *a
*a
aFaculty of Science, Ontario Tech. University, Oshawa, Ontario, Canada. E-mail: liliana.trevani@uoit.ca
bInstituto Nacional de Tecnologia Industrial, Buenos Aires, Argentina
cUniversidad de San Martin, San Martin, Buenos Aires, Argentina
dComision Nacional de Energia Atomica, San Martin, Buenos Aires, Argentina
eChemistry Department, Trent University, Peterborough, Ontario, Canada
First published on 29th April 2020
Abstract
In this work, a comparative study between three carbon materials has been carried out to investigate the impact of the micro/mesoporous structure of the carbon substrate on their adsorption capabilities. The study included two commercial carbons: Darco KB-G (AC), and Vulcan XC-72R (VC). The third carbon material was a mesoporous material (MC), with tailored micro/mesoporous structure and surface area obtained by carbonization of a resorcinol–formaldehyde (RF) polymer gel using both soft and hard template materials. Melamine was used as a model adsorbate in both acid and alkaline solutions. For all carbons, melamine adsorption was found to be pH dependent with higher adsorption from alkaline solutions than from acidic solutions. To the best of our knowledge, these are the first reported values for the adsorption of melamine to these carbon materials. Adsorption data obtained using the Langmuir model were compared with theoretical studies involving melamine as a building block in the self-assembly of molecular structures on carbon substrates, and analyzed using the results of several characterization studies carried out as part of this research work, some of which include nitrogen and CO2 adsorption isotherms, Raman spectroscopy, powder X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), and transmission electron microscopy (TEM).
1. Introduction
Carbon is an excellent adsorbent material, owing mainly to its electronic and porous structure, high surface area, and chemical inertness. It has been used for water purification since ancient times.1–3 Applications have ranged from the adsorption of dye in runoff from manufacturing and textile industries,4 the removal of mercury from waterways5,6 and pesticides from agricultural soil and runoff,7,8 to the removal of radioactive materials from water and soil around nuclear plants.9 In this study, we focused on the adsorption of melamine, a nitrogen-rich compound, 1,3,5-triazine-2,4,6-triamine. This adsorbate is of interest as it is extensively used in the production of wood-based products, where its roles include uses in coatings, adhesives, and flame retardants. Its broader applications also include use as a plasticizer on concrete,10 and paper and textile materials.11 As a result of its extended use, water and soil contamination by melamine and its decomposition products could take place.Even though the adsorption of melamine on polymeric substrates, such as organic–inorganic hybrid melamine imprinted materials12–14 and monolithic polymeric cartridges with specific recognition sites for the extraction of melamine15 have been investigated in the past, the studies on carbon are scarce despite the fact that activated carbons have been extensively used as adsorbent material for organic species in aqueous media.5,16,17 A better understanding of the adsorption of melamine on micro and mesoporous carbon materials could contribute to developing new materials with high adsorptive capacity for melamine. As adsorbents, recent studies have shown the potential of carbon blacks (CBs), with mesoporous and microporous structure for the adsorption of humid acids,3 mercury,6 carbofuran,7L-histidine,18 and radioactive materials.9 These studies have also included Vulcan XC 72R (Cabot), a type of carbon commonly used as catalyst support on fuel cell applications,19 and investigated as adsorbent material for phenol and 1-naphthol.20
In this work, we present a comparative study on the adsorption of melamine on three carbon materials with distinct surface areas, pore size distributions, and oxygen contents: Darco KB-G (AC), Vulcan XC-72R (VC), and a synthetic carbon with micro/mesoporous structure (MC). Special efforts were dedicated to characterizing the carbon substrates using gas adsorption experiments, Raman spectroscopy, XRD, XPS, TEM, and other techniques to get a thorough insight into the melamine adsorption process and differences between carbon materials. Theoretical monolayer loadings for the adsorbate molecule were calculated based on the size of the molecule and the surface area of the carbon, and compared with experimental and literature values for model carbon surfaces.21–24
2. Experimental
2.1. Materials and methods
DARCO KB-G activated carbon (AC, Sigma Aldrich, Oakville, Canada) and Vulcan XC-72R carbon black (VC, Fuel Cell Store) were ground with an agate mortar and pestle, dried at 80 °C in a vacuum oven overnight, and stored in sealed vials in a desiccator. The following chemicals were obtained from Sigma-Aldrich and used as received: formaldehyde (37 wt% in H2O), fumed silica (0.2–0.3 μm avg. part. size), glycerol (≥99%), melamine (99%), methanol (≥99.9%), poly-diallydimethylammonium chloride solution (PDADMAC, 20 wt% in H2O), resorcinol (≥99.0%), hydrochloric acid (35–37%), and sodium hydroxide (50 wt% in water). Water used in these experiments was deionized through a Milli-Q deionization system (Millipore Q-Gard T2, Millipore Quantum TEX); and it met the requirements for ASTM Type 1 water, with a resistivity above 18 MΩ cm. Gases used for the synthesis and analysis were purchased from Praxair and used without further purification: argon (99.999%, AR5.0UH-T), CO2 (99.9%, CD3.0-KS), extra dry air (AI0.0XD-T), helium (99.999%, HE5.0UH-T), hydrogen (99.999%, HY5.0UH-T), and nitrogen (99.995%, Ni5.0UH-T).2.2. Synthesis of mesoporous carbon
The procedure was based on the synthesis developed by Fuentes-Quezada and co-workers25 but involved a different sized SiO2 hard-template. In this method, two solutions (A and B) had to be prepared. Solution A was obtained by mixing 2 g resorcinol, 1 g PDADMAC (soft-template), 45 g H2O and 0.4 g sodium acetate, and Solution B prepared by adding 3.5 g glycerol, 1.25 g silica (hard-template) and 4 g methanol in 45 g H2O. Both solutions were sonicated for 30 minutes to ensure proper mixing. Solution A was then heated with stirring at ∼65 °C for 10 minutes to help dissolution and dispersion of the reactants, then Solution B was added, and the temperature was raised to 90 °C. Heating continued with vigorous stirring for 3 hours, with 1.3 mL of formaldehyde added after 20 minutes of heating and 2.8 mL of formaldehyde added after 65 minutes of heating. The solution was then cooled, suction filtered through P42 filter paper, and dried overnight in a vacuum oven at 80 °C to produce the final resin. The solid was ground with an agate mortar and pestle, and carbonized in a tube furnace at 950 °C for 2 hours in a nitrogen atmosphere. The resulting carbon material was washed for 24 hours with 3 M NaOH under reflux to dissolve the SiO2 nanoparticles, followed by a 24 hours Soxhlet extraction in water to remove any residual NaOH.2.3. Carbon characterization
The structural properties of the carbon samples were investigated using both Raman spectroscopy and powder X-ray diffraction. Raman spectra were measured using a Renishaw inVia Raman Spectrometer with a 532 nm solid state laser source with a 50 mW nominal power. The spectra were collected from 100 cm−1 to 4000 cm−1 at 0.5% laser power, 15 s exposure time, 10 accumulations, with a binning setting of 3. The analysis of the spectra was performed using Origin Pro 2018 software. Powder X-ray diffraction analysis was performed using a Rigaku Ultima IV X-ray diffractometer with Cu Kα radiation (λ = 0.15418 nm) at 40 kV (44 mA). The diffractograms were collected at 2θ angels from 10° to 90° with a step size of 1.5°.Nitrogen and carbon dioxide adsorption experiments were carried out to determine the surface area and pore size distribution of the carbon materials using a Micrometrics TriStar II Plus system. Typically 0.05–0.1 g of sample was vacuum degassed for 24 hours at 110 °C prior to adsorption. Data analysis was performed with Micromeretics MicroActive software.
Surface functional groups were identified by Fourier transform infrared spectroscopy (FTIR) on a PerkinElmer Spectrum 100 FT-IR Spectrometer using a Horizontal Attenuated Total Reflectance (HATR) sampling accessory and a DTGS detector. X-ray photoelectron spectroscopy (XPS) measurements were obtained on a ThermoFisher ESCALAB 250Xi with monochromatic Al Kα radiation (1486.6 eV) and a spot size of 900 microns. The functional groups on the surface of AC and VC were also analyzed by Boehm titration.
Thermogravimetric analysis (TGA) was used to evaluate the extent of removal of the SiO2 hard template. These were carried out on an SDT Q600 Simultaneous TGA/DSC from TA Instruments under air (50 mL min−1) at a scan rate of 10 °C min−1 from 30 to 1000 °C.
2.4. Melamine adsorption determination
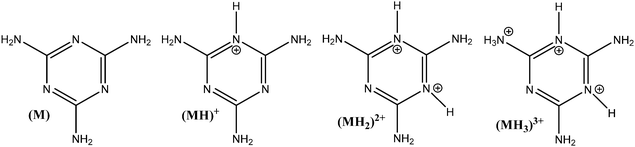
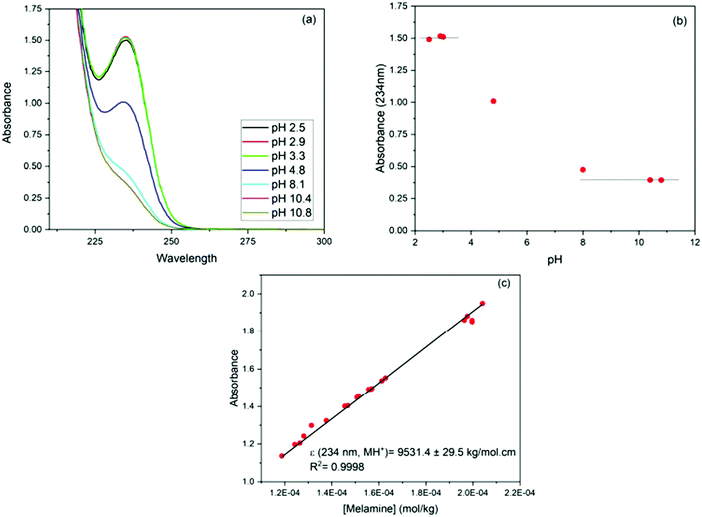
The influence of adsorbent dosage and melamine solution concentration range was optimized to achieve the best conditions for the quantification of melamine in solution, before and after adsorption, and in all the carbon materials used in these studies. Initial experiments involved different adsorbent dosages, in conjunction with multiple methods for the adsorbate detection and quantification. The melamine solution concentration range was selected by taking into account the solubility of melamine in water (acid and alkaline conditions), and a measurable level in solution before and after the adsorption experiment. Since melamine (M) is a base, it can undergo several acid/base equilibrium reactions in aqueous solution and form different protonated species (see Fig. 1). Based on the acid–base equilibria constants reported by Sal’nikov et al.,26 only M is present at pH greater than 7 and MH+ is the predominant species between pH 2 and 6, as shown in Fig. S1 in the ESI† where the stability region for the different protonated species (MH+), (MH22+), (MH33+) and (M2H+) that can form are summarized.26,27To confirm the speciation diagram for melamine accurately describes the speciation in solution as a function of pH, mainly in acid media, the changes in the UV-visible absorption spectrum of melamine were also investigated. As shown in Fig. 2, the absorbance at λ = 234 nm increases as the pH decreases and remains constant in the pH region where MH+ is the predominant species in solution (Fig. S1, ESI†). Consequently, to ensure that the adsorption experiments were carried out with only one species in solution (M or MH+), the adsorption studies were performed in 0.01 M NaOH (pH ∼ 12) and 0.01 M HCl (pH ∼ 2–3) at 30 °C. The Lambert–Beer law is obeyed in the concentration ranged adopted in this study as shown in Fig. 2.
For the adsorption studies, ∼40 mg of carbon was suspended in 100 g of melamine solution (2 × 10−4 to 7 × 10−3 mol kg−1 of solution) and left to equilibrate at a constant temperature in an Excella E25 Incubator Shaker for at least 4 days. After equilibration, samples were filtered through a syringe filter (0.45 μm Teflon filters) to remove adsorbent. The concentration of melamine in the solutions before and after adsorption was determined using UV-visible spectroscopy (Cary 50 Bio UV-Visible Spectrometer, 300–190 nm, slow scan rate). Prior to acquiring the UV-visible spectrum, the pH of all solutions was adjusted to pH 3 to ensure that all of the melamine was present as a single species.
The melamine adsorption was calculated for each carbon material with eqn (1):
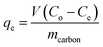 | (1) |
The Langmuir28 and Freundlich29 models were both used to fit the experimental data to be able to compare with other studies. In both cases, Origin Pro 2018 software was used to determine the best fit and regression parameters. According to the Langmuir model, the equilibrium adsorbate uptake, qe, as a function of the equilibrium concentration of adsorbate in solution, Ce is given by eqn (2):
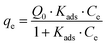 | (2) |
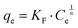 | (3) |
To confirm that the addition of carbon did not introduce a significant change in the pH of the solutions, control experiments under the same conditions but without melamine were performed in which 40 mg of carbon was mixed with 100 g of solution, with the pH tested before and after stirring for 24 hours in a closed container to minimize the contact with air. The carbon was shown to not change the pH of the solutions.
3. Results and discussion
3.1. Analysis of carbon characterization results
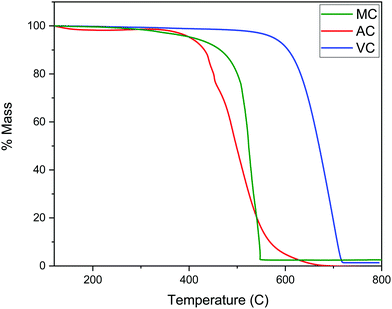
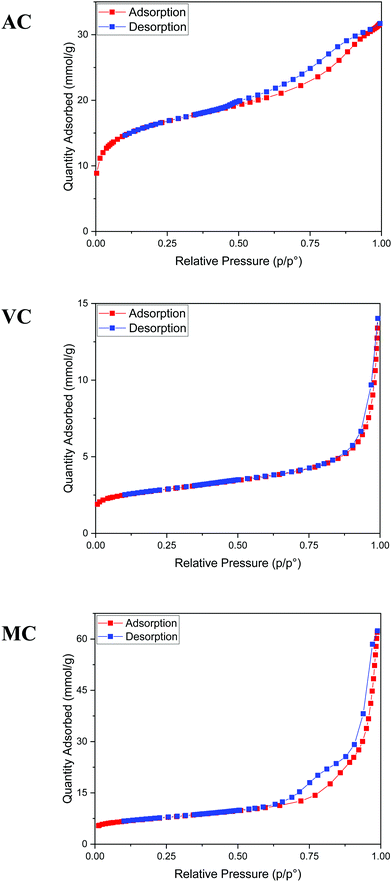
As described in the Experimental section, the R–F polymers were carbonized at 950 °C under N2 and washed for 24 hours with 3 M NaOH to dissolve the SiO2 hard template. Thermogravimetric analysis of the carbonized samples after washing and drying the products under vacuum at 80 °C for 48 hours showed the majority of the silica present in the sample was successfully removed, with a remnant silica content lower than 2 to 3 wt% (Fig. 3). The thermograms also show the combustion of AC and MC, takes place at a significantly lower temperature than VC, likely due to the higher degree of graphitization of VC when compared with the other two carbon samples.The texture of the carbon materials was investigated by gas adsorption/desorption experiments. The nitrogen adsorption isotherms for the VC and AC commercial carbons are compared with that obtained for the MC sample in Fig. 4. The presence of mesopores is evidenced by the hysteresis loop characteristic of capillary condensation at high pressure (type IV with H1 hysteresis, IUPAC classification isotherm).30 As expected, this feature is more pronounced in MC than in VC and AC, due to the fact that the synthesis was carried out in the presence of both a polyelectrolyte and a hard-template. BET surface areas were calculated as 1315 m2 g−1 for AC, 592 m2 g−1 for MC and 246 m2 g−1 for VC. A comparison with published data and available information for the commercial materials from the manufacturers indicates that the BET surface area for AC is lower than the value reported by the company for this material (1700 m2 g−1), but consistent with an independent determination performed in an alternative system. The value obtained for VC is in quite good agreement with the BET areas reported in other studies31,32 and by the manufacturer (∼240 m2 g−1).
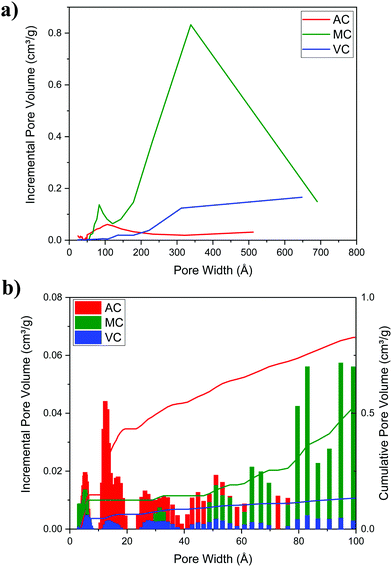
Fig. 5a illustrates typical BJH incremental pore size distribution curves obtained from the N2 desorption isotherms at 77 K for the carbon materials, while the NLDFT incremental and cumulative pore size distribution plots for AC, MC, and VC from CO2 adsorption isotherms at 273 K are shown in Fig. 5b. The pore volumes obtained from the N2 desorption isotherms were 0.83 cm3 g−1 for AC, 2.17 cm3 g−1 for MC and 0.45 cm3 g−1 for VC, with maximum pore radii at 62 Å, 189 Å and 175 Å, respectively. In the case of MC, the distribution is bimodal, a narrow peak at ∼60 Å, and a broad distribution in the mesopore region (100 to 200 Å) that it is likely due to the large size of the SiO2 nanoparticle templates and the destabilization of the structure upon its dissolution. These results are in good agreement with the TEM images obtained for the MC and shown in Fig. 6, where a distribution of mesopores with pore sizes between 100 and 200 Å is clearly visible. The volume in micropores (size <5.59 Å) obtained using the NLDFT model for the adsorption of CO2 at 273 K for AC, MC, and VC, were found to be 0.020 cm3 g−1, 0.036 cm3 g−1, and 0.0039 cm3 g−1, while the total volume for pores with sizes less than ∼10 Å were 0.075 cm3 g−1, 0.083 cm3 g−1, and 0.014 cm3 g−1, respectively. The results show AC, the material with the larger surface area, has the larger content of micropores, while VC, and mainly MC have a more developed mesopore structure.
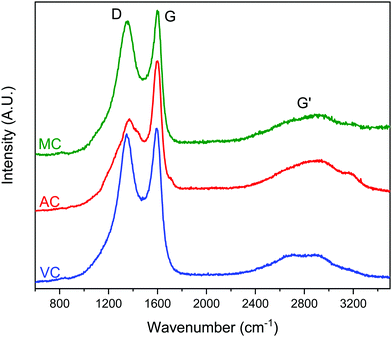
Typical Raman spectra are summarized in Fig. 7. The spectra do not show significant differences between the samples. The expected D and G bands of carbon at ∼1360 cm−1 and 1600 cm−1, respectively, can be clearly seen, where the D band corresponds to the disordered or defect content of the carbon and G bands corresponds to the graphitic, ordered component of the material. The ratio of the intensity of these bands, ID/IG, is a useful measure of the degree of graphitization,33,34 The lower the ID/IG ratio, the higher the content of sp2 hybridized carbon correlating to a more graphitic structure, and less sp3 hybridized carbon correlating to a more amorphous structure. Integration of the D and G bands after deconvolution allowed the calculation of the ID/IG ratios for the three carbon samples: 1.8 (AC), 1.6 (MC) and 1.7 (VC). Based on these results, AC should present the higher content of carbon defects, while MC and VC have a more graphitic structure.33 However, the differences are small, and it is difficult to make an assessment. Nevertheless, the higher ID/IG ratios for AC is in good agreement with the surface oxygen contents calculated from the XPS spectra: 13.0 atomic% for AC, 4.9 atomic% for MC, and 2.3 atomic% for VC. The Boehm titration method also used to quantify the surface functional groups on AC and VC are summarized in Table 1. AC, which contained 13 atomic% O according to XPS data, had by far the greatest number of acidic groups by Boehm titration, while VC, which had an O content of only 2.3 atomic%, contained only a negligible number of acidic groups. A similar study was not performed on MC because of the amount of carbon required for this determination.
| Carbon | O content (atomic%) | Total acidic groups | Phenolic groups | Lactonic groups | Carboxylic groups |
|---|---|---|---|---|---|
| AC | 13.0 | 342 μmol | 158 μmol | 17 μmol | 169 μmol |
| VC | 2.3 | Negligible content – unable to be determined with this method | |||
The X-ray diffraction patterns for VC, AC and MC are shown in the ESI† (Fig. S2). Similar bands are present in the three cases, but the lines corresponding to the 002, 100 or 101 and 110 planes of graphite are more pronounced in VC, indicating a more graphitic structure. The VC spectrum is also very similar to spectra for the same material reported in the literature.34
3.2. Melamine adsorption studies on AC, MC, and VC
The results summarized in Fig. 8 show the melamine uptakes for AC, MC, and VC, in both alkaline (0.1 M NaOH) and acidic (0.1 M HCl) media conditions at 30 °C. It is evident that the adsorption of melamine in alkaline media is significantly more favorable than in acidic solutions at similar equilibrium concentrations, and it is also strongly dependent on the surface area of the adsorbent materials. Scanning tunneling microscope (STM) images reported by Zhang et al.21 for the adsorption of melamine on highly oriented pyrolytic graphite (HOPG) in water showed melamine is able to form well organized molecular arrangements by interaction with the carbon substrates and other molecules of melamine through hydrogen bonding between melamine molecules, due to the presence of amine groups (hydrogen donors) and N atoms of the central ring (hydrogen acceptors). From the five different configurations considered in the study, the most stable were the C-top, N-top, and cross, where the nitrogen in the amine groups adsorbs in the center of the graphene rings.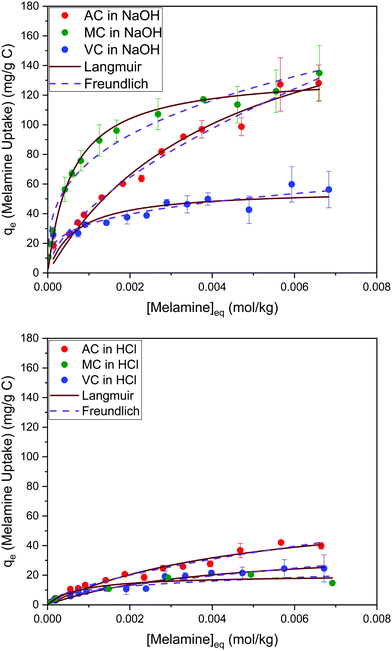 | ||
| Fig. 8 Adsorption isotherms for melamine on AC, MC, and VC in 0.01 M NaOH (top) and 0.01 M HCl (bottom) aqueous solutions at 30 °C. | ||
Optimized structures for melamine on different adsorption sites on graphene obtained using density functional theory (DFT) have been recently reported by Quesne-Turin et al.22 The study showed the adsorption and 2D self-organization process are the result of intermolecular interaction, and molecule–surface interactions to a lesser extent. The authors reported the adsorption energy increases from the monomer to the 2D-network, and the total stabilization energy on the surface decreases in the same range. Based on these findings, the authors speculate that melamine molecules are adsorbed alone or through dimers before forming a hexagonal porous supramolecular network. These results explain why the adsorption in acid and alkaline media are significantly different. In acid media, the interaction between the protonated melamine molecules, and between melamine and the carbon ring, is likely less favorable, resulting in very low adsorption values. Even electrostatic interactions will be absent at low pH values because of the protonation of the oxygen functional groups on carbon.
On the other hand, in alkaline media, MC and VC show a higher melamine uptake at low concentrations (H type isotherm based on Giles categorization35). Although this cannot be used to definitively analyze the isotherms, it could indicate that adsorption on AC is less favorable at low concentrations, perhaps due to the microporous structure of this material.
The Langmuir and Freundlich model fitting parameters are summarized in Table 2. The obtained melamine uptake for each carbon material expressed in mg melamine per g C are 208.7, 135.0, and 56.4 for AC, MC, and VC respectively. Following the expected trend, the amount of melamine required for the formation of a monolayer on carbon per gram of sorbent decreases as the BET surface area of the carbon adsorbent decreases (1315 m2 g−1, 592 m2 g−1, and 222 m2 g−1 for AC, MC, and VC, respectively). Due to the significant difference in surface area between materials, it is not surprising that normalization by surface area significantly changes this trend (Fig. 9), with monolayer saturation values per m2 of adsorbent material in alkaline media equal to 0.15, 0.23, and 0.23 mg melamine per m2 C, for AC, MC, and VC, respectively. AC, with a significantly higher oxygen content and larger micropores is able to adsorb less melamine than the other studied carbon materials. In terms of the affinity of each type of carbon for melamine, the higher the Kads value in the Langmuir model, the higher the affinity of that particular carbon for melamine. These Kads values are 232.6, 1682.9 and 1497.6 kJ mol−1 for AC, MC and VC, respectively. The results match the shape of the isotherms, as MC and VC both have very large Kads values, indicating a higher affinity for melamine than AC. The adsorption constant values were used to calculate the Gibbs energy of adsorption (ΔGads) using eqn (4).
ΔGads = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Kads) ln(Kads) | (4) |
| Carbon | Adsorption in 0.1 M HCl | Adsorption in 0.1 M NaOH | ||||
|---|---|---|---|---|---|---|
| Langmuir model | ||||||
| Q 0 (mg per g C) | K ads (kg mol−1) | r 2 | Q 0 (mg per g C) | K ads (kg mol−1) | r 2 | |
| AC | 71.2 ± 11.3 | 200.8 ± 56.4 | 0.94 | 208.7 ± 21.5 | 232.6 ± 44.9 | 0.97 |
| MC | 20.2 ± 3.0 | 1268.3 ± 852.8 | 0.90 | 135.0 ± 4.0 | 1682.9 ± 201.1 | 0.98 |
| VC | 39.9 ± 5.4 | 257.7 ± 68.4 | 0.94 | 56.4 ± 4.9 | 1497.6 ± 549.1 | 0.64 |
| Carbon | Adsorption in 0.1 M HCl | Adsorption in 0.1 M NaOH | ||||
|---|---|---|---|---|---|---|
| Freundlich model | ||||||
| K F (mg per g C) | n | r 2 | K F (mg per g C) | n | r 2 | |
| AC | 924.2 ± 231.0 | 0.616 ± 0.045 | 0.96 | 2620.7 ± 439.7 | 0.596 ± 0.030 | 0.98 |
| MC | 108.6 ± 79.0 | 0.350 ± 0.129 | 0.77 | 685.2 ± 96.8 | 0.321 ± 0.024 | 0.97 |
| VC | 477.4 ± 146.8 | 0.578 ± 0.055 | 0.94 | 216.5 ± 45.5 | 0.273 ± 0.036 | 0.86 |
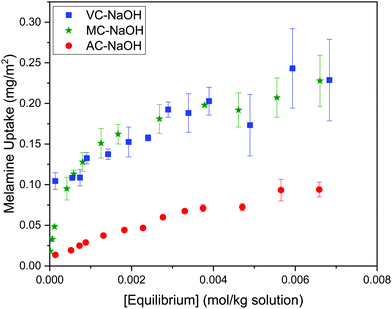 | ||
| Fig. 9 Adsorption isotherms for melamine on AC, MC and VC at 30 °C, normalized by carbon BET surface area. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cell = 1.05 nm2). The theoretical maximum number of molecules of melamine adsorbed per gram carbon was converted to milligrams per gram of carbon by dividing by Avogadro's number (NA) and multiplying by the molar mass of melamine (Mmelamine = 126.12 g mol−1):
cell = 1.05 nm2). The theoretical maximum number of molecules of melamine adsorbed per gram carbon was converted to milligrams per gram of carbon by dividing by Avogadro's number (NA) and multiplying by the molar mass of melamine (Mmelamine = 126.12 g mol−1):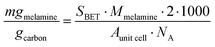 | (5) |
As shown in Table 4, the calculated monolayer values obtained by adopting the simplifying assumption that melamine forms a densely packed adlayer on carbon, that high-resolution STM images showed is not the case, and are significantly higher than those obtained in this study. Clearly, the assumption that the carbon surface is a continuous graphite plane is not a sufficiently sophisticated model for high surface area carbons, highlighting the need for accurate experimental adsorption data. In acid media, a similar comparison cannot be made because melamine will be protonated (MH+) and it is impossible to make any further analysis. Despite the limitations, the results would indicate that the adsorption of melamine on mesoporous carbons such as MC and VC is more favorable than in AC, perhaps due to the size of the solvated melamine molecule.
| Carbon | Surface area (m2 g−1) | Langmuir monolayer (in NaOH) (mg g−1) | Calculated melamine monolayer (eqn (5)) (mg g−1) | % difference between exp. and calc. values |
|---|---|---|---|---|
| AC | 1315 | 209 | 526 | 40 |
| MC | 592 | 135 | 237 | 57 |
| VC | 222 | 56 | 89 | 63 |
4. Conclusions and future work
This study examined the adsorption of the small triazine molecule melamine to three carbon materials; Darco KB-G, an activated carbon used for purification in pharmaceutical and food applications, Vulcan XC-72R, a carbon black primarily used in polymer electrolyte membrane fuel cells and electrochemical studies on the field of catalysis, and a mesoporous carbon synthesized from a resorcinol–formaldehyde resin, which employed both hard and soft templates to provide a highly porous material. The adsorption isotherms were fit with both Langmuir and Freundlich models, and to the best of our knowledge, these are the first adsorption studies for melamine involving these carbon materials. Langmuir monolayer uptakes were significantly larger in alkaline solution, which as discussed can only be due to the fact that the unprotonated melamine can interact more efficiently with the carbon substrate, but also form HN⋯H hydrogen bonding between adjacent melamine molecules. This opens another interesting avenue for remediation studies, since it may be possible to release adsorbed melamine from carbon by decreasing the pH to release the adsorbed species on demand. More research into this potential application is required, but it could lead to a simple and reusable adsorbent to remove melamine from solution.When comparing the adsorption isotherms for the three carbons in alkaline media, it was verified that the Langmuir monolayer adsorption follows the trend of surface area; AC has the largest surface area, and a melamine uptake of 209 mg g−1, followed by MC with 135 mg g−1 and finally VC with 56 mg g−1. This trend is as expected, as materials with a greater surface area usually contain more adsorption sites, increasing the amount of material that can be adsorbed. However, the surface normalized adsorption values showed that VC and MC have a greater affinity for melamine, but only MC is likely to find application as an adsorbent due to its significantly higher surface area. The MC solids produced for this study has a high surface area and porous structure, with one of the reasons for this being that the silica hard template is not removed until after the carbonization procedure to prevent the pores from collapsing.
This work seeks to serve as the first steps in the study of the adsorption of melamine on carbon materials with the expectation that the reported findings can be extended to other carbon materials such as graphene or CNTs, as a stepping stone toward surface modification for applications in the fields of self-assembled and electrochemical materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A special thanks to Mr Oliver Strong from Trent University, for the complementary N2 and CO2 adsorption data, and Dr Rana Sodhi from the University of Toronto, who performed the XPS analysis for our samples. This work would not have been possible without the support of the Faculty of Science (Ontario Tech University), the Council of Ministers of Education of Canada for the Emerging Leaders in the Americas Program (ELAP) Scholarship who facilitated Gonzalo Montiel's visit. Liliana Trevani also wants acknowledge the Natural Sciences and Engineering Research Council of Canada, Discovery Grant Program (RGPIN/005820-2017), for financial support.References
- F. Çeçen, Activated carbon for water and wastewater treatment: integration of adsorption and biological treatment, Ferhan Çeçen and Özgür Aktas, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 1st edn, 2011 Search PubMed.
- N. Hagemann, K. Spokas, H.-P. Schmidt, R. Kägi, A. M. Böhler and D. T. Bucheli, Water, 2018, 10(2), 182–201 CrossRef.
- W. Libbrecht, A. Verberckmoes, J. W. Thybaut, P. Van Der Voort and J. De Clercq, Langmuir, 2017, 33, 6769–6777 CrossRef CAS PubMed.
- S. J. Allen, G. McKay and J. F. Porter, J. Colloid Interface Sci., 2004, 280, 322–333 CrossRef CAS PubMed.
- W. Liu, X. Zhao, T. Wang, J. Fu and J. Ni, J. Mater. Chem. A, 2015, 3, 17676–17684 RSC.
- X. Lu, J. Jiang, K. Sun, J. Wang and Y. Zhang, Mar. Pollut. Bull., 2014, 78, 69–76 CrossRef CAS PubMed.
- A. K. M. Mydul Islam, J.-I. Hwang, S.-E. Lee and J.-E. Kim, Desalin. Water Treat., 2016, 57, 21512–21523 CrossRef CAS.
- H.-Y. Wang, H. Wang, L.-L. Tang, Y.-H. Dong, L. Zhao and G. Toor, Environ. Sci. Pollut. Res., 2014, 21, 979–985 CrossRef CAS PubMed.
- D. Yamaguchi, K. Furukawa, M. Takasuga and K. Watanabe, Sci. Rep., 2014, 4, 6053 CrossRef PubMed.
- M. Pei, D. Wang, X. Hu, Y. Zhao, Y. Xu, J. Wu and D. Xu, J. Appl. Polym. Sci., 2004, 94, 2251–2256 CrossRef CAS.
- V. A. Dehabadi and H. J. Buschmann, Textiles: History, Properties and Performance and Applications, 2014, pp. 367–382 Search PubMed.
- T. S. Anirudhan, J. Christa and J. R. Deepa, Food Chem., 2017, 227, 85–92 CrossRef CAS PubMed.
- F. Arfaoui, A. Khlifi, M. Bargaoui, M. Khalfaoui and R. Kalfat, Chem. Afr., 2018, 1, 175–185 CrossRef CAS.
- J. Yu, C. Zhang, P. Dai and S. Ge, Anal. Chim. Acta, 2009, 651, 209–214 CrossRef CAS PubMed.
- E. M. Dursun, R. Üzek, N. Bereli, S. Şenel and A. Denizli, React. Funct. Polym., 2016, 109, 33–41 CrossRef CAS.
- D. Chinn and C. J. King, Ind. Eng. Chem. Res., 1999, 38, 3738–3745 CrossRef CAS.
- S. C. Smith and D. F. Rodrigues, Carbon, 2015, 91, 122–143 CrossRef CAS.
- A. Vinu, K. Z. Hossain, G. Satish Kumar and K. Ariga, Carbon, 2006, 44, 530–536 CrossRef CAS.
- A. G. Oshchepkov, A. Bonnefont, S. N. Pronkin, O. V. Cherstiouk, C. Ulhaq-Bouillet, V. Papaefthimiou, V. N. Parmon and E. R. Savinova, J. Power Sources, 2018, 402, 447–452 CrossRef CAS.
- L. Zuo, S. Yu, L. Cheng and E. Du, Korean J. Chem. Eng., 2013, 30, 714–723 CrossRef CAS.
- X. Zhang, T. Chen, Q. Chen, L. Wang and L.-J. Wan, Phys. Chem. Chem. Phys., 2009, 11, 7708–7712 RSC.
- A. Quesne-Turin, J. Touzeau, Y. J. Dappe, B. Diawara, F. Maurel and M. Seydou, Superlattices Microstruct., 2017, 105, 139–151 CrossRef CAS.
- H. Medina, Y. C. Lin, D. Obergfell and P. W. Chiu, Adv. Funct. Mater., 2011, 21, 2687–2692 CrossRef CAS.
- V. León, A. M. Rodriguez, P. Prieto, M. Prato and E. Vázquez, ACS Nano, 2014, 8, 563–571 CrossRef PubMed.
- E. Fuentes-Quezada, E. de la Llave, E. Halac, M. Jobbágy, F. A. Viva, M. M. Bruno and H. R. Corti, Chem. Eng. J., 2019, 360, 631–644 CrossRef CAS.
- Y. I. Sal’nikov, G. A. Boos, I. S. Ryzhkina, S. G. Fattakhov, G. A. Chmutova and G. R. Zaripova, Russ. J. Gen. Chem., 2009, 79, 1074 CrossRef.
- K. G. Chattaraj and S. Paul, J. Chem. Inf. Model., 2018, 58, 1610–1624 CrossRef CAS PubMed.
- I. I. Langmuir, J. Am. Chem. Soc., 1918, 40(9), 1361–1403 CrossRef CAS.
- W. Rogers and M. Sclar, J. Phys. Chem., 1932, 36, 2284–2291 CrossRef CAS.
- M. Thommes, K. Kaneko, V. Neimark Alexander, P. Olivier James, F. Rodriguez-Reinoso, J. Rouquerol and S. W. Sing Kenneth, Pure Appl. Chem., 2015, 87, 1051 CAS.
- C. Odetola, Doctor of Philosophy, Materials Chemistry, University of Ontario Institute of Technology, 2017 Search PubMed.
- C. Odetola, L. Trevani and E. B. Easton, J. Power Sources, 2015, 294, 254–263 CrossRef CAS.
- N. Shimodaira and A. Masui, J. Appl. Phys., 2002, 92, 902–909 CrossRef CAS.
- T. Kottakkat, A. K. Sahu, S. Anwar, S. Pitchumani, S. Parthasarathi and A. Shukla, J. Electrochem. Soc., 2011, 158, B622 CrossRef.
- C. Hinz, Geoderma, 2001, 99, 225–243 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00097c |
| This journal is © The Royal Society of Chemistry 2020 |