Open Access Article
Open Access ArticlePhase stability of the layered oxide, Ca2Mn3O8; probing interlayer shearing at high pressure†
Laura J.
Vera Stimpson
ab,
Kevin J. W.
Etherdo-Sibley
a,
Christopher J.
Ridley
 c,
Craig L.
Bull
c,
Craig L.
Bull
 *c and
Donna C.
Arnold
*c and
Donna C.
Arnold
 *a
*a
aSchool of Physical Sciences, University of Kent, Canterbury, Kent CT2 7NH, UK. E-mail: d.c.arnold@kent.ac.uk
bFaculty of Science, Engineering and Social Sciences, Canterbury Christ Church University, Canterbury, Kent CT1 1QU, UK
cISIS Neutron and Muon Source, Rutherford Appleton Laboratories, Chilton, Didcot OX11 0QX, UK. E-mail: craig.bull@stfc.ac.uk
First published on 5th August 2020
Abstract
We have performed high-pressure neutron diffraction studies on the layered oxide, Ca2Mn3O8. Studies up to approximately 6 GPa at temperatures of 120 and 290 K demonstrate that there are no structural phase transitions within this pressure range. Fits of the unit-cell volume to a Birch-Murngahan equation of state gives values for the bulk modulus of 137(2) GPa and 130(2) GPa at temperatures of 290 K and 120 K respectively possibly suggesting that Ca2Mn3O8 is more compressible at lower temperature. Furthermore, compression along the principal axes are anisotropic on the local scale. Comparison of individual bond lengths and bond angle environments further demonstrate that compression is complex and likely results in a shearing of the layers.
1 Introduction
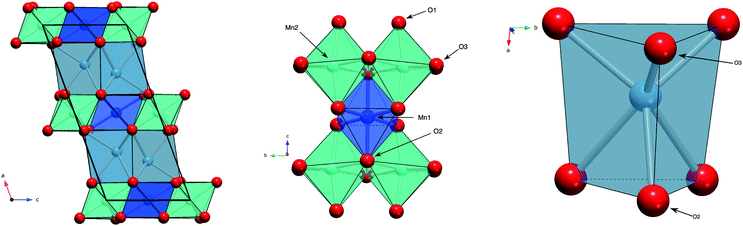
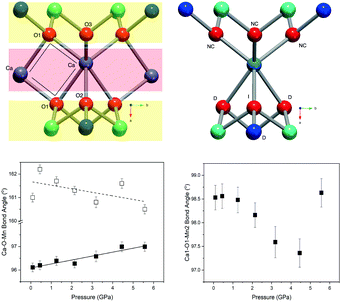
Layered metal oxides continue to attract extensive attention due to their large compositional flexibility and wide variety of potential applications. For example, applications in renewable energy1–7 and catalysis8–10 have been reported. The prototypical layered transition metal materials are the delafossite family typified by the formulae ABO2 (where A is a monovalent cation such as Na+ or Cu+ and B is a trivalent transition metal such as Fe3+ or Mn3+). The structure can be described by BO6 layers with the A+ cations situated between these layers. When B is a magnetic ion with unpaired electrons the triangular connectivity between these species often results in the realisation of exotic magnetic states.11–16More recently, interest is growing in the layered transition metal oxide, Ca2Mn3O8, first reported by Horowitz et al. in 1978.17 They showed that Ca2Mn3O8 crystallises with a monoclinic C2/m layered structure described by Mn3O84− sheets, formed from edge sharing MnO6 octahedra and separated by trigonal bipyramidal CaO6 sites as shown in Fig. 1.17–19 In contrast with delafossites, these materials have a nominal formulae of Ca0.5Mn0.75O2 as a result the B-site cation layers are incomplete (when compared with the triangular lattice exhibited by delafossite materials) with a quarter of the triangular lattice (Mn4+ octahedral) sites vacant. This leads to a network of ordered voids within the 2D layers realising a ‘bow-tie’ connectivity of the Mn4+ ions (Fig. 1).17–19 The location of this void alternates between layers giving rise to ABAB stacking in the lattice a-direction.17–19 White et al. later characterised the magnetic behaviour of the material as antiferromagnetic from SQUID magnetometry.20 As with delafossite materials, Ca2Mn3O8 has been investigated for the catalytic splitting of water21–27 and as a potential battery electrode.28 However, the understanding of the structure–property relationships in Ca2Mn3O8 has largely been limited by the low crystallinity of the as synthesised materials.29
Previously, we have demonstrated that synthetic route can have a large effect on the morphology observed.29 Solid-state methods give large spherical particles comprised of small crystallites, sol–gel methods produce nano-sized particles and hydrothermal methods yield flake-like geometries with large surface areas.29 However, all synthetic routes led to materials with low crystallinity making further analysis difficult. Recently, we developed a molten salt synthetic route which allowed us to synthesise highly crystalline Ca2Mn3O8 bulk materials.30 The high crystallinity of these materials allowed us to perform more comprehensive studies of the thermal stability and magnetic behaviour of Ca2Mn3O8.30,31 Low temperature studies (1.8–300 K) showed that Ca2Mn3O8 orders antiferromagnetically with an ↑↑↓↓ arrangement of the magnetic spins at a Néel temperature (TN) of approximately 58 K.30 Additionally, an invariant behaviour below 130 K is seen in the lattice parameter, b and the monoclinic β angle. This occurs at the same temperature as a deviation from Curie–Weiss behaviour observed in magnetic susceptibility measurements and is consistent with short-range spin correlations.30 Data collected between 300 and 1273 K show that the monoclinic structure is remarkably stable up to a temperature of approximately 1200 K before it decomposes into the perovskite, CaMnO3 and marokite, CaMn2O4 phases.31 Moreover, electrical measurements confirm that Ca2Mn3O8 is an electronic conductor in the temperature range, 400–700 K with an activation energy of approximately 0.50(1) eV.31
Given the interesting nature of Ca2Mn3O8 and the phase stability of the C2/m structure as a function of temperature it is of importance to determine the distortion of this structure on the application of hydrostatic pressure. Applied pressure is an effective way to change co-ordination environments and tune property behaviour driving very different distortion behaviour upon increasing pressure. For example, in the perovskite family of materials there are examples of both decreasing and increasing structural distortions which are controlled by the relative compressibilities of the two types of polyhedra present within the structure.32 A number of compressibility studies (both experimental33–46 and computational47–50) have been performed on CuFeO2 and related rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) delafossites. Structural studies show that the compression of the lattice is anisotropic with the compressibility within the lattice c direction (between the layers) being far larger than that of the lattice a direction (within the layers).40–45 In CuFeO2 the R
m) delafossites. Structural studies show that the compression of the lattice is anisotropic with the compressibility within the lattice c direction (between the layers) being far larger than that of the lattice a direction (within the layers).40–45 In CuFeO2 the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure has been shown to be stable up to pressure of approximately 18 GPa before transformation to a monoclinic, C2/c phase.42 At approximately 23 GPa there is a second partial transformation of the structure to a trigonal P
m structure has been shown to be stable up to pressure of approximately 18 GPa before transformation to a monoclinic, C2/c phase.42 At approximately 23 GPa there is a second partial transformation of the structure to a trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase resulting from an interatomic valence change from Cu1+/Fe3+ sites in the low pressure phases to Cu2+/Fe2+ above 23 GPa.42 In contrast in CuGaO2 and CuAlO2 the R
m phase resulting from an interatomic valence change from Cu1+/Fe3+ sites in the low pressure phases to Cu2+/Fe2+ above 23 GPa.42 In contrast in CuGaO2 and CuAlO2 the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure is stable up to a pressures of 28 GPa and 35 GPa respectively.40,43 Above these pressures there is an irreversible transition (in both CuGaO2 and CuAlO2) to an unidentified phase which seems to be driven primarily by the Cu site. The pressure dependent magnetism has also been extensively studied in CuFeO2.33–39,46 At ambient pressure CuFeO2 exhibits two distinct antiferromagnetically ordered states.46 The first magnetic transition occurs At 14 K (TN1) with the spins ordering with an incommensurately modulated collinear spin density wave.46 Below 11 K (TN2) a second magnetic phase transition occurs with the magnetic spins now adopting a collinear commensurate four sub-lattice (4SL) ↑↑↓↓ ordering.46 At TN2 there is also a lowering of the symmetry from rhombohedral to monoclinic. With applied pressure the transition temperature of the spin density wave (TN1) increases.46 In contrast the behaviour below TN2 is far more complex. With increasing pressure the transition temperature falls slightly and a number of pressure induced magnetic phase transitions occur. Firstly, a transition to an incommensurately modulated proper screw ordered state is observed at approximately 3 GPa. This is followed by a transition to an incommensurate state which has signatures of both cycloidal and proper screw configurations at approximately 4 GPa. Finally, at 6 GPa only the high temperature incommensurate spin density wave is observed (i.e. there is only a single magnetically ordered state).46 More recently, more complex magnetic correlations as a function of both applied pressure and magnetic field have been reported.51
m structure is stable up to a pressures of 28 GPa and 35 GPa respectively.40,43 Above these pressures there is an irreversible transition (in both CuGaO2 and CuAlO2) to an unidentified phase which seems to be driven primarily by the Cu site. The pressure dependent magnetism has also been extensively studied in CuFeO2.33–39,46 At ambient pressure CuFeO2 exhibits two distinct antiferromagnetically ordered states.46 The first magnetic transition occurs At 14 K (TN1) with the spins ordering with an incommensurately modulated collinear spin density wave.46 Below 11 K (TN2) a second magnetic phase transition occurs with the magnetic spins now adopting a collinear commensurate four sub-lattice (4SL) ↑↑↓↓ ordering.46 At TN2 there is also a lowering of the symmetry from rhombohedral to monoclinic. With applied pressure the transition temperature of the spin density wave (TN1) increases.46 In contrast the behaviour below TN2 is far more complex. With increasing pressure the transition temperature falls slightly and a number of pressure induced magnetic phase transitions occur. Firstly, a transition to an incommensurately modulated proper screw ordered state is observed at approximately 3 GPa. This is followed by a transition to an incommensurate state which has signatures of both cycloidal and proper screw configurations at approximately 4 GPa. Finally, at 6 GPa only the high temperature incommensurate spin density wave is observed (i.e. there is only a single magnetically ordered state).46 More recently, more complex magnetic correlations as a function of both applied pressure and magnetic field have been reported.51
In this paper we have explored the pressure–temperature phase diagram for Ca2Mn3O8 using neutron powder diffraction. We demonstrate that the C2/m structure is shown to be robust up to pressures of approximately 6 GPa at temperatures of both 290 and 120 K. Compression behaviour is shown to be complex and largely results from a shearing of the layers.
2 Materials and method
2.1 Sample synthesis and characterisation
Ca2Mn3O8 was synthesised using a molten salt method as previously reported by us.30 Briefly, stoichiometric ratios of CaCO3 (Sigma Aldrich, ≥99%), MnCO3 (Sigma Aldrich, ≥99%) and a eutectic mixture of KCl/NaCl (350% w/w) were mixed and reacted for 48 hours at 973 K followed by a second heating cycle of 24 hours at 973 K. After both heating cycles, the material was quenched to room temperature. Between heating cycles the material was washed and dried under ambient conditions and an additional 350% (w/w) eutectic mixture of KCl/NaCl was added for the second heating.Phase purity was confirmed using a Rigaku Miniflex 600 powder X-ray diffractometer (40 kV and 15 mA, with λ = 1.5406 Å) over a 2θ range of 10° to 70° (data not shown here).
2.2 High-pressure diffraction
Neutron powder diffraction (NPD) data were collected under applied pressures of 0–6 GPa at 290 K (room temperature) and 0–5 GPa at 120 K, using the PEARL diffractometer at the ISIS Neutron and Muon Facility (UK).52 A powdered sample of Ca2Mn3O8 was loaded into toroidal profile anvils machined from zirconia toughened alumina, encapsulated in a null scattering TiZr gasket and sealed in the Paris-Edinburgh press with an applied load of 6 tonnes.53,54 Time-of-flight neutron powder diffraction patterns were collected in ∼1 GPa increments for ∼4 hours each. Data were focused, normalised and intensity corrected for anvil attenuation using in-house software.52,55 Rietveld refinements were performed using the GSAS suite of programs (full details are provided in the ESI†).56,57 The data collection at 120 K was performed in the same manner described above except we used a modified Paris-Edinburgh press which was cooled with liquid N2 cooling rings and is described in detail elsewhere.52 In both experiments a small piece of lead was included in the gasket chamber and used as a pressure marker, and a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (by volume) mix of perdueterated methanol
1 (by volume) mix of perdueterated methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol was used to ensure compression was made under hydrostatic conditions.58,59
ethanol was used to ensure compression was made under hydrostatic conditions.58,59
3 Results and discussion
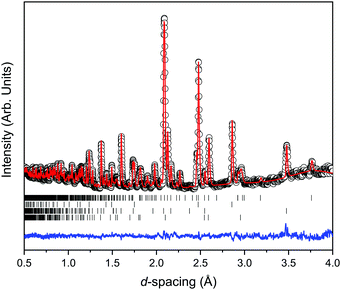
Fig. 2 shows the room temperature time-of-flight diffraction pattern of Ca2Mn3O8 as collected on the PEARL instrument at the sealing load of 6 tonnes in the Paris-Edinburgh press. The associated Rietveld refinement is also shown. Table 1 shows the results of the Rietveld refinement compared to those published previously.18 The Rietveld fit to the data clearly indicates an excellent fit to the monoclinic, C2/m, model expected for Ca2Mn3O8.18,30,31 Additional phases of Pb (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) from the pressure calibrant and, ZrO2 (P42/nmc) and Al2O3 (R
m) from the pressure calibrant and, ZrO2 (P42/nmc) and Al2O3 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) from the anvil were also refined.
c) from the anvil were also refined.
| Parameter | This study | Previous study18 |
|---|---|---|
| a (Å) | 11.0212(6) | 11.014(4) |
| b (Å) | 5.8465(3) | 5.851(3) |
| c (Å) | 4.9428(3) | 4.942(2) |
| β (°) | 109.785(4) | 109.73(5) |
| Unit cell volume (Å3) | 299.707(3) | 299.78 |
| Ca x | 0.722(6) | 0.72442(3) |
| Ca z | 0.6613(12) | 0.66593(7) |
| Mn(2) y | 0.25100(15) | 0.25914(4) |
| O(1) x | 0.0980(4) | 0.10059(7) |
| O(1) y | 0.2220(6) | 0.22158(15) |
| O(1) z | 0.3894(8) | 0.39171(17) |
| O(2) x | 0.5955(6) | 0.59726(11) |
| O(2) z | 0.08918(12) | 0.90202(25) |
| O(3) x | 0.6042(5) | 0.60385(11) |
| O(3) z | 0.9585(10) | 0.96258(26) |
| wRp | 2.43 | 3 |
| χ 2 | 1.027 | — |
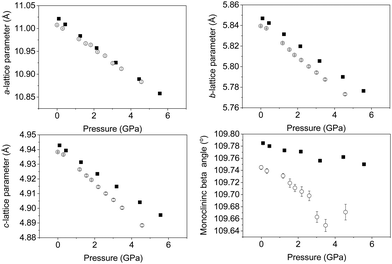
Upon increasing pressure at temperatures of both 290 and 120 K there is no change in the diffraction pattern beyond that expected with increasing pressure. Rietveld refinement of the structural model permits the lattice parameters of the monoclinic cell to be determined and with increasing pressure they show a continuous decrease as shown in Fig. 3. We find no evidence for a change in symmetry (at either 120 or 290 K) and thus conclude that the C2/m crystal symmetry is maintained up to the highest pressure studied (∼6 GPa) confirming the robust nature of the C2/m phase. This is consistent with studies on related delafossite materials which are also seen to be stable over this pressure range.40–45 Refinement profiles and data tables are provided in the ESI,† for data collected at all pressure points at both temperatures. There is a clear difference in the rate of compression of the three crystallographic axes as a function of temperature. The a- and b-lattice parameter shows very little difference in compression rate irrespective of temperature. However, the c-axis shows a greater compression rate at 120 K when compared to the 290 K data as shown by the change in slope shown in Fig. 3. This is also seen significantly in the behaviour of the monoclinic unit-cell angle (β). The beta angle decreases from initial values of 109.785(4)° and 109.745(4)° at 290 and 120 K respectively at ambient pressure to 109.750(5)° and 109.671(13)° at 290 and 120 K at pressures of 5.6 GPa and 4.6 GPa respectively possibly suggesting that the lattice is more compressible at low temperature. Overall, the structure is becoming less distorted with increasing pressure as suggested by the decrease in monoclinic cell angle (β) consistent with what has been observed in other layered delafossite materials.40
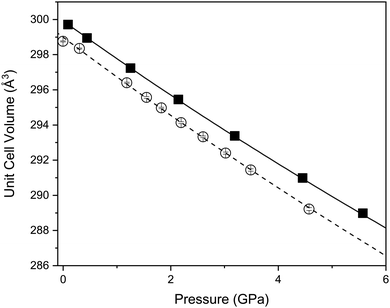
Fig. 4 shows the variation of the unit-cell volume with increasing pressure at 290 and 120 K. At both temperatures the cell volume decreases smoothly with increasing pressure indicating no structural changes consistent with lattice parameter behaviour. The variation of the volume has been fitted with a Birch-Murnaghan equation of state. At 290 K the determined bulk modulus (B0) is 136.8(20) GPa with a pressure derivative (B′) of 4.5(5) (Table 2). Such a bulk modulus is comparable with other layered oxides such as CuFeO2 (156 GPa and 2.6),44,45 PbCoO2 (225 GPa and 0.7) and CuGaO2 (202 GPa and 3.9).40 In Ca2Mn3O8 there is a small decrease in the bulk modulus upon cooling to 120 K (Table 2).
| Parameter | 290 K | 120 K |
|---|---|---|
| a A second order fit is made to the 120 K data set with an implied B′ value of 4. | ||
| V 0 (Å3) | 299.92(5) | 298.99(6) |
| B 0 (GPa) | 137(2) | 130(2) |
| B′ | 4.5(5) | 4a |
| Median compressibility K1 | 2.49(2) | 2.51(5) |
| Direction of K1 (X1) | ≈0.97a + 0.3c | = b |
| Median compressibility K2 | 2.03(3) | 2.61(7) |
| Direction of K2 (X2) | =−b | ≈−0.8a + 0.6c |
| Median compressibility K3 | 1.59(3) | 2.11(5) |
| Direction of K3 ((X3)) | ≈c | ≈−0.3a − c |
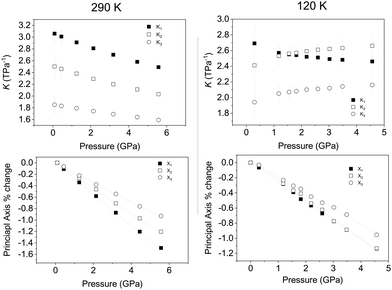
We have established that upon compression at 290 and 120 K there is no change in crystal symmetry of Ca2Mn3O8 with increasing pressure. However, compression behaviour can only be understood directly from unit cell dimensions when they are orthogonal, i.e. when they lie coincident with the principal axes of the strain tensor. For non-orthogonal axes (as is the case here), these must be reformulated into a Cartesian set. We have determined the principal axes (their relation to the unit-cell axes), and their corresponding compressibilities,60 for both temperatures. Table 2 shows the determined bulk modulus (B0) and median compressibilities (Kn) of the corresponding principal axis (Xn). It can be seen that the compressibility is anisotropic which is consistent with that reported for rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) delafossite materials.40–45 The median compressibilities of the principal axis X1 and X2 at 290 and 120 K respectively show very similar values (see Table 2) both of these axes are principally along the a direction (Fig. 5). The principal axis X2 and X1 at 290 & 120 K respectively lie parallel to the b-axis with the median compressibility being greater at low temperature (Table 2). For the third principal axis X3 at 290 & 120 K the median compressibility (K3) is greater at 120 K. In general the three principal axes all show very different median compressibilities to each other. However, at 120 K the values of K1 and K2 are similar in value. The actual compressibilities of all axes decrease with increasing pressure at 290 K as seen in Fig. 5. However, the compressibilities of X2 and X3 increase with increasing pressure. The fact that some median compressibilities increase upon cooling suggest that some changes must occur to the structure or electronic properties determining the bond strength upon cooling. This could possibly be related to short range magnetic correlations which are known to propagate at temperatures below approximately 130 K at ambient pressure.30 In order to understand this further the behaviour of the individual bond lengths and polyhedra need to be understood upon compression.
m) delafossite materials.40–45 The median compressibilities of the principal axis X1 and X2 at 290 and 120 K respectively show very similar values (see Table 2) both of these axes are principally along the a direction (Fig. 5). The principal axis X2 and X1 at 290 & 120 K respectively lie parallel to the b-axis with the median compressibility being greater at low temperature (Table 2). For the third principal axis X3 at 290 & 120 K the median compressibility (K3) is greater at 120 K. In general the three principal axes all show very different median compressibilities to each other. However, at 120 K the values of K1 and K2 are similar in value. The actual compressibilities of all axes decrease with increasing pressure at 290 K as seen in Fig. 5. However, the compressibilities of X2 and X3 increase with increasing pressure. The fact that some median compressibilities increase upon cooling suggest that some changes must occur to the structure or electronic properties determining the bond strength upon cooling. This could possibly be related to short range magnetic correlations which are known to propagate at temperatures below approximately 130 K at ambient pressure.30 In order to understand this further the behaviour of the individual bond lengths and polyhedra need to be understood upon compression.
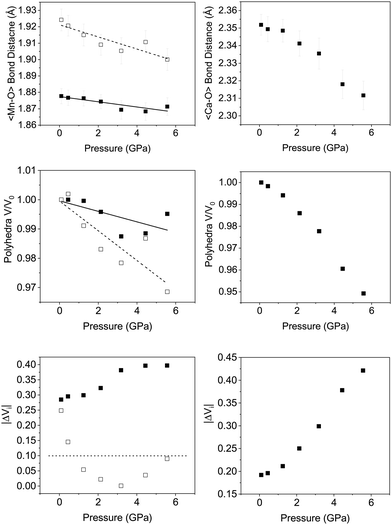
Fig. 6 shows the variation in the average Mn–O bond lengths in the two crystallographically distinct MnO6 octahedra. Both octahedra (Mn(1) and Mn(2)) display a decrease in the average bond length and individually the bond lengths within the octahedra show the same behaviour (see ESI†). The average Mn(2)O6 bond lengths show a greater compressibility than those of the Mn(1)O6 (Fig. 6). This behaviour is also reflected in the rate of change of the polyhedral volume with pressure (Fig. 6); the volume of the Mn(1)O6 polyhedra decreases at a lower rate compared to that of the larger Mn(2)O6 polyhedra. However, for both polyhedra no measurable change in distortion is seen. Within the Mn(1)O6 octahedra there is a clear contraction of the Mn(1)–O(1) bond lengths which lie in the a–b plane (see ESI†). In contrast for the most part there is little change in the Mn(1)–O(2) bond lengths, which predominantly lie in the c-lattice plane within this octahedral unit (Fig. 1). There is a decrease in the Mn(2)–O(1) bond length with increasing pressure, however, we see very little change in the Mn(2)–O(3) bond lengths (see ESI†). We note that Mn(2)–O(1) and Mn(2)–O(3) bonds predominantly lie in the lattice a–b plane. Likewise, we see a change in the Mn(2)–O(2) bond lengths (lying predominantly along the c-lattice direction) with increasing pressure. There is very little change in the Mn–O–Mn bond angles, suggesting there is no rotation of the MnO6 octahedra or buckling of the layers. Additionally, whilst both octahahedral sites contribute to lattice contraction in the a and b directions only the Mn(2)O6 octahedra drives the contraction of the layers in the c-lattice direction. This is perhaps not surprising given that the MnO6 octahedra are edge-shared within the layers consistent with the relatively small change in dimensions seen in the c lattice parameter when compared to the a and b lattice parameters.
As described previously, in Ca2Mn3O8, the calcium cation is sited between the MnO6 layers within a six coordinate trigonal bipyramidal site as shown in Fig. 1. The contraction of these bonds is a little more complex with all three bond lengths (Ca–O(1), Ca–O(2) and Ca–O(3)) contributing to lattice contraction in all three crystallographic directions. The average Ca–O bond length (shown in Fig. 6) decreases with increasing pressure. The rate of decrease is greater than the Mn–O bond contraction. Also Fig. 6 shows a significant decrease in CaO6 polyhedral volume with increasing pressure.
Looking at the individual Ca–O bonds within the polyhedra, there is only a small change in the Ca–O(1) bond length with increasing pressure whilst both the Ca–O(2) and Ca–O(3) bond lengths show a clear contraction. This would seem to suggest that the CaO6 polyhedra become increasingly distorted with increasing pressure. Previous work using the difference in the absolute bond valence sum (|ΔVi|) has suggested that a value of >0.1 is a result of strain within a polyhedron.32 |ΔVi| for the CaO6 polyhedra shows a clear increase in value with increasing pressure for which R0 = 1.967 Å, B = 0.37 and formal expected charge of the calcium ion as 2+. The individual bond distances within the octahedra compress at different rates as described in the ESI,† and gives rise to an increase in geometric distortion of the octahedra as suggested by |ΔVi| (Fig. 6). Indeed for the CaO6 polyhedra the initial value is 0.2 and this doubles upon application of a pressure of ∼6 GPa. This is in contrast with the behaviour of the MnO6 polyhedra where the Mn(2)O6 shows no real strain or changes with increasing pressure and only the Mn(1)O6 polyhedra show an increase in strain suggested by the bond valence difference from 0.28 to 0.4 at 5.6 GPa (for both octahedra R0 = 1.753 Å, B = 0.37) with a formal charge on the manganese ion of 4+. Again within each individual octahedra the individual Mn–O bonds compress at different rates and this leads to the difference in overall behaviour suggested by |ΔVi|.
In contrast with the Mn–O–Mn bond angles, there are systematic changes in the bond angles associated with the calcium site (as shown in the ESI†). The Ca–O(1)–Ca bond angle shows a small increase with increasing pressure. This effectively acts to pull the layers closer together as shown in Fig. 7. The interlayer stacking in Ca2Mn3O8 is ABAB with the intralayer voids formed within the MnO6 framework shifted with respect to each other in adjacent layers.17–20,29–31 This means the Ca–O–Mn bond environments are different above and below the Ca2+ cation as shown in Fig. 7. These environments also alternate as you move between Ca2+ cations within the layer. The Ca–O(1)–Mn1 and Ca–O(1)–Mn(2) bond angles are each described by two different values depending on if the angle describes bond angles linked to the ‘top’ or ‘bottom’ layer (as is depicted in the arrangement in Fig. 7). In fact all bond angles associated with the top layer (Ca–O(1)–Mn(1), Ca–O(1)–Mn(2) and Ca–O(3)–Mn(2)) all show little change with increasing pressure. In contrast those bond angles associated with the bottom layer show consistent changes with increasing pressure. In addition to the decreasing bond angle trends described above for Ca–O(1)–Mn(1) and Ca–O(1)–Mn(2), the Ca–O(2)–Mn(2) and Ca–O(2)–Mn(1) (non-bonding) bond angles both subtly increase with increasing pressure. This suggests that a shearing (consistent with the decrease of the β angle) of the layers contributes to the overall contraction in the a-lattice direction. This is consistent with the larger contractions seen in the interlayer dimensions in the delafossites (in this case the c-lattice direction).40–43,45 From these data we can also suggest that the shearing effect occurs uniformly across the material, as we see no evidence to support buckling or superstructure formation. However, considering the ‘average’ nature of these experiments we cannot rule out local or modulation effects. Further work is necessary to elucidate the local behaviours in these materials.
4 Conclusions
In summary we have investigated the temperature-pressure phase diagram of the layered oxide, Ca2Mn3O8 at temperatures of 290 K and 120 K and pressures up to 6 GPa. These studies demonstrate that there is a smooth decrease in the lattice parameters and unit cell volume with increasing pressure. Compression of the structure is largely anisotropic and predominantly occurs in the interlayer direction(s) as opposed to the intralayer directions consistent with data reported for the compression of similar layered oxides.40–45 On the local scale compression behaviour is far more complex. Bond lengths and bond angle values suggest that there is little tilting or strain associated with the MnO6 octahedra. In contrast the CaO6 trigonal bipyramidal site becomes increasingly strained with increasing pressure. Moreover, contraction appears to be driven by one side of the CaO6 polyhedra with the other side remaining largely unchanged. The nature of the structure means that this behaviour alternates between neighbouring Ca2+ ions which results in a shearing of the layers. These studies provide insight into the compression behaviour of Ca2Mn3O8 which may be useful for optimising dopant (chemical pressure) studies, as well as providing a deeper understanding which will allow optimisation of this material for application.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Both L. J. V. and K. J. W. E. are grateful for the awards of EPSRC DTA studentships. We are thankful to the ISIS Neutron and Muon User facility for the provision of beamtime on PEARL (RB1930086).61Notes and references
- R. Manickam, V. Yesuraj and K. Biswas, Mater. Sci. Semicond. Process., 2020, 109, 104928 CrossRef CAS.
- P. Beraslegui, C.-W. Tai and M. Valvo, J. Power Sources, 2018, 401, 386–396 CrossRef.
- D. Nayak, P. K. Jha, S. Ghosh and V. Adyam, J. Power Sources, 2019, 438, 227025 CrossRef CAS.
- L. M. Zheng, Z. Q. Wang, M. S. Wu, B. Xu and C. Y. Ouyang, J. Mater. Chem. A, 2019, 7, 6053–6061 RSC.
- M. P. Down, E. Martinez-Perinon, C. W. Foster, E. Lorenzo, G. C. Smith and C. E. Banks, Adv. Energy Mater., 2019, 9, 1803019 CrossRef.
- M. Tato, R. Shironishi, M. Hagiwara and S. Fujihara, ACS Energy Mater., 2020, 3, 1979–1987 CrossRef CAS.
- P. Yardanov, W. Sigle, P. Kaya, M. E. Gruner, R. Pentcheva, B. Keimer and H. U. Habermuer, Phys. Rev. Mater., 2019, 3, 085403 CrossRef.
- T. I. Draskovic and Y. Wu, ChemCatChem, 2017, 9, 3837–3842 CrossRef CAS.
- Y. W. Deng, D. H. Xiong, H. Gao, J. Wu, S. K. Verma, B. S. Lutz and X. J. Zhao, Dalton Trans., 2020, 49, 3519–3524 RSC.
- F. Podjaski, D. Weber, S. Y. Zhang, L. Diehl, R. Eger, V. Duppel, E. Alarco-Llado, G. Richter, F. Haase and A. F. I. Morral, Nat. Catal., 2020, 3, 55–63 CrossRef CAS.
- R. L. Dally, R. Chisnell, L. Harriger, Y. H. Liu, J. W. Lynn and S. D. Wilson, Phys. Rev. B, 2018, 98, 144444 CrossRef CAS.
- F. Orlandi, E. Aza, I. Bakaimi, K. Kiefer, K. Klemke, B. Zorko, A. Arcon, C. Stock, G. D. Tsibidis, M. A. Green, P. Manuel and A. Lappas, Phys. Rev. Mater., 2018, 2, 074407 CrossRef CAS.
- A. Zorko, O. Adamopoulos, M. Komelj, D. Arcon and A. Lappas, Nat. Commun., 2014, 95, 3222 CrossRef PubMed.
- T. Nakajima, N. Terada, S. Mitsuda and R. Bewley, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 134414 CrossRef.
- T. Nakajima, A. Suno, S. Mitsuda, N. Terada, S. Kimura, K. Kaneko and H. Yamauchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184401 CrossRef.
- A. M. L. Lopes, G. N. P. Oliveira, T. M. Mendonca, J. A. Moreira, A. Almeida, J. P. Aravjo, V. S. Amaral and J. G. Correla, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014434 CrossRef.
- H. S. Horowitz and J. M. Longo, Mat. Res. Bull., 1978, 13, 1359–XX CrossRef CAS.
- G. B. Ansell, M. A. Modrick, J. M. Longo, K. R. Poeppeimeler and H. S. Horowitz, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1795–1797 CrossRef.
- H. S. Horowitz and J. M. Longo, Inorg. Synth., 1983, 22, 73–XX CAS.
- T. R. White, W. S. Glaunsinger, H. S. Horowitz and J. M. Longo, J. Solid State Chem., 1979, 29, 205 CrossRef CAS.
- M. M. Najafpour, N. Pashaei and S. Nayeri, Dalton Trans., 2012, 41, 4799 RSC.
- M. M. Najafpour and D. J. Sedigh, Dalton Trans., 2013, 42, 12173 RSC.
- A. Ramirez, P. Bogdanoff, D. Friedrich and S. Fiechter, Nano Energy, 2012, 1, 282 CrossRef CAS.
- E. Braktash, I. Zaharieva, M. Schroder, C. Goebel, H. Dau and A. Thomas, Dalton Trans., 2013, 42, 16920 RSC.
- X. Han, T. Zhang, J. Du and F. Cheng, Chem. Sci., 2013, 4, 368 RSC.
- J. Yang, H. Yu, Y. Wang, F. Qi, H. Liu, L.-L. Lou, K. You, W. Zhou and S. Liu, Catal. Sci. Technol., 2019, 9, 6659 RSC.
- A. Gagrani, M. Alsultan, G. F. Swigers and T. Tsuzuki, Catal., 2020, 10, 2152 RSC.
- Y. J. Park and M. A. Doeff, Solid State Ionics, 2006, 177, 893–XX CrossRef CAS.
- L. J. Vera Stimpson, S. Ramos, G. B. G. Stenning, M. Jura, S. Parry, G. Cibin and D. C. Arnold, Dalton Trans., 2017, 46, 14130 RSC.
- L. J. Vera Stimpson, E. E. Rodriguez, C. M. Brown, G. B. G. Stenning, M. Jura and D. C. Arnold, J. Mater. Chem. C, 2018, 6, 4541–4548 RSC.
- L. J. Vera Stimpson, J. A. McNulty, F. D. Morrison, A. Mahajan, E. E. McCabe, A. S. Gibbs, G. B. G. Stenning, M. Jura and D. C. Arnold, J. Alloys Compd., 2020, 843, 155633 CrossRef CAS.
- J. Zhao, N. L. Ross and R. J. Angel, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 263–271 CrossRef CAS PubMed.
- T. Nakajima, Y. Iguchi, H. Tamatsukuri, S. Mitsuda, Y. Yanasami, H. Nakao and N. Terada, J. Phys. Soc. Jpn., 2013, 82, 114711 CrossRef.
- T. Nakajima, S. Mitsuda, K. Takahashi, K. Yoshitami, K. Masuda, C. Kaneko, Y. Honma, S. Kobayashi, H. Kitazawa, M. Kosaka, N. Aso, Y. Uwatoko, N. Terada, S. Wakimoto, M. Takeda and K. Kakurai, J. Phys. Soc. Jpn., 2012, 81, 094710 CrossRef.
- H. Tamatsukuri, S. Mitsuda, T. Nakamura, K. Takata, T. Nakjima, K. Prokes, F. Yakaichiya and K. Kiefer, Phys. Rev. B., 2017, 95, 174108 CrossRef.
- T. Nakajima, S. Mitsuda, J. T. Haraldsen, R. S. Fishman, T. Hong, Y. Terada and N. Uwatoko, Phys. Rev. B., 2012, 85, 144405 CrossRef.
- T. Nakajima, S. Mitsuda, T. Nakamura, H. Ishii, T. Haku, Y. Honma, M. Kosaka, N. Aso and Y. Uwakoto.
- N. Terada, N. Qureshi, L. C. Chapon and T. Osakabe, Nat. Commun., 2018, 9, 4368 CrossRef PubMed.
- W. M. Xu, G. R. Hearne and M. P. Pasternak, Phys. Rev. B., 2016, 94, 035155 CrossRef.
- J. Pellier-Porres, A. Segura, C. Ferrer-Roca, D. Martinez-Garcia, J. A. Sans, E. Martinez, J. P. Itie, A. Polian, F. Baudelet, A. Munoz, P. Rodriguez-Hernandez and P. Munsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 024109 CrossRef.
- M. Hasagawa, M. Tanaka, T. Yagi, H. Takei and A. Inoue, Solid State Commun., 2003, 128, 33 Search PubMed.
- W. M. Xu, G. K. Rozenberg, M. P. Pasternak, M. Kertzer, A. Kurnosov, L. S. Dubrovinsky, S. Pascarelli, M. Munoz, M. Vaccari, M. Hanfland and R. Jeanloz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104110 CrossRef.
- A. Pellier-Porres, A. Segura, C. Ferrer-Roca, P. Munsch and D. Kim, J. Phys.: Condens. Matter., 2013, 25, 115406 CrossRef PubMed.
- T. R. Zhao, M. Hasegawa, H. Takei, T. Kondo and T. Yagi, Jpn. J. Appl. Phys., 1996, 35, 3535 CrossRef CAS.
- T. R. Zhao, M. Hasegawa, T. Kondo, T. Yagi and H. Takei, Mat. Res. Bull., 1997, 32, 151 CrossRef CAS.
- N. Terada, D. D. Khalyavin, P. Manuel, T. Osakabe, P. G. Radaelli and H. Kitazawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 220403 CrossRef.
- A. Miura, M. Wessel and R. Dronskowski, J. Ceram. Soc. Jpn., 2011, 119, 663 CrossRef CAS.
- A. Nakanishi and H. Katayama-Yoshida, J. Phys. Soc. Jpn., 2011, 80, 024706 CrossRef.
- D. Upadhyay, A. Piatap and P. K. Jha, J. Raman Spec., 2019, 50, 603 CrossRef CAS.
- J. Pellicer-Porres, A. Segura, E. Martinez, A. M. Saitta, A. Polian, J. C. Cherun and B. Canny, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064301 CrossRef.
- H. Tamatsukuri, S. Mitsuda, T. Shimizu, M. Fujihala, H. Yokota, K. Takehara, Y. Imariaka, A. Nakao and K. Munakata, Phys. Rev. B., 2019, 100, 201105 CrossRef CAS.
- C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Press. Res., 2016, 36, 493–511 CrossRef.
- W. G. Marshall and D. J. Francis, J. Appl. Crystallogr., 2002, 35, 122–125 CrossRef CAS.
- J. M. Besson, R. J. Nelmes, G. Hamel, J. S. Loveday, G. Weill and S. Hull, Physica B, 1992, 180, 907–910 CrossRef.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Meth. A, 2014, 764, 156–166 CrossRef CAS.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report (LAUR), 2004, 86, 748 Search PubMed.
- S. Klotz, J. C. Chervin, P. Munsch and G. L. Marchand, J. Phys. D: Appl. Phys., 2009, 42, 075413 CrossRef.
- A. D. Fortes, RAL Technical Reports, 2019, RAL-TR-2019-002 Search PubMed.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- D. C. Arnold and C. L. Bull, 2019, DOI:10.5286/ISIS.E.RB1930086.
Footnote |
| † Electronic supplementary information (ESI) available: ESI includes full refinement details of all collected data sets as well as additional information and graphical material to support the work presented here. See DOI: 10.1039/d0ma00464b |
| This journal is © The Royal Society of Chemistry 2020 |