A type-II blue phosphorus/MoSe₂ van der Waals heterostructure: improved electronic and optical properties via vertical electric field

Abstract

Building novel van der Waals (vdW) heterostructures is of great interest and is important to improve the performance of individual two-dimensional materials. Using first-principles calculations, we demonstrate that the constructed blue phosphorus/MoSe₂ (P₂/MoSe₂) vdW heterostructure has a unique type-II band alignment and a suitable bandgap (about 1.63 eV) for optoelectronic applications. Its electronic and optical properties depend strongly on the applied vertical electric field. The quasi-particle bandgap of the P₂/MoSe₂ can be linearly modulated by about 1.11 eV under the applied electric field and the type-II band alignment persists in a broad range. Meanwhile, the negative electric field induces a significant red-shift of the optical absorption edge of P₂/MoSe₂, greatly enhancing its absorption for the visible and near-infrared lights, which is desirable for optoelectronic applications. More importantly, the observed interlayer excitons with large binding energy (more than 600 meV) can be preserved under the applied electric field, being very much beneficial for the real separation of photoexcited carriers. These results indicate that the P₂/MoSe₂ vdW heterostructure can become a good candidate for optoelectronic devices.

---

1 Introduction

In recent years, the precise transfer of the produced two-dimensional (2D) materials has led to an emerging new class of materials, van der Waals (vdW) heterostructures.^1–8 vdW heterostructures, formed by vertically stacking two dissimilar 2D materials, can exhibit more desirable properties than their components due to interlayer coupling. For example, the interlayer coupling induced by vdW interactions can cause an ultrafast separation of photoexcited carriers^9–11 and long lifetimes of indirect excitons in the vdW heterostructure.^12,13 Such novel properties in vdW heterostructures can be utilized to explore their applications for photovoltaics and optoelectronics. Previously, an efficient flexible photovoltaic device based on graphene/MoS₂ was reported, achieving an external quantum efficiency of above 30%.¹⁴ A p–n diode based on black phosphorene/MoS₂ obtains broad-band photodetection and sunlight harvesting.¹⁵ The vdW heterostructures for other versatile applications also have been reported, including electrocatalysts,^16,17 Li⁺/Na⁺ ion batteries,^18,19 and supercapacitors.^20,21 In addition, the external electric field has also been considered as an effective way to further optimize the properties of vdW heterostructures. The electric-field tunable semiconductor-to-metal transition is observed in black phosphorene/MoS₂,²² MoS₂/MX₂ (M: Mo, W, and Cr; X = Se, and S),²³ and black phosphorene (MoSSe)/blue phosphorene heterostructures,^24,25 suggesting a new application of these systems in semiconductor devices. More importantly, the external electric field can significantly manipulate the optical properties of the vdW heterostructure by changing the band alignment and interlayer coupling.^26,27 For example, in the WSe₂/graphene vdW heterostructure, the external electric field enhances photoluminescence (PL) intensity of excitons by more than 40 times and induces a maximum blue-shift of 50 meV of exciton peaks.²⁸

Among 2D materials, the hexagonal MoSe₂ monolayer has desirable properties, such as a direct bandgap of 1.60 eV,^29,30 optical absorbance of 5–10% for the incident sunlight, and a photo flux of 4.6 mA cm⁻².³¹ Monolayer MoSe₂-based field effect transistors can also obtain an on/off current ratio as high as 10⁶ and an intrinsic carrier mobility of up to 500 cm² V⁻¹ s⁻¹ at 100 K.³² In 2016 the blue phosphorus (P₂) monolayer with in-plane hexagonal structure was firstly synthesized on Au(111) by a molecular beam epitaxial growth approach.³³ Furthermore, theoretical studies have demonstrated that it has intriguing structural and electronic properties, such as its stability at room temperature,^34,35 moderate bandgap of approximately 2.0 eV,^35,36 and room-temperature carrier mobility of over 10³ cm² V⁻¹ s⁻¹.³⁷ These good properties in MoSe₂ and P₂ monolayers can draw enormous interest, suggesting great potential in optoelectronic devices. Besides, the MoSe₂ and P₂ monolayers with similar hexagonal structure^35,38 have distinct differences in constituents and chemical bonding, which may form a large potential difference and band offsets between the two layers. Meanwhile, it suggests that the hybrid band structure, band alignment at the heterointerface, and even interlayer coupling in the vdW heterostructure based on MoSe₂ and P₂ monolayers, can be manipulated by an external electric field. Previously, MoSe₂-based vdW heterostructures, such as WS₂/MoSe₂^39,40 and WSe₂/MoSe₂,⁴¹ have been achieved by transfer methods. Therefore, the fabrication of a P₂/MoSe₂ vdW heterostructure is anticipated and their properties are of great interest.

In this work, we construct five P₂/MoSe₂ vdW heterostructures by stacking the P₂ and MoSe₂ monolayers. Using density-functional theory (DFT) connected with the G₀W₀ + Bethe–Salpeter equation (BSE) method, we investigated the P₂/MoSe₂ vdW heterostructure, focusing on the structure, electronic and optical properties, and the effect of vertical electric field. Our calculations show that its electronic band structure and optical response are very sensitive to the size and orientation of the applied electric field.

2 Computational method

The electronic and optical properties of the systems were attained via a three-step procedure. First, we used a plane-wave basis set and a norm-conserving pseudopotential⁴² to achieve the ground states, which was performed by the Quantum Espresso code.⁴³ Electron exchange and correlation were treated by generalized gradient approximation (GGA) along with the Perder–Burke–Ernzerhof (PBE) functional.⁴⁴ The 4s²4p⁶4d⁵5s¹ of Mo, 4s²4p⁶ of Se, and 3s²3p³ of P were used as valence electrons. The cutoff energy for wave function was set to be 70 Ry. To eliminate the interaction between spurious replicate images, a vacuum region of 20 Å along the c-axial direction was inserted for the systems. The Brillouin zone integrations adopted a k-point grid of 18 × 18 × 1. The weak interaction between two layers was considered via a vdW-DF approach.^45,46 When structures were fully relaxed, the force applied on each atom and the total energy of the system were converged within the 0.01 eV Å⁻¹ and 10⁻⁴ eV, respectively. To avoid the errors induced by the periodic boundary condition, dipole correction was considered in the systems. Furthermore, an external sawtooth potential along the c-axial direction was also used to simulate the effect of an applied electric field.⁴⁷ The phonon dispersion relations of the systems were obtained by performing phonon calculations from density functional perturbation theory.⁴⁸

Then, the G₀W₀ approximation⁴⁹ was used to obtain quasi-particle (QP) band structures. The convergence of quasi-particle bandgap with respect to the number of unoccupied bands, the size of dielectric matrix and the k-point grid was carefully checked and a convergence of 100 meV was assured in the systems. Finally, the coupled electron–hole excitation energies and exciton wave functions were obtained by solving the Bethe–Salpeter equation (BSE).^50,51 The 1218 bands (unoccupied bands: 1200, and occupied bands: 18) and random phase approximation were involved to attain the converged dielectric function. A fine k-point grid (54 × 54 × 1), 38 bands (20 unoccupied bands), was utilized to obtain the converged optical spectra. The G₀W₀ and BSE calculations were performed via the YAMBO code.⁵²

3 Results and discussion

3.1 Geometric structure and stability

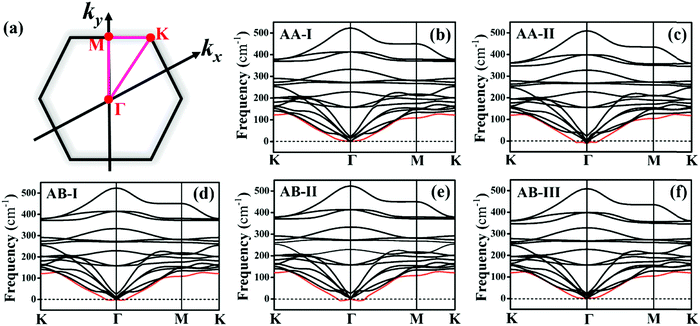
Before investigating the P₂/MoSe₂ vdW heterostructure, it is necessary to understand the geometries and electronic properties of P₂ and MoSe₂ monolayers. Their optimized geometric structures are provided in Fig. S1 of the ESI,† in which the lattice constants are a_P2 = b_P2 = 3.322 Å for the P₂ monolayer and a_MoSe2 = b_MoSe2 = 3.269 Å for the MoSe₂ monolayer. The bond lengths of P–P and Mo–Se are 2.271 Å and 2.549 Å, respectively. The obtained structural parameters are in good accordance with previous studies.^35,53,54 To examine the electronic properties of the P₂ and MoSe₂ monolayers, the quasi-particle band structures with many-body interaction included, are calculated by the single-shot G₀W₀ method and the results are exhibited in Fig. S2 (ESI†). It can be found that the P₂ monolayer is an indirect semiconductor with a wide quasi-particle gap of 3.350 eV, while the MoSe₂ monolayer has a direct bandgap of 2.300 eV at K-point. Interestingly, the gap of the MoSe₂ monolayer is fixed at the visible-light region, suggesting its potential for visible-light-driven optoelectronics. The predicted quasi-particle bandgaps agree well with previous reports (3.530 eV for P₂ monolayer; 2.260 eV for MoSe₂ monolayer).^54–56

Due to small lattice mismatch (approximately 1.6%) between the P₂ and MoSe₂ monolayers, five P₂/MoSe₂ vdW heterostructures are constructed by the 1 × 1 primitive cells of the P₂ and MoSe₂ monolayers, as shown in Fig. 1. The lattice mismatch is calculated by 2(a_P2 − a_MoSe2)/(a_P2 + a_MoSe2). To verify the thermal stability of the five possible stacking configurations, the formation energies (E_f) are firstly calculated to assess them using the equation E_f = E₁ − E₂ − E₃, where E₁, E₂, and E₃ are the total energies of the P₂/MoSe₂, P₂ monolayer, and MoSe₂ monolayer, respectively. The estimated formation energies are all negative for these designed configurations (as seen in Table S1, ESI†), suggesting that the fabrications of P₂/MoSe₂ vdW heterostructures should be feasible from a thermodynamic point of view. Among these constructed vdW heterostructures, the AA-I stacking shows the most stable structure by the lowest formation energy of −0.212 eV per unit cell. We further verify the dynamical stability of these heterostructures by calculating their phonon spectra, which are shown in Fig. 2(b)–(f). The observed phonon spectra of AA-I and AB-III stacking structures have no negative frequencies, while the other three stacking configurations (AA-II, AB-I, and AB-II) have negligible imaginary frequencies around the Γ-point. The calculation results of phonon dispersion indicate that the AA-I and AB-III configurations have more dynamical stability than the other three configurations. In addition, as a comparison, the structural parameters of the five configurations are also listed in Table S1 (ESI†). There is little difference in the lattice constant, bond length, and interlayer distance for the five stacking configurations, which will result in similar band dispersion, as seen in Fig. S3 (ESI†). In the following sections, we only investigate the most stable AA-I configuration among five stacking configurations.

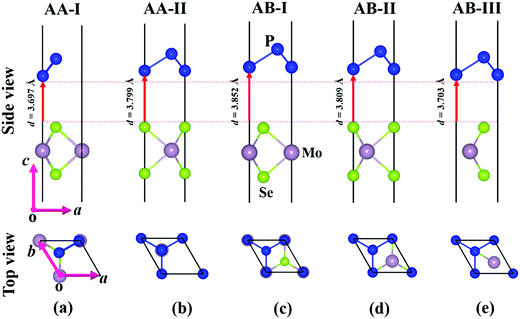Fig. 1 Optimized structures of P₂/MoSe₂ vdW heterostructures with different stacking configurations: (a) AA-I, (b) AA-II, (c) AB-I, (d) AB-II, and (e) AB-III.

Fig. 2 (a) High-symmetric path (K–Γ–M–K) of the first Brillouin zone of hexagonal lattice, K (1/3, 1/3, 0), Γ (0, 0, 0), and M (0, 1/2, 0). Phonon spectra of P₂/MoSe₂ vdW heterostructures with different stacking configurations: (b) AA-I, (c) AA-II, (d) AB-I, (e) AB-II, and (f) AB-III.

3.2 Electronic and optical properties

Fig. 3(a) shows the quasi-particle band structure of the AA-I stacking P₂/MoSe₂ vdW heterostructure at the single-shot G₀W₀ level. Compared with the isolated P₂ and MoSe₂ monolayers, the P₂/MoSe₂ vdW heterostructure has a relatively narrow indirect gap of 1.630 eV due to the preserved band structures of the two monolayers. This phenomenon has also been observed in other semiconducting vdW heterostructures, such as WS₂/MoS₂, blue phosphorene/BSe, and blue phosphorus/Mg(OH)₂.^58–60 To understand the layer contributions to the highest occupied state (VBM) and the lowest unoccupied state (CBM) of the P₂/MoSe₂, the partial charge distributions of the CBM and VBM are calculated and the results are exhibited in Fig. 3(a) right. It is found the CBM and VBM of the P₂/MoSe₂ are contributed by the P₂ and MoSe₂ layers, respectively, suggesting it has a type-II characteristic of band alignment and good charge separation. To check the charge transfer between the P₂ and MoSe₂ layers, it is necessary to obtain the work functions (Φ) of the isolated P₂ and MoSe₂ monolayers. The Φ can be calculated by the definition: Φ = E_VAC − E_VBM, in which E_VAC and E_VBM are the vacuum potential and VBM energy, respectively.⁶¹ The obtained work functions are 6.96 eV for the P₂ monolayer and 5.46 eV for the MoSe₂ monolayer, respectively. Owing to a relatively large difference (1.50 eV) in the work functions between the P₂ and MoSe₂ monolayers, electrons can easily migrate from the MoSe₂ layer into the P₂ layer after forming the P₂/MoSe₂ vdW heterostructure. The work function of P₂/MoSe₂ is also estimated to be 4.95 eV, being less than those of the isolated monolayers due to the interlayer coupling. Also, the calculated two band edges of the heterostructure relative to the vacuum level are located at −3.32 eV (CBM) and −4.95 eV (VBM), which cannot wholly straddle water redox potentials (reduction potential: −4.44 eV; oxidation potential: −5.67 eV) at pH = 0. However, the P₂/MoSe₂ vdW heterostructure satisfies the reduction level in water splitting. Upon illuminating the P₂/MoSe₂, the photoexcited electrons collected in the P₂ layer due to the type-II band alignment will drive the hydrogen reduction reaction generating hydrogen (2H⁺ + 2e⁻ → H₂), as shown in Fig. S4 (ESI†), suggesting it could be a potential hydrogen production material.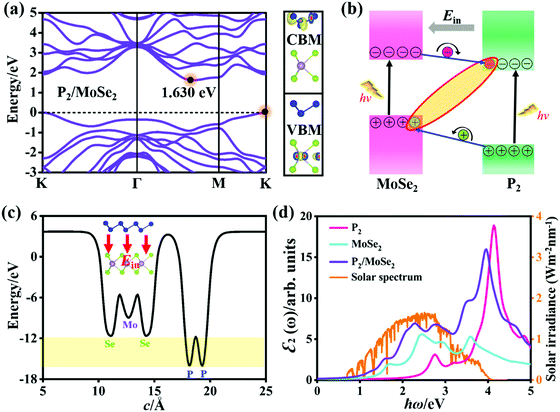

Fig. 3 (a) Quasi-particle band structure and decomposed charge density (CBM and VBM) of the P₂/MoSe₂ vdW heterostructure (isosurface: 3.0 × 10⁻³ e Å⁻³). (b) Schematic diagram of the band alignment between the two layers in P₂/MoSe₂ and charge separation at the P₂–MoSe₂ interface. (c) Planar average electrostatic potential of the P₂/MoSe₂ along the c-axial direction. The direction of built-in electric field (E_in) is inset. (d) Optical absorption spectra of the P₂ and MoSe₂ monolayers, and P₂/MoSe₂ including the interaction between photoexcited electrons and holes, in comparison with the incident AM 1.5G solar irradiance.⁵⁷ Polarized light along the a-axial direction and Lorentzian broadening (0.15 eV) are used in these spectra.

Fig. 3(b) shows the charge separation at the P₂–MoSe₂ interface and the formation of indirect excitons when illuminating the P₂/MoSe₂ vdW heterostructure. The photoexcited electrons and holes are inclined to spontaneously separate into the opposite layers by the potential offsets. The formed indirect excitons will prolong the lifetime of photoexcited carriers, being very useful for optoelectronic devices. In fact, the indirect charge-transfer exciton has been observed experimentally in other vdW heterostructures (like MoS₂/WS₂, MoS₂/MoSe₂, and MoS₂/WSe₂) by time resolved measurements^9,62 and photoluminescence quenching.^58,63,64 In addition, the planar average electrostatic potential is also computed and presented in Fig. 3(c). The depth of potential of the MoSe₂ layer is smaller than that of the P₂ layer by about 4 eV, indicating that the built-in electric field (E_in) has been formed in the MoSe₂–P₂ interface. The direction of the E_in is pointed from the P₂ layer to the MoSe₂ layer (as seen in the inset of Fig. 3(c)), which will play an important role in further facilitating charge separation, i.e. the photoexcited electron (hole) is accelerated to flow from the MoSe₂ (P₂) layer to the P₂ (MoSe₂) layer under the E_in (as in Fig. 3(b)). As a result, the E_in can promote the separation of photoexcited electron–hole pairs in the P₂/MoSe₂ vdW heterostructure.

On the other hand, the excitonic behavior of the P₂/MoSe₂ vdW heterostructure should have a striking difference with those of the isolated P₂ and MoSe₂ monolayers owing to the existence of a potential gradient across the P₂–MoSe₂ interface. In order to obtain their exact optical properties, we solved the BSE equation based on the G₀W₀ calculations, which has fully included the many-body interactions (electron–electron and electron–hole interactions) in real systems. Fig. 3(d) shows the imaginary parts ε₂(ω) of the dielectric functions of the P₂ monolayer, MoSe₂ monolayer, and the P₂/MoSe₂ heterostructure, i.e. the optical absorption spectra. It can be found that the P₂/MoSe₂ heterostructure has a wide absorption range from the near-infrared to the near-ultraviolet. The optical spectrum of the P₂/MoSe₂ is dominated by the MoSe₂ layer in the energy of 0–2 eV, while the absorption ranging from 2 eV to 5 eV is contributed by both the MoSe₂ and P₂ layers. Compared with the isolated P₂ and MoSe₂ monolayers, the P₂/MoSe₂ vdW heterostructure has a marked enhancement of optical absorption in a broad light-harvesting range, spanning from 1.64 eV (visible light) to 4.15 eV (near-ultraviolet light). The enhanced optical absorption in the P₂/MoSe₂ vdW heterostructure should originate from the interlayer coupling and charge transfer between the two single layers as well as the overlap of the electronic states. In addition, for the incident AM 1.5G solar irradiance, the P₂/MoSe₂ vdW heterostructure can also absorb a considerable part, as shown in Fig. 3(d), which could be used in optoelectronic devices based on the solar irradiance.

3.3 Effects of vertical electric fields on electronic and optical properties

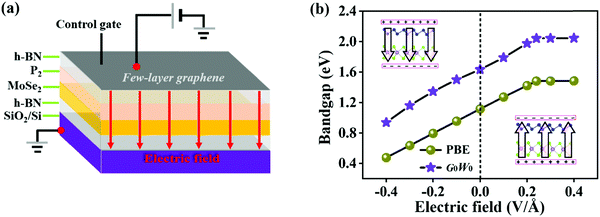
To explore the effect of electric field on the electronic properties of the P₂/MoSe₂ vdW heterostructure, an electric field (E_ef) perpendicular to the stacking layers is applied on the heterostructure, ranging from −0.4 V Å⁻¹ to 0.4 V Å⁻¹ with the step of 0.1 V Å⁻¹. The phonon spectrum of P₂/MoSe₂ at the electric field of 0.4 V Å⁻¹ is also calculated to check its dynamical stability, as presented in Fig. S5 (ESI†). Only a small imaginary frequency of −1.8 cm⁻¹ close to the Γ point is observed in the P₂/MoSe₂, suggesting it has dynamic stability under the observed electric field. The positive direction of vertical electric field is pointed from the MoSe₂ layer to the P₂ layer along the c-axial direction. Experimentally, a controlled vertical electric field can be realized by a double-gated configuration without changing the charge carrier concentration in the P₂/MoSe₂ vdW heterostructure, as shown in Fig. 4(a). Fig. 4(b) shows the various bandgaps under different electric-field strengths from the PBE and G₀W₀ methods. The G₀W₀ method can correct the band structure of the semiconductor at the PBE level to obtain a credible quasi-particle bandgap by shifting the conduction (valence) band up (down). It can be seen that the quasi-particle bandgap of the P₂/MoSe₂ heterostructure can be significantly tuned in a wide range from 0.94 eV (E_ef = −0.4 V Å⁻¹) to 2.05 eV (E_ef = 0.4 V Å⁻¹). Although the PBE method underestimates the bandgap of the semiconducting material, the trend of bandgap variation in the two methods is roughly the same in the observed electric field range, in which the bandgap linearly increases with E_ef from −0.4 V Å⁻¹ to 0.24 V Å⁻¹ and shows little change from 0.24 V Å⁻¹ to 0.4 V Å⁻¹. To shed more light on the variable bandgap, the projected band structures of P₂/MoSe₂ under variable electric fields is calculated and presented in Fig. 5(a)–(e). It is found that the CBM (A point) belonging to the P₂ layer is very sensitive to E_ef, in which the A point is slowly elevated in the range of −0.4 to 0.2 V Å⁻¹, leading to the increasing bandgap of the P₂/MoSe₂. In fact, the CBM has been shifted to the B point located at the MoSe₂ layer at E_ef = 0.24 V Å⁻¹, shown in Fig. 5(f), suggesting that the type-II band alignment in the P₂/MoSe₂ heterostructure is converted to type-I at E_ef = 0.24 V Å⁻¹. When the E_ef is larger than 0.24 V Å⁻¹, the invariable bandgap of the P₂/MoSe₂ should be attributed to the insensitive B point to the applied electric field. Interestingly, for the P₂/MoSe₂ vdW heterostructure, the retained type-II heterointerface in a wide range from −0.4 to 0.24 V Å⁻¹, together with broadly tunable bandgap, will endow it with potential applications in the optoeletronics and solar energy conversion.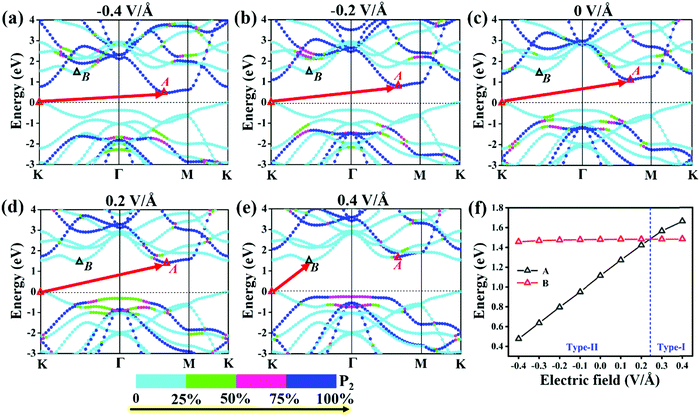

Fig. 4 (a) Schematic of double-gated P₂/MoSe₂ device. (b)Evolution of bandgap as a function of the vertical electric field in the P₂/MoSe₂ vdW heterostructure. Two insets show the positive and negative directions of the vertical electric field, respectively.

Fig. 5 (a)–(e) Projected band structures of the P₂/MoSe₂ vdW heterostructure and (f) relative positions of “A” and “B” to the VBM at PBE level under a variable electric field.

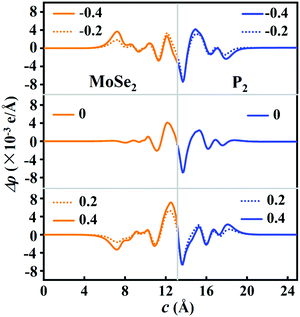
To obtain more physical insight into the P₂/MoSe₂ heterostructure, the planar-averaged electron density difference is also calculated along the c-axial direction under the E_ef, as shown in Fig. 6. When applying an enhanced positive E_ef, more electrons (Δq) flow from the P₂ layer to the MoSe₂ layer, which will generate an interlayer dipole moment P, causing the electric polarized field E_epf across the interlayer region of the P₂/MoSe₂. The direction of the E_epf points from the P₂ layer to the MoSe₂ layer, being opposite with the positive direction of the E_ef. Such an E_epf across the P₂–MoSe₂ interface is beneficial to the separation of photoexcited carriers on the interface, shown in Fig. S6 (ESI†). On the contrary, more electrons tend to transfer from the MoSe₂ layer to the P₂ layer under an increased reverse E_ef. Bader charge analysis further verifies that Δq = 1.15 × 10⁻²e, 4.9 × 10⁻³e, and −1.2 × 10⁻³e are transferred from the P₂ layer to MoSe₂ layer at E_ef = 0.4 V Å⁻¹, 0 V Å⁻¹, and −0.4 V Å⁻¹, respectively. Furthermore, the magnitude of electric polarized field (E_epf) can be estimated by E_epf = P/ε₀·ε_r·S₀·d. P is the size of the dipole moment and P = |Δq|·d, ε₀ and ε_r are the permittivity of free space and relative dielectric constant (ε₀ = 8.850 × 10⁻¹² F m⁻¹, ε_r = 1.0), respectively, S₀ is the interface area of the P₂/MoSe₂ (S₀ = 9.380 × 10⁻²⁰ m²), and d is the interlayer equivalent distance (d = 3.697 × 10⁻¹⁰ m). The calculated E_epf under different E_ef values can be found in Table S2 (ESI†). When E_ef is strengthened to 0.40 V Å⁻¹, the induced E_epf with opposite direction can be as large as 0.22 V Å⁻¹, which is comparable to the applied vertical electric field. Thus, the vertical electric field may not only effectively tailor the carrier concentrations of the MoSe₂ and P₂ layers, but also change the interlayer coupling at the P₂–MoSe₂ heterointerface.

Fig. 6 Planar-averaged electron density difference across the P₂/MoSe₂ vdW heterostructure under various electric fields of −0.4 V Å⁻¹, −0.2 V Å⁻¹, 0 V Å⁻¹, 0.2 V Å⁻¹, and 0.4 V Å⁻¹. The orange (blue) region corresponds the the MoSe₂ (P₂) layer.

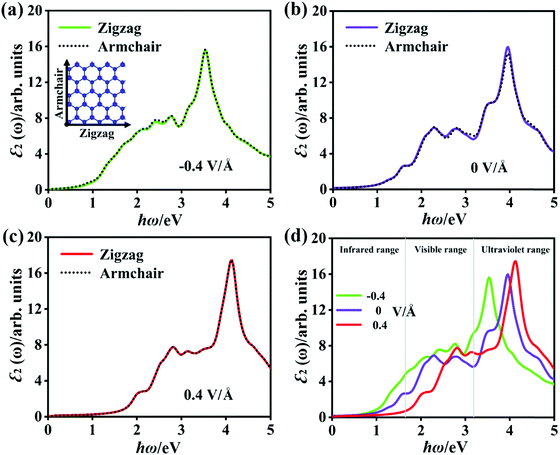
As mentioned before, there is a significant difference in the band structure of the P₂/MoSe₂ vdW heterostructure under different vertical electric fields. To further investigate the variation in the optical properties of the P₂/MoSe₂ at different electric field strengths, we calculated the ε₂(ω) of the P₂/MoSe₂ at electric fields of −0.4 V Å⁻¹, 0 V Å⁻¹, and 0.4 V Å⁻¹ and the results are plotted in Fig. 7, in which two polarized lights along the zigzag (a-axial) and armchair directions are adopted, respectively. From Fig. 7(a)–(c), strong isotropy is observed between ε₂ (zigzag) and ε₂ (armchair), suggesting that the isotropic nature of optical absorption in the P₂/MoSe₂ vdW heterostructure can be retained under the observed electric fields. When the negative electric field is applied on the P₂/MoSe₂, its absorption edge moves toward low energy (as seen in Fig. 7(d)), enhancing the optical absorption for the near-infrared and visible lights. The red-shift of the optical spectrum originates from the decrease of the bandgap of the P₂/MoSe₂ under the negative electric field, while the positive electric field pushes the absorption edge to a high-energy region due to the increase of bandgap. The blue-shift of the absorption edge results in the blue-shift of the highest absorption peak, positioned at 3.535 eV, 3.944 eV, and 4.135 eV for −0.4 V Å⁻¹, 0 V Å⁻¹, and 0.4 V Å⁻¹, respectively. Meanwhile, the intensity of the highest peak is strengthened from −0.4 V Å⁻¹ to 0.4 V Å⁻¹, suggesting that the absorption of the P₂/MoSe₂ for the near-ultraviolet light becomes more active under the positive electric field.

Fig. 7 (a)–(c) The optical absorption spectra of the P₂/MoSe₂ vdW herterostructure along the two polarized-light directions (Zigzag and Armchair) at the vertical electric fields of −0.4 V Å⁻¹, 0 V Å⁻¹, and 0.4 V Å⁻¹. The Zigzag and Armchair directions are inset. These calculated spectra have included the electron–hole interaction. (d) The comparable optical absorption spectra along the zigzag polarized-light direction (i.e. the a-axial direction) under different electric fields. A Lorentzian broadening of 0.15 eV is applied in the calculations of the optical spectra.

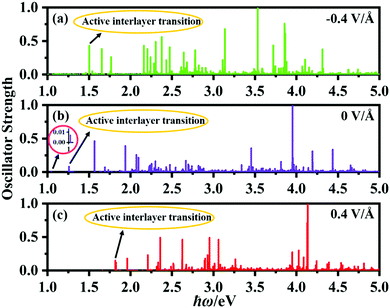
Fig. 8 shows the calculated oscillator strengths of the excited states of the P₂/MoSe₂ vdW herterostructure under the electric field of −0.4 V Å⁻¹, 0 V Å⁻¹, and 0.4 V Å⁻¹, suggesting that the vertical electric field can significantly influence the photoexcited behavior of P₂/MoSe₂. Based on the oscillator strength selection rules, we analyze the transition of P₂/MoSe₂ under the three electric fields. For the primitive P₂/MoSe₂ vdW heterostructure, the low-energy spectrum of 0–2 eV is mainly contributed by the MoSe₂ layer (as seen in Fig. 3(d)), which means that the intralayer excitons of the MoSe₂ layer dominate the low-energy spectrum. However, an active interlayer transition is also found at the energy position of about 1.26 eV, which comes from the vertical transition between the VBM and CBM at certain non-high-symmetric point T(5/18, 1/3, 0) near high-symmetric K point. The partial charge distributions of VBM and CBM at the T point can be found in Fig. S7 (ESI†), in which the VBM (CBM) is mainly contributed by the MoSe₂ (P₂) layer. Another inactive interlayer transition is also observed at about 1.05 eV although its oscillator strength is very small (as seen in the inset of Fig. 8(b)), which is mainly between the VBM and CBM at the K point. The active interlayer transition can induce the formation of an interlayer exciton (i.e. indirect exciton), whose binding energy is estimated to be 670 meV by the method of the energy difference between the quasi-particle energy and excitation energy. For the cases of −0.4 V Å⁻¹ and 0.4 V Å⁻¹, active interlayer transitions occur at 1.50 eV and 1.82 eV, respectively (marked in Fig. 8(a) and (c)), which generate two corresponding interlayer excitons. For the −0.4 V Å⁻¹, the active interlayer transition comes from the vertical transition between the VBM (MoSe₂ layer) and CBM (P₂ layer) at the K point, which is different to that of the primitive P₂/MoSe₂, while the active interlayer transition under the electric field of 0.4 V Å⁻¹ is from the VBM (MoSe₂ layer) to the second conduction band (P₂ layer) at the K point. The two observed interlayer excitons also possess considerable binding energies of 614 meV for −0.4 V Å⁻¹ and 628 meV for 0.4 V Å⁻¹, which is comparable with that of the primitive P₂/MoSe₂. These interlayer excitons found in the P₂/MoSe₂ heterostructure are beneficial to facilitate the separation of photoexcited carriers, which is very important for applications in photovoltaics and photocatalytic water splitting. On the basis of the above results, we can draw a conclusion that the bandgap of the P₂/MoSe₂ vdW heterostructure can be modulated in a broad range and its optical properties can also be tuned effectively by applying the vertical electric field.

Fig. 8 (a)–(c) Calculated oscillator strengths of excited states of the P₂/MoSe₂ vdW herterostructure in the energy range of 1–5 eV for vertical electric fields of −0.4 V Å⁻¹, 0 V Å⁻¹, and 0.4 V Å⁻¹. The polarized light is along the zigzag direction.

4 Conclusions

In summary, we performed first-principles calculations to investigate the effect of vertical electric field on the electronic and optical properties of the constructed P₂/MoSe₂ vdW heterostructure. We found that the AA-stacking P₂/MoSe₂ with more stability has an intrinsic type-II band alignment, in which photoexcited electrons (holes) migrate from the MoSe₂ (P₂) to the P₂ (MoSe₂) layer. The estimated quasi-particle bandgap can be tuned effectively from 0.94 eV (−0.4 V Å⁻¹) to 2.05 eV (0.4 V Å⁻¹) by the vertical electric field. A transition from type-II to type-I can be observed under a moderate electric field of 0.24 V Å⁻¹. More interestingly, P₂/MoSe₂ possesses a strong and broad optical absorption ranging from the near-infrared to near-ultraviolet. Under the negative electric field, the optical absorption of the P₂/MoSe₂ heterostructure for the visible and near-infrared light can be enhanced significantly. The active interlayer excitons with binding energy more than 600 meV are observed under the applied vertical electric field, being favorable to effectively separate the photoexcited electron–hole pairs. The electric field-tunable electronic and optical properties of the P₂/MoSe₂ vdW heterostructure make it a potential candidate for optoelectronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Research Fund (No. 1052931610) of Jiangsu University of Science and Technology.

References

1. C. V. Nguyen, M. Idrees, H. V. Phuc, N. N. Hieu, N. T. T. Binh, B. Amin and T. V. Vu, Phys. Rev. B, 2020, 101, 235419.
2. T. V. Vu, N. V. Hieu, H. V. Phuc, N. N. Hieu, H. D. Bui, M. Idrees, B. Amin and C. V. Nguyen, Appl. Surf. Sci., 2020, 507, 145036.
3. I. Shahid, S. Ahmad, N. Shehzad, S. Yao, C. V. Nguyen, L. Zhang and Z. Zhou, Appl. Surf. Sci., 2020, 523, 146483.
4. S. Fan, Q. A. Vu, M. D. Tran, S. Adhikari and Y. H. Lee, 2D Mater., 2020, 7, 022005.
5. Q. Lv and R. Lv, Carbon, 2019, 145, 240–250.
6. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439.
7. H. Lim, S. I. Yoon, G. Kim, A.-R. Jang and H. S. Shin, Chem. Mater., 2014, 26, 4891–4903.
8. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419.
9. X. Hong, J. Kim, S.-F. Shi, Y. Zhang, C. Jin, Y. Sun, S. Tongay, J. Wu, Y. Zhang and F. Wang, Nat. Nanotechnol., 2014, 9, 682.
10. Q. Zheng, W. A. Saidi, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, Nano Lett., 2017, 17, 6435–6442.
11. X. Niu, Y. Li, Y. Zhang, Q. Zheng, J. Zhao and J. Wang, J. Mater. Chem. C, 2019, 7, 1864–1870.
12. P. Rivera, J. R. Schaibley, A. M. Jones, J. S. Ross, S. Wu, G. Aivazian, P. Klement, K. Seyler, G. Clark, N. J. Ghimire, J. Yan, D. G. Mandrus, W. Yao and X. Xu, Nat. Commun., 2015, 6, 6242.
13. B. Miller, A. Steinhoff, B. Pano, J. Klein, F. Jahnke, A. Holleitner and U. Wurstbauer, Nano Lett., 2017, 17, 5229–5237.
14. L. Britnell, R. M. Ribeiro, A. Eckmann, R. Jalil, B. D. Belle, A. Mishchenko, Y.-J. Kim, R. V. Gorbachev, T. Georgiou, S. V. Morozov, A. N. Grigorenko, A. K. Geim, C. Casiraghi, A. H. C. Neto and K. S. Novoselov, Science, 2013, 340, 1311–1314.
15. Y. Deng, Z. Luo, N. J. Conrad, H. Liu, Y. Gong, S. Najmaei, P. M. Ajayan, J. Lou, X. Xu and P. D. Ye, ACS Nano, 2014, 8, 8292–8299.
16. P. Xiong, X. Zhang, H. Wan, S. Wang, Y. Zhao, J. Zhang, D. Zhou, W. Gao, R. Ma, T. Sasaki and G. Wang, Nano Lett., 2019, 19, 4518–4526.
17. Z. Yuan, J. Li, M. Yang, Z. Fang, J. Jian, D. Yu, X. Chen and L. Dai, J. Am. Chem. Soc., 2019, 141, 4972–4979.
18. Y.-T. Du, X. Kan, F. Yang, L.-Y. Gan and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2018, 10, 32867–32873.
19. C. Zhao, C. Yu, B. Qiu, S. Zhou, M. Zhang, H. Huang, B. Wang, J. Zhao, X. Sun and J. Qiu, Adv. Mater., 2018, 30, 1702486.
20. X. Wang, H. Li, H. Li, S. Lin, J. Bai, J. Dai, C. Liang, X. Zhu, Y. Sun and S. Dou, J. Mater. Chem. A, 2019, 7, 2291–2300.
21. W. Liu, Z. Wang, Y. Su, Q. Li, Z. Zhao and F. Geng, Adv. Energy Mater., 2017, 7, 1602834.
22. L. Huang, N. Huo, Y. Li, H. Chen, J. Yang, Z. Wei, J. Li and S.-S. Li, J. Phys. Chem. Lett., 2015, 6, 2483–2488.
23. N. Lu, H. Guo, L. Li, J. Dai, L. Wang, W.-N. Mei, X. Wu and X. C. Zeng, Nanoscale, 2014, 6, 2879.
24. L. Huang and J. Li, Appl. Phys. Lett., 2016, 108, 083101.
25. D. Chen, X. Lei, Y. Wang, S. Zhong, G. Liu, B. Xu and C. Ouyang, Appl. Surf. Sci., 2019, 497, 143809.
26. K. Rahimi, Phys. Chem. Chem. Phys., 2020, 22, 7412–7420.
27. S. Gao, L. Yang and C. D. Spataru, Nano Lett., 2017, 17, 7809–7813.
28. Y. Li, J.-K. Qin, C.-Y. Xu, J. Cao, Z.-Y. Sun, L.-P. Ma, P. A. Hu, W. Ren and L. Zhen, Adv. Funct. Mater., 2016, 26, 4319–4328.
29. S. Tongay, J. Zhou, C. Ataca, K. Lo, T. S. Matthews, J. Li, J. C. Grossman and J. Wu, Nano Lett., 2012, 12, 5576–5580.
30. J. S. Ross, S. Wu, H. Yu, N. J. Ghimire, A. M. Jones, G. Aivazian, J. Yan, D. G. Mandrus, D. Xiao, W. Yao and X. Xu, Nat. Commun., 2013, 4, 1474.
31. M. Bernardi, M. Palummo and J. C. Grossman, Nano Lett., 2013, 13, 3664–3670.
32. B. Chamlagain, Q. Li, N. J. Ghimire, H.-J. Chuang, M. M. Perera, H. Tu, Y. Xu, M. Pan, D. Xaio, J. Yan, D. Mandrus and Z. Zhou, ACS Nano, 2014, 8, 5079–5088.
33. J. L. Zhang, S. Zhao, C. Han, Z. Wang, S. Zhong, S. Sun, R. Guo, X. Zhou, C. D. Gu, K. D. Yuan, Z. Li and W. Chen, Nano Lett., 2016, 16, 4903–4908.
34. J. Guan, Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 113, 046804.
35. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
36. B. Ghosh, S. Nahas, S. Bhowmick and A. Agarwal, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115433.
37. J. Xiao, M. Long, X. Zhang, J. Ouyang, H. Xu and Y. Gao, Sci. Rep., 2015, 5, 9961.
38. A. Ramasubramaniam, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115409.
39. D. Kozawa, A. Carvalho, I. Verzhbitskiy, F. Giustiniano, Y. Miyauchi, S. Mouri, A. H. Castro Neto, K. Matsuda and G. Eda, Nano Lett., 2016, 16, 4087–4093.
40. E. M. Alexeev, D. A. Ruiz-Tijerina, M. Danovich, M. J. Hamer, D. J. Terry, P. K. Nayak, S. Ahn, S. Pak, J. Lee, J. I. Sohn, M. R. Molas, M. Koperski, K. Watanabe, T. Taniguchi, K. S. Novoselov, R. V. Gorbachev, H. S. Shin, V. I. Fal’ko and A. I. Tartakovskii, Nature, 2019, 567, 81–86.
41. P. K. Nayak, Y. Horbatenko, S. Ahn, G. Kim, J.-U. Lee, K. Y. Ma, A.-R. Jang, H. Lim, D. Kim, S. Ryu, H. Cheong, N. Park and H. S. Shin, ACS Nano, 2017, 11, 4041–4050.
42. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
43. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
46. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2005, 95, 109902.
47. L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304.
48. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
49. L. Hedin, Phys. Rev., 1965, 139, A796–A823.
50. E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232.
51. M. Rohlfing and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944.
52. A. Marini, C. Hogan, M. Grüning and D. Varsano, Comput. Phys. Commun., 2009, 180, 1392–1403.
53. T. Böker, R. Severin, A. Müller, C. Janowitz, R. Manzke, D. Voß, P. Krüger, A. Mazur and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235305.
54. M. M. Ugeda, A. J. Bradley, S.-F. Shi, F. H. da Jornada, Y. Zhang, D. Y. Qiu, W. Ruan, S.-K. Mo, Z. Hussain, Z.-X. Shen, F. Wang, S. G. Louie and M. F. Crommie, Nat. Mater., 2014, 13, 1091–1095.
55. A. J. Bradley, M. M. Ugeda, F. H. da Jornada, D. Y. Qiu, W. Ruan, Y. Zhang, S. Wickenburg, A. Riss, J. Lu, S.-K. Mo, Z. Hussain, Z.-X. Shen, S. G. Louie and M. F. Crommie, Nano Lett., 2015, 15, 2594–2599.
56. C. E. P. Villegas, A. S. Rodin, A. Carvalho and A. R. Rocha, Phys. Chem. Chem. Phys., 2016, 18, 27829–27836.
57. The AM 1.5G Spectrum Was Taken from the NREL Website: http://Rredc.Nrel.Gov/Solar/Spectra/Am1.5 and Integrated with the Trapezoid Rule.
58. Y. Gong, J. Lin, X. Wang, G. Shi, S. Lei, Z. Lin, X. Zou, G. Ye, R. Vajtai, B. I. Yakobson, H. Terrones, M. Terrones, B. K. Tay, J. Lou, S. T. Pantelides, Z. Liu, W. Zhou and P. M. Ajayan, Nat. Mater., 2014, 13, 1135–1142.
59. B.-J. Wang, X.-H. Li, R. Zhao, X.-L. Cai, W.-Y. Yu, W.-B. Li, Z.-S. Liu, L.-W. Zhang and S.-H. Ke, J. Mater. Chem. A, 2018, 6, 8923–8929.
60. B.-J. Wang, X.-H. Li, X.-L. Cai, W.-Y. Yu, L.-W. Zhang, R.-Q. Zhao and S.-H. Ke, J. Phys. Chem. C, 2018, 122, 7075–7080.
61. N. A. Lanzillo, A. J. Simbeck and S. K. Nayak, J. Phys.: Condens. Matter, 2015, 27, 175501.
62. F. Ceballos, M. Z. Bellus, H.-Y. Chiu and H. Zhao, ACS Nano, 2014, 8, 12717–12724.
63. S. Tongay, W. Fan, J. Kang, J. Park, U. Koldemir, J. Suh, D. S. Narang, K. Liu, J. Ji, J. Li, R. Sinclair and J. Wu, Nano Lett., 2014, 14, 3185–3190.
64. M.-H. Chiu, M.-Y. Li, W. Zhang, W.-T. Hsu, W.-H. Chang, M. Terrones, H. Terrones and L.-J. Li, ACS Nano, 2014, 8, 9649–9656.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00413h

---