Open Access Article
Open Access ArticleNanoparticles shape-specific emergent behaviour on liquid crystal droplets†
Zeynep
Sumer
 and
Alberto
Striolo
and
Alberto
Striolo
 *
*
Department of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: a.striolo@ucl.ac.uk
First published on 9th December 2019
Abstract
Self-assembly attracts enormous research attention because it is at the core of important applications ranging from medical treatments to renewable energy production. Among several classes of self-assembling materials, liquid crystals (LCs) and nanoparticles yield ordered structures under well-defined thermodynamic conditions and could yield supra-molecular aggregates, respectively. In this work, nanoparticle self-assembly on LC nano-droplets is investigated. The LC nano-droplets act as templating agents on which homogeneous and Janus nanoparticles of various geometrical features are adsorbed. LC mesogens and water have low mutual solubility, and under the conditions chosen the LCs yield bipolar nano-droplets. Particle self-assembly on oil nano-droplets is also considered for comparison. Our results reveal that the mesogens can direct the assembly of the nanoparticles. This effect is mainly governed by the nanoparticle size and shape. In some cases, strong evidence of emergent behaviour is observed depending on entropic forces that arise because of the shape and patchiness of the nanoparticles. For example, while one small spherical homogeneous particle does not show preferential adsorption on specific LC nano-droplet locations, 100 spherical nanoparticles preferentially agglomerate at the nano-droplet boojums, providing evidence of emergent behaviour. On the contrary, Janus spherical nanoparticles do not show such a strong emergent behaviour. Cylindrical NPs manifest the opposite trend: while homogeneous nano-cylinders do not exhibit orientational order on the LC nano-droplet, Janus ones either locate at the LC nano-droplet boojums or orient towards the direction vector of bipolar droplets. Quantification of the orientational order within the LC nano-droplets suggests that the self-assembly of the LC mesogens does not significantly change upon nanoparticle adsorption. These simulations clearly suggest an interplay between nanoparticle size, shape and chemical composition upon their self-assembly on LC nano-droplets. The results could be helpful for the design of new sensors and for the directed self-assembly of advanced materials.
Design, System, ApplicationSelf-assembly of liquid crystals (LCs) is crucial for a variety of high-end applications ranging from sensors to displays. Towards designing supra-molecular aggregates for such applications, it is crucial to better understand nanoparticle (NP)–LC interactions. Yet, this area is not yet fully explored by either theoretical or experimental studies. To aid future system design and engineering for such systems, we conducted computational studies to quantify the molecular driving forces responsible for the collective behaviour of LC molecules in the presence of NPs. We focused on NPs with different shapes, sizes, and chemical functionalities. LC droplets dispersed in aqueous medium were considered as templates for guiding the self-assembly of the NPs. The LC droplets were prepared in the bipolar nematic phase. Our results yield a comprehensive map of NP–LC interactions at the nanoscale, revealing that the NP shape could be equally important as NP size in driving assembly. In addition, our results show that the chemical functionality, in particular homogeneous vs. Janus NPs, have strong effects on the NP assembly on the LC droplets. The results suggest that a balance among different driving forces is essential to develop advanced supra-molecular devices. |
1. Introduction
The spontaneous organization of matter has yet to be fully understood despite the fact that controlling the assembly of materials that vary in size and shape over multiple length scales could enable advancements in science and technology. Among other self-assembling structures, nanoparticles and liquid crystals could be used, e.g., in optical devices and pharmaceuticals.1,2 In these and other futuristic applications, such nano-sized elements could provide the building blocks for supra-molecular engineered materials.3We consider here two classes of self-assembling materials: nanoparticles (NPs) and liquid crystals (LCs). Many have documented how NPs can show various degrees of self-assembly, depending on the particle morphology and on the system thermodynamic conditions.4–11 Bulk NP self-assembly has been investigated12–14 as well as NP self-assembly onto interfaces.15–19 LCs provide the foundation for mature electronic applications20 as well as for putative applications as chemical sensors, bacterial detectors, and so forth.21,22 In such multi-component systems, the LC behaviour depends on system composition, the presence of emulsions, temperature and other thermodynamic conditions.23
When NPs and LCs are simultaneously present, interesting features emerge, in which NPs and LCs guide each other's self-assembly, yielding sometimes unexpected results. For example, de Pablo and co-workers suggested that NP-covered LC droplets could lead to functional patchy particles and sensing devices,24 and very recently, Kumacheva and co-workers investigated the morphogenesis of LC droplets at increasing particle content within cholesteric (Ch) LC droplets doped with cellulose nanocrystals (CNCs).25 The results suggested that Ch-CNC droplets affect the particle alignment and vice versa. The size dependency of the results was also discussed.26 De Pablo and co-workers reported that small NPs do not manifest a preferred adsorption site on LC droplets, while large NPs prefer boojums, which are defect regions on the LC droplet surfaces and therefore act as attractive wells for the NPs.24 Defects are inevitable on LC droplets, and because such defects could yield natural templates for smaller molecules or crystals such as copolymers or particles to adsorb on, they might be useful for developing future technological applications. Others considered LC-in-LC colloids by utilizing droplets of cholesteric CNC phases27 or hybrid colloidal fluids of biaxial phases.28
In this work, we report a systematic study on LC nano-droplets on which NPs of different sizes, shapes and chemistry are adsorbed, with particular emphasis on self-assembly. We consider NPs of different sizes and shapes as well as surface chemistry. To enable a meaningful comparison, we modelled NPs similar in size and roughness but different in shape. To better interpret the results in light of literature observations, it is beneficial to classify colloidal particles based on anisotropy. Thus, NPs are categorically identified as spheroids (discs and ellipses), spheres, rods, faceted polyhedra, branched structures and colloidal molecules, patterned or not.29 In our study, six shapes were considered: discs, ellipses, spheres, cylinders, cubes, and stars. For each NP shape, we simulated both homogeneous and Janus particles,30 given the increasing importance of patterned particles in the field. Other criteria can be used to classify nanomaterials, e.g., anisotropy dimensions, patch size, curvature radius and so forth.9 These characteristics change for the NPs considered in this work because of the different shapes simulated. When comparing NPs of different shapes, we ensured that the NP volume and bead density were maintained constant.
In our simulations, the NPs were introduced within systems in which nano-droplets of nematic LC molecules were dispersed in a water medium. Our simulations differ from most of those available in the literature for similar systems because the latter tend to constrain LC and NPs within simulation boxes of spherical geometry. Our systems are designed to explicitly and realistically consider LC droplets dispersed in an aqueous solvent to attempt filling two gaps in the literature: (i) our simulations are meant to complement experiments by providing information regarding the local structure of NPs in contact with LC molecules and by analyzing how such structure changes when interactions change, and (ii) our simulations are meant to complement continuum-level analysis, which is intrinsically applicable to large systems as well as other simulations available in the literature, in which LC molecules and NPs are both constrained within spherical cavities. Our analysis focused on the self-organisation of the NPs on the LC droplets. The results showed that the NP shape is an important descriptor of the NPs' collective behaviour on the droplet surfaces: NPs might form smectic structures on the droplets' equators or assemble at the boojums, depending on their shape. Our results show that NP adsorption does not cause a significant alteration from the bipolar alignment of LC molecules within the droplets. Indeed, only minor changes in nano-droplet asphericity and orientational orders are observed as a function of NP surface density.
The remainder of this manuscript is organised as follows: in section 2 we describe the simulation details as implemented in this work. In section 3 we show representative results, focusing on the effects of NP shape and size on self-assembly. The behaviour of individual particles is also quantified and compared to that of a larger number of NPs on the LC nano-droplets which allows us to highlight emergent phenomena relevant for self-assembly. In section 4 we summarize our main conclusions, and we comment on their possible relevance for practical applications and future research.
2. Models
2.1. Nanoparticles and liquid crystal mesogens
The simulations presented here are conducted within a coarse-grained representation. Details regarding the models implemented for describing water and LC mesogens are reported elsewhere.31,32 In short, in our coarse-grained representation, one water ‘bead’, indicated with W in what follows, represents 5 water molecules (i.e., the degree of coarse graining was set equal to 5). The LC mesogens are rod-like molecules composed of 6 beads connected with a harmonic spring. Within these molecules, bond length [Ebond = kbond × (r − r0)2] and bond bending [Eangle = kangle × (θ − θ0)2] potentials are implemented to maintain rigid rod-like structures. In our implementation, r0 = 0.6, θ0 = 180°, kbond = 100kBT/r2, and kangle = 100kBT. These parameters yield rather rigid LC molecules, whose phase diagram in the bulk was described elsewhere.31In this work, we considered nanoparticles of six different shapes, and for each NP shape, two NP sizes were simulated. In Fig. 1, we provide schematic representations for shapes and sizes of the ‘small’ NPs used here. The NPs considered are spheroids (i.e., oblate and prolate ellipsoids), spheres, cylindrical rods, cubes, and star-shaped. The volume of each small NP ranges between 3.7 and 5.4r3. Each NP is composed of different beads: rod-shaped NPs contain 112 beads, star-shaped NPs contain 154 beads, and each of the other NPs contain 125 beads. The density of beads within the volume of the NPs is in the range 23.1–33.0 beads per r3. To test the effect of particle size, we considered also ‘large’ NPs. In these simulations, because of computing power limitations only one NP was simulated on one LC droplet. To generate the ‘large’ NPs, the dimensions shown in Fig. 1 were increased three-fold. Following our prior work, the large NPs were hollow. Surface bead density and roughness were maintained constant among the large NPs.
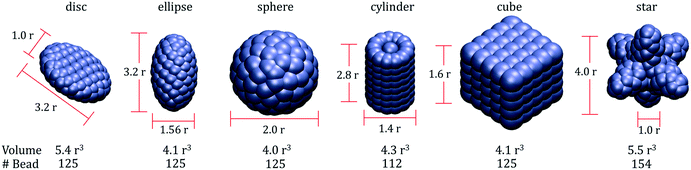 | ||
| Fig. 1 Sizes and volumes of the ‘small’ nanoparticles (NPs) modelled in this work. Left to right: disc, ellipse, sphere, rod, cube and star-shaped NPs. | ||
When modelling LCs, it is important to be able to differentiate between different structures. Following conventional simulation approaches, the order of LC molecules was quantified by the orientational order parameter (S). As we discussed in our previous studies,31,32S is calculated by the ensemble average of the traceless second-rank tensor (Q) for each molecule that is considered an integral part of a LC nano-droplet:
 | (1) |
2.2. Simulation details
The simulations were conducted by implementing the dissipative particle dynamics (DPD) algorithm in the LAMMPS software package.34,35 The NVE ensemble was implemented, with integration time Δt = 0.01τ, corresponding to ∼14.9 ps.32 Each simulation run included 3 × 106 steps, the last 106 of which were considered part of the production run and were used for analysis. In other words, out of the 0.447 μs of each simulation, the last 0.149 μs were considered for generating the results presented here. During the production phase, one system configuration (i.e., one frame) was recorded at 0.0149 μs intervals, yielding 100 frames for the system. The protocols implemented for data collection were described previously.32 For pulling/pushing of NPs (described in section 3.3) we implemented the software PLUMED.36The results presented in sections 3.1 and 3.2 were obtained for systems in which one LC nano-droplet was present, of radius ∼13.6r. In these simulations, 100 NPs were inserted per simulation, the system density was 3.03 ± 0.01 bead per r3, the temperature 0.62–0.63kBT, and the pressure ∼17.10 ± 1.17kBT/r3. Fluctuations in temperature and pressure are caused by the presence of rigid structures in the systems. In these simulations, the fluid was characterised by pressures and temperatures of ∼20.66 ± 0.08kBT/r3 and ∼0.62kBT, respectively. The results presented in section 3.3 were obtained for systems with density ∼2.85 ± 0.002 bead per r3, temperature ∼0.62kBT, and pressure ∼19.94 ± 0.03kBT/r3.
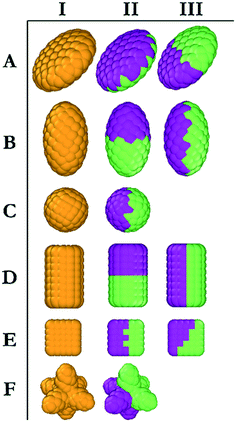
In DPD, repulsion coefficients, αij, determine the strength of the conservative force between beads i and j. To discuss the interaction parameters, we refer to Fig. 2, in which homogeneous and Janus NPs are represented schematically. The NPs shown in yellow (column I in Fig. 2) were described by moderate repulsive interactions with both water beads and LC beads. In this case, NP/water and NP/LC interactions were described by αij = 35kBT/r. For Janus particles (columns II and III in Fig. 2), we increased the conservative repulsive forces between the medium and the corresponding side of the nanoparticle. Explicitly, purple (hydrophilic) NP beads interacted with water and LC beads via potentials described by αij = 25 and αij = 50kBT/r, respectively; green (hydrophobic) NP beads interacted with water and LC beads via interactions described by αij = 50 and αij = 10kBT/r, respectively. The DPD parameterization is completed by imposing αij = 50kBT/r among beads of different types and αij = 25kBT/r among beads of the same type. This parameterization ensures conditions of low mutual solubility between LCs and water.32 Each system was simulated three times with different initial configurations. Equilibration was considered achieved when the same density profiles were observed. Further confirmation that equilibration was achieved was attained via visual analysis. In fact, the final simulation snapshots obtained from three independent simulations of the same system showed the same alignment among the simulated NPs, which constitutes the body of results presented in the remainder of the manuscript.
3. Results and discussion
3.1. Self-assembly of nanoparticles on nano-droplets (LC and oil)
In this section, we investigate the collective self-assembly of ‘small’ nanoparticles (see Fig. 1 for their dimensions) adsorbed on nano-droplets. We compared LC and oil nano-droplets, although the discussion focuses on LC droplets. The results obtained on oil droplets are reported in the ESI.† The NPs considered are shown in Fig. 2, and they are named based on the row and column within which they are located in this figure. To conduct these simulations, we added disc (A), ellipse (B), sphere (C), rod (D), cube (E) and star (F) NPs to simulation boxes in which one nano-droplet was pre-equilibrated. For each NP, we considered homogeneous (type I) and Janus NPs; in some cases, two types of Janus NPs were prepared for a given NP shape (type II and III, respectively). In total, we prepared 16 NPs of similar volumes and bead densities. In each simulation, 100 NPs of the same type are added to a water/LC droplet system. The system containing the LC droplet immersed in water was characterised in our prior work. For the present study, we chose droplets of radius 13.6r.32In Fig. 3(right), we represent the last frame of each simulation for each of the simulated systems to provide a visual summary of the results. The molecular coordinates representative of these frames are provided in the ESI.† To quantify the results, we compute the density profile of the NP center as a function of the distance from the center of the LC nano-droplet. The results are reported in Fig. 3(left). In this representation, the LC nano-droplet surface is located at radial distances 13.6–15.6r from the nano-droplet center. This region is identified in Fig. 3 by two vertical lines, which allows us to compare results on different systems. Below we summarise the results obtained for 16 different NPs in total.
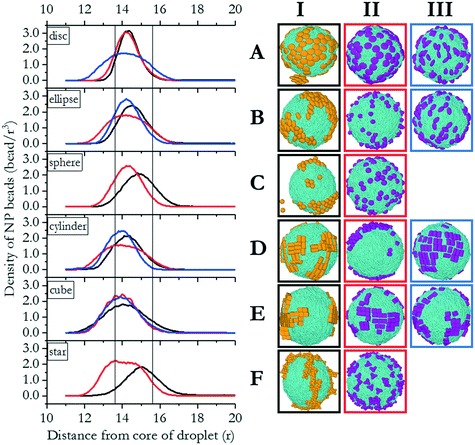 | ||
| Fig. 3 Left: density profiles of NP beads with respect to the distance from the droplet core. Lines in the graph indicate the interface, located at radial distances in the range between 13.6 and 15.6r. Right: corresponding snapshots of LC droplets with disc, ellipse, sphere, rod, cube and star shaped nanoparticles (A–F), respectively. In the ESI† we provide coordinates for the various systems summarised in this figure. | ||
The results obtained for prolate ellipsoids (group B NPs in Fig. 2) are also shown in Fig. 3. We observed that homogenous ellipse particles (B.I) were not homogeneously distributed on the droplet surface. They rather form surface clusters within which the NPs remain parallel to the droplet direction vector. Experimental data showed that spheroids with different aspect ratios yield honeycomb structures on two-dimensional surfaces.37 Honeycomb structures were observed in our simulations as well. Additionally, NPs oriented along the direction of LC molecules in the droplet. Our results suggest that the orientation of the ellipsoids adsorbed on the LC nano-droplets could be manipulated by the preferred orientation of the mesogens. In our simulations, the droplet boojums function as poles and the ellipsoidal NPs are distributed on the droplet surface as compass needles. This feature, however, is lost when Janus spheroidal NPs are considered (i.e., see B.II NPs in Fig. 3). The latter NPs were observed to be randomly distributed over the droplet surface. Since these NPs are adsorbed normal to the droplet surface, their orientation could not be quantified. Due to deeper penetration within the droplet surface, B.II NPs show a wider peak in the density profiles shown in Fig. 3 because of density fluctuations in the radial direction. Ellipsoidal B.III NPs, on the other hand, manifest similar orientation to the B.I NPs, although B.III NPs do not assemble in clusters as B.I NPs tend to do. As a consequence, the density profiles obtained for B.I and B.III NPs are similar and narrower than those obtained for B.II NPs. The results also show that ellipsoidal B.III NPs are oriented parallel to the direction vector of the LC droplet, similar to the results described for A.III NPs. This is further evidence that shape-dependent entropic forces yield a patterned alignment that does not exist when the B.III NPs adsorb on oil droplets (Fig. S1†).
The simulation results shown in Fig. 3 also show, contrary to our expectations, that for Janus spherical NPs (type C.II in Fig. 2), neither clustering and preferential localization at the boojums occurred. This was observed both on LC and oil droplets, in both of which the density profiles were also similar. These observations suggest that effective NP–LC interactions at the droplet could strongly affect the NP self-assembly, perhaps overcoming the energetic and entropic advantages of accumulating on the boojums.
It is perhaps interesting to observe that for small spheroidal (discs and ellipsoids) and small spherical NPs, NP clustering was achieved when the NPs were chemically homogeneous, and that in all cases honeycomb structures were obtained, which is coherent with previous findings.19,37,38 Due to more attractive NP–LC interactions than NP-NP ones, spherical Janus NPs distributed rather uniformly on the droplet surface.
In the following sections we quantify the behaviour of NPs that yield smectic order on the LC nano-droplet surface: cylindrical and cubic NPs.
When cylindrical Janus NPs had their two faces vertically separated, as in D.III NPs, they preferentially adsorbed on the LC droplet equator rather than the boojums. Although they have the same aspect ratio as D.II NPs, their morphology caused a much shorter attractive region on the LC nano-droplet, and the D.III NPs could not penetrate the droplet surface. In this case, the LC molecules clearly acted as templating agents and directed the NPs to be parallel to the droplet direction vector. The templating properties of rigid LC molecules cause the preferential orientation for D.III NPs, just as they did for A.III NPs. As in the case of A.III NPs, we ascribed these results to entropic patchiness of D.III NPs. However, it should be noted that this alignment was not observed for D.I NPs. The combination of these results suggests that moderate attraction between LC mesogens and rod-like NPs (D.I) did not induce ordering, and the NPs clustered on the droplet surface with no preferential orientation. The Janus D.III NPs, on the other hand, oriented parallel to the LC molecules. On the contrary, highly attractive interactions caused D.II NPs to penetrate through the droplet surface and accumulate at the droplet boojums.
Homogeneous cubic NPs (particles E.I in Fig. 3) yield clusters on the LC nano-droplet surface. These NP clusters preferentially locate on the equator, similarly to what was observed for cylindrical D.I NPs. However, because, as opposed to nano-rods, E.I particles have equal length in all directions, the preferential orientation they exhibit cannot be ascribed to their anisotropic shape. Glotzer and co-workers reported that perfect spherical particles prefer to assemble within the fcc crystal structure, whereas perfect cubes prefer simple cubic structures.9 We observed the same behaviour on LC droplets, with cubic NPs yielding clusters on the droplet surface that arrange in a simple cubic form.
Janus cubic particles (E.II and E.III NPs) yield smaller clusters than those formed by E.I NPs, but the behaviour is similar. Although E.II NPs are cubically faceted and E.III NPs are tetrahedrally faceted once they became Janus NPs, they did not exhibit strong differences in their surface alignment. Morphological differences between E.II and E.III NPs did not cause any observable difference among the NP self-assembled structures, as can be seen in Fig. 3.
Our analysis reveals that NPs with facets, e.g., cylinders and cubes, achieve smectic order on the LC nano-droplet surface. This is consistent with literature reports in which experiments were conducted to study the self-assembly of gold nanorods with high aspect ratio37 and that of 2D perovskite nanoplatelets.41 In addition to what was available in the literature, our simulation results suggest that the interactions with LC molecules, which create the driving forces, determine where NPs accumulate on the surface of LC nano-droplets. The NP morphology, on the other hand, creates the entropic forces that dictate whether NPs self-assemble yielding a directional order. As was previously reported, entropic patchiness plays a contribution towards the preferential orientation of NPs, where the enthalpic interactions are the dominating force.9 This explains why LC molecules do not always affect the location and orientation of NPs but can act as a template under specific conditions.
The results summarised in Fig. 3 showed that enthalpy-driven molecular mechanisms drive the NPs to be preferentially adsorbed at the LC nano-droplet boojums or in other locations. It is worth pointing out that small NPs with the same shape can yield different behaviour due to morphologically different LC-attractive regions exposed on their surface. Most homogeneous NPs considered here show similar behaviour when they are adsorbed on LC droplets as they do on flat LC interfaces. For example, they yield smectic order or honeycomb structures, depending on their morphology. In addition, some of the NPs considered here show preferential adsorption on the LC droplet equatorial regions and do not move towards the boojums, even though the topological defects are accumulated at the boojums. Bead-to-bead interactions between nanoparticles and LC molecules are important in determining the preferential NP adsorption location on the droplet surface, as the NP size and shape are. When moderate attractions are present, NPs may or may not preferentially adsorb on the droplet tips (this is evident for homogeneous NPs). When strong attractions are present, NPs might prefer to assemble side-to-side with LC molecules, yielding parallel orientation along the LC droplet meridians. In such situations, it appears that NP–LC interactions dominate size and shape effects. Namely, once the enthalpy-driven preferential adsorption occurs, entropic forces affect the NP orientation. This effect is very distinct on elongated NPs (e.g., ellipsoidal and cylindrical ones, as well as Janus discs), which orient along the droplet directional vector.
3.2. NP effects on LC mesogen self-assembly
In this section, we investigate how NP assemblies affect the orientation of LC mesogens within the droplets. In our prior report, the properties of LCs in the absence of NPs were quantified.32 In summary, LC molecules in water formed a droplet that is bipolar and in the nematic phase. The droplet size chosen for this study was small enough to allow for meaningful simulations to be completed, yet larger than a molecular cluster. The temperature used in the present simulations was chosen so that the droplet was nematic, yet with sufficient molecular mobility to achieve equilibrated systems.32To quantify how the NPs affect the LC orientation, in Fig. 4 we show pictorially the probability distributions of LC molecules with respect to their location within the nano-droplet and second-rank tensors (Q). The algorithm for the calculation of the second-rank tensor is defined in section 2.1. For reference, in Fig. 4 we report results obtained for the LC nano-droplet with no adsorbed NPs, so that the effect of NP adsorption can be quantified by comparison. For brevity, in Fig. 4 we consider only NPs from group I in Fig. 3, i.e., homogenous NPs. This is because the results are similar to those reported in Fig. 4 for the corresponding homogeneous NPs and are provided in the ESI.† Analysis of the simulation results shows that the NPs have a slight impact on the order of the LC mesogens. When such an effect is observed, it always remains local, specifically on the droplet surface, i.e., NP adsorption does not affect the LC order throughout the whole droplet. At the core of the liquid droplets, almost no LC molecules show a second-rank tensor lower than 0.4 in any of the systems considered. This indicates that all LC molecules are oriented in nematic, almost smectic structures. As we move towards the nano-droplet surface, the results suggest that most of the LC mesogens remain parallel to the direction vector, although the number of LC molecules that are tilted or perpendicular increases from core to surface. These results are similar for all the nanoparticle types considered. Exceptions are observed for D.I and E.I NPs (cylinders and cubes, respectively), in which case the results suggest that the NPs interact with the smectic alignment of LC mesogens on the nano-droplet surface. In fact, the results in Fig. 4 suggest that these NPs cause a slightly higher probability of observing the second-rank tensor of 1.0 near the droplet surface. As explained above, entropic effects probably cause the NPs to interact with the LC mesogens, in qualitative agreement with observations from the literature,42 and the results in Fig. 4 suggest that a synergistic phenomenon is taking place, with the NPs orienting because of the LCs, but vice versa, the NPs also templating further LC alignment.
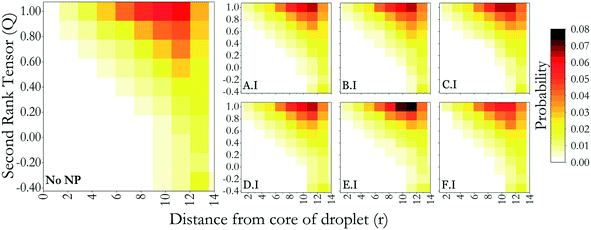 | ||
| Fig. 4 Probability distributions of LC mesogens with respect to their locations and second-rank tensors, for pristine LC droplets and for LC droplets that were exposed to group I NPs, as shown in Fig. 2. Similar results for group II and III NPs are provided in the ESI.† | ||
The global orientational order for all LC droplets considered in Fig. 4 varies between 0.55 and 0.63, as indicated in Fig. 5(a). This means that all droplets are nematic, with orientational order. Upon NP adsorption, the LC droplets remain bipolar, although slight deformations were observed. The droplets with adsorbed NPs showed shapes ranging from perfectly spherical to slightly elongated droplets. To quantify the droplet deformation, we calculated the asphericity. The asphericity quantifies the shape deviation from a perfect sphere, with 0 denoting such a perfect sphere.32 Asphericity values are given in Fig. 5(a). The asphericity of the droplet with no NPs adsorbed was 0.23 ± 0.04. The highest asphericity value was obtained for LC droplets with adsorbed E.I NPs (i.e., 0.28 ± 0.03) followed by LC droplets with adsorbed D.I NPs (i.e., 0.22 ± 0.02). For reasons that were explained in Fig. 4, the E.I and D.I NPs have stronger interactions with the LC droplets, resulting in droplet deformations. The smallest LC droplet asphericity was observed when star-shaped NPs (F.I) adsorbed, yielding an asphericity of ∼0.14 ± 0.03. In general, when NPs other than those with facets adsorb, the asphericity of the LC droplet decreases compared to values obtained for the LC droplet with no NPs.
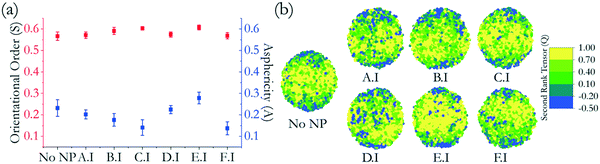 | ||
| Fig. 5 (a) Orientational orders (square) and asphericity (sphere) and (b) map of LCs on droplets color-coded by their second-rank tensor that were exposed to group I nanoparticles. Groups II and III are provided in the ESI.† | ||
To relate the change in second-rank tensor with respect to the location of the LC molecules on the droplet, we draw color-coded maps in Fig. 5(b). The results show that the orientation changes from parallel to perpendicular as we move from the equator to the boojums of the droplets. The yellow portion of the droplet represents the mesogens that are almost parallel to the direction vector located in the equatorial region. The dark blue regions, located near the boojums, represent the mesogens that are almost perpendicular to the direction vector, pointing to the droplet tips. Such an assembly is consistent with planar anchoring with water molecules, as reported previously.24 Some of the results in Fig. 5(b), for example, those for A.I and D.I NPs, show that some LC mesogens locally changed orientation from parallel to perpendicular in the equatorial region (see blue dots). This is the local effect due to NP adsorption. The results in Fig. 5 suggest that no significant change occurred in the orientation of the LC molecules upon NP adsorption, although slight shape deformations took place, as described in Fig. 5(a). Li et al., surveying experimental results, suggested that often liquid crystalline ordering is insensitive to colloidal assembly, although this is not the case when the NPs are able to penetrate into LC droplets.25 Our results are consistent with this observation, as the simulated NPs affect the orientation of LC molecules locally, but this effect is not strong enough to change the global orientational order within the droplets.
3.3. Effect of NP size
The results presented in sections 3.1 and 3.2 were obtained for NPs whose size is comparable to the length of one LC mesogen (‘small’ NPs in the nomenclature implemented herein). We concluded that when multiple NPs adsorb on one LC droplet, emerging phenomena can occur, depending on the NP features, with, in some cases, preferential adsorption sites and alignment between adsorbed NPs being observed. Because previous research revealed that spherical nanoparticles preferentially locate at the boojums of biaxial LC droplets if they are large enough,24 in this section we systematically investigate the effect of NP size. We simulated NPs whose features are shown in Fig. 2, maintaining the same aspect ratios used to prepare the NPs simulated in Fig. 3, yet increasing the NP size three times along each dimension. To put these changes in perspective, the LC droplet-to-NP volume ratio was ∼2500 in section 3.1, while it is ∼90 for the systems discussed in section 3.3. Because of computing power limitations, we studied only 1 NP adsorbed on one LC nano-droplet. Focusing on a single NP offers the added benefit of more clearly identifying size-dependent properties for NP-droplet self-assembly, as emergent phenomena such as those highlighted for small NPs, which might appear should multiple NPs be simulated, could hinder the interpretation of the simulation results. By systematically investigating NPs of different shapes and chemical features (i.e., homogeneous vs. Janus), our results highlight the ability of LC nano-droplets to template the preferential adsorption of particles depending on NP size, shape and surface properties.To ensure that the results presented are representative of truly equilibrated states, we conducted additional analyses, which are discussed in the ESI.† The algorithm is shown schematically in Fig. 6. From the final configuration obtained from one typical DPD simulation run (left in Fig. 6) we used a pulling algorithm to desorb the Janus particle from the interface. Then, we dislocated the NP along the aqueous phase until it was above a different region of the LC droplet (middle in Fig. 6), and we allowed it to adsorb again on the droplet. Additional equilibrium simulations (3 million additional steps) were then conducted to test whether the NP would return to the original preferential location (right in Fig. 6). This test was conducted for Janus NPs, and the results suggested that the simulations discussed below had indeed reached equilibrium. Only Janus NPs were used for this test because only these NPs showed preferential adsorption on defined locations on the droplet surface. At the end of the algorithm summarised in Fig. 6, the results showed that the NPs that had shown preferential adsorption at the droplet tips (B.II, D.II, and F.II NPs) moved back to the tips after manipulation. The NPs that moderately prefer boojums also moved back towards these locations (A.II, A.III, and C.II). The other NPs remained within the equatorial region of the LC nano-droplets (B.III, D.III, E.II and E.III). Details of these simulations can be found in the ESI.†
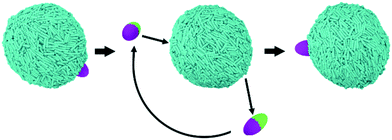 | ||
| Fig. 6 Schematic representation of the algorithm implemented to test whether the DPD simulations discussed below for ‘large’ NPs adsorbed on LC droplets had reached equilibrium. Further details are provided in the ESI.† | ||
In Fig. 7 the results obtained for the simulation of single ‘large’ NPs adsorbed on LC nano-droplets are summarised. In this figure, we report the last frames of our simulations. In what follows we discuss the results for each NP morphological feature.
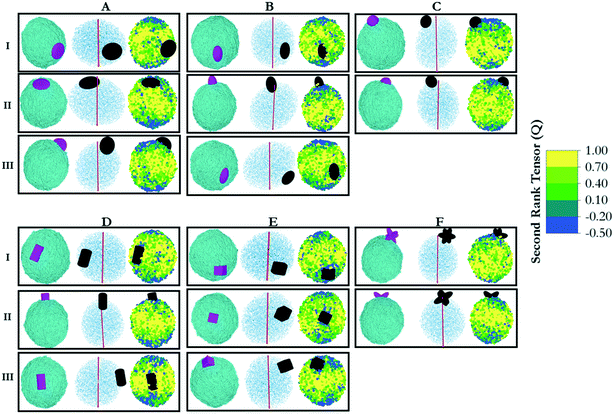 | ||
| Fig. 7 (Left) Simulation snapshots of droplets with large particles, (middle) their representation with direction vectors and (right) colour-coded LC molecules with respect to their second-rank tensor (Q). Each panel title represents the corresponding NP in the notation shown in Fig. 2 for disc, ellipse, sphere, rod, cube and star shaped nanoparticles (A–F), respectively. | ||
The results obtained for group B NPs (ellipsoids) show that B.I and B.III NPs are excluded from the polar regions, while B.II NPs preferentially assemble at the droplet tip. Homogeneous B.I and Janus B.III NPs show some preference for the droplet equators. In these positions, the templating propensity of the LC mesogens becomes evident: due to their vertical alignment with respect to the droplet poles, the mesogens contribute to align the NPs along the same direction. These results strengthen the argument of enthalpic forces being the main driving force in directing the organisation of NPs on LC nano-droplet surfaces, with entropic forces providing a contribution, not necessarily dominant, to the driving force. Bead-to-bead interactions described by the DPD parameters (see section 2) for B.I and B.III NPs ensure that B.I and B.III NPs remain on the equatorial region of the LC droplet, while B.II moved towards the boojums. These differences in behaviour were observed even though the NP geometry is the same for these 3 NPs. Entropic forces could not affect the position of B.I and B.III NPs, yet they could change their orientation, which is parallel to the direction vector of the droplet.
The results obtained for group C NPs (spheres) show that these NPs migrate towards the droplet boojums regardless of their surface features (i.e., homogeneous vs. Janus). It is worth noting that neither C.I nor C.II NPs adsorb at the droplet tip, unlike the ellipsoidal B.II NPs. Our simulation results indicate that the dimensions of a NP affect its alignment. Elongated particles exhibit similar behaviour to block polymers, which can penetrate through the LC droplet surface and move towards the boojums within certain ranges of attractive interactions between polymers and mesogens.32 Therefore, if a particle is long enough to penetrate the surface of a LC droplet, it likely migrates towards its tip. A large NP does not necessarily penetrate the LC surface, yet it can still migrate towards the boojums, but perhaps it remains within the arctic/antarctic circle rather than reaching the droplet tip.
None of the cube-shaped NPs, as can be seen in Fig. 7, group E, manifested a distinct preferential adsorption site on the LC nano-droplet. Both homogeneous and Janus cubic NPs distributed randomly on the droplet surface. After the detachment/attachment process described in Fig. 6, the cubic NPs simply stayed where they were put back on the droplet surface. Comparing these results to those obtained for elongated NPs clearly quantifies the importance of NP aspect ratio in determining preferential adsorption sites on LC droplets. The cubic NPs considered here did not have sides long enough to penetrate through the droplet surface, which our results show is a strong mechanism to drive the NPs towards the LC droplet tips, and, being equally long in all three directions, could not show a preferential orientation either because entropic forces were not strong enough, as opposed to results obtained for elongated NPs just discussed.
The results presented in this section suggest that parameters such as shape and attractiveness are equally important as the NP size in determining the preferential adsorption site for NPs on LC nano-droplets. As in the examples of disks (A.I), ellipsoidal (B.I) and cylindrical (D.I) NPs, not all large NPs necessarily move towards the boojums. Some prefer to locate at the equator. The results also show that entropy-driven self-assembly is only possible if enthalpic forces are too strong or oppose such an assembly. The results also suggest that chemical functionalisation yielding Janus structures, for some NPs, can alter the preferential adsorption sites for NPs on LC droplets, which could provide a useful handle to create self-assembled structures with the desired morphology and size for a variety of applications.
4. Conclusions
In this study, the adsorption and self-assembly of nanoparticles on liquid crystal droplets was investigated using coarse-grained molecular simulations. The results strongly suggest that several factors determine both the existence of preferential adsorption sites on LC droplets and the orientation of the adsorbed NPs. In fact, small particles that were not expected to have a preferred location on the droplet surface showed strong evidence of emergent phenomena. Additionally, the results highlighted marked changes in behaviour for Janus NPs when compared to their homogeneous counterparts. This suggests that the NP–LC molecule interactions are also important parameters, in addition to the NP size, in controlling the NP self-assembly on LC droplets. Overall, for the systems considered here, the simulation results qualitatively suggest that enthalpic forces predominantly determine the preferential adsorption location for NPs, while entropic forces affect the orientation of the NPs, when possible.The nanoparticle adsorption on liquid crystal droplets had no significant impact on the overall LC molecules' orientation within the droplet. The reason is that the NPs considered did not penetrate through the droplet surface. Further, in our systems there are no ligands or stabilizing agents, which are often present in experimental studies.43,44 Therefore, there is limited interaction between the particles and the droplet as a whole.
With regard to increasing the nanoparticle size, our simulations confirmed that the NPs must be above a certain size threshold to exhibit preferential adsorption location on, e.g., the LC droplet boojums. Our results conclusively show that the NP shape is also an important parameter that can be used to control the preferential adsorption site. For example, two NPs of similar size but different shape can show different preferential adsorption sites. As was the case for small NPs, the NP surface chemistry is also important, as was quantified by comparing the results obtained for homogeneous vs. Janus particles of the same size and shape.
While following studies could clarify the effect of NP functionalisation and surface chemistry on preferential adsorption and self-assembly on LC droplets, the results presented here are helpful for enhancing our quantitative understanding of self-assembly towards designing protocols to direct the assembly of chosen particles into supra-molecular structures for advanced material applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Generous allocations of computing time were provided by the Research Computing Platforms Support – University College London. The authors acknowledge useful discussions with Prof. Martin Lisal of the Czech Academy of Sciences.References
- M. Dienerowitz, M. Mazilu and K. Dholakia, J. Nanophotonics, 2008, 2, 021875 CrossRef.
- S. M. Dizaj, F. Lotfipour, M. Barzegar-Jalali, M. H. Zarrintan and K. Adibkia, Mater. Sci. Eng., C, 2014, 44, 278–284 CrossRef CAS PubMed.
- S. C. Glotzer, Science, 2004, 306, 419–420 CrossRef CAS PubMed.
- P. Bačová, E. Glynos, S. H. Anastasiadis and V. Harmandaris, ACS Nano, 2019, 13, 2439–2449 Search PubMed.
- M. Borówko, W. Rżysko, S. Sokołowski and T. Staszewski, Soft Matter, 2018, 14, 3115–3126 RSC.
- N. K. Hansoge, T. Huang, R. Sinko, W. Xia, W. Chen and S. Keten, ACS Nano, 2018, 12, 7946–7958 CrossRef CAS PubMed.
- E. S. Harper, B. Waters and S. C. Glotzer, Soft Matter, 2019, 15, 3733–3739 RSC.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168 CrossRef CAS PubMed.
- G. van Anders, N. K. Ahmed, R. Smith, M. Engel and S. C. Glotzer, ACS Nano, 2013, 8, 931–940 CrossRef PubMed.
- Z. Zhang, M. A. Horsch, M. H. Lamm and S. C. Glotzer, Nano Lett., 2003, 3, 1341–1346 CrossRef CAS.
- Y. Zhang, M. Cao, G. Han, T. Guo, T. Ying and W. Zhang, Macromolecules, 2018, 51, 5440–5449 CrossRef CAS.
- F. Huang, Y. Lv, L. Wang, P. Xu, J. Lin and S. Lin, Soft Matter, 2016, 12, 6422–6429 RSC.
- Q. Li, Z. Wang, Y. Yin, R. Jiang and B. Li, Macromolecules, 2018, 51, 3050–3058 CrossRef CAS.
- Y.-D. Yan, Y.-H. Xue, H.-Y. Zhao, H. Liu, Z.-Y. Lu and F.-L. Gu, Macromolecules, 2019, 52, 6169–6180 CrossRef CAS.
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021 RSC.
- Y. Ning, F. C. Meldrum and S. P. Armes, Chem. Sci., 2019, 10, 8964–8972 RSC.
- F. Sicard and A. Striolo, in Anisotropic Particle Assemblies, Elsevier, 2018, pp. 167–200 Search PubMed.
- X. Zhao, G. Yu, J. Li, Y. Feng, L. Zhang, Y. Peng, Y. Tang and L. Wang, ACS Sustainable Chem. Eng., 2018, 6, 4105–4114 CrossRef CAS.
- T. M. Ruhland, A. H. Gröschel, N. Ballard, T. S. Skelhon, A. Walther, A. H. Müller and S. A. Bon, Langmuir, 2013, 29, 1388–1394 CrossRef CAS PubMed.
- D. Demus, J. W. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Handbook of Liquid Crystals, Volume 2A: Low Molecular Weight Liquid Crystals I: Calamitic Liquid Crystals, John Wiley & Sons, 2011 Search PubMed.
- P. Bao, D. A. Paterson, P. L. Harrison, K. Miller, S. Peyman, J. C. Jones, J. Sandoe, S. D. Evans, R. J. Bushby and H. F. Gleeson, Lab Chip, 2019, 19, 1082–1089 RSC.
- M. Khan, A. R. Khan, J.-H. Shin and S.-Y. Park, Sci. Rep., 2016, 6, 22676 CrossRef CAS PubMed.
- N. L. Abbott, Y. Kim, J. Noh and K. Nayani, Soft Matter, 2019 Search PubMed.
- J. K. Whitmer, X. Wang, F. Mondiot, D. S. Miller, N. L. Abbott and J. J. de Pablo, Phys. Rev. Lett., 2013, 111, 227801 CrossRef PubMed.
- Y. Li, N. Khuu, E. Prince, M. Alizadehgiashi, E. Galati, O. D. Lavrentovich and E. Kumacheva, Sci. Adv., 2019, 5, eaav1035 CrossRef PubMed.
- Y. Li, J. J.-Y. Suen, E. Prince, E. M. Larin, A. Klinkova, H. Thérien-Aubin, S. Zhu, B. Yang, A. S. Helmy and O. D. Lavrentovich, Nat. Commun., 2016, 7, 12520 CrossRef CAS PubMed.
- G. Chu, G. Vasilyev, R. Vilensky, M. Boaz, R. Zhang, P. Martin, N. Dahan, S. Deng and E. Zussman, Langmuir, 2018, 34, 13263–13273 CrossRef CAS PubMed.
- H. Mundoor, S. Park, B. Senyuk, H. H. Wensink and I. I. Smalyukh, Science, 2018, 360, 768–771 CrossRef CAS PubMed.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557 CrossRef PubMed.
- A. Walther and A. H. Müller, Soft Matter, 2008, 4, 663–668 RSC.
- Z. Sumer and A. Striolo, Phys. Chem. Chem. Phys., 2018, 20, 30514–30524 RSC.
- Z. Sumer and A. Striolo, Soft Matter, 2019, 15, 3914–3922 RSC.
- B. Jerome, Rep. Prog. Phys., 1991, 54, 391 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- N. R. Jana, Angew. Chem., Int. Ed., 2004, 43, 1536–1540 CrossRef CAS PubMed.
- M. Rahimi, T. F. Roberts, J. C. Armas-Pérez, X. Wang, E. Bukusoglu, N. L. Abbott and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5297–5302 CrossRef CAS PubMed.
- M. Škarabot and I. Muševič, Soft Matter, 2010, 6, 5476–5481 RSC.
- E. P. Lewandowski, M. Cavallaro Jr, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142–15154 CrossRef CAS PubMed.
- C. Bi, S. Wang, S. V. Kershaw, K. Zheng, T. Pullerits, S. Gaponenko, J. Tian and A. L. Rogach, Adv. Sci., 2019, 1900462 CrossRef PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2011, 6, 609–614 CrossRef PubMed.
- W. Feng, L.-D. Sun and C.-H. Yan, Langmuir, 2011, 27, 3343–3347 CrossRef CAS PubMed.
- L. M. Rossi, J. L. Fiorio, M. A. Garcia and C. P. Ferraz, Dalton Trans., 2018, 47, 5889–5915 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00153k |
| This journal is © The Royal Society of Chemistry 2020 |