Understanding the role of electrons in the magnetism of a colossal permittivity dielectric material†
Adam
Berlie
 *ab,
Ian
Terry
b,
Stephen P.
Cottrell
a,
Wanbiao
Hu
c and
Yun
Liu
c
*ab,
Ian
Terry
b,
Stephen P.
Cottrell
a,
Wanbiao
Hu
c and
Yun
Liu
c
aISIS Neutron and Muon Facility, Science and Technology Facilities Council, Chilton, Oxfordshire OX11 0QX, UK. E-mail: adam.berlie@stfc.ac.uk
bDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK
cResearch School of Chemistry, Australian National University, Acton, Canberra 2601, Australia
First published on 21st August 2019
Abstract
Creating new materials that show potential for technological devices is one of the most important and active areas of solid state chemistry and physics. For data storage, multiferroics present some great advantages due to the coupling of their electrical and magnetic properties. The discovery of In and Nb co-doped rutile (Hu et al. Nat. Mater. 12, 821) presented a material that was perfect for capacitive devices; with high permittivity and low loss, which was attributed to localised polarisable defects within the crystal structure, though other work has suggested internal blocking barriers at grain boundaries as being responsible for the dielectric properties. Here we report on the magnetic properties of this material and shown that magnetic ordering occurs at room temperature and below, with the Curie temperature depending upon doping levels. Moreover, muon spin relaxation measurements suggest that the magnetic order is confined to grain boundaries or areas where the defects can cluster. This implies that a strong magneto-electronic coupling could exist within In- and Nb-co-doped rutile close to room temperature, though the inhomogeneous nature of the magnetism suggests that the coupling may be optimised in nanoparticles or thin films where defect clustering could be promoted.
New conceptsCo-doped rutile TiO2 is an extremely novel dielectric material with both high permittivity and low loss; the ideal candidate to be used in devices. This system uses localised electron defects to result in a polarisable dipole moment that gives us a high capacitance. However, one thing that has been completely overlooked and not considered is studying the magnetic properties, we have addressed this utilising the extremely novel muon spectroscopy technique, and have found that there is a remnant magnetic component that depends strongly on doping level. Of all the work on these co-doped materials no-one has spent time considering the magnetic properties and this is very exciting stuff. We have shown that there is a huge amount of promise where one can tune the magnetic transition temperature with doping level and this now extends this material from purely a dielectric material to something more like a multiferroic where there is a strong coupling of the electrical and magnetic behaviours. This result is a bit of a game-changer where we can now begin to look at this family of doped materials for different applications not just within capacitance devices. |
The interplay of magnetism and dielectric behaviour is crucial for many materials that have technological potential, such as multiferroics, and understanding this is essential for the design of new compounds.1–3 Within capacitors one wants a dielectric material that has high permittivity and low loss, with various promising materials being synthesised and measured.4–7 One advancement was the colossal permittivity that resulted from the co-doping of In(III) and Nb(V) ions within TiO2 rutile and was attributed to defect induced localised electronic moments.7 These localised electrons can be easily polarised with an electric field resulting in the high permittivity and electron spin resonance measurements highlighted two distinct spin centres within the sample. Furthermore the permittivity and loss both showed features at 50 K, which was attributed to a spin freezing phenomena.7 Additional work by other groups has suggested that grain boundaries are important with regards to the dielectric response8 and similar behaviour has been seen in an amorphous thin film.9 However, in all cases there has been no distinct/clear agreement on the microscopic origin of the colossal permittivity. A detailed study of the nature of the magnetic state associated with electronic dipoles has not been carried out. Such an investigation is very important as it may be that the magnetic and electrical properties are strongly coupled. In fact, grain boundaries can also be important in their own right as they have been shown to have associated magnetic structure,10 illustrating the importance of understanding these types of materials. Our work provides insight into the spin freezing effect associated with defects and shows the onset of static magnetic ordering where the particle/grain surface boundaries (and potentially the particle surface area) are likely to be important.
Samples were synthesised using the method outlined by Hu et al.,7 with 3 levels of co-doping; 1, 5 and 10%. All samples were characterised in a similar way to that described in ref. 7.
Magnetic susceptibility measurements were conducted using a Quantum Design MPMS-XL using the DC transport method and VSM-SQUID. The background diamagnetic susceptibility of rutile TiO2 was calculated to be χD = −2.89 × 10−11 m3 kg−1 by using Pascal's constants.11 Muon spectroscopy experiments were done at the ISIS Neutron and Muon Source on the EMU and MUSR spectrometers. Both a closed cycle refrigerator (CCR) and He flow cryostat were used to cool the sample; each set-up will have its own intrinsic background. μSR is a fantastic local probe of weak magnetism, where the muon will couple to magnetic moments (both electronic and nuclear) over a few nanometres and since the muon life time is 2.2 μs, it is sensitive to dynamics on the MHz scale. Pulses of muons are implanted in the sample and the directional decays of the muon are measured in forward and backward detectors, the asymmetry between the two detector banks provides information on the muon spin depolarisation. From looking at the asymmetry and the depolarisation rate, one can gain information on both static and dynamic properties of the magnetic moments with the sample.
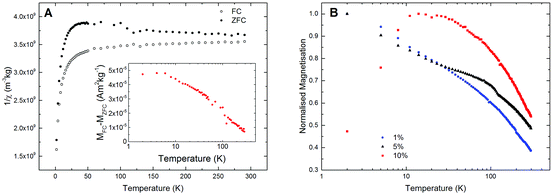
Magnetic susceptibility measurements (Fig. 1A) are shown for the 5% co-doped sample. The temperature dependent inverse susceptibility demonstrates that paramagnetic species have been produced, though if one were creating local non-interacting Ti3+ defects, this would manifest itself as a Curie, tail where a plot of 1/χ vs. T should be linear. This is not the case and there is a remnant component that exists from 2 K to above room temperature. It should also be noted that we believe the noise in the ZFC curve at approximately 100 K in Fig. 1A is sample-related and not intrinsic to the measurement. The inset to Fig. 1A shows the growth of this remnant component as temperature decreases and there is an apparent plateau at low temperatures. To supplement this, additional experiments were conducted on all three samples (Fig. 1B) where they were cooled in an applied field of 1 T and at base temperature (2 K) the field was reduced to 1 mT; this was to prevent a small negative residual field being trapped in the superconducting solenoid. The moment was then measured on warming and was normalised with respect to the highest remnant moment observed for each sample so that their magnetic responses could be compared. In all cases the measurement highlights the behaviour of the remnant component where there is a strong temperature dependence across all three samples. It is clear that a non-zero remnant magnetic moment exists at room temperature and the curvature of each samples' magnetisation temperature dependence suggest Curie or blocking temperatures above 400 K. For the 10% sample, the low temperature data are anomalous since there is a clear maximum in the moment at ∼20 K and within the 5% sample we also see an anomaly at around 100 K. These data are indicative of there being clusters of moments that are able to interact giving rise to magnetic hysteresis. However, it is unlikely that this is a homogeneous magnetic response and there are likely a range of cluster sizes with different intra- and inter-cluster interaction energies.
The magnetic data illustrate that there is something of interest within the spin freezing region and a strong remnant component in the magnetisation. Further insight into the nature of the inhomogeneous magnetism of the doped rutile samples was obtained by using the muon spin relaxation (μSR) technique.
A ZF μSR experiment was performed on all samples where, at high temperatures, a very broad Kubo–Toyabe relaxation was observed, which is attributed to dephasing of the muon polarisation by quasi-static randomly orientated nuclear moments.12 At low temperatures the relaxation becomes more exponential in character, which is an indication that the muons are sensitive to the slowing down of electronic magnetic fluctuations entering the experimental timescale. Therefore all the spectra were fit with a multiplication of a Kubo–Toyabe and an exponential function:
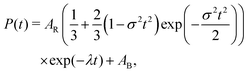 | (1) |
It is likely that the anomalously high values for AB are a consequence of inhomogeneity within the samples. At low temperatures (approximately 12 K) the baseline is sample dependent where the 1% has the highest baseline. This also suggests that a large number of muons are being stopped within regions where there is no electronic or nuclear magnetism that can cause the muon polarisation to dephase; hence the implantation site for such muons is quite removed from any defects associated with the dopants. For example, the 1% sample has 2% of the Ti sites occupied by dopants. On average, there should be about one dopant atom per 25 unit cells whilst in the case of the 10% sample, there would be one dopant atom per 2.5 unit cells. Given dimensions of rutile's unit cell,15 this implies mean defect separations of 70 to 100 Å for a 1% sample while this would be 7 to 10 Å in the case of a 10% sample. A muon is influenced by local magnetic moments of ∼20 Å away from its implantation site. It is therefore likely that, at least in the case of the 10% and 5% samples, the dopants are not homogeneously distributed throughout the sample and are probably located within grain boundaries or close to the surfaces of individual grains, which have less stopping power for muons than bulk material. DFT studies have suggested that segregation of dopants to grain boundaries is likely to occur in rutile TiO2.16 This type of behaviour has been seen within ZnO particles where there was a large non-relaxing baseline from the bulk of the material with a small relaxing component from the electronic magnetism present within the grain boundaries.14 The relaxing fraction of muons is related to the muons stopping near defects with electronic or nuclear moments that cause a relaxation of the muon spin polarisation. A simple ratio of the relaxing fraction to the baseline (Table 1) demonstrates that low doping results in a relatively large baseline contribution. In previous work on rutile, the baseline has been shown to be negligible where a full asymmetry was observed to be depolarised by the intrinsic behaviour of the rutile sample.19 The values of σ are similar and this would highlight that the field distribution from these nuclear moments is similar between samples, thus confirming that the high temperature Kubo–Toyabe behaviour is related to the In and Nb nuclear moments.
| Fitting parameter | 10% sample | 5% sample | 1% sample |
|---|---|---|---|
| A R/AB | 0.92(3) | 0.52(1) | 0.35(1) |
| σ (MHz) | 0.082(4) | 0.112(8) | 0.097(1) |
| λ (MHz) | 0.088(4) | 0.138(8) | 0.150(10) |
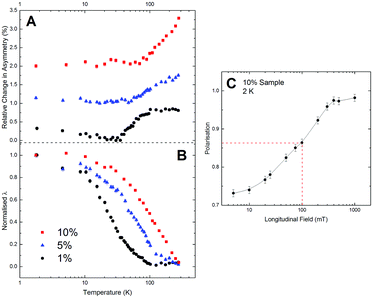
Muon spectra were collected over a wide temperature range and the fitting parameters obtained from their analyses are shown in Fig. 2. Scaling was used to account for the data overlap between high and low temperatures that was taken in separate sample environments. The relative change in the relaxing asymmetry is plotted in Fig. 2A. The change in the asymmetry is very small, given that a full asymmetry is ∼23%. This small relaxing component is likely to be due to the fact that only a small amount of each sample contains magnetic moments that are able to relax the muon polarisation, i.e. muon spin relaxation occurs only in dilute, specific areas of the sample. The muon relaxation rate, λ, was normalised at low temperatures (see Fig. 2B) and the trend is similar for all samples, where there appears to be a gradual increase in λ as the temperature is decreased. It is clear that the point at which λ begins to increase rapidly occurs at different temperatures for each doping concentration. These rises in λ are a consequence of the increasing importance of muon spin depolarisation due to the electronic magnetic moments within the samples. Moreover, there is a strong similarity between the temperature dependent changes in λ and the variation of the remnant magnetisation shown in Fig. 1B. The decrease in the asymmetry and the rise of λ correspond to the same temperature regions and show a similar trend; this mutual behaviour is an indication of the existence of static magnetic ordering. The decrease in the asymmetry may be interpreted as being a result of the internal fields from the ordering of electronic moments becoming high enough to dephase muons outside of the experimental time window, and so there is a missing fraction, (a decrease in the number of detected muons) at the lowest temperatures. The flattening out of λ at low temperatures is indicative of a competing process causing the muon spin to dephase, these could be from persistent electronic fluctuations that would be present when the paramagnetism dominates or if the sample has entered a quasi-static state where you are left with a broad static field distribution. At high temperatures where λ → 0 the muon is considered to be in the motionally narrowed state; i.e. the fluctuations are too fast for the experimental time-scale. For the 10% sample, both the asymmetry and relaxation rate are still changing even at room temperature supporting the idea that a ferromagnetic state exists in the material with a Curie or blocking temperature greater than 300 K. Further evidence for the static nature of the magnetism is from the longitudinal field sweep (Fig. 2C) where one is able to decouple the muons from their surroundings by applying a field along the direction of the initial muon polarisation. Since there is a full recovery of the muon polarisation at high fields this indicative of a static magnetically ordered system, where the mid-point along the curve can be taken as an estimate of the internal field that the muon is coupled to; ∼100 mT. This value is too high to be a shallow donor state or decoupling from nuclear magnetism, thus it is a decoupling from a static magnetically frozen/ordered state.17
The behaviour of muons within pure rutile has been studied previously.18–22 Below 10 K the muon forms a shallow donor state near a Ti3+ defect where the ionisation energy of this state has been reported to be 0.9 meV.20 Above 10 K, the muon becomes dynamic where the diffusion rate is beyond the timescale of the measurement and so no relaxation is observed, as a result the baseline increases. This also indicates that our high baseline is a consequence of muons stopping in the pure rutile structure. No paramagnetic muonium is observed unless one induces oxygen vacancies within the sample.18 In our case the relaxation we are interested in is above 10 K and so the influence of the shallow donor state is negligible. Our data do not mimic that of pure rutile and so the results we have presented must be due to the doping.
All samples show broad and continuous magnetic transitions that are due to the onset of short range order at the grain boundaries and may be percolative in nature as seen in other doped systems.23,24 It has also been shown that a small amount (1–5%) of magnetic cations can create local magnetic polarons from oxygen vacancies leading to room weak temperature ferromagnetism.27 As the doping increases, the wavefunction of the neighbouring polarons overlap and a coherent magnetic state can be observed; even as little as 2% doping of Fe or 7% doping of Co in a TiO2 matrix has resulted in observable ferromagnetism,28,29 thus the percolation limit is fairly small. Within dilute magnetic semiconductors, the shape of the magnetisation, or critical behaviour, has been shown to be important,25,26 as the difference in convex or concave nature of the transition is related to the polaron interactions and carrier densities.
The low temperature behaviour shown in Fig. 2B is curious as a flattening out of λ can imply persistent dynamics from the electronic moments such as that observed in spin liquids in an applied longitudinal field30,31 or from low dimensional systems, where in Rb4Cu(MoO4)3 no long range order is seen down to 50 mK.32 However, since there is also a paramagnetic component in magnetic susceptibility, this would also manifest itself as a low temperature feature in the μSR data, such as an increase in the relaxation rate, however, the shallow donor state in pure rutile may also contribute.20
Overall we see evidence for strong dynamics associated with the electronic moments, with possible persistent dynamics at low temperatures, but the field distribution that the muon is sensitive to must be fairly broad. We have also shown that there are two muon stopping sites within the sample, one within the bulk, where no relaxation of muon spins is observed, and the other probably closer to grain boundaries, where relaxation is observed. The similar behaviour between the muon data and remnant magnetisation data is especially poignant as it shows that both techniques are measuring the same phenomena, where there is a strong correlation between doping level and strength of interaction. This work may help to explain the two different spin centres observed within the ESR measurements of Hu et al.,7 where the less intense ESR peak could be due to the magnetic defects at grain boundaries studied within this work. However, what is clear is that the spin freezing observed in the original work of Hu et al.7 is of great interest as it appears to be magnetic order which exits close to room temperature. Thus co-doped rutile TiO2:Nb,In exhibits both a colossal permittivity and ferromagnetism which may interact to produce magneto-electric coupling close to room temperature. We have also shown the usefulness and validity of the μSR technique to study these types of dilute grain-boundary systems, which is something that could be exploited within other compounds.
With more research it is hoped that one will be able to utilise the interplay between the magnetism and dielectric behaviour to create defect pinned multiferroics. Since the TC is strongly dependent on doping levels, creating more surface or grain boundaries with high doping levels may be able to allow the ordered magnetic state to exist above room temperature, offering a realistic potential for future applications, which would then have promising applications. Therefore the synthesis of doped nanoparticles seems like a sensible next step in the continuing search for novel technological materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Ruth Berlie for her artwork and Pauline Bott for helping proof read our manuscript.References
- M. Bibes and A. Barthélémy, Nat. Mater., 2008, 7, 425 CrossRef CAS PubMed.
- W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759 CrossRef CAS.
- S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13 CrossRef CAS PubMed.
- M. T. Buscaglia, M. Viviana, V. Buscaglia, L. Mitoseriu, A. Testino, P. Nanni, Z. Zhao, M. Nygren, C. Harnagea, D. Piazza and C. Galassi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064114 CrossRef.
- M. A. Subramanian, D. Li, N. Duan, B. A. Reisner and A. W. Sleight, J. Solid State Chem., 2000, 151, 323 CrossRef CAS.
- A. P. Ramirez, et al., Giant dielectric constant response in a copper-titanate, Solid State Commun., 2000, 115, 217 CrossRef CAS.
- W. Hu, Y. Liu, R. L. Withers, T. J. Frankcombe, L. Norén, A. Snashall, M. Kitchin, P. Smith, B. Gong, H. Chen, J. Schiemer, F. Brink and J. Wong-Leung, Nat. Mater., 2013, 12, 821 CrossRef CAS PubMed.
- J. Li, F. Li, Y. Zhuang, L. Jin, L. Wang, X. Wei, Z. Xu and S. Zhang, J. Appl. Phys., 2014, 116, 074105 CrossRef.
- Z. Gai, Z. Cheng, X. Wang, Z. Lanling, N. Yin, R. Abah, M. Zhao, F. Hong, Z. Yu and S. Dou, J. Mater. Chem. C, 2014, 2, 6790 RSC.
- S. Farokhipoor, C. Magén, S. Venkatesan, J. Íñiguez, C. J. M. Daumont, D. Rubi, E. Snoeck, M. Mostovoy, C. de Graaf, A. Müller, M. Döblinger, C. Scheu and B. Noheda, Nature, 2014, 515, 379 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- The nuclear moments present within the samples are: Nb (I = + 9/2), In (I = + 9/2) as well as 47Ti (I = −5/2; 7.44% abundance) and 49Ti (I = − 7/2; 5.41% abundance).
- The background of the CCR and sample holder was measured using hematite powder which resulted in Abg = 3.8%.
- T. Tietze, P. Audehm, Y.-C. Chen, G. Schutz, B. B. Straumal, S. G. Protasova, A. A. Mazilkin, P. B. Straumal, T. Prokscha, H. Luetkens, Z. Salman, A. Suter, B. Baretzky, K. Fink, W. Wenzel, D. Danilov and E. Goering, Sci. Rep., 2015, 5, 8871 CrossRef CAS.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53 CrossRef CAS.
- W. Körner and C. Elsässer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205315 CrossRef.
- ed. S. L. Lee, S. H. Kilcoyne and R. Cywinski, Muon Science: Muons in Physics, Chemistry and Materials, IOP Publishing, Bristol and Philadelphia, 1999 Search PubMed.
- H. Ariga, K. Shimomura, K. Ishida, F. Pratt, Y. Yoshizawa, W. Higemoto, E. Torikai and K. Asakura, JPS Conf. Proc., 2014, 2, 010307 Search PubMed.
- B. B. Baker, Y. G. Celebi, R. L. Lichti, H. N. Bani-Salameh, P. W. Mengyan and B. R. Carroll, Phys. Proc., 2012, 30, 101 CrossRef CAS.
- R. C. Vilão, R. B. L. Vieira, H. V. Alberto, J. M. Gil, A. Weidinger, R. L. Lichti, B. B. Baker, P. W. Mengyan and J. S. Lord, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081202(R) CrossRef.
- S. F. J. Cox, J. L. Gavartin, J. S. Lord, S. P. Cottrell, J. M. Gil, H. V. Alberto, J. Pioto Duarte, R. C. Vilão, N. Ayres de Campos, D. J. Keeble, E. A. Davis, M. Charlton and D. P. van der Werf, J. Phys.: Condens. Matter, 2006, 18, 1079 CrossRef CAS.
- K. Shimomura, R. Kadono, A. Koda, K. Nishiyama and M. Mihara, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075203 CrossRef.
- J. Wu and C. Leighton, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174408 CrossRef.
- J. P. Clancy, A. Lupascu, H. Gretarsson, Z. Islam, Y. F. Hu, D. Casa, C. S. Nelson, S. C. LaMarra, G. Cao and Y.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054409 CrossRef.
- S. Das Sarma, H. Hwang and A. Kaminski, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155201 CrossRef.
- A. Kaminski and S. Das Sarma, Phys. Rev. Lett., 2002, 88, 247202 CrossRef CAS.
- J. M. D. Coey, M. Venkatesan and C. B. Fitzgerald, Nat. Mater., 2005, 4, 173 CrossRef CAS.
- Z. Wang, J. Tang, L. D. Tung, W. Zhou and L. Spinu, J. Appl. Phys., 2003, 93, 7870 CrossRef CAS.
- Y. Matsumoto, M. Murakami, T. Shono, T. Hasegawa, T. Fukumura, M. Kawasaki, P. Ahmet, T. Chikyow, S.-Y. Koshihara and H. Koinuma, Science, 2001, 291, 854 CrossRef CAS PubMed.
- C. Orain, L. Clark, F. Bert, P. Mendels, P. Attfield, F. H. Aidoudi, R. E. Morris, P. Lightfoot, A. Amato and C. Baines, J. Phys.: Conf. Ser., 2014, 551, 012004 CrossRef.
- B. Fåk, E. Kermarrec, L. Messio, B. Bernu, C. Lhuillier, F. Bert, P. Mendels, B. Koteswararao, F. Bouquet, J. Ollivier, A. D. Hillier, A. Amato, R. H. Colman and A. S. Wills, Phys. Rev. Lett., 2012, 109, 037208 CrossRef PubMed.
- T. Lancaster, P. J. Baker, F. L. Pratt, S. J. Blundell, W. Hayes and D. Prabhakaran, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184404 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh00983c |
| This journal is © The Royal Society of Chemistry 2020 |