Open Access Article
Open Access ArticleBroadband solar absorption with silicon metamaterials driven by strong proximity effects†
Ankit
Chauhan
 a and
Gil
Shalev
a and
Gil
Shalev
 *ab
*ab
aSchool of Electrical & Computer Engineering, Ben-Gurion University of the Negev, POB 653, Beer-Sheva 8410501, Israel. E-mail: glshalev@bgu.ac.il
bThe Ilse-Katz Institute for Nanoscale Science & Technology, Ben-Gurion University of the Negev, POB 653, Beer-Sheva 8410501, Israel
First published on 2nd April 2020
Abstract
Absorption of the solar radiation over a wide spectral range is of utmost importance to applications related to the harvesting of solar energy. We numerically demonstrate broadband solar absorption enhancement employing a metamaterial in the form of arrays composed of subwavelength silicon truncated inverted cones, henceforth referred to as light funnel (LF) arrays. We show that the broadband absorption efficiency of an unoptimized LF array is 36% greater compared with an optically-maximized NP array. We show that photon trapping in LF arrays is motivated by proximity effects related to the optical overlap between LFs. We make the distinction between two types of optical overlap: weak overlap in which the coupling between the sparse array modes and the impinging illumination increases with array densification, and strong overlap where the array densification introduces new highly absorbing modes. We show that in nanopillar (NP) arrays the optical intensity inside the NPs decreases upon densification and the overall increase in absorptivity is due to increase in filling ratio (as was also shown by others), while the densification of LF arrays increases the optical intensity inside the individual LF and with the concurrent increase in filling ratio concludes light trapping much superior to that of NP arrays. Light trapping governed by strong proximity effects was not reported to date, and we believe it is an important paradigm for miniaturized lab-on-chip technologies.
Introduction
Harvesting solar photons is important to applications related to solar energy conversion.1–4 The theoretical basis of light trapping was historically developed in terms of geometrical optics and utilized total internal reflections between the absorber and the environment;5 it was shown that by texturing the front and back absorber surfaces the optical length inside the absorber increases and generates the 4n2 upper limit, where n is the absorber index of refraction, of the absorption enhancement factor for a Lambertian cell (the Yablonovitch limit). Equivalently, a randomly textured surface is as a system of infinite periodicity6,7 in which each impinging plane wave can couple to at least one guided mode.8 Light trapping in the ‘wave optics’ regime has been the subject of a considerable amount of experimental and theoretical works. It was numerically shown that arrays of subwavelength design can add wave vectors to the incident light by diffraction, for example, and in this manner increase the absorber optical excitation.9–11 Absorption enhancement of the solar light over a wide spectral range with ordered or disordered gratings of subwavelength semiconducting features was shown experimentally and numerically.4,12–30Theoretically, Sheng et al. showed that beyond the 4n2 absorption improvement is possible over a given spectrum as the presence of thick grating modifies the overall density of states of the grating-substrate complex.31 Yu et al. theoretically described the excitation of wave guide modes in a Lambertian thin slab with shallow grating on top and concluded that for an efficient light trapping one needs to maximize the number of available waveguide modes and minimize the number of diffraction orders. They showed that 2D grating inherently results in higher absorption enhancement compared with 1D grating, and, more importantly, described broadband absorption enhancement of 12n2 with a 2D grating.8,32 Callahan et al. argued for light trapping beyond the 4n2 limit if one is to increase the optical states of the absorbing film.33 Trapping of photons and absorption in a wide spectral range in substrate-less arrays have been the focus of extensive research, as well. Kosten et al. developed a ray optics model and reproduced the 4n2 limit for theoretical substrate-less arrays of vertical microwires.34 Sturmberg et al. delineated an absorption improvement in free-floating nanopillar (NP) arrays and showed how improvement is governed with adequate modal pairing with the impinging illumination, medium power centering inside the NPs and Fabry–Perot resonances.35 Lin and Povinelli examined free-floating NP arrays with a relatively large periodicity and demonstrated absorption improvement governed by the excitation of guided modes coupled with field concentration within the NPs.36 Finally, Shalev et al. numerically showed that the absorption in NP arrays is optimized with large-diameter NPs with a repressed absorption cross-section.20
We recently introduced a new paradigm for absorption of the solar light over a wide spectral range that is based on light-funnel (LF) arrays, where a LF is a subwavelength cone (or hyperboloid) reversed relative to the impinging wave front.37–42 The inherent LF continuum diameters entails a wide range of resonanting wavelengths for a single mode.43 We numerically showed that substrate-less LF arrays provide absorption improvement of the solar spectrum in comparison with optimized NP arrays. Also, we studied LF arrays on top of thin films, and showed that the grating-film composites exhibit high absorption at wavelengths >900 nm which is attributed to either excitations of the LFs, excitations of the films, or concurrent excitations of arrays and the films. We also demonstrated photon capture at the 4n2 limit for the LF array-film composite.
Presently, we examine the transition from a sparse LF array into a dense LF array. We also revisit this transition for NP arrays which allows us to identify the difference between the two systems and to pinpoint the origin of the unique mechanism of light trapping in LF arrays.
Methods
The electromagnetic wave solver (Synopsys Inc.) is used for the 3D finite-difference time-domain (FDTD) computations. The calculations (λ = 400–1100 nm in 20 nm intervals) are performed for an infinite square array in which a unit cell is considered with a periodic boundary conditions in the x–y directions. Complementary perfectly matched layers boundary condition is considered for the z-dimension. The spatially-resolved power (time-averaged Poynting vector (SAV)) and the absorbed photon density (APD) are spectrally extracted. The absorbed, reflected and transmitted photons are calculated for each wavelength using detectors surrounding the unit cell. According, the reflectivity, and transmissivity are extracted. In order to ensure the precision of the FDTD calculations, the mesh size is smaller than 0.1 of the wavelengths in the materials. The weighted absorption efficiency (ηabs) is the weighted average of the absorptivity and the solar radiation (AM 1.5G), and the weighted Qabs is extracted similarly. The material properties are adopted from ref. 44.Results and discussion
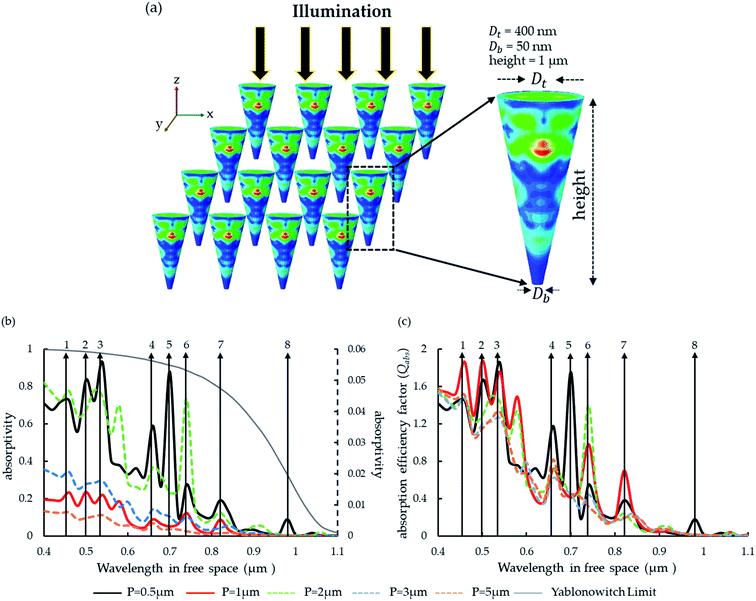
Fig. 1a presents a substrate-less free-floating LF array. Fig. 1b provides the dependency of a LF array absorptivity on the array periodicity (P), and the 4n2 limit is presented as well. The LF array is composed of LFs with a bottom diameter (Db) of 50 nm, a top diameter (Dt) of 400 nm, and height (H) of 1 μm; it was previously shown that such LFs provide optimal broadband absorption of the solar radiation.37–39 In order to unravel the transition from isolated LFs in to a LF array, we will follow the strong absorption peaks marked and numbered in Fig. 1b. For P = 5 μm the fields of the LFs weakly overlap and we approximate adjacent LFs to be optically isolated from each other. Three absorption peaks are evident for P = 5 μm (peak 1 = 460 nm, peak 3 = 540 nm and peak 4 = 660 nm) which reflect the excitation of localized leaky Mie modes characteristic of isolated LFs;43 these three peaks are also present for the smaller periods. For P = 3 μm there is an additional absorption peak (peak 6 = 740 nm) that persists also for smaller periods, and which reflects the excitation of a new mode associated with the optical overlap of adjacent LFs; this excitation marks the transition from light trapping governed by the excitation of isolated Mie modes into light trapping governed by excitations of Bloch-like modes. P = 2 μm and P = 1 μm each introduce an additional peak that persists for smaller P (peak 7 = 820 nm and peak 2 = 500 nm, respectively), and peak 5 (700 nm) and peak 8 (980 nm) emerge at P = 0.5 μm.In order to follow the progression of peak formation with period we next examine the respective absorption efficiency factor (Qabs) spectra which inherently excludes the contribution of the filling ratio (i.e. volume of a single LF divided by the volume of a unit cell) to the absorptivity. Qabs defines the potential of a subwavelength feature to self-concentrate light and is considered as Qabs = Cabs/(π/4Dt2), where Cabs is the absorption cross-section and Dt is the particle projected top diameter.45Fig. 1c presents the dependency of the Qabs spectra on P for a single LF. The locations of peaks 1–8 are marked as well. First, note that Qabs peaks 1, 3, 4 do not change much between P = 5 μm and P = 3 μm which confirms the initial assumption that for P = 5 μm the LFs are, to a good approximation, electromagnetically isolated for the respective wavelengths. Next, it is apparent that a smaller period implies a higher Qabs as the strongest peaks are for P = 0.5 μm and 1 μm except for peak 6 which is highest for P = 2 μm. This suggests that light trapping in LF arrays is strongly modulated by the optical overlap of adjacent LFs, and that the strong absorptivity peaks in Fig. 1b are not solely a density effect but also due to strong light confinement in the individual LFs. Hence, the increased LF density not only affects the filling ratio but rather introduces slow Bloch-like modes in which the intensity is locally concentrated in the individual LFs.35
Fig. 2 presents the optical intensity distribution for the selected absorption peaks 1, 4 and 5 presented in Fig. 1b, c, and absorption peaks 2, 3, 6, 7, 8 are provided in the ESI.† Intensity x and y cuts for peak 1 are shown for P = 1 (maximum Qabs) μm in which the vertical location of the strongest excitation is marked. The z-cuts show the progression of the strongest excitation for all considered periods. Note that for P = 2, 3, 5 the excitation does not change, which agrees with Fig. 1c. Higher optical coupling between the excitation and the impinging illumination, i.e. higher excitation amplitude due to higher leakage rate between the impinging illumination and excitation, is apparent for P = 1 μm and a decrease in coupling is recorded for P = 0.5 μm, which agrees with Fig. 1c where peak 1 Qabs is maximized for P = 1 μm. Similar behavior is also recorded for peaks 2, 6, 7 (see ESI†) in which the dependency of the absorption peaks on the period exhibits a maxima behavior (peak 2 exhibits two strong excitations). Hence, upon coalescence of isolated LFs into an array, the optical coupling with the impinging illumination increases to a maximum after which a decrease is recorded. Peaks 3, 4 (see ESI† for peak 3) also present a similar behavior only these are maximized for the smallest period. Peaks 5 and 8 (see ESI† for peak 8) reveal a different behavior. Four strong excitations are evident in peak 5 where three are located at the upper part of the LF and an additional one is located at the LF bottom. Remarkably, the three top excitations reflect the excitation of new modes in contrast with the bottom excitation which reflects stronger coupling between the impinging illumination and the isolated excitation. Hence, a distinction needs to be made between two types of optical overlap between LFs; the first type is the weak overlap that reflects coupling enhancement between the impinging illumination and the excitation, and the second type is the strong overlap which entails the introduction of a new excitation. To conclude, the strong absorptivity for peaks 5 and 8 agrees with the respective high Qabs values which reflect the excitation of several modes that are the result of the strong overlap regime. Finally, note that for peaks 5 and 8 strong overlap is only apparent at the top of the LF where the proximity effect is greater than at the LF bottom.
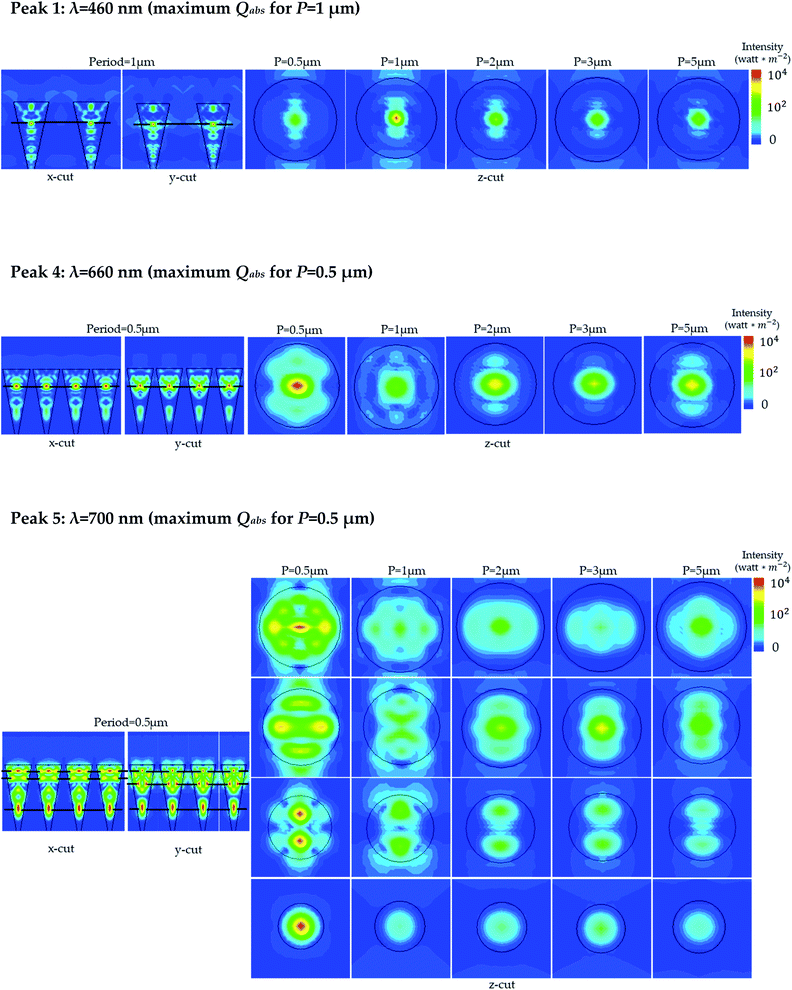 | ||
| Fig. 2 Intensity distributions for the strong Qabs peaks marked in Fig. 1c. On the left side the x and y intensity cross-sections for the period of maximum Qabs in which the vertical location of the strongest excitation is marked. Intensity cross-sections along the z-axis of the strongest excitation for the different periodicities are shown on the right. | ||
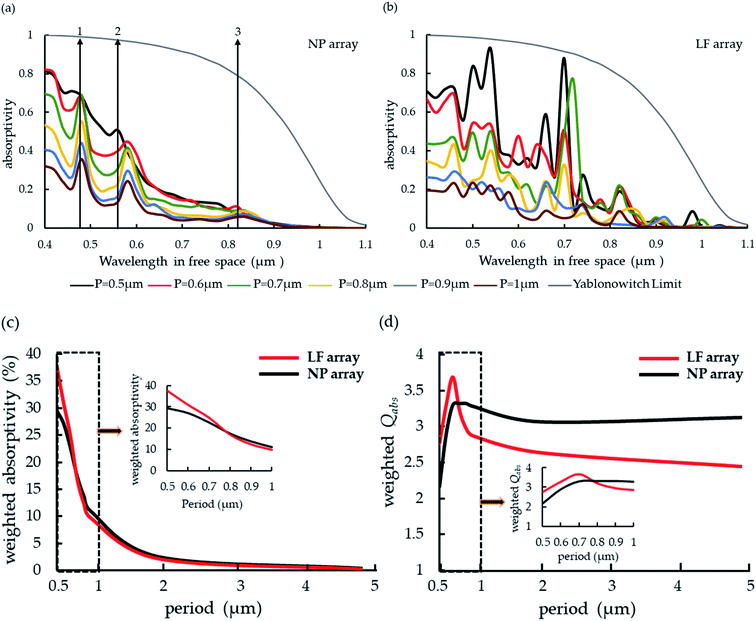
Next, in order to better understand the significance of weak and strong field overlap in LF arrays, we compare the period dependency of LF arrays with that of optimized NP arrays, that is NP diameter of 400 nm and H = 1 μm. Fig. 3a and b present the absorptivity for periods of 0.5 μm to 1 μm (0.1 μm interval) for NP and LF arrays, respectively, in which the LF array geometry is identical to the one used in Fig. 1. The NP arrays in Fig. 3a present three absorption peaks at 480 nm, 580 nm and a weaker one at 820 nm which are period-independent except for P = 0.5 μm in which the absorption peaks are blue shifted as described previously.12,46 The dependency of the LF arrays absorptivity spectra in Fig. 3b is starkly different and more complex; the LF array of P = 1 μm presents multiple peaks some of which are apparent also for the smaller periods while others vanish. Fig. 3c presents the variation of the weighted absorptivity, that is the absorptivity averaged with the AM1.5G radiation, with the array period of NP and LF arrays (P = 2, 3, 4, 5 μm are shown as well). It is apparent that for sparse arrays the broadband absorption of the NP array is slightly greater whereas for denser arrays the LF array absorption over a wide spectral range is substantially improved. In sparse arrays, pairing of the incoming light into localized radial modes is more efficient in NP arrays, whereas in dense LF arrays the impinging illumination couples more efficiently into slow Bloch-like photonic modes.35,43 Finally, as shown in Fig. 3c, the densification process produces maximum absorption at P = 0.5 μm for both arrays, in which the LF array exhibits weighted absorptivity that is 36% greater than that of the optically-optimized NP array. Fig. 3d shows the weighted Qabs (〈Qabs〉) where for high P values the NP 〈Qabs〉 is higher which is consistent with the observation that in sparse arrays the impinging illumination interacts more efficiently with the NP localized Mie modes. On the other hand, the LF 〈Qabs〉 is higher for dense arrays which supports the assumption of efficient coupling of the impinging illumination with slow Bloch modes in which the intensity is localized in the LFs. Also interesting is the maxima behavior of the LF array 〈Qabs〉 which increases for decreasing P till P = 0.7 μm and suggests intensity increase in the individual LF, whereas for smaller P the intensity in the LFs decreases similarly to NP arrays. However, the linear increase in LF array absorptivity for P = 0.5–1 μm suggests that the absorptivity enhancement of LF array for P = 0.5 μm is a result of both efficient coupling into slow Bloch modes and a higher filling ratio.
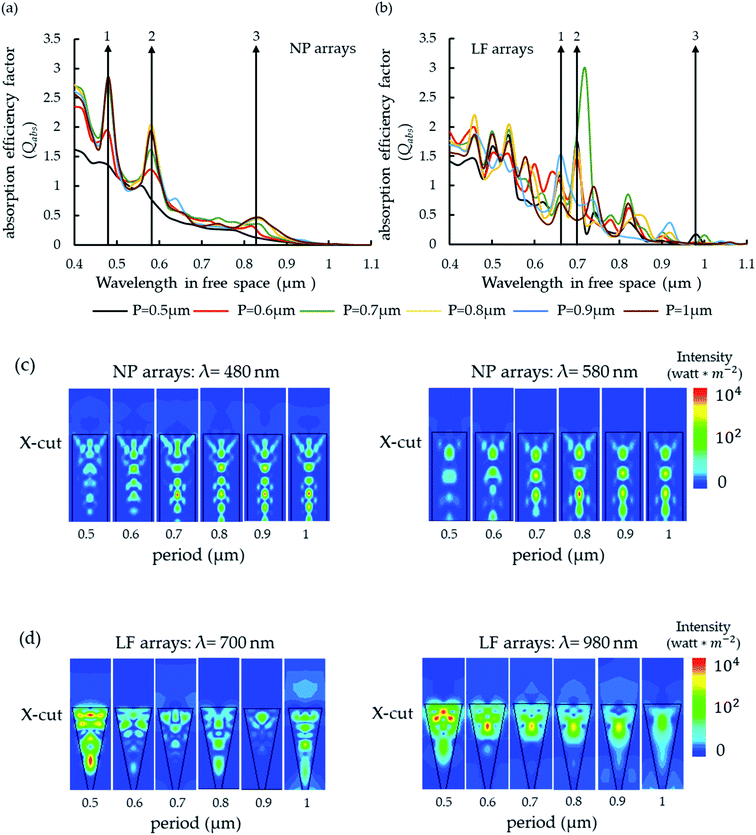
Fig. 4a and b present the Qabs spectra for NP arrays and LF arrays presented in Fig. 3a and b, respectively. The NP arrays exhibit three strong Qabs peaks (marked in Fig. 4a) that corresponds with the NP absorptivity peaks (Fig. 3a). Also, the Qabs peaks are higher for the sparser arrays; this implies that the coalescence of a sparse array into a dense array entails a decrease in the absorption cross-section of the individual NPs and therefore the absorptivity increase is due to the higher filling ratio, as reported previously by others.35 Specifically, note that the array of highest filling ratio (P = 0.5 μm) exhibits the highest absorptivity albeit the lowest Qabs spectrum and the almost complete vanishing of the three characteristic Qabs peaks. In other words, in order to maximize the absorptivity of a NP array, the absorption cross-section of the individual NPs has to decrease.20 The behavior is very different for LF arrays: the strong Qabs peaks do not necessarily correspond with the absorptivity peaks of the sparser array (Fig. 3b). On the contrary, note, for example, the three P = 0.5 μm Qabs high peaks at λ = 660 nm, 700 nm and 980 nm (these Qabs peaks are marked in Fig. 4b) with Qabs values of 1.17, 1.75 and 0.17, respectively, which are much higher than the P = 1 μm array Qabs values of 0.71, 0.41 and 0.01, respectively. Moreover, the absorptivity at these wavelengths (λ = 660 nm, 700 nm and 980 nm) is considerably higher for the P = 0.5 μm with 0.6, 0.88 and 0.09 compared with P = 1 μm absorptivity of 0.09, 0.05 and 0.001, respectively. Clearly, unlike the coalescence of NP arrays in which the increased absorptivity is entirely due the higher filling ratio, the coalescence of LF arrays generates higher absorptivity that is a result of higher filling ratio coupled with higher absorption cross-section of the individual LFs. This suggests that light trapping in LF arrays is driven by weak and/or strong field overlap. Fig. 4c and d present intensity x-cut (see ESI† for intensity y-cut) of NPs for λ = 480 nm and 580 nm and LFs for λ = 700 nm and 980 nm for the different periodicities, respectively. Again, the nature of light trapping in NP arrays is entirely different from light trapping in LF arrays; evidently, NPs are more strongly excited when isolated (consistent with the discussion above), whereas for LFs the excitation increases with decreasing periodicity. In other words, the origin of the absorption peaks in dense NP array is strong excitations of isolated NPs, that are somewhat decreased upon increase in array density coupled with a high filling ratio; hence, unlike LF arrays, field overlap in NP arrays is detrimental to the absorptivity and therefore no weak or strong overlap is observed. On the other hand, in LF arrays the absorption peaks are due to weak or strong optical overlap coupled with higher filling ratio.
Conclusions
LF arrays are a promising approach toward the efficient harvesting of the solar spectrum as well as interesting and insightful system for the investigation of coupling light into matter. In the current work we identified the underlying mechanism for light trapping in LF arrays, and we demonstrated how this mechanism is different from light trapping in optimized NP arrays. We believe the underlying mechanism of light trapping in LF arrays could also be utilized to provide design rules for the development of other light trapping schemes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support by the Israel Ministry of Energy.References
- J. R. Maiolo, B. M. Kayes, M. D. Kelzenberg, M. A. Filler, M. C. Putnam, H. A. Atwater and N. S. Lewis, High Aspect Ratio Silicon Wire Array Photoelectrochemical Cells, J. Am. Chem. Soc., 2007, 129, 12346–12347 CrossRef CAS PubMed.
- Y. Nishijima, K. Ueno, Y. Kotake, K. Murakoshi, H. Inoue and H. Misawa, Near-Infrared Plasmonassisted Water Oxidation, J. Phys. Chem. Lett., 2012, 3(10), 1248–1252 CrossRef CAS PubMed.
- D. B. Ingram and S. Linic, Water Splitting on Composite Plasmonic-Metal/Semiconductor Photoelectrodes: Evidence for Selective Plasmon-Induced Formation of Charge Carriers near the Semiconductor Surface, J. Am. Chem. Soc., 2011, 133(14), 5202–5205 CrossRef CAS PubMed.
- K. T. Fountaine, W.-H. Cheng, C. R. Bukowsky and H. A. Atwater, Near-Unity Unselective Absorption in Sparse InP Nanowire Arrays, ACS Photonics, 2016, 3(10), 1826–1832 CrossRef CAS.
- E. Yablonovitch, Statistical Ray Optics, J. Opt. Soc. Am., 1982, 72(7), 899 CrossRef.
- I. Tobías, A. Luque, A. Martí, I. Tobías, A. Luque and A. Martí, Light Intensity Enhancement by Diffracting Structures in Solar Cells Light Intensity Enhancement by Diffracting Structures in Solar Cells, J. Appl. Phys., 2008, 104, 034502 CrossRef.
- P. W. Anderson, Absence of Diffusion in Certain Random Lattices, Phys. Rev., 1958, 109, 1492–1505 CrossRef CAS.
- Z. Yu, A. Raman and S. Fan, Fundamental Limit of Nanophotonic Light Trapping in Solar Cells, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(41), 17491–17496 CrossRef CAS PubMed.
- C. Rockstuhl and F. Lederer, Photon Management by Metallic Nanodiscs in Thin Film Solar Cells, Appl. Phys. Lett., 2009, 94(213102), 1–3 Search PubMed.
- S. Mokkapati, F. J. Beck, A. Polman, K. R. Catchpole, S. Mokkapati, F. J. Beck, A. Polman and K. R. Catchpole, Designing Periodic Arrays of Metal Nanoparticles for Light-Trapping Applications in Solar Cells, Appl. Phys. Lett., 2009, 95(053115), 1–4 Search PubMed.
- B. R. A. Pala, J. White, E. Barnard, J. Liu and M. L. Brongersma, Design of Plasmonic Thin-Film Solar Cells with Broadband Absorption Enhancements, Adv. Mater., 2009, 21, 3504–3509 CrossRef.
- L. Hu and G. Chen, Analysis of Optical Absorption in Silicon Nanowire Arrays for Photovoltaic Applications, Nano Lett., 2007, 7(11), 3249–3252 CrossRef CAS PubMed.
- P. Spinelli, M. A. Verschuuren and A. Polman, Broadband Omnidirectional Antireflection Coating Based on Subwavelength Surface Mie Resonators, Nat. Commun., 2012, 3, 692 CrossRef CAS PubMed.
- S. K. Kim, X. Zhang, D. J. Hill, K. D. Song, J. S. Park, H. G. Park and J. F. Cahoon, Doubling Absorption in Nanowire Solar Cells with Dielectric Shell Optical Antennas, Nano Lett., 2015, 15(1), 753–758 CrossRef CAS PubMed.
- Y. Li, M. Li, P. Fu, R. Li, D. Song, C. Shen and Y. Zhao, A Comparison of Light-Harvesting Performance of Silicon Nanocones and Nanowires for Radial-Junction Solar Cells, Sci. Rep., 2015, 5, 11532 CrossRef CAS PubMed.
- A. B. Wong, S. Brittman, Y. Yu, N. P. Dasgupta and P. Yang, Core-Shell CdS-Cu2S Nanorod Array Solar Cells, Nano Lett., 2015, 15(6), 4096–4101 CrossRef CAS PubMed.
- A. Nowzari, M. Heurlin, V. Jain, K. Storm, A. Hosseinnia, N. Anttu, M. T. Borgström, H. Pettersson and L. Samuelson, A Comparative Study of Absorption in Vertically and Laterally Oriented InP Core-Shell Nanowire Photovoltaic Devices, Nano Lett., 2015, 15(3), 1809–1814 CrossRef CAS PubMed.
- J. Wallentin, N. Anttu, D. Asoli, M. Huffman, I. Aberg, M. H. Magnusson, G. Siefer, P. Fuss-Kailuweit, F. Dimroth and B. Witzigmann, et al., InP Nanowire Array Solar Cells Achieving 13.8% Efficiency by Exceeding the Ray Optics Limit, Science, 2013, 339(6123), 1057–1060 CrossRef CAS PubMed.
- G. Vescovi, D. Asoli, U. Naseem, J. P. Gilboy, C. Sundvall, A. Dahlgren, K. E. Svensson, N. Anttu, M. T. Bj and L. Samuelson, A GaAs Nanowire Array Solar Cell with 15.3% Efficiency at 1 Sun, IEEE Journal of Photovoltaics, 2016, 6(1), 185–190 Search PubMed.
- G. Shalev, S. Schmitt, G. Brönstrup and S. Christiansen, Maximizing the Ultimate Absorption Efficiency of Vertically-Aligned Semiconductor Nanowire Arrays with Wires of a Low Absorption Cross-Section, Nano Energy, 2015, 12, 801–809 CrossRef CAS.
- Y.-F. Huang, S. Chattopadhyay, Y.-J. Jen, C.-Y. Peng, T.-A. Liu, Y.-K. Hsu, C.-L. Pan, H.-C. Lo, C.-H. Hsu and Y.-H. Chang, et al., Improved Broadband and Quasi-Omnidirectional Anti-Reflection Properties with Biomimetic Silicon Nanostructures, Nat. Nanotechnol., 2007, 2(12), 770–774 CrossRef CAS PubMed.
- S. Jeong, M. D. McGehee and Y. Cui, All-Back-Contact Ultra-Thin Silicon Nanocone Solar Cells with 13.7% Power Conversion Efficiency, Nat. Commun., 2013, 4(May), 2950 CrossRef PubMed.
- H. Savin, P. Repo, G. von Gastrow, P. Ortega, E. Calle, M. Garín and R. Alcubilla, Black Silicon Solar Cells with Interdigitated Back-Contacts Achieve 22.1% Efficiency, Nat. Nanotechnol., 2015, 10, 1–6 CrossRef PubMed.
- M. L. Brongersma, Y. Cui and S. Fan, Light Management for Photovoltaics Using High-Index Nanostructures, Nat. Mater., 2014, 13(5), 451–460 CrossRef CAS PubMed.
- E. Garnett and P. Yang, Light Trapping in Silicon Nanowire Solar Cells, Nano Lett., 2010, 10(3), 1082–1087 CrossRef CAS PubMed.
- E. R. Martins, J. Li, Y. Liu, V. Depauw, Z. Chen, J. Zhou and T. F. Krauss, Deterministic Quasi-Random Nanostructures for Photon Control, Nat. Commun., 2013, 4, 2665 CrossRef PubMed.
- M.-C. van Lare and A. Polman, Optimized Scattering Power Spectral Density of Photovoltaic Light-Trapping Patterns, ACS Photonics, 2015, 2(7), 822–831 CrossRef CAS.
- A. Gaucher, A. Cattoni, C. Dupuis, W. Chen, R. Cariou, M. Foldyna, L. Lalouat, E. Drouard, C. Seassal and P. Roca I Cabarrocas, et al., Ultrathin Epitaxial Silicon Solar Cells with Inverted Nanopyramid Arrays for Efficient Light Trapping, Nano Lett., 2016, 16(9), 5358–5364 CrossRef CAS PubMed.
- J. He, P. Gao, M. Liao, X. Yang, Z. Ying, S. Zhou, J. Ye and Y. Cui, Realization of 13.6% Efficiency on 20 Mm Thick Si/Organic Hybrid Heterojunction Solar Cells via Advanced Nanotexturing and Surface Recombination Suppression, ACS Nano, 2015, 9(6), 6522–6531 CrossRef CAS PubMed.
- Z. Y. Wang, R. J. Zhang, S. Y. Wang, M. Lu, X. Chen, Y. X. Zheng, L. Y. Chen, Z. Ye, C. Z. Wang and K. M. Ho, Broadband Optical Absorption by Tunable Mie Resonances in Silicon Nanocone Arrays, Sci. Rep., 2015, 5, 7810 CrossRef CAS PubMed.
- P. Sheng, A. N. Bloch and R. S. Stepleman, Wavelength-Selective Absorption Enhancement in Thin-Film Solar Cells Wavelength-Selective Absorption Enhancement in Thin-Film Solar Cells, Appl. Phys. Lett., 1983, 43(6), 579–581 CrossRef CAS.
- Z. Yu, A. Raman and S. Fan, Fundamental Limit of Light Trapping in Grating Structures. Opt, Express, 2010, 18(53), 366–380 CrossRef PubMed.
- D. M. Callahan, J. N. Munday and H. a. Atwater, Solar Cell Light Trapping beyond the Ray Optic Limit, Nano Lett., 2012, 12(1), 214–218 CrossRef CAS PubMed.
- E. D. Kosten, E. L. Warren and H. A. Atwater, Ray Optical Light Trapping in Silicon Microwires: Exceeding the 2n(2) Intensity Limit. Opt, Express, 2011, 19(4), 3316–3331 CrossRef CAS PubMed.
- B. C. P. Sturmberg, K. B. Dossou, L. C. Botten, A. A. Asatryan, C. G. Poulton, C. M. de Sterke and R. C. McPhedran, Modal Analysis of Enhanced Absorption in Silicon Nanowire Arrays. Opt, Express, 2011, 19(S5), A1067 CrossRef CAS PubMed.
- C. Lin and M. L. Povinelli, Optical Absorption Enhancement in Silicon Nanowire Arrays with a Large Lattice Constant for Photovoltaic Applications. Opt, Express, 2009, 17(22), 19371–19381 CrossRef CAS PubMed.
- G. Shalev and S. W. Schmitt, Embrechts, Heidemarie Brönstrup, G.; Christiansen, S. Enhanced Photovoltaics Inspired by the Fovea Centralis, Sci. Rep., 2015, 5, 8570 CrossRef CAS PubMed.
- A. Prajapati, Y. Nissan, T. Gabay and G. Shalev, Broadband Absorption of the Solar Radiation with Surface Arrays of Subwavelength Light Funnels, Nano Energy, 2018, 54, 447–452 CrossRef CAS.
- A. Prajapati, Y. Nissan, T. Gabay and G. Shalev, Light Trapping with Silicon Light Funnel Arrays, Materials, 2018, 11(3), 1–9 CrossRef PubMed.
- A. Prajapati, A. Chauhan, D. Keizman and G. Shalev, Approaching the Yablonovitch Limit with Free-Floating Arrays of Subwavelength Trumpet Non-Imaging Light Concentrators Driven by Extraordinary Low Transmission, Nanoscale, 2019, 11, 3681–3688 RSC.
- S. S. P. Konedana, E. Vaida, V. Viller and G. Shalev, Optical Absorption beyond the Yablonovitch Limit with Light Funnel Arrays, Nano Energy, 2019, 59, 321–326 CrossRef CAS.
- G. Marko, A. Prajapati and G. Shalev, Broadband Absorption of the Solar Radiation with Arrays of Subwavelength Nonimaging Light Concentrators, Nano Energy, 2019, 61, 275–283 CrossRef CAS.
- K. T. Fountaine, C. G. Kendall and H. A. Atwater, Near-Unity Broadband Absorption Designs for Semiconducting Nanowire Arrays via Localized Radial Mode Excitation. Opt, Express, 2014, 22(S3), A930 CrossRef CAS PubMed.
- E. D. Palik, Handbook of Optical Constants of Solids, Academic, 1985 Search PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-VCH, Weinheim, 1998, Vol. 16 Search PubMed.
- F. J. Bezares, J. P. Long, O. J. Glembocki, J. Guo, R. W. Rendell, R. Kasica, L. Shirey, J. C. Owrutsky and J. D. Caldwell, Mie Resonance-Enhanced Light Absorption in Periodic Silicon Nanopillar Arrays, Opt. Express, 2013, 21(23), 287–291 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00711c |
| This journal is © The Royal Society of Chemistry 2020 |