Solid wetting-layers in inorganic nano-reactors: the water in imogolite nanotube case

Abstract

By combined use of wide-angle X-ray scattering, thermo-gravimetric analysis, inelastic neutron scattering, density functional theory and density functional theory molecular dynamics simulations, we investigate the structure, dynamics and stability of the water wetting-layer in single-walled aluminogermanate imogolite nanotubes (SW Ge-INTs): an archetypal system for synthetically controllable and monodisperse nano-reactors. We demonstrate that the water wetting-layer is strongly bound and solid-like up to 300 K under atmospheric pressure, with dynamics markedly different from that of bulk water. Atomic-scale characterisation of the wetting-layer reveals organisation of the H₂O molecules in a curved triangular sublattice stabilised by the formation of three H-bonds to the nanotube's inner surface, with covalent interactions sufficiently strong to promote energetically favourable decoupling of the H₂O molecules in the adlayer. The evidenced changes in the local composition, structure, electrostatics and dynamics of the Ge-INT's inner surface upon the formation of the solid wetting-layer demonstrate solvent-mediated functionalisation of the nanotube's cavity at room temperature and pressure, suggesting new strategies for the design of nano-rectors towards potential control of chemical reactivity in nano-confined volumes.

---

1 Introduction

Nano-confinement of reactants, reaction solvent, and (co-)catalysts is a by now established route to the creation of local chemical environments markedly different from the corresponding bulk-phase analogues.^1–9 Driven by the often unexpected and appealing effects of nano-confinement on chemical and physical properties, development of nano-reactors towards rational control of chemical reactivity by design has turned into one of the most thriving areas of contemporary research in chemistry.^10–21 For such a control to be truly rational, accurate understanding of the atomistic details of a given reaction in terms of stoichiometry, structure and interactions is required, together with quantification of the mutual effects that the nano-confined species and the nano-confining reactor exert on one another. However, to our knowledge, this has not been achieved to date with simultaneous resolution of the systems' stoichiometry, structure and dynamics.^1–21

Taking the first steps towards a generalised solution to this unfortunate stalemate, here we illustrate the combined use of Thermo-Gravimetric Analysis (TGA), Wide-Angle X-ray Scattering (WAXS), Inelastic Neutron Scattering (INS) and Density Functional Theory Molecular Dynamics (DFT-MD) simulations for quantitative resolution of the atomistic details of the intimate interface between an archetypal quaternary alumino-germanate imogolite nanotube and, the most ubiquitous among the inorganic solvents, water. The combined approach enables quantitative characterisation of the intimate nanotube–water interface in terms of its atomic structure, dynamics and mutual effects at play in the temperature range between 10 K and room temperature (300 K) at ∼1 bar pressure, laying the basis for a systematic study of the effects of different water-soluble reactants in the nano-reactor considered.

Even in its bulk form, water shows ‘anomalous' properties compared to most liquids. These anomalies stem from the specific local tetrahedral organisation of its hydrogen bond network.^22,23 This network can be significantly modified when water is confined in one^24–26 or two dimensions,²⁷ inducing electronic re-hybridisation at the interface with the nano-confining container²⁸ and the emergence of new physico-chemical properties. Examples include the emergence of a new state of square ice²⁹ in graphene nanocapillaries, which has been shown to respond to the presence of ions by forming ultralong polarisation chains,³⁰ or the coexistence of different phases of two-dimensional water in hydrophilic nanoporous materials.²⁷ The potential of nano-confinement induced, emergent new states of water for sustainable energy and nanofluidics applications has also been recently recognised,³¹ motivating a growing number of studies ranging from development of high-voltage aqueous electrolyte lithium-ion batteries^32,33 to innovative proton³⁴ and water transport³⁵ strategies.

In all these cases, the physico-chemical properties of the emergent states for the nano-confined phases of water are typically rationalised in terms of distortions in the local tetrahedral environment and/or in terms of frustration of its hydrogen-bond network, as evidenced experimentally,^26,36 with very limited effects on the nano-confining host.

Definition of suitable nano-containers, enabling extremely low loading of nano-confined water, and resulting in physical decoupling of the nano-confined water molecules, has also been achieved, revealing exciting new low-temperature quantum physics. Examples of decoupled water molecules in the literature range from the isolation and characterisation of metastable ortho water in endohedral H₂O@C₆₀ composites³⁷ to tunnelling delocalised quantum states for the protons of water nano-confined in the beryl mineral.³⁸

However, in spite of the many recent achievements, quantitative characterisation of the role of nano-container/water interactions and mutual effects on the composite's structure and dynamics at chemistry relevant temperatures is, to the best of our knowledge, missing, motivating the present study. Additional motivations for the present study can be found in the current lack of proof of concepts on whether nano-reactors of suitably tailored surfaces can induce, by means of favourable chemical interactions, room temperature, standard pressure decoupling of the nano-confined water molecules. We recall that, to date, decoupling of nano-confined water molecules in nanoporous materials has only been achieved by physical separation in the small cavities (5.1 Å diameter) of beryl³⁸ which, together with the presence of even narrower (∼2.8 Å diameter) bottlenecks, limits the system's appeal as a viable nano-reactor.

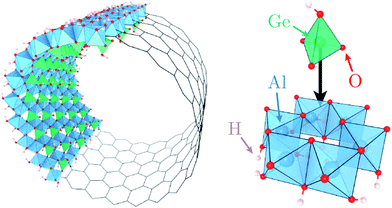
Motivated by these elements, here we characterise quantitatively the structure and dynamics of one mono-layer of water adsorbed on the inner surface of a quaternary oxide nanotube of the imogolite family,³⁹ specifically a single-walled (SW) aluminogermanate GeAl₂O₇H₄ imogolite-like nanotube (Ge-INT). The inner diameter of the SW Ge-INT is about 2.8 nm,⁴⁰ ∼5.5 times that of the larger cavities (5.1 Å) in beryl,³⁸ allowing water loading substantially higher than one H₂O molecule per periodic repeat unit. The Ge-INT's wall consists of an octahedral gibbsite-like layer [Al(OH)₃] with isolated O₃GeOH tetrahedron units sharing three oxygen atoms, Fig. 1. The presence of dangling hydroxyl OH groups warrants strong hydrophilicity of the inner cavity, offering competing interactions to the water–water ones.

Fig. 1 Polyhedral representation of a SW Ge-INT where O₃Al(OH)₃ octahedra (in blue) are arranged to form a honeycomb network and O₃GeOH tetrahedra (in green) are placed right above each octahedral cavity.

By combining DFT-MD simulations and INS measurements on samples with quantitatively resolved atomic structure and water loading, we demonstrate that the nanotube–water interactions are sufficiently strong to (i) create a stable wetting-layer that, at room pressure (1 bar), remains solid up to 300 K, (ii) decouple the water molecules in the wetting-layer, leading to the emergence of a novel two-dimensional (2D) curved structure in which water molecules are bound exclusively to the nanotube's germanol groups, and (iii) significantly alter the dynamics of the hosting nanotubes with water-induced softening of the nanotubes' inner hydroxyl stretching modes as large as ∼150 meV (∼1210 cm⁻¹). Notably, the 2D nanotube–water interface is observed to present consistently harmonic dynamics in the 10–300 K temperature range. These results pave the way to a systematic study of the effects of different water loadings and water-soluble reactants in complex oxide-based nanoreactors starting from, but not limited to, the imogolite family.

2 Methods

The procedure used to synthesise SW Ge-INTs and to prepare powder samples is described in ref. 40 and 41. Nanotubes are separate (not bundled) in the powder (see the inset in Fig. S2 in the ESI†). The same powder sample was used in two different states for INS experiments: a partially hydrated (pHyd) state, with a water wetting-layer in the cavity, and a dry state. The pHyd state is obtained by preheating the sample for 12 hours at 90 °C, whereas the dry state is obtained by heating it at 220 °C. The sample was sealed in an aluminium cell after heating, so that the pressure is about 1 bar at room temperature. Based on thermogravimetric analysis (reported in the ESI†), treatment at 90 °C is sufficient to cause desorption of additional water from the nanotube's cavity and its relatively hydrophobic outer (AlOH decorated) surfaces.^42,43

DFT geometric optimisations at 0 K and DFT-MD simulations at 150 K were performed with the CP2K/Quickstep package.⁴⁴ Computational details can be found in the ESI.† Two models were considered for the simulations: a water-devoid dry nanotube (dry) and a nanotube with a water wetting-layer in the cavity (pHyd), with a one-to-one ratio between the water molecules and germanium atoms in the system, as per the results of the thermogravimetric analysis.

For the nanotube itself, its chiral indices and axial period were determined from the X-ray scattering diagram obtained by following the methodology developed in ref. 45 and detailed in the ESI.† DFT and DFT-MD simulations were accordingly carried out on a nanotube of chiral parameter equal to (22, 0) with twenty-two Ge atoms along the circumference. One tubular unit cell comprises forty-four GeAl₂O₇H₄ units.

Inelastic neutron scattering investigations were performed using the neutron spectrometers IN4C and IN1-LAGRANGE at the Institut Laue-Langevin. On IN1-LAGRANGE, measurements were done at 10 K, while on IN4C the evolution of the spectra was investigated in the temperature range from 10 K to 300 K. On IN4C, inelastic spectra were recorded using a set of two incident neutron wavelengths λ = 0.9 Å and 1.7 Å, with the largest wavelength allowing the measurement of low frequency modes. The raw data were normalised to incoming flux and corrected from the sample holder contribution by measuring an empty cell under the same conditions. IN4C data were rescaled to merge with IN1 data around 60 meV, to provide a single spectrum over a large energy range, from a few meV to 500 meV. Data were processed to obtain the so-called generalised density of state (GDOS) which is a neutron weighted observable.⁴⁶

3 Results and discussion

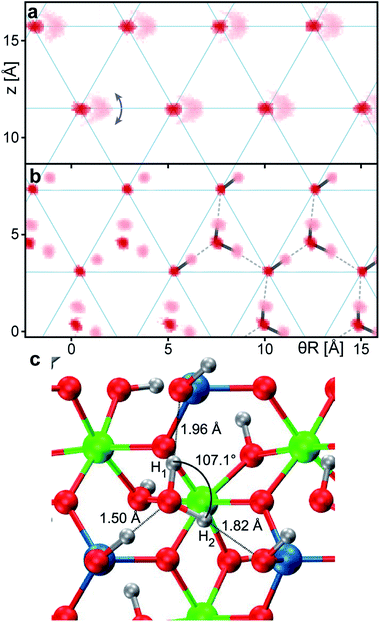
Fig. 2a and b show the atomic density maps calculated from the DFT-MD trajectories for the dry and pHyd nanotube, respectively. As shown in Fig. 2a, the nanotube's inner oxygen atoms are arranged in a triangular lattice. DFT-MD simulations reveal peculiarly large (∼1 Å) amplitude motions for the inner hydrogen atoms, H_in (also see Fig. S4a†). These large amplitude motions are suppressed by the presence of the water wetting-layer (Fig. 2b), pointing to strong interactions between the nanotubes and the water molecules. The water molecules form a strongly bound wetting-layer with an adsorption energy (E_ads) of −0.712 eV per H₂O molecule at the PBE level. Due to the very favourable interactions with the nanotube's inner surface, the wetting-layer sits very close to the surface of the nanotube, with radial distances between the water oxygen atoms and the nanotube's H_in being shorter than 1 Å (Fig. S4b†). As shown in Fig. 2b, the water molecules in the wetting-layer arrange in an ordered triangular sublattice, where only one triangular site over two in-between germanol groups is occupied by a water molecule. Each water molecule forms three H-bonds with the germanol groups of the Ge-INT’s inner surface, satisfying the geometric H-bonding criteria proposed in ref. 47. Optimisation of the pHyd Ge-INT's geometry reveals asymmetric adsorption of the H₂O molecules on the Ge-INT's inner surface, leading to one very short (1.50 Å) H-bond and two larger (1.82 Å and 1.96 Å) ones (see Fig. 2). Importantly, with the shortest H₂O–H₂O intermolecular distance of 3.15 Å, there are no additional H-bonds between water molecules in the layer.

Fig. 2 DFT-MD atomic density colour map (T = 150 K) for (a) the dry Ge-INT and (b) the partially hydrated (pHyd) Ge-INT. The horizontal axis corresponds to the curvilinear coordinate along a circle of radius R, the mean radial atomic coordinate; the vertical axis is the z coordinate along the nanotube axis. Oxygen and hydrogen densities are shown in red and pink, respectively. Only the inner O and H atoms of the Ge-INT's wall are shown for the sake of clarity. The O atoms of the nanotube form a triangular lattice, marked in light blue. The arrow in (a) marks the large amplitude motion of inner hydroxyls, H_in in the dry nanotube. On the right part of (b), continuous grey lines represent the OH bonds within the water molecule. Dotted grey lines highlight the H-bonds in the system. (c) DFT optimised geometry (T = 0 K) for the pHyd Ge-INT with the corresponding H-bond distances. Al: green, Ge: blue, O: red, H: grey.

To the best of our knowledge, such a configuration and decoupling have not been previously observed for water in differently hydrophilic structures^27,48 or on metal⁴⁹ adsorption substrates, pointing to a critical role of the triangular GeOH lattice (Fig. 2a) in promoting interactions sufficiently large to induce separation of the H₂O molecules in the adlayer. We return to this point at the end of this section by quantifying the different interactions at play in the pHyd Ge-INT.

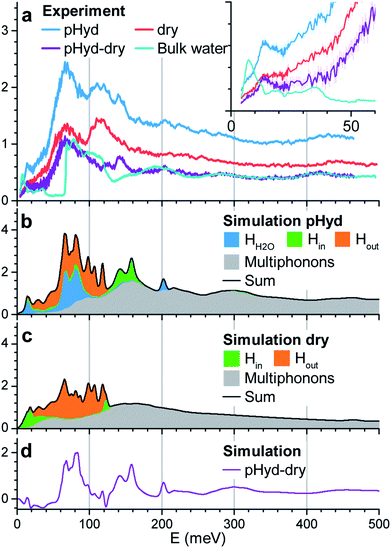
We now turn to INS study of the dry and pHyd nanotubes and the ensuing quantification of the role of the water–nanotube interactions in the dynamics of the composite system. Given the very large incoherent neutron cross-section for H atoms, only the vibrations of the hydrogen atoms contribute to the experimental generalised density of state (GDOS). Fig. 3a reports the GDOS of the pHyd and dry Ge-INTs at T = 10 K§, and their difference spectrum, together with the GDOS for a pure water sample (hereafter referred to as bulk water).

Fig. 3 (a) Generalised densities of states (GDOS) for the dry nanotubes (red trace), the partially hydrated (pHyd) nanotubes (blue) and bulk ice (cyan). Experiments were performed at 10 K. The difference between the GDOS for the dry and pHyd nanotubes is shown in purple. The inset reports a zoom in image of the data in the 0–60 meV range. (b and c) DFT-MD derived GDOS (T = 150 K) for the pHyd (b) and dry (c) nanotubes (solid black line). The calculated GDOS for the nanotube's inner (H_in) and outer (H_out) H atoms are displayed as orange and green filled peaks, respectively. The calculated GDOS for the H atoms of the water molecules (H_H2O) is shown as blue filled peaks. The grey area corresponds to the multiphonon contribution. (d) Difference between the calculated total GDOS for the pHyd and dry nanotubes.

Since the neutron intensity is directly proportional to the number of H atoms present in the sample, one can derive the water content of the pHyd nanotube by first integrating the difference spectrum, and dividing the result by the integral of the pHyd spectrum. The procedure returns an intensity loss of ∼39%, in good agreement with the amount of water estimated from thermogravimetric analysis, which was one molecule of water H₂O per GeAl₂O₇H₄ entity (33% hydrogen loss on drying).

As evident from Fig. 3a, the drying process, leading to complete removal of H₂O from the nanotube, affects significantly the measured GDOS: the intensity of the low energy peak at about 15 meV for the pHyd sample is strongly reduced for the dry nanotube (see the inset in Fig. 3a). The same conclusion holds for the intense and broad band with maximum intensity at ∼70 meV.

The measured spectrum of bulk water is dominated by a broad asymmetric contribution centred at ∼70 meV and shows an almost identical profile to the difference spectrum above ∼160 meV. Based on these similarities, one can attribute the peaks at ∼70 meV and ∼200 meV to, respectively, the libration and bending modes of the H₂O molecules in the wetting-layer.

The low-energy range (≤50 meV) of the INS spectrum for bulk water is dominated by vibrational translational modes around 6 meV and between 20 and 35 meV.⁵⁰ These modes are well separated by a 20 meV gap from the sharp onset of the libration band (∼60 meV). In the difference spectrum, a well-defined peak at 15 meV is found. Then, the GDOS-intensity increases continuously at higher energies, filling the gap up to the libration band. Additional peaks are also clearly visible in the difference spectrum around ∼125 meV and 145 meV. As these peaks are not present for bulk water, and are sensitive to the presence of the wetting-layer, they necessarily stem from vibrations specific to the intimate H₂O–Ge-INT interface. Although they cannot be unambiguously assigned to either H₂O or Ge-INT specific vibrations on the basis of the INS results alone, the availability of MD-DFT simulations enables us to overcome this shortcoming.

We simulated atom-resolved GDOS from the DFT-MD trajectories and the corresponding atom-specific velocity autocorrelation functions (VACFs), as detailed in the ESI.† DFT-MD trajectories were propagated at 150 K (not 10 K) to allow for a computationally faster equilibration of the system and thermalisation of the constituting atoms. Fig. 3b and c report the calculated GDOS for the dry and pHyd Ge-INTs, together with the corresponding difference. Spectral filtering, detailed in the ESI,† allows straightforward visualisation of the atomic displacements contributing to the vibrational modes in a selected energy window.

The simulated GDOS for the pHyd nanotube (Fig. 3b) reproduces closely the major features of the experimental data. The peaks in the GDOS for the water molecules of the wetting-layer can be readily assigned to a bending mode at 200 meV (Fig. S10c†), a wide librational band starting at ∼40 meV (see Fig. S10b†), and an additional mode centred around 15 meV. This mode is specific to the H₂O molecules in the wetting-layer. It corresponds to local translational motions of the whole water molecule trapped in the triangular germanol site (see Fig. S10a†). These translational motions involve displacements in the three directions of space, both within the plane locally parallel to the nanotube wall and perpendicular to it, with amplitudes of about 0.1 Å.

The Ge-INT's contributions to the simulated spectrum are due to (i) modes involving displacements of the H atoms of the inner germanol groups (H_in modes) and (ii) modes involving displacements of the H atoms of the aluminol groups on the outer surface of the nanotube (H_out modes). For the pHyd nanotube, the H_out modes contribute to the 20–130 meV energy window. Conversely, the H_in modes are clustered in a doubly peaked feature with maximum intensities at around 140 meV and 160 meV (Fig. 3b). Interestingly, the wagging modes of terminal hydroxyls on the (110) surface of rutile-structured tin oxide are calculated at the same energies.⁵¹ This doubly peaked feature is clearly visible also in the experimental difference spectrum, although at slightly smaller energies (125 meV and 145 meV), so that it can now be assigned to the H_in modes. Also according to the simulations, the two peaks are associated with scissoring and twisting modes of the Ge–O–H fragment, respectively. As shown in Fig. S9a and b,† the twisting mode corresponds to the displacement of the H atom in a plane locally parallel to the inner surface of the nanotube. Conversely, the scissoring mode corresponds to bending of the Ge–O–H fragment towards and away from the Ge-INT's surface.

In contrast to the H_out modes, the H_in twisting and scissoring modes are found to be highly sensitive to the presence of the wetting-layer (Fig. 3c). Specifically, in the absence of interacting H₂O molecules, the scissoring mode is softened to about 120 meV while the twisting mode is broadened and downshifted to about 20 meV. Its softening is responsible for the negative values below 50 meV in the difference spectrum between the calculated GDOS of the pHyd and dry nanotubes in Fig. 3d.

No negative values are observed in the experimental GDOS-difference shown in Fig. 3a. However, analysis of the atomic displacements for the twisting mode reveals large amplitude motions of the H_in atoms (Fig. S8b†), already visible in Fig. 2a. Accordingly, harmonic approximation of the system's vibrations, implicit in the approach used to calculate vibrational DOS from the VACF,⁵² should not hold for this mode, causing the observed deviations between experimental and calculated GDOS traces. Regardless of the quantitative disagreement between the calculated and experimental GDOS differences below 50 meV, the conclusion of a very soft local potential determining the orientation of the inner OH bonds in dry Ge-INTs should thus be qualitatively correct. The spectral signature of such an anharmonic movement is closer to that of a diffusive mode (in the form of a quasielastic scattering) or of a damped harmonic oscillator than to a classical molecular vibration. Its observation is, therefore, conditioned by the energy resolution of the spectrometer. More experimental insights into the H_in twisting could thus be obtained thanks to quasi-elastic experiments with different energy windows.

Above 50 meV, it is interesting to note the rather good agreement between the GDOS measured at 10 K and calculated at 150 K. Except for the H_in twisting in the dry Ge-INT, the vibrational modes do not imply particularly large amplitude motions. Therefore one can reasonably consider them as rather harmonic between 10 K and 150 K, so that the corresponding features in the GDOS should not be strongly temperature dependent.

The observed sensitivity of the low energy, large amplitude twisting mode for the Ge-INT's H_in atoms invites comparison and discussion against available results for the chemically analogous, yet synthesised under different conditions,⁵³ double-walled (DW) Ge-INT. In spite of the same composition, SW Ge-INTs have an inner diameter (2.8 nm) twice as large as DW Ge-INTs (1.4 nm).^40,54 Accordingly, H-bonding interactions between the H_in atoms in DW Ge-INTs are expected to be stronger than those in SW Ge-INTs and thus our conclusions on highly flexible inner O–H_in bonds in dry SW Ge-INTs may not be transferable to DW-INTs. Importantly, analysis of the shape of the stretching band measured by infrared spectroscopy for DW Ge-INTs at low relative humidity ratio⁵⁵ indicates four-fold (not three-fold) coordination for the water molecules wetting the inner surfaces of DW Ge-INTs. Given the DW Ge-INTs' 1.4 nm inner diameter, and the geometry of H₂O, four-fold coordination of water molecules is necessarily achieved by the mixing of H₂O–H₂O and H₂O–INT H-bonding in the wetting-layer, as in aluminosilicate imogolite nanotubes.⁵⁶ Altogether, these elements point to the composition, local structure and curvature of the SW Ge-INTs as being crucial for the occurrence of suitably spaced, thence weakly H-bonded and highly flexible O–H_in bonds in the dry INT, which can in turn adjust optimally to the H₂O molecules in the wetting-layer. The increase of the nanotube's curvature (decrease of its diameter) leads to highly mobile and labile wetting-layers or clusters, with mixed H₂O–H₂O and H₂O–INT H-bonding connectivity.

Fig. 4 reports a comparison between the temperature dependent GDOS for bulk water and the Ge-INT H₂O wetting-layer in the 10–300 K range. We recall that, as shown in Fig. 3, the difference between the GDOS for the dry and pHyd Ge-INTs contains only the water translational mode and a librational component in the 1–80 meV energy window. Thus, the GDOS results in this energy window are exclusively due to the water wetting-layer on the Ge-INT's inner surface. The bulk water spectrum reveals the anharmonic character of the lattice modes, with progressive broadening and damping of the GDOS features with an increase of temperature from 10 K to 250 K. The melting to the liquid state is further demonstrated by the complete loss of the ice characteristic translational modes at 300 K. By contrast, the trace for the wetting-layer results to be almost temperature independent. This shows that the structure of the wetting-layer is kept unchanged and its dynamics are rather harmonic up to temperatures as high as 300 K, reiterating an extremely strong affinity adsorption between the Ge-INT's inner surface and the H₂O wetting-layer. This observation demonstrates that the H₂O wetting-layer remains solid-like up to 300 K. Finally, it should be noted here that the diffusion of water molecules into the first layer of two-dimensional oxide surfaces can also be considerably reduced by strong hydrogen bonds with the surface.⁵⁷

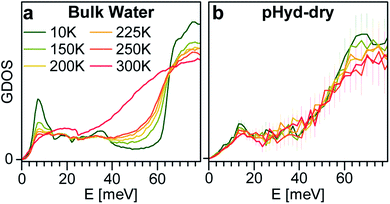Fig. 4 Generalised density of state (GDOS) as a function of temperature: (a) bulk water and (b) GDOS of pHyd nanotubes minus GDOS of dry nanotubes.

DFT simulations suggest that the increased resilience to melting of the wetting-layer with respect to bulk water stems from the strong interactions experienced by the H₂O in contact with the Ge-INT. At the PBE level, the calculated cohesive energy (E_coh) for hexagonal I_h ice is −0.666 eV per molecule, in semi-quantitative agreement with previously published PBE results for more extended basis-sets than those used here (TZV2P: −0.706 eV per molecule, QZV2P: −0.678 eV per molecule).⁵⁸ For the H₂O molecules in the wetting-layer, the calculated E_ads is −0.712 eV per molecule. E_coh and E_ads, defined in the ESI,† are conceptually equivalent and can be directly compared. Such a comparison indicates that in spite of the reduced number of H-bonds (three instead of four), the water molecules are more strongly bonded in the wetting-layer than in ice. We thus find that the formation of three 1.50 Å, 1.80 Å and 1.96 Å H-bonds, as present in the wetting-layer, is energetically favoured over formation of four 1.77 Å H-bonds, as present in the optimised structure of ice I_h. Calculation of the harmonic zero-point vibrational energies (ZPEs, defined in the ESI†) for the H₂O molecules in I_h ice (0.498 eV per molecule) and in the wetting-layer (0.526 eV per molecule) does not alter this conclusion. Addition of the vibrational ZPE to the calculated E_ads (E_coh) of the wetting-layer (I_h ice) results in corrected energies of −0.186 eV per molecule (−0.168 eV per molecule).

Analysis of the pHyd Ge-INT's atom-projected electronic density of states (PDOS) enables one to appreciate why the H₂O–Ge-INT interactions in the pHyd Ge-INT are stronger than the H₂O–H₂O ones in I_h ice. For the sake of clarity, we recall that the electronic PDOS is to be understood as the atom-specific contribution to the number of (Kohn–Sham DFT) electronic states per unit of energy for the adopted simulation cell, that is, the energy-dependent atom-specific contribution to the Kohn–Sham states (eigenvalues) at 0 K.

Fig. 5a shows the electronic rehybridisation between the Ge-INT and the H₂O molecules, leading to broader H₂O-PDOS features spanning most of the Ge-INT's valence band (VB) and indicative of covalent bonding of the H₂O molecules with the Ge-INT. Simulation of the wetting-layer's PDOS in the absence of the Ge-INT leads to three well-defined PDOS peaks, due to the H₂O HOMO, HOMO-1 and HOMO-2 (Kohn–Sham) states, with no intermediate band-like PDOS feature in between them. These results indicate that the H₂O–Ge-INT electronic re-hybridisation and the ensuing enhancement of the covalent component of the H₂O bonding with the Ge-INT increase the interaction energy experienced by the molecules, with respect to fewer covalent regimes as present in I_h ice. Atom-resolved analysis of the PDOS for the wetting-layer, shown in Fig. 5b, shows the electronic re-hybridisation to be mostly due to the O-atoms of the H₂O molecules as expected based on their substantially shorter (1.50 Å) H-bond distance.

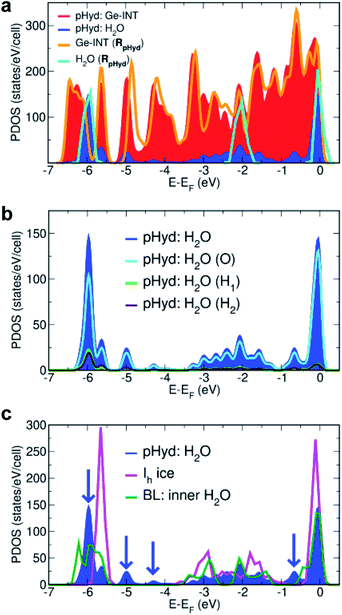Fig. 5 (a) Calculated atom-projected electronic density of states (PDOS) for the pHyd Ge-INT and its constituents. The Ge-INT's and wetting-layer's contributions to the PDOS are labelled “pHyd: Ge-INT” and “pHyd: H₂O”, respectively. The calculated PDOS for an isolated Ge-INT [Ge-INT(R_pHyd)] and the H₂O wetting-layer [H₂O(R_pHyd)] in the pHyd optimised geometry (R_pHyd) are also shown for comparison. (b) Atom-resolved analysis of the PDOS for the wetting-layer (pHyd: H₂O) using the same labelling as in Fig. 2. (c) Comparison between the calculated PDOS for the Ge-INT's wetting-layer (pHyd: H₂O), hexagonal ice (I_h ice), and the inner layer in the reference H₂O cylindrical bilayer (BL), also see Fig. S12 in the ESI.† Blue arrows point towards additional features in pHyd: H₂O compared to I_h ice, illustrating its stronger covalent character.

Mulliken (Hirshfeld) charge analysis of the pHyd Ge-INT reveals that the interfacial electronic re-hybridisation results in transfer of 0.065e per molecule (0.013e per molecule), equivalent to 2.86e (0.572e) per Ge-INT periodic unit, from the H₂O molecules to the nanotube. Consistent with the change in the Ge-INT's PDOS in the presence of the wetting-layer (Fig. 5a), and as visualised in Fig. S11 in the ESI,† the effects of such an interfacial electronic re-hybridisation span the whole Ge-INT, and not just its immediate interface with the H₂O molecules.

Further evidence of the leading role of the Ge-INT/H₂O interfacial electronic rehybridisation in the stabilisation of the H₂O molecules is provided by comparison of the calculated PDOS for the Ge-INT's wetting-layer, I_h ice, and the inner layer of a reference H₂O cylindrical bilayer (BL) with the same local H-bonding connectivity as in pHyd Ge-INTs (also see Fig. S12 in the ESI†). As shown in Fig. 5c, neither the I_h ice nor the BL traces present band-like PDOS features as the wetting-layer in Ge-INTs, confirming the crucial role of the Ge-OH triangular lattice in the enhancement of the covalent component at the interface. The calculated adsorption energy (E_ads) of 0.268 eV per molecule for the H₂O in the reference BL, 0.444 eV per molecule smaller in absolute value than for the pHyd Ge-INT and accounting for a 62% reduction in the interactions experienced, further strengthens this point.

Although aware of the challenges of semi-local XC-functionals, such as PBE used here, in describing non-covalent interactions in condensed phases of H₂O,^59–63 we expect the calculated enhancement of the covalent component of the Ge-INT/H₂O bonding in comparison with interactions in I_h to be qualitatively meaningful which is demonstrably due to electronic re-hybridisation (Fig. 5) rather than non-covalent interactions.

As previously calculated and discussed in ref. 45 and 64–66, INTs present a permanent dipole density (μ_σ) across their wall, with accumulation of the opposite charge at the inner and outer surface. Following the procedure detailed in ref. 66, we calculate a μ_σ of 38.5 mD Å⁻² for SW Ge-INTs, with a negative inner charge. The adsorption of the wetting-layer, leading to the most electronegative O-atoms of the H₂O molecules facing the centre of the Ge-INT's cavity, increases the pHyd Ge-INT's wall dipole density ∼2.3 times, resulting in a μ_σ of 88.4 mD Å⁻². As shown in Fig. S13 in the ESI,† such an increase of the Ge-INT's wall dipole density markedly affects the electrostatics inside the cavity with a ∼1.3 eV shift of the vacuum electrostatic plateau inside the nanotube's cavity. Given the increased μ_σ for the pHyd Ge-INT with respect to the dry Ge-INT, and the calculated sensitivity of the electron acceptor/donor states of nano-confined species to the cavity electrostatics,^65,66 these results suggest that the pHyd Ge-INTs may be substantially more effective as redox co-catalysts than the pristine dehydrated Ge-INT.

We finally note that although not detectable in the experimental GDOS traces owing to the strong multiphonon contribution at high energies, MD-DFT simulations of the dry and pHyd Ge-INTs indicate that the H₂O–nanotube interactions also affect the high-energy modes of the Ge-INTs, specifically the H_in bending and stretching modes. As evident from the calculated vibrational density of states shown in Fig. S5 and S6 in the ESI,† formation of the H₂O wetting-layer leads to a large ∼150 meV softening for the inner hydroxyl's stretching mode, along with hardening of the bending (scissoring and twisting) modes, as already discussed above. As a result, the energy gap between hydroxyl bendings and hydroxyl stretching is strongly reduced, so that the, vibration mediated, energy dissipation pathways in the pHyd nanotubes should be noticeably different from those in the dry system. This result encourages future theoretical and experimental research on the potential of solid wetting-layers in nano-reactors for control of the (electron–phonon and phonon–phonon mediated) pathways for energy dissipation during chemical reactions.

4 Conclusions

Our study demonstrates that the water wetting-layer in SW Ge-INTs is strongly bound and solid-like up to 300 K under atmospheric pressure. Atomic-scale characterisation of the wetting-layer reveals organisation of the H₂O molecules in a curved triangular sublattice stabilised by the formation of enhanced H-bonds between the adsorbed molecule and the highly flexible Ge-INT's inner hydroxyls. The controllable diameter of Ge-INTs allows water–nanotube interactions to be sufficiently strong to account for energetically favoured decoupling of the H₂O molecules, suppressing H-bonding between water molecules in the wetting-layer, yet enhancing the overall stability of the adlayer by means of covalent interactions between the nanotube and the oxygen of the adsorbed H₂O molecules. Given the evidenced changes in the local composition, structure, electrostatics and dynamics of the Ge-INT's inner surface upon the formation of the solid wetting-layer, the present results open up exploration of solvent-based strategies for functionalisation of the inner surface of nanotubes and nano-reactors in general.

Author contributions

PL, SR, GT and EP conceptualized the project. SR and PL supervised the experiments and their analysis and GT supervised DFT calculations. The sample was synthesized by MSA and EP. WAXS and TGA results were obtained by GM, MSA, EP, SR and PL. Inelastic neutron scattering experiments were performed by GM, MSA, ARC, EP, AO, MJR, PL and SR. Their analysis based on DFT-MD trajectories was made by GM, LF, SR and PL, on the basis of dedicated software developed by GM. DFT calculations were carried out by ZC, LML and GT. GM, SR, GT and PL wrote the manuscript, which has been checked by all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

GT, ZC and LML acknowledge support from the EPSRC (EP/I004483/1) and Royal Society (NAF-R1-180242). This work used the ARCHER (UKCP Consortium, EPSRC UK EP/P022189/2) and UK Materials and Molecular Modelling Hub (EPSRC UK EP/P020194/1) High-Performance Computing facilities. GT benefited from a visiting researcher grant from the CNRS. This project has received financial support from the CNRS through the International Emerging Actions program (no. 08216) and from the French ANR agency (grant number ANR-18-CE09-0001). We also acknowledge the ILL for beam time and Olivier Meulien for technical assistance during the INS investigations.

Notes and references

1. L. K. Yeung and R. M. Crooks, Nano Lett., 2001, 1, 14–17.
2. J. Lee, J. C. Park and H. Song, Adv. Mater., 2008, 20, 1523–1528.
3. J. Ge, Q. Zhang, T. Zhang and Y. Yin, Angew. Chem., Int. Ed., 2008, 47, 8924–8928.
4. Y.-S. Hu, X. Liu, J.-O. Müller, R. Schlögl, J. Maier and D. Su, Angew. Chem., Int. Ed., 2009, 48, 210–214.
5. Z. Chen, Z.-M. Cui, F. Niu, L. Jiang and W.-G. Song, Chem. Commun., 2010, 46, 6524–6526.
6. F. Sastre, V. Fornés, A. Corma and H. García, J. Am. Chem. Soc., 2011, 133, 17257–17261.
7. F. Sastre, V. Fornés, A. Corma and H. García, Chem.–Eur. J., 2012, 18, 1820–1825.
8. A. Lu and R. K. O'Reilly, Curr. Opin. Biotechnol., 2013, 24, 639–645.
9. J. Lee, S. M. Kim and I. S. Lee, Nano Today, 2014, 9, 631–667.
10. S. H. Petrosko, R. Johnson, H. White and C. A. Mirkin, J. Am. Chem. Soc., 2016, 138, 7443–7445.
11. B. Maiti, A. Abramov, R. Pérez-Ruiz and D. Díaz Díaz, Acc. Chem. Res., 2019, 52, 1865–1876.
12. H. Tian, J. Liang and J. Liu, Adv. Mater., 2019, 1903886.
13. L. Li, Z. Yang, W. Fan, L. He, C. Cui, J. Zou, W. Tang, O. Jacobson, Z. Wang, G. Niu, S. Hu and X. Chen, Adv. Funct. Mater., 2019, 1907716.
14. Y. Wang, W. Zhang, J. Guo, W. Duan and B. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 38016–38022.
15. J. Yu, F. Zhao, W. Gao, X. Yang, Y. Ju, L. Zhao, W. Guo, J. Xie, X.-j. Liang, X. Tao, J. Li, Y. Ying, W. Li, J. Zheng, L. Qiao, S. Xiong, X. Mou, S. Che and Y. Hou, ACS Nano, 2019, 13, 10002–10014.
16. W. Zhu, Z. Chen, Y. Pan, R. Dai, Y. Wu, Z. Zhuang, D. Wang, Q. Peng, C. Chen and Y. Li, Adv. Mater., 2019, 31, 1800426.
17. M. Debnath, S. Sasmal, D. Podder and D. Haldar, ACS Omega, 2019, 4, 13872–13878.
18. M. Yuan, H. Zhang, C. Yang, F. Wang and Z. Dong, ChemCatChem, 2019, 11, 3327–3338.
19. N. Alarcos, B. Cohen, M. Ziółek and A. Douhal, Chem. Rev., 2017, 117, 13639–13720.
20. S. Murcia-López, M. C. Bacariza, K. Villa, J. M. Lopes, C. Henriques, J. R. Morante and T. Andreu, ACS Catal., 2017, 7, 2878–2885.
21. W. Lv, L. Li, M. Xu, J. Hong, X. Tang, L. Xu, Y. Wu, R. Zhu, R. Chen and W. Huang, Adv. Mater., 2019, 31, 1900682.
22. F. Franks, The Physics and Physical Chemistry of Water, Springer, US, 3rd edn, 1972.
23. K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim, J. Park, K. H. Nam, T. Katayama and A. Nilsson, Science, 2017, 358, 1589–1593.
24. S. Cambré, B. Schoeters, S. Luyckx, E. Goovaerts and W. Wenseleers, Phys. Rev. Lett., 2010, 104, 207401.
25. A. I. Kolesnikov, J.-M. Zanotti, C.-K. Loong, P. Thiyagarajan, A. P. Moravsky, R. O. Loutfy and C. J. Burnham, Phys. Rev. Lett., 2004, 93, 035503.
26. S. Dalla Bernardina, E. Paineau, J.-B. Brubach, P. Judeinstein, S. Rouzière, P. Launois and P. Roy, J. Am. Chem. Soc., 2016, 138, 10437–10443.
27. J.-M. Zanotti, P. Judeinstein, S. Dalla-Bernardina, G. Creff, J.-B. Brubach, P. Roy, M. Bonetti, J. Ollivier, D. Sakellariou and M.-C. Bellissent-Funel, Sci. Rep., 2016, 6, 25938.
28. G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, J. Am. Chem. Soc., 2008, 130, 1871–1878.
29. G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Nature, 2015, 519, 443–445.
30. I. Strauss, H. Chan and P. Král, J. Am. Chem. Soc., 2014, 136, 1170–1173.
31. A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 0091.
32. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943.
33. J. Lim, K. Park, H. Lee, J. Kim, K. Kwak and M. Cho, J. Am. Chem. Soc., 2018, 140, 15661–15667.
34. Z. Cao, Y. Peng, T. Yan, S. Li, A. Li and G. A. Voth, J. Am. Chem. Soc., 2010, 132, 11395–11397.
35. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190.
36. S. Roy, D. Skoff, D. V. Perroni, J. Mondal, A. Yethiraj, M. K. Mahanthappa, M. T. Zanni and J. L. Skinner, J. Am. Chem. Soc., 2016, 138, 2472–2475.
37. C. Beduz, M. Carravetta, J. Y.-C. Chen, M. Concistrè, M. Denning, M. Frunzi, A. J. Horsewill, O. G. Johannessen, R. Lawler, X. Lei, M. H. Levitt, Y. Li, S. Mamone, Y. Murata, U. Nagel, T. Nishida, J. Ollivier, S. Rols, T. Rõõm, R. Sarkar, N. J. Turro and Y. Yang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12894–12898.
38. A. I. Kolesnikov, G. F. Reiter, N. Choudhury, T. R. Prisk, E. Mamontov, A. Podlesnyak, G. Ehlers, A. G. Seel, D. J. Wesolowski and L. M. Anovitz, Phys. Rev. Lett., 2016, 116, 167802.
39. N. Yoshinaga and S. Aomine, Soil Sci. Plant Nutr., 1962, 8, 22–29.
40. M. S. Amara, E. Paineau, S. Rouzière, B. Guiose, M.-E. M. Krapf, O. Taché, P. Launois and A. Thill, Chem. Mater., 2015, 27, 1488–1494.
41. E. Paineau, M. S. Amara, G. Monet, V. Peyre, S. Rouzière and P. Launois, J. Phys. Chem. C, 2017, 121, 21740–21749.
42. B. Creton, D. Bougeard, K. S. Smirnov, J. Guilment and O. Poncelet, Phys. Chem. Chem. Phys., 2008, 10, 4879–4888.
43. A. Fernandez-Martinez and L. Michot, in Developments in Clay Science, Elsevier, 2016, vol. 7, pp. 202–222.
44. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
45. G. Monet, M. S. Amara, S. Rouzière, E. Paineau, Z. Chai, J. D. Elliott, E. Poli, L.-M. Liu, G. Teobaldi and P. Launois, Nat. Commun., 2018, 9, 2033.
46. H. Schober, J. Neutron Res., 2014, 17, 109–357.
47. M. Ferrario, M. Haughney, I. R. McDonald and M. L. Klein, J. Chem. Phys., 1990, 93, 5156–5166.
48. T. R. Prisk, C. Hoffmann, A. I. Kolesnikov, E. Mamontov, A. A. Podlesnyak, X. Wang, P. R. C. Kent and L. M. Anovitz, Phys. Rev. Lett., 2018, 120, 196001.
49. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
50. K. Amann-Winkel, M.-C. Bellissent-Funel, L. E. Bove, T. Loerting, A. Nilsson, A. Paciaroni, D. Schlesinger and L. Skinner, Chem. Rev., 2016, 116, 7570–7589.
51. H.-W. Wang, M. J. DelloStritto, N. Kumar, A. I. Kolesnikov, P. R. Kent, J. D. Kubicki, D. J. Wesolowski and J. O. Sofo, J. Phys. Chem. C, 2014, 118, 10805–10813.
52. J. M. Dickey and A. Paskin, Phys. Rev., 1969, 188, 1407–1418.
53. E. Paineau, G. Monet, V. Peyre, C. Goldmann, S. Rouzière and P. Launois, Langmuir, 2019, 35, 12451–12459.
54. M.-S. Amara, E. Paineau, M. Bacia-Verloop, M.-E. M. Krapf, P. Davidson, L. Belloni, C. Levard, J. Rose, P. Launois and A. Thill, Chem. Commun., 2013, 49, 11284–11286.
55. Y.-Y. Liao, P. Picot, J.-B. Brubach, P. Roy, A. Thill and S. Le Caër, J. Phys. Chem. C, 2019, 123, 19768–19777.
56. L. Scalfi, G. Fraux, A. Boutin and F.-X. Coudert, Langmuir, 2018, 34, 6748–6756.
57. E. Mamontov, L. Vlcek, D. J. Wesolowski, P. T. Cummings, J. Rosenqvist, W. Wang, D. R. Cole, L. M. Anovitz and G. Gasparovic, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys, 2009, 79, 051504.
58. D. Pan, L.-M. Liu, G. A. Tribello, B. Slater, A. Michaelides and E. Wang, J. Phys.: Condens. Matter, 2010, 22, 074209.
59. K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168.
60. B. Santra, A. Michaelides and M. Scheffler, J. Chem. Phys., 2009, 131, 124509.
61. R. A. DiStasio, B. Santra, Z. Li, X. Wu and R. Car, J. Chem. Phys., 2014, 141, 084502.
62. M. Chen, H.-Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein, J. P. Perdew and X. Wu, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846–10851.
63. J. G. Brandenburg, A. Zen, D. Alfè and A. Michaelides, J. Chem. Phys., 2019, 151, 164702.
64. G. Teobaldi, N. S. Beglitis, A. J. Fisher, F. Zerbetto and W. A. Hofer, J. Phys.: Condens. Matter, 2009, 21, 195301.
65. E. Poli, J. D. Elliott, L. E. Ratcliff, L. Andrinopoulos, J. Dziedzic, N. D. M. Hine, A. A. Mostofi, C.-K. Skylaris, P. D. Haynes and G. Teobaldi, J. Phys.: Condens. Matter, 2016, 28, 074003.
66. J. D. Elliott, E. Poli, I. Scivetti, L. E. Ratcliff, L. Andrinopoulos, J. Dziedzic, N. D. M. Hine, A. A. Mostofi, C.-K. Skylaris, P. D. Haynes and G. Teobaldi, Adv. Sci., 2017, 4, 1600153.

---

Footnotes

† Electronic supplementary information (ESI) available: Thermogravimetric analysis, determination of the nanotube chiral indices from X-ray scattering measurements, computational details of DFT and DFT-MD simulations, atomic density maps, partial vibrational densities of state, trajectory spectral filtering, and additional DFT results. See DOI: 10.1039/d0na00128g

‡ First author of DFT study.

§ Absolute renormalisation of the measured and calculated DOS of the dry and pHyd systems was performed by applying the same renormalisation factor, so that the integral over the energy of the DOS for the pHyd system is equal to six (the number of H atoms per Ge atom).

---