Open Access Article
Open Access ArticleMechanistic insight into biopolymer induced iron oxide mineralization through quantification of molecular bonding†
K. K.
Sand‡§
 *ab,
S.
Jelavić§
*ab,
S.
Jelavić§
 c,
S.
Dobberschütz
c,
P. D.
Ashby
b,
M. J.
Marshall
d,
K.
Dideriksen¶
c,
S.
Dobberschütz
c,
P. D.
Ashby
b,
M. J.
Marshall
d,
K.
Dideriksen¶
 c,
S. L. S.
Stipp||
c,
S. N.
Kerisit
a,
R. W.
Friddle
c,
S. L. S.
Stipp||
c,
S. N.
Kerisit
a,
R. W.
Friddle
 e and
J. J.
DeYoreo
*af
e and
J. J.
DeYoreo
*af
aPhysical Sciences Division, Pacific Northwest National Laboratory, Richland, WA, USA. E-mail: kas84@aber.ac.uk; james.DeYoreo@pnnl.gov
bMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA, USA
cNano-Science Center, Department of Chemistry, University of Copenhagen, Denmark
dBiologic Sciences Division, Pacific Northwest National Laboratory, Richland, WA, USA
eSandia National Laboratories, Livermore, California 94550, USA
fDepartment of Material Science and Engineering, University of Washington, Seattle, WA, USA
First published on 15th June 2020
Abstract
Microbial production of iron (oxyhydr)oxides on polysaccharide rich biopolymers occurs on such a vast scale that it impacts the global iron cycle and has been responsible for major biogeochemical events. Yet the physiochemical controls these biopolymers exert on iron (oxyhydr)oxide formation are poorly understood. Here we used dynamic force spectroscopy to directly probe binding between complex, model and natural microbial polysaccharides and common iron (oxyhydr)oxides. Applying nucleation theory to our results demonstrates that if there is a strong attractive interaction between biopolymers and iron (oxyhydr)oxides, the biopolymers decrease the nucleation barriers, thus promoting mineral nucleation. These results are also supported by nucleation studies and density functional theory. Spectroscopic and thermogravimetric data provide insight into the subsequent growth dynamics and show that the degree and strength of water association with the polymers can explain the influence on iron (oxyhydr)oxide transformation rates. Combined, our results provide a mechanistic basis for understanding how polymer–mineral–water interactions alter iron (oxyhydr)oxides nucleation and growth dynamics and pave the way for an improved understanding of the consequences of polymer induced mineralization in natural systems.
Introduction
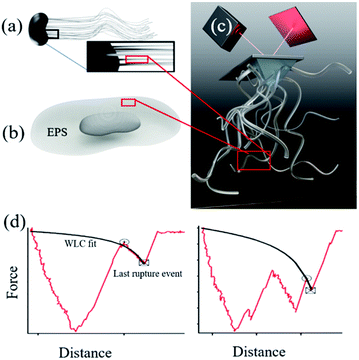
Microbially produced iron (oxy)hydroxides have a large impact on the global iron cycle1 and have influenced the creation of an oxygen-rich atmosphere.2 For common iron oxidizers such as Gallionella (Fig. 1a) and iron reducers such as Shewanella (Fig. 1b) we find nanoparticles of hydrated iron phases on their filamentous polysaccharide rich stalks3 and extracellular polymeric substances (EPS) respectively.4,5 This intimacy suggests that the organic compounds are involved in the nucleation process of the iron phases. The microbial polymers are known to strongly affect subsequent nanoparticle behaviour in soils and sediments such as growth,6–9 transformation,10,11 aggregation9,11,12 and reactivity.3,11,13,14 Yet, we do not know if the polymers drive the nucleation or if they merely adsorb at the already formed nanoparticles. In the case of directed control of polymers over nanoparticle nucleation, the formation of nanoparticles can occur at a lower driving force (e.g. supersaturation) than currently assumed, which will add to the significance of microbial biomineralization in the iron and carbon cycles. Currently, the physicochemical controls exerted by these biopolymers on iron (oxyhydr)oxide behaviour is poorly understood which makes it difficult to assess the impact of such interactions on an environmental level.Iron (oxyhydr)oxides are common products of aqueous processes and are readily found in soils and sediments.15 In solution, iron (oxyhydr)oxides form by attachment of primary entities such as ionic complexes16 or poorly to well crystalline nanoparticles.6,17–20 The size of the primary entities is between ∼1–4 nm.6,16 In oxic environments, ferrihydrite (∼Fe8.2O8.5(OH)7.4·3H2O), an iron (oxyhydr)oxide with the smallest particle size among iron oxides, is one of the most stable phases at the nanoscale21 and is generally the first one to precipitate. It is poorly crystalline, has highly charged surface sites and transforms to other iron (oxyhydr)oxides over time.22 At circumneutral pH, a common product of ferrihydrite transformation is hematite (Fe2O3), which is the most stable macroscopic iron oxide.21,23 Hematite has a low surface charge and well developed crystal faces, where the most stable crystal face is the {00.1}.24,25 The formation of ferrihydrite in solution26,27 and its subsequent transformation28,29 has long been investigated but the mechanisms underlying the nucleation of iron (oxyhydro)oxides and their transformation behaviour on substrates, such as biopolymers, is lacking.
Considering the principles of nucleation theory, there are two main processes by which polymers can facilitate nucleation: by locally increasing the ion activity and the supersaturation30 or by decreasing the free interfacial energy of the polymer–nuclei–solution system, γ.31,32 One hypothesis is that microbial polymers decrease γ for iron (oxyhydr)oxide formation, thus reducing the system's free energy barrier to nucleation, ΔG*, which is proportional to γ3 through:33
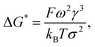 | (1) |
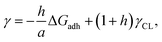 | (2) |
It has been difficult to experimentally determine ΔGadh at the bond level between minerals and polymer assemblies (polymer brush) such as polysaccharide and EPS. DFS is an atomic force microscopy (AFM) based technique that have been used to address binding between a polymer and a substrate. DFS measures the force required to rupture the bond, fr, between a substrate and a polymer attached to the AFM tip (Fig. 1c), as a function of loading rate, lr. This approach has traditionally been challenging to apply for a polymer brush because of both analytical challenges related to interpret the non-linear dependence of extension as well as unravelling the unknown amount of bonds clustered at the probe–surface contact. The latter has been circumvented by having just one (or a few) molecules on the tip. However, a polymer brush is a better representation of a natural system and would allow us to take intramolecular forces between the biopolymers into account. Recently, however, a new approach was formulated where direct information about the interaction between extendable polymer brushes and mineral surfaces was obtained.36 The approach is polymer brush-based dynamic force spectroscopy (DFS).36 The polymer brush-based approach provides a way for extracting rupture forces that approximate single polymer events from a polymer coated probe. This technique is highly relevant for natural systems when polymers often occur in close proximity and polymer–polymer interactions take part in the overall binding. We used alginate polysaccharide as a model for polysaccharide rich bacterial stalks and EPS extracted from Shewanella as a real representation of the extracellular environment where bacteria influence iron (oxyhydr)oxide precipitation. Besides polysaccharides, EPS can contain proteins, nucleic acids, phospholipids and humic substances37 but polysaccharides have been shown to play a decisive role in iron (oxyhydr)oxide crystallisation and geochemical cycling.3,38,39 We covalently attached alginate and EPS to AFM tips and collected force curves from surfaces of either ferrihydrite nanoparticles or a polished, single crystal of hematite {00.1} (Fig. S1†). The large hematite crystal ensures that we are probing only this most stable and most represented face. The nanoparticulate ferrihydrite substrate ensures that we are probing a variety of possible surfaces characteristic for such a poorly crystalline and yet structurally unresolved iron (oxyhydr)oxides.
If indeed the polymers decrease γ, we would expect the polymer–nuclei-solution system to form smaller nuclei compared to a polymer-free system because a lower nucleation barrier would result in more nuclei compared to a system with a higher barrier. Thus, we tested the results from the binding experiments performed on ferrihydrite and hematite surfaces to bulk nucleation experiments. For the bulk experiments, we coprecipitated alginate-containing and alginate-free ferrihydrite and used pair distribution function (PDF) and transmission electron microscopy (TEM) to determine the resulting particle size. In addition, we used cryogenic X-ray photoelectron spectroscopy (XPS) and thermogravimetric analysis (TGA) to gain information on the transformation processes. Additionally, we used density functional theory (DFT) to support the findings. Our results are consistent across scales, from single-molecule binding experiments and simulations to bulk nucleation studies.
Experimental
Preparation of hematite and ferrihydrite substrates for DFS
We used the {00.1} face from a polished, single crystal of hematite as a substrate for DFS measurements. The {00.1} face was cleaned in 1 M NaOH at 60 °C for 1 h to remove fatty contamination, sonicated for 20 min to remove particulate contaminants, rinsed with ultradeionised water (MilliQ, resistivity 18.2 MΩ cm) and plasma cleaned for 10 min prior to use. This cleaning procedure results with hematite adventitious carbon content of 6.9 ± 0.7 at%.40 The hematite substrate was imaged using Cypher ES™ Environmental to confirm the flatness of the surface and the absence of a particulate contamination ((ESI), Fig. S1†).For preparation of ferrihydrite substrate, we used reagent grade NaOH (Sigma Aldrich, ≥98%) and Fe(NO3)3·9H2O (Sigma Aldrich, ≥98%). The ferrihydrite substrate was made by nucleating iron (oxyhydr)oxide on freshly cleaved muscovite (Ted Pella Inc., mica grade V-3) using the protocol of Jun et al.41 After 20 minutes, we obtained a substrate of closely packed ferrihydrite particles. The adventitious carbon content of such prepared ferrihydrite substrate, measured with XPS, was 8.3 ± 0.4 at%. Prior to DFS experiments, a ferrihydrite substrate was imaged in air or liquid using a Cypher ES™ Environmental or a MFP3D AFM to confirm uniform coverage (Fig. S1†).
Tip functionalization
We functionalised the tips with (a) alginate (Pronova UP LVM, Novamatrix, Norway) and (b) a saccharide-rich and protein-poor (ratio 3.64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) EPS fraction extracted from the biofilm of Shewanella oneidensis strain MR-1, using the procedure from Cao et al.42 To functionalize the tips, the alginate and EPS were covalently attached to sharpened silicon nitride MSCT tips from Bruker (nominal spring constant, k = 0.01–0.6) using the protocol from Sletmoen et al.43 Briefly, the AFM tips were thoroughly rinsed using 3 sequences of ethanol and MilliQ water and after drying, they were plasma cleaned for 10 minutes, then silanized in freshly prepared 1% (v/v) solution of trimethoxysilylpropyl–diethylenetriamine and 1 mM acetic acid, for 20 min at room temperature, then rinsed in MilliQ water. 1-(3-Dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride (EDAC) was used as a coupling agent between the amino groups of the silanized AFM tips and the carboxylate on the polysaccharide. 0.5 mg ml−1 EDAC was incubated for 1 h with 20 μg ml−1 alginate or EPS in 50 mM boric acid, pH 5.8.
1) EPS fraction extracted from the biofilm of Shewanella oneidensis strain MR-1, using the procedure from Cao et al.42 To functionalize the tips, the alginate and EPS were covalently attached to sharpened silicon nitride MSCT tips from Bruker (nominal spring constant, k = 0.01–0.6) using the protocol from Sletmoen et al.43 Briefly, the AFM tips were thoroughly rinsed using 3 sequences of ethanol and MilliQ water and after drying, they were plasma cleaned for 10 minutes, then silanized in freshly prepared 1% (v/v) solution of trimethoxysilylpropyl–diethylenetriamine and 1 mM acetic acid, for 20 min at room temperature, then rinsed in MilliQ water. 1-(3-Dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride (EDAC) was used as a coupling agent between the amino groups of the silanized AFM tips and the carboxylate on the polysaccharide. 0.5 mg ml−1 EDAC was incubated for 1 h with 20 μg ml−1 alginate or EPS in 50 mM boric acid, pH 5.8.
DFS data acquisition
DFS is a method to directly measure the forces between a complex organic molecules and a mineral surface. These forces are then recalculated into bond parameters used to derive thermodynamic parameters such as ΔGadh. DFS measurements were made using an Asylum MFP3D AFM at 20 °C in 10 mM NaCl (Sigma Aldrich, ≥99.5%). 10 mM NaCl solution was used to minimise the repulsive van der Waals forces between the tip and substrate and to avoid possible complexation between PS/EPS and divalent cations. All solutions were filtered through a 0.22 μm filter (Whatman) prior to use. To avoid damage to the tip during the force measurements, we used the minimum trigger force possible (in general, 120 pN) and determined the true cantilever spring constant at the end of the measurement. The spring constant was measured using the thermal calibration method,44 at a trigger point of 2500 pN. Subsequently, the tip was discarded. During the DFS measurements, we used a constant approach rate of 500 nm s−1 and a dwell time of 1 s. We collected force curves for seven retraction velocities, for each experiment, ranging from 5 nm s−1 to 10 μm s−1, to sample energy profiles in both the near equilibrium and far from equilibrium regimes. The retraction velocity was changed every 5 force curves, while the tip probed random points on the surface. This approach minimized the effect of local mineral heterogeneities. A minimum of 20 such cycles was made for each experiment, resulting in at least 700 force curves per experiment.DFS data analysis
We used the single bond theory developed by Friddle et al.45 for data interpretation, where fr is plotted against the lr. We used the polymer brush-based approach developed by Sand et al.36 for the data treatment. In brief, to approximate single polymer event, we only considered the rupture events that most likely represent the rupture/bond breaking between a single polymer and the substrate. Because of tip geometry, the last rupture event, i.e. the event where the tip is furthest from the substrate, has the highest likelihood of representing a single rupture event. To further discriminate between multiple and single rupture events, we applied the worm-like chain (WLC) model to that last rupture event to estimate the number of interacting molecules, N, involved in the rupture: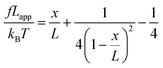 | (3) |
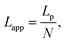 | (4) |
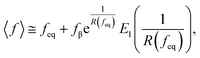 | (5) |
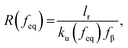 | (6) |
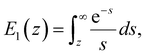 | (7) |
We calculated the adhesion free energy per unit length following the polymer brush-based approach.36 Manohar et al.,47 related feq to the adhesion free energy per unit length, γadh, by:
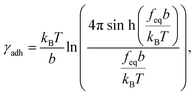 | (8) |
| γadh ≈ feq. | (9) |
The free energy of adhesion per monomer then follows as:
| ΔGadh = γadhlmono ≈ feqlmono, | (10) |
Density functional theory (DFT)
Plane-wave DFT calculations were performed with the projector augmented-wave (PAW)50,51 method, as implemented in the ab initio total energy and molecular dynamics program VASP (Vienna Ab initio Simulation Package).52–54 The calculations made use of the Perdew–Burke–Ernzerhof (PBE)55,56 generalized gradient approximation (GGA) of the exchange-correlation potential. The rotationally-invariant variant to the DFT+U approach57 was employed to treat the Fe 3d electrons with an effective on-site parameter Ueff of 3.81 eV,58 on the surface of interest to this work. A plane-wave cutoff energy of 600 eV was used throughout. A 2 × 2 hydroxyl-terminated {00.1} hematite slab with 4 iron bilayers was constructed from the crystallographic structure of Blake et al.59 An alginate monomer was initially placed with its center of mass approximately 5 Å above the surface. A constant volume ab initio molecular dynamics (AIMD) simulation was then run at 50 K for 5 ps to let the alginate monomer bind to the surface. The AIMD simulation was followed by energy minimization with the conjugate gradient approach. Energy minimizations of the isolated hematite surface and alginate monomer were performed to calculate the alginate adsorption energy at the {00.1} surface. An energy minimization with 3 water monolayers was also made to compare the alginate adsorption energy to that of water.Synthesis of hematite and ferrihydrite nanoparticles, and their coprecipitates and complexes with alginate
Hematite was precipitated following the protocol of Barton et al.,60 by slowly dripping 60 ml of 2 M iron(III) nitrate (Fe(NO3)3·9H2O) (Sigma Aldrich, ≥98%) solution into 750 ml of boiling MilliQ. The reaction time was approximately 30 min, after which the solution was removed from the heater and left overnight, at a room temperature, to cool. The next day, the solution was poured into MilliQ water rinsed dialysis bags (Spectra/Por tubing) and dialyzed against MilliQ water until the conductivity of solution approached that of MilliQ water (7 days).Ferrihydrite was prepared following the method of Schwertmann and Cornell.23 We added 1 g Fe(NO3)3·9H2O (Sigma Aldrich, ≥98%) to 12.5 ml MilliQ water and dropwise added 1 M NaOH at 2 ml min−1 under vigorous stirring. When pH reached 6.8, the titration was stopped and the precipitates centrifuged and rinsed 3 times in MilliQ water.
When ferrihydrite was coprecipitated with alginate polysaccharide (Pronova UP LVM, Novamatrix, Norway), alginate was added to MilliQ water to obtain a total concentration of 0.1% PS. The PS-MilliQ solution was adjusted with 1 M HCl to pH 2.5 before starting the titration, which was made in the same way as for the pure ferrihydrite precipitate. Once the titration stopped, the suspension was centrifuged and rinsed 3 times in MilliQ water.
Hematite could not have been coprecipitated with alginate because the water-boiling temperature during the synthesis would degrade the alginate. To make TGA and cryoXPS analyses comparable for ferrihydrite and hematite, we prepared mixtures of ferrihydrite with alginate, and hematite with alginate. We added ferrihydrite and hematite powders to 10 mM NaCl, 0.1% (w/w) alginate solution and kept the specific surface area/liquid ratio the same. The 15 ml PET tubes containing alginate–iron (oxy/hydr)oxide complexes were shaken overnight, ultracentrifuged and washed by ultracentrifugation with 45 ml of 10 mM NaCl solution to remove excess alginate, then freeze-dried.
Characterisation of (alginate-) ferrihydrite and (alginate-) and hematite nanoparticles
Results and discussion
For all force curves, we observed the characteristic saw tooth pattern for polymer detachment (red curves in Fig. 1d) that arises from multiple rupture events. After extracting the curves approximating single polymer interactions36 we plotted the average rupture force (fr) for single polymers as a function of the average loading rate (lr) of alginate–hematite, alginate–ferrihydrite and EPS–ferrihydrite systems (Fig. 2a–c). The observed trends for frvs. lr exhibit the characteristic shape of DFS curves, that cross the two fundamental regimes of bond breaking: the near equilibrium plateau at low lr and the kinetic regime of increasing fr at high lr45,72 (grey text in Fig. 2a).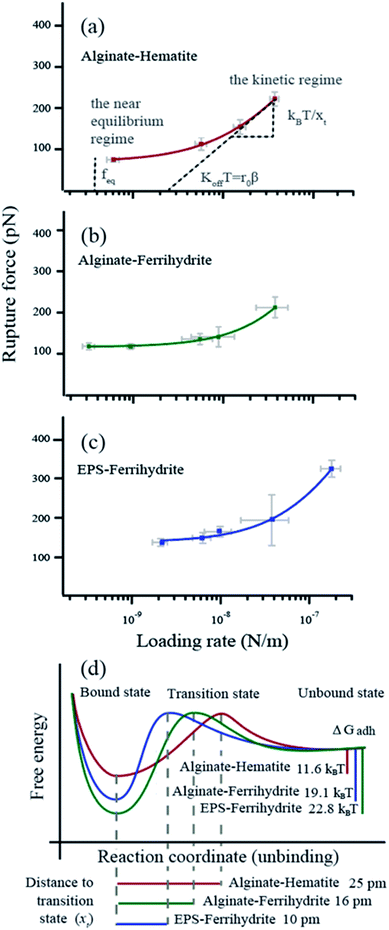 | ||
| Fig. 2 Dynamic force data displayed as rupture force in pN vs. loading rate in N m−1 (a–c) The data points represent the values for each velocity pool with standard errors. The curve (red, purple or green) is a fit to the single bond model. The parameters obtained from the fitting are d listed in Table 1. The intercept between the plateau of rupture forces in the near equilibrium regime and the y-axis defines the feq, the slope of the kinetic regime defines the xt and the intercept between a tangent of the kinetic regime and the x-axis (r0) defines the koff (β = e−0.557xt/kBT). (d) Reaction coordinates for unbinding from a bound state. Alg-alginate; EPS-extracellular polymer substance; FHY-ferrihydrite; HEM-hematite; ΔGadh-the crystal-polymer binding free energy. | ||
We applied the single bond analysis45 adopted for polymers36 to our dynamic force spectra (Fig. 2a–c) and extracted the equilibrium force (feq), the intrinsic unbinding rate (koff), and the distance between transition states (xt). Knowing feq, we obtained the crystal–polymer binding Gibbs free energy (ΔGadh) using eqn (8)–(10). The parameters and standard errors are presented in Fig. 2d and Table 1. While the EPS–ferrihydrite bond properties are similar to those for alginate–ferrihydrite, both are distinct from the properties of the alginate–hematite bond. ΔGadh is slightly higher for EPS–ferrihydrite (22.8 ± 1 kBT) than for alginate–ferrihydrite (19.1 ± 0.3 kBT) but both are nearly twice greater than for alginate–hematite (11.6 ± 0.6 kBT). EPS–hematite was previously shown to be 8.6 kBT (using a similar approach).36 Similarly, xt and koff for the ferrihydrite systems are indistinguishable, within experimental error, whereas koff is ∼4 times smaller for the alginate–hematite bond. koff is a measure of the kinetic barrier to bond breaking and the higher values for ferrihydrite imply that the bond strength of (E)PS to ferrihydrite is stronger than to hematite.
| x t (pm) | k off (s−1) | f eq (pN) | ΔGadhd (kBT) | |
|---|---|---|---|---|
| a x t, the distance to the transition state. b k off, the intrinsic unbinding rate. c f eq, the equilibrium rupture force. d ΔGadh, the crystal–polymer binding free energy. Numbers in grey represent the standard error. | ||||
| Alginate–hematite | 25 ± 5 | 74 ± 18 | 71 ± 4 | 11.6 ± 0.6 |
| Alginate–ferrihydrite | 10 ± 8 | 240 ± 94 | 116 ± 2 | 19.1 ± 0.3 |
| EPS–ferrihydrite | 16 ± 8 | 307 ± 180 | 139 ± 6 | 22.8 ± 1.0 |
Effects of bond strength on iron oxide nucleation
The values of ΔGadh can now be used to evaluate the impact of polymer–mineral interaction on γ and on ferrihydrite and hematite nucleation (eqn (2)). To calculate γ, we need the crystal–liquid interfacial free energy, γCL, which is difficult to measure experimentally but it is related to mineral solubility, Ceq, through an empirical approximation:73γCL = −18.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(Ceq) + 34.5. log(Ceq) + 34.5. | (11) |
| Alginate–hematite | Alginate–ferrihydrite | EPS–ferrihydrite | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔG adh | 28.8 kJ mol−1 | 47.3 kJ mol−1 | 56.5 kJ mol−1 | ||||||||||||
| γ CL | 224 mJ m−2 | 159 mJ m−2 | 159 mJ m−2 | ||||||||||||
| h/a | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| a γ for nucleation on the polymer as a function of area for possible interaction, a, and shape factor, h. Nucleation is favored (black) when γ < γCL and unfavorable when γ > γCL (grey). ΔGadh, the crystal–polymer binding free energy. | |||||||||||||||
| 0.3 | 147 | 219 | 243 | 255 | 262 | −30 | 88 | 128 | 148 | 159 | −76 | 65 | 112 | 136 | 150 |
| 0.5 | 96 | 216 | 256 | 276 | 288 | −156 | 41 | 107 | 140 | 160 | −233 | 3 | 81 | 121 | 144 |
| 0.8 | 20 | 211 | 275 | 307 | 327 | −345 | −29 | 76 | 128 | 160 | −457 | −91 | 35 | 98 | 135 |
The results raise the question of why EPS promotes iron oxide nucleation more than alginate. The bond dynamics explored here are expected to be driven by electrostatic interactions between negatively charged groups of EPS and alginate and positively charged iron oxide surface sites. First, we note that the covalent bond between polysaccharide molecules anchored to an AFM tip and the substrate breaks at about 2 nN (ref. 74) and our DFS data show that our measured rupture forces are well below such a value. Thus, the stronger feq and ΔGadh found for EPS is likely to reflect compositional differences between EPS and alginate. In addition to COO−, EPS also contains proteins and lipids.42,75 The amine groups from the proteins are positively charged while the phosphate groups are negatively charged and both could contribute to binding. Beside the electrostatic contribution from the functional groups, the difference in feq between alginate–ferrihydrite and EPS–ferrihydrite could be caused by differences in steric effects between polymer and substrate and/or variations in oxygen–oxygen interactions between the functional groups.32
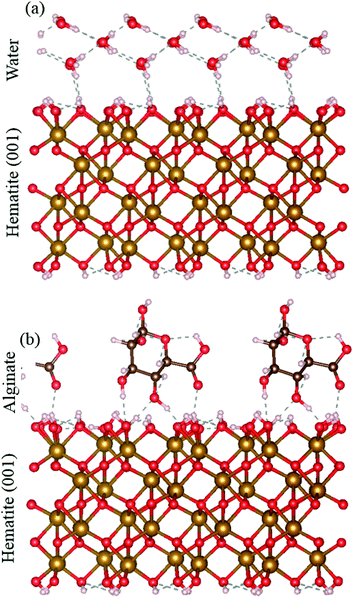
The solubilities for ferrihydrite and hematite are a function of in the DFS approach, we only measure the strongest bond, but in a bulk system, a number of bonds act between alginate and the mineral surface. We used DFT to compare the adsorption energy of the full alginate monomer and water molecules to a hematite {00.1} face. Even at neutral conditions, i.e., where the interaction between the mineral surface and the alginate monomer exclude the electrostatic contribution, alginate adsorption still has a significantly more favorable adsorption energy than water (that represents a pure system). The alginate monomer binds to the hematite surface through two alcohol groups and a carboxyl group and involves a total of four hydrogen bonds; adsorption energy is −1.11 eV. In contrast, a single water molecule interacts with the surface through two hydrogen bonds; adsorption energy of −0.43 eV. Even under neutral conditions, the hematite–alginate bond is significantly more exothermic than the hematite–water bond (−1.11 vs. −0.43 eV per molecule) and the alginate interaction results in stronger surface binding per molecule than water (Fig. 3).
Nucleation in the bulk system: the size of ferrihydrite coprecipitated with alginate
The conclusion that polysaccharides, whether alginate or EPS, decrease the nucleation barrier for ferrihydrite formation is supported by a parallel set of experiments where ferrihydrite nanoparticles were coprecipitated with alginate (we did not attempt to coprecipitate hematite with alginate because alginate starts to degrade rapidly at water boiling temperature).When the interfacial free energy is low, we expect more nucleation sites, promoting the growth of smaller crystals than in a system with fewer nucleation events. TEM (Fig. 4) and PDF analysis (details in Section 9-ESI†) of our precipitates show that the alginate-coprecipitated ferrihydrite particles are slightly smaller and that there is a high coverage of ferrihydrite particles on the polymer (essentially 100% in Fig. 4b). Although smaller crystals can also be produced if the growth of the nuclei is inhibited by the polymer, the qualitative TEM results are consistent with the conclusion that the biopolymers decrease the interfacial free energy which is expected to enhance nucleation rates of the iron (oxyhydr)oxides relative to nucleation in a solution.
 | ||
| Fig. 4 TEM images of (a) pure ferrihydrite and (b) alginate–ferrihydrite. Average grain size in nm is given in the upper right corner for n = 22. Experiments done in duplicates. | ||
The interfacial water of alginate–iron oxy(hydr)oxide complexes could play a role in their nucleation
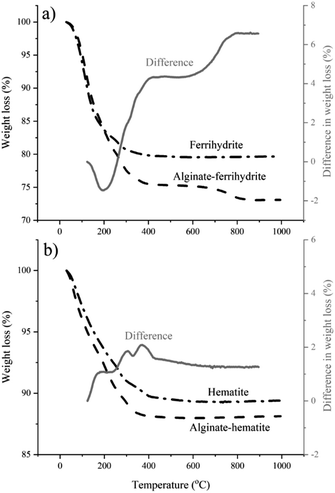
The DFS results reported here imply that the polymer–mineral interaction alone could exert control over iron (oxyhydr)oxide nucleation. However, TGA and cryoXPS show that the role of the interactions between the polymer and the surrounding aqueous medium cannot be ignored. TGA indicates a higher water content in alginate–ferrihydrite complexes compared to pure ferrihydrite (Fig. 5a) and suggests a distinct difference in thermochemical properties between the two systems. This is not the case for alginate–hematite complex that shows similar thermochemical behavior to pure hematite (Fig. 5b).These results were confirmed with cryoXPS measurements (more details in Section 10-ESI†). CryoXPS shows an increased interfacial water content of 3.7% in the alginate–ferrihydrite system compared to pure ferrihydrite (Table 3, Fig. S8†). In the alginate–hematite system, there is a decrease in the interfacial water content compared to pure hematite (Table 3, Fig. S9†). The reason for the decrease of the interfacial water content upon the complexation of hematite with alginate is unknown. This extra, more strongly bound water in the alginate–ferrihydrite interface region is expected to influence the interfacial energy and reaction rates and could explain increased ferrihydrite transformation rates in the central part of bacterial polysaccharide filaments.3
| O 1sb (atom %) | Interfacial H2O contentc (%) | ΔH2O content (%) | |||
|---|---|---|---|---|---|
| a V-vitrified sample, i.e., the spectrum from the sample analysed at cryogenic conditions, and RT-room temperature sample, i.e., the spectrum acquired from the sample analysed at ambient temperature. b High-resolution spectra of O 1s region of all samples can be found in the ESI. c Values are calculated by subtracting the oxygen content of the RT sample from the V sample. | |||||
| Ferrihydrite | MilliQ | Va | 90.1 | 8.4 | +3.7 |
| RTa | 81.7 | ||||
| 0.1% alginate | V | 68.6 | 12.1 | ||
| RT | 56.5 | ||||
| Hematite | MilliQ | V | 83.6 | 7.1 | −1.8 |
| RT | 76.5 | ||||
| 0.1% alginate | V | 70 | 5.3 | ||
| RT | 64.7 | ||||
Conclusion
We investigated biopolymer induced precipitation of iron (oxyhydr)oxides by measuring the interfacial free energy of the polymer–nuclei-solution system. We looked into the precipitation of ferryhidrite and hematite because they are common iron biominerals. As model bacterial biopolymers, we used alginate polysaccharide and extracellular polymeric substance extracted from the biofilm of Shewanella oneidensis. We used dynamic force spectroscopy to determine the equilibrium force and Gibbs free energy of binding between ferrihydrite and hematite substrates and biopolymers. Our rationale was that the stronger the energy of binding, the lower the barrier towards nucleation. We used the Gibbs free energy of binding to determine the interfacial free energy of the biopolymer–iron (oxyhydr)oxide-solution system (heterogeneous nucleation) and compared it to the interfacial free energy of iron (oxyhydr)oxide-solution system (homogeneous nucleation).The higher feq for ferrihydrite than hematite is likely caused by higher charge density at the surface. Microbial polymers can, through strong mineral binding (high feq), decrease the nucleation barriers for ferrihydrite and direct nucleation on the polymers. Our results for complex polymer systems parallel observations of the impact of organic molecules on carbonate mineral formation by marine organisms.33,34 In both systems, the influence of the charge state of the polymer and polymer–solvent–mineral interactions, reflected in the polymer–mineral γ, suggests that electrostatic interactions are important for binding and in determining interfacial energies and hence, for controlling nucleation. In addition to electrostatic interactions, the DFT simulations suggest that hydrogen bonding might be an additional source of biopolymer–iron oxide binding. Our results on thermal stability and interfacial water content of polymer–mineral complexes imply that the polymer–solvent interactions can also impact the mineral transformation kinetics from the initial, transient disordered phase the final, stable phase. Thus, our data show that a combination of polymer–mineral and polymer–solvent interactions control the dynamics of iron oxide mineralization from the first appearance to final form. Finally, our results highlight that microbial polymers can decrease the barriers for nucleation which is expected to lead to enhanced nucleation of iron (oxyhydr)oxides at low driving forces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We sincerely thank Dr Halei Zhai, Dr Jinhui Tao and Dr Christina Newcomb for helpful discussion on DFS, Kirstine Bach for generation of 3D figures and renderings, Dr Nico Bovet for useful comments on cryoXPS, Dr Glen Waychunas for providing the hematite sample and Dr Caroline Ajo-Franklin and Dr Kevin Rosso for encouragement and intellectual input. Funding for data collection and interpretation and for molecular simulations was provided by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences (OBES), Chemical Sciences, Geosciences and Biosciences Division through its Geosciences Program at Pacific Northwest National Laboratory (PNNL), which is operated by Battelle for the U.S. DOE under Contract DE-AC05-76RL01830. Analytical method development was supported by Sandia National Laboratories, a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. The research was performed using the Environmental and Molecular Sciences Laboratory, which is a DOE Office of Science Scientific User Facility (SUF) sponsored by the Office of Biological and Environmental Research operated by PNNL, under proposal 48274 and a U.S. DOE Office of Science Early Career Award (Project 60385). This research also used resources of U.S. DOE OBES SUFs, the Advanced Photon Source and the Molecular Foundry, which are operated for the DOE OBES by, respectively, Argonne National Laboratory under Contract No. DE-AC02-06CH11357 and LBNL under Contract No. DE-AC02-05CH11231. SJ, SD, KD and SLSS were supported by the running budget of the Materials Chemistry Research Section, University of Copenhagen.Notes and references
- K. O. Konhauser, FEMS Microbiol. Rev., 1997, 20, 315–326 CrossRef CAS.
- D. E. Canfield, Nature, 1998, 396, 450 CrossRef CAS.
- C. S. Chan, G. D. Stasio, S. A. Welch, M. Girasole, B. H. Frazer, M. V. Nesterova, S. Fakra and J. F. Banfield, Science, 2004, 303, 1656–1658 CrossRef CAS PubMed.
- J. Miot, K. Benzerara, G. Morin, A. Kappler, S. Bernard, M. Obst, C. Férard, F. Skouri-Panet, J.-M. Guigner, N. Posth, M. Galvez, G. E. Brown and F. Guyot, Geochim. Cosmochim. Acta, 2009, 73, 696–711 CrossRef CAS.
- C. S. Chan, S. C. Fakra, D. C. Edwards, D. Emerson and J. F. Banfield, Geochim. Cosmochim. Acta, 2009, 73, 3807–3818 CrossRef CAS.
- J. F. Banfield, S. A. Welch, H. Zhang, T. T. Ebert and R. L. Penn, Science, 2000, 289, 751–754 CrossRef CAS PubMed.
- S. Vollrath, T. Behrends and P. V. Cappellen, Geomicrobiol. J., 2012, 29, 550–560 CrossRef CAS.
- S. Vollrath, T. Behrends, C. B. Koch and P. V. Cappellen, Geochim. Cosmochim. Acta, 2013, 108, 107–124 CrossRef CAS.
- A. Zegeye, M. Etique, C. Carteret, C. Ruby, P. Schaaf and G. Francius, J. Phys. Chem. C, 2014, 118, 5978–5987 CrossRef CAS.
- C. B. Kennedy, S. D. Scott and F. G. Ferris, Chem. Geol., 2004, 212, 269–277 CrossRef CAS.
- C. Mikutta, R. Mikutta, S. Bonneville, F. Wagner, A. Voegelin, I. Christl and R. Kretzschmar, Geochim. Cosmochim. Acta, 2008, 72, 1111–1127 CrossRef CAS.
- C. W. Neil, J. R. Ray, B. Lee and Y.-S. Jun, Environ. Sci.: Nano, 2016, 3, 647–656 RSC.
- K. Eusterhues, A. Hädrich, J. Neidhardt, K. Küsel, T. F. Keller, K. D. Jandt and K. U. Totsche, Biogeosciences, 2014, 11, 4953–4966 CrossRef.
- R. E. Cooper, K. Eusterhues, C.-E. Wegner, K. U. Totsche and K. Küsel, Biogeosciences, 2017, 14, 5171–5188 CrossRef CAS.
- U. Schwertmann and R. M. Cornell, in The Iron Oxides, John Wiley & Sons, Ltd, 2004, pp. 1–7 Search PubMed.
- J. Scheck, B. Wu, M. Drechsler, R. Rosenberg, A. E. S. Van Driessche, T. M. Stawski and D. Gebauer, J. Phys. Chem. Lett., 2016, 7, 3123–3130 CrossRef CAS PubMed.
- K. M. Towe and H. A. Lowenstam, J. Ultra. Res., 1967, 17, 1–13 CrossRef CAS.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. D. Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS PubMed.
- J. Baumgartner, A. Dey, P. H. H. Bomans, C. Le Coadou, P. Fratzl, N. A. J. M. Sommerdijk and D. Faivre, Nat. Mater., 2013, 12, 310–314 CrossRef CAS PubMed.
- K. M. Ø. Jensen, H. L. Andersen, C. Tyrsted, E. D. Bøjesen, A.-C. Dippel, N. Lock, S. J. L. Billinge, B. B. Iversen and M. Christensen, ACS Nano, 2014, 8, 10704–10714 CrossRef CAS PubMed.
- A. Navrotsky, L. Mazeina and J. Majzlan, Science, 2008, 319, 1635–1638 CrossRef CAS PubMed.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2015, 158, 179–198 CrossRef CAS.
- U. Schwertmann and R. M. Cornell, in Iron Oxides in the Laboratory, John Wiley & Sons, Ltd, Weinheim, Federal Republic of Germany, 2nd edn, 2000, pp. 121–134 Search PubMed.
- G. Waychunas, T. Trainor, P. Eng, J. Catalano, G. Brown, J. Davis, J. Rogers and J. Bargar, Anal. Bioanal. Chem., 2006, 386, 2255 CrossRef CAS.
- T. Hiemstra and W. H. Van Riemsdijk, Geochim. Cosmochim. Acta, 2009, 73, 4423–4436 CrossRef CAS.
- C. M. Flynn, Chem. Rev., 1984, 84, 31–41 CrossRef CAS.
- M. Zhu, C. Frandsen, A. F. Wallace, B. Legg, S. Khalid, H. Zhang, S. Mørup, J. F. Banfield and G. A. Waychunas, Geochim. Cosmochim. Acta, 2016, 172, 247–264 CrossRef CAS.
- U. Schwertmann and E. Murad, Clays Clay Miner., 1983, 31, 277–284 CrossRef CAS.
- Y. Cudennec and A. Lecerf, J. Solid State Chem., 2006, 179, 716–722 CrossRef CAS.
- P. J. M. Smeets, K. R. Cho, R. G. E. Kempen, N. A. J. M. Sommerdijk and J. J. De Yoreo, Nat. Mater., 2015, 14, 394–399 CrossRef CAS PubMed.
- A. E. Nielsen, J. Cryst. Growth, 1984, 67, 289–310 CrossRef CAS.
- Q. Hu, M. H. Nielsen, C. L. Freeman, L. M. Hamm, J. Tao, J. R. I. Lee, T. Y. J. Han, U. Becker, J. H. Harding, P. M. Dove and J. J. D. Yoreo, Faraday Discuss., 2013, 159, 509–523 RSC.
- A. J. Giuffre, L. M. Hamm, N. Han, J. J. D. Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U.S.A., 2013, 110, 9261–9266 CrossRef CAS PubMed.
- L. M. Hamm, A. J. Giuffre, N. Han, J. Tao, D. Wang, J. J. D. Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 1304–1309 CrossRef CAS PubMed.
- J. J. D. Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef.
- K. K. Sand, R. W. Friddle and J. J. DeYoreo, Sci. Rep., 2017, 7, 8663 CrossRef CAS PubMed.
- J. Wingender, T. R. Neu and H.-C. Flemming, in Microbial Extracellular Polymeric Substances: Characterization, Structure and Function, ed. J. Wingender, T. R. Neu and H.-C. Flemming, Springer Berlin Heidelberg, Berlin, Heidelberg, 1999, pp. 1–19 Search PubMed.
- C. S. Hassler, V. Schoemann, C. M. Nichols, E. C. V. Butler and P. W. Boyd, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 1076 CrossRef CAS PubMed.
- C. S. Hassler, E. Alasonati, C. A. Mancuso Nichols and V. I. Slaveykova, Mar. Chem., 2011, 123, 88–98 CrossRef CAS.
- S. Jelavić, D. J. Tobler, T. Hassenkam, J. J. D. Yoreo, S. L. S. Stipp and K. K. Sand, Chem. Commun., 2017, 53, 12700–12703 RSC.
- Y.-S. Jun, B. Lee and G. A. Waychunas, Environ. Sci. Technol., 2010, 44, 8182–8189 CrossRef CAS PubMed.
- B. Cao, L. Shi, R. N. Brown, Y. Xiong, J. K. Fredrickson, M. F. Romine, M. J. Marshall, M. S. Lipton and H. Beyenal, Environ. Microbiol., 2011, 13, 1018–1031 CrossRef CAS PubMed.
- M. Sletmoen and B. T. Stokke, Biomacromolecules, 2004, 5, 1288–1295 CrossRef CAS PubMed.
- N. A. Burnham, X. Chen, C. S. Hodges, G. A. Matei, E. J. Thoreson, C. J. Roberts, M. C. Davies and S. J. B. Tendler, Nanotechnology, 2002, 14, 1–6 CrossRef.
- R. W. Friddle, A. Noy and J. J. D. Yoreo, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 13573–13578 CrossRef CAS PubMed.
- A. Noy and R. W. Friddle, Methods, 2013, 60, 142–150 CrossRef CAS PubMed.
- S. Manohar and A. Jagota, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021805 CrossRef PubMed.
- S. Manohar, A. R. Mantz, K. E. Bancroft, C.-Y. Hui, A. Jagota and D. V. Vezenov, Nano Lett., 2008, 8, 4365–4372 CrossRef CAS PubMed.
- M. A. K. Williams, A. Marshall, R. G. Haverkamp and K. I. Draget, Food Hydrocolloids, 2008, 22, 18–23 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- X. Huang, S. K. Ramadugu and S. E. Mason, J. Phys. Chem. C, 2016, 120, 4919–4930 CrossRef CAS.
- R. L. Blake, R. E. Hessevick, T. Zoltai and L. W. Finger, Am. Mineral., 1966, 51, 123–129 CAS.
- L. E. Barton, K. E. Grant, T. Kosel, A. N. Quicksall and P. A. Maurice, Environ. Sci. Technol., 2011, 45, 3231–3237 CrossRef CAS PubMed.
- A. P. Hammersley, S. O. Svensson and A. Thompson, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 346, 312–321 CrossRef CAS.
- P. J. Chupas, X. Qiu, J. C. Hanson, P. L. Lee, C. P. Grey and S. J. L. Billinge, J. Appl. Crystallogr., 2003, 36, 1342–1347 CrossRef CAS.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS.
- F. M. Michel, V. Barrón, J. Torrent, M. P. Morales, C. J. Serna, J.-F. Boily, Q. Liu, A. Ambrosini, A. C. Cismasu and G. E. Brown, Proc. Natl. Acad. Sci. U.S.A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, Science, 2007, 316, 1726–1729 CrossRef CAS PubMed.
- A. Shchukarev and S. Sjöberg, Surf. Sci., 2005, 584, 106–112 CrossRef CAS.
- A. Shchukarev, Adv. Colloid Interface Sci., 2006, 122, 149–157 CrossRef CAS PubMed.
- A. Shchukarev and M. Ramstedt, Surf. Interface Anal., 2017, 49, 349–356 CrossRef CAS.
- K. Shimizu, A. Shchukarev, P. A. Kozin and J.-F. Boily, Langmuir, 2013, 29, 2623–2630 CrossRef CAS PubMed.
- S. Jelavić, A. R. Nielsen, S. L. S. Stipp and N. Bovet, Langmuir, 2018, 34, 7011–7020 CrossRef PubMed.
- R. W. Friddle, P. Podsiadlo, A. B. Artyukhin and A. Noy, J. Phys. Chem. C, 2008, 112, 4986–4990 CrossRef CAS.
- O. Söhnel, J. Cryst. Growth, 1983, 63, 174–176 CrossRef.
- M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727–1730 CrossRef CAS PubMed.
- B. Cao, B. Ahmed, D. W. Kennedy, Z. Wang, L. Shi, M. J. Marshall, J. K. Fredrickson, N. G. Isern, P. D. Majors and H. Beyenal, Environ. Sci. Technol., 2011, 45, 5483–5490 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00138d |
| ‡ Current address: Geography & Earth Sciences, Aberystwyth University, UK. |
| § Current address: Section for GeoGenetics, Globe Institute, Faculty of Health and Medical Sciences, University of Copenhagen, Denmark. |
| ¶ Current address: Department of Geochemistry, Geological Survey of Denmark and Greenland (GEUS), Denmark. |
| || Current address: Department of Physics, Technical University of Denmark, Denmark. |
| This journal is © The Royal Society of Chemistry 2020 |