Refractive index of nanoconfined water reveals its anomalous physical properties
T. H. H.
Le
 *ab,
A.
Morita
*ab,
A.
Morita
 cd and
T.
Tanaka
cd and
T.
Tanaka
 bef
bef
aDepartment of Applied Chemistry, Graduate School of Engineering, The University of Tokyo, Bunkyo, Tokyo 113-8656, Japan
bInnovative Photon Manipulation Research Team, RIKEN Center for Advanced Photonics, Wako, Saitama 351-0198, Japan. E-mail: thu.le@riken.jp
cDepartment of Chemistry, Graduate School of Science, Tohoku University, Sendai, Miyagi 980-8578, Japan
dElements Strategy Initiative for Catalysts and Batteries (ESICB), Kyoto University, Nishikyo, Kyoto 615-8520, Japan
eMetamaterials Laboratory, RIKEN Cluster for Pioneering Research, Wako, Saitama 351-0198, Japan
fInstitute of Post-LED Photonics, Tokushima University, Minami-Jyosanjima, Tokushima 770-8560, Japan
First published on 27th April 2020
Abstract
Despite extensive studies on the distinctive properties of water confined in a nanospace, the underlying mechanism and significance of the lengthscale involved in the confinement effects are still subjects of controversy. The dielectric constant and the refractive index in particular are key parameters in modeling and understanding nanoconfined water, yet experimental evidence is lacking. We report the measurement of the refractive indices of water in 10–100 nm spaces by exploiting the confinement of water and localized surface plasmons in a physicochemically well-defined nanocavity. The results revealed significantly low values and the scaling behavior of the out-of-plane refractive index n⊥ of confined water. They are attributed to the polarization suppression at the interfaces and the long-range correlation in electronic polarization facilitated by the strengthened H-bonding network. Using the refractive index as a sensing probe, we also observed anomalous stability of water structures over a wide range of temperature. Our measurement results provide essential feedback information for benchmarking water models and molecular interactions under nanoconfinement. This study also opens up a new methodology of using plasmon resonance in characterizing nanoconfined molecules and chemical reactions, and thus gives us fundamental insight into confinement effects.
New conceptsTheoretical studies have predicted the suppression of the dielectric constant and refractive index of water confined in a nanospace, yet no clear experimental evidence has been reached due to the lack of characterization methods. We report the measurement of the refractive indices of water confined in 10–100 nm spaces by employing a sensing device that allows the confinement of water molecules and localized surface plasmons inside physicochemically well-defined nanocavities. Our device consists of a metal mirror and an array of periodic nanorods separated by a nanofluidic channel. It generates a quadrupole plasmon resonance that exhibits a uniform enhanced electric field oscillating in the out-of-plane direction. It thus allows us to selectively probe the out-of-plane refractive index n⊥ of water in the nanocavity with pronounced sensitivity. It is worth noting that this confinement characteristic cannot be obtained by using conventional dipole plasmons. Moreover, our device fabrication approach enables a facile and well-controlled method to functionalize the nanocavities to give the system of interest. This is essential to elucidate the confinement effects and ensure high reproducibility of measurements. These first experimental results of n⊥ give fundamental insight into the dielectric properties and behaviors of water under moderate confinement of a 10–100 nm lengthscale. |
Introduction
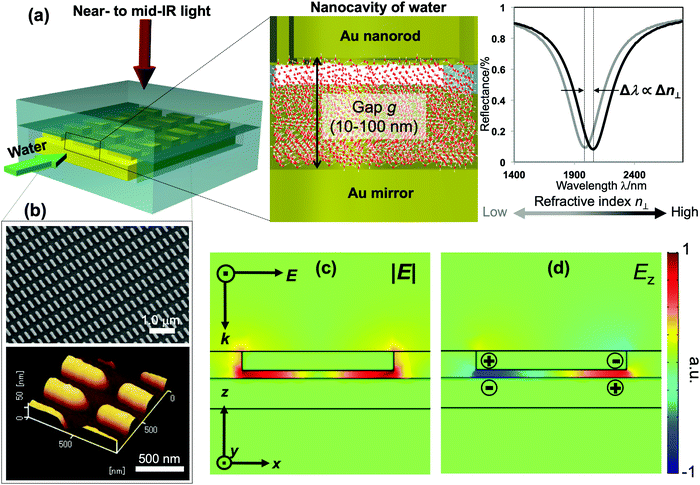
Distinctive properties and dynamics of nanoconfined water from those of bulk water have been intensively investigated in experimental and theoretical studies. Examples include the modification of the hydrogen-bonding (H-bonding) network,1–7 slow dynamics,8 peculiar phase transitions,9–11 high proton mobility,12–14etc. Although the term “nanoconfined water” usually refers to the extreme confinement in several-nanometer geometries of carbon nanotubes or graphene nanoslabs, recently similar effects have also been confirmed in weak and moderate confinement on the 10–100 nm scale. The latter one, in fact, currently attracts much attention for both fundamental interest and practical relevance, because liquids on this lengthscale can be controlled by nanofluidic operation, while, at the same time, remarkable confinement effects are present.6–8,11–15 The dielectric constant and particularly the refractive index (i.e., the dielectric constant at optical frequencies) are essential for modeling and elucidating the underlying mechanism and lengthscales involved in nanoconfinement effects. Theoretical studies predicted the decrease of molecular polarizability at interfacial water, which consequently lowers the dielectric constant and refractive index (RI) of water under extreme nanoconfinement,16–19 yet measurements are very challenging. Attempts to assess the RI of confined water by interferometry techniques have been made in several studies but no clear conclusion has been reached due the large uncertainty and errors in measurement.20–24Surface plasmon resonance (SPR) has been a major technique of choice for RI sensing. SPR sensors exploit the extreme susceptibility of the enhanced electromagnetic field generated on a propagating or localized surface plasmon polariton to detect a subtle change in the RI of the surrounding medium. However, SPR sensors so far have focused on engineering the enhancement factors to improve the sensitivity, rather than tailoring other features of the plasmon fields for functional detection. In this study, we demonstrate a nanofluidic device embedded with a unique plasmonic metamaterial structure that is purposely designed to exhibit an enhanced field localized in a nanocavity of water. This plasmon field is exploited to measure the RI of water confined within the cavity as the shifts of plasmon resonances. Our device comprises a gold (Au) mirror and an array of periodic Au nanorods separated by a nanofluidic channel of 10–100 nm in depth. Liquids are introduced into the nanochannel forming a nanocavity bounded by two Au interfaces, as described in Fig. 1(a). Under normal incidence, this structure generates a quadrupole mode, in which most of the plasmon energy is trapped inside the fluidic cavity and its enhanced electric field oscillates in the out-of-plane direction (i.e., the direction perpendicular to the confining walls). It thus allows us to probe the out-of-plane refractive index n⊥ of water in the cavity with ultrahigh sensitivity.
Results and discussion
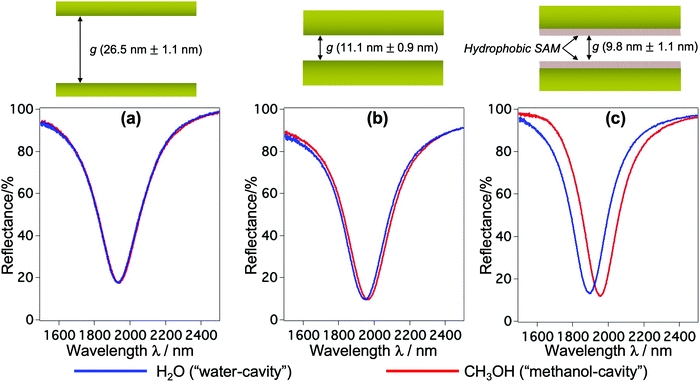
The fabrication follows a previously reported method.7,25 The gap g between the nanorods and Au mirror can be precisely fabricated at ∼nm accuracy, and its interfacial properties can be tuned from hydrophilicity to hydrophobicity by chemical modification. This top-down fabrication approach enables a facile and well-controlled method to functionalize the nanocavities to give the system of interest, and allows us to elucidate the nanoconfinement effect. Fig. 1(b) shows the SEM and AFM images of representative structures used in our devices. The numerical calculation of the corresponding system carried out by the finite-element-method (FEM) reveals that under linearly polarized radiation at normal incidence there is a strong resonant mode, in which an electric dipole is resonantly excited in the upper Au nanorod with dipole orientation along the incident electric field. This dipole plasmon mode induces an opposite dipole, which is its own mirror image, in the Au mirror. The interference of these two dipoles forms a quadrupole mode (i.e., magnetic dipole mode or metal–insulator–metal perfect absorber mode). This is a non-radiative mode that thus leads to a total anti-reflection.7,25 Since the structure does not transmit light, most of the light energy is absorbed and accumulated inside the nanogap as plasmon enhanced fields, as shown in the electric field |E| in Fig. 1(c). The formation of the quadrupole mode is clearly indicated in the out-of-plane electric field Ez profile (Fig. 1(d)). Notably, at resonance, Ez is the dominant component of E; even the background field is in parallel with the confining walls. It enables the selective probing of the out-of-plane refractive index n⊥, which is expected to be greatly affected by the geometrical restriction rather than the in-plane component n‖. The plasmon enhanced field performs as a sensing probe with sensitivity determined by its field intensity. It is worth noting that the quadrupole mode works as a parallel plate capacitor with a uniform field distribution in the z-direction. This property is eventually a key feature to characterize nanoconfinement effects using plasmons. Since confined water might exhibit heterogeneous layered structures whose properties vary with the layers in the confining direction, the measurement should give cumulative information on interfacial and inner molecules, effectively averaging their contributions over the confining gap. Therefore, the sensing probe should exhibit the same sensitivity in every layer to ensure that the measured value represents the average value of the overall cavity. This kind of field distribution cannot be obtained in conventional dipole plasmon modes in nanoantenna or surface plasmon polariton systems, in which the enhanced fields attenuate rapidly away from the surfaces.We fabricated several devices of different nanogaps g from 10 nm to 80 nm with tailored interfacial properties, and investigated their optical responses. The nanorod structures were purposely designed so that when water is used to fill the devices all devices exhibit the above-mentioned quadrupole resonance at the same frequency of ∼5100 cm−1. At this near-infrared (NIR) wavelength, the absorption (i.e., the imaginary part of the dielectric permittivity) of water is negligibly small, and the shifts of resonant wavelengths purely reflect the property of the RI (i.e., the real part of the dielectric permittivity). At the same time, compared to visible or shorter NIR ones, the interband absorption of the metal (Au) is suppressed, resulting in the improvement of the Q-factors. Devices filled with water (i.e., “water-cavity”), methanol (i.e., “methanol-cavity”) and other organic solvents were measured using an FT-IR spectrometer under linear polarization along the long axis of the nanorods. Strong reflectance dips, which are attributed to the quadrupole modes, are confirmed in the reflectance spectra in Fig. 2. Surprisingly, the relative positions of plasmon resonances in the water-cavities and methanol-cavities vary in devices of different configurations. For hydrophilic cavities of a small gap, the plasmon resonance in the water-cavity exhibits a blue-shift with respect to that of the methanol-cavity, while those blue-shifts are alleviated in larger gaps (Fig. 2(a) and (b)). Since the blue-shift implies a relatively low RI, the results evidence a decrease in n⊥ of water confined in small nanogaps. Whereas even in the same confining size (∼10 nm), the water-cavity with hydrophobic interfaces shows a pronounced blue-shift compared to that of the hydrophilic ones (Fig. 2(b) and (c)). It can be concluded from this result that both the confining sizes and interfacial properties have notable effects on lowering the RI of water.
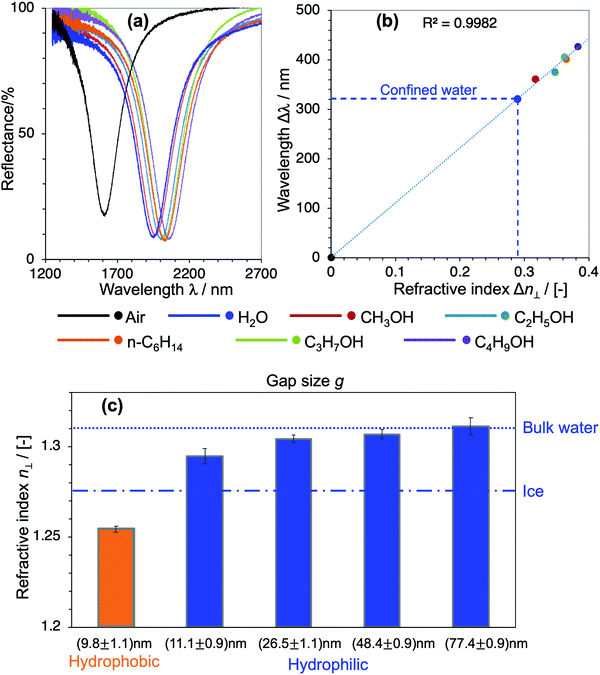
To quantitatively determine the value of the RI in SPR, generally, liquids with known RI are used as references for calibrating the sensitivity of the sensor. In our devices, however, choosing appropriate reference liquids is a big concern because confinement might have an influence on all liquids. It is common sense that water owes its characteristic dielectric properties to the polarity of its molecules, and the continuous three-dimensional (3D) network of H-bonds. This nature and the strength of the H-bonds are very unique to water, and they are even essentially different to those in polar solvents with H-bonds such as alcohols. Upon confinement, the H-bonding network in water is further strengthened to form a highly-ordered water structure, which is generally addressed as the physical origin of the distinctive properties of nanoconfined water.1–7,16,19 Indeed, compared to a large number of nanoconfinement effects found in water, there is no obvious evidence of such effects on alcohols nor other kinds of organic solvents. Based on this fact, here we used alcohols and n-hexane as reference liquids with their RI values in the literature to calibrate the sensitivity of the corresponding devices and evaluate n⊥ of the nanoconfined water. Fig. 3(a) shows the optical responses of the devices when they are filled with air, water and organic solvents, respectively. Their shifts of resonant wavelengths (with respect to the value in devices filled with air) were extracted as Δλ, while the RI differences of the corresponding filling liquids and air Δn were calculated from their bulk values in the literature, respectively.26–30 Δλ was then plotted against Δn and a prominent linear relationship was achieved. The unknow n⊥ value of confined water was obtained by projecting its Δλ to the calibration line, as described in Fig. 3(b). We repeated such experiments and the same analysis method for all devices of nanogap g ranging from 10 nm to 80 nm. The definite n⊥ values of water confined in the corresponding devices are summarized in Fig. 3(c). The result obviously shows a statistically significant difference of n⊥ values in devices of different confining sizes and interfacial properties. In hydrophilic cavities, n⊥ gradually decreases with decreasing gap g, and it approaches an intermediate value between bulk water and hexagonal ice at a ∼10 nm gap, while it recovers to the bulk value at a gap of 80 nm. On the other hand, in a ∼10 nm cavity of a hydrophobic interface, the RI exhibits an anomalously low value. Not only is it much smaller than in comparison with hydrophilic interfaces of the same gap, but the value is even smaller than that of hexagonal ice. Although the suppression of the out-of-plane dielectric constant ε⊥ of water under confinement has been reported in previous atomistic simulations and experimental studies,16–19 to the best of our knowledge this is the first experimental proof of reduction of n⊥ and its scaling behavior in moderate confinement of 10–100 nm lengthscale.
The RI is conventionally represented in terms of the density and molecular polarizability by the famous Lorentz–Lorenz equation.31 Previous studies agreed that extreme confinement of a monolayer or bilayer of water can induce a change in the electronic band structure of water that results in a decrease of the water density, but the overall water density becomes equal to the bulk values when pores have a diameter of 10 nm or larger.32,33 Accordingly, the reduced RI is hardly explained by the perturbation of the density under moderate confinement in our case. On the other hand, it has been generally accepted that water at a liquid–solid interface exhibits a suppressed dielectric constant.34,35 For example, there is a high density of water with planar H-bonds coupled with the hydrophobic interface (i.e., dangling water), and these planar H-bonds restrict water from reorienting along the direction perpendicular to the confining walls. It consequently results in a large suppression of the out-of-plane dielectric constant.33–35 A similar effect appears in water on hydrophilic interfaces due to the strong interactions of water with hydrophilic molecules, which leads to the reduced affinity of interfacial water molecules to align perpendicular to the surfaces.36 This means that, even though the degree of reduction is different, in both cases aligning the water molecules close to the surface under an electric field applied in the out-of-plane direction becomes energetically demanding. Therefore, the decrease of n⊥ of confined water can be partially attributed to the interfacial water. This interpretation is consistent with the scaling behavior of n⊥ observed in Fig. 3(c), in which the contribution of interfacial water decreases with an increasing gap. It also agrees well with the significant reduction of n⊥ found in cavities of hydrophobic interfaces. However, it cannot fully explain the effect of confinement on the RI, since such interfacial water is reported to be extending to several water layers away from the surface (less than 1 nm).34–36 In contrast, our result unveils the effect presented up to a mesoscale dimension corresponding to more than 30 layers of water. Our findings thus have a great impact on elucidating the underlying physical origin of the nanoconfinement.
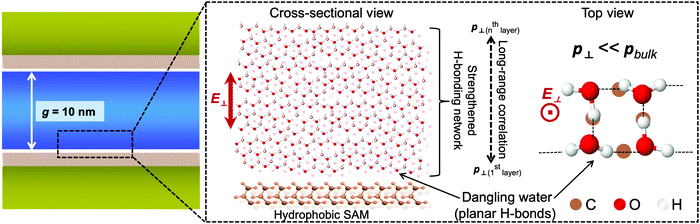
Here the network structure of H-bonds in water was taken into consideration. The 3D H-bonding network accounts for the strong correlation of orientation in water, and the extent of intermolecular correlation, often denoted with the Kirkwood g factor, is known to be sensitive to the boundary condition of dielectrics. For example, MD simulations reported a dramatic reduction in the dielectric constant of water clusters.37 This effect might affect the dielectric properties of water, including the RI, in a range longer than predicted. We use the schematic water model represented in Fig. 4 to summarize and elucidate remarkable findings from our results. Interfacial water exhibits specific molecular structures that hinder the electronic polarization of water in the out-of-plane direction. This generates a reduction of n⊥ of water at interfaces, even though the degree of reduction is much more pronounced in cases of hydrophobic interfaces. The confinement affects the RI by facilitating the effects of interfacial water in a much longer range via the correlation in electronic polarization. This correlation is mediated by the strengthening of the H-bonding network under geometrical restriction. Our results also suggest that the confinement might have some certain effects on the electronic and vibrational band structures of water. It is thus of significance for benchmarking water models, and in calculations of the absorption spectrum of confined water.
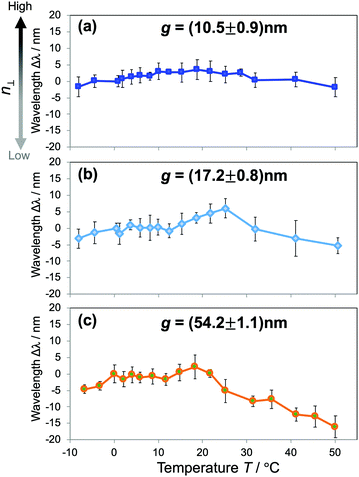
To get further insight into the water structures in confined spaces, we employed the RI as a sensing probe to examine the thermodynamic behavior of water. In bulk water, the RI reaches a maximum value at just below 0 °C and decreases with increasing temperature, or liquid water in the bulk exhibits a negative thermo-optic coefficient dn/dT. It is primarily attributed to the change of water structures as the temperature increases. The increase of temperature usually induces a progressive destruction of H-bonds that leads to the reduction of the density. Here we investigated the dependence of n⊥ on temperature. The temperature T of the overall device was controlled at an accuracy of 0.1 °C by a Peltier-type thermoelectric control system within the temperature range of −10 °C to 50 °C. The shifts of resonant wavelengths Δλ at the corresponding temperatures were measured and plotted against T. The results of hydrophilic devices of gaps g ranging from 10 to 50 nm in Fig. 5 reveal a distinctive dn/dT behavior of confined water that is much deviated from that of the bulk. For water confined in 10–20 nm gaps (Fig. 5(a and b)), it is obvious from the graphs that the resonant wavelengths stay unchanged with the temperature increase, indicating a constant n⊥ over a wide range of T. Whereas, water confined in larger gaps (Fig. 5(c)) experiences a dispersion curve of n⊥ with T comparable to that of bulk water, shown in the clear decrease of Δλ with increasing T, especially in the high temperature regime. The results indicate the anomalous stability of water structures as confined in small gaps, and they can also be attributed to the modification of the H-bonding network of water under confinement. The strong confinement does not only facilitate highly ordered water structures at room temperature (i.e., ice-like structures), but also keeps water molecules associated when the temperature increases, resulting in a net decrease of the enthalpy of nanoconfined water. It maintains the density, the molecular polarization, and consequently the n⊥ of confined water. Those effects appear more pronounced in small gaps, and gradually lessened in larger ones. It should be noted that this result is in good agreement with the reduction and the scaling behavior of the RI in Fig. 3(c). The probing of the RI allows us to assess and unveil an intriguing thermodynamic behavior of nanoconfined water. Similar phenomena such as peculiar phase transitions, the increase of the boiling temperature and the decrease of the melting temperature were reported for water under extreme confinement;9,11,21 however, this is the first observation of this kind of effect in moderate confinement of ∼10 nm.
Conclusion
We demonstrated a plasmonics–nanofluidics hybrid device to detect the RI of liquids in a nanocavity with exceptionally high sensitivity, and succeeded in characterizing the out-of-plane RI of water under moderate confinement of 10–100 nm lengthscale. We observed significantly low values of n⊥, along with their dependence on the interfacial properties and confining sizes. The hindering of molecular polarization at interfacial water and the long-range correlation in the electronic polarizability mediated by the strengthening of the H-bonding network in nanoconfined water are attributed to be the physical origin of the reduced n⊥. Employing the RI as a sensing probe, we also confirmed anomalous stability of water structures over a wide range of temperature, which is also explained by the strengthened H-bonds. This study has offered a new perspective in understanding long-range water-mediated interactions, which is crucial in biological systems such as the hydration or stabilization of DNA and proteins, ion solvation, molecular transport, and chemical reactions in confined geometries. The measured n⊥ values provide essential feedback information for a more accurate parametrization of water models, and intermolecular interactions under nanoconfinement.Methods
Device fabrication
The fabrication of the measurement device was described in our previous report.7,25ϕ 50.0 mm SiO2 substrates (Sigma Koki-BK7), which were custom-polished up to optical grade, were used. SiO2 substrates were cleaned in piranha solution (H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2 = 3
H2O2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) before fabrication. On one SiO2 substrate, ϕ 0.7 mm through-holes serving as inlets and outlets for introducing fluidics were drilled at specific positions in advance. Those holes were also used as markers for position alignment. The substrate was then coated with 300 nm-thick ZEP-520A resist (Zeon) and a thin layer of conducting polymer Espacer 300Z (Showa Denko). Nanorod patterns were written by electron beam lithography (Elionix ELS-7700). After developing in methyl butyl ketone, the substrate was coated with a 3 nm Cr (adhesion layer)/50 nm Au film by thermal evaporation. It was then lifted-off in tetrahydrofuran with the assistance of sonication. The achieved Au nanorod arrays were observed and analyzed by scanning electron microscopy (Hitachi SU8010) under a 5.0 kV acceleration voltage. The dimensional parameters of the nanorod array were finely tuned so that all devices exhibit the above-mentioned quadrupole resonance at the same frequency of ∼5100 cm−1 when they are filled with water. For example, the length and width of the nanorod structure used in the device appearing in Fig. 3(a) are 360 nm and 96 nm, and the corresponding pitches are 550 nm and 300 nm, respectively.
1) before fabrication. On one SiO2 substrate, ϕ 0.7 mm through-holes serving as inlets and outlets for introducing fluidics were drilled at specific positions in advance. Those holes were also used as markers for position alignment. The substrate was then coated with 300 nm-thick ZEP-520A resist (Zeon) and a thin layer of conducting polymer Espacer 300Z (Showa Denko). Nanorod patterns were written by electron beam lithography (Elionix ELS-7700). After developing in methyl butyl ketone, the substrate was coated with a 3 nm Cr (adhesion layer)/50 nm Au film by thermal evaporation. It was then lifted-off in tetrahydrofuran with the assistance of sonication. The achieved Au nanorod arrays were observed and analyzed by scanning electron microscopy (Hitachi SU8010) under a 5.0 kV acceleration voltage. The dimensional parameters of the nanorod array were finely tuned so that all devices exhibit the above-mentioned quadrupole resonance at the same frequency of ∼5100 cm−1 when they are filled with water. For example, the length and width of the nanorod structure used in the device appearing in Fig. 3(a) are 360 nm and 96 nm, and the corresponding pitches are 550 nm and 300 nm, respectively.
On another SiO2 substrate, large microchannels (design width: 400 μm; depth: 5 μm) were fabricated for guiding fluidics into the nanochannels, by employing UV photolithography and reactive ion etching using CF4/O2 gas. It corresponds to the bottom substrate in Fig. 1(a). After that, nanochannel patterns (design width: 200 μm; length: 400 μm) were written onto the same substrate by UV photolithography. Careful position alignment was necessary to ensure that the nanochannels bridged the inlet and outlet microchannels. After developing, the substrate was immersed into buffered hydrofluoric acid solution (BHF 1.25%) for wet etching of nanochannels. The depth of the nanochannels was finely controlled by the immersion time, with an approximate etching rate of 0.7 nm s−1. The etched substrate was cleaned again in piranha solution to remove all the contamination. Finally, mirror patterns were written inside the nanochannels by UV photolithography, following by the deposition of 3 nm Cr and a thick Au film. After lift-off, this generated an Au mirror film inside the nanochannel. The thickness of the Au mirror was finely controlled to tune the final nanogap g to the desired value. It was verified that the nanogap g could be controlled to several nanometers (experiment-to-experiment accuracy).
Chemical modification of Au surfaces
In the chemical modification of Au surfaces by a superhydrophobic self-assembled monolayer (SAM), the two post-fabrication substrates were immersed in a solution of 1.0 mM 1-octadecanethiol (Wako Chemicals) in dehydrated ethanol (Wako Chemicals). After 48 hours, the substrates were rinsed in dehydrated ethanol several times before drying under a nitrogen gas flow. A 21.5 Å thick SAM with a thiol head-group was chemisorbed on the Au surface.Characterization of nanogaps g
The depth of the nanochannel d at the mirror layer was measured by employing a surface profiler (KLA Tencor, P-16). The height h of the fabricated nanorod array was evaluated using an atomic force microscope (AFM) (SII, Nano Navi IIs Nanocute). Both measurements present sub-nanometer accuracy, and the profiling data indicate that both the Au mirror and Au nanorod exhibit a surface roughness (Rms) of less than 1.0 nm. Finally, the nanogap g was calculated by subtracting the channel depth d at the mirror part from the height h of the Au nanorods. After evaluating the nanogap g, the two substrates were bonded together to form a sealed fluidic device.Bonding of the device
The two substrates underwent surface activation by UV/O3 treatment in 30 min. Right after the treatment, the substrates were cleaned in ultra-pure water to fully activate the –OH groups on the SiO2 surfaces. The alignment of the top nanorod array and the bottom mirror was carried out under a 4× microscope. It was verified that the fabricated device could tolerate applied pressure up to 360 kPa, which corresponded to a flow velocity of 26 μm s−1.IR reflectance measurement
The reflectance property of the fabricated device was characterized by using a Fourier-transform infrared spectrometer (FT-IR) equipped with a microscope (JASCO, FT/IR-6300FV + VIRT-3000) with a frequency resolution of 1 cm−1. All spectra were measured at normal incident angle through an objective lens with an NA of 0.57, which corresponds to a maximum collective angle of 34.8°. All the experiments here employed the first mode (e.g., quadrupole mode), in which the incident angle dependencies on the coupling coefficients and resonant wavelength are negligibly small. Therefore, we conclude that the effect of the oblique incidence in our measurement can be ignored. To improve the signal-to-noise ratio of the IR signal, the sample chamber was purged with dry nitrogen gas, and a liquid nitrogen-cooled highly-sensitive MCT (HgCdTe) detector was used. The size of each fabricated nanorod array was 80 × 80 μm2, while the measurement area was 50 × 50 μm2. For the experiments in Fig. 2 and 3, the temperature T of the devices was stabilized at 20 °C by a Peltier-type thermoelectric control system throughout the FT-IR measurements. Since the structures act as an absorber, a subtle local temperature increase might occur. To ensure a fair comparison of the measured RI, we controlled the absorbance of all structures at the same level, and assume that all devices are measured at the same temperature.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by MEXT Grants-in-Aid for Scientific Research 15H06856, 19K15454 and Research Foundation for Opto-Science and Technology. We would like to thank RIKEN Emergent Matter Science Research Laboratory for the usage of nanofabrication facilities.References
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Formation of Ordered Ice Nanotubes Inside Carbon Nanotubes, Nature, 2001, 412, 802–805 CrossRef CAS PubMed.
- G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Square Ice in Graphene Nanocapillaries, Nature, 2015, 519, 443–445 CrossRef CAS PubMed.
- S. D. Bernardina, E. Paineau, J.-B. Brubach, P. Judeinstein, S. Rouzière, P. Launois and P. Roy, Water in Carbon Nanotubes: the Peculiar Hydrogen Bond Network Revealed by Infrared Spectroscopy, J. Am. Chem. Soc., 2016, 138, 10437–10443 CrossRef PubMed.
- P. Rotureau, J. P. Renault, B. Lebeau, J. Patarin and J. C. Mialocq, Radiolysis of Confined Water: Molecular Hydrogen Formation, Chem. Phys. Chem., 2005, 6, 1316–1323 CrossRef CAS PubMed.
- G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, Water Confined in Nanotubes and Between Graphene Sheets: a First Principle Study, J. Am. Chem. Soc., 2008, 130, 1871–1878 CrossRef CAS PubMed.
- S. Le Caër, S. Pin, S. Esnouf, Q. Raffy, J. Ph. Renault, J.-B. Brubach, G. Creff and P. Roy, A Trapped Water Network in Nanoporous Material: the Role of Interfaces, Phys. Chem. Chem. Phys., 2011, 13, 17658–17666 RSC.
- T. H. H. Le, A. Morita, K. Mawatari, T. Kitamori and T. Tanaka, Metamaterials-Enhanced Infrared Spectroscopic Study of Nanoconfined Molecules by Plasmonics–Nanofluidics Hydrid Device, ACS Photonics, 2018, 8, 3179–3188 CrossRef.
- K. Bhattacharyya and B. Bagchi, Slow Dynamics of Constrained Water in Complex Geometries, J. Phys. Chem. A, 2000, 104, 10603–10613 CrossRef CAS.
- V. V. Chaban, V. V. Prezhdo and O. V. Prezhdo, Confinement by Carbon Nanotubes Drastically Alters the Boiling and Critical Behavior of Water Droplets, ACS Nano, 2012, 6, 2766–2773 CrossRef CAS PubMed.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Nanoscale Hydrodynamics: Enhanced Flow in Carbon Nanotubes, Nature, 2005, 438, 44 CrossRef CAS PubMed.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phase Transitions Induced by Nanoconfinement in Liquid Water, Phys. Rev. Lett., 2009, 102, 050603 CrossRef PubMed.
- T. Tsukahara, A. Hibara, Y. Ikeda and T. Kitamori, NMR Study of Water Molecules Confined in Extended Nanospaces, Angew. Chem., Int. Ed., 2007, 46, 1180–1183 CrossRef CAS PubMed.
- D. B. Spry, A. Goun, K. Glusac, D. E. Moilanen and M. D. Fayer, Proton Transport and the Water Environment in Nafion Fuel Cell Membranes and AOT Reverse Micelles, J. Am. Chem. Soc., 2007, 129, 8122–8130 CrossRef CAS PubMed.
- T. Tsukahara, K. Mawatari and T. Kitamori, Integrated Extended-nano Chemical Systems on a Chip, Chem. Soc. Rev., 2010, 39, 1000–1013 RSC.
- T. H. H. Le, K. Mawatari, H. Shimizu and T. Kitamori, Detection of Zeptomole Quantities of Nonfluorescent Molecules in a 101 nm Nanochannel by Thermal Lens Microscopy, Analyst, 2014, 139, 2721–2725 RSC.
- A. Schlaich, E. W. Knapp and R. R. Netz, Water Dielectric Effects in Planar Confinement, Phys. Rev. Lett., 2016, 117, 048001 CrossRef PubMed.
- H.-B. Cui, K. Takahashi, Y. Okano, H. Kobayashi, Z. Wang and A. Kobayashi, Dielectric Properties of Porous Molecular Crystals that Contain Polar Molecules, Angew. Chem., Int. Ed., 2005, 44, 6508–6512 CrossRef CAS PubMed.
- H. Itoh and H. Sakuma, Dielectric Constant of Water as a Function of Separation in a Slab Geometry: A Molecular Dynamics Study, J. Chem. Phys., 2015, 142, 184703 CrossRef PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Anomalously Low Dielectric Constant of Confined Water, Science, 2007, 360, 1339–1342 CrossRef PubMed.
- P. Kekicheff and O. Spalla, Refractive Index of Thin Aqueous Films Confined Between Two Hydrophobic Surfaces, Langmuir, 1994, 10, 1584–1591 CrossRef CAS.
- M. M. Kohonen and H. K. Christenson, Capillary Condensation of Water Between Rinsed Mica Surfaces, Langmuir, 2000, 16, 7285–7288 CrossRef CAS.
- D. F. Kienle and T. L. Kuhl, Analyzing Refractive Index Profiles of Confined Fluids by Interferometry, Anal. Chem., 2014, 86, 11860–11867 CrossRef CAS PubMed.
- D. F. Kienle and T. L. Kuhl, Analyzing Refractive Index Profiles of Confined Fluids by Interferometry Part II: Multilayer and Asymmetric Systems, Anal. Chim. Acta, 2016, 936, 236–244 CrossRef CAS PubMed.
- D. F. Kienle and T. L. Kuhl, Density and Phase State of a Confined Nonpolar Fluid, Phys. Rev. Lett., 2016, 117, 036101 CrossRef PubMed.
- T. H. H. Le and T. Tanaka, Plasmonics–Nanofluidics Hydrid Metamaterial: an Ultrasensitive Platform for Infrared Absorption Spectroscopy and Quantitative Measurement of Molecules, ACS Nano, 2017, 11, 9780–9788 CrossRef CAS PubMed.
- E. Sani and A. Dell'Oro, Spectral Optical Constants of Ethanol and Isopropanol from Ultraviolet to Far Infrared, Opt. Mater., 2016, 60, 137–141 CrossRef CAS.
- A. Tuntomo, C. Tien and S. Park, Optical Constants of Liquid Hydrocarbonfuels, Combust. Sci. Technol., 1992, 84, 133–140 CrossRef CAS.
- L. H. Liu and C. Wang, Temperature-Dependent Optical Constants of Liquid Isopropanol, n-Butanol, and n-Decane, Appl. Opt., 2018, 57, 3003–3011 CrossRef PubMed.
- J. E. Bertie, S. L. Zhang, H. H. Eysel, S. Baluja and M. K. Ahmed, Infrared Intensities of Liquids XI: Infrared Refractive Indices from 8000 to 2 cm−1, Absolute Integrated Intensities, and Dipole Moment Derivatives of Methanol at 25 °C, Appl. Spectrosc., 1993, 47, 1100–1114 CrossRef CAS.
- K. F. Palmer and D. Williams, Optical Properties of Water in the Near Infrared, J. Opt. Soc. Am., 1974, 64, 1107–1110 CrossRef CAS.
- H. Frohlich, Theory of Dielectrics, Clarendon Press, Oxford, 2nd edn, 1958 Search PubMed.
- F. M. Etzler and D. M. Fagundus, The Extent of Vicinal Water - Implications from the Density of Water in Silica Pores, J. Colloid Interface Sci., 1987, 115, 513–519 CrossRef CAS.
- A. W. Knight, N. G. Kalugin, E. Coker and A. G. Ilgen, Water Properties Under Nano-scale Confinement, Sci. Rep., 2019, 9, 8246 CrossRef PubMed.
- M. D. Boamah, P. E. Ohno, F. M. Geiger and K. B. Eisenthal, Relative Permittivity in the Electrical Double Layer from Nonlinear Optics, J. Chem. Phys., 2018, 148, 222808 CrossRef PubMed.
- M. C. F. Wander and A. E. Clark, Structural and Dielectric Properties of Quartz–Water Interfaces, J. Phys. Chem. C, 2008, 112, 19986–19994 CrossRef CAS.
- S. Varghese, S. K. Kannam, J. S. Hansen and S. P. Sathian, Effect of Hydrogen Bonds on the Dielectric Properties of Interfacial Water, Langmuir, 2019, 35, 8159–8166 CrossRef CAS PubMed.
- S. Saito and I. Ohmine, Translational and Orientational Dynamics of a Water Cluster (H2O)108 and Liquid water: Analysis of Neutron Scattering and Depolarized Light Scattering, J. Chem. Phys., 1995, 102, 3566–3579 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |